Modulation Format Identification and OSNR Monitoring Based on Multi-Feature Fusion Network
Abstract
1. Introduction
2. Proposed Scheme
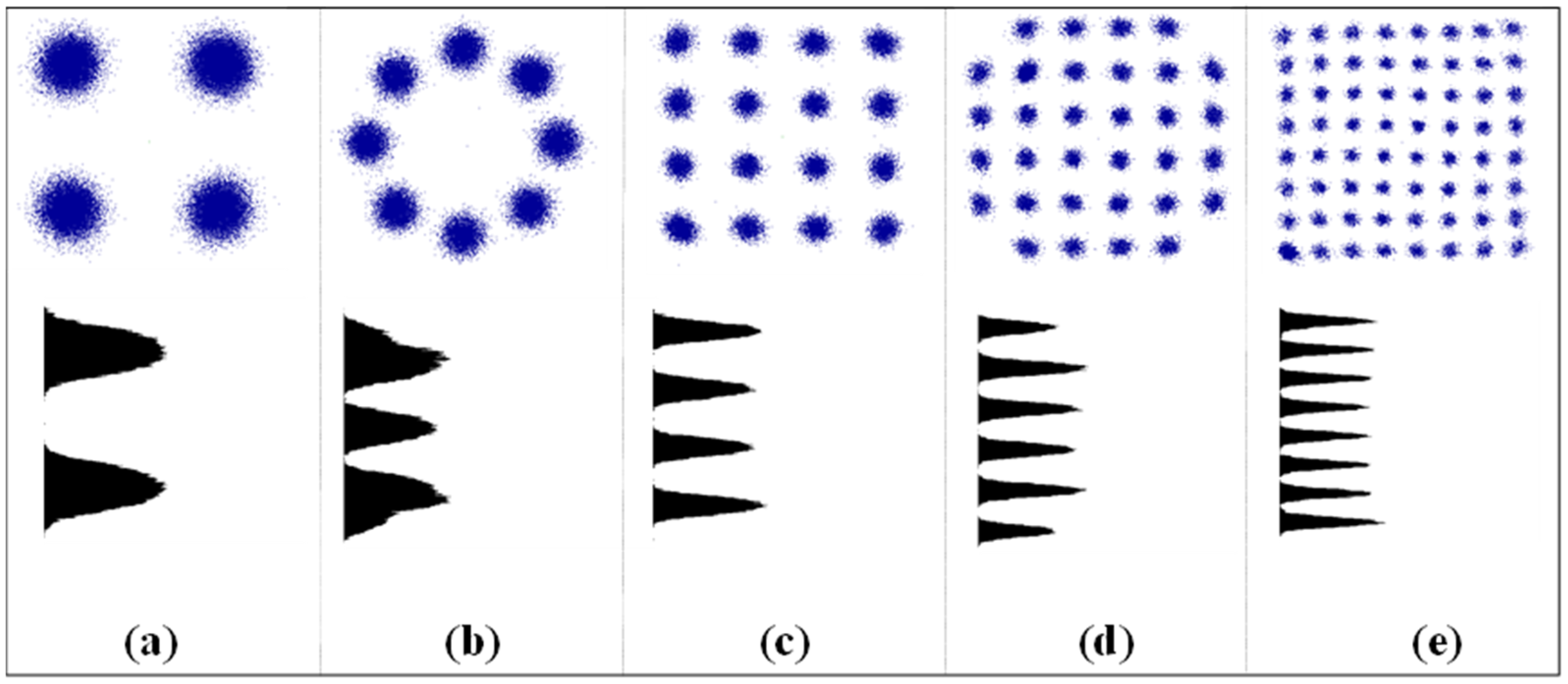
2.1. Data Pre-Processing
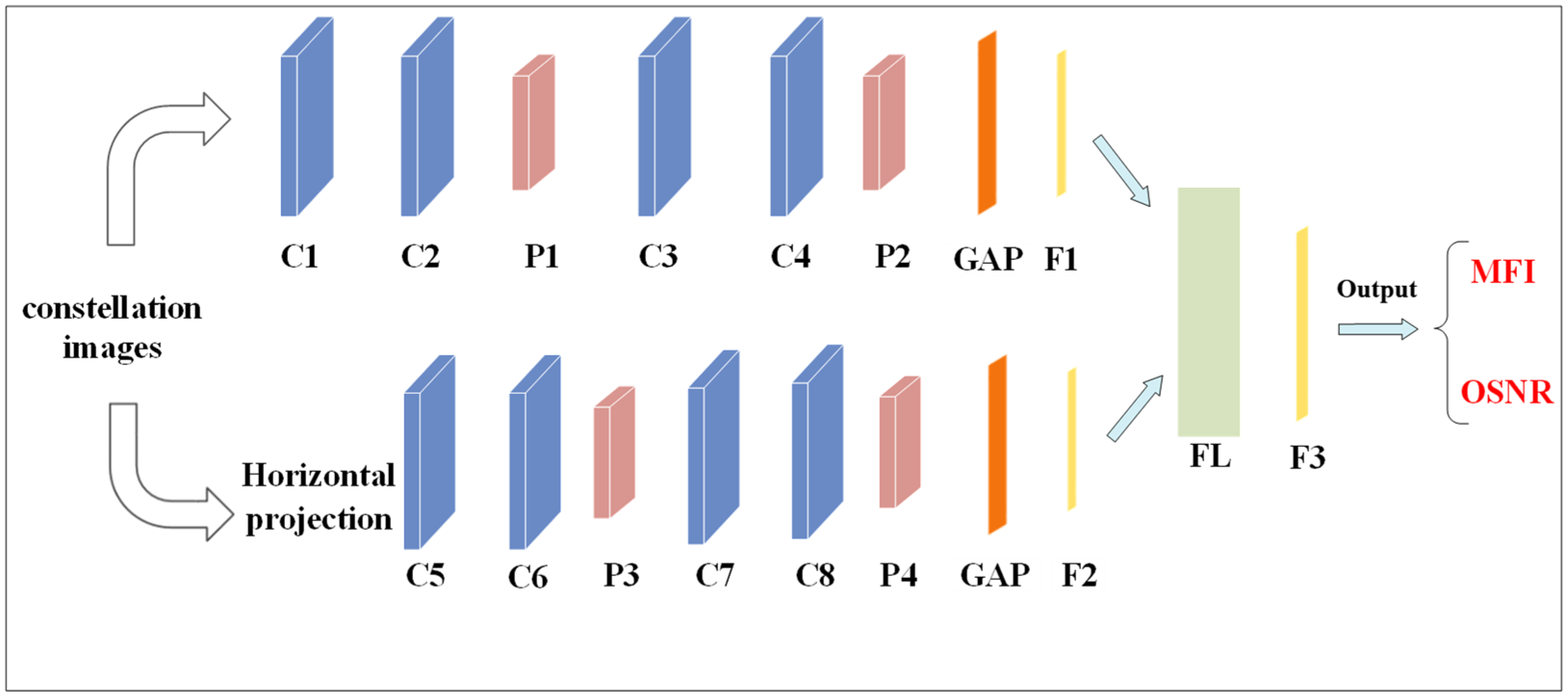
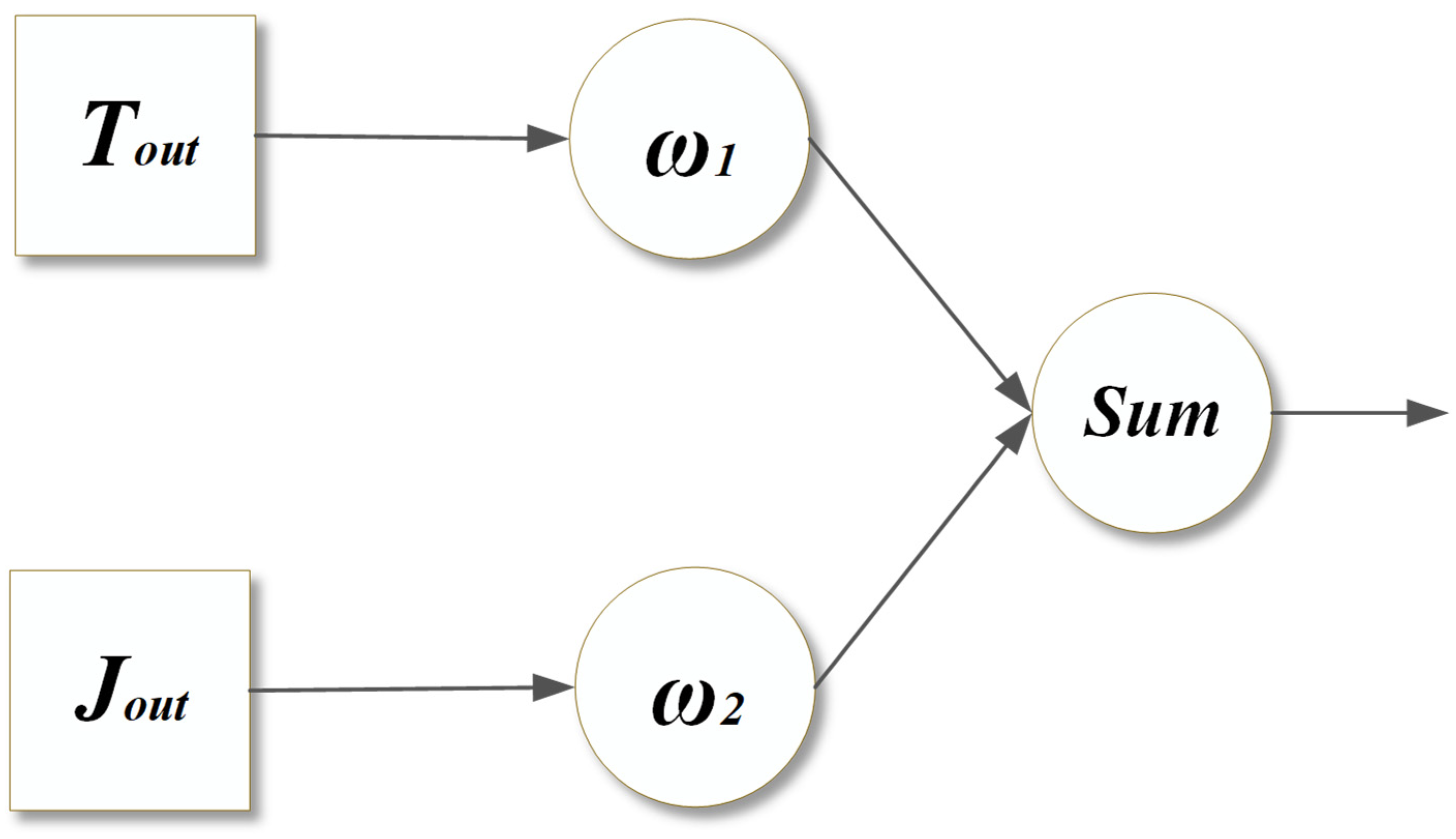
2.2. System Structure
3. Simulation Setup
4. Results and Discussion
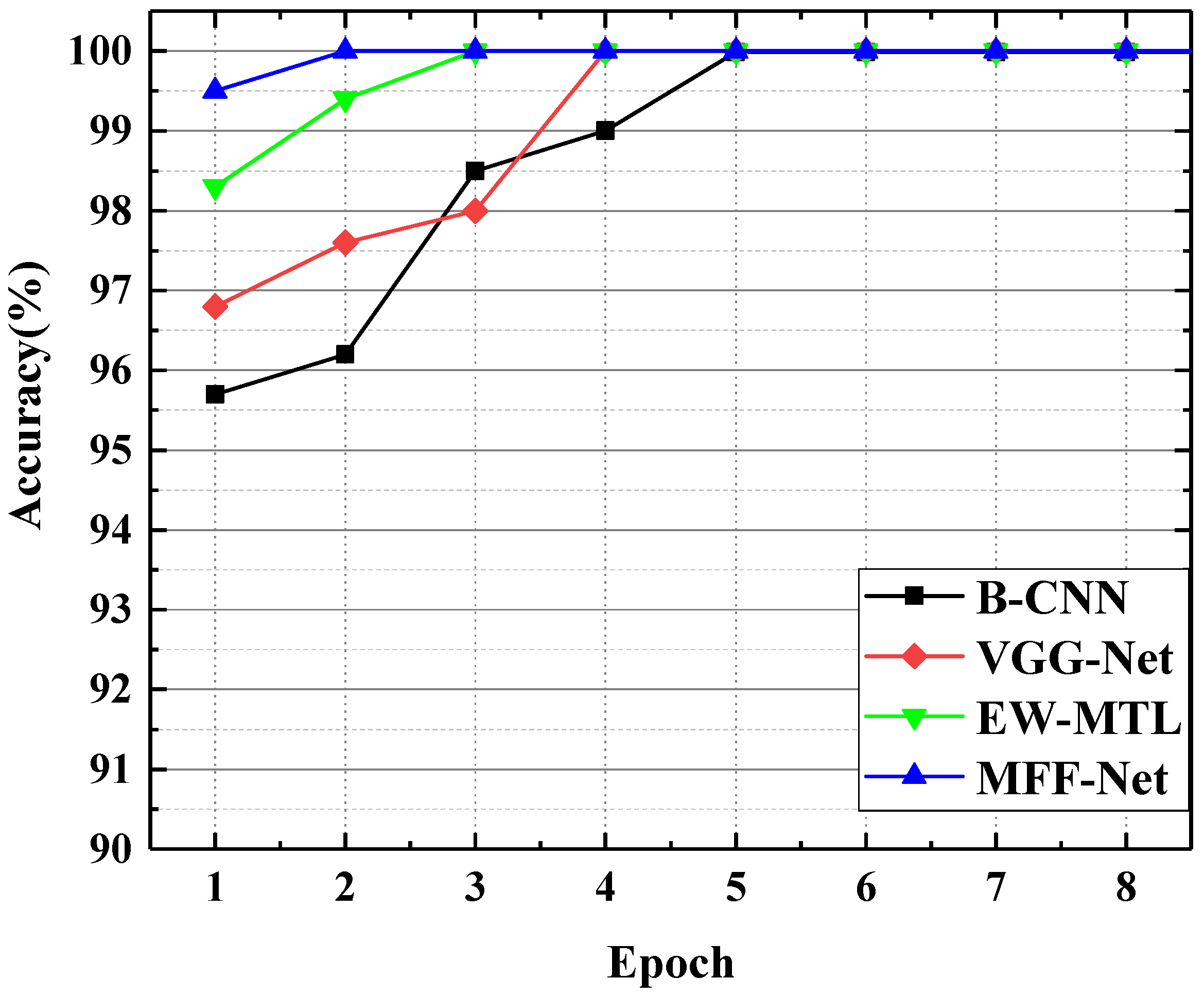
4.1. Modulation Format Identification
4.2. OSNR Monitoring
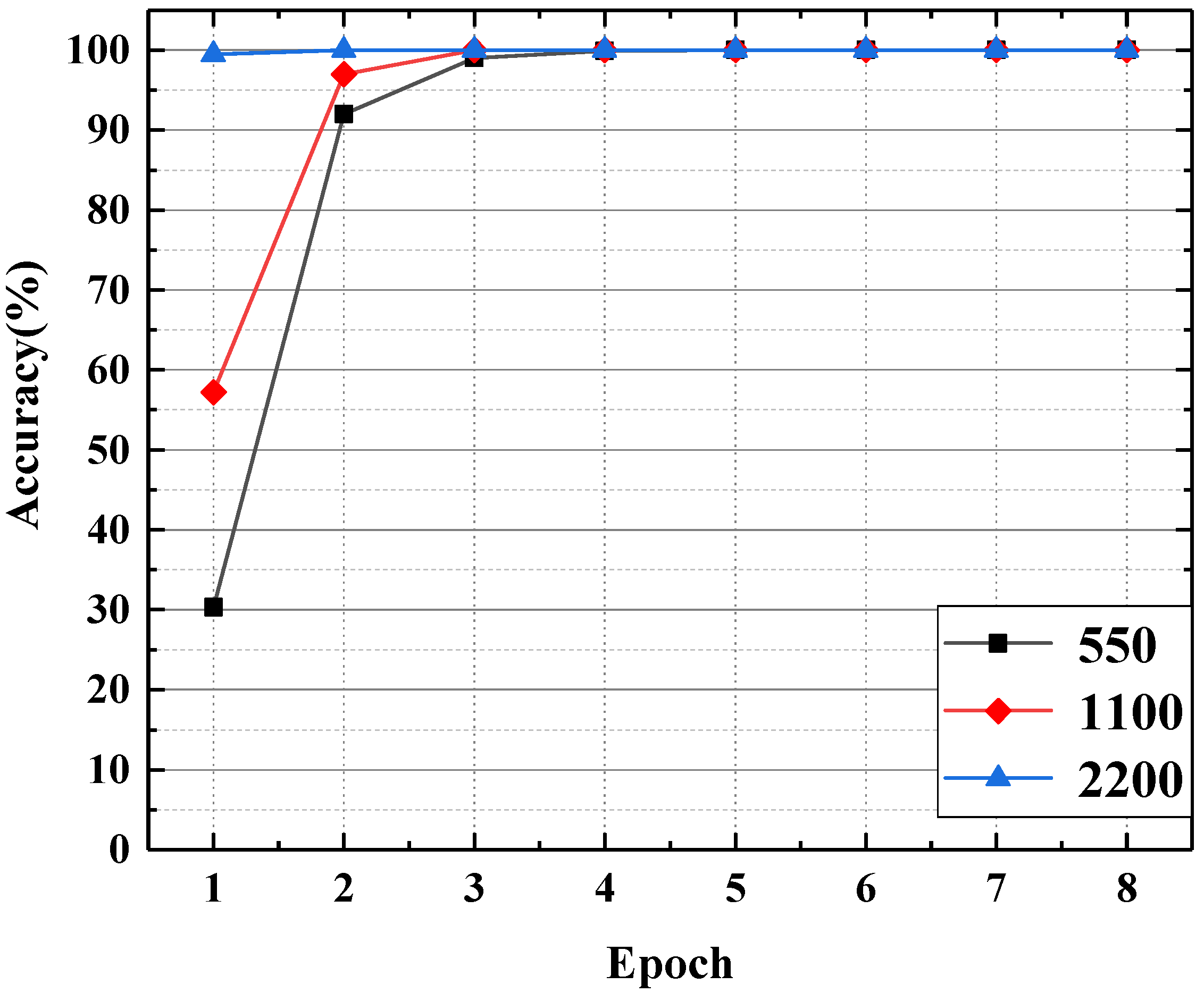
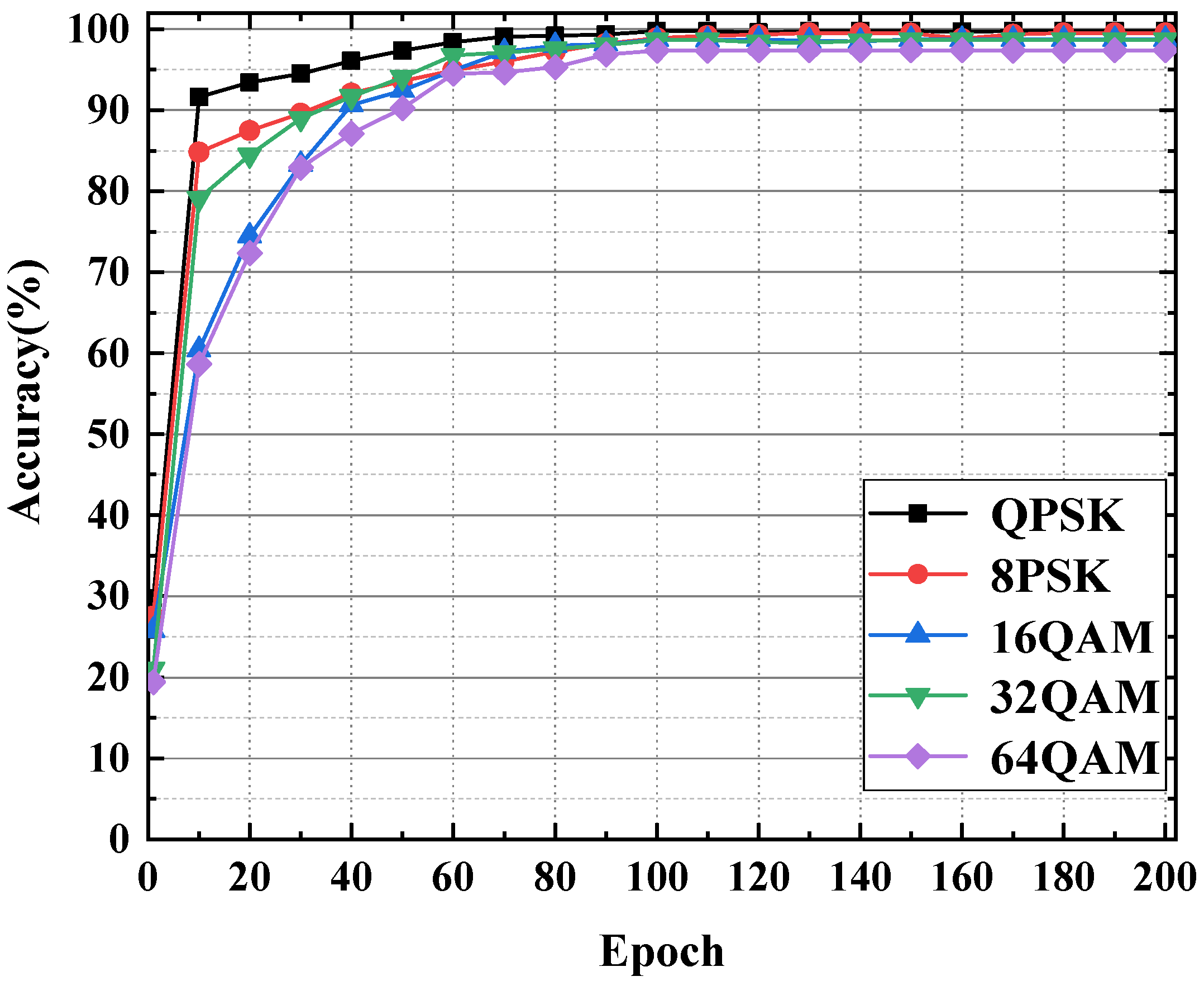
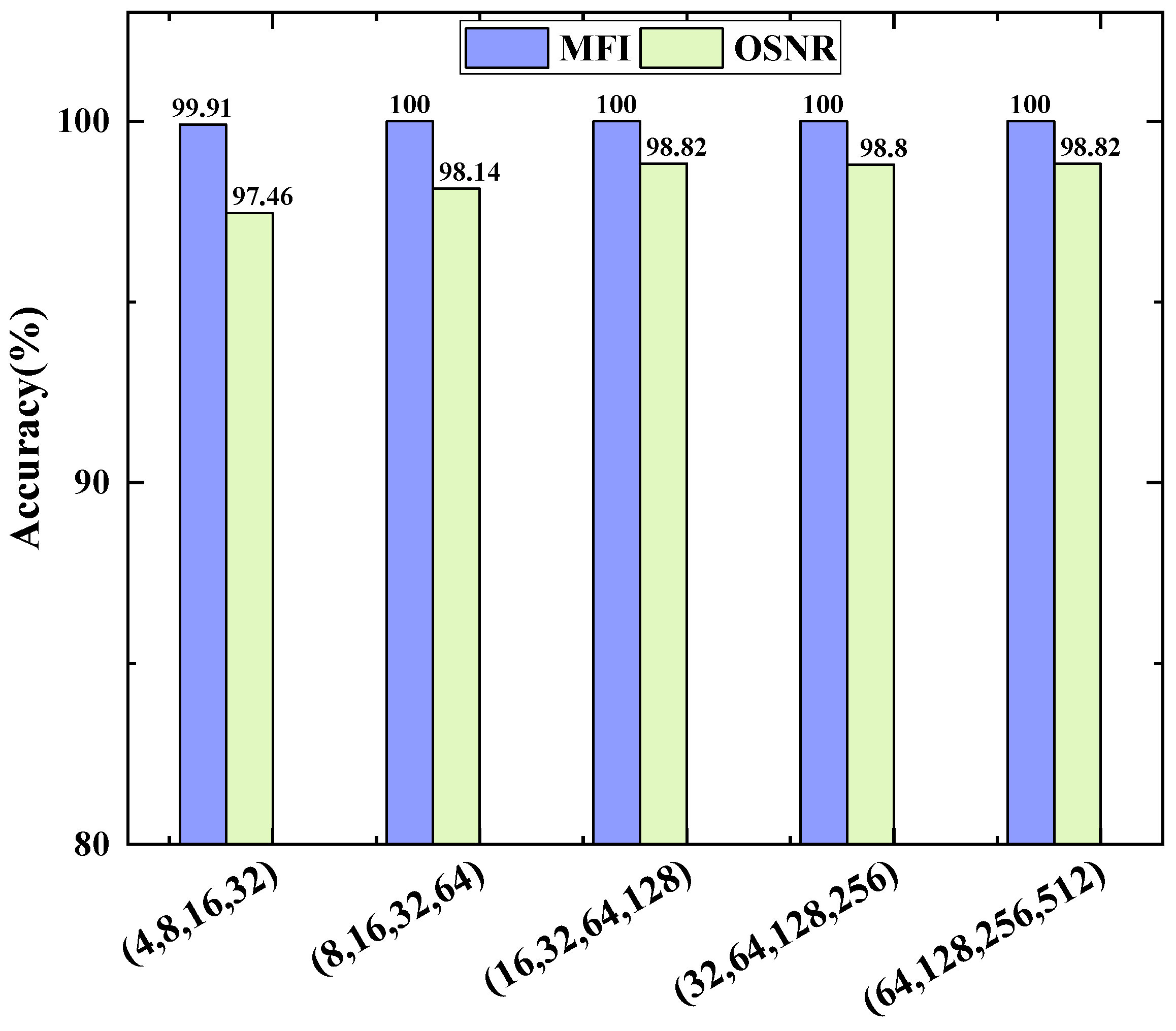
4.3. Model Structure
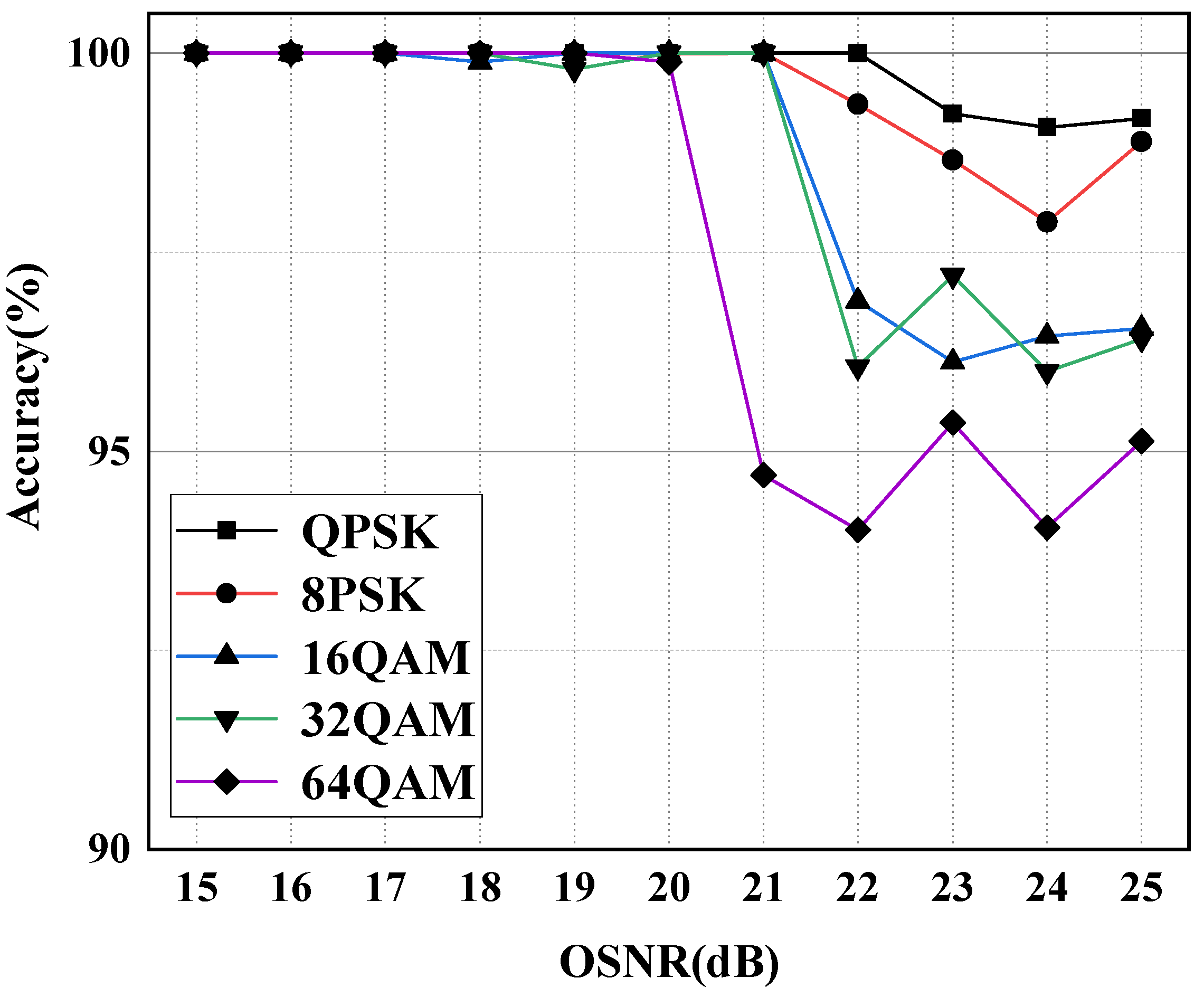
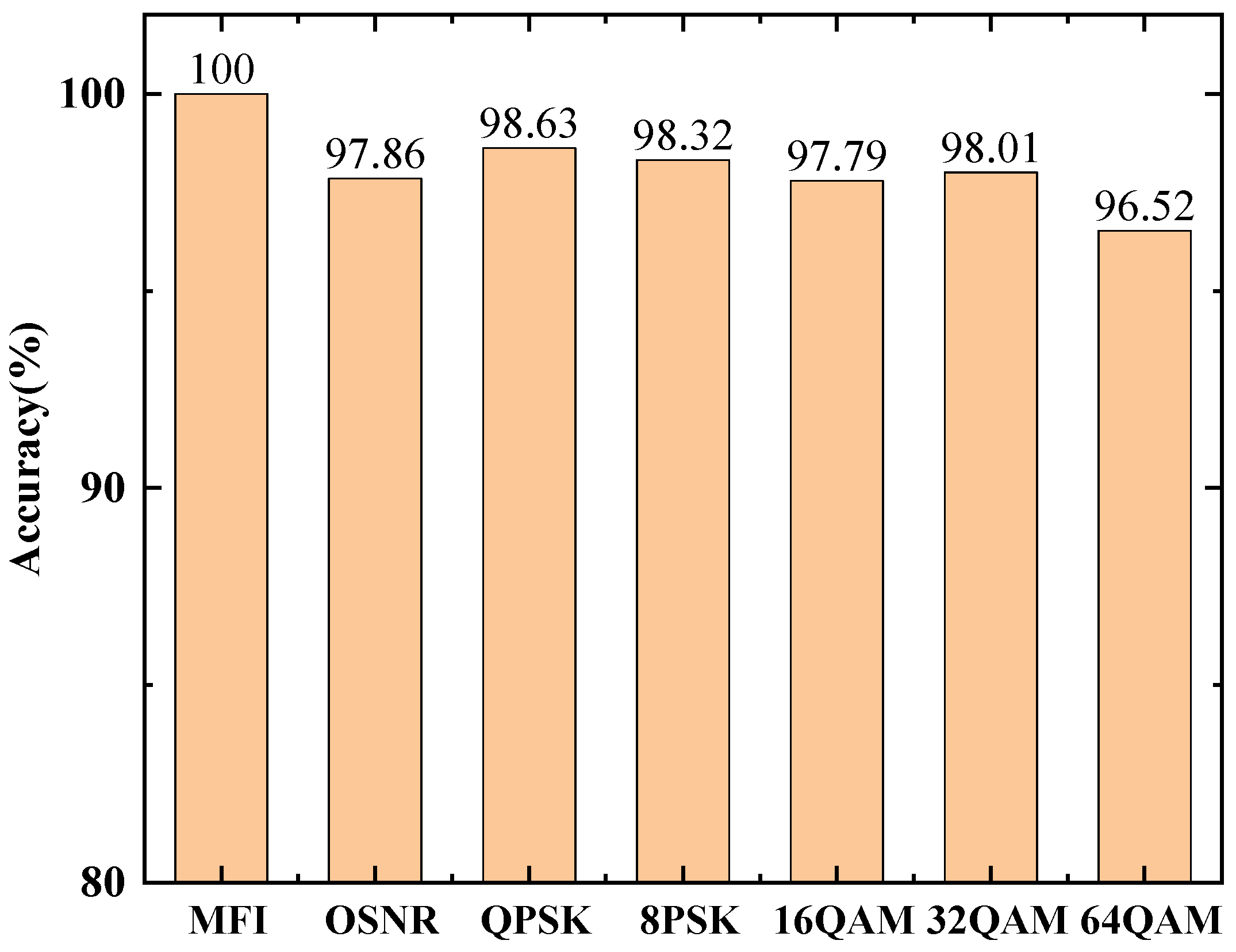
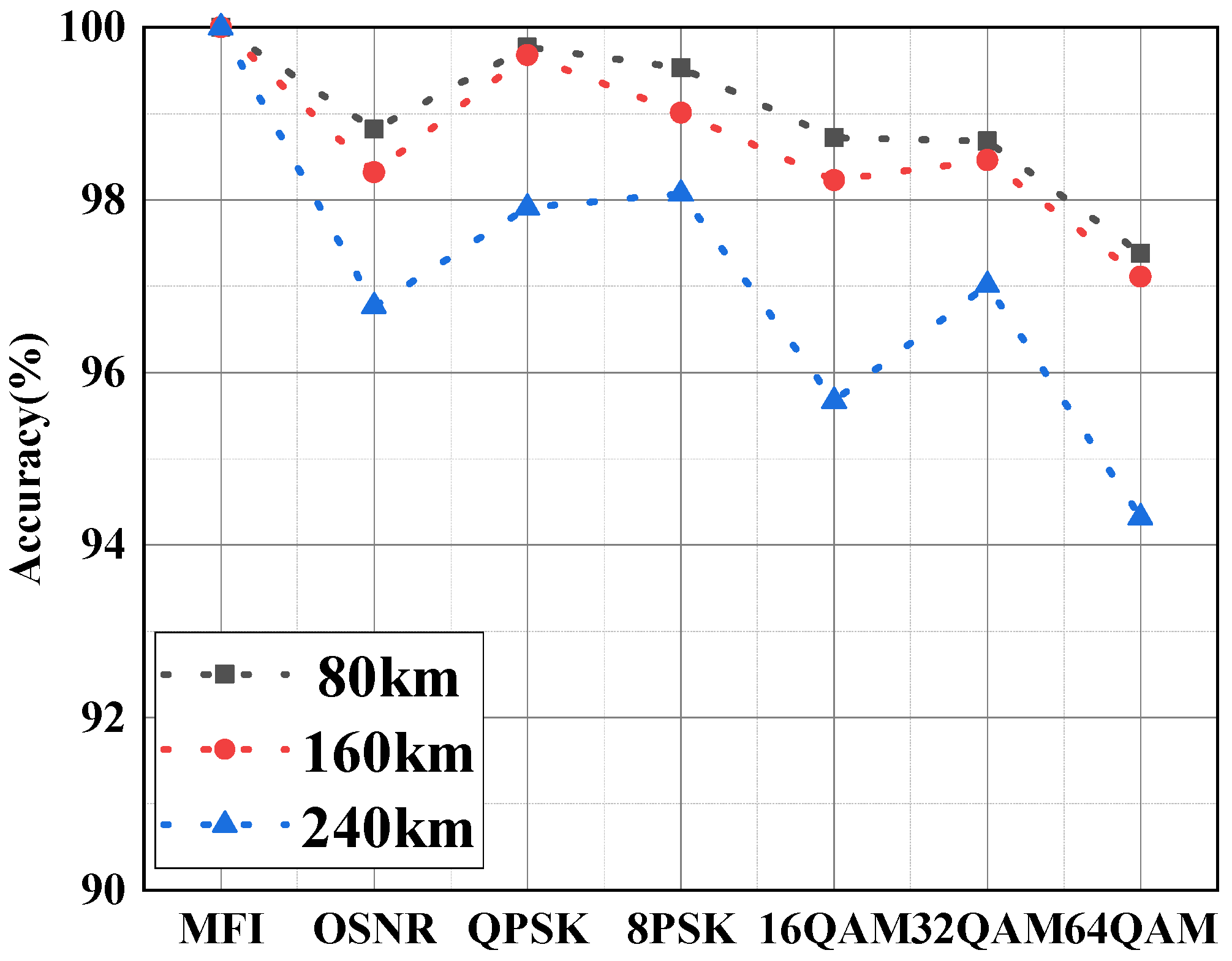
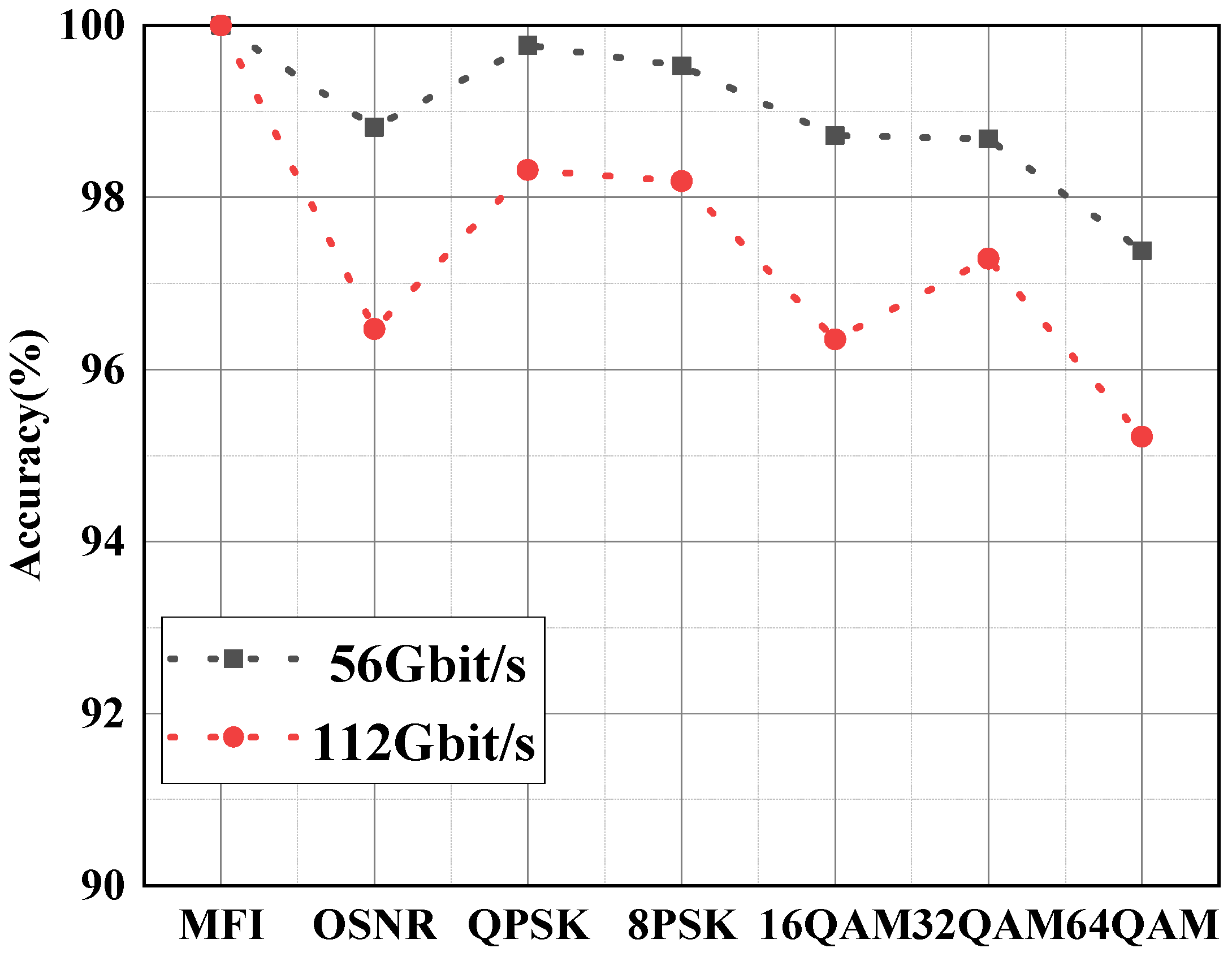
4.4. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saif, W.S.; Esmail, M.A.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Machine Learning Techniques for Optical Performance Monitoring and Modulation Format Identification: A Survey. IEEE Commun. Surv. Tutor. 2020, 22, 2839–2882. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, P.; Dong, C.; Lu, Y.; Chuanqi, L. Intelligent equally weighted multi-task learning for joint OSNR monitoring and modulation format identification. Opt. Fiber Technol. 2022, 71, 102931. [Google Scholar] [CrossRef]
- Saif, W.S.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Optical Performance Monitoring in Mode Division Multiplexed Optical Networks. J. Light. Technol. 2021, 39, 491–504. [Google Scholar] [CrossRef]
- Pan, Z.; Yu, C.; Willner, A.E. Optical performance monitoring for the next generation optical communication networks. Opt. Fiber Technol. 2010, 16, 20–45. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.; Mayrovouniotis, M.L. Deep learning in photonics: Introduction. Photonics Res. 2021, 9, 2327–9125. [Google Scholar]
- Wang, D.; Zhang, M.; Li, J.; Li, Z.; Li, J.; Song, C.; Chen, X. Intelligent constellation diagram analyzer using convolutional neural network-based deep learning. Opt. Express 2017, 25, 17150–17166. [Google Scholar] [CrossRef]
- Wan, Z.; Yu, Z.; Shu, L.; Zhao, Y.; Zhang, H.; Xu, K. Intelligent optical performance monitor using multi-task learning based artificial neural network. Opt. Express 2019, 27, 11281–11291. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Morikawa, H. Convolutional Neural Network-Based Optical Performance Monitoring for Optical Transport Networks. J. Opt. Commun. Netw. 2019, 11, A52–A59. [Google Scholar] [CrossRef]
- Wang, D.; Wang, M.; Zhang, M.; Zhang, Z.; Yang, H.; Li, J.; Li, J.; Chen, X. Cost-effective and data size—Adaptive OPM at intermediated node using convolutional neural network-based image processor. Opt. Express 2019, 27, 9403–9419. [Google Scholar] [CrossRef]
- Yu, Z.; Wan, Z.; Shu, L.; Hu, S.; Zhao, Y.; Zhang, J.; Xu, K. Loss weight adaptive multi-task learning based optical performance monitor for multiple parameters estimation. Opt. Express 2019, 27, 37041–37055. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.N.; Zhong, K.; Zhou, X.; Al-Arashi, W.H.; Yu, C.; Lu, C.; Lau, A.P.T. Joint OSNR monitoring and modulation format identification in digital coherent receivers using deep neural networks. Opt. Express 2017, 25, 17767–17776. [Google Scholar] [CrossRef]
- Zheng, J.; Lv, Y. Likelihood-Based Automatic Modulation Classification in OFDM with Index Modulation. IEEE Trans. Veh. Technol. 2018, 67, 8192–8204. [Google Scholar] [CrossRef]
- Lin, X.; Eldemerdash, Y.A.; Dobre, O.A.; Zhang, S.; Li, C. Modulation Classification Using Received Signal’s Amplitude Distribution for Coherent Receivers. IEEE Photonics Technol. Lett. 2017, 29, 1872–1875. [Google Scholar] [CrossRef]
- Liu, G.; Proietti, R.; Zhang, K.; Lu, H.; Yoo, S.B. Blind modulation format identification using nonlinear power transformation. Opt. Express 2017, 25, 30895–30904. [Google Scholar] [CrossRef] [PubMed]
- Yi, A.; Liu, H.; Yan, L.; Jiang, L.; Pan, Y.; Luo, B. Amplitude variance and 4th power transformation based modulation format identification for digital coherent receiver. Opt. Commun. 2019, 452, 109–115. [Google Scholar] [CrossRef]
- Khan, F.N.; Zhou, Y.; Lau, P.T.A.; Lu, C. Modulation format identification in heterogeneous fiber-optic networks using artificial neural networks. Opt. Express 2012, 20, 12422–12431. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Zhang, M.; Li, Z.; Li, J.; Fu, M.; Cui, Y.; Chen, X. Modulation Format Recognition and OSNR Estimation Using CNN-Based Deep Learning. IEEE Photonics Technol. Lett. 2017, 29, 1667–1670. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, A.; Guo, P.; He, P. OSNR and nonlinear noise power estimation for optical fiber communication systems using LSTM based deep learning technique. Opt. Express 2018, 26, 21346–21357. [Google Scholar] [CrossRef]
- Wang, C.; Fu, S.; Wu, H.; Luo, M.; Li, X.; Tang, M.; Liu, D. Joint OSNR and CD monitoring in digital coherent receiver using long short-term memory neural network. Opt. Express 2019, 27, 6936–6945. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, J.; Hu, S.; Zhu, M.; Song, Y.; Qiu, K. Transfer learning assisted deep neural network for OSNR estimation. Opt. Express 2019, 27, 19398–19406. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, M.; Ma, Y.; Zhao, Y.; Chen, W.; Shen, G. Intelligent adaptive coherent optical receiver based on convolutional neural network and clustering algorithm. Opt. Express 2018, 26, 18684–18698. [Google Scholar] [CrossRef] [PubMed]
- Eltaieb, R.A.; Farghal, A.E.A.; Ahmed, H.E.-D.H.; Saif, W.S.; Ragheb, A.M.; Alshebeili, S.A.; Shalaby, H.M.H.; El-Samie, F.E.A. Efficient Classification of Optical Modulation Formats Based on Singular Value Decomposition and Radon Transformation. J. Light. Technol. 2019, 38, 619–631. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, D.; Zhang, N.; Xu, H.; Zhang, X.; Zhang, H.; Li, Y. Identifying Probabilistically Shaped Modulation Formats Through 2D Stokes Planes With Two-Stage Deep Neural Networks. IEEE Access 2020, 8, 6742–6750. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, J.; Huang, Z.; Li, L. Going Deeper into OSNR Estimation with CNN. Photonics 2021, 8, 402. [Google Scholar] [CrossRef]
- Yang, L.; Xu, H.; Bai, C.; Yu, X.; You, K.; Sun, W.; Guo, J.; Zhang, X.; Liu, C. Modulation Format Identification Using Graph-Based 2D Stokes Plane Analysis for Elastic Optical Network. IEEE Photonics J. 2021, 13, 7901315. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Li, Y. Multi-feature fusion point cloud completion network. World Wide Web 2021, 25, 1551–1564. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Gan, C. Multimodality Fusion for Node Classification in D2D Communications. IEEE Access 2018, 6, 63748–63756. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, Z.; Wan, Z.; Hu, S.; Shu, L.; Zhang, J.; Xu, K. Low Complexity OSNR Monitoring and Modulation Format Identification Based on Binarized Neural Networks. J. Light. Technol. 2020, 38, 1314–1322. [Google Scholar] [CrossRef]
- Lv, H.; Zhou, X.; Huo, J.; Yuan, J. Joint OSNR monitoring and modulation format identification on signal amplitude histograms using convolutional neural network. Opt. Fiber Technol. 2021, 61, 102455. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Kandeepan, S.; Wang, K. Machine Learning Applications for Short Reach Optical Communication. Photonics 2022, 9, 30. [Google Scholar] [CrossRef]

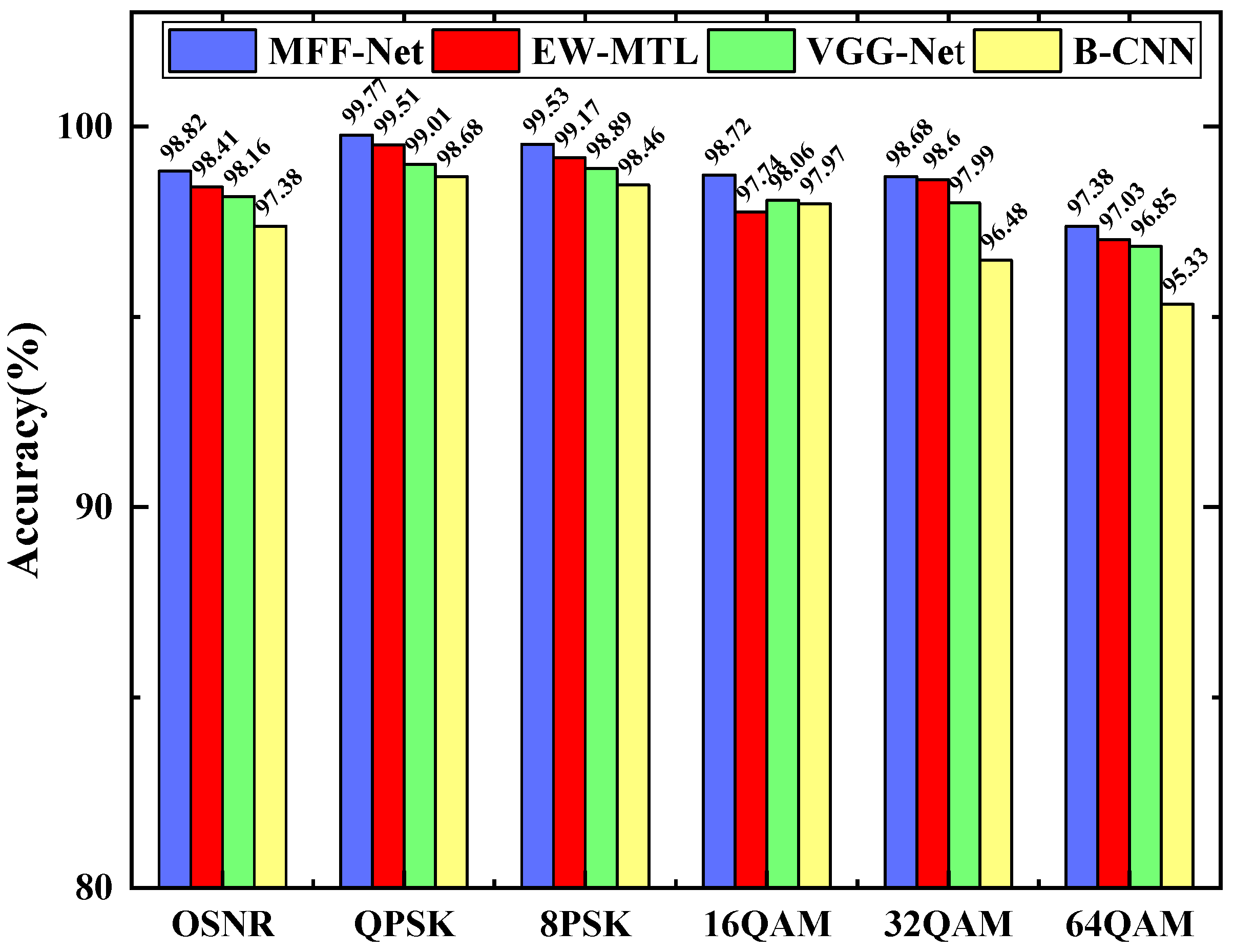


| Model Type | MFF-Net | B-CNN | VGG-Net | EW-MTL | CNN | LSTM |
|---|---|---|---|---|---|---|
| OSNR Accuracy | 98.82% | 97.38% | 98.16% | 98.41% | 97.13% | 95.53% |
| Total Parameters | 2.64 × 105 | 1.63 × 108 | 4.27 × 106 | 4.76 × 105 | 2.51 × 106 | 4.80 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ma, J.; Liu, J.; Lu, J.; Zeng, X.; Luo, M. Modulation Format Identification and OSNR Monitoring Based on Multi-Feature Fusion Network. Photonics 2023, 10, 373. https://doi.org/10.3390/photonics10040373
Li J, Ma J, Liu J, Lu J, Zeng X, Luo M. Modulation Format Identification and OSNR Monitoring Based on Multi-Feature Fusion Network. Photonics. 2023; 10(4):373. https://doi.org/10.3390/photonics10040373
Chicago/Turabian StyleLi, Jingjing, Jie Ma, Jianfei Liu, Jia Lu, Xiangye Zeng, and Mingming Luo. 2023. "Modulation Format Identification and OSNR Monitoring Based on Multi-Feature Fusion Network" Photonics 10, no. 4: 373. https://doi.org/10.3390/photonics10040373
APA StyleLi, J., Ma, J., Liu, J., Lu, J., Zeng, X., & Luo, M. (2023). Modulation Format Identification and OSNR Monitoring Based on Multi-Feature Fusion Network. Photonics, 10(4), 373. https://doi.org/10.3390/photonics10040373




