Multipurpose Laser Instrument for Interplanetary Ranging, Time Transfer, and Wideband Communications ^†

Abstract

In this paper, we discuss the design and feasibility of a multifunctional laser instrument capable of precision ranging, time transfer, and wideband communications over interplanetary distances throughout our solar system. To simplify the communications discussion, On-Off Keying (OOK) is assumed for the high bandwidth (MHz to GHz) modulation format, and the required laser powers and transmit and receive apertures are determined for each Earth–planet link as a function of data rate. Optimization of the transmitter and receiver antenna gains is reviewed. It is further assumed that the spacecraft is in orbit about the planet of interest in order to justify the need for large data downloads rates and that single-photon sensitive detector arrays can be utilized to aid in the acquisition, detection, and tracking of the opposite terminal. Satellite acquisition and tracking is complicated by the long one-way propagation distances (up to 40 AU), the finite speed of light, the orbital and rotational velocities of the two planets, and, if applicable, the spacecraft orbital speed about the planet. Taking advantage of the highly circular and coplanar planetary orbits within our solar system, point ahead angles are estimated for all combinations of possible Earth–planet positions revealing solar orbital geometries where planetary motion does not introduce a need for point ahead angles. Finally, possible methods for simplifying the initial mutual acquisition of the planetary and Earth terminals and maintaining the coalignment of their respective optical systems is discussed.

1. Introduction

The first ruby laser was reported by Theodore Maiman in 1960 [1], and researchers were quick to propose exciting new applications, especially in space. This was largely due to the fact that, for a given initial beam diameter, infrared and visible light diverges orders of magnitude less rapidly than RF or microwave frequencies, allowing much more energy to impinge on the target. In 1964, Dr. Henry Plotkin and his team at NASA Goddard Space Flight Center in Greenbelt, MD reported the first successful laser ranging to an artificial satellite equipped with retroreflectors, which reflected a portion of the incoming laser light back to its source [2]. Since that time, dozens of artificial satellites have been tracked to support a number of scientific and engineering programs. In 1998, the International Laser Ranging Service (ILRS) was created to better coordinate international tracking, orbit determination, and scientific processing of the data [3]. Figure 1 shows the current global distribution of satellite laser ranging (SLR) stations. The largest concentration of stations can be found in Europe and East Asia. As will be discussed later, these existing stations can likely be used by researchers to test future deep space laser transponder and communications systems.

As early as 1969, following the placement of a retroreflector array on the Moon by the Apollo 11 astronauts, a team of scientists successfully measured the range to the Moon with centimeter accuracy [4]. Today, a total of five retroreflector arrays reside on the lunar surface, i.e., three installed by Apollo astronauts and two French retroreflector arrays attached to Soviet Lunakhod landers. However, since the optical losses for the roundtrip to a passive reflector vary as R⁻⁴ (where R is the range), for decades, only three large meter-class telescopes, located, respectively, on mountaintops in southern France and NASA-supported sites at the University of Texas and the University of Hawaii, were capable of detecting return signals. Subsequently, a large telescope in Matera, Italy was added to the roster, but the larger 3.5 m telescope at Apache Point Observatory in Sunspot, New Mexico, USA made a huge difference in data yield as well as providing unprecedented ranging precision at the few millimeter level [5].

2. Two-Way Laser Transponders for Interplanetary Ranging and Time Transfer

Given the weak lunar return signals and the resultant dependence of successful lunar ranging on large telescopes, the present author suggested the use of two-way laser transponders to extend both precision ranging and time transfer capabilities over interplanetary distances [6]. As with lasercom systems, the signal strength varies as R⁻² instead of R⁻⁴ as in SLR to passive reflectors. Figure 2 illustrates the manner in which range and relative time can be transferred between Earth and the spacecraft. Subsequent to this concept, range and time offsets between an Earth-based clock, located at the 1.2 m telescope at NASA Goddard Space Flight Center, and the Mercury Laser Altimeter (MLA) mission, enroute to Mercury at a distance of roughly 22 million km, with an estimated 20 cm range accuracy [7]. A few months later, over 500 laser pulses transmitted by the same 1.2 m Earth station were observed by NASA’s Mars Orbiter Laser Altimeter (MOLA) at a distance of 80 million km. MOLA had previously mapped the surface of Mars, but, unfortunately, the onboard laser was no longer operational, and a return laser signal was not possible [8]. With the exception of a wideband optical transceiver operating in the MHz to GHz range, the hardware and operational requirements are similar, and the various operations can be consolidated within a single interplanetary instrument. The addition of the transceiver also permits the ability to transfer a coded value of the time at the start of the coded sequence from Earth to the interplanetary spacecraft, and vice versa, while a series of coded signals traded between the two terminals can also provide the range rate, resulting in accurate atomic clock offsets, range, and range rate between the two terminals as described in Figure 2 [6].

3. The Advantages and Disadvantages of Lasers over Microwaves in Deep Space Operations

The principal advantage of lasers in deep space operations is that the divergence of the transmitted optical beam is proportional to the ratio of the wavelength λ to the transmit aperture D. The Deep Space Network Ka-band microwave antennas operate at sub-centimeter wavelengths, and the resulting beam divergence is roughly 4–5 orders of magnitude larger for a comparable antenna diameter operating at popular laser wavelengths in the visible and near infrared. The corresponding reduction in received energy at the Earth terminal greatly reduces the achievable data bandwidth. For example, microwave communications bandwidths from the NASA New Horizons Flyby Mission to Pluto to Earth were typically limited to between 1 and 4 KHz, and the acquired data took months to download. A second advantage of lasers is that charged particles in the interplanetary solar plasma cannot follow optical frequencies. Thus, there is no need for solar plasma models or corrections via dual wavelength methods and no propagation delays due to Earth’s ionosphere. Overall, laser systems require both lower power transmitters and smaller optical antennas (telescopes) and are therefore more lightweight and consume less prime power for a given link.

On the negative side, the low beam divergence at optical frequencies requires more precise pointing knowledge and tracking at both terminals whose optical axes must remain coaligned during wideband laser communications. For interplanetary links, coalignment is further complicated by the enormous distances involved (up to 40 AU for the outermost planets) and the finite speed of light, requiring point ahead angles to compensate for the rapid and different orbital velocities of the Earth and subject planet about the Sun; therefore, initial acquisition of the opposite planet will likely rely on optical tracking of the sunlit planet combined with accurate orbital models to determine the proper look-ahead angles. Finally, if the laser beams are too narrow, they may illuminate a relatively small portion of the planetary surface, especially in the case of the giant planets, Jupiter and Saturn.

Table 1. Planetary parameters relevant to the acquisition and tracking of the opposite terminal during wideband communications between Earth and the planet under investigation. The angular radii for Earth and the planet it is communicating with corresponds to the angular spread seen by the opposite terminal at the average interplanetary distance. The actual distance can vary between RPE_ave+/− 1 AU.

Planet Name	Solar Distance (AU)	Planet Diameter (km)	Planet Orbital Period (Years)	Planet Rotational Speed (km/h)	Mean Earth to Planet Distance (AU)	Mean One-Way Light Transit Time (min)	Mean Planet Angular Radius (µrad)	Mean Earth Angular Radius (µrad)
Mercury	0.38	4879	0.2	10.83	1	8.3	16.42	40.93
Venus	0.72	12,104	0.6	6.52	1	8.3	40.73	42.93
Earth	1.00	12,758	1.0	1574	0	0	NA	NA
Mars	1.52	6792	1.9	866	1.52	12.6	15.04	28.24
Jupiter	5.2	142,984	11.9	45,583	5.2	43.0	92.52	8.25
Saturn	9.54	120,536	29.5	36,840	9.54	78.8	42.51	4.50
Uranus	19.2	51,118	84	14,794	19.2	158.6	8.96	2.24
Neptune	30.1	48,528	164.8	9719	30.1	248.3	5.43	1.43
Pluto	39.5	2376	248	47.18	39.5	326.3	0.20	1.09

lists the relevant solar system parameters needed to assess required look-ahead angles related to planetary rotation. Rotational velocities about the polar axis of the planets also cause periodic interruptions in link availability and can further complicate acquisition and tracking. As a result, each terminal must point to where the opposite terminal will be when the light arrives or, in hunter’s terminology, “lead the duck”. Furthermore, unlike microwaves, link availability can be negatively affected by weather and clouds at an Earth ground terminal. Large aperture astronomical telescopes located on mountaintops can greatly mitigate this problem but not totally eliminate it. A possible alternative means of eliminating atmospheric effects and interruptions in link availability is to use a large Earth-orbiting telescope, such as NASA’s 2.4 m aperture Hubble Space Telescope [9], and relay the high bandwidth planetary data to an Earth station via conventional high bandwidth microwave systems.

At or near the minimum Earth–planet range, the Earth, as viewed from the planet, is solidly located in front of the solar disk and the background solar radiation will likely overwhelm the planetary terminal, while at or near the maximum Earth–planet range, the Sun will physically block both links.

One can probably assume that the need for high bandwidth communications implies that the deep space terminal is not a lander but instead is orbiting the planet of interest and collecting voluminous data to be transmitted back to Earth. A polar orbit would provide maximum information and coverage. In this instance, the impact of the planetary atmosphere on the interplanetary lasercom link is eliminated, and the plane of the polar orbit can be oriented to provide uninterrupted visibility to the Earth station(s) for long periods of time. Nevertheless, the polar orbit adds yet another planetary terminal motion that must be accounted for in pointing the Earth telescope, and vice versa. All of these issues will be addressed in later sections.

Finally, as with any new technology, lasers have a somewhat limited space heritage, lifetime, and reliability compared to more mature but data-limited microwave systems. However, several Q-switched Nd:YAG (λ = 1.06 μ) multinational laser altimeters have already operated for years in orbits about the Earth, Moon, Mars, Mercury, and occasional asteroids, and several are planned to operate in orbit about planetary moons. Although most have operated at low repetition rates (<40 pulses per second), NASA’s ICESat-2, launched in 2018, operates in single photon mode with six beams from a single Q-switched Nd:YAG laser operating at a 10 KHz pulse rate, resulting in 60,000 altimetry measurements per second from a 500 km Earth orbit. Unfortunately, none of these low repetition rate, space-qualified lasers are suited for wideband (MHz to GHz) laser communications.

4. Advantages of Single Photon Detector (SPD) Arrays

Single photon sensitivity can significantly reduce link requirements on laser power and/or telescope aperture size. Furthermore, arrays of such detectors allow the system to monitor a much larger angular region of space in order to sense a weak return on the perimeter of the array and guide the pointing mechanism to the central pixel in order to coalign the telescopes at both ends of the communications link [10]. Single photon sensitive detectors and arrays have been used successfully in a wide variety of laser sensors including:

Laser ranging to both retroreflector-equipped satellites (e.g., NASA Goddard 2 KHz NGSLR [10]) and orbiting space debris (e.g., Graz Austria SLR station [11]).

Multibeam airborne (e.g., Sigma Space, six million surface measurements per second using a 532 nm 60 kHz Q-switched laser split into 100 beamlets and the returns recorded by a 10 × 10 pixel array [12]) and spaceborne laser altimetry (e.g., NASA ICESat-2 in a 500 km orbit, 60,000 measurements per second with six beamlets from a single 10 kHz laser [13].

Moon to Earth laser communications (NASA HQ/MIT LLCD Mission) demonstrated PPM modulation at 620 Mbits/s [14].

Accurate ranging and time transfer between Earth-based and space-based atomic clocks for improved spacecraft positioning and trajectory adjustment during transit to the planet.

Currently available single photon sensitive array detectors include microchannel plate photomultiplier tubes (MCP/PMTs), in which the tube anode can be segmented with each segment having its own output, single-photon avalanche photodiodes (SPADs), Geiger-mode avalanche photodiodes (GM/APDs), and more recently nanowire detectors. It must be mentioned, however, that GM/APDs (typically used at 1064 nm) are unable to record multiple photons per bit and therefore do not appear to be well suited to the communications application. Commercially available SPADs have demonstrated detection efficiencies as high as 70% at 532 nm, and recent nanowire experiments have suggested similar efficiencies are possible.

5. Interplanetary Laser Communications

Of the proposed applications, high bandwidth interplanetary laser communications over distances of up to 40 AU (e.g., Pluto) place the greatest engineering burden on the instrument. In this paper, we will consider the case of On-Off Keying (OOK), a simple communication code which transmits a series of ones (detection) and zeros (no detection). If we assume a detector with single-photon sensitivity, the probability of NOT detecting a ”one” pulse is given by P(ND) = 1 − exp (−n) where n is the number of photons incident on the receive detector in that bit. From Figure 3, we see that for n = 7, 14, and 21, respectively, the probability of not correctly detecting a “one” is one in a thousand (KHz), one in a million (MHz), and one in a billion (GHz). Having an expected multiphoton response for a “one” also helps to reject false alarms for a “zero”, due to either internal receiver noise or low-level background light passed through a narrowband spectral filter, by allowing the imposition of a threshold count below which the bin is considered a “zero”.

In OOK mode, the laser pulse train could be either a rapidly modulated CW beam or alternatively a repetitively pulsed Q-switched or mode-locked laser whose pulsewidths are shorter than the desired bit interval, e.g., <1 μs for 1 MHz systems or <1 ns for 1 GHz systems. Other modulation approaches are certainly possible, such as the pulse position modulation (PPM) used in the highly successful 622 MHz LLCD mission between the Earth and Moon mentioned previously.

Early space-based laser communications efforts in the 1970s and beyond were mostly directed toward near-Earth applications to satellites. They dealt with a wide range of issues such as device technology, including lasers, detectors, optical antennas, precision beam pointing mechanisms, modulation methods, etc. Because of the relatively short propagation paths, a wide range of laser sources were considered spanning the infrared and visible wavelengths. The best papers on these subjects published before 1991 were collected and published by the SPIE Optical Engineering Press in a book entitled “Selected Papers on Free-Space Laser Communications” edited by David L. Begley [15]. A more recent book on the subject has been compiled by Hamid Hemmati, a former researcher at the Jet Propulsion Laboratory (JPL) [16].

The link equations allow us to estimate the laser power and telescope apertures required to achieve the desired data rates between Earth and the planet under study. Fortunately, the orbits of the planets about the Sun are coplanar (with the exception of Pluto) and highly circular. In performing the link analyses, we will use the average Earth–planet distance, R_ave, which under the assumption of quasi-circular orbits is equal to the orbital radius of the planet about the Sun. The actual range can vary within R_ave − AU and R_ave + AU. However, as mentioned previously, at or near the minimum interplanetary distance, the Earth is viewed against the extremely bright background of the Sun, while at or near the maximum distance, the Sun is physically blocking the optical path between the Earth and the planet. We will also ignore any transmission or scattering losses in the atmosphere since these can be largely mitigated by utilizing an astronomical telescope on a mountaintop or alternatively a large orbiting telescope, such as NASA’s 2.4 m Hubble Telescope, which in polar orbit would not experience interruptions in service due to Earth rotation. As for the planetary terminal, the need for high bandwidth communications would suggest a satellite in a near-polar orbit outside the planetary atmosphere and oriented for maximum visibility to the Earth station.

Table 1 provides a list of planetary characteristics relevant to interplanetary communications from which one can estimate the approximate range of link distances between the Earth and the planetary probe as well as the relative velocities of the two terminals and the angular uncertainties during initial acquisition and subsequent tracking of the opposite terminal. Choosing telescope (optical antenna) designs that minimize the transmitter beam divergence and ensure that the received light is fully captured by the detector array is crucial and has been previously studied in detail [17] and will be used in the upcoming link analysis.

The number of laser photons received at the Earth station is given by the equation

n_rE = n_tPη_tPG_tPG_rEη_rEη_dER_PE⁻²

(1)

where

• n_tP = the number of photons per pulse/bit emitted by the planetary laser
• ή_tP = the optical efficiency of the planetary transmit optics
• G_tP = the transmitter gain of the planetary telescope (optical antenna)
• G_rE = the receiver gain of the Earth telescope (optical antenna)
• η_rE = the optical efficiency of the Earth receive optics
• η_dE = the optical efficiency of the Earth detector
• R_PE = range between the Earth and planetary terminals

The corresponding equation for the Earth to planet optical uplink is obtained by interchanging the Es and Ps in Equation (1) to yield

$${\eta }_{rP}=n_{tE}{\eta }_{tE}{G}_{tE}{G}_{rP}{\eta }_{rP}{\eta }_{dP}{R}_{PE}^{-2}$$

(2)

According to Figure 4, aluminum or silver coatings applied to the primary and secondary mirrors of both terminals would result in a total transmission of about 72% at three candidate wavelengths of 1550, 1064, and 532 nm, but the shortest wavelength laser at 532 nm (frequency-doubled Nd:YAG) would produce the highest gain. Additional antireflection or high reflectivity coatings on other optical elements in the path would add only about 0.25% loss per surface. For our sample link calculations, we will assume three additional transmitting or dielectrically-coated reflective elements in each of the two telescopes of an additional total loss of 3%. The Earth receiver also includes a narrowband filter whose transmission can be as high as 95% assuming no direct illumination of the detector by the Sun, which would require a much narrower bandwidth with a lower transmission. Thus, we will assume an estimated total coating loss of η_tot = 72 (0.97) (0.95) = 0.66.

The gain of a transmitting optical antenna is given by [17]

$$G_T=\frac{4\pi A_T}{{\lambda }^2}{g}_T\left({\alpha }_T,{\beta }_T,{\gamma }_T,X_T\right)$$

(3)

where A_T is the area of the telescope primary mirror, λ is the laser wavelength, α_T = a/ω where a is the physical radius of the transmitting primary mirror and ω is the Gaussian beam radius at the telescope exit aperture, γ_T = b/a where b is the physical radius of the secondary mirror, X_T = 2πa_T sinφ/λ = πD_T sinφ/λ where φ is the pointing error, D_T is the diameter of the transmitting telescope, and β_T = 0 unless the outgoing beam is purposely defocused to create a wider beam angle as might occur during initial acquisition of the opposite terminal. Thus, once the two terminals are locked onto each other, we can set X_T = β_T = 0 and the gain equation simplifies to

$$\begin{array}{l}{G}_T=\frac{4\pi A_T}{{\lambda }^2}{g}_T\left({\alpha }_T,0,{\gamma }_T,0\right)\\ =\frac{4\pi A_T}{{\lambda }^2}\frac{2}{{\alpha }_T^2}\left\{\exp \left(-2{\alpha }_T^2\right)+\exp {\left(-2{\alpha }_T^2{\gamma }_T^2\right)}^{-}-2\exp \left[-{\alpha }_T^2\left(1+{\gamma }_T^2\right)\right]\right\}\end{array}$$

(4)

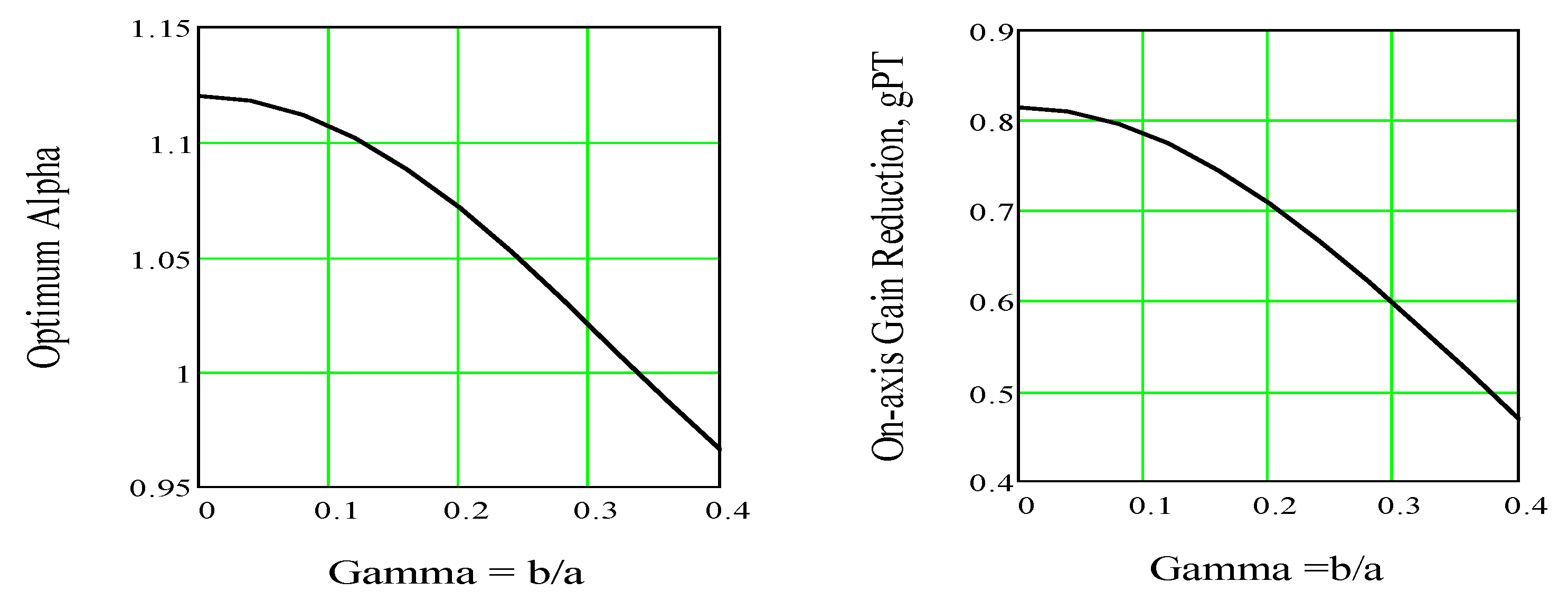
For a given obscuration ratio, the value of α_T which maximizes the transmitter antenna gain, is given by

$${\alpha }_T^{opt}=1.12-1.30{\gamma }_T^2+2.12{\gamma }_T^4$$

(5)

Similarly, the gain of the receiving antenna is given by [18]

$$G_R=A_R\left(1-{\gamma }_R^2\right){\eta }_{RD}$$

(6)

where A_R is the area of the receive telescope primary mirror, γ_R is the receiver obstruction ratio of the secondary mirror, and η_RD has a maximum value of 0.95 if πR_D/λF_E > 0.7 where R_D is the detector radius and F_E is the Earth telescope F-number, i.e., the ratio of the receive telescope focal length over the primary diameter [18].

If we multiply both sides of Equation (1) by the photon energy hν and the desired bit frequency f_b, we generate the equation for the transmitted laser power from the planetary platform needed to generate the desired number of received photons per bit at the Earth station, i.e.,

$$P_{rE}=n_{rE}(f_b)h\nu f_b=P_{tP}{\eta }_{tot}{\eta }_{dE}\frac{{\pi }^3}{4}{g}_{tP}\left(1-{\gamma }_{rE}^2\right)\frac{{\left(D_{tP}{D}_{rE}\right)}^2}{{\left(\lambda R_{PR}\right)}^2}$$

(7)

From Equation (7), we obtain

$$P_{tP}{(D_{tP}{D}_{rE})}^2=P_{rE}{(\lambda R_{PE})}^2\frac{4}{{\pi }^3{\eta }_{tot}{\eta }_{dE}{g}_{tP}(1-{\gamma }_{rE}^2)}$$

(8)

In Equation (8), P_rE is the desired received power at the Earth station. For example, if we want to limit the Bit Error Rate (BER) to one per thousand in a KHz system, one per million in a MHz system, or one per billion in a GHz system, then, based on Figure 3, the desired laser power received at the Earth terminal, P_rE is equal to the photon energy hν multiplied by the desired received photons per bit n_rE and the bit frequency f_b, e.g., 7 thousand (KHz), 14 million (MHz), or 21 billion (GHz).

We will now insert our previously determined values of η_tot = 0.66 and η_dE = 0.7 into Equation (8) and further assume that a secondary mirror is not required for the smaller planetary telescope. The latter assumption implies γ_tP = 0 and g_tP = 0.81 from Figure 3. If we further assume an orbiting Earth telescope, like NASA’s 2.4 m diameter Hubble Space Telescope, the value of γ_rE = 0.3 m/2.4 m = 0.125 or (1 − γ_rE²) = 0.984.

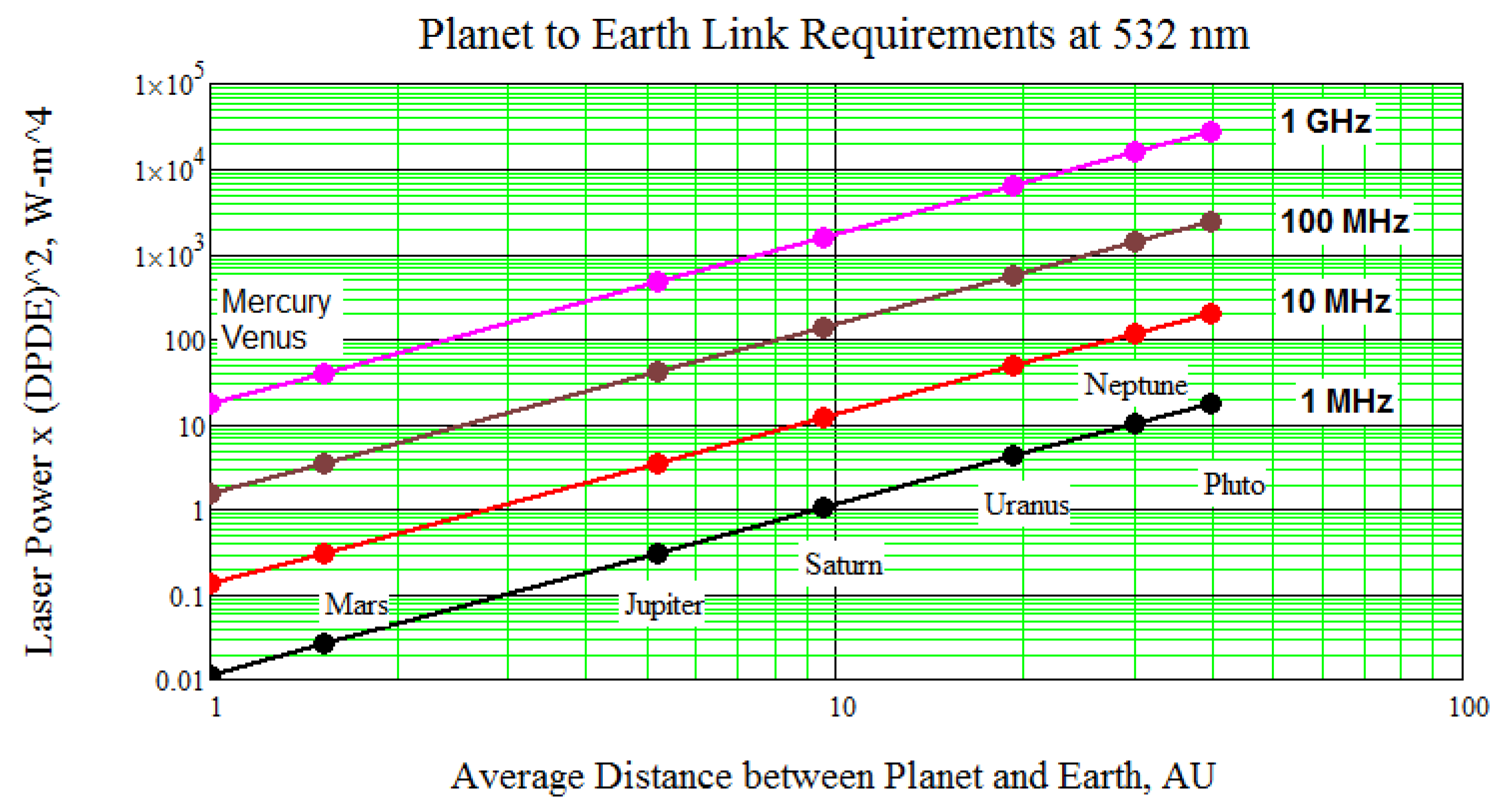
In Figure 5, the product of the transmitted laser power emitted by the planetary probe and the two telescope diameters squared (y-axis) is plotted as a function of the planetary distance (x-axis) for four candidate bit rates: 1 MHz (black), 10 MHz (orange), 100 MHz (brown), and 1 GHz (pink) for a laser wavelength of λ = 532 nm. The dots along the lines indicate the average distance of the various planets from Earth, as listed in Table 1. The graph allows the reader to quickly assess the laser power and telescope diameters needed to support a given OOK bandwidth between 1 MHz and 1 GHz.

As a simple example, let us assume that the diameter product for the transmitting and receiving Hubble Space Telescope equals 1 m² or D_tP = 1 m²/D_rE = 1 m²/2.4 m = 0.42 m. Then a 10 W laser at 532 nm combined with a 42 cm diameter planetary telescope would allow roughly 900 MHz communications from Mercury or Venus, 700 MHz from Mars, 70 MHz from Jupiter, 10 MHz from Saturn, 6 MHz from Uranus, 1 MHz from Neptune, and 900 kHz from Pluto. Using Equation (8), the required power and telescope diameters for other laser wavelengths can easily be determined from Figure 5 by multiplying the y-axis result by the square of the wavelength ratio, (λ/532 nm)², which equals 4 for a wavelength of 1064 nm (Nd:YAG) and 8.5 at 1550 nm.

6. Opposite Terminal Acquisition and Tracking

The orbits of the planets in our solar system are all nearly circular and coplanar because during the solar system’s formation the planets formed out of a disk of dust which surrounded the Sun. Pluto, however, deviates from coplanar by about 17°. Nevertheless, all of the planets in our solar system have been meticulously observed by astronomers for more than a century and their orbital characteristics (including slight deviations from the circular coplanar orbits assumed here) are therefore very well known, but the precise position of the planetary probe and the synchronization of the onboard clock with Earth clocks may not be. This is an area where the instrument’s secondary functions of precise ranging and time transfer via two-way transponder can be helpful in precisely guiding the spacecraft to its desired destination and during the initial acquisition and tracking of the opposite terminal. The latter is made much more difficult due to the huge interplanetary distances, the finite velocity of light, and 4 to 5 orders of magnitude reduction in beam divergence relative to conventional microwave-based systems. Sunlight reflected off the opposite planet can help guide the initial acquisition provided one also compensates for the planetary orbital motions and finite velocity of light. In the following analysis, we will ignore the small ellipticities in some of the planetary orbits.

Under our planetary circular orbit approximation, the Earth and planet positions can be written as

$$E=R_E\left[\begin{array}{c}\cos ({\theta }_E)\\ \sin ({\theta }_E)\end{array}\right], P=R_P\left[\begin{array}{c}\cos ({\theta }_P)\\ \sin ({\theta }_P)\end{array}\right]$$

(9)

where R_E and R_P are the orbital radii, and therefore the Earth–planet distance at time t is equal to

$$\begin{array}{c}{R}_{PE}\left(t\right)=\sqrt{{\left[R_P\cos \left({\theta }_P\right)-R_E\cos \left({\theta }_E\right)\right]}^2+{\left[R_P\sin \left({\theta }_P\right)-R_E\sin \left({\theta }_E\right)\right]}^2}\\ =\sqrt{R_E^2+R_P^2-2R_E{R}_P\cos \left[{\theta }_P\left(t\right)+{\theta }_E\left(t\right)\right]}\end{array}$$

(10)

where the time dependence of the combined angular change during the one-way laser pulse time of flight (TOF) is given by

$${\theta }_P\left(t\right)+{\theta }_E\left(t\right)={\theta }_P\left(t_0\right)+{\theta }_E\left(t_0\right)+\left({\omega }_P+{\omega }_E\right)\left(t-t_0\right)$$

(11)

and ω_P and ω_E are the angular rates of the two planetary orbits. The cosine in Equation (10) can now be approximated by

$$\begin{array}{l}\cos \left[{\theta }_P\left(t\right)+{\theta }_E\left(t\right)\right]=\\ \cos \left[{\theta }_P\left(t_0\right)+{\theta }_E\left(t_0\right)\right]\cos \left[\left({\omega }_P+{\omega }_E\right)\frac{R_{PE}}{c}\right]-\sin \left[{\theta }_P\left(t_0\right)+{\theta }_E\left(t_0\right)\right]\sin \left[\left({\omega }_P+{\omega }_E\right)\frac{R_{PE}}{c}\right]\end{array}$$

(12)

Substitution of Equation (12) into Equation (10) results in a quadratic equation for the interplanetary distance traveled by the laser pulse arriving at time t, i.e.,

$$R_{PE}^2\left(t\right)+\left\{2R_E{R}_P\cos \left[{\theta }_P\left(t_0\right)+{\theta }_E\left(t_0\right)\right]\left(\frac{{\omega }_P+{\omega }_E}{c}\right)\right\}{R}_{PE}\left(t\right)-\left(R_E^2+R_P^2\right)=0$$

(13)

with the solution

$$R_{PE}\left(t\right)=\frac{-B\pm \sqrt{B^2-4AC}}{2A}$$

(14a)

where

$$\begin{array}{l}A=1\\ B=2R_E{R}_P\cos \left[{\theta }_P\left(t_0\right)+{\theta }_E\left(t_0\right)\right]\frac{{\omega }_P+{\omega }_E}{c}\\ C=-\left(R_E^2+R_P^2\right)\end{array}$$

(14b)

Since the distance between the planets can be huge, i.e., up to 40 astronomical units (AUs), the finite speed of light, combined with the planetary and Earth angular speeds around the Sun (ω_P and ω_E) and the narrow laser beam divergences (which are 4 to 5 orders of magnitude smaller than conventional microwave systems), can complicate the initial acquisition and subsequent tracking of the opposite terminal. One attractive acquisition approach would be to have each terminal initially track the sunlit image of the opposite planet in order to narrow the search angle and then, based on our excellent knowledge of the orbital velocities and eccentricities (if any), point ahead of the viewed position to compensate for the two-way time delay.

If t₀ is the time a light signal was transmitted by the planetary terminal, t₁ = RPE1/c is the time that signal was observed at the Earth station, and t₂ = (RPE1 + RPE2)/c is the time that the Earth response reaches the planetary terminal; then, the cosine of the point ahead angle for the Earth station is given by the dot product of the interplanetary range vectors at times t₀ and t₂ divided by their respective magnitudes, RPE1 and RPE2. This leads to the following set of equations for the planetary positions at time t = t₀:

$$P\left(t_0\right)=R_P\left(\begin{array}{c}\cos {\theta }_{P0}\\ \sin {\theta }_{P0}\end{array}\right), E\left(t_0\right)=R_E\left(\begin{array}{c}1\\ 0\end{array}\right)$$

the two components of the roundtrip pulse transit times t₁ and t₂,

$$t_1=\frac{RP{E}_1}{c}, t_2=\frac{RP{E}_2}{c}$$

and the position vectors for Earth and the planet at times t₁ and t₂

$$\begin{gathered} E\left(t_1\right)=R_E\left[\begin{array}{c}\cos \left({\omega }_E{t}_1\right)\\ \sin \left({\omega }_E{t}_1\right)\end{array}\right], P(t_1)=R_P\left[\begin{array}{c}\cos ({\theta }_{P0}+{\omega }_P{t}_1)\\ \sin \left({\theta }_{P0}+{\omega }_P{t}_1\right)\end{array}\right] \\ \begin{array}{l}E\left(t_2\right)=R_E\left[\begin{array}{c}\cos \left({\omega }_E\left(t_1+t_2\right)\right)\\ \sin \left({\omega }_E\left(t_1+t_2\right)\right)\end{array}\right],\\ P(t_2)=R_P\left[\begin{array}{c}\cos \left({\theta }_{P0}+{\omega }_P\left(t_1+t_2\right)\right)\\ \sin \left({\theta }_{P0}+{\omega }_P\left(t_1+t_2\right)\right)\end{array}\right]\end{array} \end{gathered}$$

where ω_E and ω_P are the angular revolution rates of the Earth and planet about the Sun. The latter are obtained by dividing the orbit circumference, 2πR_P, by the orbital period in Table 1. The value for Earth is ω_E = 0.199 μrad/s. The vectors between the Earth and planetary terminals at the beginning and end of the roundtrip are in turn given by

$$EP\left(t_0\right)=P(t_0)-E\left(t_0\right), EP(t_2)=P(t_2)-E\left(t_2\right)$$

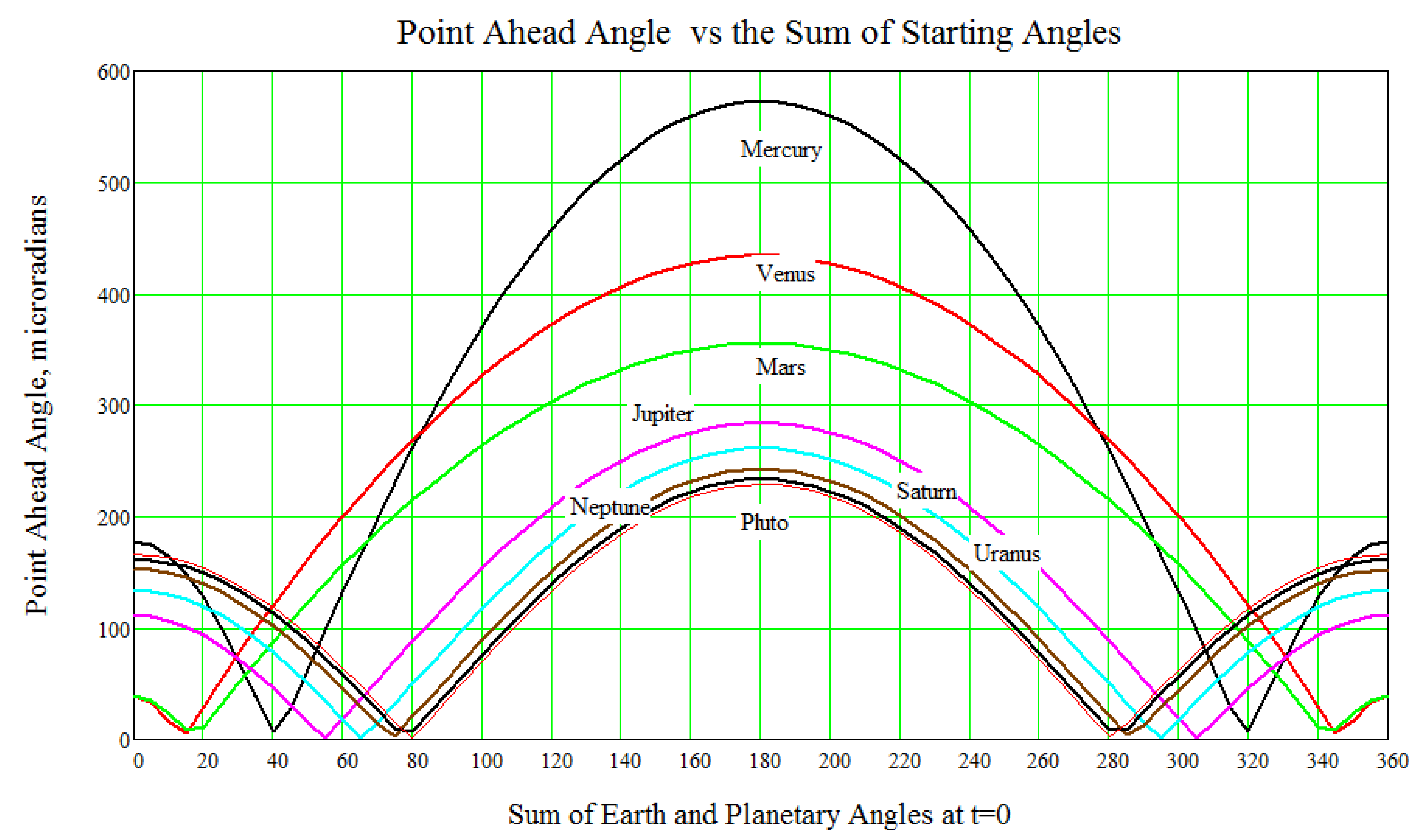
The dot product of the two vectors, divided by their magnitudes, yields the cosine of the point ahead angle. The latter is plotted for all of the planets in Figure 6 as a function of their combined start angles θ_P0 where, due to the assumed circular symmetry, we can arbitrarily set θ_E = 0 deg. For most planetary geometries, the point ahead angle is a fraction of a milliradian but still orders of magnitude greater than the angular radii of the planet as seen from Earth, as listed in Column 8, Table 1. It should also be noted that orbital geometries where the point ahead angle drops to near zero in Figure 6 would be optimum locations to initiate opposite terminal acquisition. These opportunities would occur twice per Earth year for all of the planets but with different time intervals between them.

The highest peak at θ_P0 = 180 degrees occurs for two reasons: (1) the relative planetary orbital velocities are additive because they point in opposite directions; and (2) the planets are at their maximum distance during the two-way light transit time between t₀ and t₂. The height of the central peak falls for planets farther from the Sun because they revolve more slowly and therefore add less to the Earth angular velocity contribution. In decreasing order, the peaks in Figure 6 correspond to Mercury (black), Venus (red), Mars (green, Jupiter (pink), Saturn (aqua), Uranus (brown), Neptune (black), and Pluto (red). In the case of the outer planets (Mars and beyond), the Earth’s orbital angular velocity dominates, whereas the angular velocities of Mercury and Venus exceed that of Earth and tend to increase the point ahead angle.

For an angular starting sum of 0 (or 360) degrees, a smaller point ahead peak is formed in Figure 6 because: (1) the angular velocities are in the same direction and therefore subtracted from each other; and (2) the two-way light Earth–planet transit time is at a minimum and reduced by Δt = 2AU/c relative to the 180° case discussed previously.

7. Effects of Planetary Rotation or Planetary Orbits

In addition to the relative motions of the planets about the Sun, all of the planets rotate about their polar axes which, like Earth, are not necessarily oriented perpendicular to their orbital plane about the Sun. Using the information in Columns 5 and 8 of Table 1, we can compute the angular rate of rotation for each of the planets and multiply by the light roundtrip transit time using the one-way transit time in Column 7 to compute the maximum angular point-ahead angle for a lander located on the planet’s equator. This maximum occurs when the lander is in the middle of the planet when viewed through the Earth telescope and diminishes as the lander approaches the edge of the planet prior to disappearing from view. The maximum point ahead angles due to axial rotation of the innermost planets are quite large compared to angular widths of the laser beams, i.e., 195 μrad for Mercury and 47 μrad for Venus. The point ahead angles for the outer planets are significantly greater: Mars (17 mrad), Jupiter (145 mrad), Saturn (256 mrad), Uranus (487 mrad), Neptune (528 mrad), and Pluto (69 mrad). These are all much larger than the beamwidths needed to transmit MHz or GHz bandwidths between the planets using modest laser output powers, as outlined in Figure 5. For example, the overall laser beam divergence between points that see roughly 10% of the peak illumination at the center of the beam (corresponding to only a few photons per bit) is roughly equal to the wavelength to telescope diameter ratio, λ/D. Thus, at a wavelength of 532 nm, telescope diameters between 0.25 m and 2.5 m create a full beam divergence of roughly 20 and 2 μrad respectively, orders of magnitude smaller than the angular deviations caused by planetary rotations at the equator. Only near the poles do the planetary rotations result in near zero point ahead angles. As demonstrated by Equation (8), use of longer wavelength lasers increases the beam divergence for a given pair of telescopes but also increases the laser power required to achieve the desired bit rate. For example, for a wavelength of 1064 nm, the required laser power increases by a factor of 4.

In the opinion of the author, it appears unlikely that a lander mission on the planet could gather sufficient data to require high bandwidth communications in the MHz to GHz range due to a lander’s highly limited access to information compared to an orbiting satellite. In contrast to a lander, a satellite in a properly oriented polar orbit would have access to information from the entire planet and could communicate continuously with an orbiting Earth terminal for an extended period of time before the orientation of the satellite orbital plane would have to be adjusted in order to maintain long-term Earth visibility. Furthermore, a polar orbit would negate possible transmission and scattering losses in the planetary atmosphere which might degrade the received signal strength and subsequently the achievable bit error rate.

Laser terminals in polar orbits about both planets, combined with conventional wideband microwave relays to Earth, would eliminate atmospheric transmission and scattering losses and potentially provide quasi-continuous wideband communication except for brief periods twice per Earth year, i.e., when the outer planets are at or near the minimum and maximum interplanetary distance (θ_P0 = 0 or 180 degrees) when the Sun would either blind the planetary terminal or block the beams entirely. In addition, the initial angular area of uncertainty for the location of the planetary orbiter would be constrained to a narrow circular rim defined by the orbital altitude above the planet’s surface, i.e., A_O = πDh where D is the angular diameter of the planet as viewed by the opposite terminal and h << D is the maximum altitude of the satellite. A land-based terminal, on the other hand, could be located anywhere within the angular disk, i.e., A_L = πD²/4, as listed in Columns 8 and 9 of Table 1, a factor D/4h larger. The look-ahead angle for a satellite in polar orbit about a planet of angular diameter D is roughly equal to πD/τ_orb and is plotted in Figure 7 for the various planets as a function of the orbital period.

The shape of the transmitted beams is not Gaussian as is often assumed by some authors. On the contrary, the antenna pattern of the optimized transmit telescope consists of a strong central lobe surrounded by increasingly weaker circular rings [17]. The rings result from the truncation of the Gaussian beam profile by the finite diameter of the telescope and are further modified by the presence of a secondary mirror, if any. In fact, the presence of a secondary mirror slightly reduces the intensity of the central lobe while simultaneously increasing the amplitudes of the outer rings [17]. Within the central lobe, the signal strength drops to roughly 10% of the peak value for pointing errors equal to λ/D. Thus, for the 1 GHz OOK system discussed earlier, the desired 21 received photons per bit would be reduced to about 2 photons per bit due to this pointing error, thereby resulting in an unacceptable bit error rate. It is also worth noting that the Earth terminal telescope diameter, D_E, is highly likely to be much larger than the planetary telescope diameter, D_P, requiring the Earth terminal pointing to be much more accurate in transmission mode for a two-way communications link. It is therefore extremely important to either maintain a very tight coalignment of the transmit and receive telescope optical axes or increase the laser power to compensate for the optical loss. We will now discuss a possible solution.

To expedite the acquisition and coalignment of the planetary and Earth terminals, one can include a defocusing element in each telescope and a partitioned single-photon sensitive detector array in each receiver focal plane. The defocusing element would temporarily merge the central lobe and the surrounding diffraction rings into a much broader (and therefore lower intensity) far field pattern with a mild degree of spatial modulation [17]. As mentioned briefly in Section 5, the amount of beam broadening is determined by the parameter β’ = β/2π = D²/8(λR) where D is the diameter of the telescope primary mirror and λR is again the product of the laser wavelength and the range to the opposite terminal. Figure 5 in [17] suggests that choosing the value β’ = 2.4 would increase the planetary beam spread in the far field by a factor of 7 relative to the original central lobe. This would increase the transmitted beam area for acquisition by a factor of 49, thereby greatly accelerating acquisition of the opposite terminal. However, the mean reduction in signal strength due to defocusing would be about 2 orders of magnitude. If the received photons per bit was set at 21 photons as recommended earlier for the 1 Gbps system, an off-axis detector of the same size would collect only 0.2 photons per bit. However, by summing over 100 bits (100 ns) using an integrating circuit, one could record the same number of photons as in the focused case. An attractive concept to the author would be an NxN square array (N odd) of equally sized detectors with the central communications detector sized to collect all of the light entering the telescope parallel to the optical axis. At a minimum (N = 3), the central detector would be surrounded by eight equally sized integrating detectors summing over 100 pulses and guiding the detected beam to the central detector. Other detectors with longer integration times could be added to the outer boundaries of the array (N = 5, 7, etc) if needed to further widen the FOV for faster target acquisition.

In order to minimize the aforementioned integration time during the acquisition and coalignment process, the transmitters at both terminals would be “unmodulated”. By “unmodulated”, we simply mean uncoded, i.e., no modulation of a CW beam or no ejection of pulses from the Q-switched or mode-locked pulse trains used to create “zeros” in the OOK modulation scheme. Once a signal is detected in the outer array of the receiving telescope during terminal acquisition, the affected pixels can guide the receiver pointing system into coalignment with the transmitting terminal. Coalignment can also be maintained during wideband communications by monitoring and correcting for intermittent signals occurring within the integrating array detectors adjacent to the central communications detector that might arise due to “light spillovers” resulting from small pointing errors or jitter.

The optimum size of the communications detector would be determined by the point at which a ray, parallel to the optic axis of the receiver telescope and at the edge of the primary mirror, enters the focal plane of the telescope. In order to minimize the bit error rate (BER), short integration times in integrating pixels immediately adjacent to the communications detector would possibly permit rapid corrections of small misalignments due to pointing jitter.

8. Summary

In this paper, the author has attempted to enumerate both the advantages and disadvantages of using lasers in the implementation of wideband deep space laser communications. The relatively simple On-Off Keying (OOK) would define acceptable bit error rates for the various data bandwidths (MHz to GHz). The product P_T(D_PD_E)² (laser power times the square of diameters of gain-optimized transmit and receive telescopes) needed to achieve a particular bit error rate was determined for all of the planets and is proportional to (λR)² where λ is the wavelength and R is the distance between the Earth and the planet. At the extreme outer edges of our solar system, R can be as large as 40 AU (Pluto), resulting in a two-way light transit time of up to 11 hours! During such long time intervals, any (1) relative angular motion between Earth and the subject planet in their respective voyages about the Sun, (2) rotations of each planet about its axis in the case of ground-based terminals, or alternatively (3) orbital motions of the communications terminals about their respective planets will result in a combination of multiple look-ahead angles in highly diverse directions that must be taken into account in order to maintain coalignment of the two telescope axes and the required signal strength for wideband communications in the MHz to GHz range with low bit error rates (BERs). In this paper, the approximate magnitudes of all of these look-ahead angles have been determined under the assumption of perfectly circular, coplanar planetary orbits about the Sun and circular orbits of both terminals about their respective planets. It has been noted that for all of the planets there are two time intervals per Earth year when no look-ahead angles are required to compensate for planetary orbital velocities about the Sun, making them optimum times to initiate acquisition of the opposite terminal. It is further anticipated that during future interplanetary operations both terminals will have access to the most precise planetary orbit models as well as the ability to periodically synchronize both relative position and time through the use of the two-way transponder capabilities of the optical link, as discussed in Section 2 of this paper.

As a final note, it has been shown [19] that, because of the R⁻⁴ signal strength dependence of satellite laser ranging (SLR) as opposed to the R⁻² dependence of the two-way transponder and communications applications considered here, certain satellites in the ILRS constellation can mimic the signal strengths expected from various planets throughout the solar system. These are listed in

Table 2. Satellites currently tracked by the International Laser Ranging Service (ILRS) that can mimic interplanetary links in the testing of laser transponders and communications. Because the satellite returns are only visible within a certain range of the source of the laser radiation, the Earth and planetary terminals must be collocated during the planetary simulation.

Satellite	Altitude (km)	Mean Target Cross-Section 106 m2	Minimum Transponder Range (AU)	Maximum Transponder Range (AU)
LAGEOS	6000	15	0.263	0.771
GLONASS	19,000	55	1.38	2.72
GPS	20,000	19	2.60	5.06
LRE (elliptical)	25,000	2	12.52	23.12
Apollo 15 (Moon)	384,000	1400	111.6

.