Study on the Acousto-Optic Coupling Effect of a One-Dimensional Hetero-Optomechanical Crystal Nanobeam Resonator
Abstract
1. Introduction
2. Model and Theory
2.1. Model Design
2.2. Theory
3. Results and Discussion
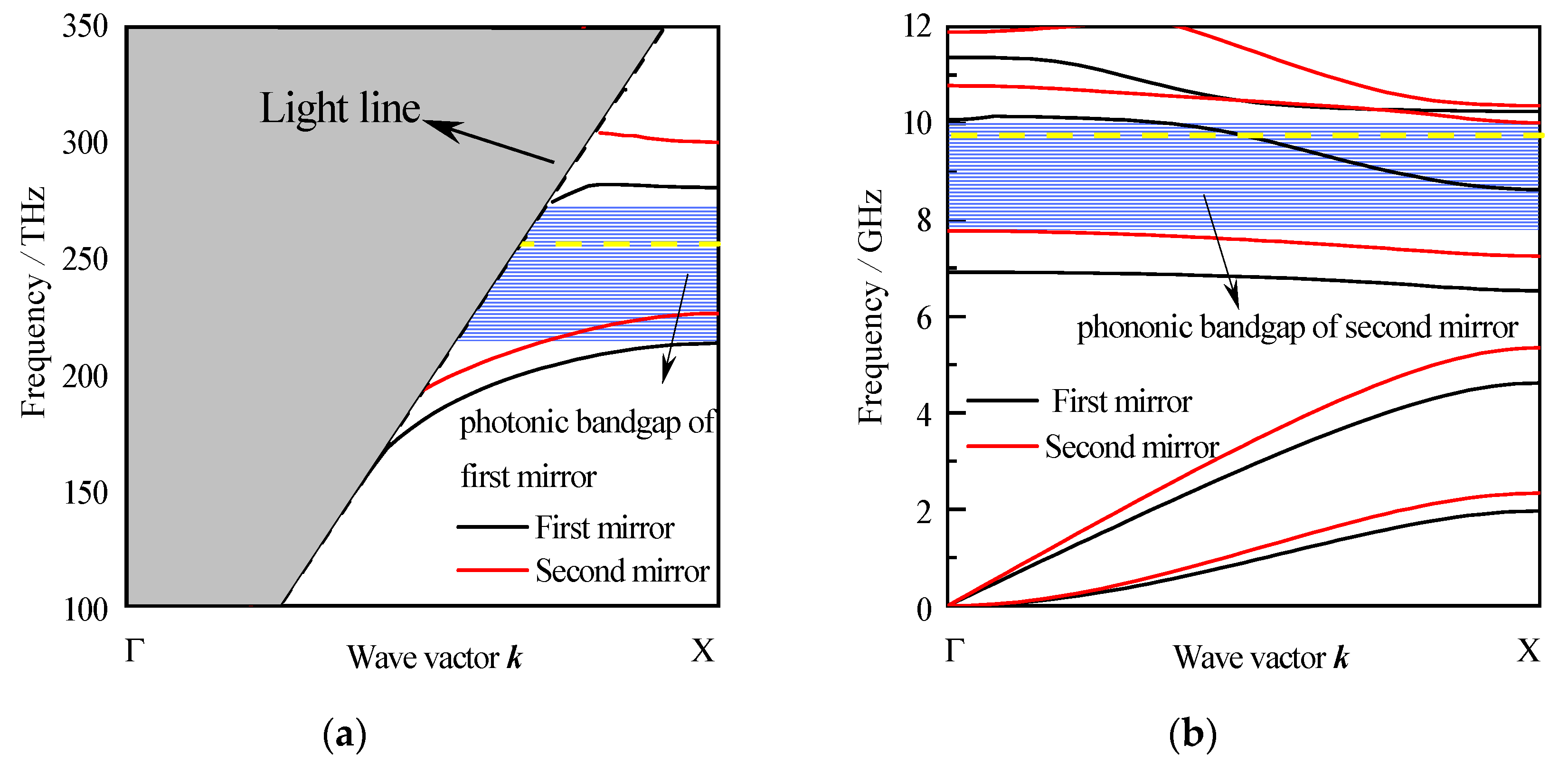
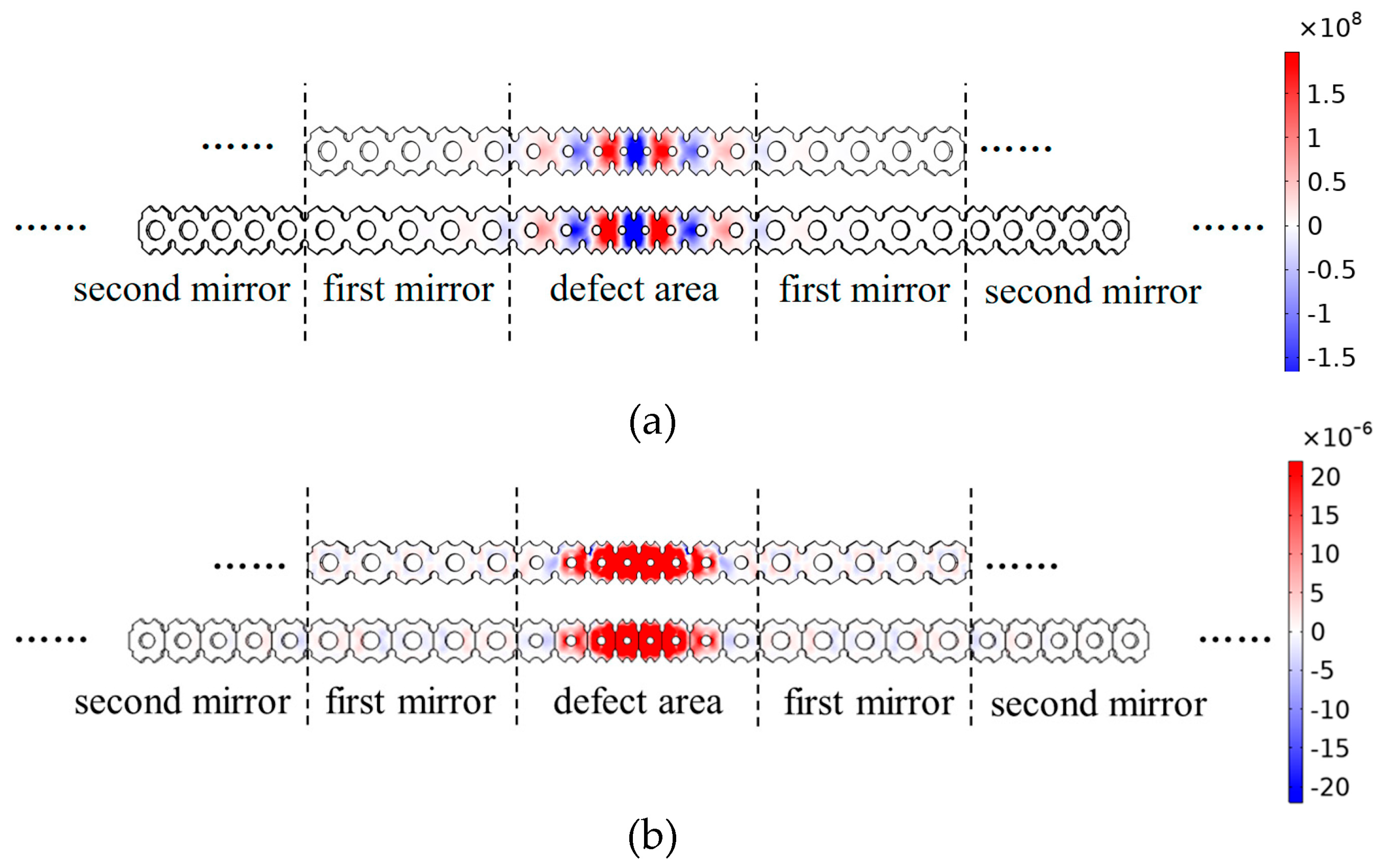
3.1. Band Structure
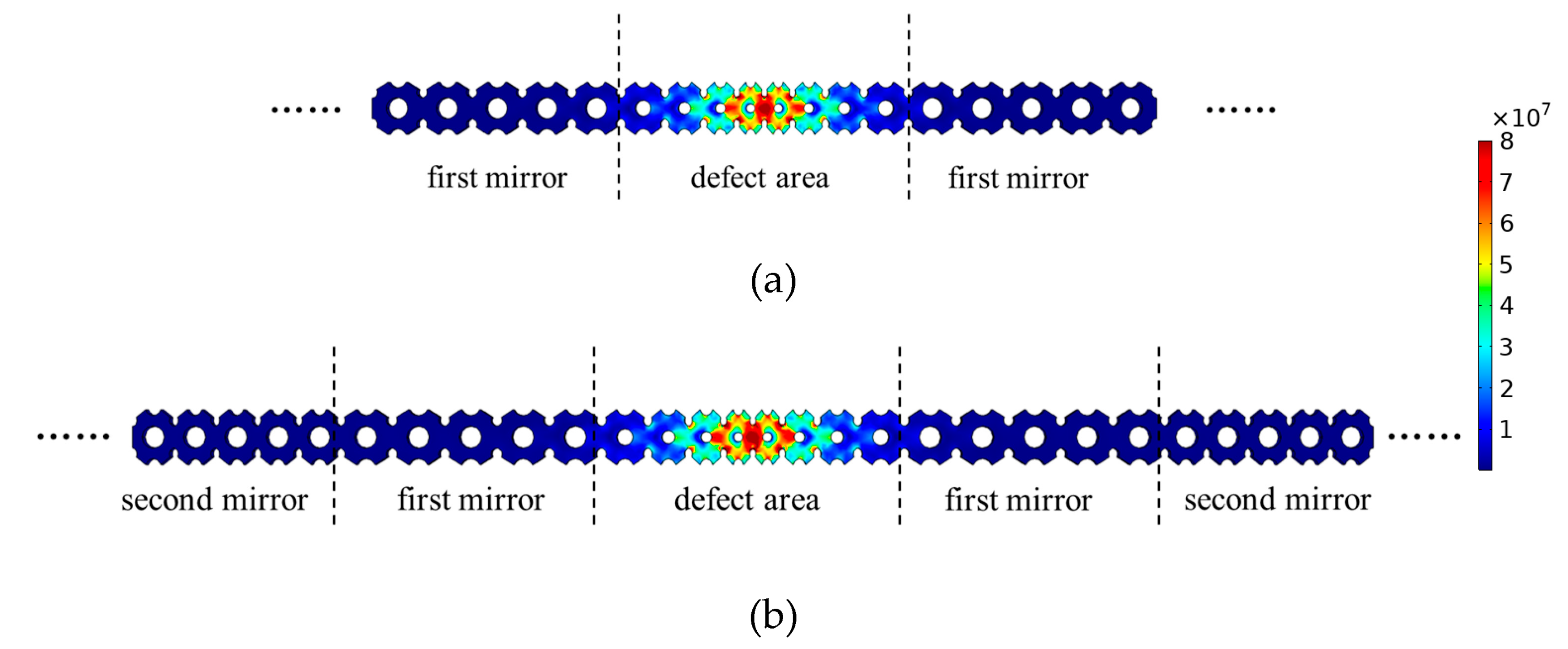
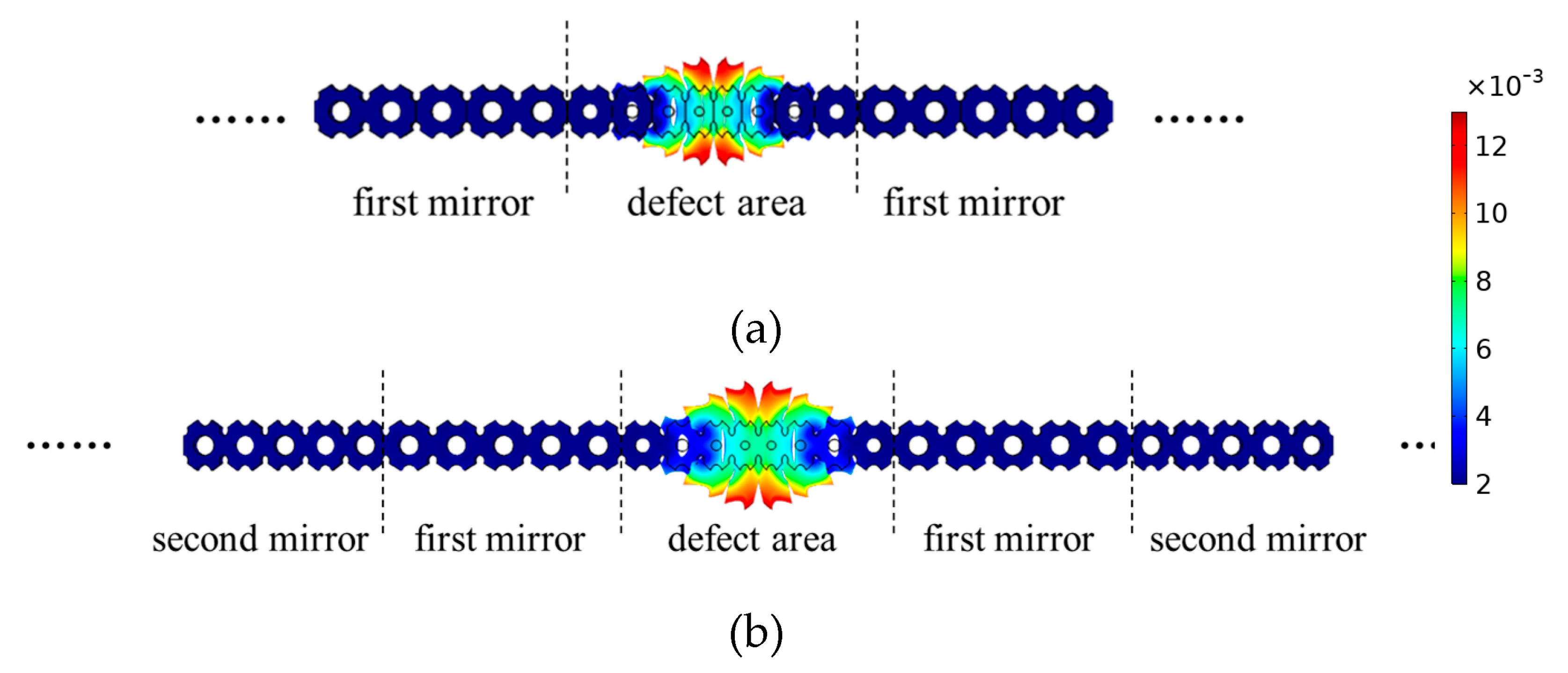
3.2. Modes and Optomechanical Coupling Rate
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- John, S. Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, M.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Nastas, A.; Iovu, M.; Tolstik, A. Effect of Corona Discharge on the Optical Properties of Thin-Film Cu–As2Se3 Structures. Opt. Spectrosc. 2020, 128, 236–240. [Google Scholar] [CrossRef]
- Ren, H.; Matheny, M.; MacCabe, G.; Luo, J.; Pfeifer, H.; Mirhosseini, M.; Painter, O. Two-dimensional optomechanical crystal cavity with high quantum cooperativity. Nat. Commun. 2020, 11, 3373. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.; Mayer Alegre, T.; Safavi-Naeini, A.; Hill, J.; Krause, A.; Gr¨oblacher, S.; Aspelmeyer, M.; Painter, O. Cooling of a levitated nanoparticle to the motional quantum ground state. Nature 2011, 478, 892–895. [Google Scholar]
- Delić, U.; Reisenbauer, M.; Dare, K.; Grass, D.; Vuletić, V.; Kiesel, N.; Aspelmeyer, M. Molecular Asymmetry and Optical Cycling: Laser Cooling Asymmetric Top Molecules. Science 2020, 478, 031022. [Google Scholar]
- Baba, T. Slow light in photonic crystals. Nat. Photonics 2008, 2, 465–473. [Google Scholar] [CrossRef]
- Maldovan, M.; Thomas, E. Simultaneous localization of photons and phonons in two-dimensional periodic structures. Appl. Phys. Lett. 2006, 88, 251907. [Google Scholar] [CrossRef]
- Sadat-Saleh, S.; Benchabane, S.; Baida, F.; Bernal, M.; Laude, V. Tailoring simultaneous photonic and phononic band gaps. J. Appl. Phys. 2009, 106, 074912. [Google Scholar] [CrossRef]
- Eichenfield, M.; Camacho, R.; Chan, J.; Vahala, K.; Painter, O. A picogram and nanometer scale photonic crystal optomechanical cavity. Nature 2009, 459, 550–555. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Chan, J.; Camacho, R.; Vahala, K.; Painter, O. Optomechanical Crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef]
- Chan, J.; Safavi-Naeini, A.; Hill, J.; Meenehan, S.; Painter, O. Optimized optomechanical crystal cavity with acoustic radiation shield. Appl. Phys. Lett. 2012, 101, 081115. [Google Scholar] [CrossRef]
- Lin, T.; Chang, C.; Hsu, J. Strong optomechanical coupling of light and highly confined acoustic phonons in slot dual-beam phoxonic crystal cavities. J. Appl. Phys. 2019, 126, 064901. [Google Scholar] [CrossRef]
- Chiu, C.; Chen, W.; Sung, K.; Hsiao, F. High-efficiency acousto-optic coupling in phoxonic resonator based on silicon fishbone nanobeam cavity. Opt. Express 2017, 25, 6076–6091. [Google Scholar] [CrossRef] [PubMed]
- Oudich, M.; El-Jallal, S.; Pennec, Y.; Djafari-Rouhani, B.; Gomis-Bresco, J.; Navarro-Urrios, D.; Sotomayor Torres, C.; Martínez, A.; Makhoute, A. Optomechanic interaction in a corrugated phoxonic nanobeam cavity. Phys. Rev. B 2014, 89, 245122. [Google Scholar] [CrossRef]
- Ma, T.; Zou, K.; Wang, Y.; Zhang, C.; Su, X. Acousto-optical interaction of surface acoustic and optical waves in a two-dimensional phoxonic crystal hetero-structure cavity. Opt. Express 2014, 22, 28443–28451. [Google Scholar] [CrossRef]
- Huang, Z.; Cui, K.; Li, Y.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y. Strong Optomechanical Coupling in Nanobeam Cavities based on Hetero Optomechanical Crystals. Sci. Rep. 2015, 5, 15964. [Google Scholar] [CrossRef]
- Cui, K.; Huang, Z.; Wu, N.; Xu, Q.; Pan, F.; Xiong, J.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y. Phonon lasing in a hetero optomechanical crystal cavity. Photonics Res. 2021, 9, 937–943. [Google Scholar] [CrossRef]
- Wu, N.; Cui, K.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y. Hetero-Optomechanical Crystal Zipper Cavity for Multimode Optomechanics. Photonics 2022, 9, 78. [Google Scholar] [CrossRef]
- Hopcroft, M.; Nix, W.; Kenny, T. What is the Young’s Modulus of Silicon? J. Microelectromech. S. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Aram, M.; Khorasani, S. Optical wave evolution due to interaction with elastic wave in a phoxonic crystal slab waveguide. Appl. Phys. B 2017, 123, 218. [Google Scholar] [CrossRef]
- Johnson, S.; Ibanescu, M.; Skorobogatiy, M.; Weisberg, O.; Joannopoulos, J.; Fink, Y. Perturbation theory for Maxwell’s equations with shifting material boundaries. Phys. Rev. E 2022, 65, 066611. [Google Scholar] [CrossRef] [PubMed]
- Biegelsen, D. Photoelastic Tensor of Silicon and the Volume Dependence of the Average Gap. Phys. Rev. Lett. 1974, 52, 1196–1199. [Google Scholar] [CrossRef]
- Presnov, D.; Kafanov, S.; Dorofeev, A.; Bozhev, I.; Trifonov, A.; Pashkin, Y.; Krupenin, V. High quality factor mechanical resonance in a silicon nanowire. JETP Lett. 2018, 108, 492–497. [Google Scholar] [CrossRef]
- Jaberzadeh, M.; Li, B.; Tan, K. Wave propagation in an elastic metamaterial with anisotropic effective mass density. Wave Motion 2019, 89, 131–141. [Google Scholar] [CrossRef]
- Li, Y.; Cui, K.; Feng, X.; Huang, Y.; Huang, Z.; Liu, F.; Zhang, W. Optomechanical crystal nanobeam cavity with high optomechanical coupling rate. J. Optics 2015, 17, 045001. [Google Scholar] [CrossRef]
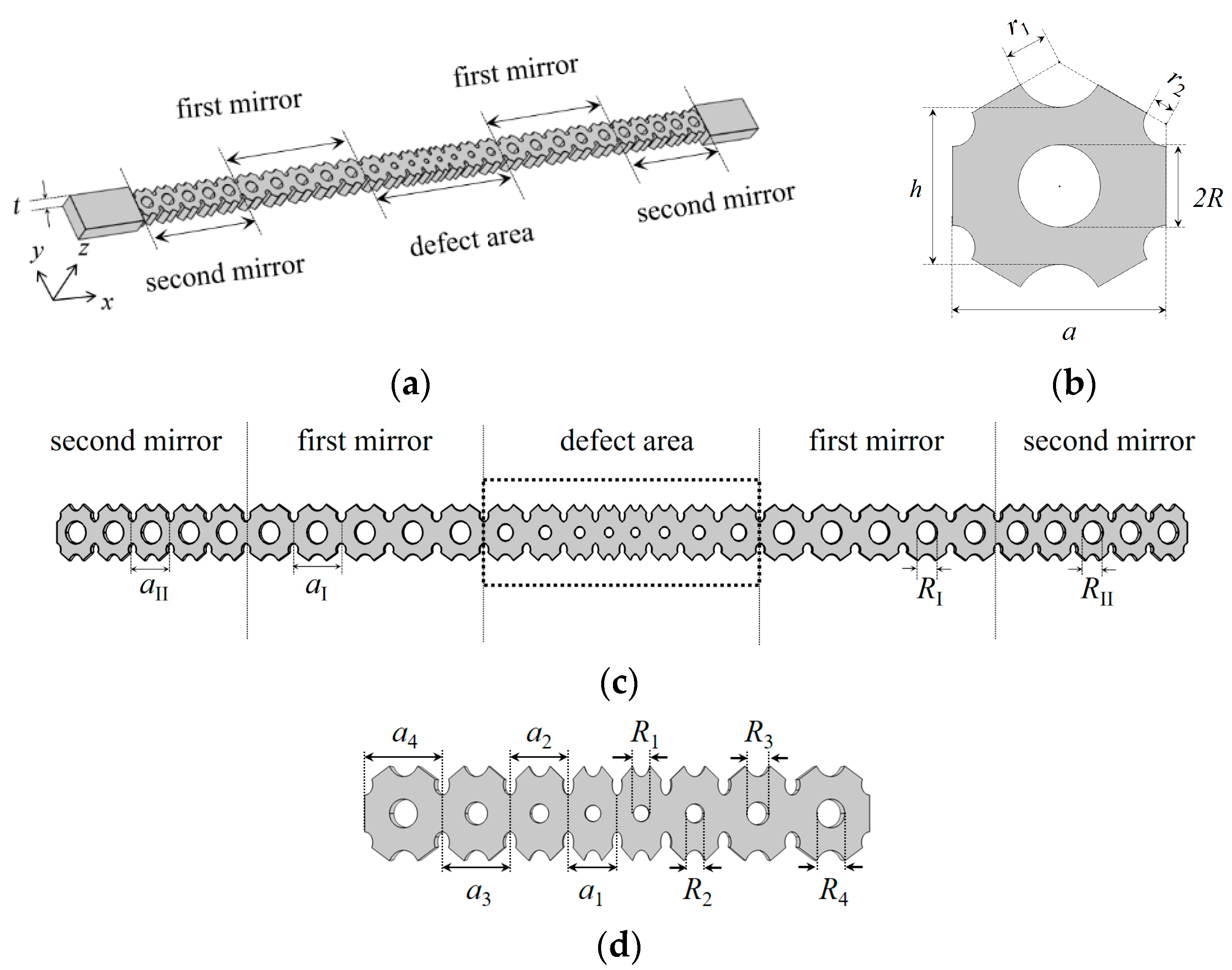
| Geometry Parameters (nm) | ||||||
|---|---|---|---|---|---|---|
| r1 | r2 | aI | aII | RI | RII | t |
| 91 | 45 | 390 | 331 | 83 | 71 | 230 |
| Structures | gmb (MHz) | gpe (MHz) | g0 (MHz) | Q | meff (fg) |
|---|---|---|---|---|---|
| Single-mirror structure | −1.04 | −2.64 | −3.68 | 1.25 × 105 | 42.75 |
| Heterostructure | −1.08 | −2.73 | −3.81 | 3.18 × 106 | 43.29 |
| Structures | g0 (MHz) | Structures | g0 (MHz) |
|---|---|---|---|
| Rectangular holes [11] | 0.22 | Circular holes [26] | 1.16 |
| Oval holes [12] | 1.10 | Round hole heterostructure [17] | 1.31 |
| Oscillator type [15] | 0.54 | Fishbone type [14] | 1.89 |
| Slit type [13] | 2.80 | The structure proposed in this paper | 3.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, J.; Wen, X.; Sun, X.; Liu, X.; Wang, Y.; Han, G. Study on the Acousto-Optic Coupling Effect of a One-Dimensional Hetero-Optomechanical Crystal Nanobeam Resonator. Photonics 2023, 10, 197. https://doi.org/10.3390/photonics10020197
Lan J, Wen X, Sun X, Liu X, Wang Y, Han G. Study on the Acousto-Optic Coupling Effect of a One-Dimensional Hetero-Optomechanical Crystal Nanobeam Resonator. Photonics. 2023; 10(2):197. https://doi.org/10.3390/photonics10020197
Chicago/Turabian StyleLan, Jianxu, Xiaodong Wen, Xiaowei Sun, Xixuan Liu, Yiwen Wang, and Genliang Han. 2023. "Study on the Acousto-Optic Coupling Effect of a One-Dimensional Hetero-Optomechanical Crystal Nanobeam Resonator" Photonics 10, no. 2: 197. https://doi.org/10.3390/photonics10020197
APA StyleLan, J., Wen, X., Sun, X., Liu, X., Wang, Y., & Han, G. (2023). Study on the Acousto-Optic Coupling Effect of a One-Dimensional Hetero-Optomechanical Crystal Nanobeam Resonator. Photonics, 10(2), 197. https://doi.org/10.3390/photonics10020197




