Analysis of Crosstalk in Multicore Fibers: Statistical Distributions and Analytical Expressions
Abstract
1. Introduction
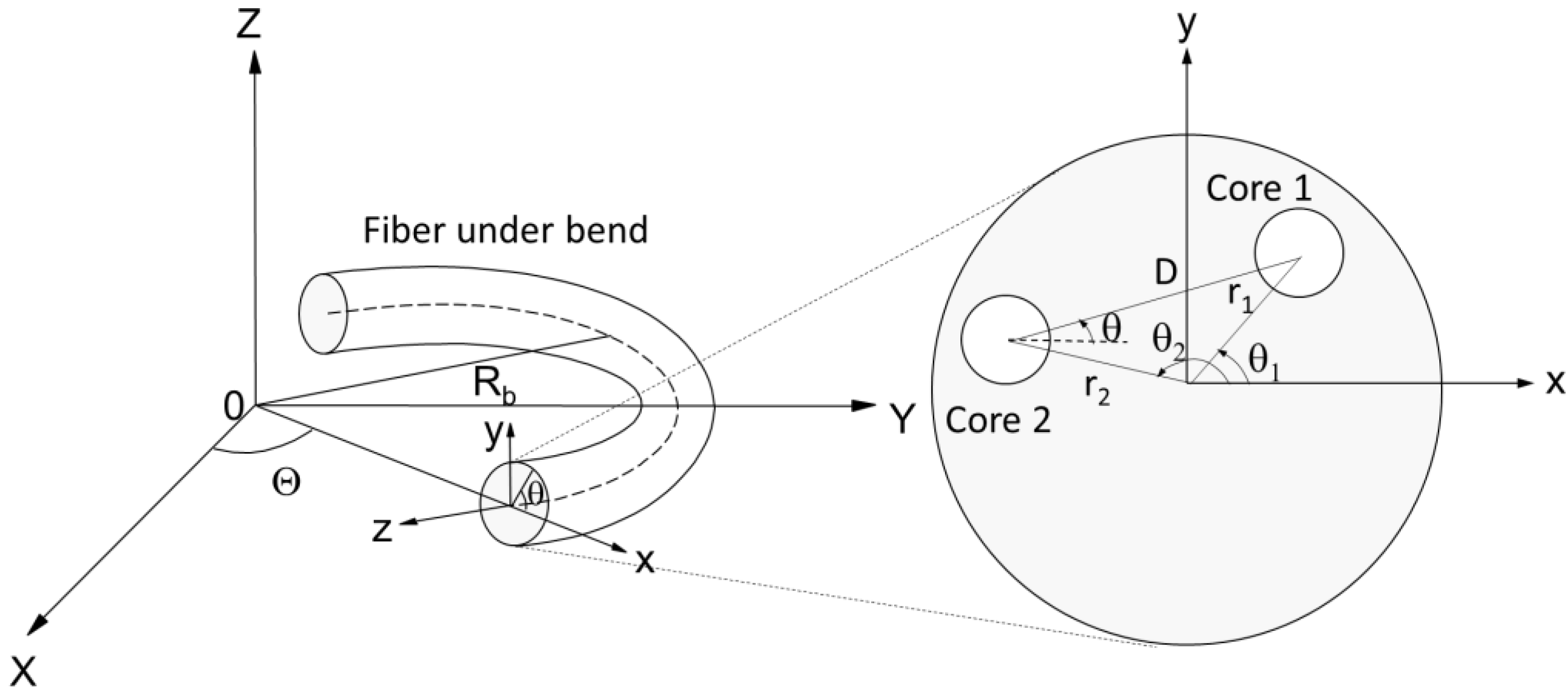
2. General Crosstalk Formulation Using CMT
3. Analytical Expressions for Average Crosstalk
3.1. Derivation of Analytical Expressions
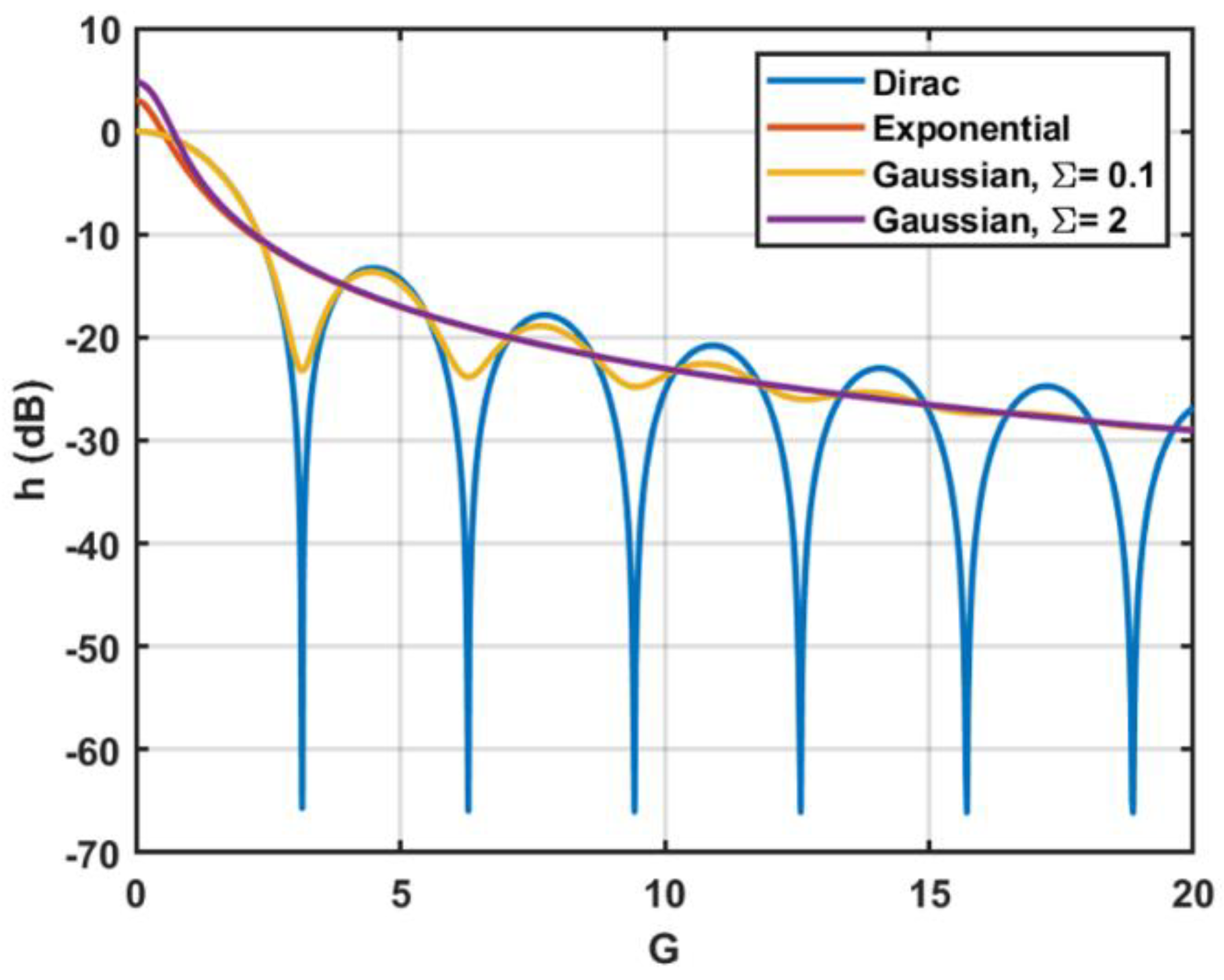
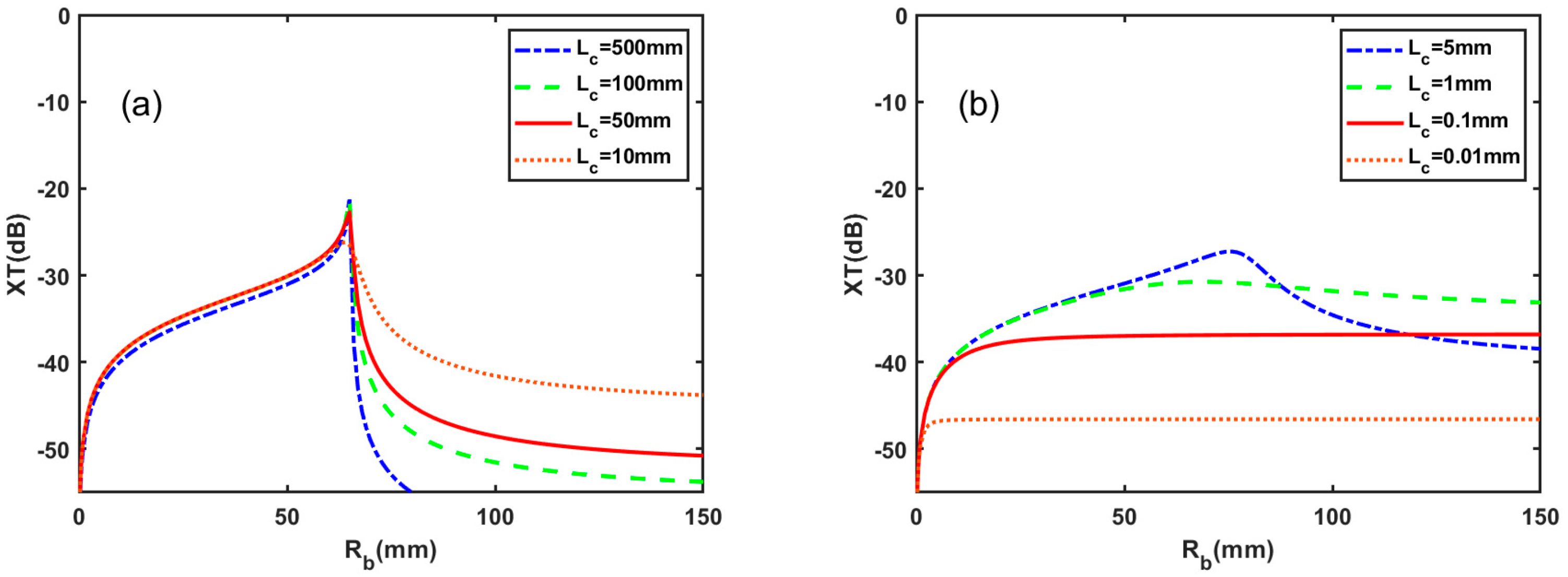
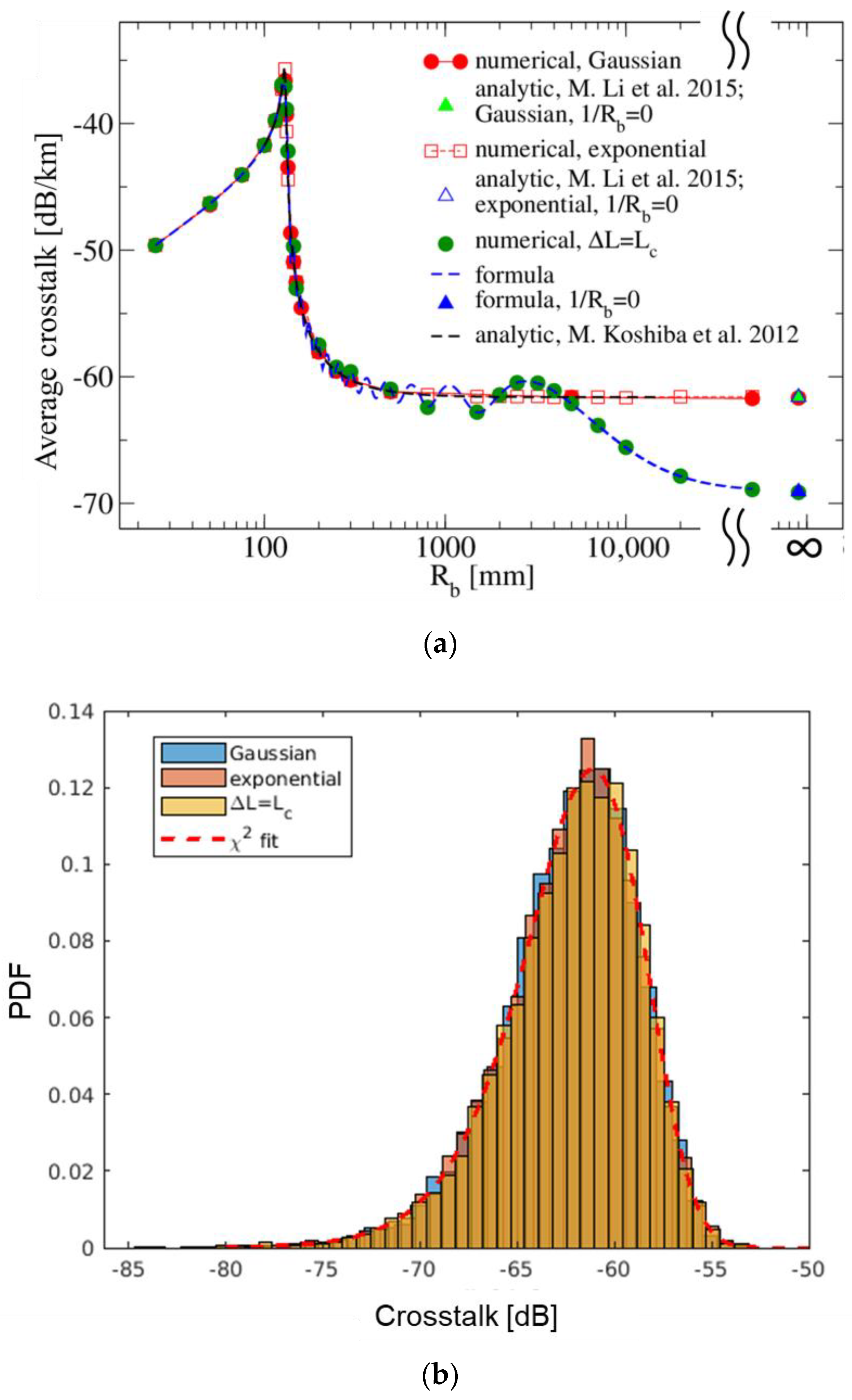
3.2. Comparison of Average Crosstalk for Different Statistical Distributions
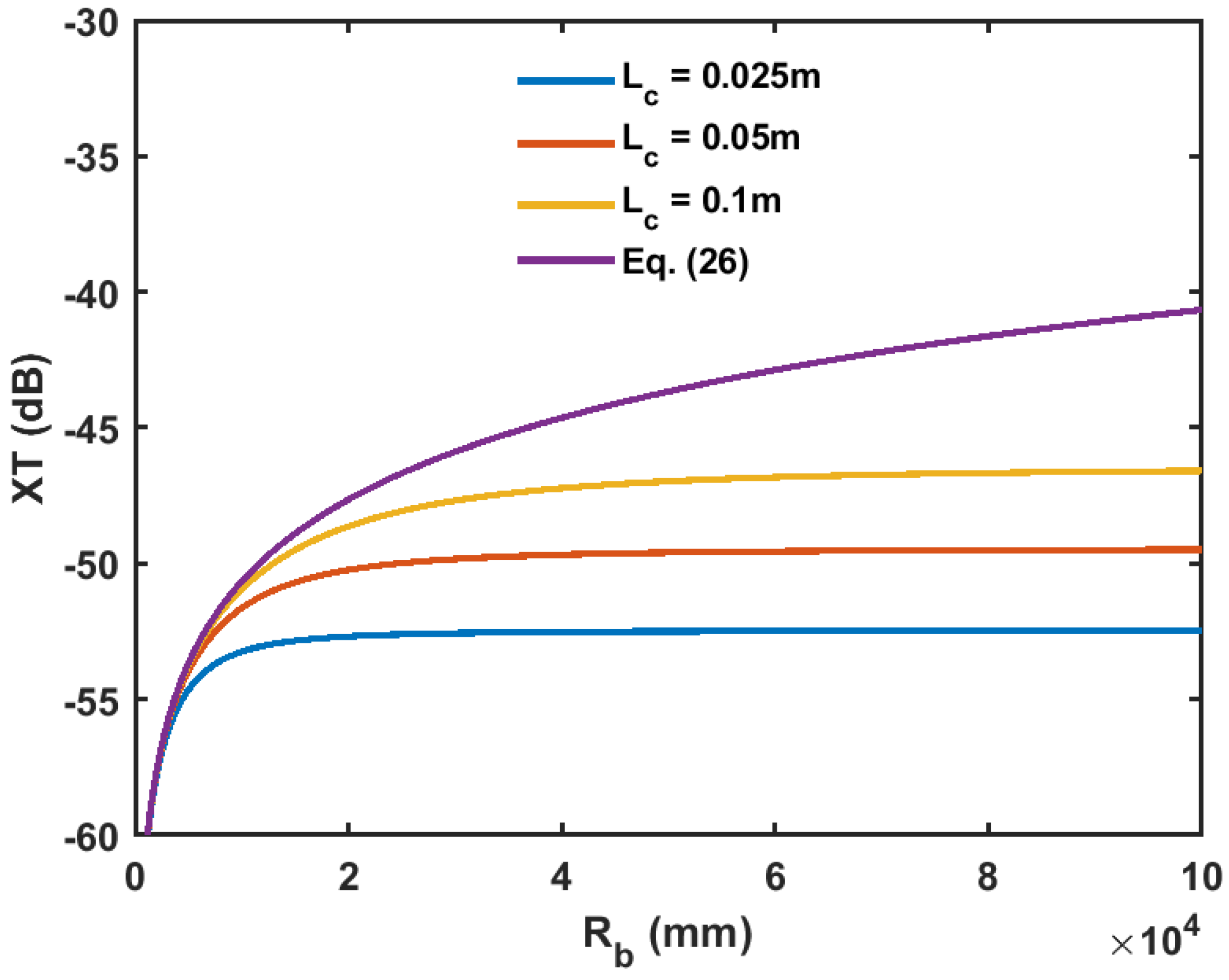
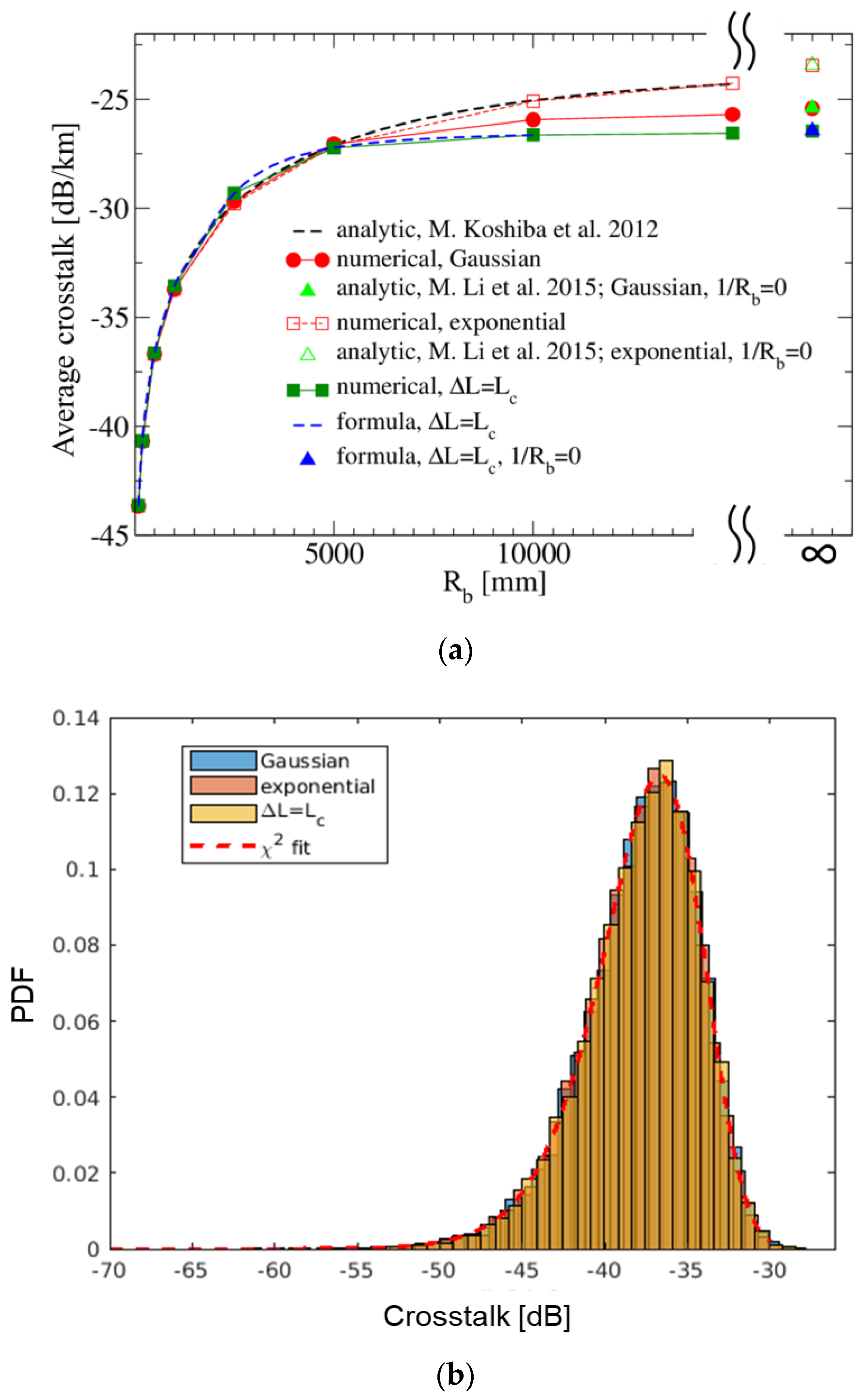
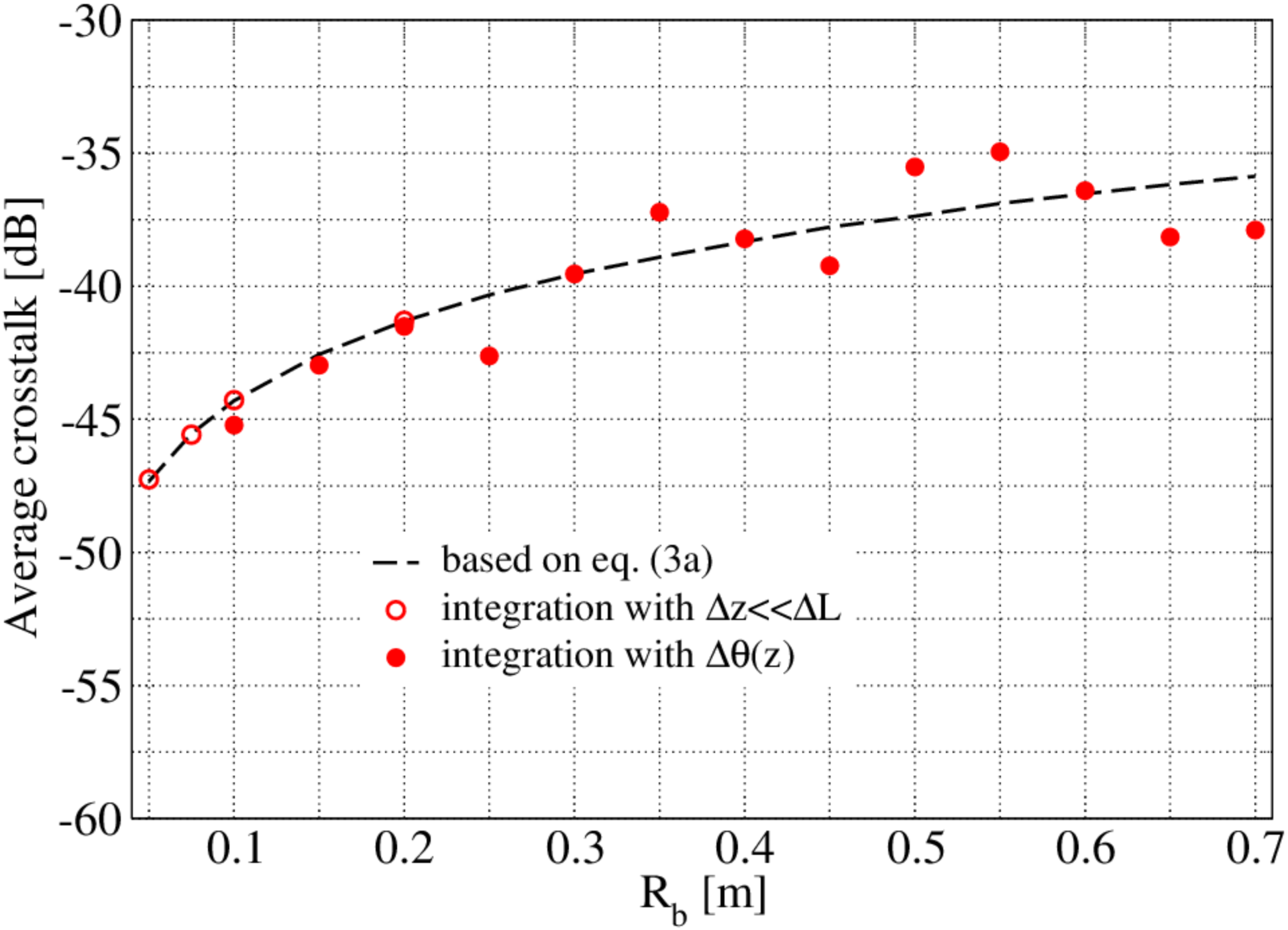
3.3. Comparison with the Results in the Literature for the Heterogeneous Case
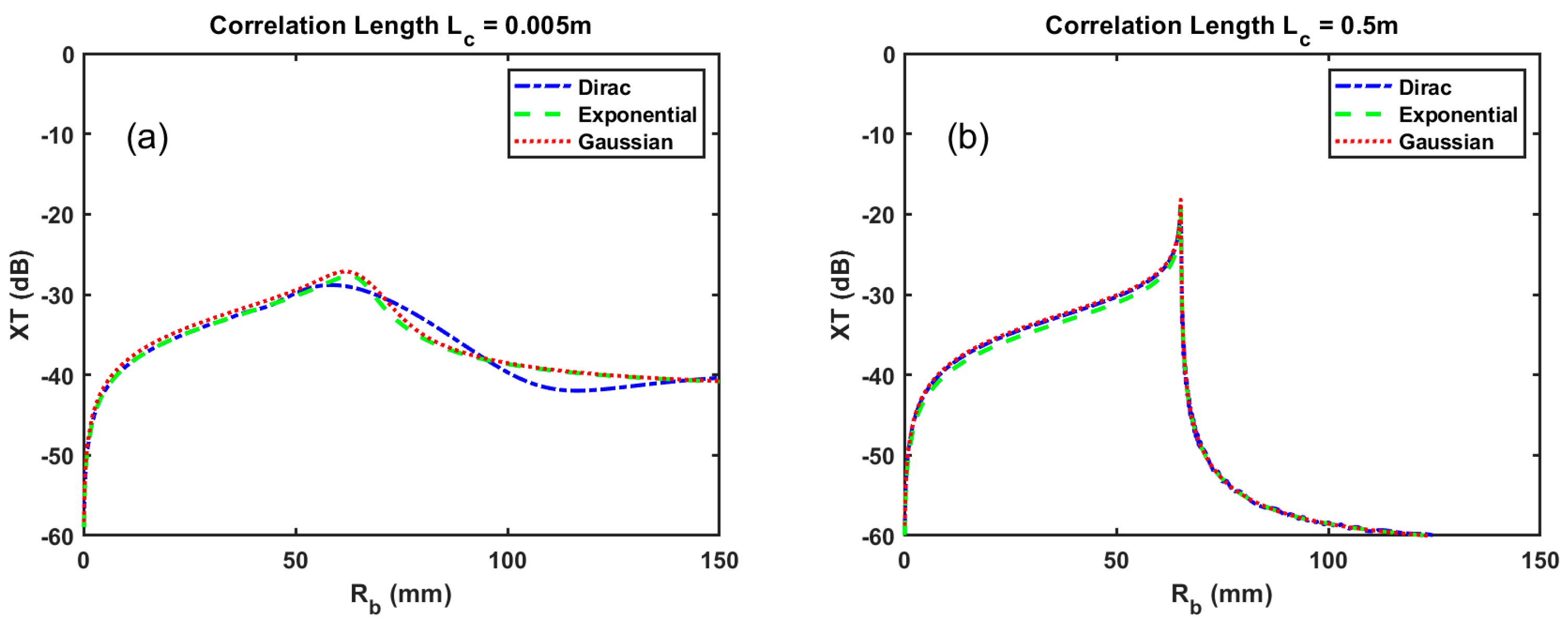
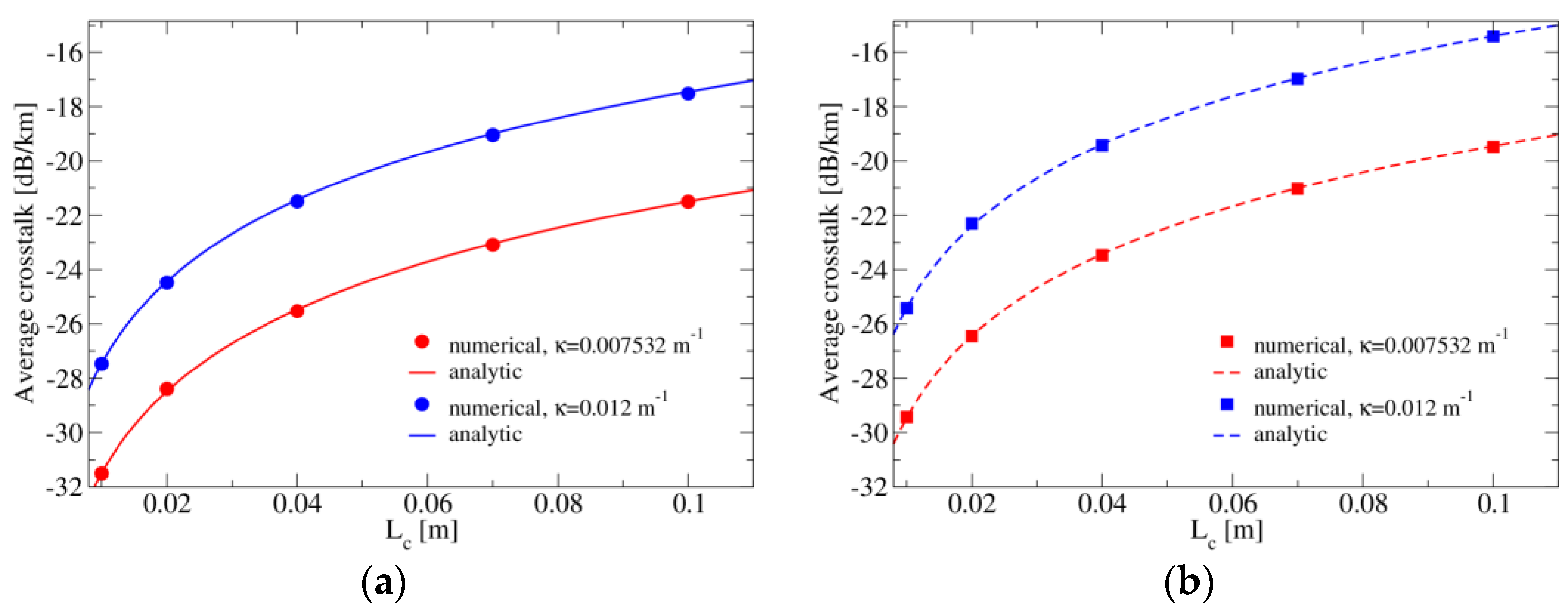
4. Numerical Simulations and Comparisons with Analytical Expressions
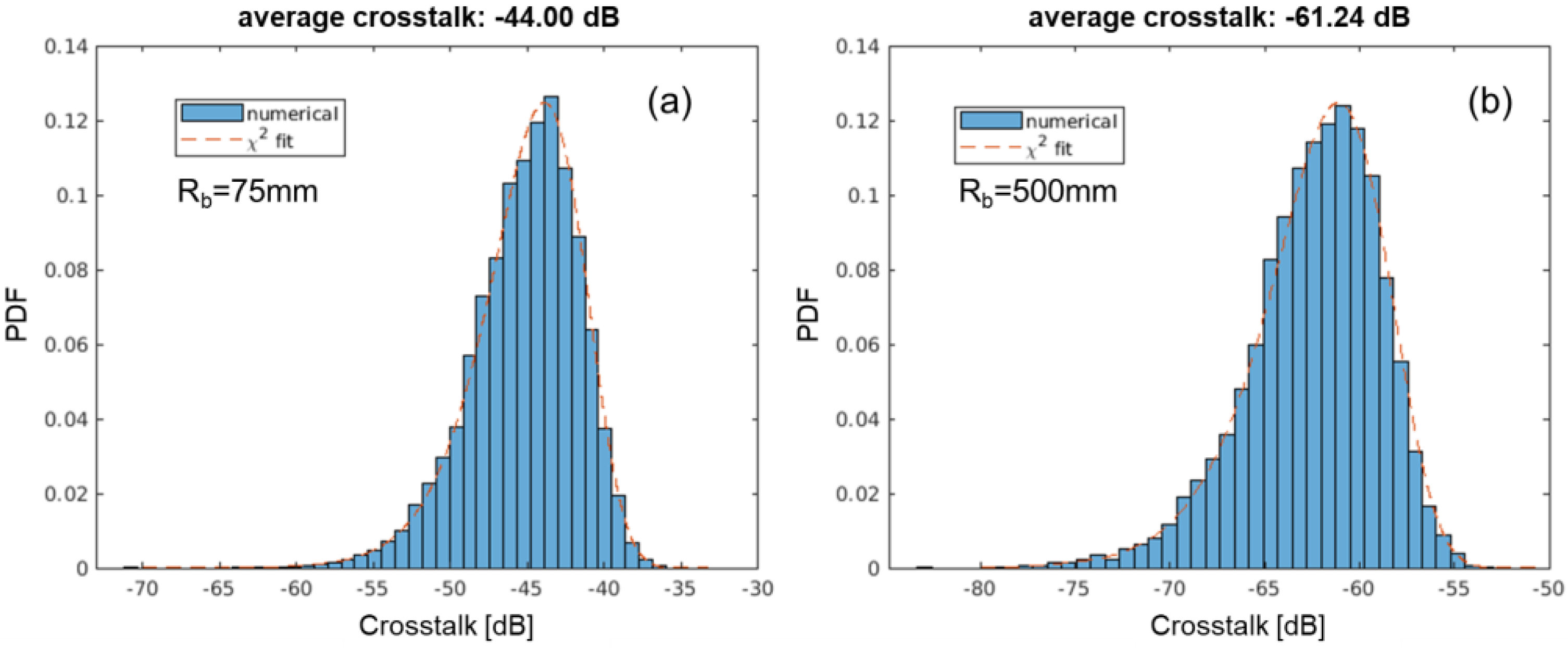
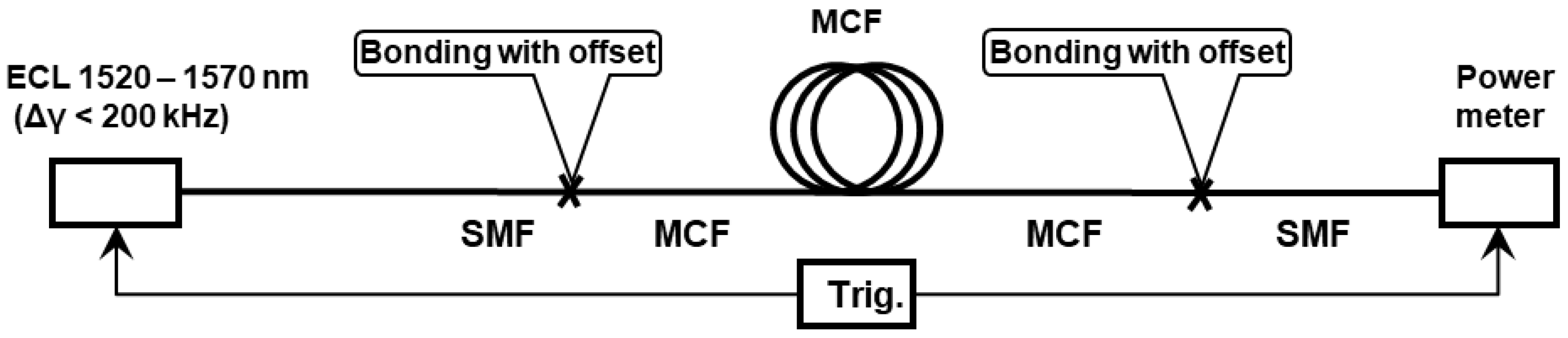
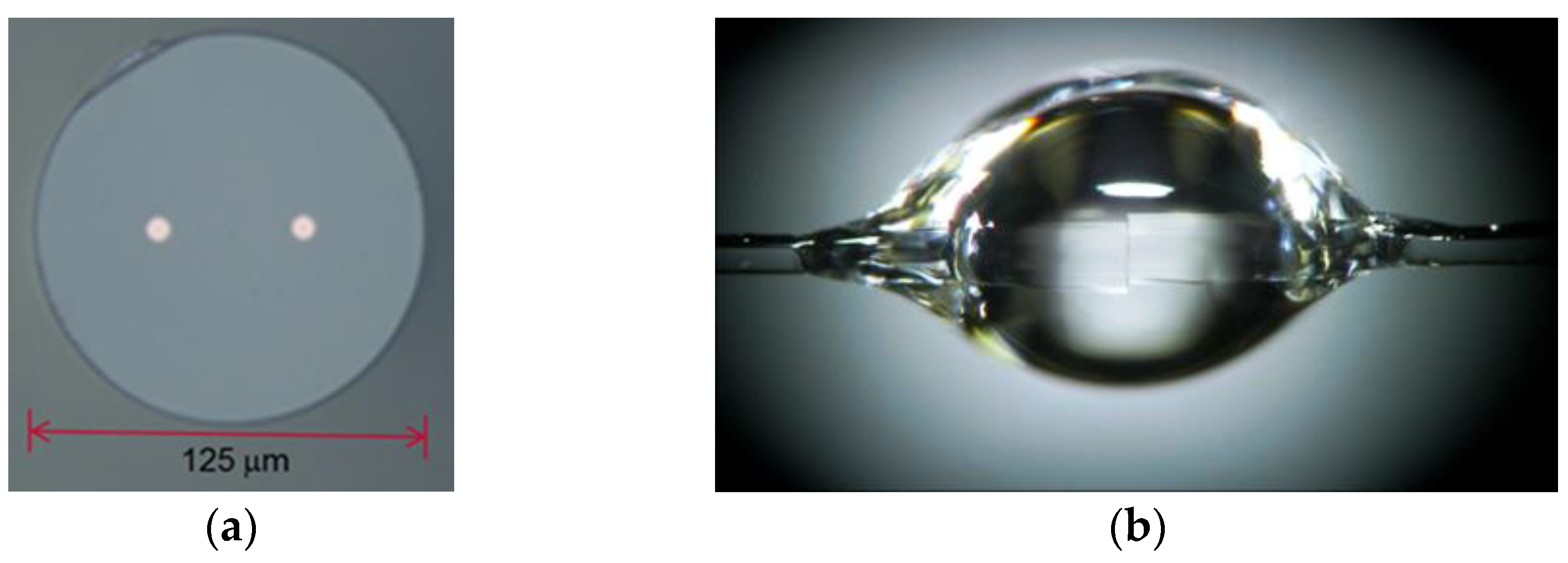
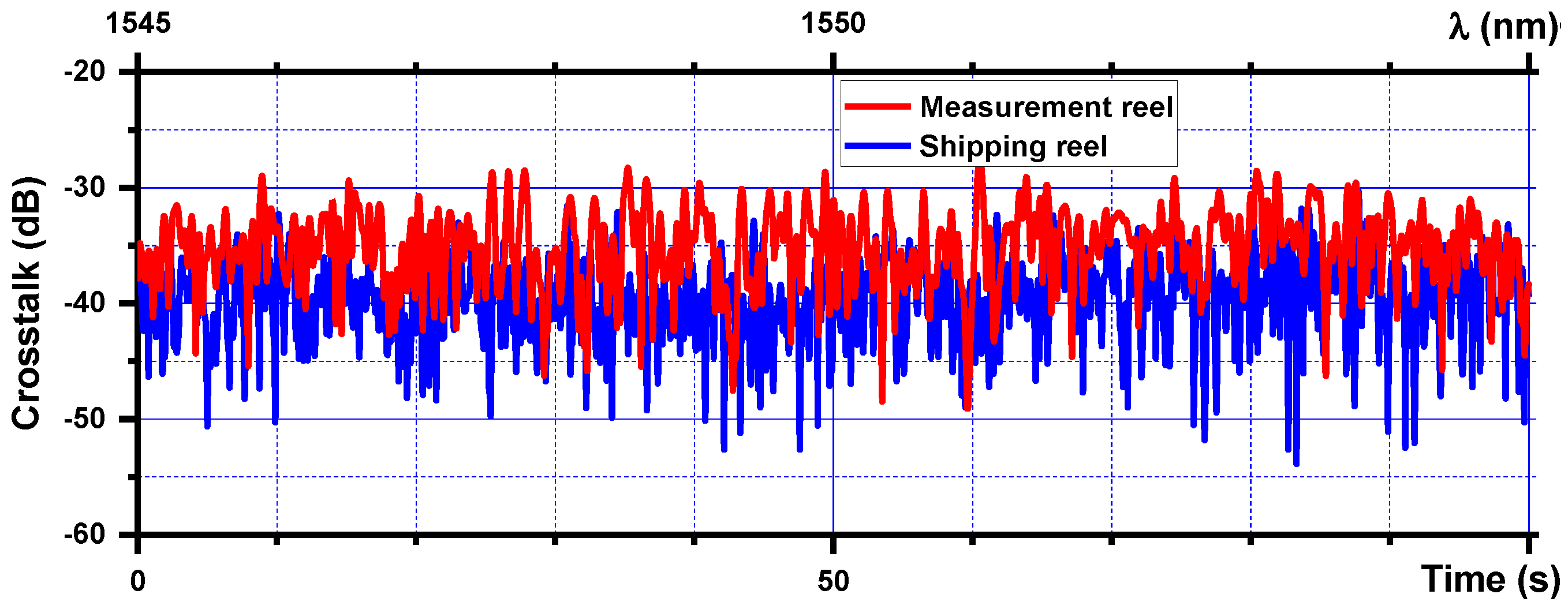
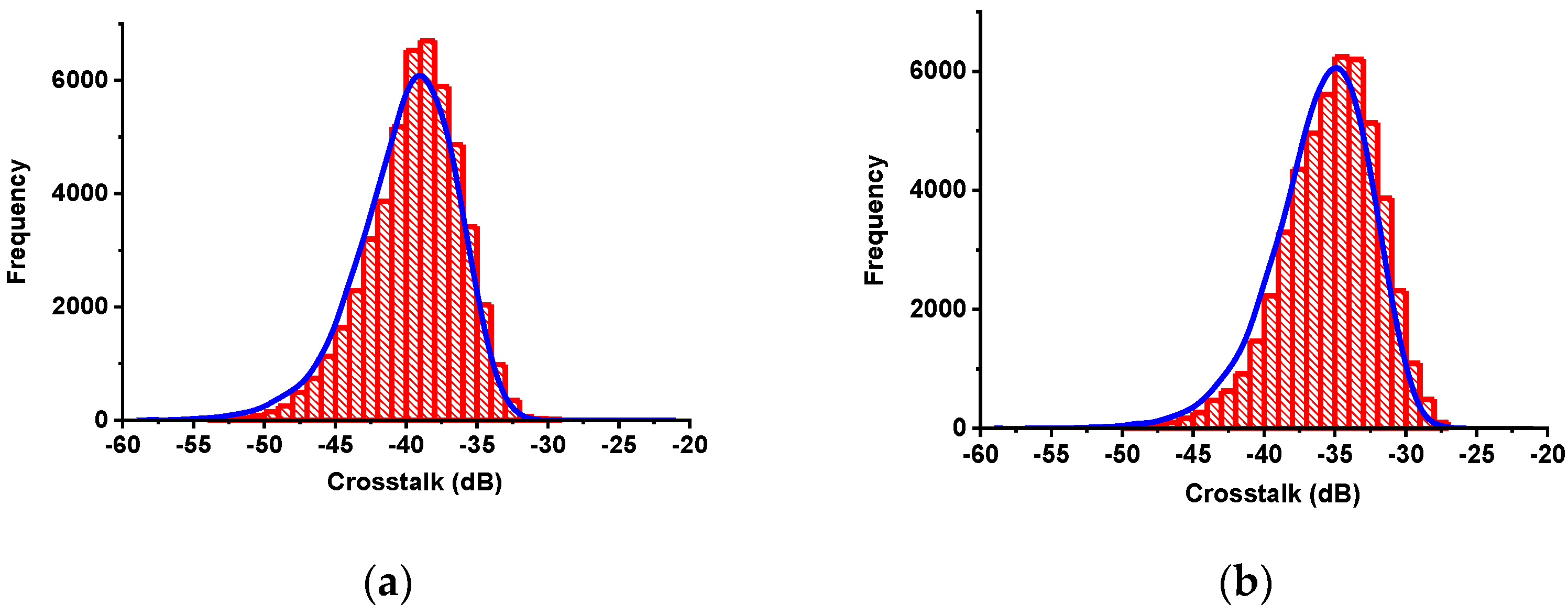
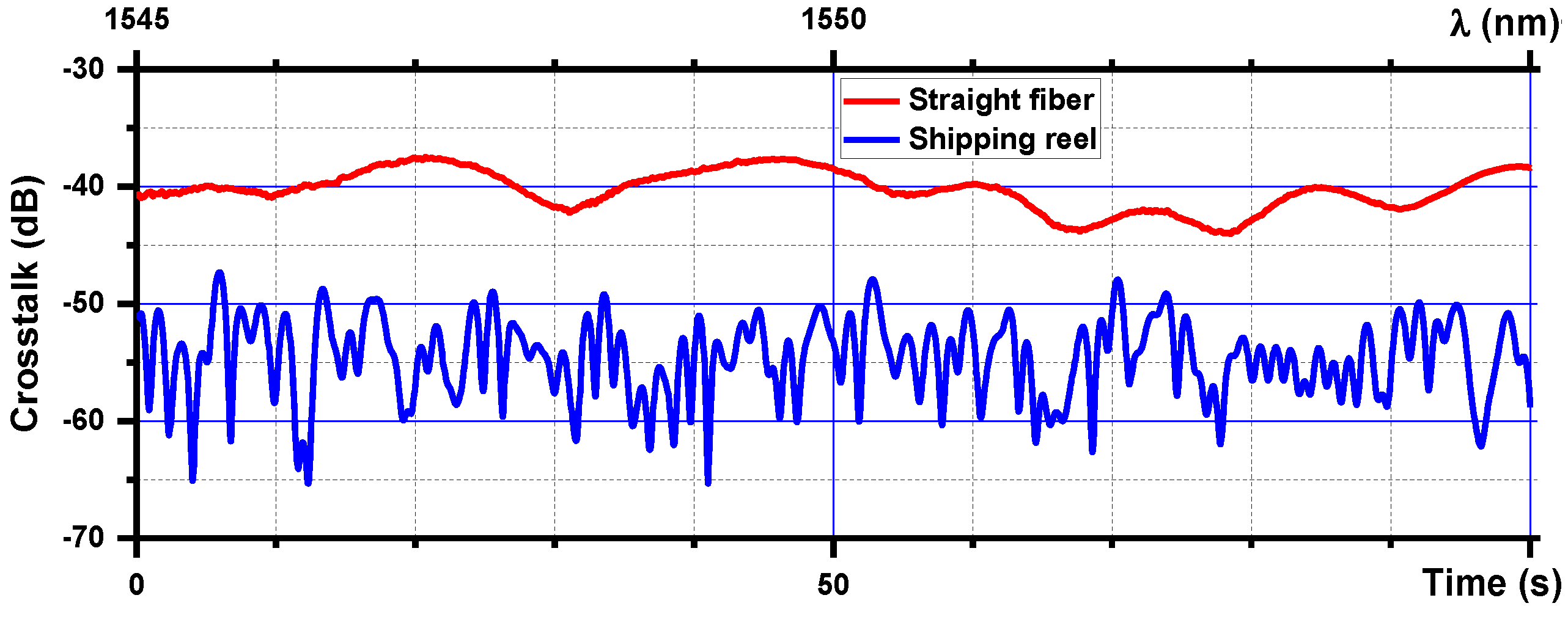
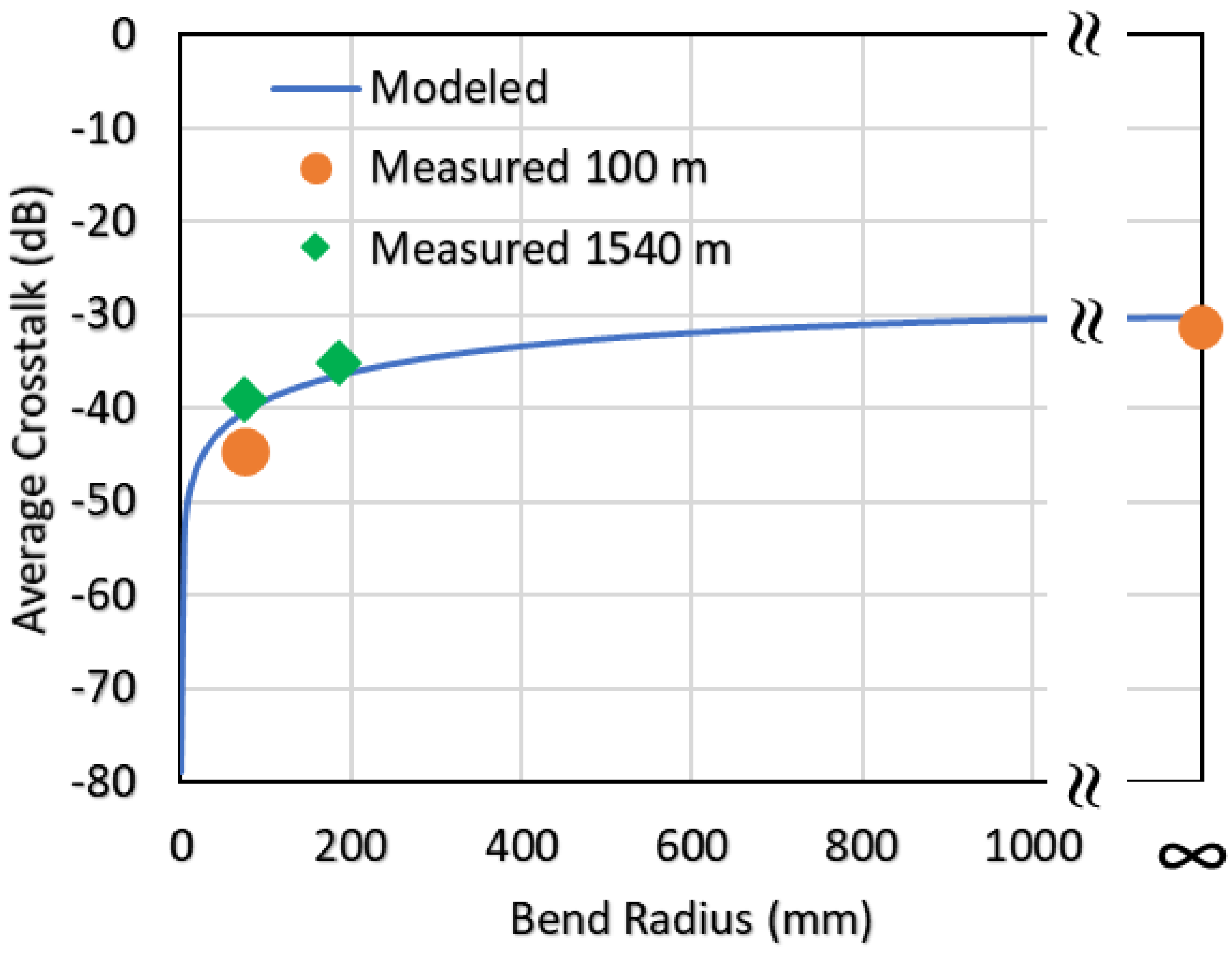
5. Experimental Characterization of MCF Crosstalk Statistical Distributions
6. Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Nakajima, K.; Sillard, P.; Richardson, D.; Li, M.; Essiambre, R.; Matsuo, S. Transmission media for an SDM-based optical communication system. IEEE Commun. Mag. 2015, 53, 44–51. [Google Scholar] [CrossRef]
- Li, M.J.; Hayashi, T. Chapter 1—Advances in Low-Loss, Large-Area, and Multicore Fibers; Willner, A.E., Ed.; Optical Fiber Telecommunications VII; Academic Press: Cambridge, MA, USA, 2020; pp. 3–50. ISBN 9780128165027. [Google Scholar] [CrossRef]
- Kunimasa, S.; Shoichiro, M. Multicore fibers for large capacity transmission. Nanophotonics 2013, 2, 441–454. [Google Scholar] [CrossRef]
- Butler, D.L.; Li, M.-J.; Li, S.; Geng, Y.; Khrapko, R.R.; Modavis, R.A.; Nazarov, V.N.; Koklyushkin, A.V. Space Division Multiplexing in Short Reach Optical Interconnects. J. Light. Technol. 2017, 35, 677–682. [Google Scholar] [CrossRef]
- Fini, J.M.; Zhu, B.; Taunay, T.F.; Yan, M.F. Statistics of crosstalk in bent multicore fibers. Opt. Express 2010, 18, 15122–15129. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Taru, T.; Shimakawa, O.; Sasaki, T.; Sasaoka, E. Design and fabrication of ultra-low crosstalk and low-loss multi-core fiber. Opt. Express 2011, 19, 16576–16592. [Google Scholar] [CrossRef] [PubMed]
- Koshiba, M.; Saitoh, K.; Takenaga, K.; Matsuo, S. Multi-core fiber design and analysis: Coupled-mode theory and coupled-power theory. Opt. Express 2011, 19, B102–B111. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Li, S.; Modavis, R.A. Coupled Mode Analysis of Crosstalk in Multicore Fiber with Random Perturbations. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 22–26 March 2015; pp. 1–3. [Google Scholar]
- Nazarov, V.; Kuchinsky, S.A.; Zakharian, A.R.; Li, M.J. Crosstalk Statistical Distributions in Multicore Fibers Under Different Deployment Conditions. In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), Washington, DC, USA, 6–10 June 2021. [Google Scholar]
- Takenaga, K.; Arakawa, Y.; Tanigawa, S.; Guan, N.; Matsuo, S.; Saitoh, K.; Koshiba, M. An investigation on crosstalk in multi-core fibers by introducing random fluctuation along longitudinal direction. IEICE Trans. Commun. 2011, E94-B, 409–416. [Google Scholar] [CrossRef]
- Koshiba, M.; Saitoh, K.; Takenaga, K.; Matsuo, S. Analytical Expression of Average Power-Coupling Coefficients for Estimating Intercore Crosstalk in Multicore Fibers. IEEE Photonics J. 2012, 4, 1987–1995. [Google Scholar] [CrossRef]
- Antonelli, C.; Riccardi, G.; Hayashi, T.; Mecozzi, A. Role of polarization-mode coupling in the crosstalk between cores of weakly coupled multi-core fibers. Opt. Exp. 2020, 28, 12847–12861. [Google Scholar] [CrossRef] [PubMed]
- Cartaxo, A.V.P.; Morgado, J.A.T. New Expression for Evaluating the Mean Crosstalk Power in Weakly-Coupled Multi-Core Fibers. J. Light. Technol. 2021, 39, 1830–1842. [Google Scholar] [CrossRef]
- Wang, W.; Xiang, L.; Shao, W.; Shen, G. Stochastic Crosstalk Analyses for Real Weakly Coupled Multicore Fibers Using a Universal Semi-Analytical Model. J. Light. Technol. 2021, 39, 4503–4510. [Google Scholar] [CrossRef]
- Marcuse, D. Theory of Dielectric Optical Waveguides, 2nd ed.; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Hayashi, T.; Taru, T.; Shimakawa, O.; Sasaki, T.; Sasaoka, E. Characterization of Crosstalk in Ultra-Low-Crosstalk Multi-Core Fiber. J. Light. Technol. 2012, 30, 583–589. [Google Scholar] [CrossRef]
- Gan, L.; Shen, L.; Tang, M.; Xing, C.; Li, Y.; Ke, C.; Tong, W.; Li, B.; Fu, S.; Liu, D. Investigation of channel model for weakly coupled multicore fiber. Opt. Express 2018, 26, 5182–5199. [Google Scholar] [CrossRef] [PubMed]
- Alves, T.; Soeiro, R.; Cartaxo, A. Probability Distribution of Intercore Crosstalk in Weakly Coupled MCFs With Multiple Interferers. IEEE Photonics Technol. Lett. 2019, 31, 651–654. [Google Scholar] [CrossRef]
- Hayashi, T.; Sasaki, T.; Sasaoka, E.; Saitoh, K.; Koshiba, M. Physical interpretation of intercore crosstalk in multicore fiber: Effects of macrobend, structure fluctuation, and microbend. Opt. Express 2013, 21, 5401–5412. [Google Scholar] [CrossRef] [PubMed]
- Alves, T.M.F.; Cartaxo, A.V.T.; Rebola, J.L. Stochastic Properties and Outage in Crosstalk-Impaired OOK-DD Weakly-Coupled MCF Applications with Low and High Skew × Bit-Rate. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 4300208. [Google Scholar] [CrossRef]
- Cartaxo, A.V.T.; Alves, T.F.M. Discrete changes model of inter-core crosstalk of real homogeneous multi-core fibers. J. Light. Technol. 2017, 35, 2398–2408. [Google Scholar] [CrossRef]
- Soeiro, R.O.J.; Alves, T.M.F.; Cartaxo, A.V.T. Dual Polarization Discrete Changes Model of Inter-Core Crosstalk in Multi-Core Fibers. IEEE Photonics Technol. Lett. 2017, 29, 15. [Google Scholar] [CrossRef]


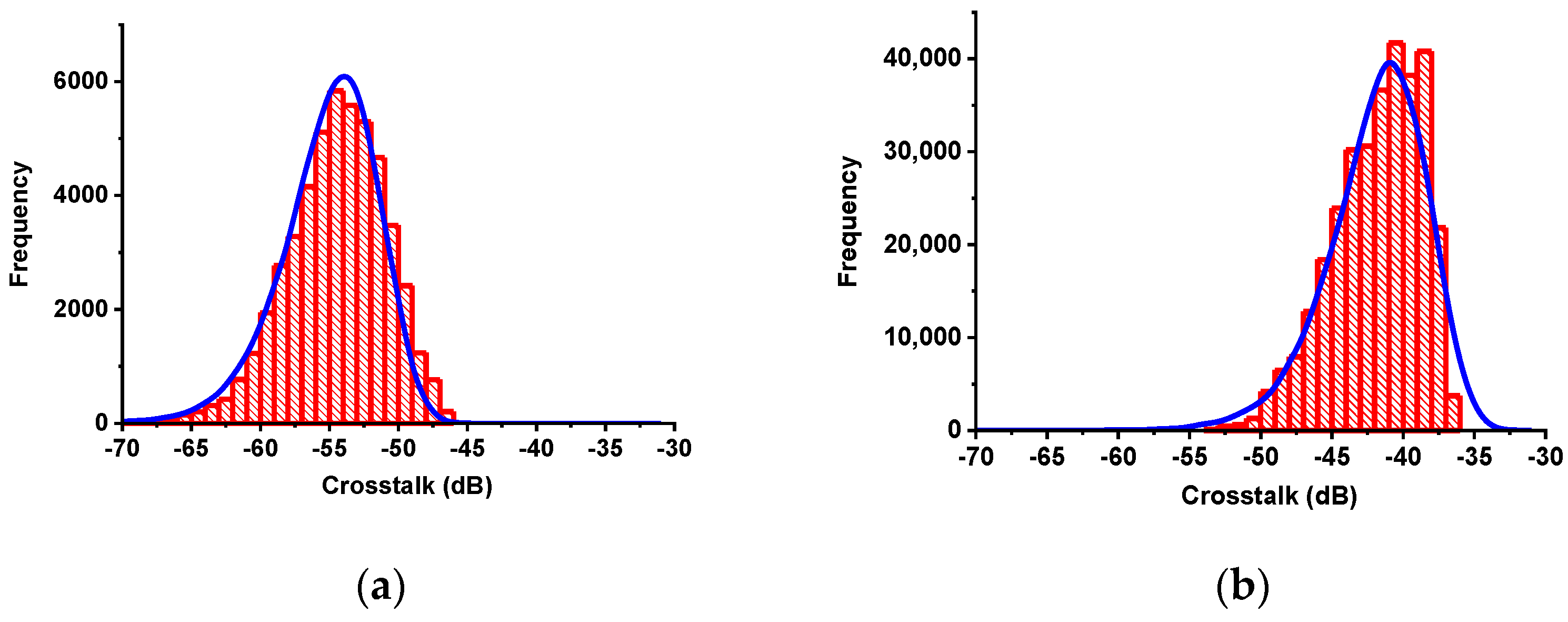
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ng, K.; Nazarov, V.; Kuchinsky, S.; Zakharian, A.; Li, M.-J. Analysis of Crosstalk in Multicore Fibers: Statistical Distributions and Analytical Expressions. Photonics 2023, 10, 174. https://doi.org/10.3390/photonics10020174
Ng K, Nazarov V, Kuchinsky S, Zakharian A, Li M-J. Analysis of Crosstalk in Multicore Fibers: Statistical Distributions and Analytical Expressions. Photonics. 2023; 10(2):174. https://doi.org/10.3390/photonics10020174
Chicago/Turabian StyleNg, Kam, Vladimir Nazarov, Sergey Kuchinsky, Aramais Zakharian, and Ming-Jun Li. 2023. "Analysis of Crosstalk in Multicore Fibers: Statistical Distributions and Analytical Expressions" Photonics 10, no. 2: 174. https://doi.org/10.3390/photonics10020174
APA StyleNg, K., Nazarov, V., Kuchinsky, S., Zakharian, A., & Li, M.-J. (2023). Analysis of Crosstalk in Multicore Fibers: Statistical Distributions and Analytical Expressions. Photonics, 10(2), 174. https://doi.org/10.3390/photonics10020174




