Abstract
For photoelectric theodolite, the mirror is the core optical component, so it is of great significance to design and optimize a mirror with excellent overall performance. In order to comprehensively consider the contradictory objectives of mass, natural frequency, and RMS under gravity, a multiobjective optimization method based on the performance analysis of two-parameter coupling was proposed. On the basis of the performance law, a suitable solution for balancing multiple objective functions is obtained by introducing manual intervention. The results show that compared with the traditional empirical design of mirrors, the first-order natural frequency, mass, and RMS performance of the optimized mirror are improved by 18.64%, 0.1%, and 15.58%, respectively. The frequency/Mass ratio and 1/(RMS*Mass) ratio are increased by 18.72% and 18.59%, respectively. Its comprehensive performance has been improved. This method is effective and provides a reference for the design of photoelectric theodolite and other mirrors.
1. Introduction
Photoelectric theodolite is a typical photoelectric tracking measurement device, which can accurately measure the external ballistic parameters of the airborne target in real time and record its flight attitude at the same time. It has the advantages of strong anti-interference ability and high measurement accuracy. As an important part of the optical system, the surface precision of the primary mirror plays a key role in imaging quality. With the improvement of observation resolution and light-gathering ability, the aperture of theodolite becomes larger and larger, increasing the aperture of the mirror will make its shape accuracy more susceptible to the influence of gravity and ambient temperature. In order to ensure the accuracy and system stability of the photoelectric theodolite, it is necessary to design the primary mirror structure to meet the index requirements in order to reduce the deformation of the primary mirror during the working process [1]. This improves the surface shape accuracy and image quality of the primary mirror. The general requirement for the face shape accuracy of the primary mirror is that the RMS value of the machined mirror is less than λ/40 (λ = 632.8 nm). Therefore, many efforts are focused on the research of high-performance, low-cost, lightweight mirrors [2,3,4]. One difficulty in developing optical devices is to minimize the quality of mirrors without compromising their stiffness. To solve this problem, some methods should be adopted during the development of mirror design, such as the choice of materials and structures [5,6]. In terms of materials, Zerodur and ULE are traditional optical materials, while silicon carbide (SiC) has been considered the most promising optical material due to its excellent properties [7,8,9]. Silicon carbide is a semiconductor compound with high covalent bond strength. Due to its unique thermal and mechanical properties, such as good wear resistance, good thermal stability, small coefficient of thermal expansion, and high hardness characteristics, it has a wide range of technical applications. Silicon carbide has been widely used in optical devices, nanotechnology, and nuclear material science for decades [10,11]. For example, since 1990, foreign telescopes such as Hubble, SST, and KST have used Be and ULE materials [12,13,14,15,16]. Since 2010, better-performing SiC material was chosen as the material for the primary mirror for the Herschel telescope [17,18,19]. In terms of structure, the main structures of the reflector are the rib, flanging, etc. The coupling between these structural shapes plays a crucial role in the influence of mirror performance. Therefore, it is an important research work of engineering significance to explore the mechanism of the influence of the coupling of structural parameters on performance and to seek the optimization method of the mirror from the essential law.
Many studies have analyzed and optimized lightweight mirrors. Kihm et al. [20] proposed a design method for a 1 m lightweight mirror in a space optical system. He divided the dimensional design into two separate problems, i.e., mirror design, and flexible design, and applied a multiobjective genetic algorithm to optimize the reflector. Butova et al. [21] used the method of parameter optimization to optimize the mirror, which is more than 1 m. A light mirror with a small optical surface deflection is obtained. Inspired by the topology optimization method considering casting constraints, Liu et al. [22] proposed an optimization model for mirror back configuration design, through which the distribution and height of ribs on the mirror back could be optimized simultaneously. Shao et al. [23] obtained key parameters by analyzing the sensitivity of primary mirror size parameters on performance. The parameter optimization is realized by the photomechanical analysis under multiple loads. Qu et al. [24] proposed a method that combines topological optimization with multiobjective function and parameter optimization. The new configuration design has an obvious advantage. Chen et al. [25] proposed an integrated photomechanical design method and optimized the parameters of the mirror and the bipod curved supports. All of the above research on mirror analysis and optimization have laid a foundation for subsequent improvement. Through previous studies, it is found that the traditional parameter-optimized method is to change a certain variable of the mirror through the computer, and the other parameter values are unchanged. Then, the influence of each parameter on mirror performance is analyzed one by one. However, only a simple analysis model can be obtained without considering the influence of different structural parameters on the overall performance of the mirror. With the change of parameters, the performance of one kind is improved while the performance of another kind is degraded. The optimization results cannot be directly applied to the practice. Moreover, only a certain structure can be obtained, according to the set objective function, which can only optimize a certain performance of the mirror. This optimization structure cannot guarantee simultaneous improvement of multiple performances. There are also some primary mirrors that are lightened using the topology optimization method. The method has the limitation that it cannot simultaneously optimize the global design of the key structural dimensions of the primary mirror.
On the basis of previous studies, this paper intends to solve the following research problems. The primary mirror of Φ672 mm in a photoelectric theodolite was taken as the research object, and the mirror configuration was designed by the empirical formula. Through the method of parametric modeling, the main structural parameters (such as rib, outer wall, center hole, etc.) were analyzed by parameter coupling, so as to summarize the law of the influence of parameter coupling on the performance. Compared with the sensitivity of a single structural variable, this method can obtain a more intuitive numerical representation and variation trend of the parameters on the performance. This model design is more common in other structural performance analyses. In addition, the problem to be solved is how to carry out a multiobjective size optimization based on the results of the parameter coupling analysis to achieve a comprehensive improvement of mirror performance. The expected performance improvement of the mirror was set by human intervention, and the feasible region was planned to meet the expected performance analysis results. In the different performance results obtained by multiple parameter variables, the intersection of the feasible region is selected. By selecting a series of parameter values in the intersection set, the data of different structure sizes can be obtained correspondingly and the performance of the mirror obtained by any group of data is better than that of the initial mirror. A multiobjective optimization of stiffness, mass, and surface shape was achieved. This method is based on the analysis content to guide the structural optimization and can be applied to the structural analysis and improvement under different working conditions.
2. The Initial Structure
2.1. Design of the Initial Structure of the Mirror
In this paper, according to the structure of a certain type of photoelectric theodolite, the semienclosed mirror was designed as the initial structure according to the actual working conditions and empirical formula of the mirror. The inside of the mirror is a traditional triangular lightweight hole, which is equipped with three support holes and a center hole. The initial mirror structure is shown in Figure 1.
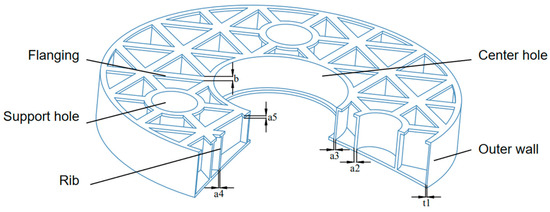
Figure 1.
Semienclosed initial mirror model.
The main structural parameters of the mirror include the thickness of the mirror (A), the thickness of the outer wall (t1), the radius of the support hole (r2), the thickness of the support hole (a2), the position of the center of the supporting hole (l2), the radius of the center hole (r3), the thickness of the center hole (a3), the thickness of the rib (a4), the thickness of the flanging (a5), the width of the flanging (b), and the height of the mirror (H). The structural parameters of the initial mirror are shown in Table 1. After the initial mirror structure is determined, COMSOL software is used for parametric modeling. Thus, the time of repeated modeling during the process of analysis is reduced when the parameter values of different structures are changed, which is convenient for analysis and comparison.

Table 1.
Structural parameter values of the initial mirror (mm).
2.2. Material of the Mirror
The material properties of the mirror are also very important to its performance. The existing commonly used mirror materials are SiC, ultralow expansion glass ULE, microcrystalline materials, Be, etc. The inherent properties of materials, such as density, Young’s modulus, Poisson’s ratio, and thermal expansion coefficient, directly affect the inherent properties of mirrors in static and dynamic environments. So the primary consideration at the beginning of structural design is material selection [26]. According to the actual working condition requirements of the photoelectric theodolite, the distribution and transportation are mostly based on vehicles, ships, or aircraft. It is necessary to measure the adaptability of the mechanical properties of different materials to working conditions. In addition, theodolite is mostly located in a harsh outdoor environment, which is obviously affected by temperature and wind load factors. Therefore, the material thermal physical properties are also an important index affecting the working accuracy of the mirror. Gravity is one of the main reasons to influence the precision of surface shape, so it is necessary to select materials with a high stiffness and a high lightweight degree as much as possible. The properties of common materials are shown in Table 2 [27].

Table 2.
Properties of common materials.
SiC material has the advantages of moderate density, nontoxicity, small coefficient of linear expansion, and high thermal conductivity. It is a widely used ceramic material [28]. Currently, there are more than 200 crystalline modifications of silicon carbide. Different crystalline modifications have different properties. By stacking several identical structures in different orders, different crystalline modifications can be obtained. For example, α-SiC is the most common crystalline form of silicon carbide and it has a hexagonal crystal structure similar to wurtzite, as shown in Figure 2a. β-SiC has a diamond-like sphalerite crystal structure, as shown in Figure 2b. Another common silicon carbide, 4H-SiC, which has a hexagonal crystal structure, is shown in Figure 2c. However, as a compound with a strong covalent bond (up to 88% covalent bond composition), the difference between grain boundary energy and the surface energy of SiC is very small, so it is difficult to form a grain boundary in the sintering process. Usually, the sintering of silicon carbide needs to be achieved by means of admixtures, pressure, or siliconizing. Reaction-bonded silicon carbide (RB-SC) generally uses α-SiC and carbon as raw materials. In the process of sintering, carbon reacts with liquid silicon or silicon vapor to form a secondary β-SiC in the primary position, which is combined with initial α-SiC particles to form dense SiC [29]. With the development of modern optical technology, the photoelectric theodolite field needs more and more urgent optical systems with a large aperture, that are ultralightweight, and have a complex shape. Compared with the other materials in Table 2, SiC has the characteristics of high specific stiffness (it is only lower than Be), low thermal expansion rate, high thermal conductivity, good chemical stability, good optical processing, and so on. So it is a lightweight mirror material with excellent comprehensive performance [30]. These properties have made SiC the preferred material for spatial and theodolite mirrors in recent years. According to the actual working conditions of photoelectric theodolite, and the current methods of preparing materials commonly used in my organization, SiC material was selected for mirror analysis.
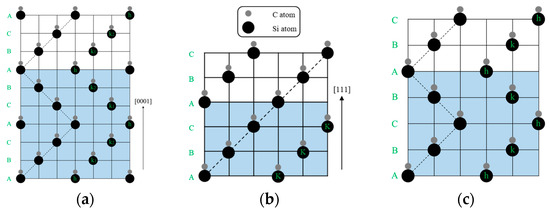
Figure 2.
Three main crystalline forms of silicon carbide. (a) (α)6H-SiC; (b) (β)3C-SiC; (c) 4H-SiC.
2.3. Performance Analysis of the Initial Structure
The natural frequency of the mirror under free vibration is an important performance index. In the free state, the natural frequency of the mirror and the position of the vibration are analyzed, in order to avoid resonance in the design of the structure. The initial mirror has meshed. After the finite element mesh is obtained, its free modes are analyzed. The vibration equation of its discrete form is shown as follows:
where is the overall quality matrix. is the overall stiffness matrix. is the damping matrix. The node displacement vector is . The velocity vector is . The acceleration vector is . Usually, the system can be viewed as undamped free simple harmonic vibration. Therefore, the form of the solution of Equation (1) is shown as follows:
where is the system amplitude vector and is the free vibration frequency. Substituting Equation (2) into Equation (1), the mode shape equation is
Equation (3) has the existence of nonzero solutions. Then, the determinant is zero. That is the following equation:
Equation (4) is the system characteristic equation or frequency equation. The eigenvalue is the natural frequency.
So, without any constraints, according to the above formula, by calculating the first 12-order characteristic frequencies of the initial mirror, after removing the first six-order rigid body displacements, the seventh-order characteristic frequency is the first-order natural frequency. Its natural frequency value is 1169.7 Hz. Figure 3 shows the free modes of orders 1–6. The first two free modes are approximately the same and they have similar natural frequencies. They bend inward from the edges of the mirror and the deformation is maximum at the four edges of the circle. The third mode shows that the center support hole has the largest deformation, and its surrounding structure protrudes outward. Its natural frequency value is about two times larger than the first natural frequency. The fourth free mode shows a total of six obvious inward or outward local deformations. Modes five and six are local modes. The natural frequency and mode shape of the mirror can be obtained by modal analysis, which can reflect the stiffness of the mirror and avoid resonance of the structure.
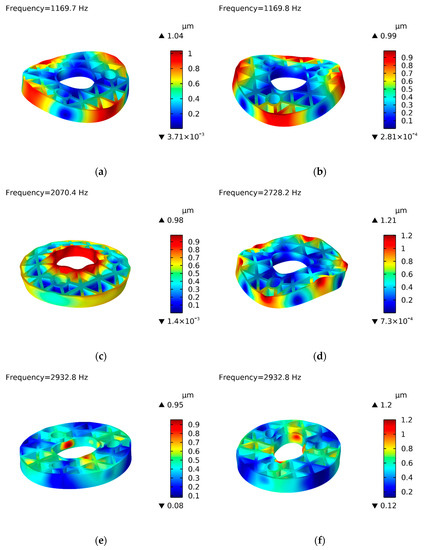
Figure 3.
Free mode analysis of the 1st−6th order of the initial mirror. (a) The first free mode shape; (b) The second free mode shape; (c) The third free mode shape; (d) The fourth free mode shape; (e) The fifth free mode shape; (f) The sixth free mode shape.
According to the above, the free modes of the initial mirror are calculated without any constraints. Next, the accuracy of surface shape and deformation under the condition of dead weight will be analyzed. As can be seen from the mirror model in Figure 1, it has three circular support holes. Simple cylinders were then added at the positions of each support hole to simulate the support structure, using them as fixed constraints. In other words, boundary conditions are set at the support hole, and its displacement is constrained to be constant at zero. The condition is that the optical axis of the SiC mirror points vertically to the zenith so that it is subjected to a 1 g gravity load under the action of three-point fixed constraints. The boundary conditions, constraints, and deformation results of the mirror under the action of dead weight are shown in Figure 4. When the mirror is in static equilibrium under its gravity, it satisfies the following equation:
where is the overall stiffness matrix, is the displacement vector, and is the external force vector.
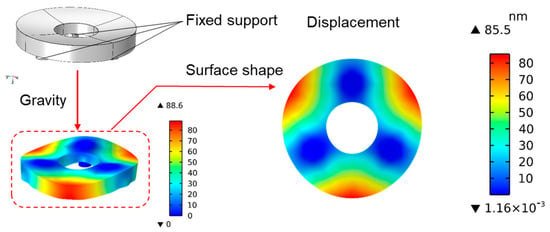
Figure 4.
Displacement of an initial SiC mirror based on three−point support (RMS = 39.56 nm).
When photoelectric theodolite is working, the face shape accuracy is related to the imaging quality. The root means square (RMS) of the surface shape is usually used to evaluate the accuracy of the surface shape. It is defined as the root mean square of the mirror normal displacement after removing the structural rigid body displacement [31,32]. RMS indicates the root mean square value of the deviation between each node of the deformed surface shape relative to the fitted surface shape:
where is the distance from the ith node to the fitted surface after deformation, and is the average distance of all nodes to the fitted surface. By calculating the mirror deformation, the quality of the mirror’s face shape can be evaluated.
The deformation of its dead weight and RMS (root mean square value of face shape) are analyzed as the reference value of the performance under the initial structure. Figure 4 shows the deformation of the initial mirror based on gravity. The maximum value is 88.6 nm, and the RMS value is 39.56 nm.
3. Parametric Coupling Analysis
There are many factors affecting the structural stiffness and surface shape accuracy of the mirror, such as the form of the lightweight hole, the degree of back closure, the thickness of the rib, the size of the support hole, etc. By analyzing the main structure size of the mirror, the stiffness of the mirror is obtained by comparing its first natural frequency (The seventh-order characteristic frequency). The comparison between stiffness and mass can analyze the influence of structural parameters on mirror performance and guide subsequent research. The RMS value under the action of gravity was analyzed to evaluate the imaging quality. The comparison between the RMS value and the mass can reflect the relationship between shape accuracy and light weight. Many factors affect the structure and performance of the mirror, such as the thickness of the flanging (a5), the width of the flanging (b), the thickness the of support hole (a2), the thickness of the center hole (a3), the thickness of the rib (a4), and the thickness of the outer wall (t1). In order, the two-parameter couplings with high correlation are grouped into a group. They were divided into three groups for parameter coupling analysis.
This paper presents the results of the influence of each parameter in a certain range on the mirror performance in the form of two-dimensional graphs. In each set of parameters, four different types of two-dimensional graphs are defined to show the results.
The first type of figure expresses the first-order natural frequencies at different sizes for a certain set of parameter combinations. It is frequency, which can show the stiffness of the mirror. When the value of the coordinate in the figure is larger, it means that the stiffness under this parameter is better. The second type of figure expresses the ratio between the natural frequency and mass of the mirror. It is frequency/mass. When the natural frequency is higher or the mass is smaller, the ratio is larger. The corresponding coordinates reflect the high “cost performance”, which not only improves the stiffness, it also reduces the quality. However, a higher value does not directly indicate better performance. Other factors should be considered. The third type of figure expresses the surface shape accuracy of the mirror based on the three-point fixed support constraint and the application of gravity. It is RMS. When the value is smaller, it means that the surface shape accuracy under the size is better. Usually, the deformation caused by gravity is one of the main reasons affecting the surface shape accuracy. The gravity depends on the quality of the mirror itself, and the light weight is a key component in the optimization design of the mirror. The purpose of light weight is not only to reduce the mass, it is also to ensure stiffness and shape accuracy. Therefore, the fourth type of graph is needed to express the relationship between the RMS value and the quality of the mirror. It is 1/(RMS*Mass). Since both RMS value and quality are seeking the minimum and appropriate value, this value needs to comprehensively consider the issue of “cost performance”. A larger value indicates better performance.
Through the above method, four kinds of results in the form of graphs can be obtained for every two related variables. They can clearly show the influence of parametric coupling on the mirror performance and the distribution law.
3.1. Coupling Analyzing the Properties of Flanging’s Thickness and Width
The flanging is located on the back of the mirror. The size of the flanging parameters determines whether the mirror is open, semiclosed, or fully closed. The thickness of flanging (a5) and the width of flanging (b) were combined. Then the combination was parametrically scanned and analyzed. The value of a5 ranges from 2 to 11 mm. The value of b ranges from 4 to 15 mm. After calculating the natural frequency and RMS values by the finite element method, a series of two-dimensional graphs of mirror performance results are obtained.
As can be seen from Figure 5, the influence of the two parameters on the performance of the mirror is different. The analysis results are shown as follows.
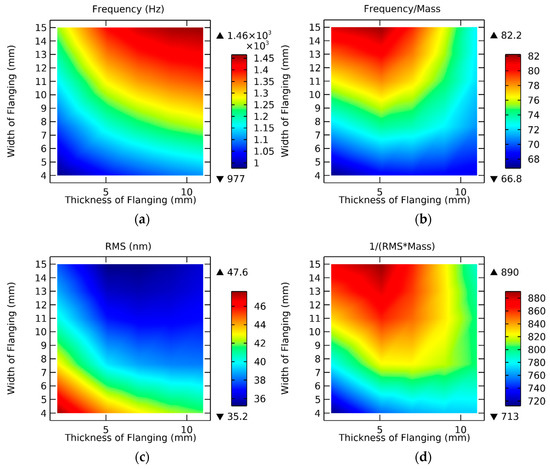
Figure 5.
Performance analysis of flanging’s thickness and width under different parameters. (a) Frequency; (b) Frequency/Mass; (c) RMS; (d) 1/(RMS*Mass).
First of all, according to the results in Figure 5a,b, under the mutual influence of the two parameters, the ratio of the first-order natural frequency to frequency/mass changes obviously. When the trend of stratification approaches the level, the results show that the width of the flanging has a high sensitivity to its corresponding performance, and the size parameter has an obvious influence on the structural performance. Increasing the value of this parameter will increase the natural frequency.
Then, since the size of the mirror along the optical axis is significantly smaller than its radial size, the mirror is more prone to deformation along the optical axis. In order to improve the bending stiffness of the mirror, the design of the mirror generally increases the flanging width value, so that it is a closed back or semiclosed structure. Under the action of gravity, Figure 5c,d show that the RMS value becomes smaller, and the surface shape accuracy is better when the increase of the flanging’s thickness and width are increased. However, if the value is too large, there will be problems such as excessive mass and manufacturing difficulties, which hinder the optimization of the mirror.
In addition, the corresponding regions of the optimal values of the four kinds of performance have intersections. It shows that the parameters in the public area can simultaneously improve the mirror structure performance.
There is one more point. When viewing Figure 5a,b longitudinally and Figure 5c,d horizontally, the coupling law of the two parameters can be clearly found. When the value of one parameter is different, the influence of another parameter’s value on the performance is different. The value of performance does not change at the same rate. That is, when one parameter takes different values, the gradient of the influence of the other coupling parameter on the performance is different.
3.2. Coupling Analyzing the Properties of the Thickness of the Support Hole and Center Hole
The support modes commonly used in mirrors include three-point support, multipoint support, center support, side support, etc. In this mirror model, the thickness of the three-point support hole (a2) and the thickness of the center hole (a3) are a set of relevant parameter values. A combined parametric scan is performed for both. The value of a2 ranges from 3 to 15 mm and the value of a3 ranges from 2 to 6 mm. The analysis results in Figure 6 are shown below.
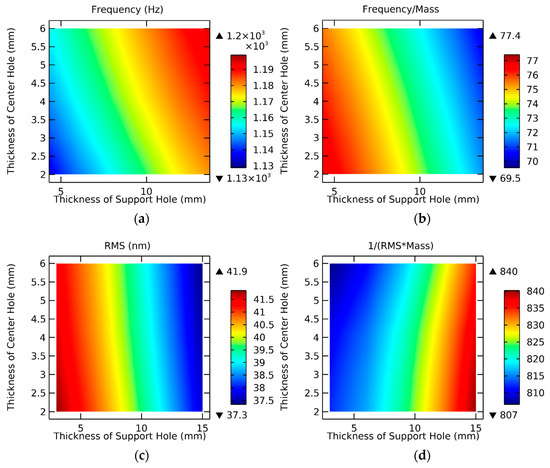
Figure 6.
Performance analysis of the thickness of the support hole and center hole under different parameters. (a) Frequency; (b) Frequency/Mass; (c) RMS; (d) 1/(RMS*Mass).
Firstly, the layering patterns of the four performance figures have similar stratification laws, which are approximately vertically distributed. The results show that the thickness of the support hole has an obvious influence on the performance of the mirror, and its parameter sensitivity is relatively large.
Secondly, the trend of the frequency/mass ratio was opposite to that of natural frequency. When the values of the two variables are smaller, the eigenvalues are larger.
Thirdly, Figure 6a–d all show that when the thickness of the support hole is larger, the corresponding performance is better. Therefore, increasing the thickness of the supporting hole is beneficial to improve the comprehensive performance of the structure.
Fourthly, although the distribution pattern is obvious, the range difference between the RMS value and 1/(RMS*Mass) is not large. The range of RMS values in the whole region was only 4.6 nm. Therefore, their values can be approximated to be equal in a wide range. These data need to be taken into account when referring to them for optimization.
Fifthly, according to Figure 6c, when the two parameters are coupled to analyze a certain performance, if the distribution law of the influence on the performance is obvious (almost horizontal or vertical), it indicates that the coupling degree of the two parameters to the performance is not high. On the contrary, if the distribution regularity of the two-dimensional performance figure is not obvious, it indicates that the two parameters have a high influence on each other and have a great impact on the performance change.
3.3. Coupling Analyzing the Properties of the Thickness of the Rib and the Outer Wall
The thickness of the rib (a4) and the outer wall (t1) are important parameters for the lightweight and structural stiffness of the mirror. The two variables were combined for parametric scanning. The value of a4 ranges from 2 to 7 mm and the value of t1 ranges from 1 to 8 mm.
As can be seen in Figure 7, the two parameters have different effects on the performance of the mirror. The analysis of the results is shown as follows.
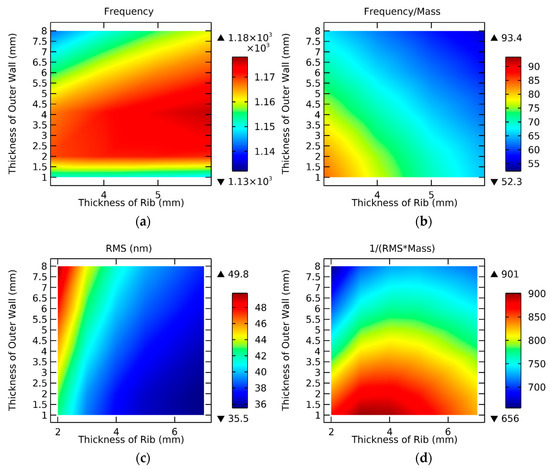
Figure 7.
Performance analysis of the thickness of the rib and outer wall under different parameters. (a) Frequency; (b) Frequency/Mass; (c) RMS; (d) 1/(RMS*Mass).
First of all, under the mutual influence of the two parameters, the distribution of natural frequency value is not obvious. However, the better value in the red region accounted for more than 50%, and the frequency value in the red region was close to each other without significant change. However, the influence of the outer wall on natural frequency is affected by the first increase and then decrease, so the excessive increase in the thickness of the outer wall will only play a negative role.
Then, the four graphs in Figure 7 show different performances, and their distribution laws are different. The contrast shows that there is a contradiction. For example, increasing the thickness of the rib can improve the natural frequency and RMS value. When the quality factor is taken into account, its cost performance will decline. This indicates that the parameter should not be increased blindly and should be considered comprehensively.
The 1/(RMS*Mass) has a large range. The maximum value is about 901 and the minimum value is about 656. Therefore, it is of great significance to be referenced and should be given priority when optimizing the structure of the mirror.
In addition, the different distribution rules in the four figures in Figure 7 show that the two parameters have different impacts on different performances. It shows that the coupling degree of the two is higher. As shown in Figure 7c, the rib has a higher sensitivity, however, as shown in Figure 7d, the outer wall has a higher sensitivity. When the value of one parameter is different, the gradient of the change of the other parameter is different.
4. Optimization
4.1. Optimized Process
In the analysis of the influence of mirror structure on performance, six variables are combined into three groups. For each group, four two-dimensional graph results about performance evaluation were obtained. To verify that the results of the parametric analysis of the main structure of the mirror can accurately reflect the performance of the structure and have application value for optimization, the above data are extended in this section. Based on the initial mirror model, the influence of the main structure size on the performance is obtained by parametric analysis. Afterward, optimization is guided by laws. Since the optimization of the mirror is not a single objective problem, it involves stiffness, mass, RMS, and other factors. For example, in general, the improvement of mass will improve the stiffness. At the same time, it also increases the influence of gravity on the shape, which makes the image quality worse. They are a set of competing factors. That is to say, when the structural parameter of the mirror is optimized, some performance will be improved, however, other performance may be weakened [33]. Therefore, in order to comprehensively improve the mirror performance, it is necessary to transform the single objective problem into a multiobjective for seeking the optimization problem. The six main structure sizes are defined as function variables and are shown in Table 3:

Table 3.
The variables are defined by each parameter.
Based on the performance analysis of the parameter coupling pair, three groups of parameter coupling were used to calculate the four performances of the mirror in turn. As shown in Figure 5, Figure 6 and Figure 7, a total of 12 performance analysis data are obtained as the basis of optimization. Then, the six variables in the three sets of coupling parameters are assigned to vector matrix X, where is the main parameter size of the initial structure. is the main structure size, which changes with the value. The change in the final structure size will affect the performance of the mirror. Although there is no explicit functional relationship between the influence of the variables of the mirror structure size on the performance, the optimization can be carried out according to the two-dimensional graph of the performance results of the variables. Based on the parameterized scan results, the feasible region is planned according to the variables and the values in the figure. The feasible region represents the expected degree of optimization. The mathematical expression is . According to each set of parameters, it is expanded as follows:
s.t.
In the above formula, Min F is the objective function. The goal of the optimization is to minimize four performance parameters, which are 1/frequency, RMS, mass/frequency, and RMS*Mass. Corner marks ij are used to represent the corresponding two-dimensional diagram, where represent three groups of variables in turn. Graph numbers a, b, c, and d (in Figure 5, Figure 6 and Figure 7) in the scan results of each group in turn are , and is the value of the performance at different X. The value of a single performance of the initial mirror is , and it is also the initial value. The optimal value of a single performance of the mirror is . is the expected improvement rate of a certain performance. is the constant term as the expected improvement of a certain performance. The two factors together determine the expected performance improvement. All of the are jointly planned to obtain the initial feasible region. Equation (9) is the range of values of the variables corresponding to structural parameters. They are selected by reference to the range values selected for structural parameters in parameter coupling analysis.
Based on the above, human intervention is added at the beginning of optimization, and constraints are set according to the requirements and expected improvement. That is, according to Equation (8), the range of the optimization domain is set in advance, and the nonconforming domain is removed from the performance data of the parameter coupling analysis. Then, the optimization is carried out based on the two-parameter coupled data and the setting of the objective function. The intersection domain is found in the retained data region of each two-dimensional graph and the points in the intersection domain are compromise solutions. In other words, the value of the points in the intersection after optimization cannot achieve the optimal performance, however, each key performance has been improved compared with the initial value. Through this process, the relevant variable X that meets the conditions in all parameter coupling groups is found. At this time, the optimization is completed. the structure size of the mirror is improved, and the performance is optimized.
4.2. Results of Optimization
Through the above method, size optimization can be achieved to obtain better mirror performance. For example, the thickness and width of the flanging are analyzed. According to the engineering requirements and the performance improvement degree of human intervention, the feasible region is planned by taking the values shown in Table 4. This plan is shown in Figure 8. The gray area is the part removed during the planning of the feasible region, which is the area that does not meet the requirements. Taking the set of intersection points in the feasible region of the four two-dimensional graphs, the size that can improve the overall performance of the mirror is obtained. A point in the intersection is the optimized point.

Table 4.
Planning of feasible regions.
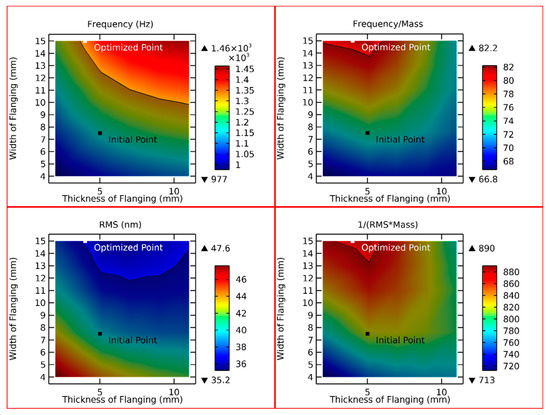
Figure 8.
Schematic diagram of an optimization.
Based on 12 performance results obtained by parametric analysis, the proposed method is used to plan and optimize the feasible region. The overall performance of the mirror is improved after the optimization of the main structural parameters. Considering the speed of the optimization, this optimization is only carried out when [X] is taken as an integer. The comparison between the optimized mirror parameters and the initial values is shown in Table 5. The comparison between the initial model and the optimized model is shown in Figure 9.

Table 5.
Comparison of parameters between the initial and improved structures (Unit: mm).
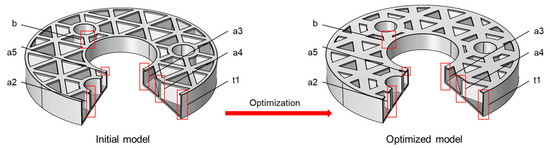
Figure 9.
Comparison of the initial mirror and the optimized mirror.
The optimized model was calculated by free mode, mass, optical axis vertical, and the influence of gravity on the face shape RMS value. Through software simulation and data processing, the first natural frequency of the optimized model is 1387.7 Hz. By calculation, the RMS of the model is 33.395 nm and the mass is 15.855 kg. The simulation result is shown in Figure 10. According to the data calculated by the initial model mentioned above, compared with the performance of the initial mirror (shown in Table 6), the performance of the optimized mirror is improved. The weight of the optimized mirror has been reduced from 15.871 kg to 15.855 kg, and it is slightly light (increased by 0.10%). At the same time, the first natural frequency is increased from 1169.7 Hz to 1387.7 Hz, and its stiffness is increased by 18.64%. The frequency/mass value is increased from 73.7 to 87.5, indicating that the cost–performance ratio between stiffness and mass is increased by 18.72%. The RMS value is decreased from 39.56 nm to 33.395 nm, indicating that the shape accuracy is increased by 15.58%. The value of 1/(RMS*Mass) is increased from 822.71 to 975.68, indicating that the cost–performance ratio between shape accuracy and mass is increased by 18.59%. The overall performance is significantly improved, which proves the practicability and reliability of the optimization method.
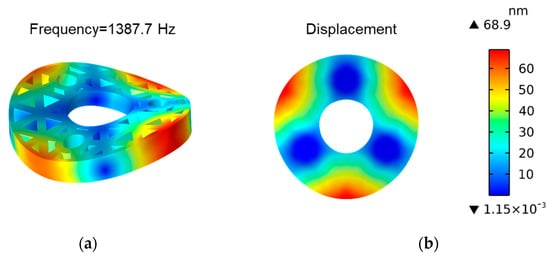
Figure 10.
Analysis of the optimized model. (a) The first free mode shape; (b) Displacement of surface shape (RMS = 33.395 nm).

Table 6.
Comparison of the performance of the initial mirror and the optimized mirror.
5. Conclusions
In this paper, a multiobjective optimization method for a SiC mirror based on dual-parameter coupling is proposed. The performance of the mirror is analyzed by using two parameter couplings. The analysis results clearly show the different parameters under the action of coupling to various properties. It improves the deficiency of only considering a single structural change without considering other factors. On this basis, the structural parameters are optimized by adding manual intervention. Compared with the structure designed based on traditional experience, the optimized mirror which uses a SiC material with better overall performance has the following properties. The weight of the optimized mirror is 15.855 kg, and it is slightly light (increased by 0.10%). At the same time, the first natural frequency is 1387.7 Hz, indicating that the stiffness increases by 18.64%. The frequency/mass value is 87.5, indicating that the cost–performance ratio between stiffness and mass increased by 18.72%. The RMS value is 33.395 nm, indicating that the accuracy of surface shape is improved by 15.58%. The value of 1/(RMS*Mass) is 975.68, indicating that the cost–performance ratio between the shape accuracy and the mass has increased by 18.59%. The result shows that this method improves the performance of the mirror and achieves a multiobjective optimization. It provides effective technical means and an engineering reference for the design of a mirror of photoelectric theodolite.
It should be noted that although this method has achieved good results in this work, due to manufacturing errors and actual working conditions in actual engineering, there may be corresponding errors compared with the expected value. In future studies, ray tracing, different optical axis angles, and temperature effects should be added to make up for the deficiency. They will make the results more realistic and universal, and experiments will be added to verify them.
Author Contributions
Conceptualization, Q.D. and Q.W.; methodology, Q.D.; software, Q.D.; validation, Q.D., C.W. and X.W. (Xiaoming Wang); formal analysis, Q.D.; investigation, Q.D.; resources, X.W. (Xiaoming Wang); data curation, X.W. (Xiaoxun Wang); writing—original draft preparation, Q.D.; writing—review and editing, Q.D.; visualization, Y.L.; supervision, C.W.; project administration, X.W. (Xiaoming Wang); funding acquisition, X.W. (Xiaoming Wang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by THE NATIONAL NATURAL SCIENCE FOUNDATION OF CHINA, grant number 6210031610.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable. The study did not involve humans.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors thank Xiaoming Wang for his theoretical guidance and academic discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, Q.; Gong, X.F. Optimization design for edge-lateral support of a medium-aperture lightweight primary mirror. Appl. Opt. 2020, 59, 10498–10505. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.M.; Xu, T.Q.; Liu, S.F.; Yang, B.; Liu, Y.N. Design of primary mirror supporting structure and lightweight of space camera. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies (AOMATT)—Advanced Optical Manufacturing Technologies, Xiamen, China, 26–29 April 2012. [Google Scholar]
- Zhang, D.D.; Li, W.Y.; Lv, Q.B.; Liu, Y.Y.; Chen, X.W. Lightweight Design and Finite Element Analysis of Primary Mirror For The Space Telescope. In Proceedings of the Optical Systems Design—Optical Design and Engineering VI, Jena, Germany, 7–10 September 2015. [Google Scholar]
- Xin, L.W.; Lin, G.C.; Hui, R.C. Finite Element Analysis of Lightweight, Active Primary Mirror. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies (AOMATT)—Large Mirrors and Telescopes, Xiamen, China, 26–29 April 2010. [Google Scholar]
- Li, X.P.; Shi, J.F.; Wang, W.; Wang, Y.J.; Fan, X.W. Review on Splicing Structure Technology of Large Aperture Space Primary Mirror. Laser Optoelectron. Prog. 2018, 55, 28–40. [Google Scholar]
- Kamiya, T.; Yasuda, S.; Okamoto, A.; Sato, S.; Ueno, H.; Mizutani, T. Material selection of 3.5-meter segmented mirror for geostationary Earth observation satellite. In Proceedings of the Symposium on Astronomical Optics—Design, Manufacture, and Test of Space and Ground Systems II held at SPIE Optical Engineering + Applications Conference, San Diego, CA, USA, 12–15 August 2019. [Google Scholar]
- Sun, N.; Zhuo, R.S.; Cong, J.F. Optimum Design of the Support System of the SiC primary Mirror with 1m Aperture. In Proceedings of the International Conference on Nanotechnology and Precision Engineering (ICNPE 2012), Guilin, China, 26–27 December 2013. [Google Scholar]
- Liu, X.Y.; Zhang, J.X.; Wu, X.X.; Li, J.F.; Guo, P.; An, Q.C. Study on the sensitivity of temperature gradient for large aperture SiC lightweight mirror based on active optics. In Proceedings of the 7th International Symposium on Advanced Optical Manufacturing and Testing Technologies (AOMATT)—Large Mirrors and Telescopes, Harbin, China, 26–29 April 2014. [Google Scholar]
- Fox, A.; Hobbs, T.; Edwards, M.; Arnold, M.; Sawyer, K. ULE (R) design considerations for a 3m class light weighted mirror blank for E-ELT M5. In Proceedings of the Conference on Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016. [Google Scholar]
- Huczko, A.; Dąbrowska, A.; Savchyn, V.; Popov, A.I.; Karbovnyk, I. Silicon carbide nanowires: Synthesis and cathodoluminescence. Phys. Status Solidi (B) 2009, 246, 2806–2808. [Google Scholar] [CrossRef]
- Ning, G.; Zhang, L.; Zhong, W.; Wang, S.; Liu, J.; Zhang, C. Damage and annealing behavior in neutron-irradiated SiC used as a post-irradiation temperature monitor. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2022, 512, 91–95. [Google Scholar] [CrossRef]
- Cheng, J. The Principles of Astronomical Telescope Design; Springer: New York, NY, USA, 2009; pp. 101–118. [Google Scholar]
- Montagnino, L.A. Test And Evaluation Of The Hubble Space Telescope 2.4-meter Primary Mirror. Proc. SPIE Int. Soc. Opt. Eng. 1986, 571, 182–190. [Google Scholar]
- Gehrz, R.D.; Roellig, T.L.; Werner, M.W.; Fazio, G.G.; Houck, J.R.; Low, F.J.; Rieke, G.H.; Soifer, B.T.; Levine, D.A.; Romana, E.A. The NASA Spitzer Space Telescope. Rev. Sci. Instrum. 2007, 78, 011302. [Google Scholar] [CrossRef] [PubMed]
- Zinn, J.W.; Jones, G.W. Kepler primary mirror assembly: FEA surface figure analyses and comparison to metrology. In Proceedings of the Conference on Optical Manufacturing and Testing VII, San Diego, CA, USA, 28–29 August 2007. [Google Scholar]
- Werner, M. The Spitzer Space Telescope. Opt. Eng. 2012, 51, 011008. [Google Scholar] [CrossRef]
- Fransen, S.; Doyle, D.; Catanzaro, B. Opto-Mechanical Modeling of the Herschel Space Telescope at ESA/ESTEC. In Proceedings of the Conference on Integrated Modeling of Complex Optomechanical Systems, Kiruna, Sweden, 15–17 August 2011. [Google Scholar]
- Minier, V.; Bonnet, R.M.; Bontems, V.; de Graauw, T.; Griffin, M.; Helmich, F.; Pilbratt, G.; Volonte, S.; Minier, V.; Bonnet, R.M.; et al. Silicon Carbide Telescope: Radical Innovation. In Inventing a Space Mission; ISSI Scientific Report Series; Springer: Cham, Switzerland, 2017; Volume 14, pp. 139–157. [Google Scholar]
- Bougoin, M.; Lavenac, J. From HERSCHEL to GAIA, 3-meter class SiC space optics. In Proceedings of the Conference on Optical Manufacturing and Testing IX, San Diego, CA, USA, 22–24 August 2011. [Google Scholar]
- Kihm, H.; Yang, H.S. Design optimization of a 1-m lightweight mirror for a space telescope. Opt. Eng. 2013, 52, 091806. [Google Scholar] [CrossRef]
- Butova, D.V.; Tolstoba, N.D.; Fleysher, A.G.; Orekhova, M.K. Optimization of the parameters of space-based mirrors. In Proceedings of the Conference on Optical Components and Materials XIV, San Francisco, CA, USA, 30 January–1 February 2017. [Google Scholar]
- Liu, S.; Hu, R.; Li, Q.; Zhou, P.; Dong, Z.; Kang, R. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope. Appl. Opt. 2014, 53, 8318–8325. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Zhang, L.; Jia, X. Optomechanical integrated optimization of a lightweight mirror for space cameras. Appl. Opt. 2021, 60, 539–546. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Jiang, Y.; Feng, L.; Li, X.; Liu, B.; Wang, W. Lightweight Design of Multi-Objective Topology for a Large-Aperture Space Mirror. Appl. Sci. 2018, 8, 2259. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Huang, B.-K.; You, Z.-T.; Chan, C.-Y.; Huang, T.-M. Optimization of lightweight structure and supporting bipod flexure for a space mirror. Appl. Opt. 2016, 55, 10382–10391. [Google Scholar] [CrossRef] [PubMed]
- Xu, H. Structural design of primary mirror subassembly for space telescope. In Proceedings of the 2nd International Conference on Mechatronics and Applied Mechanics (ICMAM2012), Hong Kong, China, 6–7 December 2012. Taipei, China, 8–9 December 2012. [Google Scholar]
- Han, Y.Y.; Zhang, Y.M.; Han, J.C.; Zhang, J.H.; Yao, W.; Zhou, Y.F. Design and finite element analysis of lightmass silicon carbide primary mirror. Trans. Nonferrous Met. Soc. China 2006, 16, S696–S700. [Google Scholar] [CrossRef]
- Lee, S.-H.; Lee, Y.-I.; Kim, Y.-W.; Xie, R.-J. Mechanical properties of hot-forged silicon carbide ceramics. Scr. Mater. 2005, 52, 153–156. [Google Scholar] [CrossRef]
- Lamon, J. A micromechanics-based approach to the mechanical behavior of brittle-matrix composites. Compos. Sci. Technol. 2001, 61, 2259–2272. [Google Scholar] [CrossRef]
- Margiotta, J.C.; Zhang, D.; Nagle, D.C. Microstructural evolution during silicon carbide (SiC) formation by liquid silicon infiltration using optical microscopy. Int. J. Refract. Met. Hard Mater. 2010, 28, 191–197. [Google Scholar] [CrossRef]
- Chen, K.; Qiu, R. Topological Optimization Design of Imaging Primary Mirror Based on Root-Mean-Square Error of Surface Figures. AcOpS 2022, 42, 99–104. [Google Scholar]
- Fengchang, L.; Wei, L.; Weiguo, Z.; Haibo, Z.; Guanyu, L.; Xiaodong, W. Topology Optimization Based Parametric Design of Balloon Borne Telescope’s Primary Mirror. Appl. Sci. 2021, 11, 5077. [Google Scholar]
- Hu, R.; Chen, W.; Li, Q.; Liu, S.; Zhou, P.; Dong, Z.; Kang, R. Design Optimization Method for Additive Manufacturing of the Primary Mirror of a Large-Aperture Space Telescope. J. Aerosp. Eng. 2016, 30, 04016093. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).