Antibunching Effects in the Hybrid Cavity–Bose–Einstein Condensates System
Abstract
1. Introduction
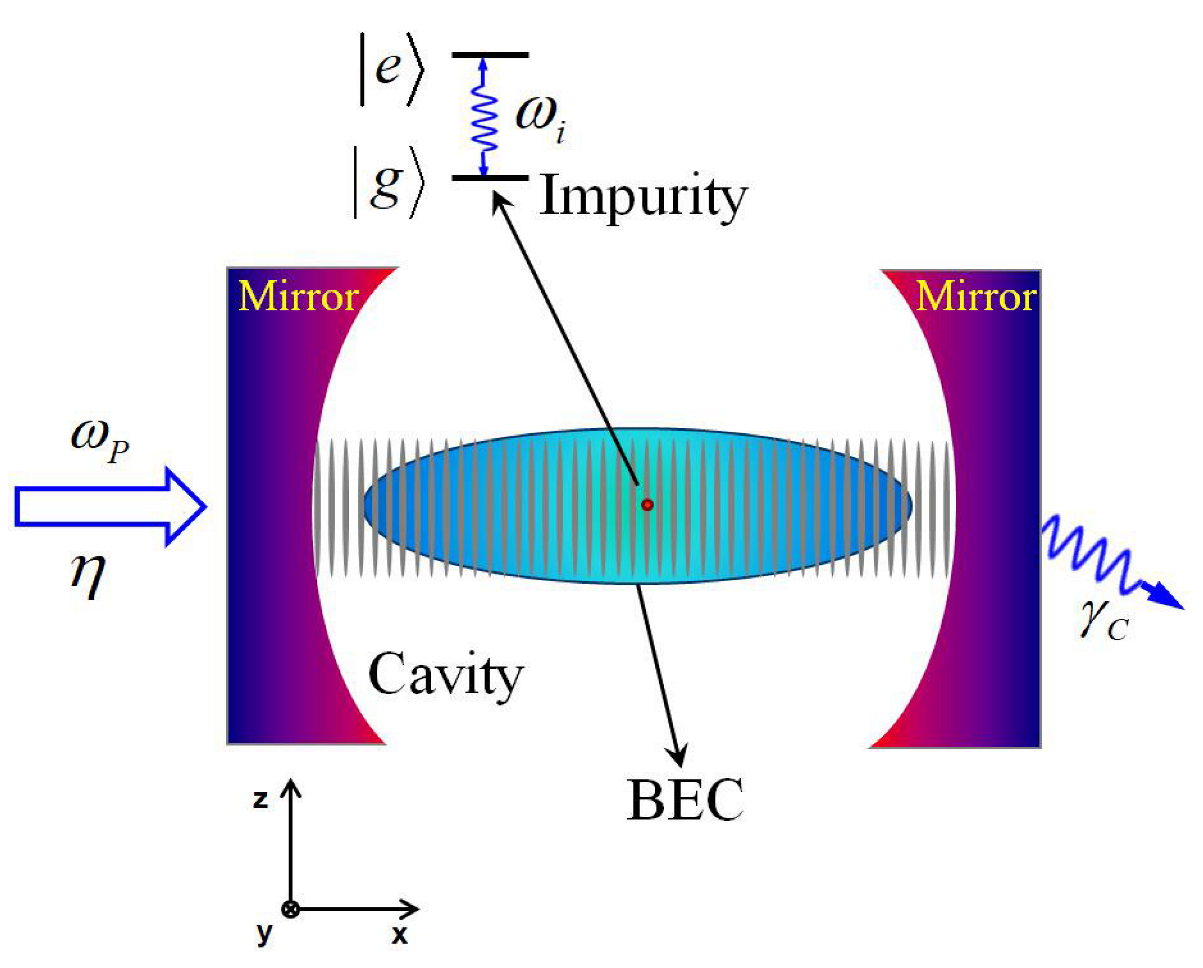
2. Physical Model and Solution
2.1. System Hamiltonian
2.2. The Eigenvalues and Eigenstates of the System
3. Anti-Bunching Effect in the Cavity
3.1. Approximate Analytical Results
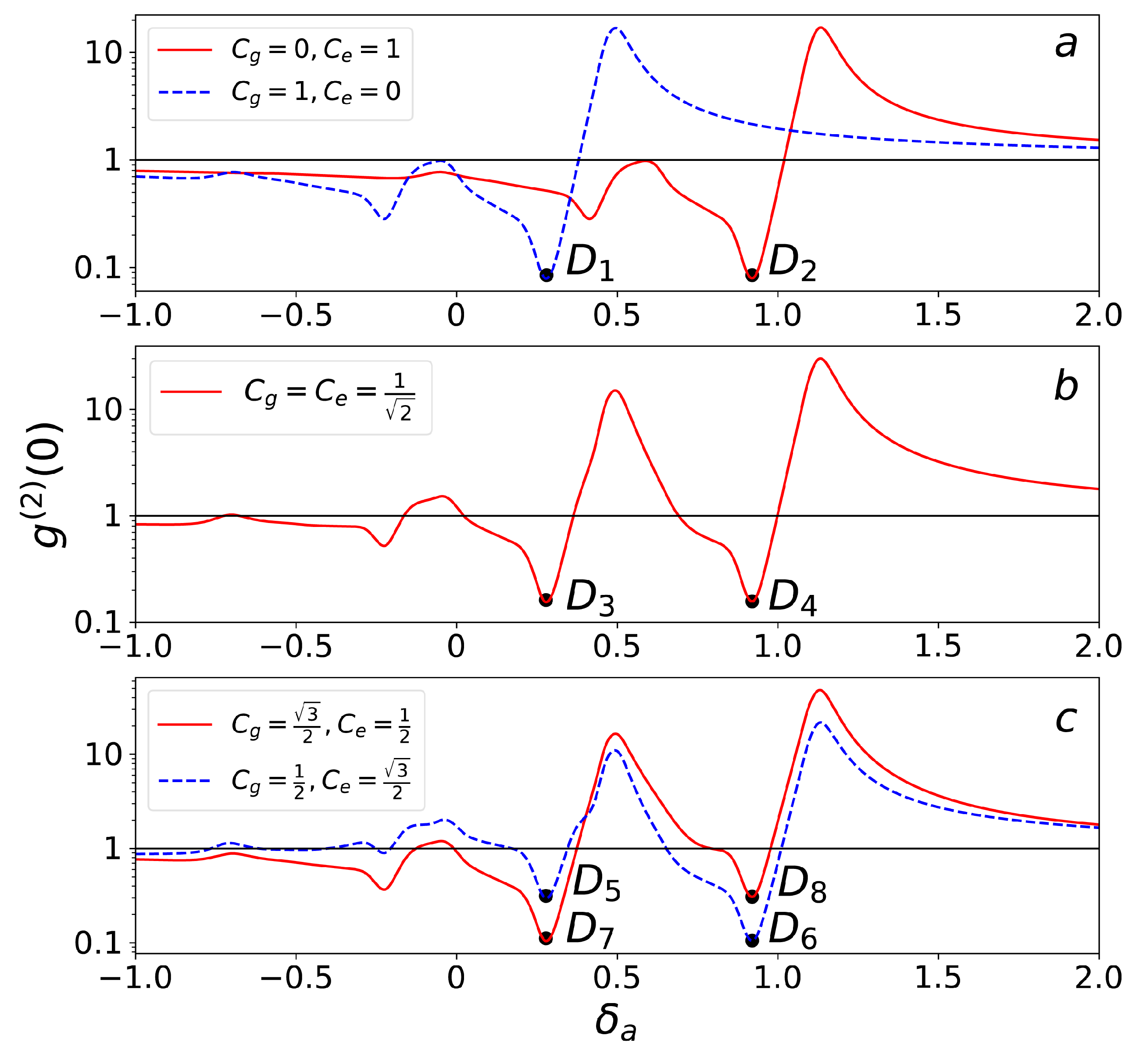
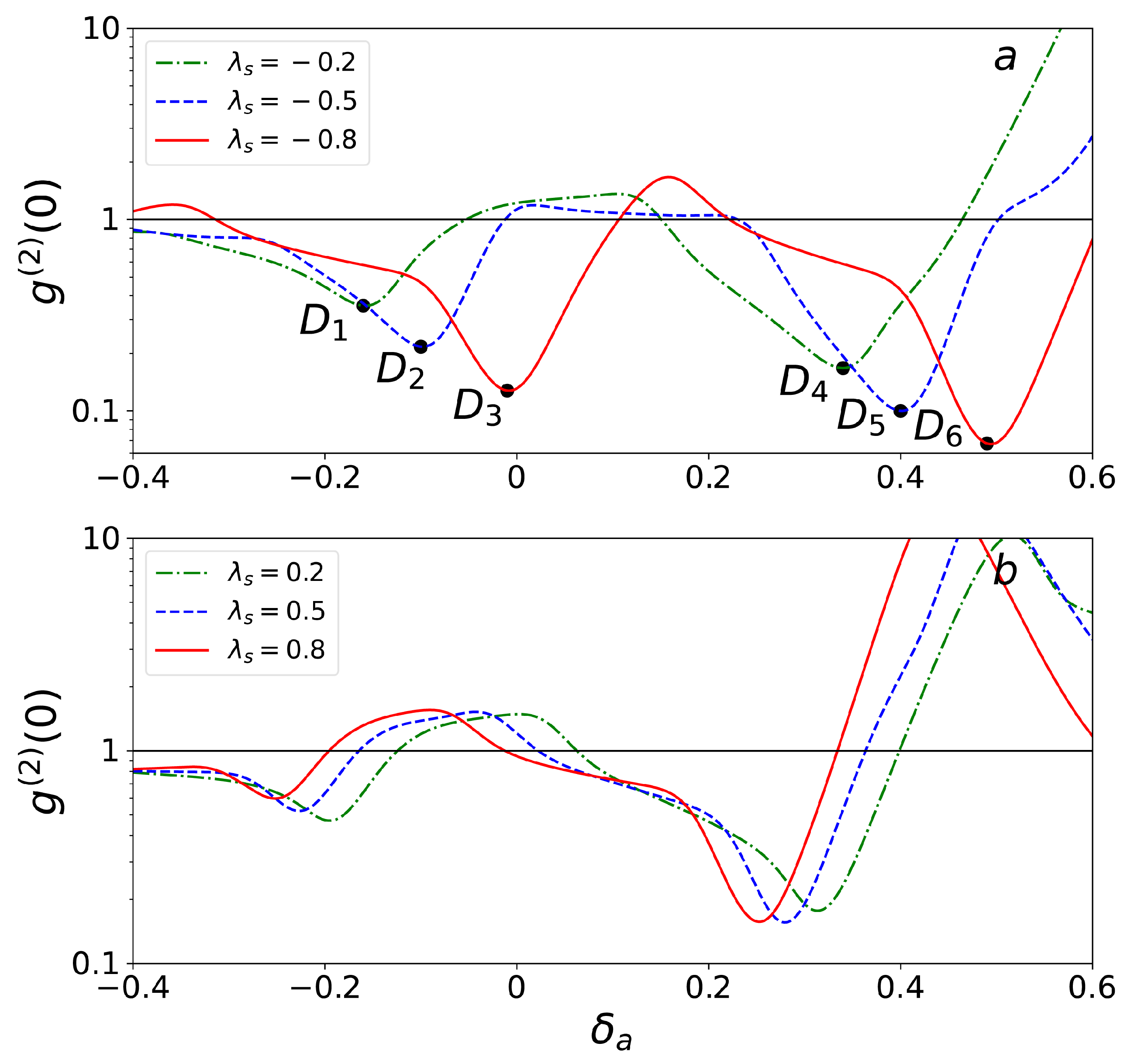
3.2. The Manipulation of Single-Photon Blockade
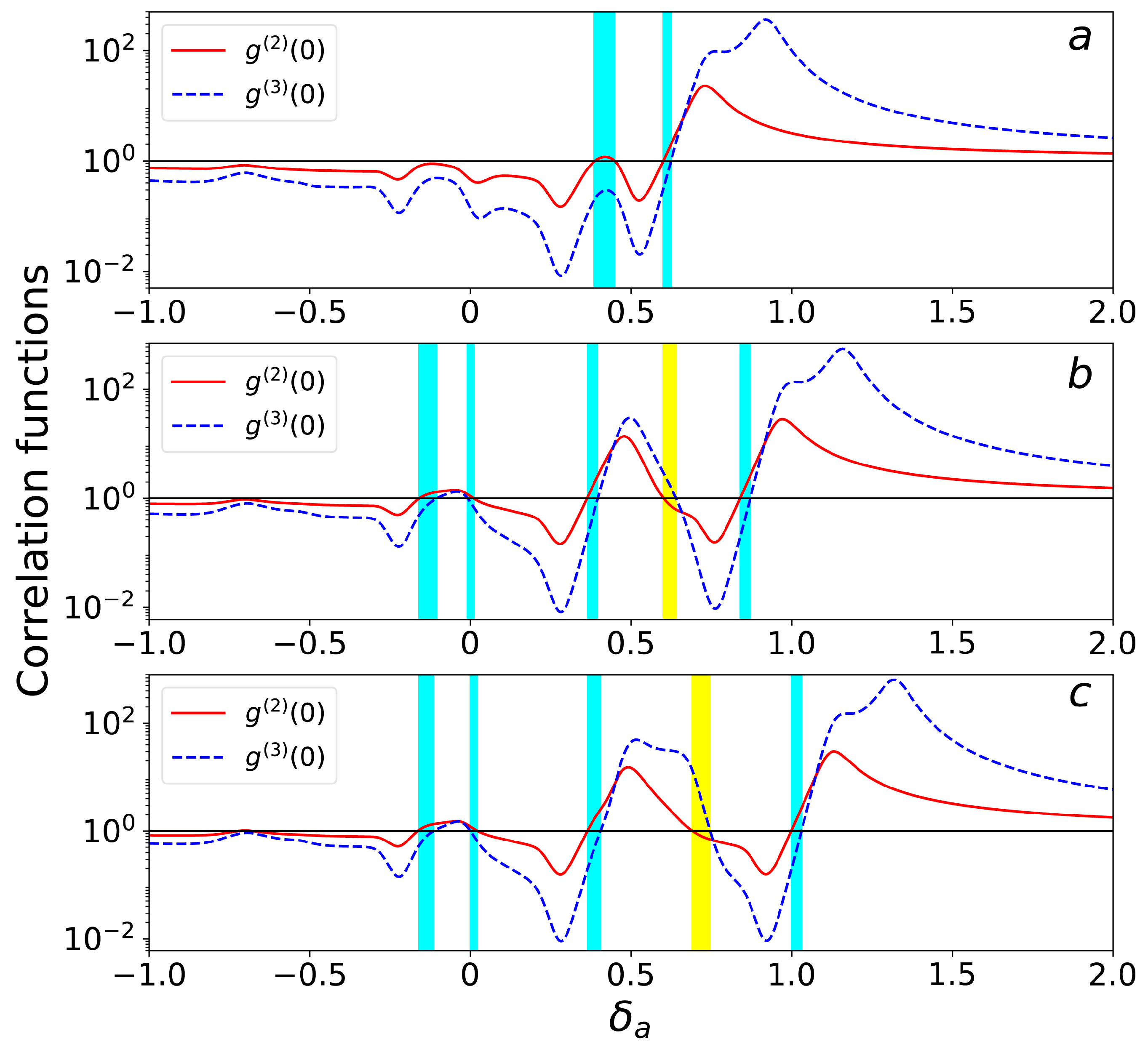
3.3. The Manipulation of Two-Photon Blockade and Non-Standard Photon Blockade
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Diagonalization of the Hamiltonian Htot
Appendix A.1. The First Step of Diagonalization
Appendix A.2. The Second Step of Diagonalization
References
- Ishizaki, K.; Noda, S. Manipulation of photons at the surface of three-dimensional photonic crystals. Nature 2009, 460, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.B.; Cho, J.W.; Lee, Y.J.; Bae, D.; Kim, S.K. High-index-contrast photonic structures: A versatile platform for photon manipulation. Light. Sci. Appl. 2022, 11, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Murray, C.R.; Pohl, T. Coherent photon manipulation in interacting atomic ensem-bles. Phys. Rev. X 2017, 7, 031007. [Google Scholar]
- Zhou, M.G.; Cao, X.Y.; Lu, Y.S.; Wang, Y.; Bao, Y.; Jia, Z.Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Experimental quantum advantage with quantum coupon collector. Research 2022, 2022, 9798679. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.B.; Li, C.L.; Xie, Y.M.; Weng, C.X.; Gu, J.; Cao, X.Y.; Lu, Y.S.; Li, B.H.; Yin, H.L.; Chen, Z.B. Homodyne detection quadrature phase shift keying continuous-variable quantum key dis-tribution with high excess noise tolerance. PRX Quantum 2021, 2, 040334. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Brune, M.; Haroche, S.; Raimond, J.M.; Davidovich, L.; Zagury, N. Manipulation of photons in a cavity by dispersive atom-field coupling: Quantum-nondemolition measurements and genera-tion of “Schrödinger cat” states. Phys. Rev. A 1992, 45, 5193. [Google Scholar] [CrossRef]
- Lu, W.; Zhai, C.; Tang, S. Measuring the pth-Order Correlation Function of Light Field via Two-Level Atoms. Photonics 2022, 9, 727. [Google Scholar] [CrossRef]
- Paul, H. Photon antibunching. Rev. Mod. Phys. 1982, 54, 1061. [Google Scholar] [CrossRef]
- Kimble, H.J.; Dagenais, M. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, S.; Li, J.; Wu, Y. Photon antibunching as a probe of trajectory information of individual neutral atoms traversing an optical cavity. Phys. Rev. A 2021, 104, 053710. [Google Scholar] [CrossRef]
- Steindl, P.; Snijders, H.; Westra, G.; Hissink, E.; Iakovlev, K.; Polla, S.; Frey, J.A.; Norman, J.; Gossard, A.C.; Bowers, J.E.; et al. Artificial coherent states of light by multiphoton interfer-ence in a single-photon stream. Phys. Rev. Lett. 2021, 126, 143601. [Google Scholar] [CrossRef]
- Muñoz-Matutano, G.; Johnsson, M.; Martínez-Pastor, J.; Rivas Góngora, D.; Seravalli, L.; Trevisi, G.; Frigeri, P.; Volz, T.; Gurioli, M. All optical switching of a sin-gle photon stream by excitonic depletion. Commun. Phys. 2020, 3, 29. [Google Scholar] [CrossRef]
- Lounis, B.; Orrit, M. Single-photon sources. Rep. Prog. Phys. 2005, 68, 1129. [Google Scholar] [CrossRef]
- Yuan, Z.; Kardynal, B.E.; Stevenson, R.M.; Shields, A.J.; Lobo, C.J.; Cooper, K.; Beattie, N.S.; Ritchie, D.A.; Pepper, M. Electrically driven single-photon source. Science 2002, 295, 102–105. [Google Scholar] [CrossRef]
- Takeuchi, S. Recent progress in single-photon and entangled-photon generation and applications. Jpn. J. Appl. Phys. 2014, 53, 030101. [Google Scholar] [CrossRef]
- Ma, X.; Fung, C.H.F.; Lo, H.K. Quantum key distribution with entangled photon sources. Phys. Rev. A 2007, 76, 012307. [Google Scholar] [CrossRef]
- Neumann, S.P.; Scheidl, T.; Selimovic, M.; Pivoluska, M.; Liu, B.; Bohmann, M.; Ursin, R. Model for optimizing quantum key distribution with continuous-wave pumped entangled-photon sources. Phys. Rev. A 2021, 104, 022406. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Srinivasan, S.J.; Schmidt, S.; Spietz, L.; Aumentado, J.; Türeci, H.E.; Houck, A.A. Dispersive photon blockade in a superconducting circuit. Phys. Rev. Lett. 2011, 107, 053602. [Google Scholar] [CrossRef]
- Liu, Y.X.; Xu, X.W.; Miranowicz, A.; Nori, F. From blockade to transparency: Control-lable photon transmission through a circuit-QED system. Phys. Rev. A 2014, 89, 043818. [Google Scholar] [CrossRef]
- Birnbaum, K.M.; Boca, A.; Miller, R.; Boozer, A.D.; Northup, T.E.; Kimble, H.J. Photon blockade in an optical cavity with one trapped atom. Nature 2005, 436, 87–90. [Google Scholar] [CrossRef] [PubMed]
- Lang, C.; Bozyigit, D.; Eichler, C.; Steffen, L.; Fink, J.M.; Abdumalikov, A.A., Jr.; Baur, M.; Filipp, S.; da Silva, M.P.; Blais, A.; et al. Observation of resonant photon blockade at micro-wave frequencies using correlation function measurements. Phys. Rev. Lett. 2011, 106, 243601. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.Q.; Nori, F. Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 2013, 88, 023853. [Google Scholar] [CrossRef]
- Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef] [PubMed]
- Brennecke, F.; Ritter, S.; Donner, T.; Esslinger, T. Cavity optomechanics with a Bose-Einstein condensate. Science 2008, 322, 235–238. [Google Scholar] [CrossRef]
- Robb, G.R.M.; Tesio, E.; Oppo, G.L.; Firth, W.J.; Ackemann, T.; Bonifacio, R. Quantum threshold for optomechanical self-structuring in a Bose-Einstein condensate. Phys. Rev. Lett. 2015, 114, 173903. [Google Scholar] [CrossRef]
- Murch, K.W.; Moore, K.L.; Gupta, S.; Stamper-Kurn, D.M. Observation of quan-tum-measurement backaction with an ultracold atomic gas. Nat. Phys. 2008, 4, 561–564. [Google Scholar] [CrossRef]
- Chauhan, A.K.; Biswas, A. Motion-induced enhancement of Rabi coupling between atomic ensembles in cavity optomechanics. Phys. Rev. A 2017, 95, 023813. [Google Scholar] [CrossRef]
- Szirmai, G.; Nagy, D.; Domokos, P. Quantum noise of a Bose-Einstein condensate in an optical cavity, correlations, and entanglement. Phys. Rev. A 2010, 81, 043639. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H. Controlling steady-state bipartite entanglement and quadra-ture squeezing in a membrane-in-the-middle optomechanical system with two Bose-Einstein condensates. Phys. Rev. A 2017, 96, 033631. [Google Scholar] [CrossRef]
- Motazedifard, A.; Dalafi, A.; Naderi, M.H. Ultraprecision quantum sensing and measurement based on nonlinear hybrid optomechanical systems containing ultracold atoms or atomic Bose-Einstein condensate. AVS Quantum Sci. 2021, 3, 024701. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H. Dispersive interaction of a Bose-Einstein condensate with a movable mirror of an optomechanical cavity in the presence of laser phase noise. Phys. Rev. A 2016, 94, 063636. [Google Scholar] [CrossRef]
- Motazedifard, A.; Dalafi, A.; Naderi, M.H.; Roknizadeh, R. Strong quadrature squeezing and quantum amplification in a coupled Bose-Einstein condensate-optomechanical cavity based on parametric modulation. Ann. Phys. 2019, 405, 202–219. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H.; Soltanolkotabi, M.; Barzanjeh, S. Nonlinear effects of atomic collisions on the optomechanical properties of a Bose-Einstein condensate in an optical cavity. Phys. Rev. A 2013, 87, 013417. [Google Scholar] [CrossRef]
- Balewski, J.B.; Krupp, A.T.; Gaj, A.; Peter, D.; Büchler, H.P.; Löw, R.; Hofferberth, S.; Pfau, T. Coupling a single electron to a Bose-Einstein condensate. Nature 2013, 502, 664–667. [Google Scholar] [CrossRef]
- Ng, H.T.; Bose, S. Single-atom-aided probe of the decoherence of a Bose-Einstein con-densate. Phys. Rev. A 2008, 78, 023610. [Google Scholar] [CrossRef]
- Wang, J.; Gacesa, M.; Côté, R. Rydberg electrons in a Bose-Einstein condensate. Phys. Rev. Lett. 2015, 114, 243003. [Google Scholar] [CrossRef]
- Schmidt, R.; Sadeghpour, H.R.; Demler, E. Mesoscopic Rydberg impurity in an atomic quantum gas. Phys. Rev. Lett. 2016, 116, 105302. [Google Scholar] [CrossRef]
- Heidemann, R.; Raitzsch, U.; Bendkowsky, V.; Butscher, B.; Löw, R.; Pfau, T. Rydberg excitation of Bose-Einstein condensates. Phys. Rev. Lett. 2008, 100, 033601. [Google Scholar] [CrossRef]
- Mukherjee, R.; Ates, C.; Li, W.; Wüster, S. Phase-imprinting of Bose-Einstein condensates with Rydberg impurities. Phys. Rev. Lett. 2015, 115, 040401. [Google Scholar] [CrossRef]
- Johnson, T.H.; Yuan, Y.; Bao, W.; Clark, S.R.; Foot, C.; Jaksch, D. Hubbard model for atomic impurities bound by the vortex lattice of a rotating bose-einstein condensate. Phys. Rev. Lett. 2016, 116, 240402. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lu, W. Transient and Fast Generation of Bose-Einstein-Condensate Macroscopic Quantum Superposition States via Impurity Catalysing. Photonics 2022, 9, 622. [Google Scholar] [CrossRef]
- Song, Y.J.; Kuang, L.M. Controlling Decoherence Speed Limit of a Single Impurity Atom in a Bose-Einstein-Condensate Reservoir. Ann. Der Phys. 2019, 531, 1800423. [Google Scholar] [CrossRef]
- Yuan, J.B.; Xing, H.J.; Kuang, L.M.; Yi, S. Quantum non-Markovian reservoirs of atomic condensates engineered via dipolar interactions. Phys. Rev. A 2017, 95, 033610. [Google Scholar] [CrossRef]
- Yuan, J.B.; Kuang, L.M. Quantum-discord amplification induced by a quantum phase transition via a cavity-Bose-Einstein-condensate system. Phys. Rev. A 2013, 87, 024101. [Google Scholar] [CrossRef]
- Li, Z.; Kuang, L.M. Controlling quantum coherence of a two-component Bose-Einstein condensate via an impurity atom. Quantum Inf. Process. 2020, 19, 188. [Google Scholar] [CrossRef]
- Li, Z.; Han, Y.; Kuang, L.M. Complementarity between micro-micro and micro-macro entanglement in a Bose-Einstein condensate with two Rydberg impurities. Commun. Theor. Phys. 2020, 72, 025101. [Google Scholar] [CrossRef]
- Lu, W.; Zhai, C.; Liu, Y.; Song, Y.; Yuan, J.; Tang, S. Berry Phase of Two Impurity Qubits as a Signature of Dicke Quantum Phase Transition. Photonics 2022, 9, 844. [Google Scholar] [CrossRef]
- Lu, W.; Zhai, C.; Liu, Y.; Song, Y.; Yuan, J.; Li, S.; Tang, S. Quantum Speed-Up Induced by the Quantum Phase Transition in a Nonlinear Dicke Model with Two Impurity Qubits. Symmetry 2022, 14, 2653. [Google Scholar] [CrossRef]
- Tan, Q.S.; Xie, Q.T.; Kuang, L.M. Effects of dipolar interactions on the sensitivity of nonlinear spinor-BEC interterometry. Sci. Rep. 2018, 8, 3218. [Google Scholar] [CrossRef]
- Tan, Q.S.; Yuan, J.B.; Jin, G.R.; Kuang, L.M. Near-Heisenberg-limited parameter es-timation precision by a dipolar-Bose-gas reservoir engineering. Phys. Rev. A 2017, 96, 063614. [Google Scholar] [CrossRef]
- Mehboudi, M.; Lampo, A.; Charalambous, C.; Correa, L.A.; García-March, M.Á.; Lewenstein, M. Using polarons for sub-nk quantum nondemolition thermometry in a bose-einstein condensate. Phys. Rev. Lett. 2019, 122, 030403. [Google Scholar] [CrossRef]
- Bruderer, M.; Jaksch, D. Probing BEC phase fluctuations with atomic quantum dots. New J. Phys. 2006, 8, 87. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X.; Chao, S.; Peng, R.; Li, C.; Zhou, L. Simultaneous blockade of a photon, phonon, and magnon induced by a two-level atom. Phys. Rev. A 2020, 101, 063838. [Google Scholar] [CrossRef]
- Alotaibi, M.F.; Khalil, E.M.; Abdel-Khalek, S.; Abd-Rabbou, M.Y.; Omri, M. Effects of the vibrating graphene membrane and the driven classical field on an atomic system coupled to a cavity field. Results Phys. 2021, 31, 105012. [Google Scholar] [CrossRef]
- Alotiabi, M.F.; Khalil, E.M.; Abd-Rabbou, M.Y. Dynamics of an atomic system associated with a cavity-optomechanical system. Results Phys. 2022, 37, 105540. [Google Scholar] [CrossRef]
- Anderson, W.R.; Veale, J.R.; Gallagher, T.F. Resonant dipole-dipole energy transfer in a nearly frozen Rydberg gas. Phys. Rev. Lett. 1998, 80, 249. [Google Scholar] [CrossRef]
- Weimer, H.; Löw, R.; Pfau, T.; Büchler, H.P. Quantum critical behavior in strongly interacting Rydberg gases. Phys. Rev. Lett. 2008, 101, 250601. [Google Scholar] [CrossRef]
- Morsch, O.; Oberthaler, M. Dynamics of Bose-Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179. [Google Scholar] [CrossRef]
- Maschler, C.; Ritsch, H. Quantum motion of laser-driven atoms in a cavity field. Opt. Commun. 2004, 243, 145–155. [Google Scholar] [CrossRef]
- Motazedifard, A.; Dalafi, A.; Bemani, F.; Naderi, M.H. Force sensing in hybrid Bose-Einstein-condensate optomechanics based on parametric amplification. Phys. Rev. A 2019, 100, 023815. [Google Scholar] [CrossRef]
- Timmermans, E.; Tommasini, P.; Hussein, M.; Kerman, A. Feshbach resonanc-es in atomic Bose-Einstein condensates. Phys. Rep. 1999, 315, 199–230. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Maschler, C.; Ritsch, H. Cold atom dynamics in a quantum optical lattice potential. Phys. Rev. Lett. 2005, 95, 260401. [Google Scholar] [CrossRef] [PubMed]
- Treutlein, P.; Steinmetz, T.; Colombe, Y.; Lev, B.; Hommelhoff, P.; Reichel, J.; Greiner, M.; Mandel, O.; Widera, A.; Rom, T.; et al. Quantum information processing in optical lattices and magnetic microtraps. Fortschritte Phys. Prog. Phys. 2006, 54, 702–718. [Google Scholar] [CrossRef]
- Savage, C.M.; Braunstein, S.L.; Walls, D.F. Macroscopic quantum superpositions by means of single-atom dispersion. Opt. Lett. 1990, 15, 628–630. [Google Scholar] [CrossRef]
- Gerry, C.; Knight, P.; Knight, P.L. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Agarwal, G.S.; Puri, R.R.; Singh, R.P. Atomic Schrödinger cat states. Phys. Rev. A 1997, 56, 2249. [Google Scholar] [CrossRef]
- Zheng, S.B.; Guo, G.C. Efficient scheme for two-atom entanglement and quantum in-formation processing in cavity QED. Phys. Rev. Lett. 2000, 85, 2392. [Google Scholar] [CrossRef]
- Xing, Y.; Qi, L.; Zhao, X.; Lü, Z.; Liu, S.; Zhang, S.; Wang, H.F. Quantum transport in a one-dimensional quasicrystal with mobility edges. Phys. Rev. A 2022, 105, 032443. [Google Scholar] [CrossRef]
- Liu, S.; Chen, Y.H.; Wang, Y.; Kang, Y.H.; Shi, Z.C.; Song, J.; Xia, Y. Generation of cat states by a weak parametric drive and a transitionless tracking algorithm. Phys. Rev. A 2022, 106, 042430. [Google Scholar] [CrossRef]
- Li, K.Z.; Xu, G.F. Robust population transfer of spin states by geometric formalism. Phys. Rev. A 2022, 105, 052433. [Google Scholar] [CrossRef]
- Nagy, D.; Domokos, P.; Vukics, A.; Ritsch, H. Nonlinear quantum dynamics of two BEC modes dispersively coupled by an optical cavity. Eur. Phys. J. D 2009, 55, 659–668. [Google Scholar] [CrossRef]
- James, D.F.; Jerke, J. Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 2007, 85, 625–632. [Google Scholar] [CrossRef]
- Hamsen, C.; Tolazzi, K.N.; Wilk, T.; Rempe, G. Two-photon blockade in an at-om-driven cavity QED system. Phys. Rev. Lett. 2017, 118, 133604. [Google Scholar] [CrossRef]
- Bin, Q.; Lü, X.Y.; Bin, S.W.; Wu, Y. Two-photon blockade in a cascaded cavi-ty-quantum-electrodynamics system. Phys. Rev. A 2018, 98, 043858. [Google Scholar] [CrossRef]
- Radulaski, M.; Fischer, K.A.; Lagoudakis, K.G.; Zhang, J.L.; Vučković, J. Photon blockade in two-emitter-cavity systems. Phys. Rev. A 2017, 96, 011801. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A.; Abo, S.I.; Chimczak, G.; Peřina, J., Jr.; Nori, F.; Miranowicz, A. Two-photon blockade and photon-induced tunneling generated by squeezing. Phys. Rev. A 2019, 100, 053857. [Google Scholar] [CrossRef]
- Zhai, C.; Huang, R.; Jing, H.; Kuang, L.M. Mechanical switch of photon blockade and photon-induced tunneling. Opt. Express 2019, 27, 27649–27662. [Google Scholar] [CrossRef]
- Hou, K.; Zhang, Z.; Zhu, C.; Yang, Y. Enhancement of the two-photon blockade effect via Van der Waals interaction. Front. Phys. 2022, 10, 979427. [Google Scholar] [CrossRef]
- Wang, H.; Gu, X.; Liu, Y.X.; Miranowicz, A.; Nori, F. Tunable photon blockade in a hybrid system consisting of an optomechanical device coupled to a two-level system. Phys. Rev. A 2015, 92, 033806. [Google Scholar] [CrossRef]
- Miranowicz, A.; Paprzycka, M.; Liu, Y.X.; Bajer, J.; Nori, F. Two-photon and three-photon blockades in driven nonlinear systems. Phys. Rev. A 2013, 87, 023809. [Google Scholar] [CrossRef]
- Dalafi, A.; Naderi, M.H.; Soltanolkotabi, M. Squeezed-state generation via atomic collisions in a Bose-Einstein condensate inside an optical cavity. J. Mod. Opt. 2014, 61, 1387–1397. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, W. Antibunching Effects in the Hybrid Cavity–Bose–Einstein Condensates System. Photonics 2023, 10, 123. https://doi.org/10.3390/photonics10020123
Li Z, Lu W. Antibunching Effects in the Hybrid Cavity–Bose–Einstein Condensates System. Photonics. 2023; 10(2):123. https://doi.org/10.3390/photonics10020123
Chicago/Turabian StyleLi, Zhen, and Wangjun Lu. 2023. "Antibunching Effects in the Hybrid Cavity–Bose–Einstein Condensates System" Photonics 10, no. 2: 123. https://doi.org/10.3390/photonics10020123
APA StyleLi, Z., & Lu, W. (2023). Antibunching Effects in the Hybrid Cavity–Bose–Einstein Condensates System. Photonics, 10(2), 123. https://doi.org/10.3390/photonics10020123



