Effect of a Femtosecond-Scale Temporal Structure of a Laser Driver on Generation of Betatron Radiation by Wakefield Accelerated Electrons
Abstract
1. Introduction
2. Methods
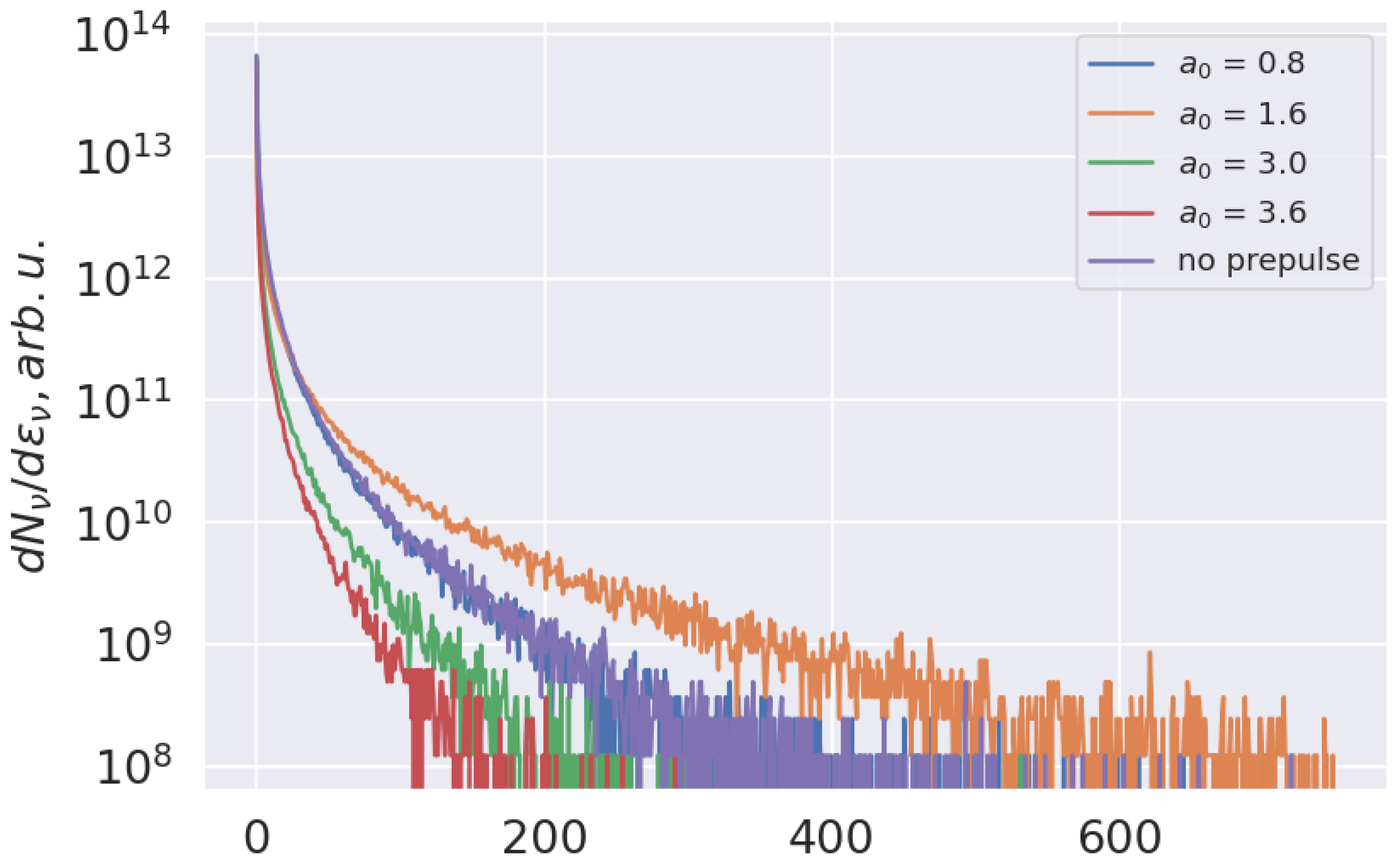
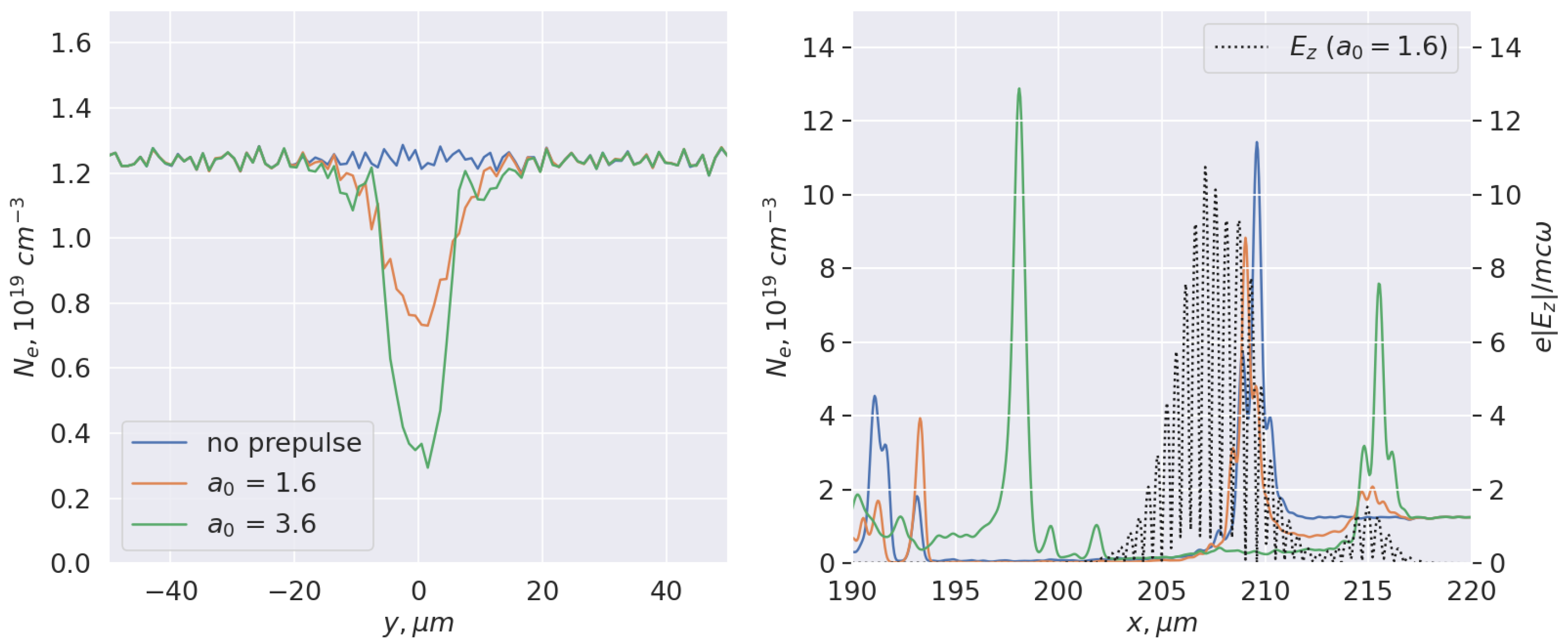
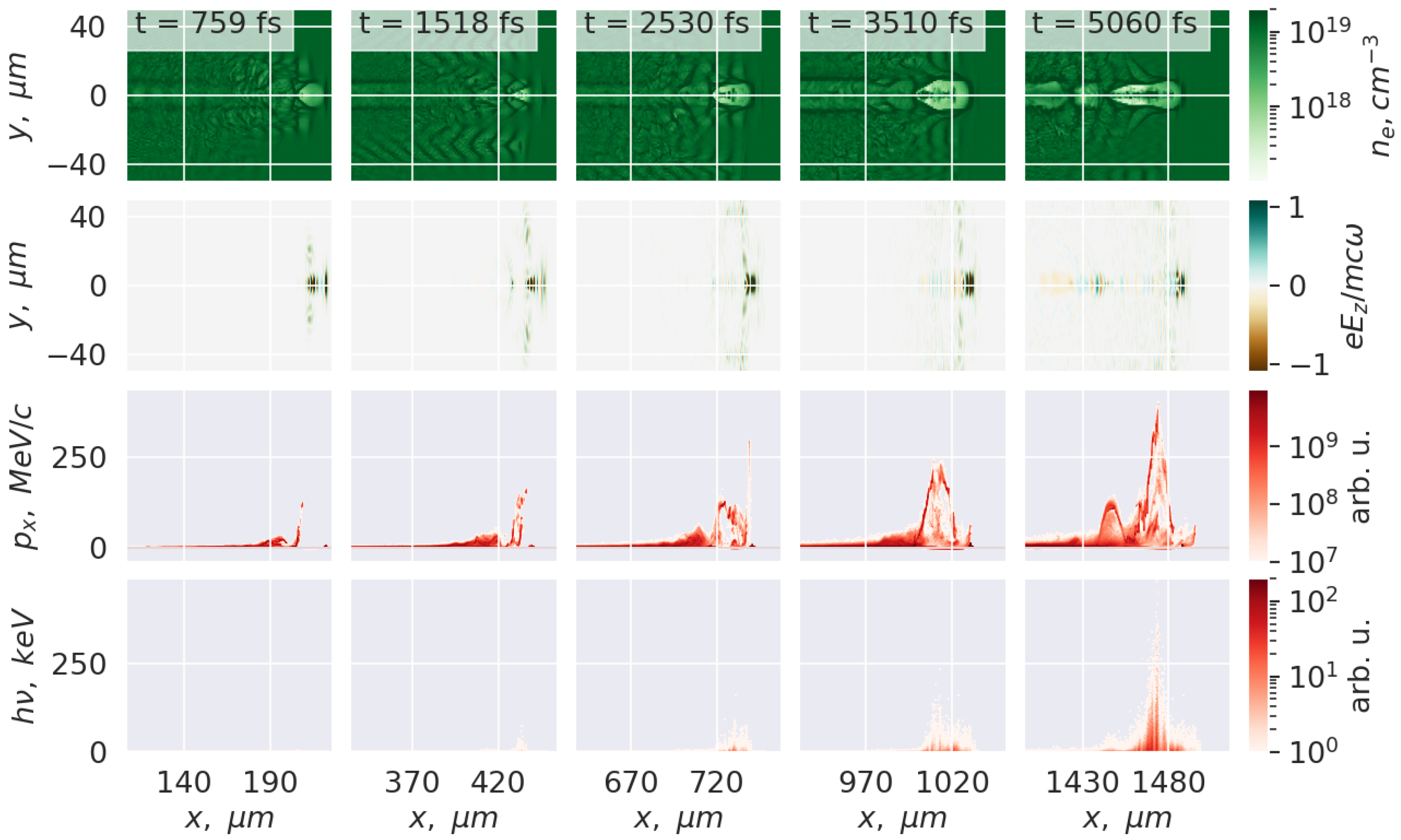
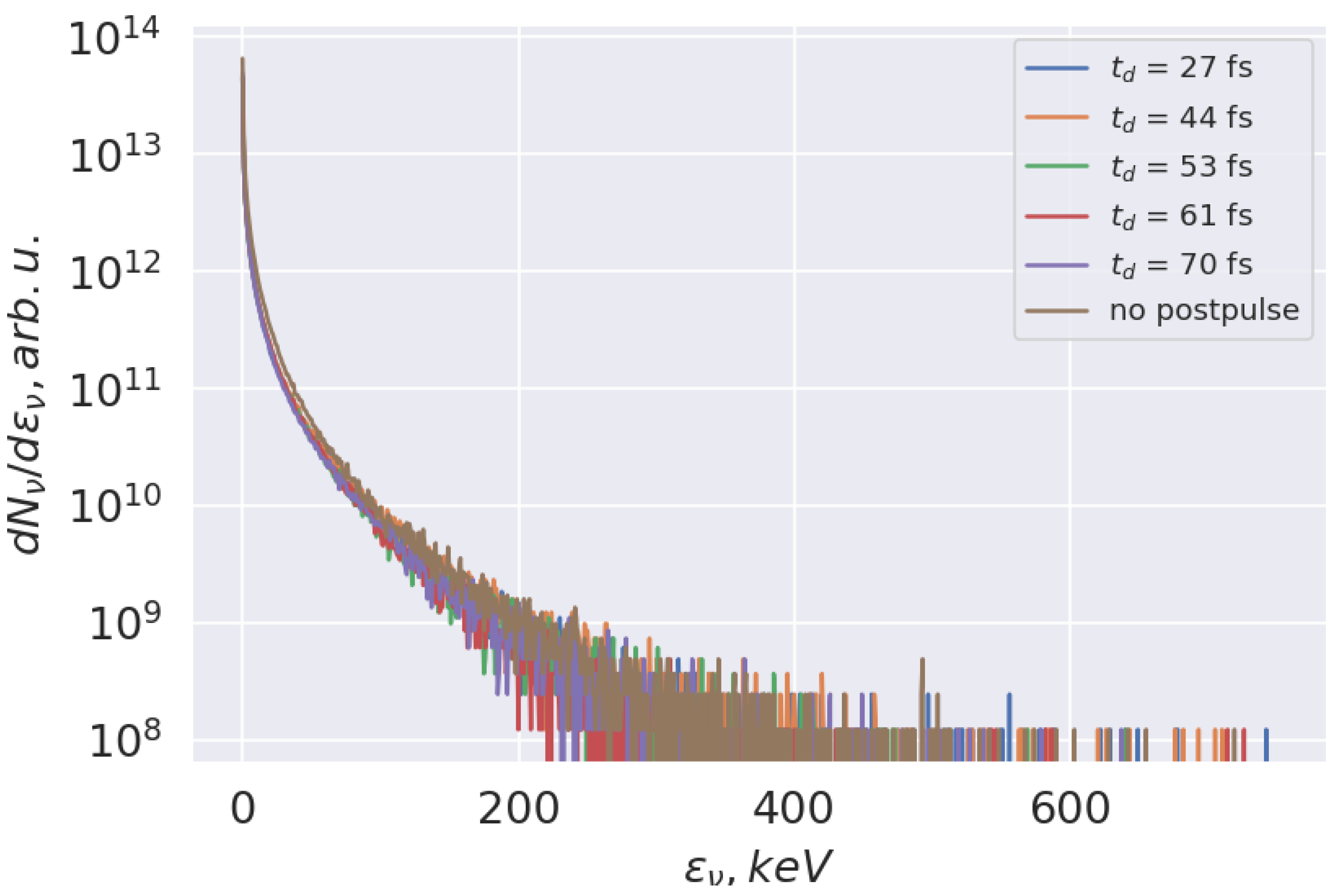
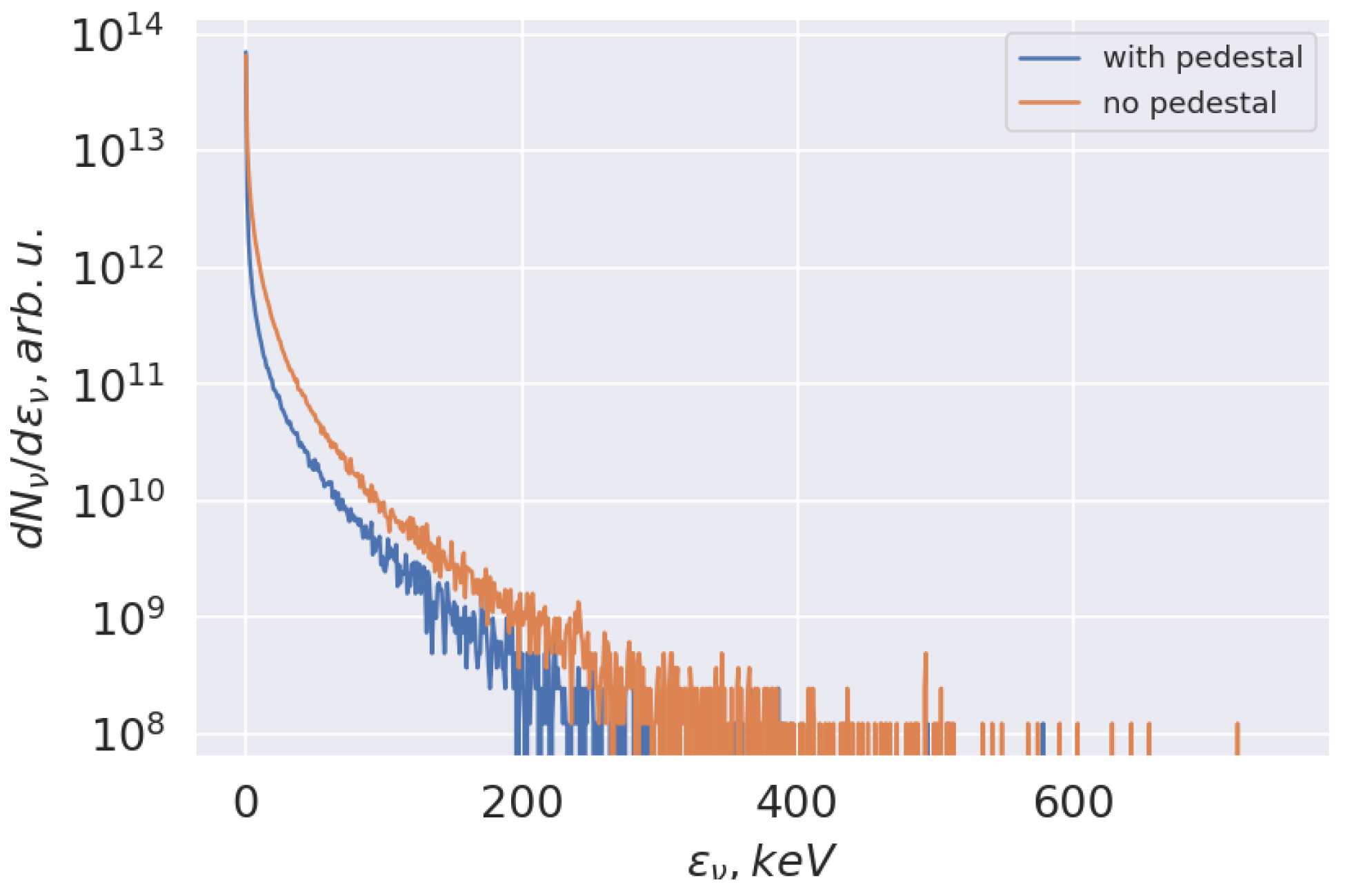
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| FWHM | Full Width at Half Maximum |
References
- Seeck, O.; Murphy, B. X-ray Diffraction: Modern Experimental Techniques; Pan Stanford Publishing: Redwood City, CA, USA, 2015. [Google Scholar]
- Sanchez-Cano, C.; Alvarez-Puebla, R.A.; Abendroth, J.M.; Beck, T.; Blick, R.; Cao, Y.; Caruso, F.; Chakraborty, I.; Chapman, H.N.; Chen, C.; et al. X-ray-based techniques to study the nano–bio interface. ACS Nano 2021, 15, 3754–3807. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Chen, S.; Powers, N.; Haden, D.; Liu, C.; Golovin, G.; Zhang, J.; Zhao, B.; Clarke, S.; Pozzi, S.; et al. Compact source of narrowband and tunable X-rays for radiography. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2015, 350, 106–111. [Google Scholar] [CrossRef]
- Flegentov, V.; Safronov, K.; Gorokhov, S.; Tishchenko, A.; Kovaleva, S.; Potapov, A.; Pavlenko, A. Pulsed laser-plasma gamma radiation source for radiography. Quantum Electron. 2021, 51, 866–872. [Google Scholar] [CrossRef]
- Davis, T.J.; Gao, D.; Gureyev, T.E.; Stevenson, A.W.; Wilkins, S.W. Phase-contrast imaging of weakly absorbing materials using hard X-rays. Nature 1995, 373, 595–598. [Google Scholar] [CrossRef]
- Najmudin, Z.; Kneip, S.; Bloom, M.S.; Mangles, S.P.D.; Chekhlov, O.; Dangor, A.E.; Döpp, A.; Ertel, K.; Hawkes, S.J.; Holloway, J.; et al. Compact laser accelerators for X-ray phase-contrast imaging. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130032. [Google Scholar] [CrossRef]
- Corde, S.; Ta Phuoc, K.; Lambert, G.; Fitour, R.; Malka, V.; Rousse, A.; Beck, A.; Lefebvre, E. Femtosecond X rays from laser-plasma accelerators. Rev. Mod. Phys. 2013, 85, 1. [Google Scholar] [CrossRef]
- Albert, F.; Thomas, A.G.R.; Mangles, S.P.D.; Banerjee, S.; Corde, S.; Flacco, A.; Litos, M.; Neely, D.; Vieira, J.; Najmudin, Z.; et al. Laser wakefield accelerator based light sources: Potential applications and requirements. Plasma Phys. Control. Fusion 2014, 56, 084015. [Google Scholar] [CrossRef]
- Umstadter, D.P. All-laser-driven Thomson X-ray sources. Contemp. Phys. 2015, 56, 417–431. [Google Scholar] [CrossRef]
- Esarey, E.; Shadwick, B.A.; Catravas, P.; Leemans, W.P. Synchrotron radiation from electron beams in plasma-focusing channels. Phys. Rev. E 2002, 65, 056505. [Google Scholar] [CrossRef]
- Kostyukov, I.; Kiselev, S.; Pukhov, A. X-ray generation in an ion channel. Phys. Plasmas 2003, 10, 4818–4828. [Google Scholar] [CrossRef]
- Kiselev, S.; Pukhov, A.; Kostyukov, I. X-ray generation in strongly nonlinear plasma waves. Phys. Rev. Lett. 2004, 93, 135004. [Google Scholar] [CrossRef] [PubMed]
- Albert, F.; Thomas, A.G.R. Applications of laser wakefield accelerator-based light sources. Plasma Phys. Control. Fusion 2016, 58, 103001. [Google Scholar] [CrossRef]
- Lu, W.; Tzoufras, M.; Joshi, C.; Tsung, F.; Mori, W.; Vieira, J.; Fonseca, R.; Silva, L. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys. Rev. Spec. Top.-Accel. Beams 2007, 10, 061301. [Google Scholar] [CrossRef]
- Gordienko, S.; Pukhov, A. Scalings for ultrarelativistic laser plasmas and quasimonoenergetic electrons. Phys. Plasmas 2005, 12, 043109. [Google Scholar] [CrossRef]
- Khazanov, E.A.; Mironov, S.Y.; Mourou, G. Nonlinear compression of high-power laser pulses: Compression after compressor approach. Phys.-Uspekhi 2019, 62, 1096. [Google Scholar] [CrossRef]
- Ginzburg, V.N.; Yakovlev, I.V.; Zuev, A.S.; Korobeynikova, A.P.; Kochetkov, A.A.; Kuz’min, A.A.; Mironov, S.Y.; Shaykin, A.A.; Shaykin, I.A.; Khazanov, E.A. Compression after compressor: Threefold shortening of 200-TW laser pulses. Quantum Electron. 2019, 49, 299–301. [Google Scholar] [CrossRef]
- Ginzburg, V.N.; Yakovlev, I.V.; Zuev, A.S.; Korobeynikova, A.P.; Kochetkov, A.A.; Kuzmin, A.A.; Mironov, S.Y.; Shaykin, A.A.; Shaikin, I.A.; Khazanov, E.A. Two-stage nonlinear compression of high-power femtosecond laser pulses. Quantum Electron. 2020, 50, 331–334. [Google Scholar] [CrossRef]
- Ginzburg, V.; Yakovlev, I.; Zuev, A.; Korobeynikova, A.; Kochetkov, A.; Kuzmin, A.; Mironov, S.; Shaykin, A.; Shaikin, I.; Khazanov, E.; et al. Fivefold compression of 250-TW laser pulses. Phys. Rev. A 2020, 101, 013829. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Fourmaux, S.; Lassonde, P.; Ginzburg, V.N.; Payeur, S.; Kieffer, J.C.; Khazanov, E.A.; Mourou, G. Thin plate compression of a sub-petawatt Ti:Sa laser pulses. Appl. Phys. Lett. 2020, 116, 241101. [Google Scholar] [CrossRef]
- Shaykin, A.; Ginzburg, V.; Yakovlev, I.; Kochetkov, A.; Kuzmin, A.; Mironov, S.; Shaikin, I.; Stukachev, S.; Lozhkarev, V.; Prokhorov, A.; et al. Use of KDP crystal as a Kerr nonlinear medium for compressing PW laser pulses down to 10 fs. High Power Laser Sci. Eng. 2021, 9, e54. [Google Scholar] [CrossRef]
- Kim, J.I.; Kim, Y.G.; Yang, J.M.; Yoon, J.W.; Sung, J.H.; Lee, S.K.; Nam, C.H. Sub-10 fs pulse generation by post-compression for peak-power enhancement of a 100-TW Ti:Sapphire laser. Opt. Express 2022, 30, 8734–8741. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, V.; Yakovlev, I.; Kochetkov, A.; Kuzmin, A.; Mironov, S.; Shaikin, I.; Shaykin, A.; Khazanov, E. 11 fs, 1.5 PW laser with nonlinear pulse compression. Opt. Express 2021, 29, 28297. [Google Scholar] [CrossRef]
- Fourmaux, S.; Lassonde, P.; Mironov, S.Y.; Hallin, E.; Légaré, F.; Maclean, S.; Khazanov, E.A.; Mourou, G.; Kieffer, J.C. Laser wakefield acceleration based x ray source using 225-TW and 13-fs laser pulses produced by thin film compression. Opt. Lett. 2022, 47, 3163. [Google Scholar] [CrossRef] [PubMed]
- Maslov, V.; Bondar, D.; Grigorencko, V.; Levchuk, I.; Onishchenko, I. Control of Characteristics of Self-Injected and Accelerated Electron Bunch in Plasma by Laser Pulse Shaping on Radius, Intensity and Shape. Probl. At. Sci. Technol. 2019, 124, 39–42. [Google Scholar] [CrossRef]
- Surmin, I.A.; Bastrakov, S.I.; Efimenko, E.S.; Gonoskov, A.A.; Korzhimanov, A.V.; Meyerov, I.B. Particle-in-Cell laser-plasma simulation on Xeon Phi coprocessors. Comput. Phys. Commun. 2016, 202, 204–210. [Google Scholar] [CrossRef]
- Gonoskov, A.; Bastrakov, S.; Efimenko, E.; Ilderton, A.; Marklund, M.; Meyerov, I.; Muraviev, A.; Sergeev, A.; Surmin, I.; Wallin, E. Extended particle-in-cell schemes for physics in ultrastrong laser fields: Review and developments. Phys. Rev. E 2015, 92, 023305. [Google Scholar] [CrossRef]
- Zhang, X.; Khudik, V.N.; Shvets, G. Synergistic Laser Wakefield/Direct Laser Acceleration in the Plasma Bubble Regime. Phys. Rev. Lett. 2015, 114, 184801. [Google Scholar] [CrossRef]
- Martyanov, M.; Mironov, S.; Starodubtsev, M.; Soloviev, A.; Kochetkov, A.; Ginzburg, V.; Shaikin, A.; Khazanov, E. Improvement of the focusability of petawatt laser pulses after nonlinear post-compression. J. Opt. Soc. Am. B 2022, 39, 1936. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sladkov, A.D.; Korzhimanov, A.V. Effect of a Femtosecond-Scale Temporal Structure of a Laser Driver on Generation of Betatron Radiation by Wakefield Accelerated Electrons. Photonics 2023, 10, 108. https://doi.org/10.3390/photonics10020108
Sladkov AD, Korzhimanov AV. Effect of a Femtosecond-Scale Temporal Structure of a Laser Driver on Generation of Betatron Radiation by Wakefield Accelerated Electrons. Photonics. 2023; 10(2):108. https://doi.org/10.3390/photonics10020108
Chicago/Turabian StyleSladkov, Andrey D., and Artem V. Korzhimanov. 2023. "Effect of a Femtosecond-Scale Temporal Structure of a Laser Driver on Generation of Betatron Radiation by Wakefield Accelerated Electrons" Photonics 10, no. 2: 108. https://doi.org/10.3390/photonics10020108
APA StyleSladkov, A. D., & Korzhimanov, A. V. (2023). Effect of a Femtosecond-Scale Temporal Structure of a Laser Driver on Generation of Betatron Radiation by Wakefield Accelerated Electrons. Photonics, 10(2), 108. https://doi.org/10.3390/photonics10020108




