Maximizing the Response of a Helium Atom at the Third Harmonic of an Intense Femtosecond Ultraviolet Pulse

Abstract

The optimal regime of three-photon resonant excitation of a helium atom via a femtosecond ultraviolet (UV) pulse was discovered and numerically studied, at which the maximum power of the third harmonic of the UV field is achieved in the spectrum of dipole acceleration (the second time derivative of the induced dipole moment) of the atom. It is shown that the optimal frequency of the UV field nearly coincides with the frequency of the three-photon transition |1s²⟩–|1s2p⟩, taking into account its shift as a result of the dynamic Stark effect, and the intensity of the UV field is dictated by the condition of maximizing the product of the populations of the |1s²⟩ and |1s2p⟩ states, averaged over the time interval during which the UV field is non-zero. For the considered UV field durations, from 10 to 100 cycles of the carrier frequency (from units to tens of femtoseconds), the optimal intensity lies in the range from 10¹⁴ W/cm² to several units of 10¹⁴ W/cm². It is shown that with an optimal choice of the frequency and intensity of the UV field, the dynamics of excitation of bound and continuum states, as well as the shape of the time envelope of the dipole acceleration of the atom, weakly depend on the duration of the UV field envelope; only their time scale changes significantly. In addition, under optimal conditions, the average power of the third harmonic signal in the dipole acceleration spectrum is practically independent of the duration of the UV field envelope.

1. Introduction

The generation of coherent radiation in the vacuum ultraviolet (VUV) and X-ray ranges is one of the topical problems of modern optics. On the one hand, interest in this problem is due to the short period of field oscillations and the possibility of generating radiation pulses of the shortest (attosecond) duration achievable today. On the other hand, the high frequency of radiation, corresponding to the photon energy comparable to or exceeding the ionization potential of an atom, makes it possible to implement regimes of light–matter interaction that are unattainable in the optical range, such as single-photon excitation or ionization of an atom from both the valence and core electronic shells, triggering Auger decay or single-photon excitation of autoionization states [1,2,3,4,5,6,7,8,9,10]. At the same time, the short wavelength of the radiation allows it to be focused into a spot with dimensions significantly smaller than the wavelength of the field in the visible/infrared (IR) range and thereby achieve record spatial resolution [11].

One of the main methods for generating coherent VUV/X-ray radiation is the high-order harmonic generation (HHG) of an optical laser field in gases or solids [12,13]. Initially, HHG was considered primarily as a method for generating a wide-band spectrum of harmonics with photon energies significantly exceeding the ionization potential of an atom. In this case, HHG occurs in the regime of tunneling ionization of the atom and is the result of a three-step process, including the release of an active electron, its acceleration in the laser field, and subsequent recombination with the parent ion [14,15]. However, in recent years, the generation of harmonics of moderate orders with photon energies lower than or on the order of the ionization potential of the atom has also attracted considerable interest [16,17,18,19,20,21,22,23,24]. In this case, HHG occurs in the process of multiphoton excitation and multiphoton ionization of the atom and is largely due to transitions between bound states. The advantages of this regime are the high efficiency of harmonic generation (compared to the tunnel ionization regime) and less stringent requirements for the intensity of the laser field. In this case, as a rule, the driver for harmonic generation is the field of the near or mid-IR range, and the order of multiphoton resonances (if any) is somewhere around ten.

As in the above-mentioned studies, this work considers the generation of harmonics under conditions of multiphoton excitation and multiphoton ionization of the atom. The main attention is paid to the properties of the lowest-order (and most intense) harmonic of the external field, namely the third harmonic. It is assumed that the fundamental frequency lies in the ultraviolet range, and the multiphoton resonance is of low order (third). This regime has significant advantages over the harmonic generation driven by the visible/IR range field. Firstly, the role of multiphoton resonances increases, and the maximum achievable efficiency of generation of below-threshold and near-threshold harmonics (with photon energies lower than or on the order of the ionization potential of the atom) increases as well. Secondly, with an increase in the fundamental frequency, the phase matching of the driving field with the radiation of its harmonics improves, which makes it possible to achieve a higher efficiency of harmonic generation in an extended medium (note, however, that the analysis of macroscopic effects is beyond the scope of this study).

In the 1970s–1990s, a number of theoretical [25,26,27,28,29] and experimental [30,31,32,33,34,35,36,37] studies were published on the generation of low-order (primarily third) harmonics of ultraviolet radiation in gases. The theoretical models used in these studies were based on (a) a phenomenological description of the nonlinear response of the medium (nonlinear susceptibility formalism), (b) a solution of the Schrödinger equation or equations for the elements of the density matrix for a two-, three-, or four-level system, and (c) on the perturbation theory corresponding to the weak field approximation, as well as a combination of these approaches. In the spectrum of the field and excitation amplitudes of stationary states (or elements of the density matrix), only the lowest-order, often the first, second, and third harmonics of the fundamental frequency, were taken into account.

In this work, the response of an atom to an external field is calculated without using the above approximations: the non-perturbative regime of laser–matter interaction is considered, and all possible harmonics of the fundamental frequency are taken into account in the spectrum of the dipole response of the atom. The harmonic generation process is analyzed using the example of helium atoms by solving the time-dependent Schrödinger equation (TDSE) in a given femtosecond UV field and calculating the induced dipole moment of the atom. Two approaches are used. The first involves the expansion of the wave function in terms of a sufficiently large number of bound states of an unperturbed atom, as well as continuum states into which electric dipole transitions from the bound states taken into account are allowed. The second approach is to numerically solve the TDSE from the first principles in a two-dimensional model using the effective one-electron potential.

The study is organized as follows. The description of the theoretical models used, and an analysis of the results obtained are given in Section 2 and Section 3, respectively. In Section 4, the conclusions are given. A significant part of the analytics, as well as the parameters of the models used, are included in the Appendices.

2. Theoretical Model

The consideration in this article is based on the TDSE solution for a helium atom in a given external field. In the electric dipole approximation, the TDSE has the form

$$i\frac{\partial }{\partial t}\left|\Psi \left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2,t\right)\right.〉=\left[{\hat{H}}_0+\hat{\overrightarrow{d}}\cdot \overrightarrow{E}\left(t\right)\right]\left|\Psi \left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2,t\right)\right.〉,$$

(1)

where $\left|\Psi \left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2,t\right)\right.〉$ is the wave function, ${\overrightarrow{r}}_1$ and ${\overrightarrow{r}}_2$ are the radius vectors of electrons in a helium atom, ${\hat{H}}_0$ is the Hamiltonian of an atom in the absence of a field, $\hat{\overrightarrow{d}}$ is the dipole moment operator, and $\overrightarrow{E}\left(t\right)$ is the external (in this case, UV) field. Here and below, atomic units are used. It is noteworthy that for the considered wavelengths of the fundamental frequency UV field, exceeding 100 nm, the dipole approximation is well satisfied [38]. Moreover, since the wavelengths of the emitted harmonics also greatly exceed the atomic dimensions, the atom can be safely considered a point-like emitter [39]. In what follows, we will assume that the UV field is linearly polarized along the z-axis and has the form

$$\overrightarrow{E}\left(t\right)={\overrightarrow{z}}_0{E}_{UV}f(t)\sin (\Omega t),$$

(2)

where ${\overrightarrow{z}}_0$ is the unit vector along the z-axis, $E_{UV}$ and $\Omega$ are the amplitude and frequency of the UV field, respectively, and $f(t)$ is the trapezoidal envelope:

$$f(t)=\left\{\begin{array}{l}0,\hspace{0.17em}\hspace{0.17em}t<0,\\ t/\left(3T\right),\hspace{0.17em}\hspace{0.17em}0\le t\le 3T,\\ 1,\hspace{0.17em}\hspace{0.17em}3T<t<\left(N_{osc}+3\right)T,\\ 1-\left(t-\left[N_{osc}+3\right]T\right)/\left(3T\right),\hspace{0.17em}\hspace{0.17em}\left(N_{osc}+3\right)T\le t\le \left(N_{osc}+6\right)T,\\ 0,\hspace{0.17em}\hspace{0.17em}t>\left(N_{osc}+6\right)T,\end{array}\right.$$

(3)

where $T=2\pi /\Omega$ is the UV field oscillation period. In accordance with Equations (2) and (3), the UV field pulse has a constant amplitude in a time interval lasting N_osc field cycles, while turning on and off the UV field is characterized by a linear increase (decrease) in its amplitude over three field cycles. In what follows, the values N_osc = 10, 30, 50, 70, and 100 are considered (most figures are given for N_osc = 30). The choice of the trapezoidal envelope allows one to simplify the interpretation of the results because this makes it possible to analyze the response of an atom to an external field with a constant amplitude over most of the time interval under consideration. In turn, this allows one to associate each combination of frequency and intensity of the UV field with a fixed ionization rate of the atom and a fixed dynamic Stark shift of energy levels (see Section 3). Note that the absolute duration of the UV field envelope is inversely proportional to its carrier frequency Ω.

As mentioned in the Introduction, the results of the calculations presented in this study were obtained using two approaches to solving the TDSE for a helium atom irradiated with a femtosecond pulse of an ultraviolet field.

The first approach is based on the expansion of the atomic wave function over a limited (sufficiently large) basis of eigenfunctions corresponding to bound states and continuum states into which electric dipole transitions from the considered bound states are allowed. This expansion has the form

$$\left|\Psi \left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2,t\right)\right.〉={\displaystyle \sum _{k=1}^{K_{\max }}{a}_k\left(t\right)\left|k\right.〉}+{\displaystyle \sum _{l=0}^{L_{\max }}{\displaystyle \underset{0}{\overset{\infty }{\int }}d\epsilon \cdot b_l\left(\epsilon ,t\right)\left|\epsilon ,l\right.〉}},$$

(4)

where $\left|k\right.〉\equiv \left|{\psi }_k\left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2\right)\right.〉$ is the spatial part of the wave function of the kth stationary state, $a_k\left(t\right)$ is the temporal factor in the same wave function, which we will further call the excitation amplitude of the state $\left|k\right.〉$, $1\le k\le K_{\max }$, and $b_l\left(\epsilon ,t\right)$ is the excitation amplitude of the continuum state $\left|\epsilon ,l\right.〉$ with energy $\epsilon >0$ and orbital momentum l, $0\le l\le L_{\max }$. 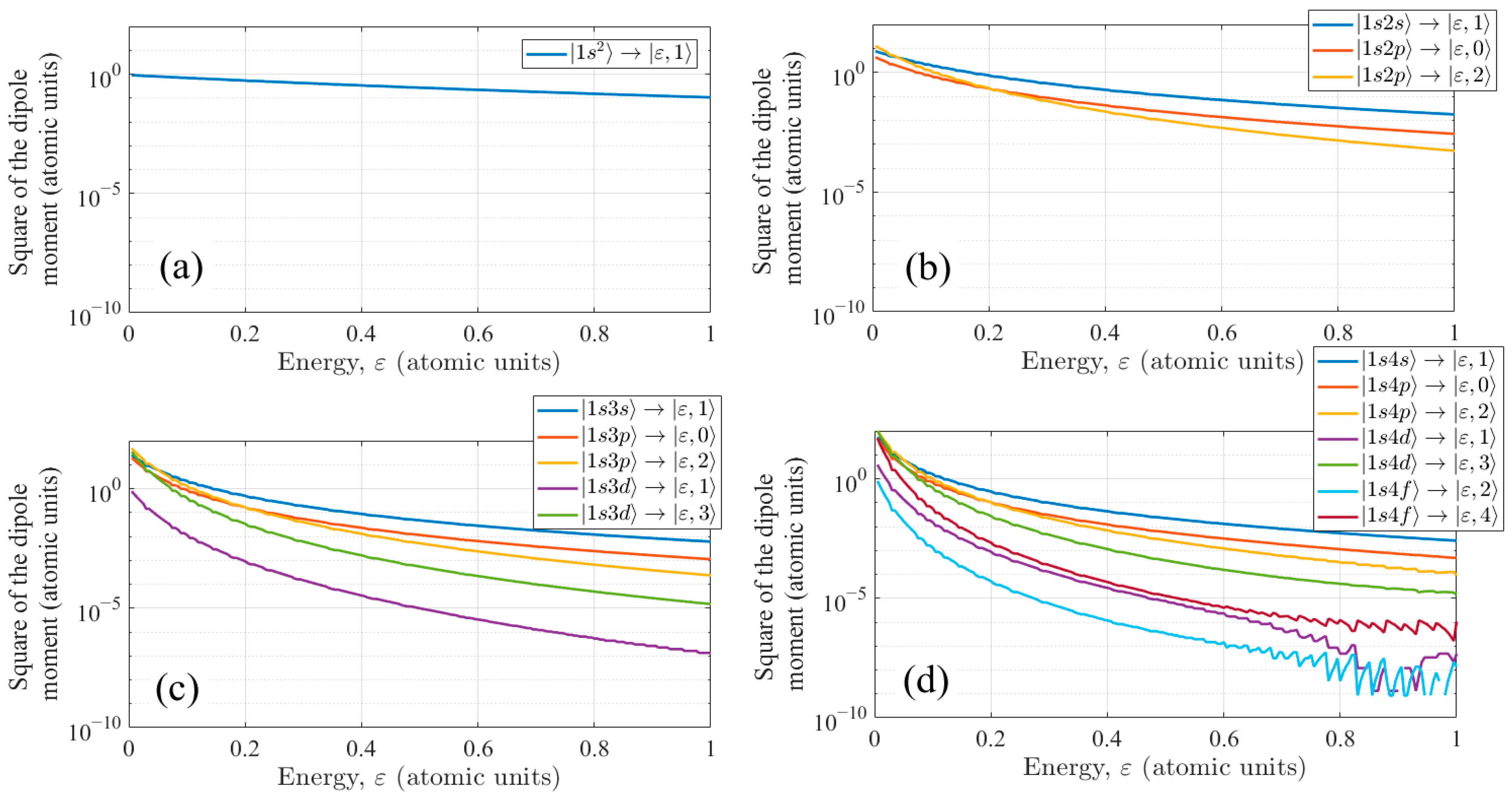In further calculations, the expansion of the wave function takes into account the first 10 bound states of the helium atom (K_max = 10), corresponding to the values of the principal quantum number n = 1,2,3,4 and the projection of the orbital momentum of the atom onto the field polarization direction m = 0 (electric dipole transitions from ground state into states with m ≠ 0 in a linearly polarized field are prohibited by selection rules). Namely, states $\left|1s^2\right.〉=\left|1\right.〉$, $\left|1s2s\right.〉=\left|2\right.〉$, $\left|1s2p\right.〉=\left|3\right.〉$, $\left|1s3s\right.〉=\left|4\right.〉$, $\left|1s3p\right.〉=\left|5\right.〉$, $\left|1s3d\right.〉=\left|6\right.〉$, $\left|1s4s\right.〉=\left|7\right.〉$, $\left|1s4p\right.〉=\left|8\right.〉$, $\left|1s4d\right.〉=\left|9\right.〉$, and $\left|1s4f\right.〉=\left|10\right.〉$ are taken into account (for brevity, here and below, the value of the projection of the orbital momentum of the atom m = 0 is not given in the designation of states). Among the continuum states, those with orbital momentum from 0 to L_max = 4 (s-, p-, d-, f-, and g-waves) are taken into account. This set of states makes it possible to quite accurately consider one-, two-, three-, four-, and five-photon transitions from the ground to lower-bound states $\left|1s2s\right.〉$ and $\left|1s2p\right.〉$ (transitions to higher-lying states are described with less accuracy). Note that the time dependences $a_k\left(t\right)$ take into account oscillations of the phase of the wave function at the natural frequencies of stationary states, which in the atomic system of units are equal to ${\mathrm{E}}_k$, where ${\mathrm{E}}_k$ is the energy of the kth stationary state in the absence of a field (state energies and other constants used are given in Appendix A). Accordingly, depending on the ratio of the values of ${\mathrm{E}}_k$ and $\Omega$, even in a weak UV field limit, the excitation amplitudes can be fast or slow functions of time on the scale of the UV field cycle.

Further, the excitation amplitudes of bound states are decomposed into harmonics of the UV field:

$$a_k\left(t\right)={\displaystyle \sum _{n=-\infty }^{\infty }{a}_{k,n}\left(t\right)\exp \left(-in\Omega t\right)},$$

(5)

where $a_{k,n}\left(t\right)$ is the Fourier component of the excitation amplitude of the kth bound stationary state.

To take into account the multiphoton ionization of an atom from the bound states under consideration, the approximation of the adiabatic exclusion of continuum states is used [40], which primarily corresponds to not taking into account transitions between continuum states. In addition, reverse transitions from continuum states to bound states are also not considered. These approximations make it possible to express the excitation amplitudes of continuum states $\left|\epsilon ,l\right.〉$ through the Fourier components of the excitation amplitudes of bound states $a_{k,n}\left(t\right)$. Ultimately, a closed system of linear differential equations for $a_{k,n}\left(t\right)$ can be written, which takes into account the decrease in absolute values of $a_{k,n}\left(t\right)$ as a result of ionization. These equations have the form

$$\frac{d{a}_{k,n}}{dt}=-\left[i\left({\mathrm{E}}_k-n\Omega \right)+{\gamma }_{k,n}(t)\right]a_{k,n}+\frac{1}{2}{\displaystyle \sum _{s=1}^{K_{\max }}f(t)E_{UV}{d}_{sk}^{(z)}\left(a_{s,n-1}-a_{s,n+1}\right)},$$

(6)

where $d_{sk}^{(z)}$ is the projection of the dipole moment of the transition from state |s〉 to state |k〉 on the z-axis, and ${\gamma }_{k,n}(t)$ is the ionization rate of the nth Fourier component of the kth state. Using the residue theory, the following expression can be obtained for ${\gamma }_{k,n}(t)$:

$$\begin{array}{r}{\gamma }_{k,n}(t)=\frac{\pi }{4}{E}_{UV}^2{f}^2(t){\displaystyle \sum _{l=0}^{L_{\max }}\left[{\left|\left.〈k\right|{\hat{d}}_z\left|{\mathrm{E}}_k+(n-1)\Omega ,l\right.〉\right|}^2\theta \left({\mathrm{E}}_k+(n-1)\Omega \right)+\right.}\\ \left.+{\left|\left.〈k\right|{\hat{d}}_z\left|{\mathrm{E}}_k+(n+1)\Omega ,l\right.〉\right|}^2\theta \left({\mathrm{E}}_k+(n+1)\Omega \right)\right],\end{array}$$

(7)

where ${\hat{d}}_z$ is the z-projection of the dipole moment operator, and $\theta (x)$ is the Heaviside unit step function. The derivation of Equations (6) and (7) is given in Appendix B.

Equations (6) and (7) were solved numerically using the fourth order one-step explicit Runge–Kutta method using the following initial conditions:

$$a_{1,0}\left(0\right)=1\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}{a}_{k,n}\left(0\right)=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}\hspace{0.17em}\mathrm{any}\hspace{0.17em}\hspace{0.17em}\left\{k,n\right\}\ne \left\{1,0\right\},$$

(8)

which imply that before exposure to the UV field, the atom is in the ground state $\left|1s^2\right.〉$ with energy ${\mathrm{E}}_1$.

This approach is a simplified and less resource-intensive implementation of the SSEA (state-specific expansion approach) method [41,42]. It makes it possible to quite accurately describe the component of the dipole response of an atom to an external field that dominates in the considered spectral range of below-threshold and near-threshold harmonics (see, for example, [43]) and is caused by transitions between bound states,

$$d_{bb}\left(t\right)\equiv \left.〈\Psi \right|{\hat{d}}_z{\left|\Psi \right.〉}_{bb}={\displaystyle \sum _{k,s=1}^{K_{\max }}{d}_{sk}^{(z)}{\displaystyle \sum _{n,m}{a}_{k,n}^{*}(t)a_{s,m}(t)\exp \left[-i\left(m-n\right)\Omega t\right]}}.$$

(9)

In Formula (9), the index bb of the induced dipole moment of an atom indicates transitions between bound states, the indices k and s number the stationary states taken into account, and the indices n and m number their Fourier components. Note that within the framework of this approach, the response of the atom due to transitions between continuum states, as well as from continuum to bound states, is not taken into account.

As usual in strong-field physics, the response of an atom to an external field will be characterized by dipole acceleration,

$${\ddot{d}}_{bb}\left(t\right)\equiv \frac{d^2}{d{t}^2}\left.〈\Psi \right|{\hat{d}}_z{\left|\Psi \right.〉}_{bb}.$$

(10)

This approach allows one to analyze the contributions of certain stationary states to the generation of harmonics and take into account the properties of a real multielectron atom (through the energies of stationary states and the dipole moments of transitions between them) by choosing the correct basis functions. For this purpose, in this study, we used the spectroscopic characteristics of a three-dimensional two-electron helium atom, calculated using the multi-configuration Hartree–Fock method (see Appendix A). Their calculation error does not exceed several percent relative to experimental data [44].

The second approach used in this article is to solve the TDSE from first principles in a two-dimensional model of a one-electron atom with an effective potential $U\left(x,z\right)$, reproducing the binding energies of ground state $\left|1s^2\right.〉$ and lowest-excited bound states $\left|1s2s\right.〉$ and $\left|1s2p\right.〉$:

$$i\frac{\partial }{\partial t}\Psi \left(x,z,t\right)=\left[-\frac{1}{2}\frac{{\partial }^2}{\partial x^2}-\frac{1}{2}\frac{{\partial }^2}{\partial z^2}+\frac{i}{c}{A}_z\left(t\right)\frac{\partial }{\partial z}+U\left(x,z\right)\right]\Psi \left(x,z,t\right),$$

(11)

where $A_z\left(t\right)=c{\displaystyle \underset{-\infty }{\overset{t}{\int }}E\left(t^{\prime }\right)d{t}^{\prime }}$ is the vector potential of the UV field, c is the speed of light in vacuum, and

$$U\left(x,z\right)=-\frac{1+\left(1+8.125r\right)e^{-8.125r}}{\sqrt{r^2+0.01}}+\frac{0.6r^6}{r^8+{10}^{-4}},r=\sqrt{x^2+z^2}.$$

(12)

The energies of the lowest stationary states and the dipole moments of transitions between them calculated in this model are given in Appendix A.

This approach has less accuracy in describing the dynamics of the localized part of the atomic wave function but takes into account recombination and all possible transitions between states of the continuum. Accordingly, the dipole response of an atom to an external field and the contribution from transitions between bound states contain components due to transitions from continuum to bound states (recombination) and transitions between continuum states. The dipole acceleration of an atom is calculated using Ehrenfest’s theorem:

$$\ddot{d}\left(t\right)\equiv E\left(t\right)+{\displaystyle \int {\Psi }^{*}\frac{\partial U}{\partial z}\Psi dx}dz,$$

(13)

where integration is carried out over the entire computational domain.

The purpose of this study is to analyze the physical mechanisms that ensure the maximization of the third harmonic energy in the spectrum of the dipole acceleration of the atom. Both approaches correspond to this goal and provide a qualitatively correct description of the process under study.

3. Calculation Results

As was shown in [45], the approaches to solving the TDSE used in this study give similar time dependences of the probability of ionization of a helium atom in a UV field with an intensity I_UV = 10¹⁴ W/cm². In the first approach, based on the expansion of the wave function in terms of the basis of stationary states, the probability of ionization is determined as

$$W_{ion}^{(1)}(t)=1-{\displaystyle \sum _{k=1}^{K_{\max }}{\left|a_k(t)\right|}^2},$$

(14)

whereas within the framework of the second approach, based on solving a two-dimensional one-electron TDSE from first principles, it has the form

$$W_{ion}^{(2)}(t)=1-{\displaystyle \underset{A}{\iint }{\left|\Psi (x,z)\right|}^{2}dxdz},$$

(15)

where the integration is carried out inside a square with side A = 100 a.u., in the center of which the core of the He atom is located. In this case, the wave functions of bound states with principal quantum numbers n = 1, 2, 3, 4 are completely contained within the integration region.

As follows from Figure 1, the frequency dependences of the ionization probability are also qualitatively similar. Figure 1 shows the probability of ionization of an atom at the end of a UV field pulse with a peak intensity I_UV = 10¹⁴ W/cm² and a constant-amplitude interval duration equal to 30 UV field cycles (N_osc = 30) as a function of its frequency. The frequency of the UV field is scanned in a range 0.18 < Ω < 0.4 that covers resonances with two-, three-, and four-photon transitions from the ground to excited bound states and corresponds to the wavelength range of the UV field from 114 nm to 254 nm. The blue curve shows the solution obtained based on expansion (4), and the red curve is based on the two-dimensional one-electron model.

As follows from Figure 1, multiphoton resonances are reproduced in both models, but their frequencies are slightly different. This is due to (a) the neglect of highly excited bound states and the use of the adiabatic continuum exclusion approximation when expanding the wave function in stationary states and (b) the difference in the dipole moments of the transitions, as well as energies of highly excited bound states, in a two-dimensional one-electron model from the corresponding parameters of a real helium atom. The best agreement in the probability of atomic ionization is achieved for a three-photon transition from state $\left|1s^2\right.〉$ to state $\left|1s2p\right.〉$, as well as two- and four-photon transitions to state $\left|1s2s\right.〉$, which is explained by the highest accuracy of both models in describing these transitions. The accuracy of the approach based on the expansion of the wave function in stationary states is due to the low probability of transitions from ground state $\left|1s^2\right.〉$ to disregarded intermediate states with n ≥ 5 during the three-photon excitation of state $\left|1s2p\right.〉$ or the two/four-photon excitation of state $\left|1s2s\right.〉$ in a real helium atom. At the same time, the two-dimensional model of the helium atom is constructed in such a way as to reproduce the energies of states $\left|1s^2\right.〉$, $\left|1s2s\right.〉$, and $\left|1s2p\right.〉$ with few percent accuracy. The dipole moments of transitions between them are reproduced with lower, but still reasonable accuracy of tens of percent (see Appendix A). Taken together with the fact that the three-photon transition to state $\left|1s2p\right.〉$ predominantly occurs through state $\left|1s2s\right.〉$, while the two- and four-photon transitions to state $\left|1s2s\right.〉$ occur through state $\left|1s2p\right.〉$, this determines the accuracy of the two-dimensional model in describing these transitions.

Let us consider in more detail the region of resonances with three-photon transitions from state $\left|1s^2\right.〉$ to the p- and f-states taken into account, 0.25 < Ω < 0.3, which corresponds to the wavelength range of the UV field from 153 nm to 183 nm. Figure 2 shows the dependence of the probability of ionization of an atom at the end of a UV field pulse on its frequency and peak intensity, calculated by expanding the atomic wave function over stationary states. Similar to Figure 1, this figure is given for UV field pulses with a constant amplitude interval duration equal to 30 carrier cycles (N_osc = 30). Note that the blue curve in Figure 1 in the frequency range 0.25 < Ω < 0.3 represents a cross-section of Figure 2 for an intensity value of 10¹⁴ W/cm². The Keldysh parameter in Figure 2 varies from 1.99 (Ω = 0.3, I_UV = 10¹⁵ W/cm²) to 23.9 (Ω = 0.25, I_UV = 10¹³ W/cm²); hence, the ionization regime is multiphoton.

As follows from Figure 2, (i) the highest probability of ionization is achieved in the vicinity of the frequencies of three-photon transitions, (ii) the absolute maximum corresponds to the vicinity of the transition |1s²〉–|1s2p〉 frequency; with increasing field intensity, (iii) the probability of ionization increases, and (iv) the resonances broaden and shift in frequency.

Next, we will focus on the resonance with the three-photon transition |1s²〉–|1s2p〉, which is characterized by the highest probability of atomic ionization and is most accurately described within the framework of the models used. For each fixed intensity of the UV field, we determine the resonance frequency using the method of multiphoton photoionization spectroscopy [46] based on the position of the maximum probability of atomic ionization in the vicinity of the frequency of the three-photon transition between the unperturbed states |1s²〉 and |1s2p〉. The dependence of the transition frequency on the UV field intensity obtained in this way is shown in Figure 2 by a black solid curve.

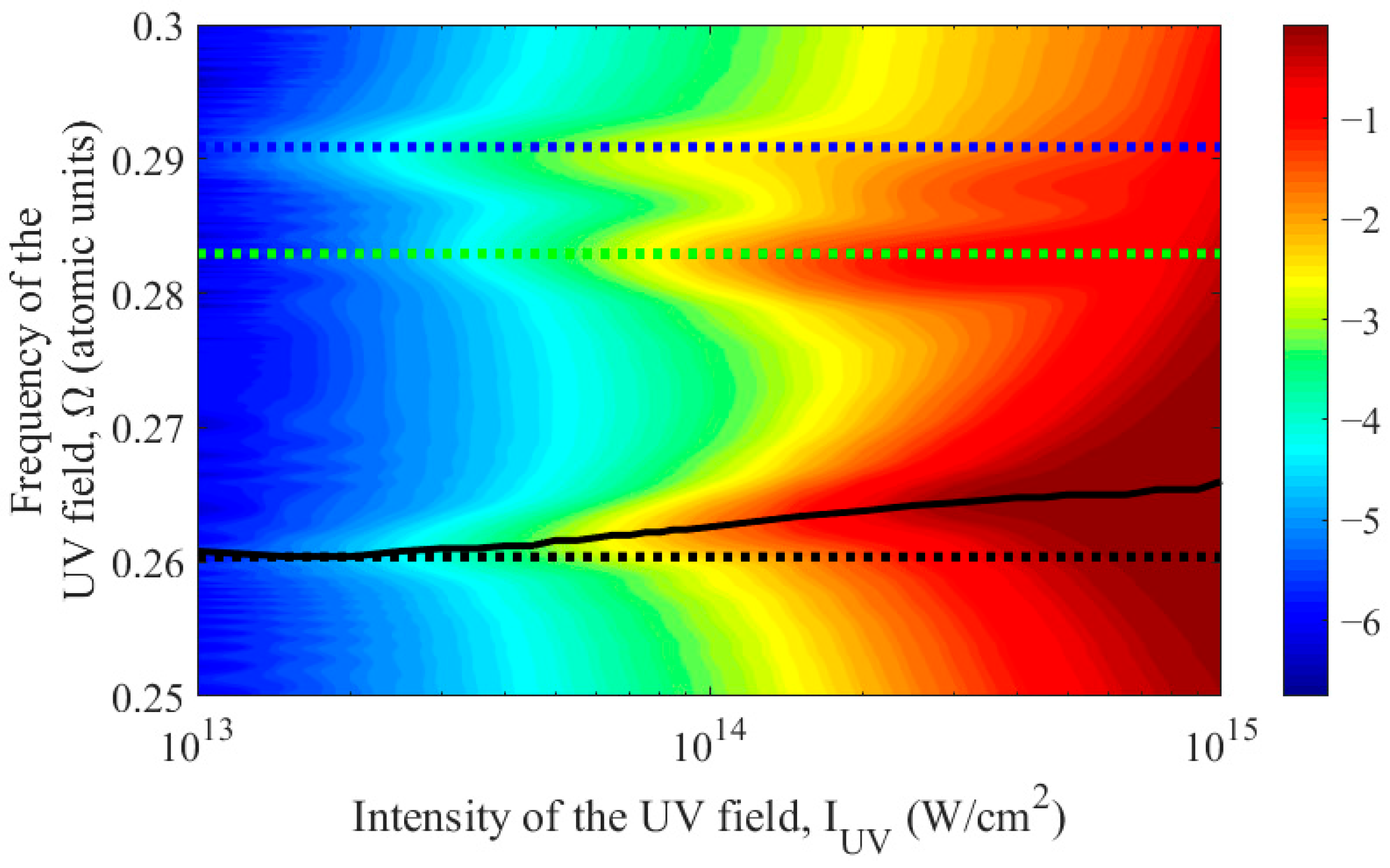
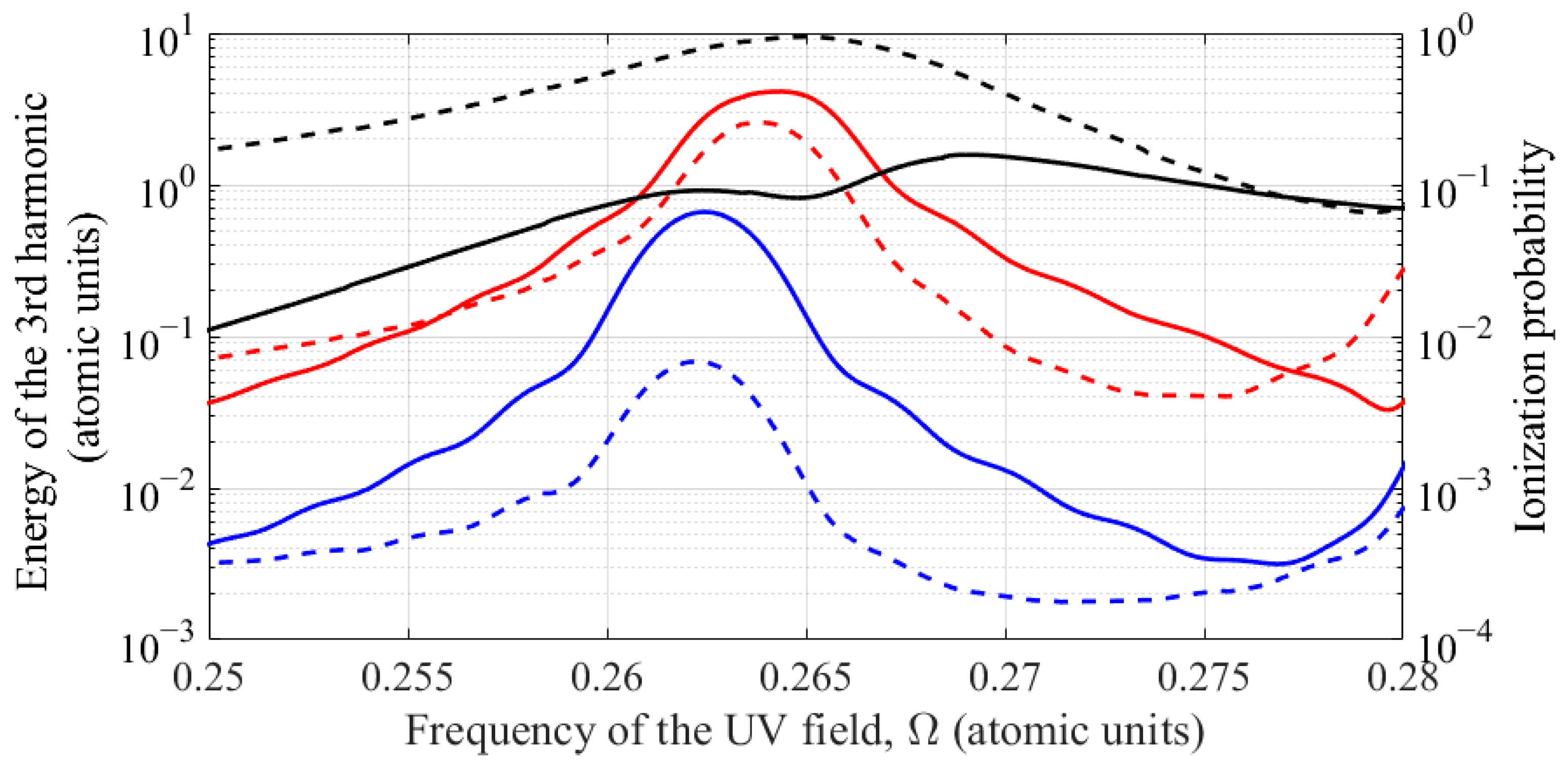
An increase in the probability of atomic ionization with increasing UV field intensity is accompanied by real and virtual excitation of bound states. As a consequence, the response of the atom to the UV field (dipole acceleration) is enriched in harmonics of the fundamental frequency. Figure 3 shows the dependence of the energy concentrated in the spectral component of the dipole acceleration of an atom (10) at the frequency of the third harmonic of the UV field (the method for calculating this quantity is described in Appendix C) on its frequency and intensity. Calculations were made for the duration of the interval of constant amplitude in the UV field envelope equal to 30 carrier cycles (N_osc = 30).

Two remarks should be made here. The energy (time-integrated square of the amplitude) of the third harmonic in the dipole acceleration spectrum was chosen as the parameter under study rather than its peak power spectral density or peak intensity. This is because, under certain conditions, the spectral and time dependences of the harmonic signal may have several maxima of comparable amplitude. In particular, this case is observed under conditions of Rabi oscillations between the resonant states of a multiphoton transition [47]. The second remark concerns the free-induction decay. Under conditions of three-photon resonance, the excited state |1s2p〉 of the atom, coupled with a dipole-allowed transition with the ground state |1s²〉, is effectively populated. As a result, after the end of the UV field pulse, the atom continues to emit at the frequency of transition |1s²〉–|1s2p〉, close to the third harmonic frequency (however, slightly different from it in the absence of a field). This radiation corresponds to free-induction decay (for details, see [48,49]). In order to separate it from the third harmonic radiation, the dipole acceleration of the atom, calculated using Formula (10) or (13), is multiplied by a temporary mask, which is non-zero only in the presence of a UV field (for more details, see Appendix C).

Similar to Figure 2, the dotted lines in Figure 3 indicate the frequencies of three-photon transitions to unperturbed states of the atom, and the solid black curve indicates the resonance frequency of the three-photon transition |1s²〉–|1s2p〉 in the UV field, determined by the maximum probability of ionization. The UV field frequency that maximizes the third harmonic energy in the dipole acceleration spectrum for a given field intensity is plotted in Figure 3 with the dashed cyan curve. As follows from Figure 3, the maximum energy of the third harmonic in the dipole acceleration spectrum is achieved at a UV field intensity I_UV = 2 × 10¹⁴ W/cm² and a frequency Ω = 0.2644 a.u. This frequency is in close proximity to the resonant frequency, Ω_res = 0.2638 a.u., of the three-photon transition to the |1s2p〉 state in the presence of a UV field of given intensity (in this case, the detuning from resonance is about 1/3 of the half-width of the resonance curve in the frequency dependence of the probability of ionization of an atom). For the specified optimal parameters, the probability of ionization at the end of the UV field pulse is approximately 24%.

As the UV field intensity decreases, the third harmonic energy (Figure 3) and, in particular, the probability of atomic ionization (Figure 2) quickly decreases. In this case, the frequency that maximizes the harmonic energy practically coincides with the frequency of the resonant three-photon transition |1s²〉–|1s2p〉 in the UV field. At the same time, for a UV field intensity exceeding the optimal value I_UV = 2 × 10¹⁴ W/cm², the value of the maximum achievable energy of the third harmonic decreases, while the detuning of the optimal (for a given intensity) frequency of the UV field from the frequency of the three-photon resonance with the |1s²〉–|1s2p〉 transition increases. With a further increase in the intensity of the UV field, the frequency that maximizes the energy of the third harmonic in the spectrum of the dipole acceleration of the atom shifts to the region of resonances with the transitions |1s²〉–|1s3p〉, |1s²〉–|1s4p〉, and |1s²〉–|1s4f〉, while the harmonic energy continues to decrease.

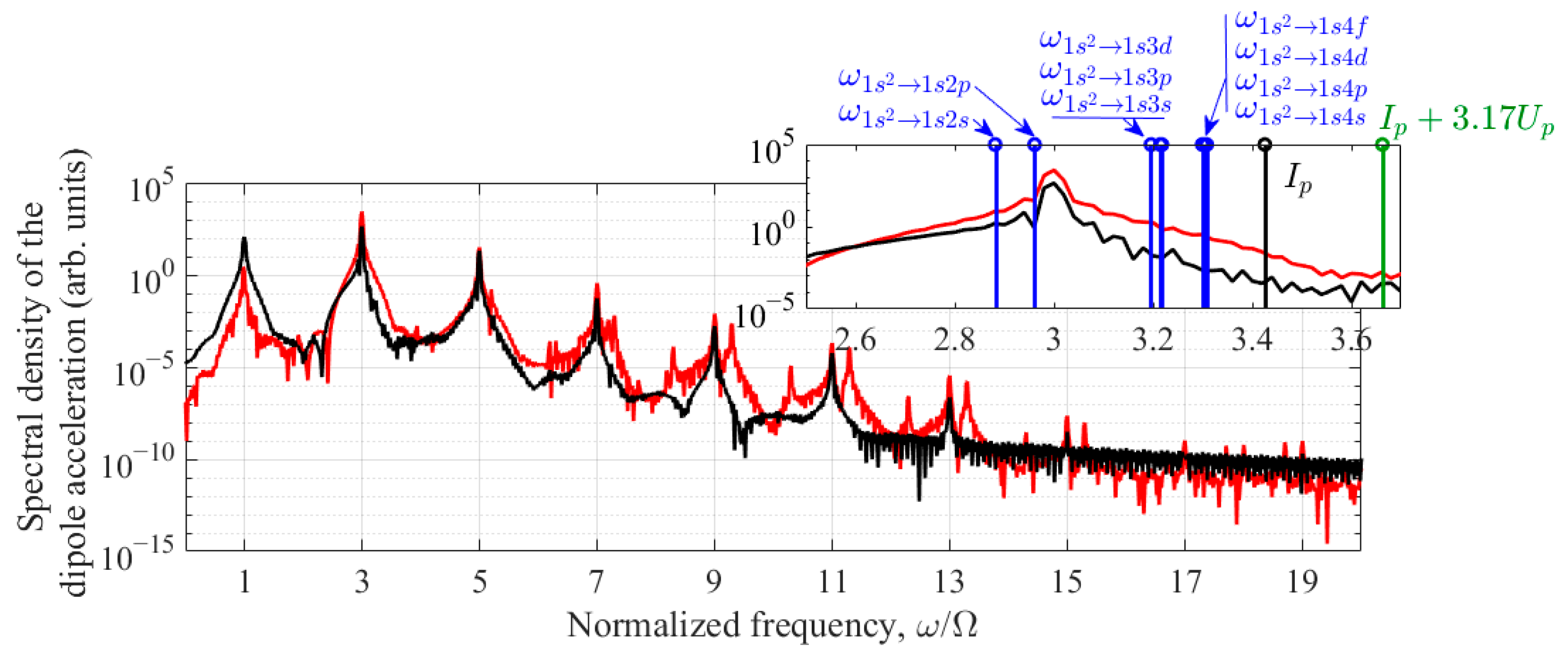
To explain this dependence, let us analyze additional figures. Figure 4 shows the frequency dependence of the power spectral density (the square of the modulus of the spectral amplitude (see Appendix C) of the dipole acceleration of an atom under conditions that maximize the energy of the third harmonic for N_osc = 30. The red curve shows the solution of Equations (6) and (7), corresponding to the expansion of the wave function in terms of the basis of stationary states (4). In this case, the third harmonic energy reaches a maximum at I_UV = 2 × 10¹⁴ W/cm² and Ω = 0.2644 a.u, see Figure 3. The black curve is obtained based on model (11) and (12). In this case, the optimum shifts towards higher UV field intensity, and the maximum is achieved at I_UV = 4 × 10¹⁴ W/cm² and Ω = 0.2730 a.u. The increase in the optimal intensity value in the two-dimensional model is most likely due to the lower probability of multiphoton excitation and the ionization of the atom, see Figure 1. Similar to Figure 3, in this case, the optimal frequency of the UV field, Ω = 0.2730 a.u., turns out to be close to the resonance frequency of the |1s²〉–|1s2p〉 transition in the UV field, which for I_UV = 4 × 10¹⁴ W/cm² in the two-dimensional model is Ω_res = 0.2720 a.u. Several conclusions can be drawn from Figure 4. Firstly, the dipole acceleration of an atom is multi-frequency. In addition to the fundamental frequency of the UV field and its third harmonic, the atomic response contains harmonics of higher orders, up to the 13th one. Secondly, for the chosen UV field parameters, the third harmonic in the dipole acceleration spectrum is dominant. In the solution of Equations (6) and (7), it is approximately 90 times more intense than the fifth harmonic, three orders of magnitude more intense than the signal at the fundamental frequency of the UV field, and four orders of magnitude more intense than the seventh harmonic. Thus, the contribution of the third harmonic to the spectrum of dipole acceleration is decisive. Third, as shown in the inset of Figure 4, under the conditions considered, the third harmonic is the only below-threshold harmonic; its frequency is comparable to the frequencies of single-photon transitions to all excited bound states of the atom and the threshold of its photoionization. The fifth and higher harmonics in the case under consideration are above the threshold. Fourthly, as shown in the inset of Figure 4, due to the small ponderomotive energy of a free electron in the UV field, U_p ≈ 0.02 a.u. << Ω, the contribution of Corkum’s mechanism of harmonic generation [14,15] under the conditions in consideration is insignificant. In addition, I_p + U_p ≈ I_p (where I_p = 0.9036 a.u. is the ionization potential of an unperturbed atom), and the shift of the energy boundary of the continuum due to the dynamic Stark effect [50] does not play a noticeable role. The fifth and final conclusion from Figure 4 is the qualitative agreement between the dipole acceleration spectra at the third, fifth, and, with less accuracy, the seventh harmonics, calculated (i) using a stationary-state basis and (ii) in a two-dimensional one-electron model of the helium atom, with appropriate (optimal in each model) UV field parameters. The differences in the shape of the spectral lines of higher harmonics are apparently due to the limited basis of the stationary states considered in the expansion (4). In this case (for the seventh and higher harmonics), two-dimensional one-electron TDSE appears to give a more physical result.

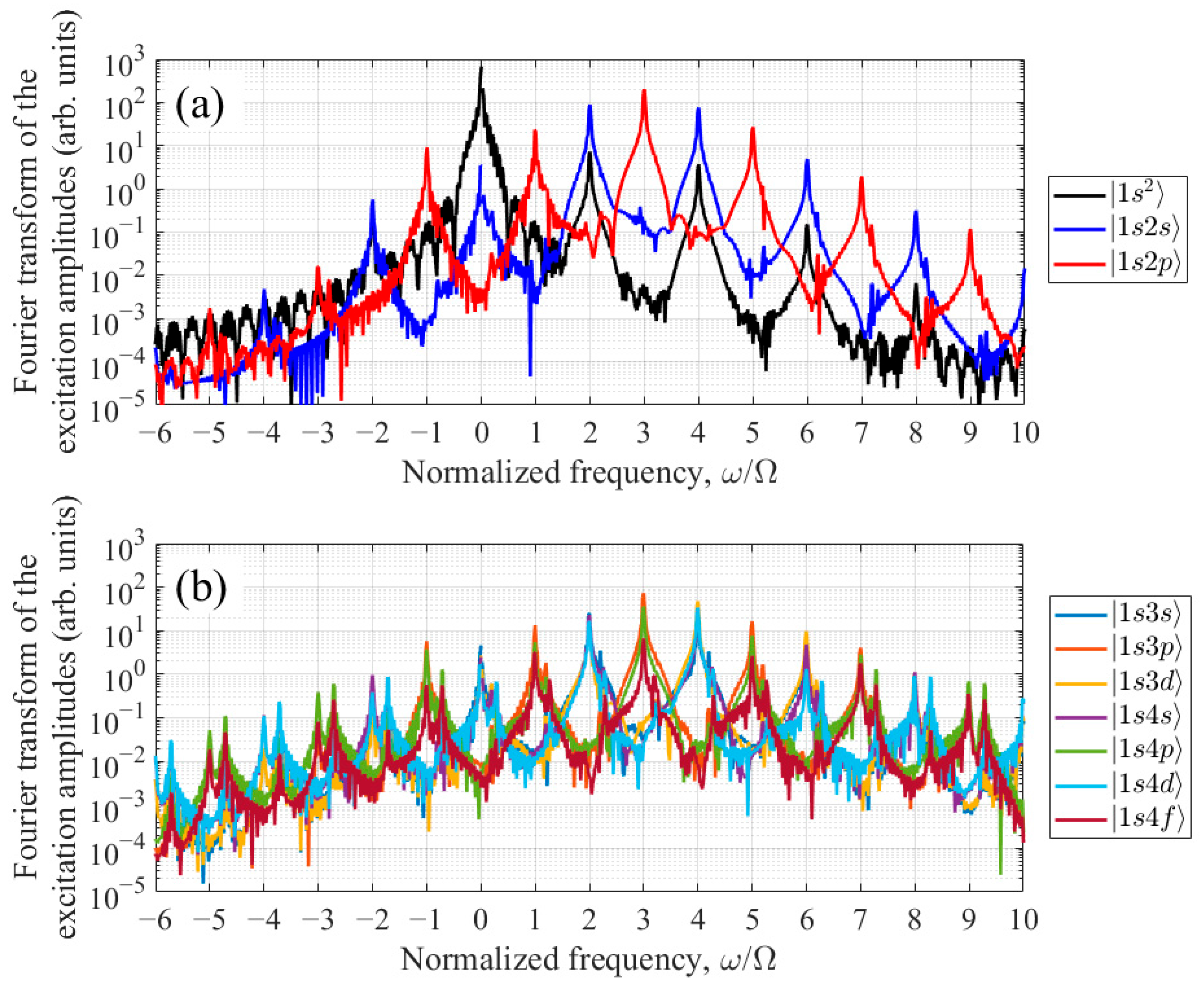
Next, we will analyze the role of various stationary states in the generation of harmonics. When using the expansion of the wave function in stationary states and the adiabatic continuum exclusion approximation, the dipole acceleration of the atom is determined by the excitation amplitudes of bound states (9) and (10). The excitation amplitude spectra of the states taken into account for N_osc = 30 (see (3)) and the optimal UV field parameters, I_UV = 2 × 10¹⁴ W/cm² and Ω = 0.2644 a.u., are shown in Figure 5. The horizontal axis shows the excitation frequency of the atom, measured from the unperturbed frequency of the ground state |1s²〉. As follows from Figure 5, the states |1s²〉, |1s2s〉, and |1s2p〉, shown in Figure 5a, have the largest excitation amplitudes, while the remaining states, Figure 5b, are excited noticeably weaker. In accordance with Equation (9), the complex amplitude of the dipole moment of an atom at the third harmonic frequency is determined by the sum of the products $d_{sk}^{(z)}{a}_{k,n}^{*}(t)a_{s,n+3}(t)$ over all considered states s and k of opposite parity and over the Fourier components of the excitation amplitudes of these states n and n + 3. As can be seen from Figure 5a, in the conditions under consideration of the even parity states, the 0th Fourier component of the excitation amplitude of the state |1s²〉, $a_{1,0}$, has the largest amplitude. Of the odd parity states, this is the case for the 3rd Fourier component of the excitation amplitude of the state |1s2p〉, $a_{3,3}$, oscillating at a frequency close to the frequency of the single-photon transition |1s²〉–|1s2p〉. Accordingly, the dominant contribution to the amplitude of the third harmonic of the UV field frequency in the spectrum of the induced dipole moment of the atom is made by the product $d_{31}^{(z)}{a}_{1,0}^{*}(t)a_{3,3}(t)$. In this case, the dipole acceleration of the atom at the third harmonic frequency is proportional to ${\Omega }^2{d}_{31}^{(z)}{a}_{1,0}^{*}(t)a_{3,3}(t)$, while its energy turns out to be proportional to ${\Omega }^4{\left|d_{31}^{(z)}\right|}^2{{\displaystyle \int \left|a_{1,0}^{*}(t)a_{3,3}(t)\right|}}^{2}dt={\Omega }^4{\left|d_{31}^{(z)}\right|}^2{{\displaystyle \int {\left|a_{1,0}(t)\right|}^2\left|a_{3,3}(t)\right|}}^{2}dt$, where integration is carried out over the time interval at which the UV field is different from zero (see Appendix C). On the other hand, due to the dominant contribution of the Fourier components a_1,0 and a_3,3 to the excitation amplitudes of the states |1s²〉 and |1s2p〉, respectively, the approximate equality is valid: ${{\displaystyle \int {\left|a_{1,0}(t)\right|}^2\left|a_{3,3}(t)\right|}}^{2}dt\approx \overline{{\left|a_1\right|}^2{\left|a_3\right|}^2}{\tau }_{UV}$, where $\overline{{\left|a_1\right|}^2{\left|a_3\right|}^2}$ denotes the time-averaged product of the populations of the states |1s²〉 and |1s2p〉, while ${\tau }_{UV}\approx N_{osc}T$ is the duration of the UV field pulse. The resulting equality is easy to interpret; namely, the energy of the third harmonic reaches its maximum under the conditions of the most effective excitation of the coherent superposition of states |1s²〉 and |1s2p〉.

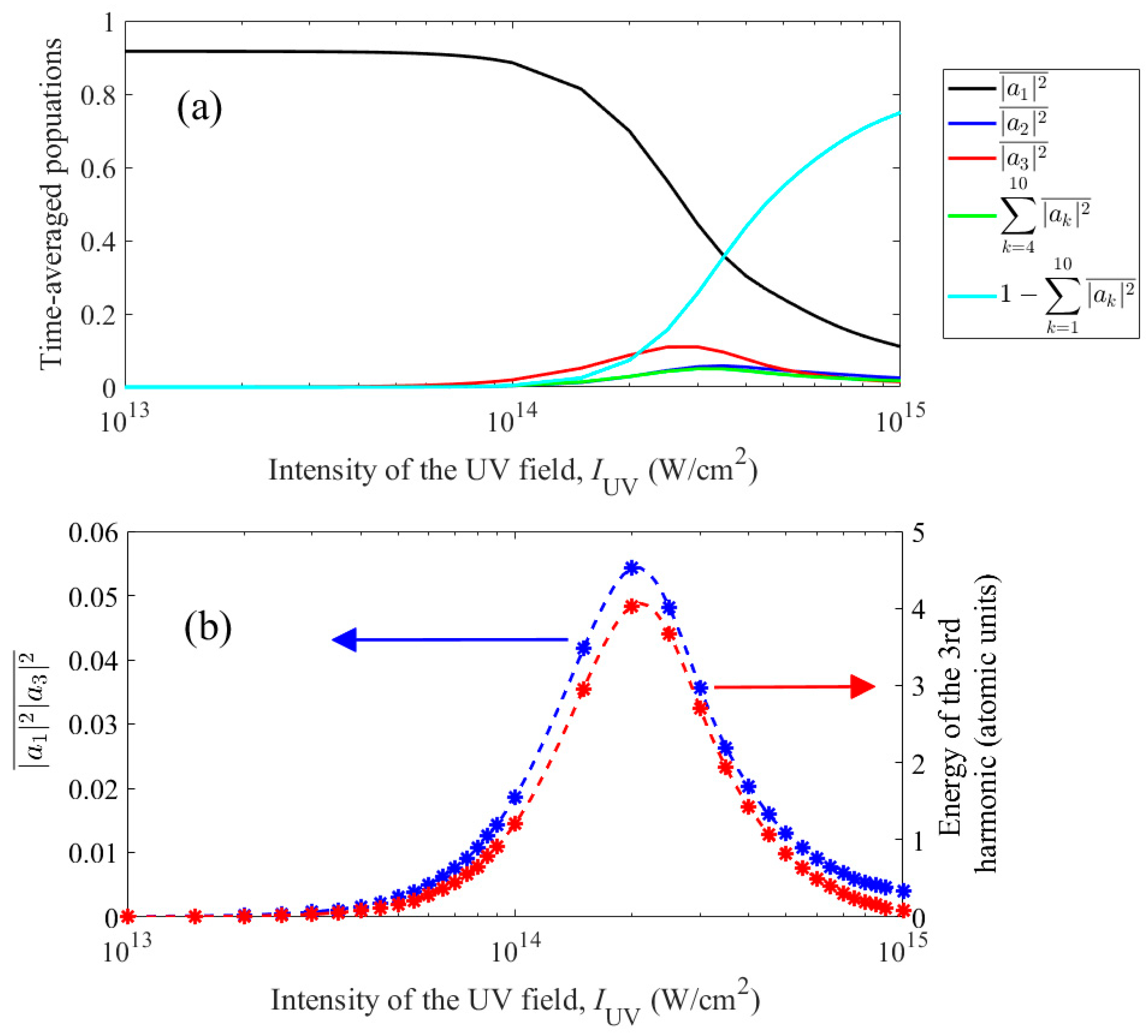
This statement is illustrated in Figure 6. The upper part of the figure (Figure 6a) shows the time-averaged populations of bound states, $\overline{{\left|a_k\right|}^2}$, and the total population of continuum states, $1-{\displaystyle \sum _k\overline{{\left|a_k\right|}^2}}$, as a function of the UV field intensity. In Figure 6, N_osc = 30 (see (3)), and the frequency of the UV field for each intensity is chosen equal to the frequency of the three-photon transition |1s²〉–|1s2p〉 in the field taking into account the dynamic Stark effect (see the black solid curve in Figure 2). The lower part of the figure (Figure 6b) shows (i) the time-averaged product of the populations of the states |1s²〉 and |1s2p〉, $\overline{{\left|a_{1s^2}\right|}^2{\left|a_{1s2p}\right|}^2}=\overline{{\left|a_1\right|}^2{\left|a_3\right|}^2}$, and (ii) the energy of the third harmonic in the spectrum of the dipole acceleration of the atom as a function of the intensity of the UV field. As can be seen from Figure 6b, up to the dimension factor, these two dependences practically coincide. Thus, to maximize the third harmonic energy, it is necessary to most effectively excite the |1s2p〉 state without excessively depleting the |1s²〉 state.

This conclusion allows us to explain the dependence of the frequency that maximizes the energy of the third harmonic in the spectrum of the dipole acceleration of an atom on the intensity of the UV field in Figure 3. In a relatively weak field, the depletion of the |1s²〉 state is not significant (see Figure 6a), and the optimum is achieved at maximum excitation of the |1s2p〉 state, i.e., when adjusting the frequency of the UV field to three-photon resonance. At the optimal UV field intensity, I_UV = 2 × 10¹⁴ W/cm², a balance is achieved between excitation of the |1s2p〉 state and depletion of the |1s²〉 state, in this case, the optimal frequency of the UV field remains in the immediate vicinity of the resonant transition frequency. With a further increase in the intensity of the UV field during resonant excitation of the |1s²〉–|1s2p〉 transition, both the populations of bound states and the third harmonic energy decrease as a result of the ionization of the atom (see Figure 6a). Accordingly, the optimal frequency of the UV field in Figure 3 moves away from the resonant one, which makes it possible to reduce the probability of ionization and, thereby, maintain a noticeable population of the |1s²〉 and |1s2p〉 states. These conclusions are confirmed in Figure 7, showing the frequency dependencies of (i) the energy of the third harmonic in the dipole acceleration spectrum and (ii) the atomic ionization probability for three different values of the UV field intensity: I_UV = 8 × 10¹³ W/cm², I_UV = 2 × 10¹⁴ W/cm², and I_UV = 5 × 10¹⁴ W/cm². While in a relatively weak UV field, the shape and position of maxima of the dependencies (i) and (ii) almost coincide, with growing UV field intensity, the difference in these dependencies increases, and for the highest considered intensity, the maximum in ionization probability coincides with a local minimum in the third harmonic energy.

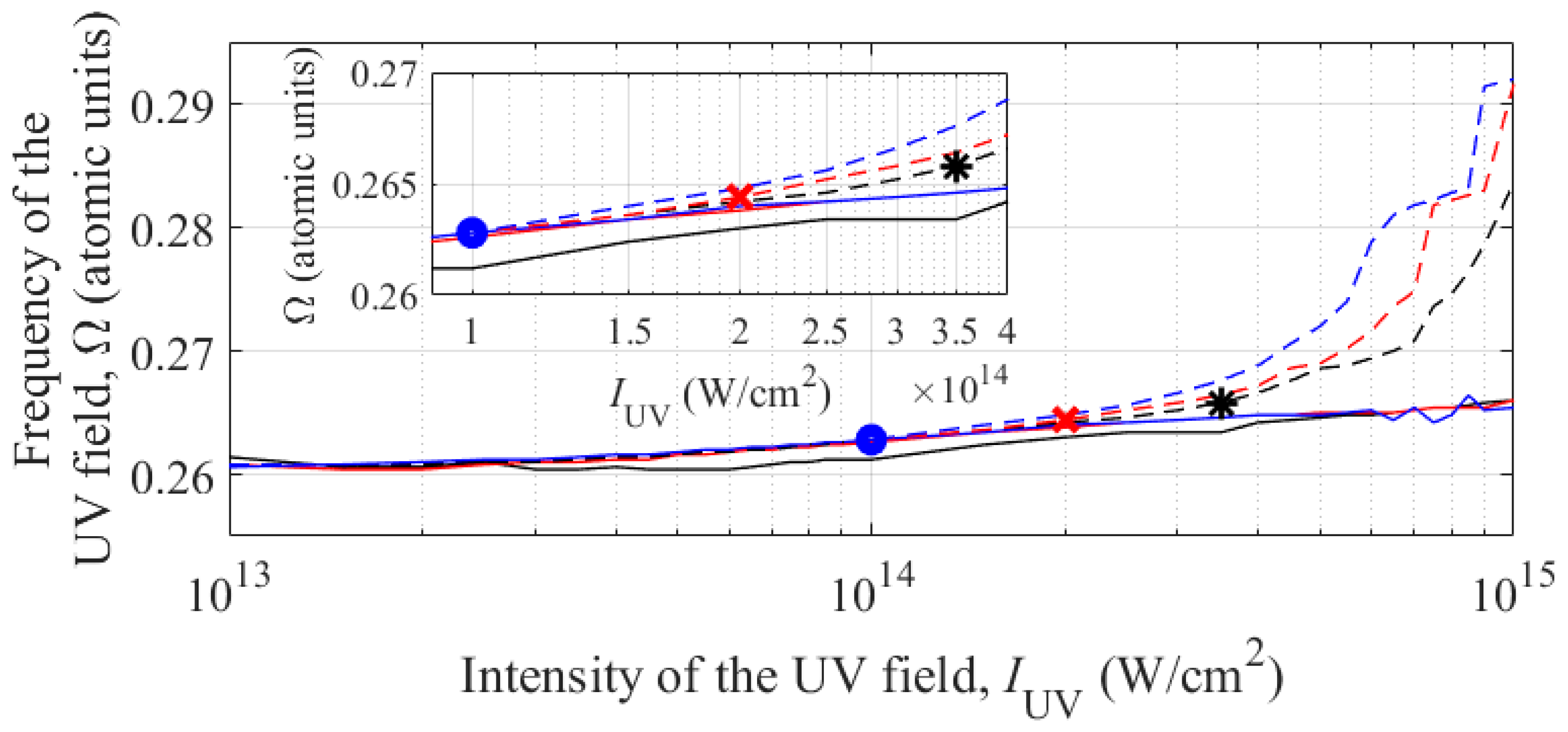
Next, using the expansion of the wave function in terms of the basis of stationary states, we study the dependence of the conditions that maximize the energy of the third harmonic in the spectrum of the dipole acceleration of an atom on the duration of the constant amplitude interval in the UV field envelope (parameter N_osc, see (3)). Figure 8 for three values of N_osc = 10, 30, and 100 shows the dependences of (i) the frequencies of the resonant three-photon transition |1s²〉–|1s2p〉 and (ii) the frequencies of the UV field that maximize the energy of the third harmonic in the dipole acceleration spectrum on the intensity of the UV field.

The resonance frequencies of the three-photon transition |1s²〉–|1s2p〉 for different durations of the UV field envelope practically coincide, which is due to the short establishing time of the dynamic Stark effect [50]. Some difference in the transition frequency is observed for the shortest pulse (N_osc = 10) and is explained by the fact that the total duration of the intervals of turning on and off the UV field (3 + 3 = 6 carrier cycles) in this case is comparable to the duration of the constant amplitude interval (10 carrier cycles). Accordingly, the time-average intensity of the UV field turns out to be noticeably lower than the peak intensity, and the Stark effect at the same peak intensity is weaker than for UV field pulses with a longer duration of the constant amplitude interval. At the same time, jumps in the position of the resonance frequency in the longest pulse (N_osc = 100) with an intensity of the order of 10¹⁵ W/cm² are explained by the extremely high, exceeding 99.99%, probability of single ionization of the atom and the unreliability of the algorithm for determining the resonance frequency under such conditions.

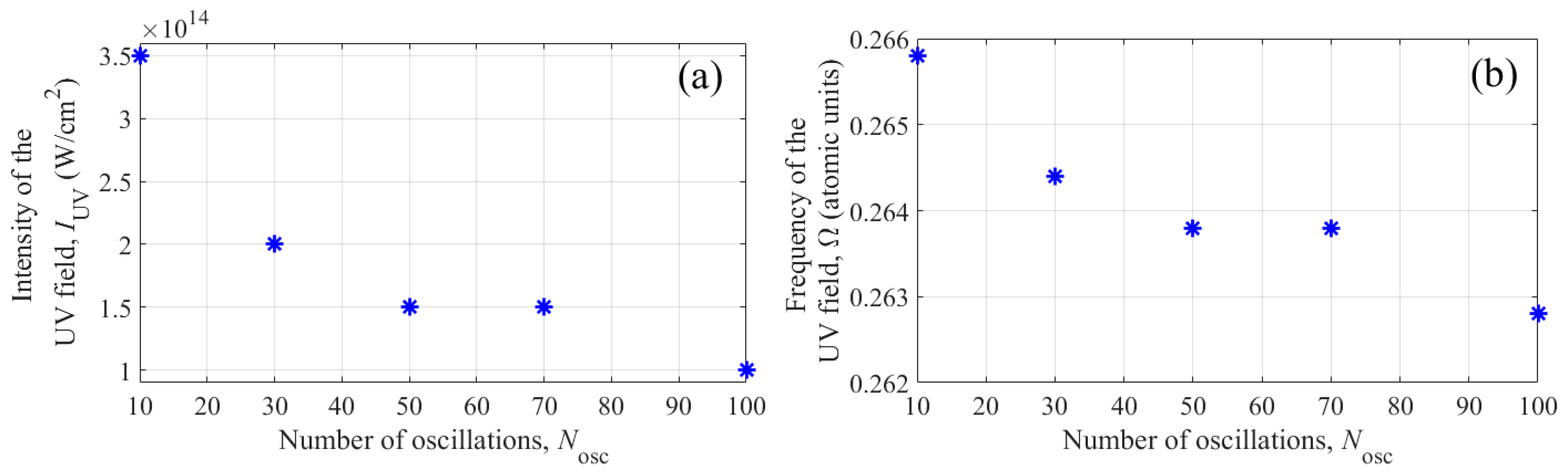
The dependences of the UV field frequencies that maximize the third harmonic energy differ more significantly for different durations of the UV field envelope. At a fixed intensity, with an increasing duration of the UV field pulse, the optimal detuning from the resonance frequency increases. At the same time, the optimal intensity of the UV field decreases with increasing envelope duration; namely, for N_osc =10, 30, and 100, the optimal values are I_UV = 3.5 × 10¹⁴ W/cm², 2 × 10¹⁴ W/cm², and 10¹⁴ W/cm², respectively. 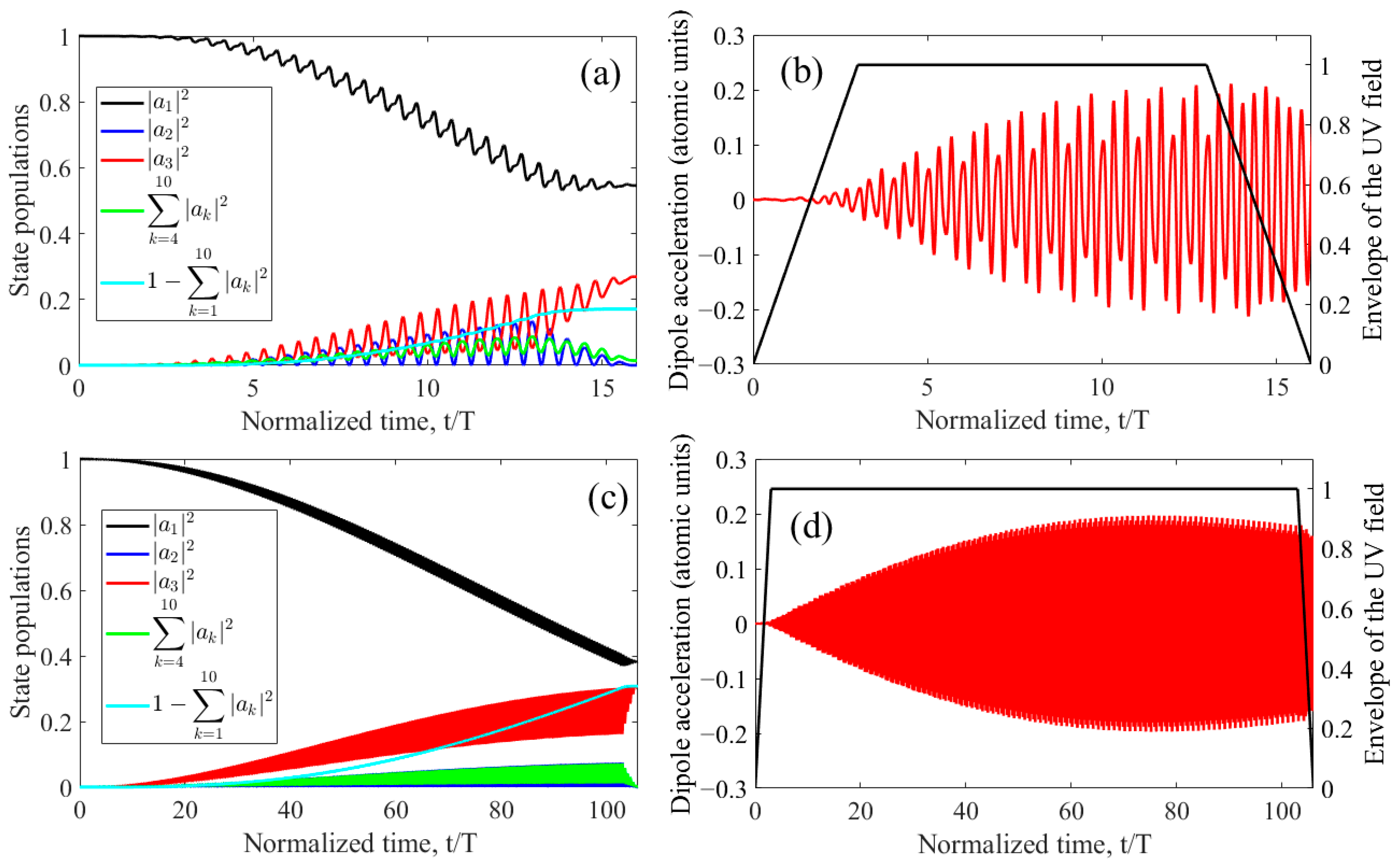To interpret these data, let us turn to Figure 9, which shows the time dependences of the populations of states |1s²〉, |1s2s〉, and |1s2p〉, as well as the total population of more highly excited bound states and the total population of states of the continuum (a,c) and electron dipole acceleration as a function of time (b,d). Figure 9a,b correspond to the UV field pulse of the shortest duration considered, N_osc = 10, while Figure 9c,d are plotted for the case of N_osc = 100.

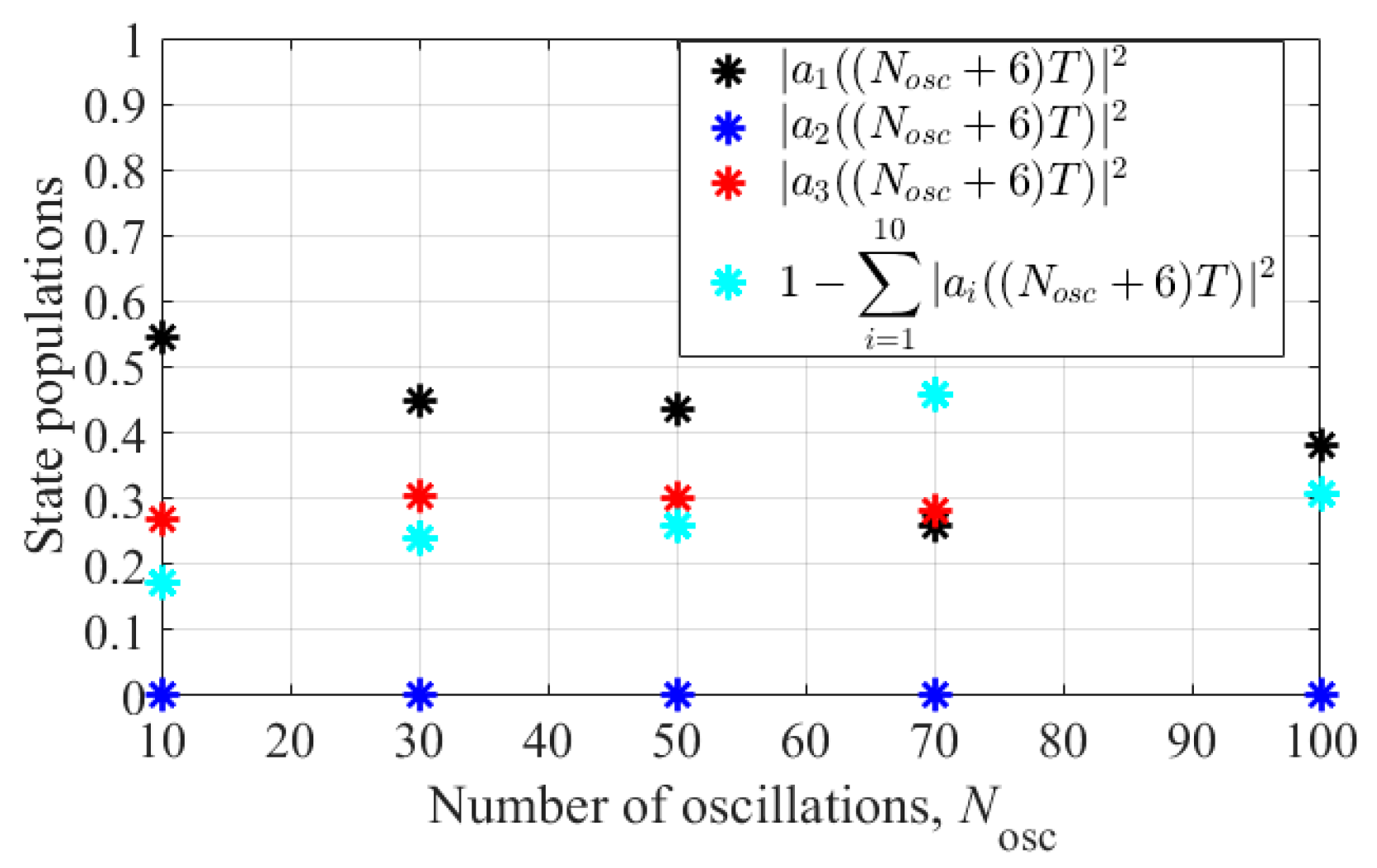
As can be seen from a comparison of Figure 9b,d, for the considered UV field parameters, which are optimal for each envelope duration, (i) the time dependences of the dipole acceleration in the interval of the constant amplitude of the UV field are similar to each other, and (ii) the peak amplitude of the dipole acceleration is approximately the same. Similar conclusions follow from Figure 9a,c, namely, with an optimal choice of UV field parameters, the dynamics of excitation of stationary states weakly depend on the duration of the field envelope, and only the time scale of the process changes significantly (proportional to the duration of the UV field pulse). Under optimal conditions, at the end of the UV pulse, the atom goes into the resonant state |1s2p〉 with a noticeable probability of about 20–30%, ionizes with a comparable probability, and remains in the ground state |1s²〉 with a probability of about 40–50%. Accordingly, the optimal parameters of the UV field are those that, for different envelope durations, provide the same (optimal) character of excitation of the atom during its interaction with the field. Thus, an increase in the optimal intensity of the UV field with a decrease in the duration of its envelope is caused by the need to provide the same (optimal) degree of excitation of the atom in a shorter interaction time.

At the same time, at a fixed intensity of the UV field, the excitation and ionization of the atom increase or decrease as the frequency of the UV field approaches or moves away from the frequency of the three-photon resonance with the |1s²〉–|1s2p〉 transition. Accordingly, with increasing duration of the UV field envelope at a fixed intensity, the optimal detuning of the field frequency from resonance increases, and with decreasing duration, and vice versa, it decreases. Note that some differences in the degree of excitation and ionization of an atom for different durations of the envelope (and, accordingly, different intensities) of the UV field (see Figure 9a,c) are due to differences in the dependences of (i) excitation probabilities and (ii) probabilities of ionization of an atom on the strength of the UV field.

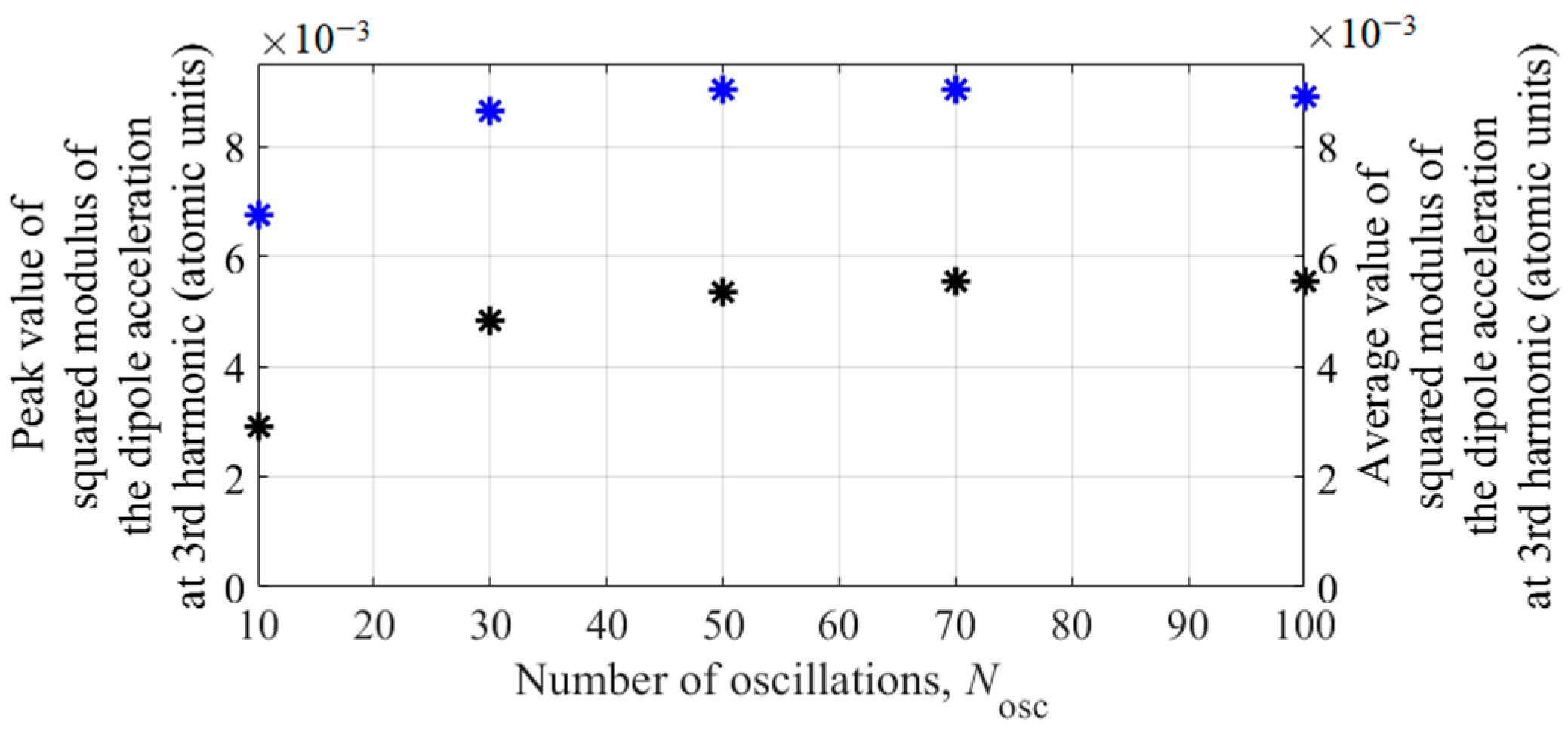
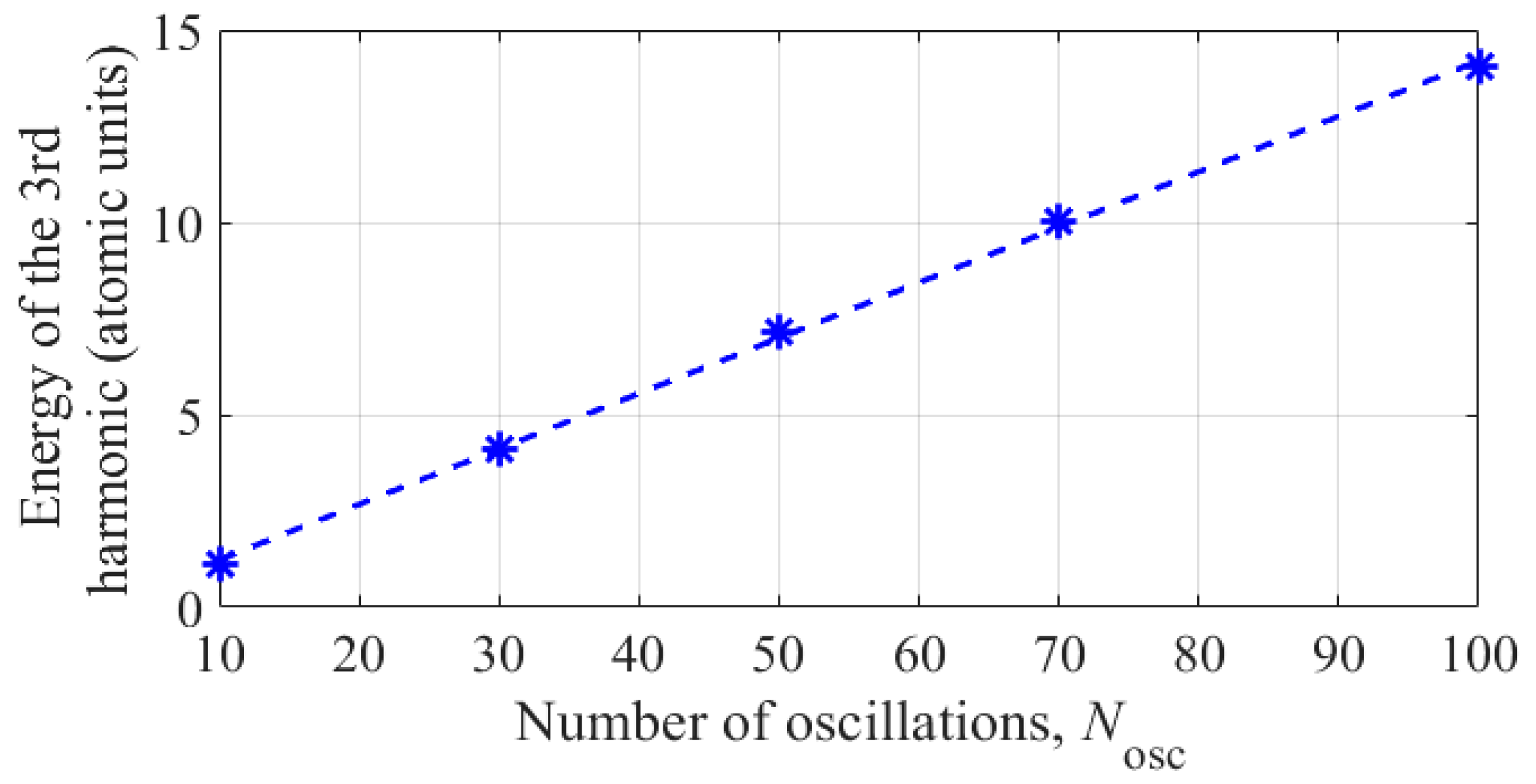
In conclusion of this section, we note that the energy concentrated in the third harmonic of the dipole acceleration of an atom varies approximately in proportion to the duration of the constant amplitude interval in the UV field envelope, see Figure 10. This means that in the conditions under consideration, the average power concentrated in the third harmonic in the spectrum of dipole acceleration of the atom does not depend on the duration of the UV field envelope. Note, however, that with the shortening of the UV field pulse envelope, to achieve the same atomic response power at the third harmonic frequency, an increase (proportional to the optimal intensity value, see Figure 8) in UV radiation power is required.

(i) The optimal parameters of the UV field, (ii) the population of states at the end of the UV field pulse with optimal intensity and frequency, and (iii) the power of the dipole acceleration of an atom at the third harmonic frequency in a UV field as functions of N_osc are given in Appendix D.

4. Conclusions

This study analyzes the conditions under which the energy of the third harmonic of the UV field in the dipole acceleration spectrum (the second time derivative of the induced dipole moment) for a helium atom reaches a maximum. The frequency range of the UV field is addressed, which includes resonances with three-photon transitions from the ground to excited bound states of the atom. It is shown that the optimal frequency of the UV field practically coincides with the frequency of the three-photon transition |1s²〉–|1s2p〉 taking into account its shift due to the dynamic Stark effect. In this case, the highest energy of the third harmonic is achieved under conditions of maximizing the time-averaged (over the duration of the UV field pulse) product of the populations of the states |1s²〉 and |1s2p〉. For the considered UV field pulses with a constant amplitude interval duration from 10 to 100 periods of field oscillations (which, for different frequencies of the UV field, corresponds to from 5 to 60 femtoseconds), the optimal UV field intensity ranges from 10¹⁴ W/cm² to several units of 10¹⁴ W/cm². Under optimal conditions, at the end of the UV pulse, the atom is excited to the resonant state |1s2p〉 with a probability of about 20–30%, ionized with a comparable probability, and remains in the ground state |1s²〉 with a probability of about 40–50%. It is shown that with an optimal choice of the frequency and intensity of the UV field, the dynamics of excitation of bound and continuum states, as well as the shape of the time envelope of the dipole acceleration of the atom, weakly depend on the duration of the UV field envelope; only their time scale changes significantly. In addition, the average power of the third harmonic signal in the dipole acceleration spectrum is also practically independent of the duration of the UV field envelope. Thus, the optimal regime of the resonant three-photon excitation of the helium atom, which maximizes the energy of the third harmonic of the UV field in its spectrum of dipole acceleration, has been found and numerically investigated.