Polarization-Based De-Scattering Imaging in Turbid Tissue-like Scattering Media
Abstract
:1. Introduction
2. Theory
2.1. Image Degradation Model
2.2. Estimation of A and A∞
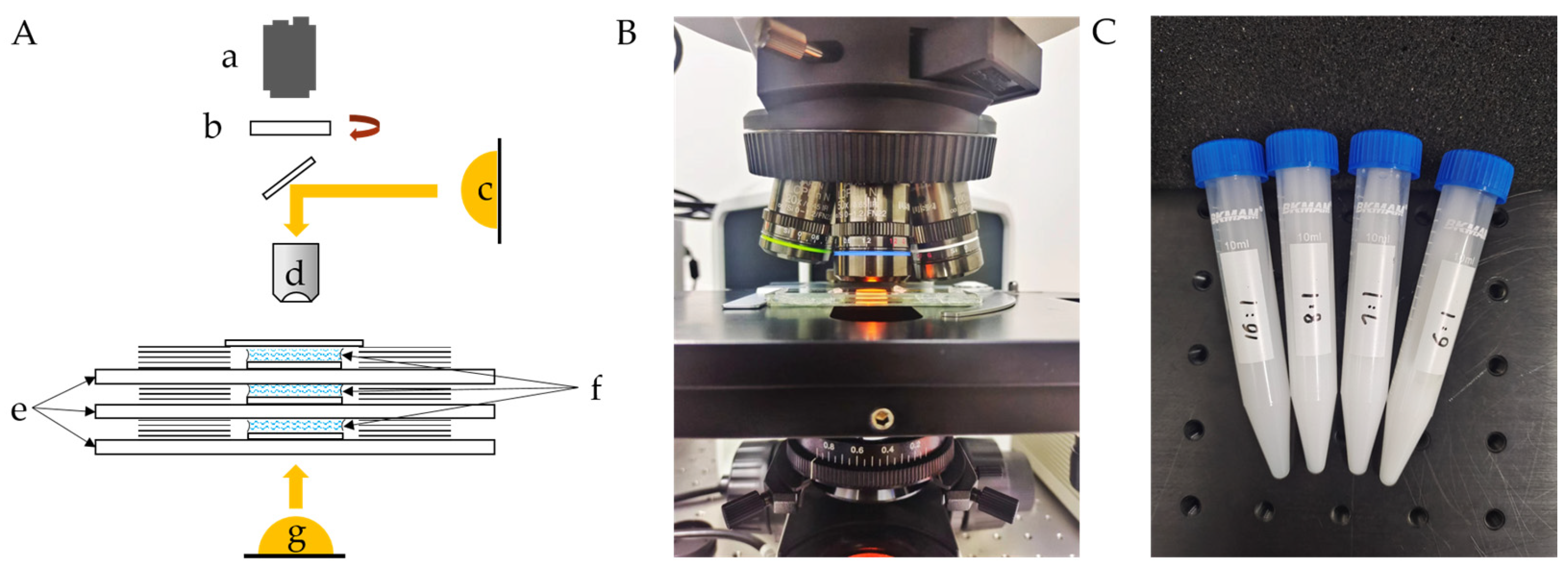
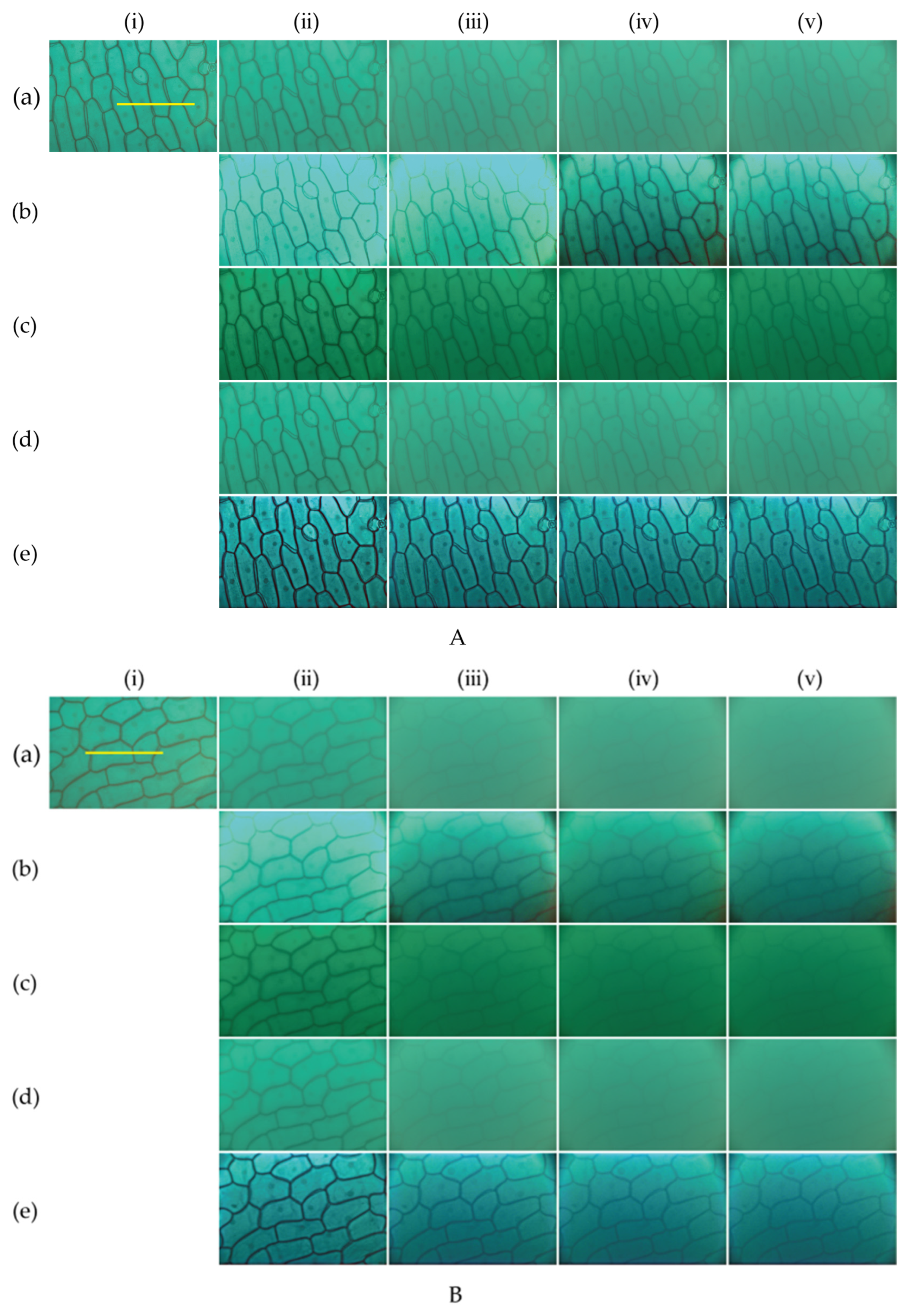
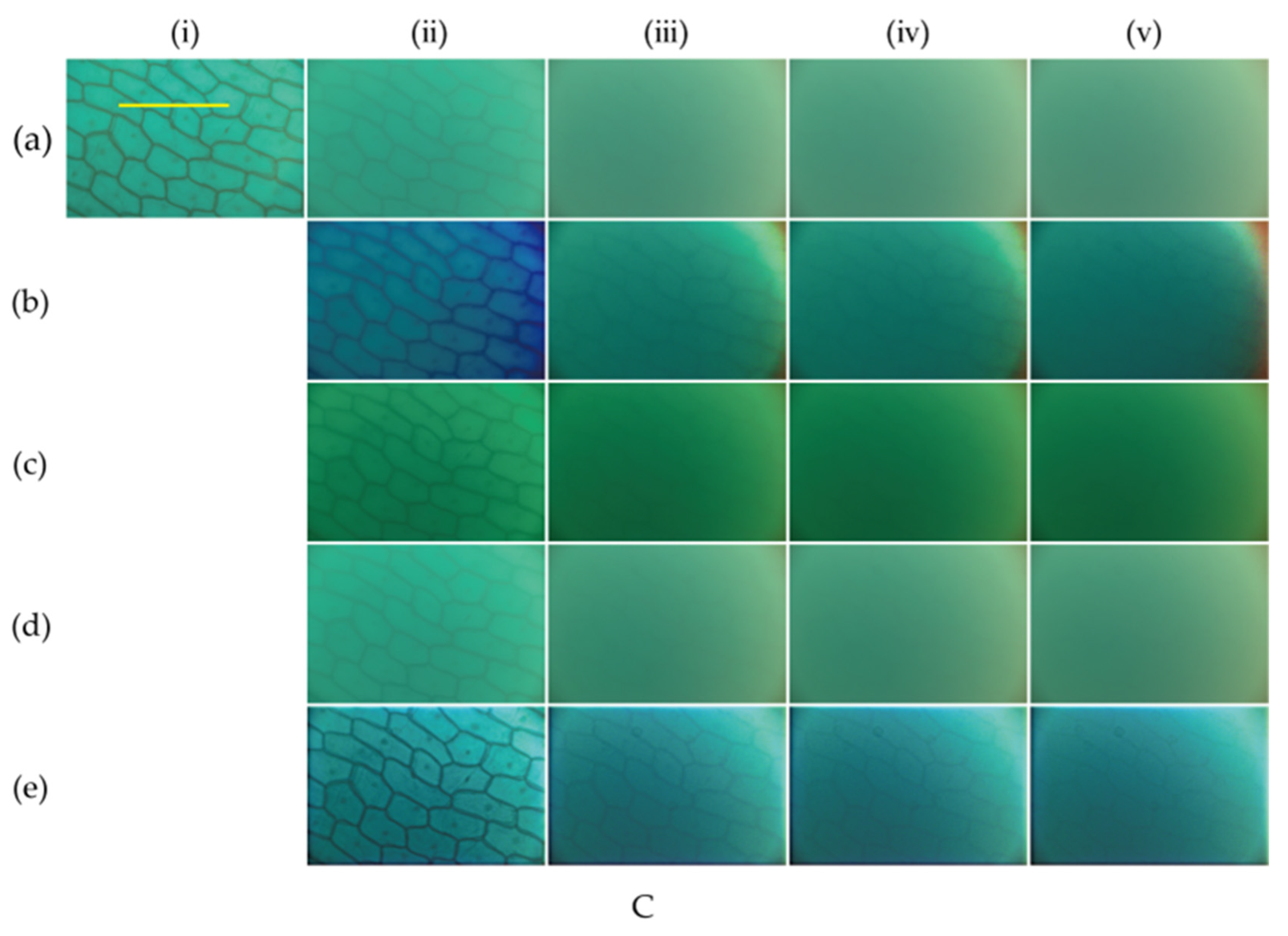
3. Experiments and Analysis
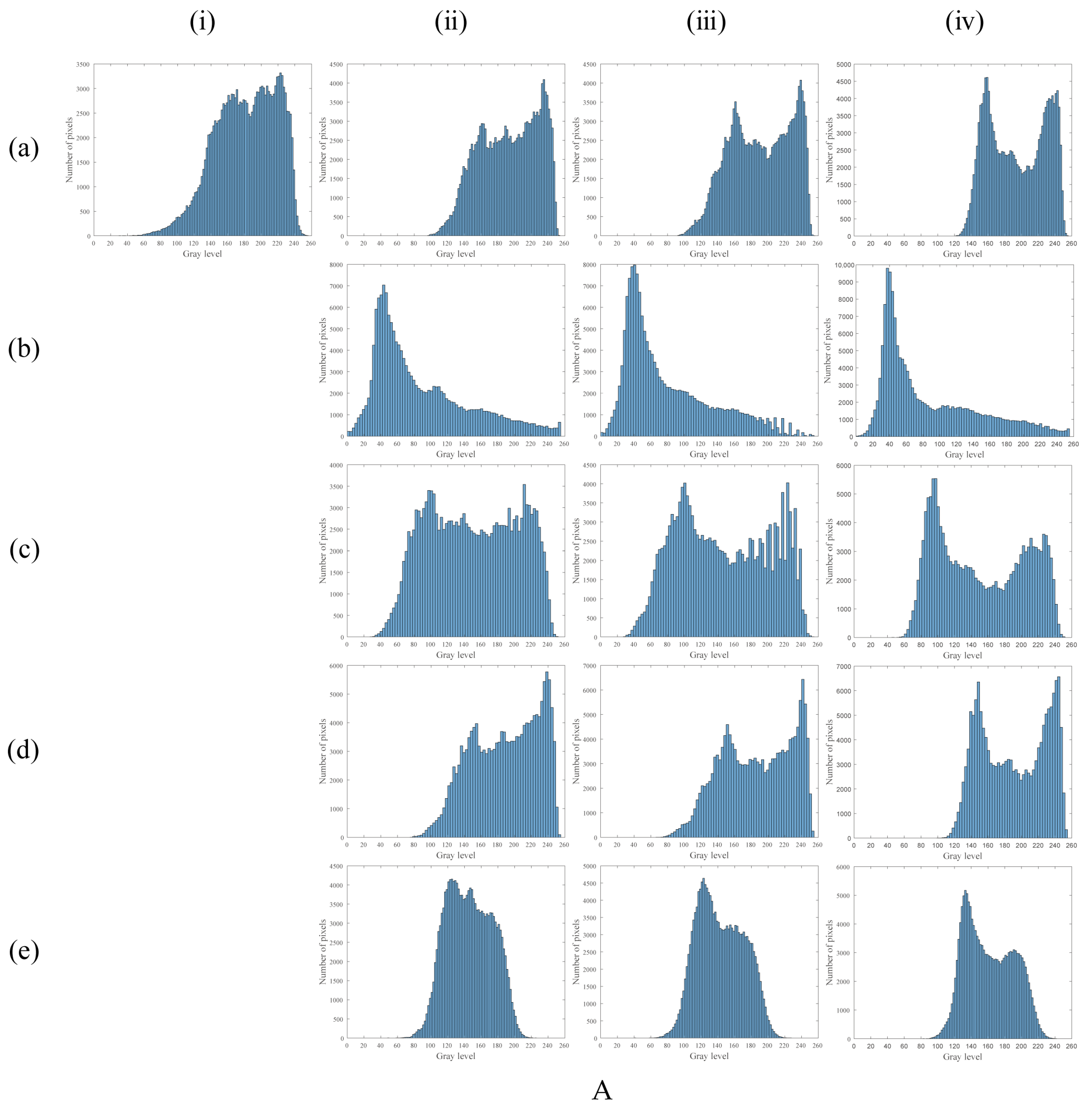
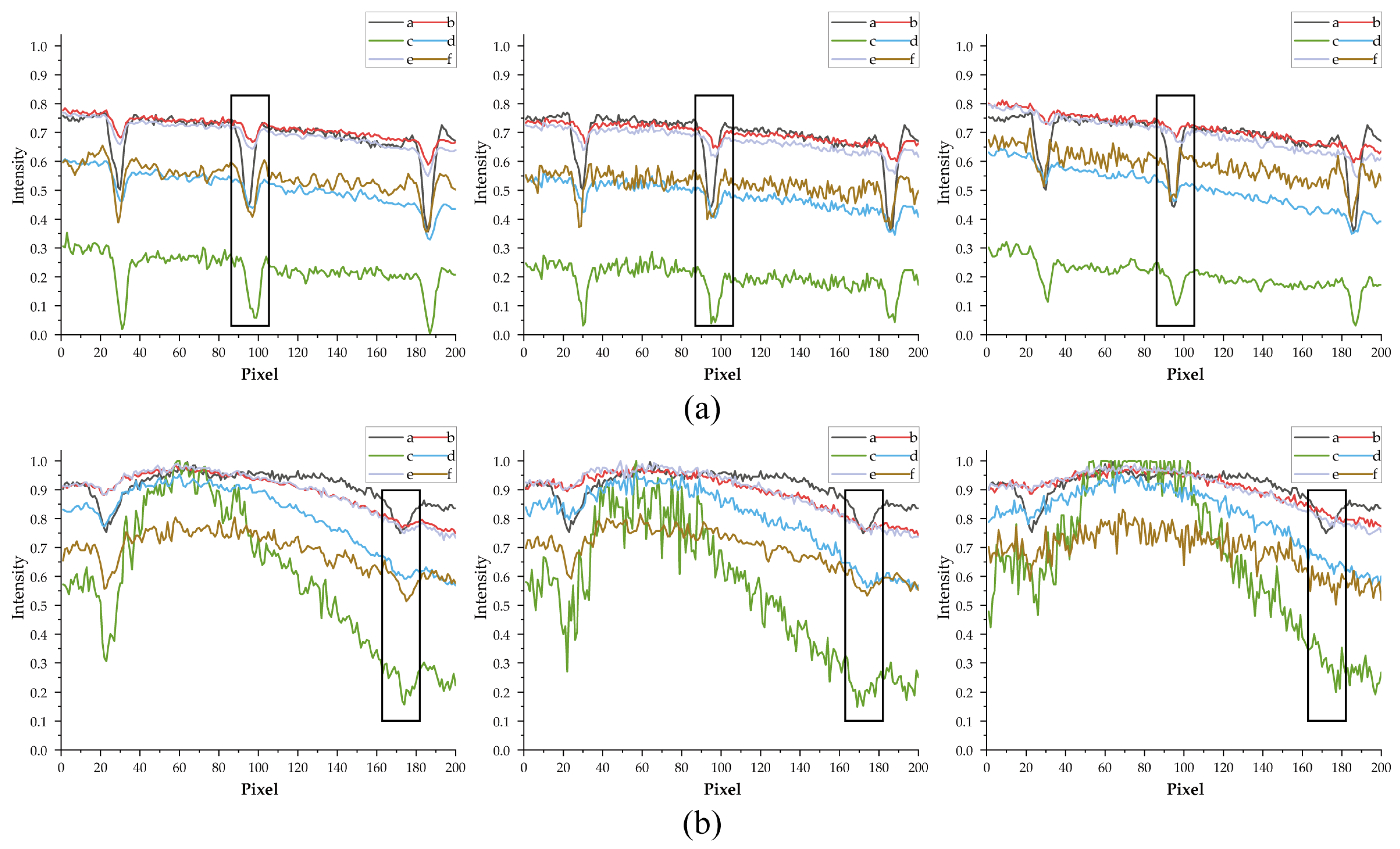
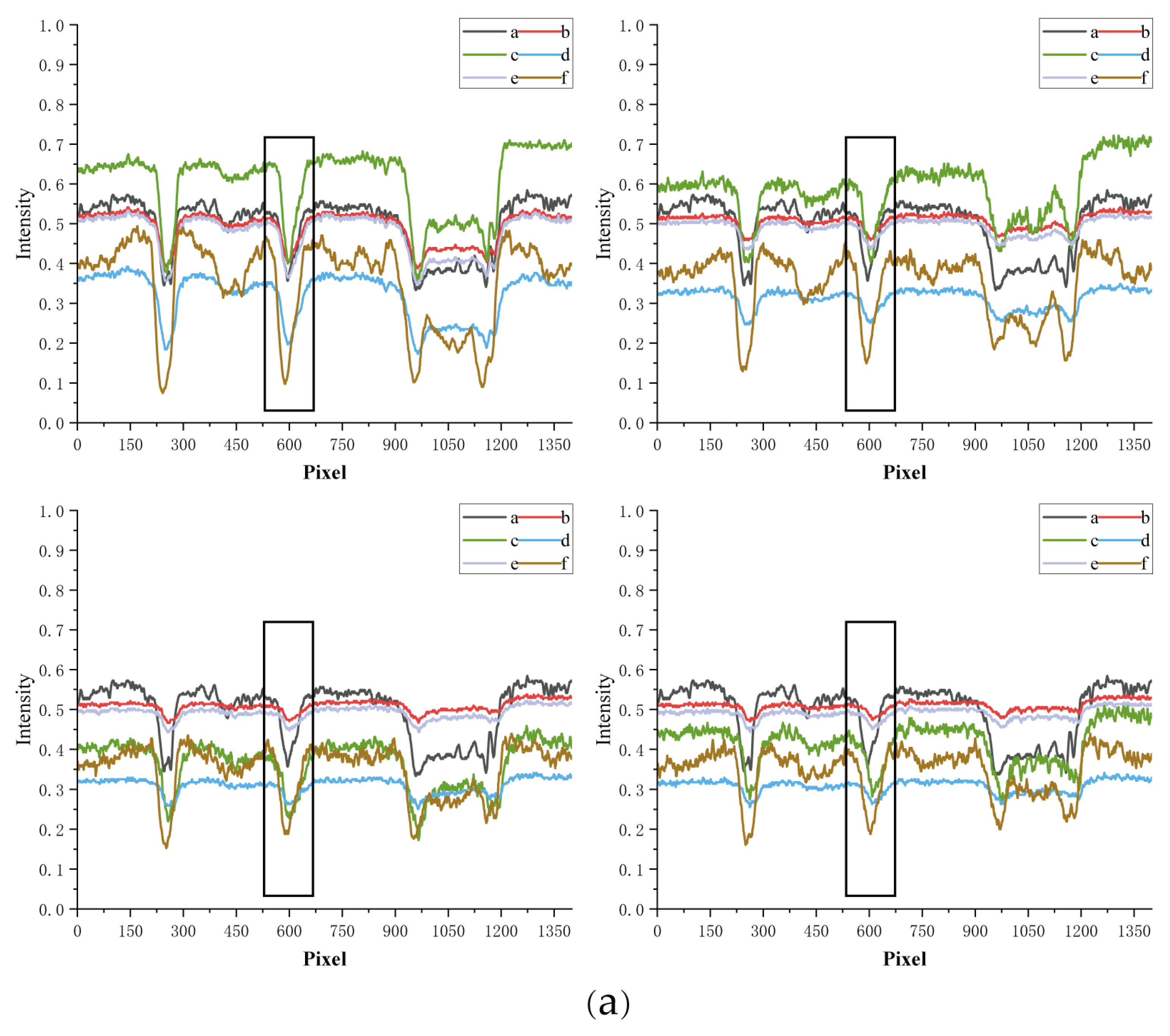
3.1. Reflected Light Source Experiment
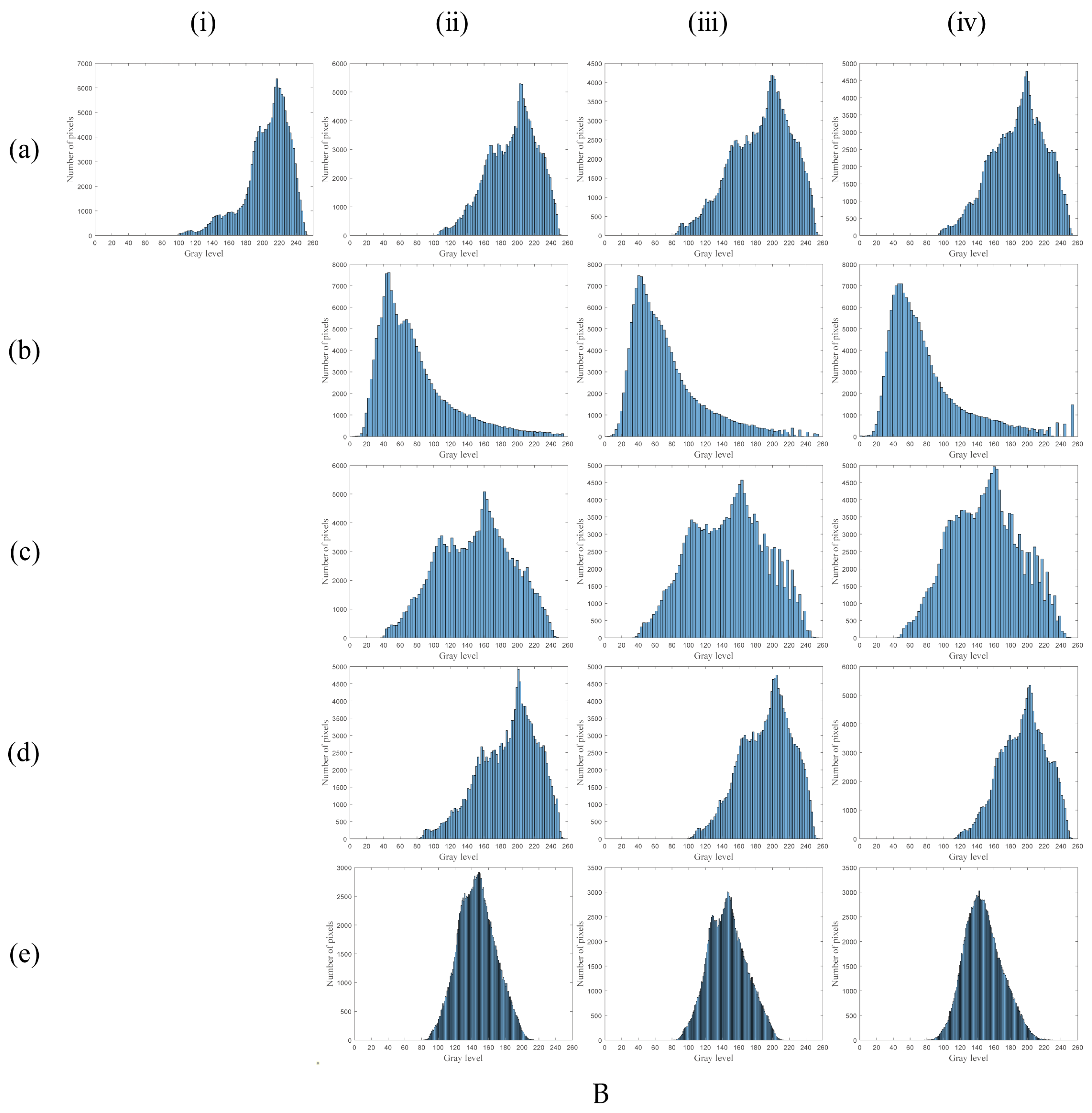
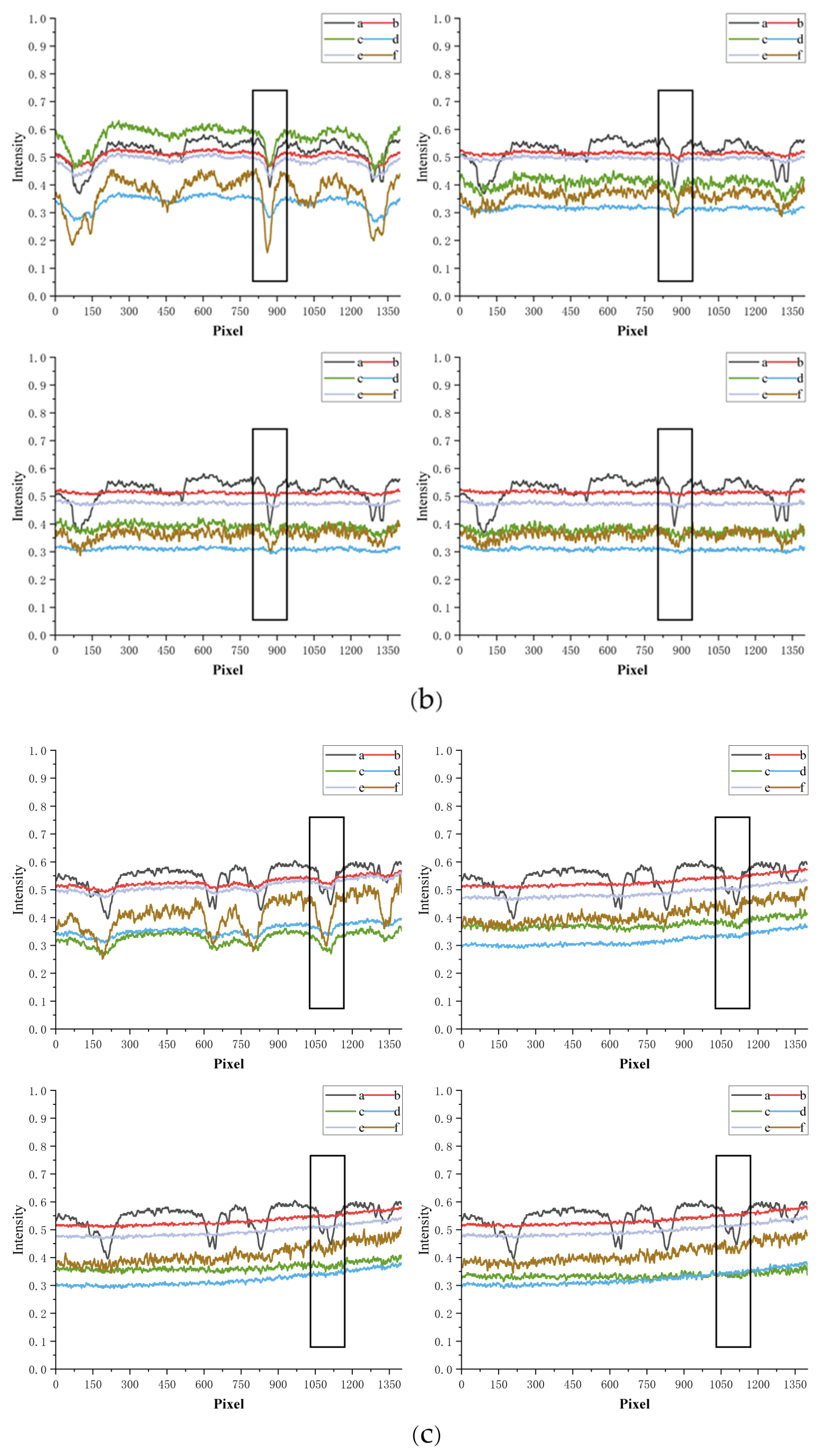
3.2. Transmitted Light Source Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Eeckhout, A.; Garcia-Caurel, E.; Garnatje, T.; Escalera, J.C.; Durfort, M.; Vidal, J. Polarimetric imaging microscopy for advanced inspection of vegetal tissues. Sci. Rep. 2021, 11, 3913. [Google Scholar] [CrossRef]
- Hafi, N.; Grunwald, M.; van den Heuvel, L.S.; Aspelmeier, T.; Chen, J.H.; Zagrebelsky, M. Fluorescence nanoscopy by polarization modulation and polarization angle narrowing. Nat. Methods 2014, 11, 579–584. [Google Scholar] [CrossRef] [PubMed]
- Ahlers, C.; Gotzinger, E.; Pircher, M.; Golbaz, I.; Prager, F.; Schutze, C. Imaging of the retinal pigment epithelium in age-related macular degeneration using polarization-sensitive optical coherence tomography. Investig. Ophthalmol. Vis. Sci. 2010, 51, 2149–2157. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; He, H.; Zeng, N.; Du, E.; Liao, R.; He, Y. Polarization Imaging and Scattering Model of Cancerous Liver Tissues. J. Innov. Opt. Health Sci. 2013, 6, 1350025. [Google Scholar] [CrossRef]
- Peng, T.; Xie, H.; Ding, Y.C.; Wang, W.C.; Li, Z.M.; Jin, D.Y. CRAFT: Multimodality confocal skin imaging for early cancer diagnosis. J. Biophotonics 2012, 5, 469–476. [Google Scholar] [CrossRef] [PubMed]
- Rey-Barroso, L.; Burgos-Fernández, F.J.; Royo, S.; Puig, S.; Malvehy, J.; Pellacani, G. Polarized Multispectral Imaging for the Diagnosis of Skin Cancer. Color Imaging Conf. 2019, 27, 381–385. [Google Scholar] [CrossRef]
- Ghosh, N.; Vitkin, I.A. Tissue polarimetry: Concepts, challenges, applications, and outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar] [CrossRef] [PubMed]
- Canabal-Carbia, M.; Rodriguez, C.; Estévez Caride, I.; Van Eeckout, A.; González-Arnay, E.; García-Caurel, E. Enhancing Biological Tissue Structures Visualization through Polarimetric Parameters. In SPIE Polarized Light and Optical Angular Momentum for Biomedical Diagnostics 2023; SPIE: San Francisco, CA, USA, 2023; Volume 12382, pp. 35–46. [Google Scholar]
- Jacques, S.L.; Roman, J.R.; Lee, K. Imaging superficial tissues with polarized light. Lasers Surg. Med. 2000, 26, 119–129. [Google Scholar] [CrossRef]
- Luthria, G.; Li, R.; Wang, S.; Prytyskach, M.; Kohler, R.H.; Lauffenburger, D.A. In vivo microscopy reveals macrophage polarization locally promotes coherent microtubule dynamics in migrating cancer cells. Nat. Commun. 2020, 11, 3521. [Google Scholar] [CrossRef]
- Tukimin, S.N.; Karman, S.B.; Ahmad, M.Y.; Wan Kamarul Zaman, W.S. Polarized Light-Based Cancer Cell Detection Techniques: A Review. IEEE Sens. J. 2019, 19, 9010–9025. [Google Scholar] [CrossRef]
- Wang, D.; Qi, J.; Huang, B.; Noble, E.; Stoyanov, D.; Gao, J. Polarization-based smoke removal method for surgical images. Biomed. Opt. Express 2022, 13, 2364–2379. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Ren, L.-Y.; Ju, H.-J.; Qu, E.-S.; Wang, Y.-L. Visibility enhancement of hazy images based on a universal polarimetric imaging method. J. Appl. Phys. 2014, 116, 173107. [Google Scholar] [CrossRef]
- Liang, J.; Ju, H.J.; Ren, L.Y.; Yang, L.M.; Liang, R.G. Generalized Polarimetric Dehazing Method Based on Low-Pass Filtering in Frequency Domain. Sensors 2020, 20, 1729. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Wei, Y.; Han, P.; Yang, K.; Bai, L.; Shao, X. Polarization-based exploration for clear underwater vision in natural illumination. Opt. Express 2019, 27, 3629–3641. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Zhu, J.; Li, H.; Zhang, X.; Guo, F.; Hou, X. Real-time underwater polarization imaging without relying on background. Opt. Lasers Eng. 2023, 169, 107721. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar]
- Zhang, S.; He, F.; Ren, W. NLDN: Non-local dehazing network for dense haze removal. Neurocomputing 2020, 410, 363–373. [Google Scholar] [CrossRef]
- Zhu, Q.; Mai, J.; Shao, L. A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar]
- Li, B.; Peng, X.; Wang, Z.; Xu, J.; Feng, D. All-in-one dehazing network. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4770–4779. [Google Scholar]
- Qin, X.; Wang, Z.; Bai, Y.; Xie, X.; Jia, H. FFA-Net: Feature fusion attention network for single image dehazing. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11908–11915. [Google Scholar]
- Bolun, C.; Xiangmin, X.; Kui, J.; Chunmei, Q.; Dacheng, T. DehazeNet: An End-to-End System for Single Image Haze Removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef]
- Narasimhan, S.G.; Nayar, S.K. Chromatic framework for vision in bad weather. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 13–15 June 2000; Volume 1, pp. 598–605. [Google Scholar]
- Schechner, Y.Y.; Narasimhan, S.G.; Nayar, S.K. Polarization-based vision through haze. Appl. Opt. 2003, 42, 511–525. [Google Scholar] [CrossRef] [PubMed]
- Vitor, A.R.; Shaus, A.; Cardoso, G.C. Image Haziness Contrast Metric Describing Optical Scattering Depth. Optics 2023, 4, 525–537. [Google Scholar] [CrossRef]
- Cai, Y.; Wei, Z.; Song, C.; Tang, C.; Han, W.; Dong, X. Optical nano-agents in the second near-infrared window for biomedical applications. Chem. Soc. Rev. 2019, 48, 22–37. [Google Scholar] [CrossRef] [PubMed]

| Original | DCP | AOD-Net | FFA-Net | PBD | ||
|---|---|---|---|---|---|---|
| Layer 1 | 7:1 | 0.044 | 0.050 | 0.058 | 0.055 | 0.100 |
| 6:1 | 0.038 | 0.071 | 0.058 | 0.051 | 0.111 | |
| 5:1 | 0.040 | 0.050 | 0.061 | 0.025 | 0.135 | |
| Layer 2 | 7:1 | 0.149 | 0.281 | 0.189 | 0.163 | 0.283 |
| 6:1 | 0.144 | 0.243 | 0.224 | 0.167 | 0.263 | |
| 5:1 | 0.077 | 0.118 | 0.112 | 0.084 | 0.118 |
| Original | DCP | AOD-Net | FFA-Net | PBD | ||
|---|---|---|---|---|---|---|
| Layer 1 | 16:1 | 0.070 | 0.107 | 0.090 | 0.080 | 0.121 |
| 8:1 | 0.031 | 0.076 | 0.041 | 0.035 | 0.106 | |
| 7:1 | 0.028 | 0.076 | 0.038 | 0.031 | 0.123 | |
| 6:1 | 0.026 | 0.074 | 0.034 | 0.028 | 0.112 | |
| Layer 2 | 16:1 | 0.043 | 0.090 | 0.058 | 0.051 | 0.131 |
| 8:1 | 0.033 | 0.104 | 0.045 | 0.036 | 0.126 | |
| 7:1 | 0.034 | 0.098 | 0.046 | 0.038 | 0.135 | |
| 6:1 | 0.033 | 0.100 | 0.044 | 0.036 | 0.126 | |
| Layer 3 | 16:1 | 0.039 | 0.074 | 0.053 | 0.045 | 0.133 |
| 8:1 | 0.036 | 0.083 | 0.049 | 0.039 | 0.117 | |
| 7:1 | 0.036 | 0.081 | 0.049 | 0.039 | 0.115 | |
| 6:1 | 0.035 | 0.083 | 0.049 | 0.039 | 0.101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Liang, J.; Jiang, Y.; Ren, L. Polarization-Based De-Scattering Imaging in Turbid Tissue-like Scattering Media. Photonics 2023, 10, 1374. https://doi.org/10.3390/photonics10121374
Zhang S, Liang J, Jiang Y, Ren L. Polarization-Based De-Scattering Imaging in Turbid Tissue-like Scattering Media. Photonics. 2023; 10(12):1374. https://doi.org/10.3390/photonics10121374
Chicago/Turabian StyleZhang, Shirong, Jian Liang, Yanru Jiang, and Liyong Ren. 2023. "Polarization-Based De-Scattering Imaging in Turbid Tissue-like Scattering Media" Photonics 10, no. 12: 1374. https://doi.org/10.3390/photonics10121374
APA StyleZhang, S., Liang, J., Jiang, Y., & Ren, L. (2023). Polarization-Based De-Scattering Imaging in Turbid Tissue-like Scattering Media. Photonics, 10(12), 1374. https://doi.org/10.3390/photonics10121374





.jpg)

