Electromagnetically Induced Transparency Spectra of 6Li Rydberg Atoms
Abstract
:1. Introduction
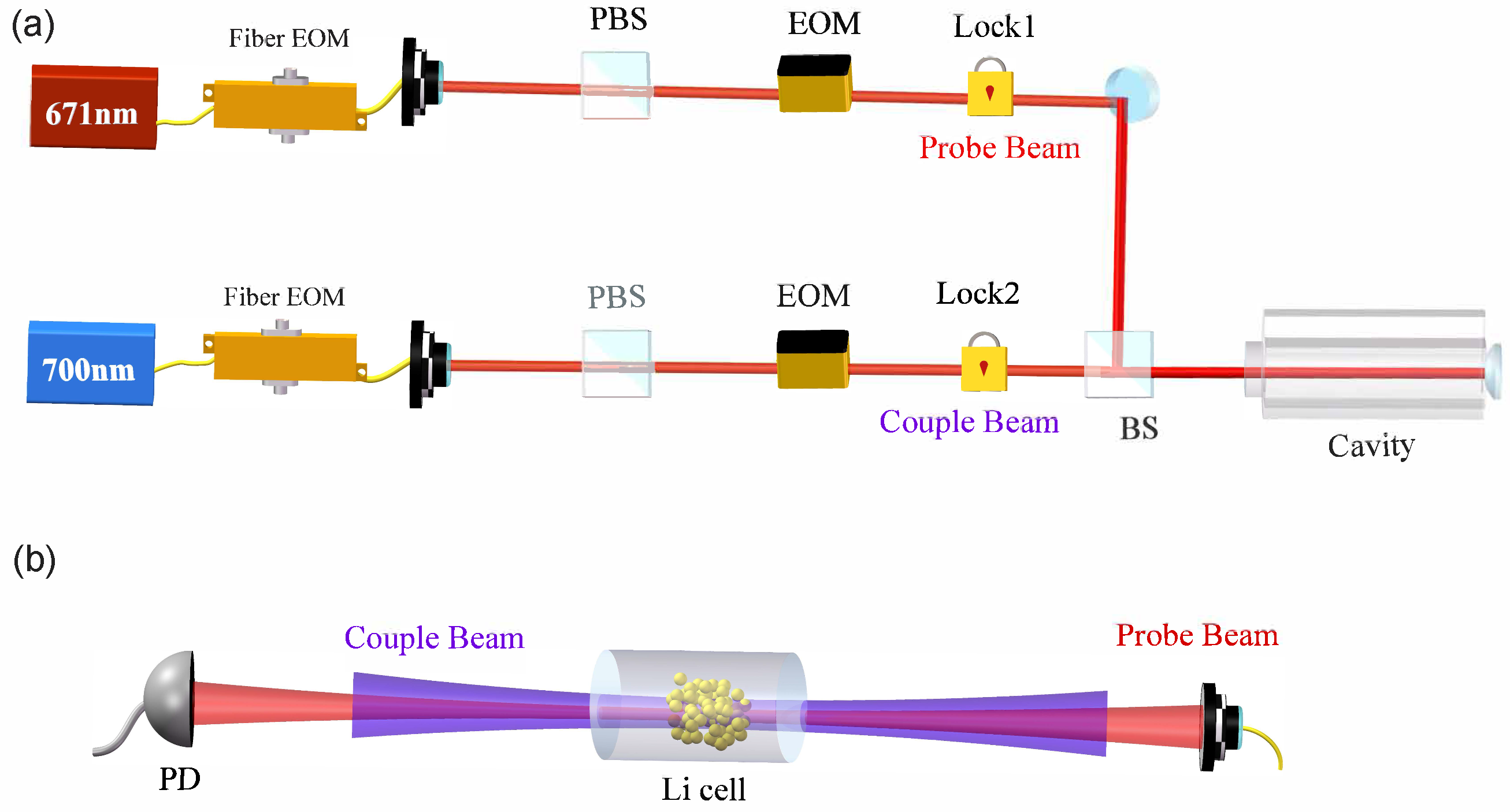
2. Experimental Methods
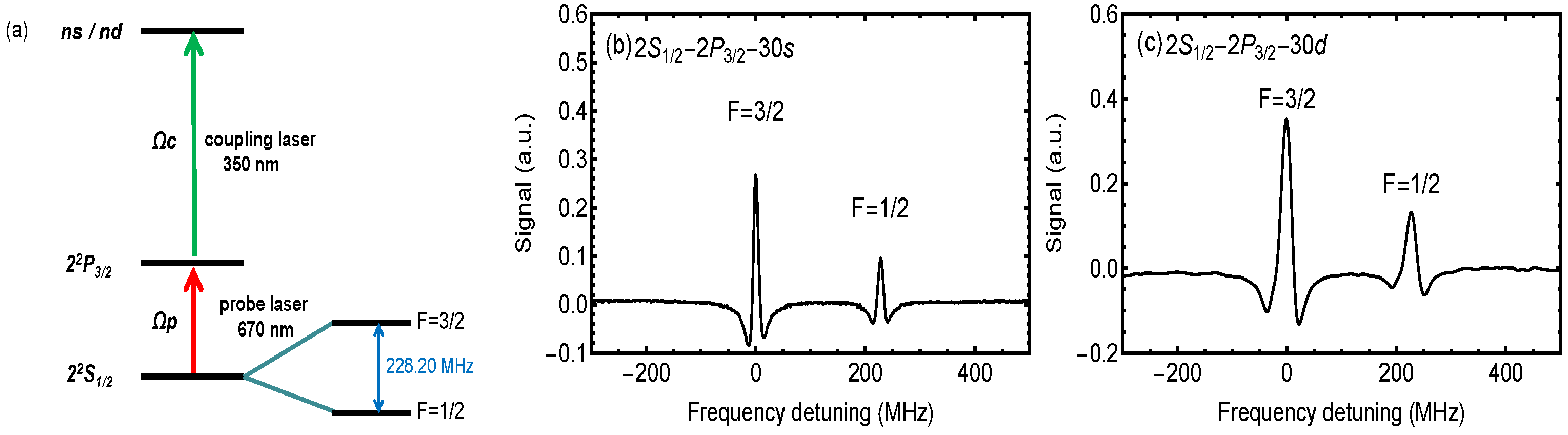
3. Measurements of EIT Spectra
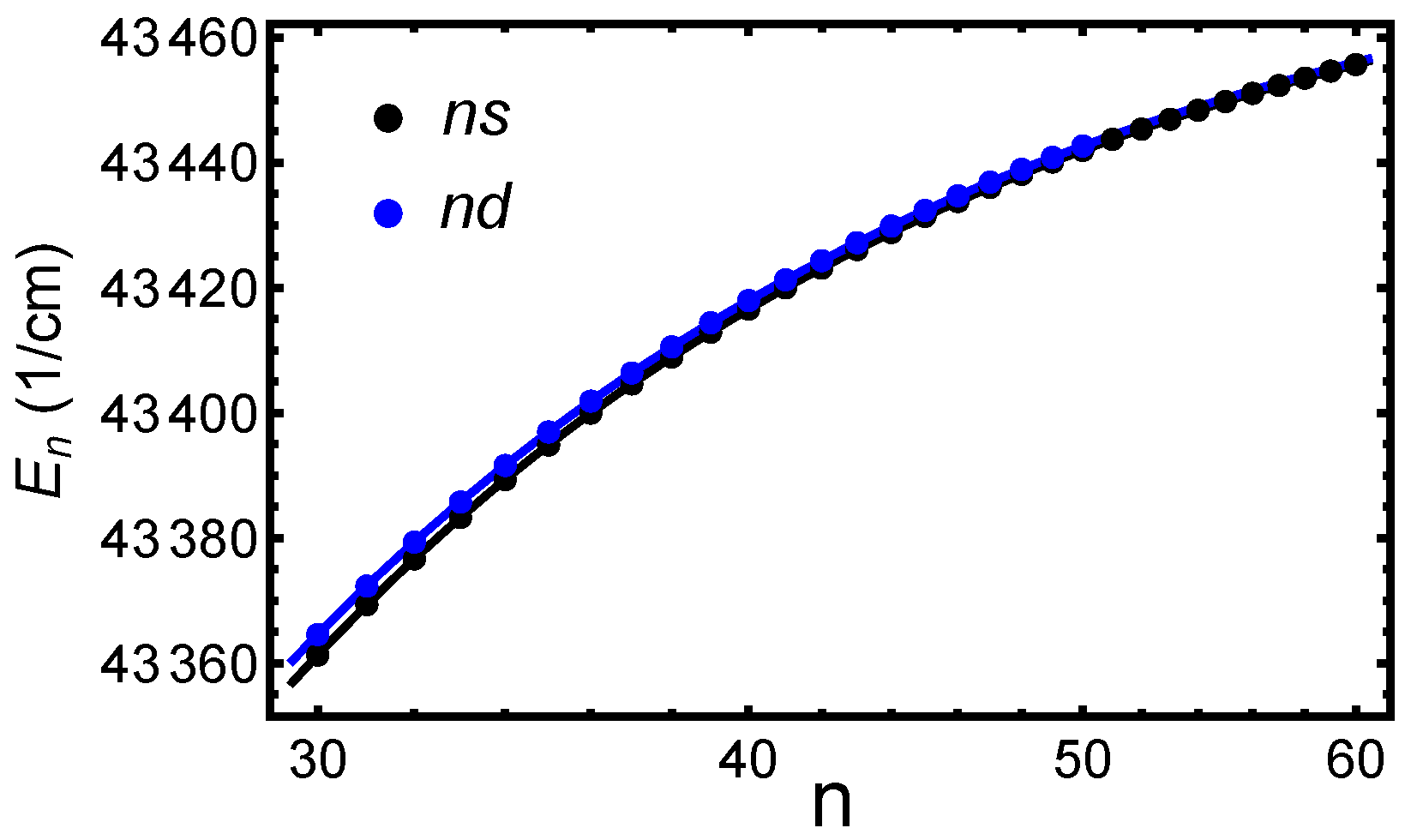
4. Quantum Defects of Li
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oks, E. Advances in Physics of Rydberg Atoms and Molecules; IOP Publishing: Bristol, UK, 2021; pp. 2053–2563. ISBN 978-0-7503-3939-1. [Google Scholar]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Dlaska, C.; Ender, K.; Mbeng, G.B.; Kruckenhauser, A.; Lechner, W.; van Bijnen, R. Quantum optimization via four-body Rydberg gates. Phys. Rev. Lett. 2022, 128, 120503. [Google Scholar] [CrossRef]
- Tiarks, D.; Baur, S.; Schneider, K.; Dürr, S.; Rempe, G. Single-photon transistor using a Förster resonance. Phys. Rev. Lett. 2014, 113, 053602. [Google Scholar] [CrossRef] [PubMed]
- Gard, B.T.; Jacobs, K.; McDermott, R.; Saffman, M. Microwave-to-optical frequency conversion using a cesium atom coupled to a superconducting resonator. Phys. Rev. A 2017, 96, 013833. [Google Scholar] [CrossRef]
- Yu, Y.; Sun, P.-F.; Zhang, Y.-Z.; Bai, B.; Fang, Y.-Q.; Luo, X.-Y.; An, Z.-Y.; Li, J.; Zhang, J.; Xu, F.; et al. Measurement-Device-Independent Verification of a Quantum Memory. Phys. Rev. Lett. 2021, 127, 160502. [Google Scholar] [CrossRef] [PubMed]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Kim, H.; Lee, W.; Lee, H.-G.; Jo, H.; Song, Y.; Ahn, J. In situ single-atom array synthesis using dynamic holographic optical tweezers. Nat. Commun. 2016, 7, 13317. [Google Scholar] [CrossRef]
- Endres, M.; Bernien, H.; Keesling, A.; Levine, H.; Anschuetz, E.R.; Krajenbrink, A.; Senko, C.; Vuletic, V.; Greiner, M.; Lukin, M.D. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 2016, 354, 1024–1027. [Google Scholar] [CrossRef]
- Barredo, D.; de Léséleuc, S.; Lienhard, V.; Lahaye, T.; Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 2016, 354, 1021–1023. [Google Scholar] [CrossRef] [PubMed]
- Sous, J.; Sadeghpour, H.R.; Killian, T.C.; Demler, E.; Schmidt, R. Rydberg impurity in a Fermi gas: Quantum statistics and rotational blockade. Phys. Rev. Res. 2020, 2, 023021. [Google Scholar] [CrossRef]
- Heidemann, R.; Raitzsch, U.; Bendkowsky, V.; Butscher, B.; Löw, R.; Pfau, T. Rydberg excitation of Bose-Einstein condensates. Phys. Rev. Lett. 2008, 100, 033601. [Google Scholar]
- Tong, D.; Farooqi, S.M.; Stanojevic, J.; Krishnan, S.; Zhang, Y.P.; Côté, R.; Eyler, E.E.; Gould, P.L. Local blockade of Rydberg excitation in an ultracold gas. Phys. Rev. Lett. 2004, 93, 063001. [Google Scholar] [CrossRef]
- Osychenko, O.N.; Astrakharchik, G.E.; Lutsyshyn, Y.; Lozovik, Y.E.; Boronat, J. Phase diagram of Rydberg atoms with repulsive van der Waals interaction. Phys. Rev. A 2011, 84, 063621. [Google Scholar] [CrossRef]
- Samajdar, R.; Ho, W.W.; Pichler, H.; Lukin, M.D.; Sachdev, S. Quantum phases of Rydberg atoms on a kagome lattice. Proc. Natl. Acad. Sci. USA 2021, 118, e2015785118. [Google Scholar] [CrossRef] [PubMed]
- Guardado-Sanchez, E.; Brown, P.T.; Mitra, D.; Devakul, T.; Huse, D.A.; Schauß, P.; Bakr, W.S. Probing the quench dynamics of antiferromagnetic correlations in a 2D quantum Ising spin system. Phys. Rev. X 2018, 8, 021069. [Google Scholar] [CrossRef]
- Zou, Y.-Q.; Berngruber, M.; Anasuri, V.S.V.; Zuber, N.; Meinert, F.; Löw, R.; Pfau, T. Observation of vibrational dynamics of orientated Rydberg-atom-ion molecules. Phys. Rev. Lett. 2023, 130, 023002. [Google Scholar] [CrossRef]
- Hummel, F.; Schmelcher, P.; Eiles, M.T. Vibronic interactions in trilobite and butterfly Rydberg molecules. Phys. Rev. Res. 2023, 5, 013114. [Google Scholar] [CrossRef]
- Zelener, B.B.; Saakyan, S.A.; Sautenkov, V.A.; Manykin, E.A.; Zelener, B.V.; Fortov, V.E.E. Efficient excitation of Rydberg states in ultracold lithium-7 atoms. JETP Lett. 2014, 100, 366–370. [Google Scholar] [CrossRef]
- Murashkin, D.A.; Saakyan, S.A.; Sautenkov, V.A.; Zelener, B.B. Measurements of quantum defect in Rydberg D-states for lithium atoms. J. Phys. Conf. Ser. 2016, 774, 012166. [Google Scholar] [CrossRef]
- Xu, W.; DeMarco, B. Velocity-selective electromagnetically-induced-transparency measurements of potassium Rydberg states. Phys. Rev. A 2016, 93, 011801. [Google Scholar] [CrossRef]
- Li, D.; Bian, G.; Miao, J.; Wang, P.; Meng, Z.; Chen, L.; Huang, L.; Zhang, J. Rydberg excitation spectrum of 40K ultracold Fermi gases. Phys. Rev. A 2021, 103, 063305. [Google Scholar] [CrossRef]
- Stoicheff, B.P.; Weinberger, E. Doppler-free two-photon absorption spectrum of rubidium. Can. J. Phys. 1979, 57, 2143–2154. [Google Scholar] [CrossRef]
- Jayaseelan, M.; Rotunno, A.; Prajapati, N.; Berweger, S.; Artusio-Glimpse, A.; Simons, M.; Holloway, C. Electromagnetically-induced-transparency spectra of Rydberg atoms dressed with dual-tone radio-frequency fields. Phys. Rev. A 2023, 108, 033712. [Google Scholar] [CrossRef]
- Mack, M.; Karlewski, F.; Hattermann, H.; Höckh, S.; Jessen, F.; Cano, D.; Fortágh, J. Measurement of absolute transition frequencies of Rb 87 to nS and nD Rydberg states by means of electromagnetically induced transparency. Phys. Rev. A 2011, 83, 052515. [Google Scholar] [CrossRef]
- Saßmannshausen, H.; Merkt, F.; Deiglmayr, J. High-resolution spectroscopy of Rydberg states in an ultracold cesium gas. Phys. Rev. A 2013, 87, 032519. [Google Scholar] [CrossRef]
- Guardado-Sanchez, E.; Spar, B.M.; Schauss, P.; Belyansky, R.; Young, J.T.; Bienias, P.; Gorshkov, A.V.; Iadecola, T.; Bakr, W.S. Quench dynamics of a fermi gas with strong nonlocal interactions. Phys. Rev. X 2021, 11, 021036. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, J.; Duffy, G.J.; Rowlands, W.J.; Akulshin, A.M. Electromagnetically induced transparency in 6Li. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3479. [Google Scholar] [CrossRef]
- Bao, S.; Zhang, H.; Zhou, J.; Zhang, L.; Zhao, J.; Xiao, L.; Jia, S. Polarization spectra of Zeeman sublevels in Rydberg electromagnetically induced transparency. Phys. Rev. A 2016, 94, 043822. [Google Scholar] [CrossRef]
- Šibalić, N.; Pritchard, J.; Adams, C.; Weatherill, K. ARC: An open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 2017, 220, 319–331. [Google Scholar] [CrossRef]
- Li, R.; Wu, Y.; Rui, Y.; Li, B.; Jiang, Y.; Ma, L.; Wu, H. Absolute Frequency Measurement of 6Li D Lines with khz-Level Uncertainty. Phys. Rev. Lett. 2020, 124, 063002. [Google Scholar] [CrossRef] [PubMed]
- Bushaw, B.A.; Drake, G.W.F.; Kluge, H.-J. Ionization energy of 6,7Li determined by triple-resonance laser spectroscopy. Phys. Rev. A 2007, 75, 052503. [Google Scholar] [CrossRef]
- Goy, P.; Liang, J.; Gross, M.; Haroche, S. Quantum defects and specific-isotopic-shift measurements in ns and np highly excited states of lithium: Exchange effects between Rydberg and core electrons. Phys. Rev. A 1986, 34, 2889. [Google Scholar] [CrossRef] [PubMed]
| n | Theory (ns, THz) | Experiment (ns, THz) | Theory (nd, THz) | Experiment (nd, THz) |
|---|---|---|---|---|
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 30 | 853.14012481 | 853.139625(2.0) | 853.238946780 | 853.238402(2.5) |
| 31 | 853.38149687 | 853.380931(1.9) | 853.471000983 | 853.470447(5.5) |
| 32 | 853.60031868 | 853.600253(2.8) | 853.681640530 | 853.681084(6.4) |
| 33 | 853.79931423 | 853.798746(1.8) | 853.873421573 | 853.872860(2.9) |
| 34 | 853.98080828 | 853.980256(4.8) | 854.048529868 | 854.047953(3.4) |
| 35 | 854.14679455 | 854.146233(5.9) | 854.208843495 | 854.208256(4.6) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 43 | 855.08189001 | 855.081821(3.2) | 855.115241259 | 855.114642(4.5) |
| 44 | 855.16408339 | 855.163507(5.7) | 855.195201873 | 855.194617(8.6) |
| 45 | 855.24081032 | 855.240745(2.7) | 855.269890967 | 855.269297(3.0) |
| 46 | 855.31254502 | 855.311976(2.6) | 855.339761976 | 855.339676(4.5) |
| 47 | 855.37971139 | 855.379642(1.9) | 855.405220550 | 855.404632(2.3) |
| 48 | 855.44268924 | 855.442116(3.8) | 855.466630577 | 855.466049(3.7) |
| 49 | 855.50181977 | 855.501250(3.1) | 855.524319130 | 855.523736(2.9) |
| 50 | 855.55741004 | 855.556839(1.6) | 855.578580965 | 855.577998(3.9) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Bao, X.; Yu, S.; Yi, L.; Ren, P.; Deng, S.; Wu, H. Electromagnetically Induced Transparency Spectra of 6Li Rydberg Atoms. Photonics 2023, 10, 1367. https://doi.org/10.3390/photonics10121367
Wu M, Bao X, Yu S, Yi L, Ren P, Deng S, Wu H. Electromagnetically Induced Transparency Spectra of 6Li Rydberg Atoms. Photonics. 2023; 10(12):1367. https://doi.org/10.3390/photonics10121367
Chicago/Turabian StyleWu, Meimei, Xin Bao, Shuxian Yu, Licheng Yi, Pingshuai Ren, Shujin Deng, and Haibin Wu. 2023. "Electromagnetically Induced Transparency Spectra of 6Li Rydberg Atoms" Photonics 10, no. 12: 1367. https://doi.org/10.3390/photonics10121367
APA StyleWu, M., Bao, X., Yu, S., Yi, L., Ren, P., Deng, S., & Wu, H. (2023). Electromagnetically Induced Transparency Spectra of 6Li Rydberg Atoms. Photonics, 10(12), 1367. https://doi.org/10.3390/photonics10121367





