Signal-to-Noise Ratio Improvement for Phase-Sensitive Optical Time-Domain Reflectometry Using a Genetic Least Mean Square Method
Abstract
:1. Introduction
2. Operating Principle
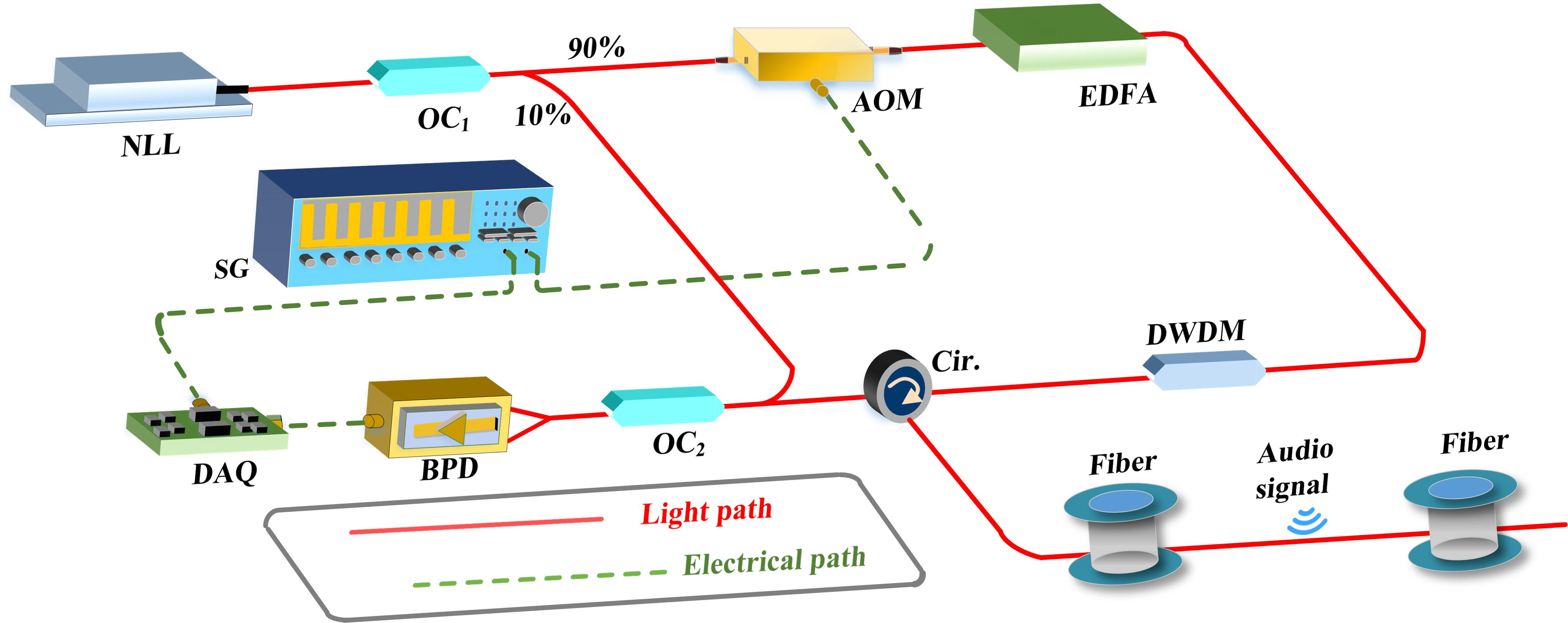
2.1. Experimental Arrangement
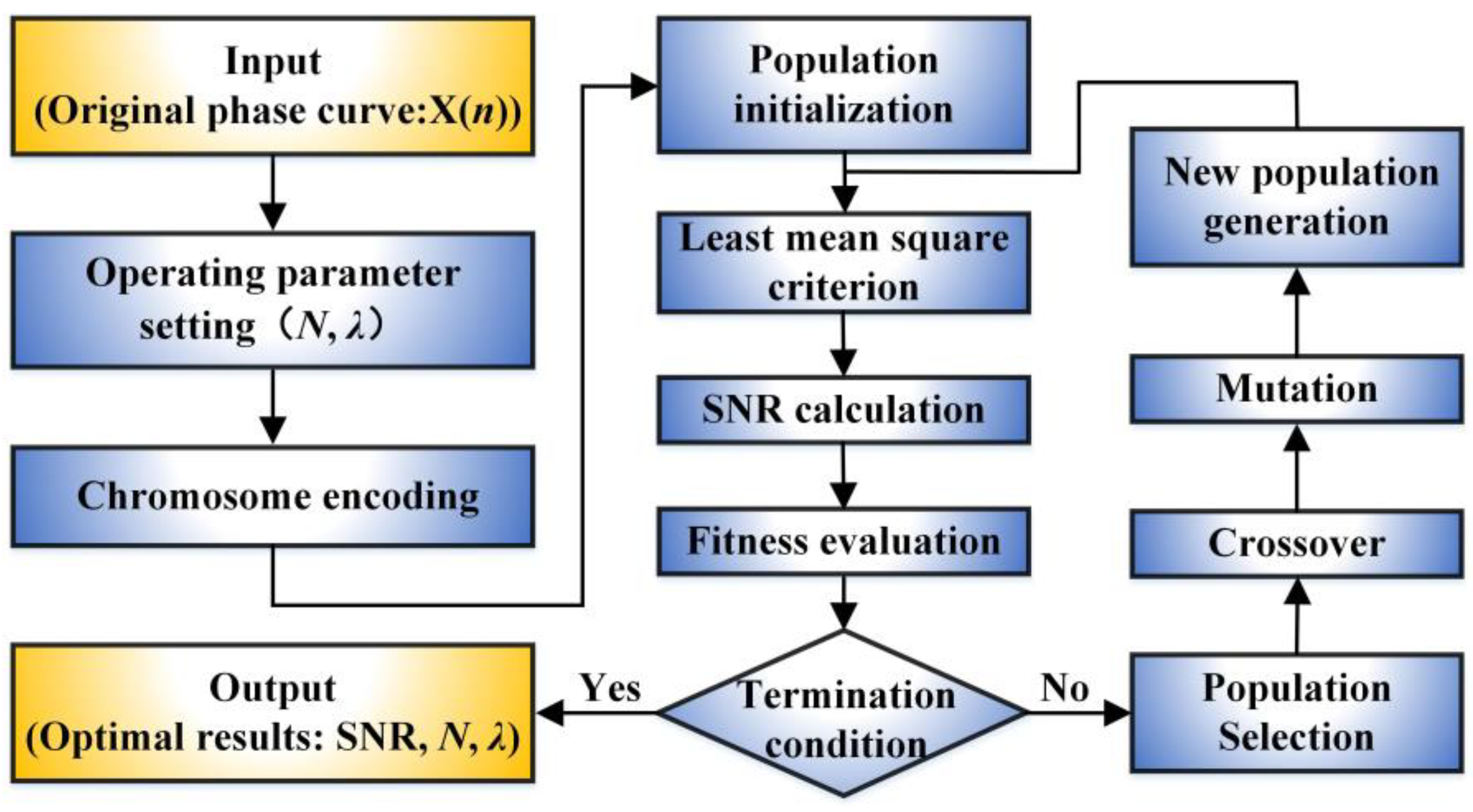
2.2. Operating Principle of the GLMS Method
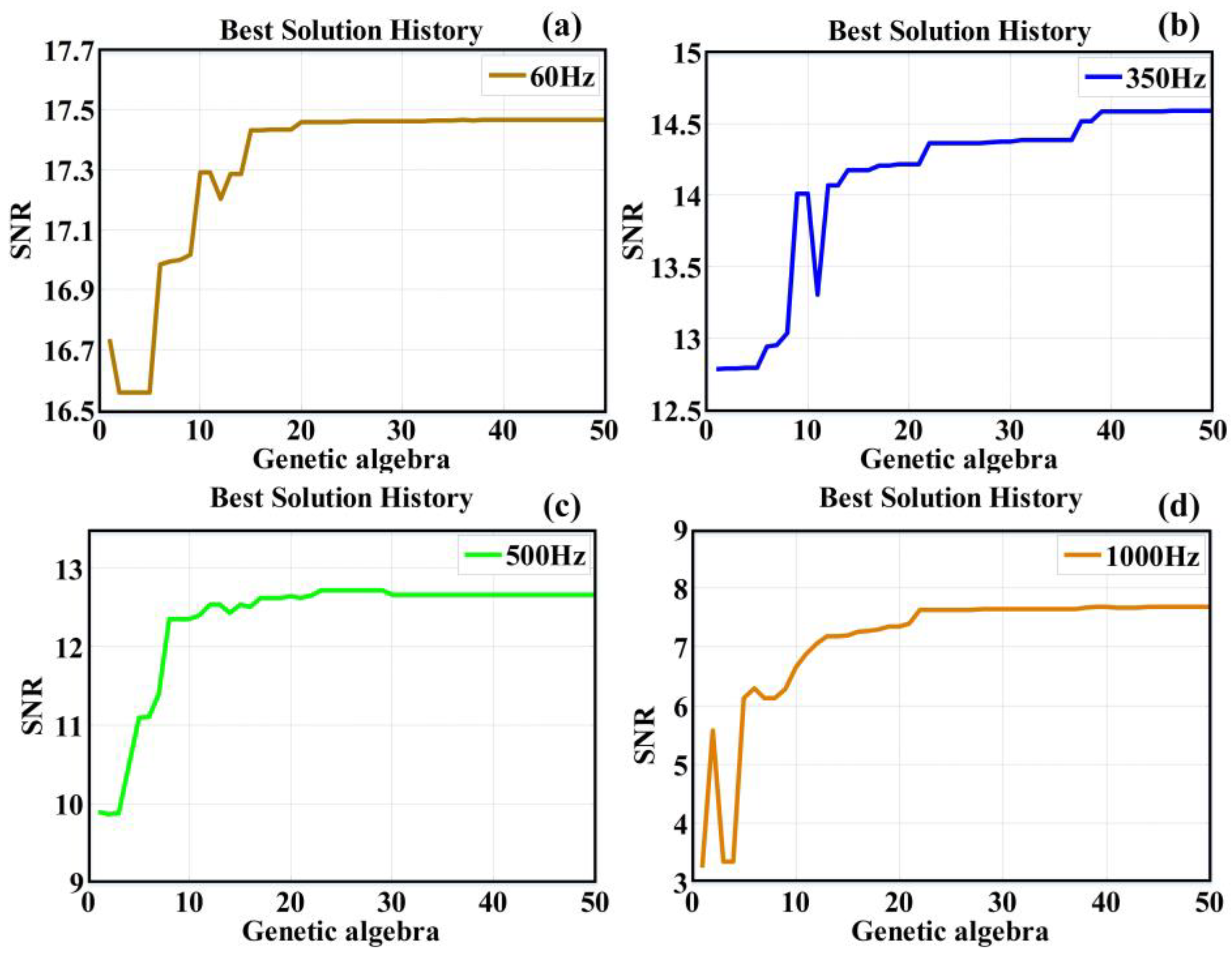
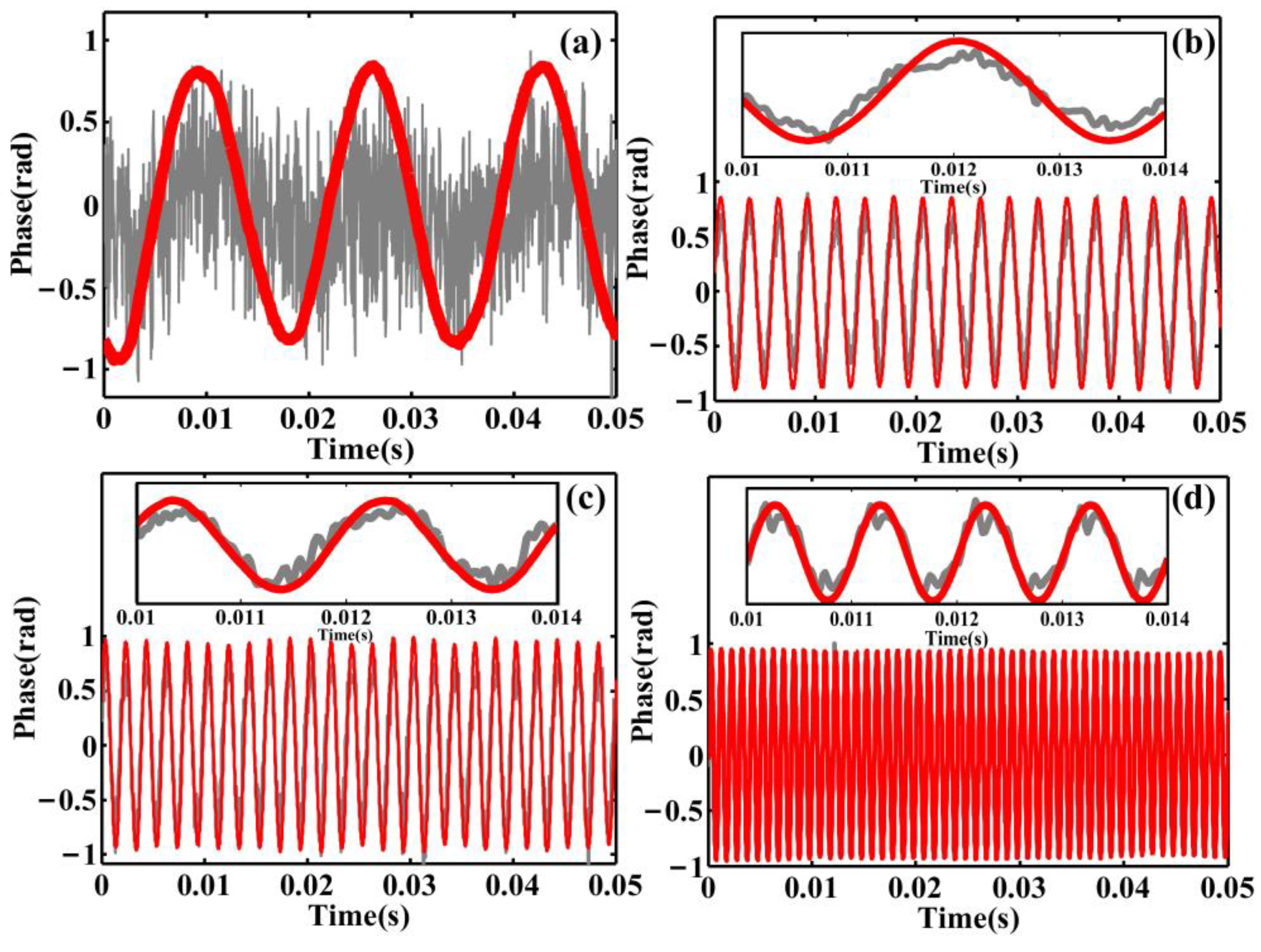
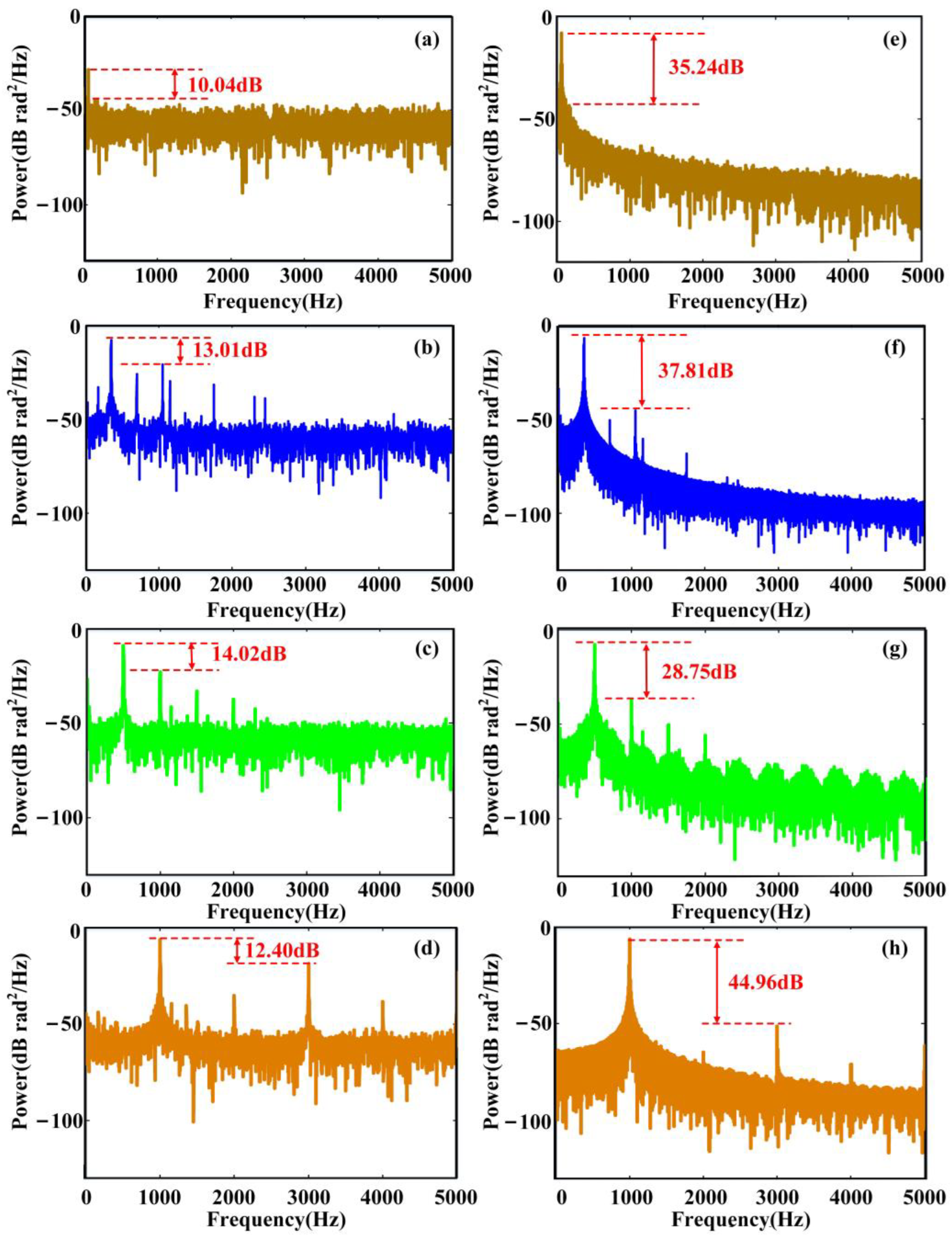
3. Experiments and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muñoz, F.; Soto, M.A. Enhancing fibre-optic distributed acoustic sensing capabilities with blind near-field array signal processing. Nat. Commun. 2022, 13, 4019. [Google Scholar] [CrossRef] [PubMed]
- Gorshkov, B.G.; Yüksel, K.; Fotiadi, A.A.; Wuilpart, M.; Korobko, D.A.; Zhirnov, A.A.; Stepanov, K.V.; Turov, A.T.; Konstantinov, Y.A.; Lobach, I.A. Scientific Applications of Distributed Acoustic Sensing: State-of-the-Art Review and Perspective. Sensors 2022, 22, 1033. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Wang, C.; Ni, J.; Zhao, W.; Li, C.; Chang, B.; Huang, S.; Wang, C.; Peng, G. Discussion on the sensitivity of optical cables based on distributed acoustic sensing. Opt. Rev. 2019, 26, 659–663. [Google Scholar] [CrossRef]
- Mateeva, A.; Lopez, J.; Potters, H.; Mestayer, J.; Cox, B.; Kiyashchenko, D.; Wills, P.; Grandi, S.; Hornman, K.; Kuvshinov, B.; et al. Distributed acoustic sensing for reservoir monitoring with vertical seismic profiling. Geophys. Prospect. 2014, 62, 679–692. [Google Scholar] [CrossRef]
- Liu, H.; Ma, J.; Yan, W.; Liu, W.; Zhang, X.; Li, C. Traffic Flow Detection Using Distributed Fiber Optic Acoustic Sensing. IEEE Access 2018, 6, 68968–68980. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M.J.; Lee, J.; Jung, H.; Kim, Y.H. Partial Discharge Monitoring Technology based on Distributed Acoustic Sensing. J. Sens. Sci. Technol. 2022, 31, 441–447. [Google Scholar] [CrossRef]
- Hussels, M.T.; Chruscicki, S.; Arndt, D.; Scheider, S.; Prager, J.; Homann, T.; Habib, A.K. Localization of Transient Events Threatening Pipeline Integrity by Fiber-Optic Distributed Acoustic Sensing. Sensors 2019, 19, 3322. [Google Scholar] [CrossRef]
- Molenaar, M.M.; Hill, D.J.; Webster, P.; Fidan, E.; Birch, B. First Downhole Application of Distributed Acoustic Sensing for Hydraulic-Fracturing Monitoring and Diagnostics. SPE Drill. Complet. 2012, 27, 32–38. [Google Scholar] [CrossRef]
- Liu, H.; Ma, J.; Xu, T.; Yan, W.; Ma, L.; Zhang, X. Vehicle Detection and Classification Using Distributed Fiber Optic Acoustic Sensing. IEEE Trans. Veh. Technol. 2020, 69, 1363–1374. [Google Scholar] [CrossRef]
- Fang, J.; Li, Y.; Ji, P.; Wang, T. Drone Detection and Localization Using Enhanced Fiber-Optic Acoustic Sensor and Distributed Acoustic Sensing Technology. J. Light. Technol. 2023, 41, 822–831. [Google Scholar] [CrossRef]
- Hua, L.; Zhu, X.; Cheng, B.; Song, Y.; Zhang, Q.; Wu, Y.; Murdoch, L.C.; Dauson, E.R.; Donahue, C.M.; Xiao, H. Distributed Acoustic Sensing Based on Coherent Microwave Photonics Interferometry. Sensors 2021, 21, 6784. [Google Scholar] [CrossRef]
- Muanenda, Y.; Faralli, S.; Oton, C.J.; Di Pasquale, F. Dynamic phase extraction in a modulated double-pulse φ-OTDR sensor using a stable homodyne demodulation in direct detection. Opt. Express 2018, 26, 687–701. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Ruiz, M.R.; Costa, L.; Martins, H.F. Distributed acoustic sensing using chirped-pulse phase-sensitive OTDR technology. Sensors 2019, 19, 4368. [Google Scholar] [CrossRef] [PubMed]
- Marcon, L.; Galtarossa, A.; Palmieri, L. High-frequency high-resolution distributed acoustic sensing by optical frequency domain reflectometry. Opt. Express 2019, 7, 13923–13933. [Google Scholar] [CrossRef] [PubMed]
- Shiloh, L.; Eyal, A. Sinusoidal frequency scan OFDR with fast processing algorithm for distributed acoustic sensing. Opt. Express 2017, 25, 19205–19215. [Google Scholar] [CrossRef]
- Li, H.; Liu, Q.; Chen, D.; Deng, Y.; He, Z. High-spatial-resolution fiber-optic distributed acoustic sensor based on Φ-OFDR with enhanced crosstalk suppression. Opt. Lett. 2020, 45, 563. [Google Scholar] [CrossRef]
- Piñeiro, E.; Sagues, M.; Loayssa, A. Compensation of Phase Noise Impairments in Distributed Acoustic Sensors Based on Optical Pulse Compression Time-Domain Reflectometry. J. Light. Technol. 2023, 41, 3199–3207. [Google Scholar] [CrossRef]
- Froggatt, M.; Moore, J. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef]
- Leviatan, E.; Eyal, A. High resolution DAS via sinusoidal frequency scan OFDR (SFS-OFDR). Opt. Express 2015, 23, 33318–33334. [Google Scholar] [CrossRef]
- Thevenaz, L.; Mafang, S.F.; Lin, J. Effect of pulse depletion in a Brillouin optical time-domain analysis system. Opt. Express 2013, 21, 14017–14035. [Google Scholar] [CrossRef]
- Peled, Y.; Motil, A.; Yaron, L.; Tur, M. Slope-assisted fast distributed sensing in optical fibers with arbitrary Brillouin profile. Opt. Express 2011, 19, 19845–19854. [Google Scholar] [CrossRef] [PubMed]
- Ip, E.; Huang, Y.; Huang, M.; Yaman, F.; Wellbrock, G.; Xia, T.; Wang, T.; Asahi, K. DAS Over 1007-km Hybrid Link With 10-Tb/s DP-16QAM Co-Propagation Using Frequency-Diverse Chirped Pulses. J. Light. Technol. 2023, 41, 1077–1086. [Google Scholar] [CrossRef]
- Muanenda, Y. Recent Advances in Distributed Acoustic Sensing Based on Phase-Sensitive Optical Time Domain Reflectometry. J. Sens. 2018, 2018, 3897873. [Google Scholar] [CrossRef]
- Sun, Y.; Li, H.; Fan, C.; Yan, B.; Chen, J.; Yan, Z.; Sun, Q. Review of a Specialty Fiber for Distributed Acoustic Sensing Technology. Photonics 2022, 9, 277. [Google Scholar] [CrossRef]
- Shang, Y.; Sun, M.; Wang, C.; Yang, J.; Du, Y.; Yi, J.; Zhao, W.; Wang, Y.; Zhao, Y.; Ni, J. Research Progress in Distributed Acoustic Sensing Techniques. Sensors 2022, 22, 6060. [Google Scholar] [CrossRef] [PubMed]
- Sha, Z.; Feng, H.; Zeng, Z. Phase demodulation method in phase-sensitive OTDR without coherent detection. Opt. Exp. 2017, 25, 4831. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, C.; Shang, Y.; Wang, C.; Zhao, W.; Peng, G.; Wang, H. Distributed acoustic sensing with Michelson interferometer demodulation. Photonic Sens. 2017, 7, 193–198. [Google Scholar] [CrossRef]
- Fang, G.; Xu, T.; Feng, S.; Li, F. Phase-Sensitive Optical Time Domain Reflectometer Based on Phase-Generated Carrier Algorithm. J. Light. Technol. 2015, 33, 2811–2816. [Google Scholar] [CrossRef]
- Pan, Z.; Liang, K.; Ye, Q.; Cai, H.; Qu, R.; Fang, Z. Phase-sensitive OTDR system based on digital coherent detection. In Proceedings of the 2011 Asia Communications and Photonics Conference and Exhibition (ACP), Shanghai, China, 13–16 November 2011; p. 83110S. [Google Scholar]
- Jiang, J.; Xiong, J.; Wang, Y.; Wang, P.; Zhang, J.; Liang, Y.; Sun, J.; Wang, Z. The Noise Lower-Bound of Rayleigh-Scattering-Pattern-Based Distributed Acoustic Sensing With Coherent Detection. J. Light. Technol. 2022, 40, 5337–5344. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Wang, S.; Xue, N.; Peng, F.; Fan, M.; Sun, W.; Qian, X.; Rao, J.; Rao, Y. Coherent Φ-OTDR based on I/Q demodulation and homodyne detection. Opt. Express 2016, 24, 853–858. [Google Scholar] [CrossRef]
- Jiang, F.; Lu, Z.; Cai, F.; Li, H.; Zhang, Z.; Zhang, Y.; Zhang, X. Low Computational Cost Distributed Acoustic Sensing Using Analog I/Q Demodulation. Sensors 2019, 19, 3753. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, J.; Gu, J.; Liu, Y.; Lu, B.; Ying, K.; Ye, L.; Ye, Q.; Qu, R.; Cai, H. Practical Performance Enhancement of DAS by Using Dense Multichannel Signal Integration. J. Light. Technol. 2021, 39, 6348–6354. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Ji, X.; Yun, F.; Rao, Y. Distributed Acoustic Sensing Based on Pulse-Coding Phase-Sensitive OTDR. IEEE Internet Things J. 2019, 6, 6117–6124. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, J.; Wu, B.; Lu, B.; Shuai, L.; Wang, Z.; Ye, L.; Ying, K.; Ye, Q.; Qu, R.; et al. High SNR Φ-OTDR with Multi-Transverse Modes Heterodyne Matched-Filtering Technology. Sensors 2021, 21, 7460. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, Z.; Zabihi, M.; Shan, Y.; Fu, S.; Wang, F.; Zhang, X.; Zhang, Y.; Zeng, B. Performance Enhancement Methods for the Distributed Acoustic Sensors Based on Frequency Division Multiplexing. Electronics 2019, 8, 617. [Google Scholar] [CrossRef]
- Tang, J.; Wang, G.; Lv, W.; Cheng, C.; Gan, W.; Yang, M. Distributed Acoustic Sensing System Based on Inserting-Zero Golay Coding with Ultra-Weak Fiber Bragg Gratings. IEEE Sens. J. 2022, 22, 15985–15990. [Google Scholar] [CrossRef]



| Acoustic Frequency | Number of Taps (N) | Step Size (λ) | SNR of the Raw Demodulated Phase | SNR of the Processed Phase by GLMS Method | SNR Increment |
|---|---|---|---|---|---|
| 60 Hz | 1965 | 4.53 × 10−5 | −0.73 dB | 17.46 dB | 18.19 dB |
| 100 Hz | 1996 | 2.00 × 10−5 | 0.35 dB | 14.04 dB | 14.37 dB |
| 150 Hz | 1985 | 1.67 × 10−6 | −3.31 dB | 20.29 dB | 23.60 dB |
| 200 Hz | 1052 | 8.30 × 10−4 | −2.88 dB | 15.86 dB | 18.74 dB |
| 250 Hz | 1839 | 5.16 × 10−7 | 0.85 dB | 18.62 dB | 17.77 dB |
| 300 Hz | 228 | 2.62 × 10−6 | −4.66 dB | 16.92 dB | 21.58 dB |
| 350 Hz | 1905 | 7.49 × 10−4 | −5.58 dB | 14.59 dB | 19.01 dB |
| 400 Hz | 1732 | 4.50 × 10−4 | −7.98 dB | 11.65 dB | 19.63 dB |
| 450 Hz | 1938 | 6.56 × 10−4 | −5.72 dB | 10.64 dB | 16.36 dB |
| 500 Hz | 189 | 9.25 × 10−6 | −2.73 dB | 12.66 dB | 15.39 dB |
| 1000 Hz | 26 | 2.68 × 10−6 | −8.11 dB | 7.68 dB | 15.79 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Liu, Z.; Zhou, X.; Wang, Y.; Bai, Q.; Jin, B. Signal-to-Noise Ratio Improvement for Phase-Sensitive Optical Time-Domain Reflectometry Using a Genetic Least Mean Square Method. Photonics 2023, 10, 1362. https://doi.org/10.3390/photonics10121362
Liu X, Liu Z, Zhou X, Wang Y, Bai Q, Jin B. Signal-to-Noise Ratio Improvement for Phase-Sensitive Optical Time-Domain Reflectometry Using a Genetic Least Mean Square Method. Photonics. 2023; 10(12):1362. https://doi.org/10.3390/photonics10121362
Chicago/Turabian StyleLiu, Xin, Zhihua Liu, Xiaoxu Zhou, Yu Wang, Qing Bai, and Baoquan Jin. 2023. "Signal-to-Noise Ratio Improvement for Phase-Sensitive Optical Time-Domain Reflectometry Using a Genetic Least Mean Square Method" Photonics 10, no. 12: 1362. https://doi.org/10.3390/photonics10121362
APA StyleLiu, X., Liu, Z., Zhou, X., Wang, Y., Bai, Q., & Jin, B. (2023). Signal-to-Noise Ratio Improvement for Phase-Sensitive Optical Time-Domain Reflectometry Using a Genetic Least Mean Square Method. Photonics, 10(12), 1362. https://doi.org/10.3390/photonics10121362





