Experimental Study on the Temporal Evolution Parameters of Laser–Produced Tin Plasma under Different Laser Pulse Energies for LPP–EUV Source
Abstract
:1. Introduction
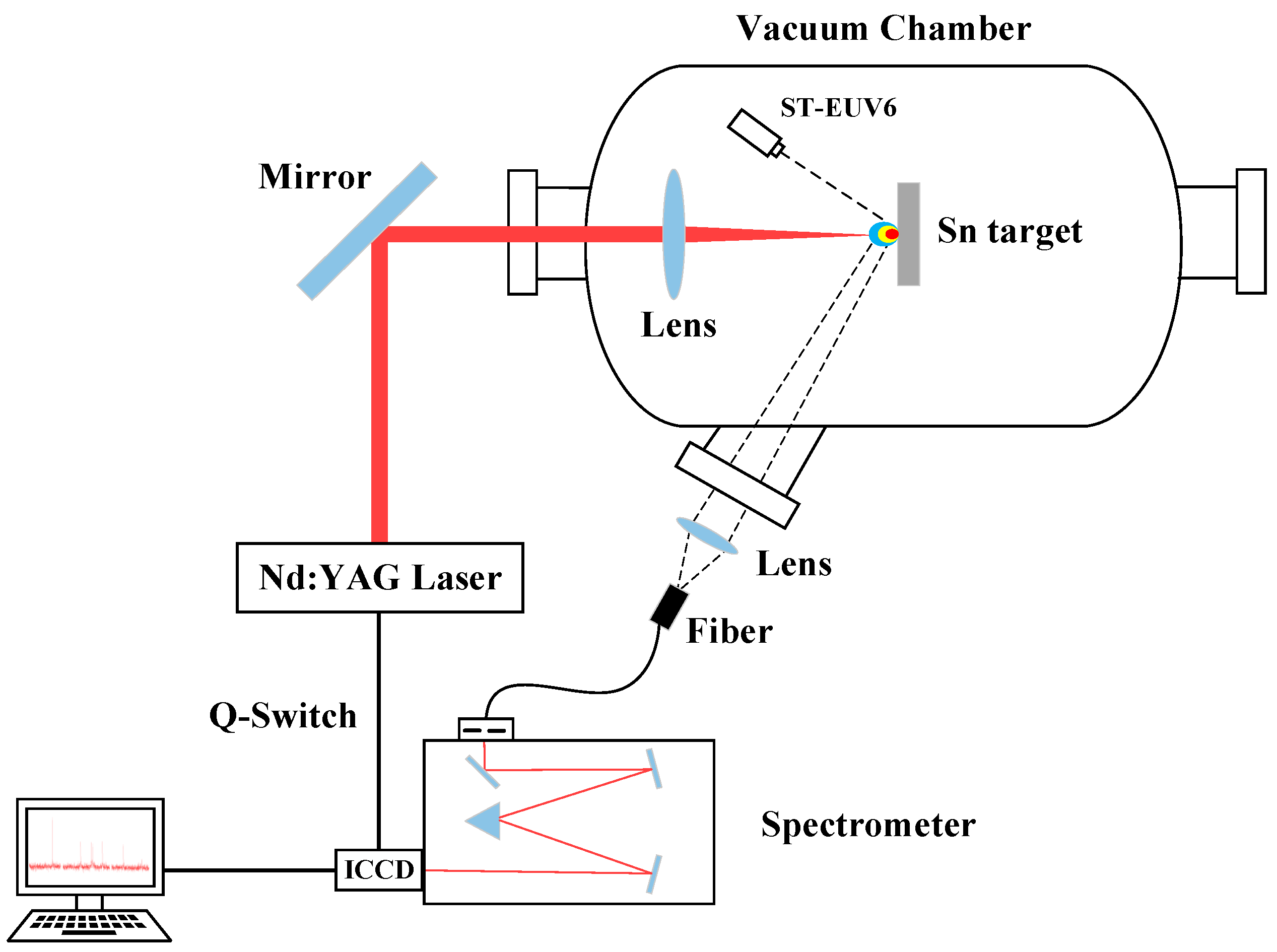
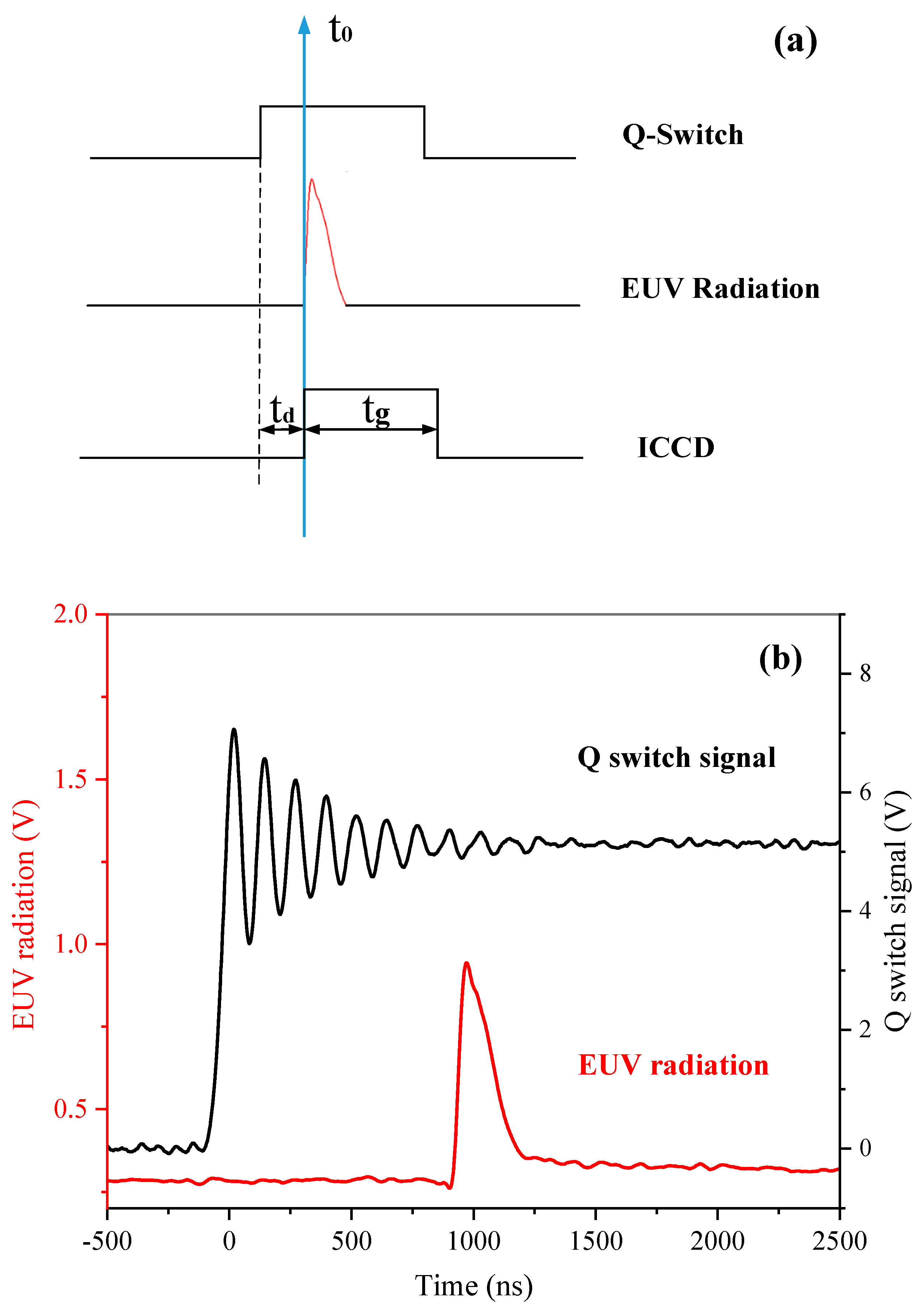
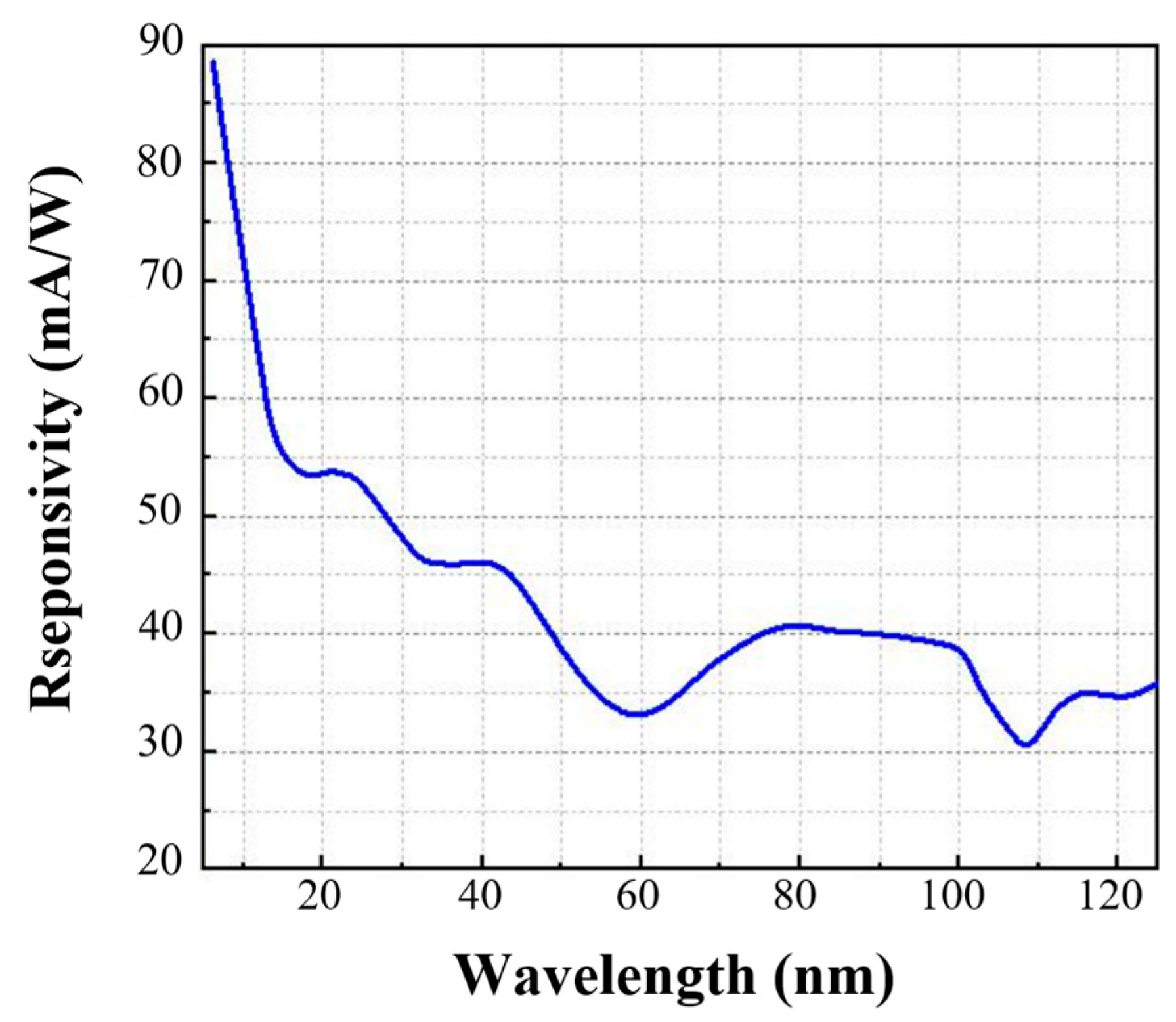
2. Experimental Setup
3. Results and Discussion
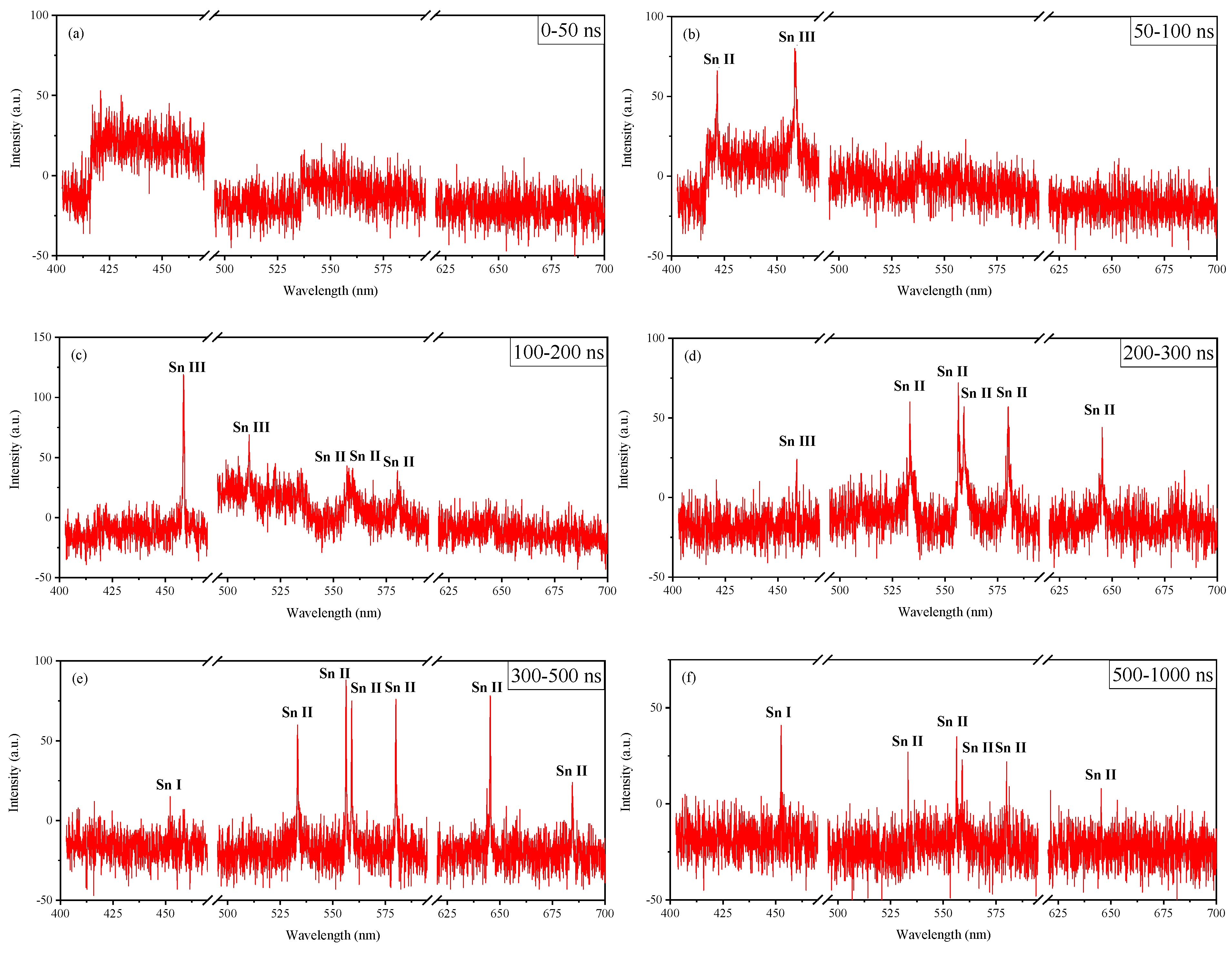
3.1. Time–Resolved Spectral Measurement of Laser–Produced Tin Plasma
3.2. Diagnosis of Electron Temperature and Electron Density in Laser–Produced Tin Plasma
3.2.1. Electron Temperature Diagnosis
3.2.2. Electron Density Diagnosis
3.3. Diagnosis of Laser–Produced Tin Plasma Parameters under Different Laser Pulse Energies
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, M.; Luo, J.; Li, F.Y.; Liu, F.; Sheng, Z.M.; Zhang, J. Tunable synchrotron-like radiation from centimeter scale plasma channels. Light Sci. Appl. 2016, 5, e16015. [Google Scholar] [CrossRef]
- Jiang, B.; Feng, C.; Li, C.; Bai, Z.; Wan, W.; Xiang, D.; Gu, Q.; Wang, K.; Zhang, Q.; Huang, D.; et al. A synchrotron-based kilowatt-level radiation source for EUV lithography. Sci. Rep. 2022, 12, 3325. [Google Scholar] [CrossRef]
- Kruecken, T. Discharge plasmas as EUV sources for future micro lithography. AIP Conf. Proc. Am. Inst. Phys. 2007, 926, 259–269. [Google Scholar]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Labat, M.; Cabadağ, J.C.; Ghaith, A.; Irman, A.; Berlioux, A.; Berteaud, P.; Blache, F.; Bock, S.; Bouvet, F.; Briquez, F.; et al. Seeded free-electron laser driven by a compact laser plasma accelerator. Nat. Photonics 2023, 17, 150–156. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Tomita, K.; Pan, Y.; Sunahara, A.; Kouge, K.; Mizoguchi, H.; Nishihara, K. Observation of plasma inflows in laser-produced Sn plasma and their contribution to extreme-ultraviolet light output enhancement. Sci. Rep. 2023, 13, 1825. [Google Scholar] [CrossRef]
- Benschop, J.; Banine, V.; Lok, S.; Loopstra, E. Extreme ultraviolet lithography: Status and prospects. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2008, 26, 2204–2207. [Google Scholar] [CrossRef]
- Torretti, F.; Sheil, J.; Schupp, R.; Basko, M.M.; Bayraktar, M.; Meijer, R.A.; Witte, S.; Ubachs, W.; Hoekstra, R.; Versolato, O.O.; et al. Prominent radiative contributions from multiply-excited states in laser-produced tin plasma for nanolithography. Nat. Commun. 2020, 11, 2334. [Google Scholar] [CrossRef]
- Zong, N.; Hu, W.M.; Wang, Z.M.; Wang, X.J.; Zhang, S.J.; Bo, Y.; Peng, Q.J.; Xu, Z.Y. Research progress on laser-produced plasma light source for 13.5 nm extreme ultraviolet lithography. Chin. Opt. 2020, 13, 28–42. [Google Scholar] [CrossRef]
- Mizoguchi, H.; Nakarai, H.; Usami, Y.; Kakizaki, K.; Fujimoto, J.; Saitou, T. High-power LPP-EUV source for semiconductor HVM: Lithography and other applications. In International Conference on Extreme Ultraviolet Lithography; SPIE: Bellingham, WA, USA, 2022; Volume 12292, pp. 255–260. [Google Scholar]
- Umstadter, K.; Graham, M.; Purvis, M.; Schafgans, A.; Stewart, J.; Mayer, P.; Brown, D. EUV light source for high-NA and low-NA lithography. In Optical and EUV Nanolithography XXXVI; SPIE: Bellingham, WA, USA, 2023; Volume 12494, pp. 335–342. [Google Scholar]
- Zeng, A. The Development of Photolithographic Technology and Machines. SHS Web Conf. EDP Sci. 2023, 163, 03021. [Google Scholar] [CrossRef]
- Harilal, S.S.; Sizyuk, T.; Hassanein, A.; Campos, D.; Hough, P.; Sizyuk, V. The effect of excitation wavelength on dynamics of laser-produced tin plasma. J. Appl. Phys. 2011, 109, 063306. [Google Scholar] [CrossRef]
- Wu, T.; Wang, X.; Tang, J. Extreme Ultraviolet and Visible Emission Spectroscopic Characterization of CO2 Laser Produced Tin Plasma for Lithography. Acta Opt. Sin. 2012, 32, 292–297. [Google Scholar]
- Lan, H.; Wang, X.B.; Zuo, D.L. Spectral and ion emission features of laser-produced Sn and SnO2 plasmas. Chin. Phys. B 2016, 25, 035202. [Google Scholar] [CrossRef]
- Lan, H.; Wang, X.; Zuo, D. Time-resolved optical emission spectroscopy diagnosis of CO2 laser-produced SnO2 plasma. Plasma Sci. Technol. 2016, 18, 902. [Google Scholar] [CrossRef]
- Amin, N.; Shaikh, N.M.; Tao, Y.; Ueno, Y.; Tillack, M.S. Influence of transverse magnetic field on dynamics of Sn plasma produced by CO2 laser. Phys. B Condens. Matter 2021, 602, 412560. [Google Scholar] [CrossRef]
- Du, Y. Study on Radiation Characteristics and Spatio-Temporal Evolution of Laser-Produced Al-Sn Plasmas. Master’s Thesis, Northwest Normal University, Lanzhou, China, 2022. [Google Scholar]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. Atomic Spectra Database: NIST Standard Reference Database. Available online: https://www.nist.gov/pml/atomic-spectradatabase (accessed on 15 August 2023).
- Harilal, S.S.; Phillips, M.C.; Froula, D.H.; Anoop, K.K.; Issac, R.C.; Beg, F.N. Optical diagnostics of laser-produced plasmas. Rev. Mod. Phys. 2022, 94, 035002. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Qian, H.; Li, K. Electron Temperature and Density of Soil Plasma Generated by Laser Ablation Fast Pulse Discharge Spectroscopy. Acta Opt. Sin. 2011, 31, 1130001. [Google Scholar]
- Moon, H.Y.; Smith, B.W.; Omenetto, N. Temporal behavior of line-to-continuum ratios and ion fractions as a means of assessing thermodynamic equilibrium in laser-induced breakdown spectroscopy. Chem. Phys. 2012, 398, 221–227. [Google Scholar] [CrossRef]
- Man, B.Y.; Dong, Q.L.; Liu, A.H.; Wei, X.Q.; Zhang, Q.G.; He, J.L.; Wang, X.T. Line-broadening analysis of plasma emission produced by laser ablation of metal Cu. J. Opt. A Pure Appl. Opt. 2003, 6, 17. [Google Scholar] [CrossRef]
- Griem, H.R.; Scott, F.R. Plasma spectroscopy. Am. J. Phys. 1965, 33, 864–865. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Djeniže, S.; Srećković, A.; Labat, J. Stark width and shift of singly-ionized tin spectral lines. Z. Phys. D At. Mol. Clust. 1990, 17, 85–86. [Google Scholar] [CrossRef]

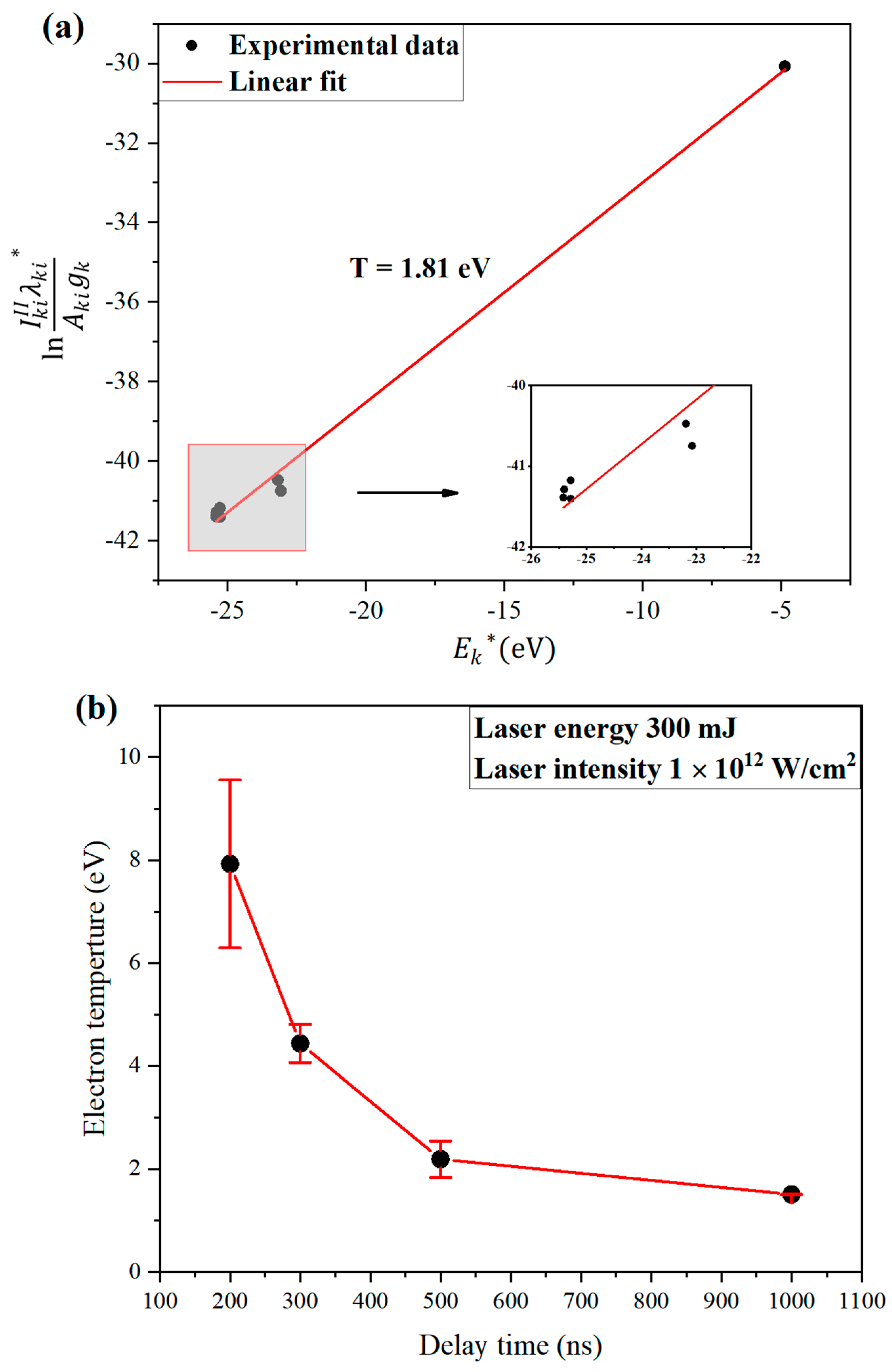
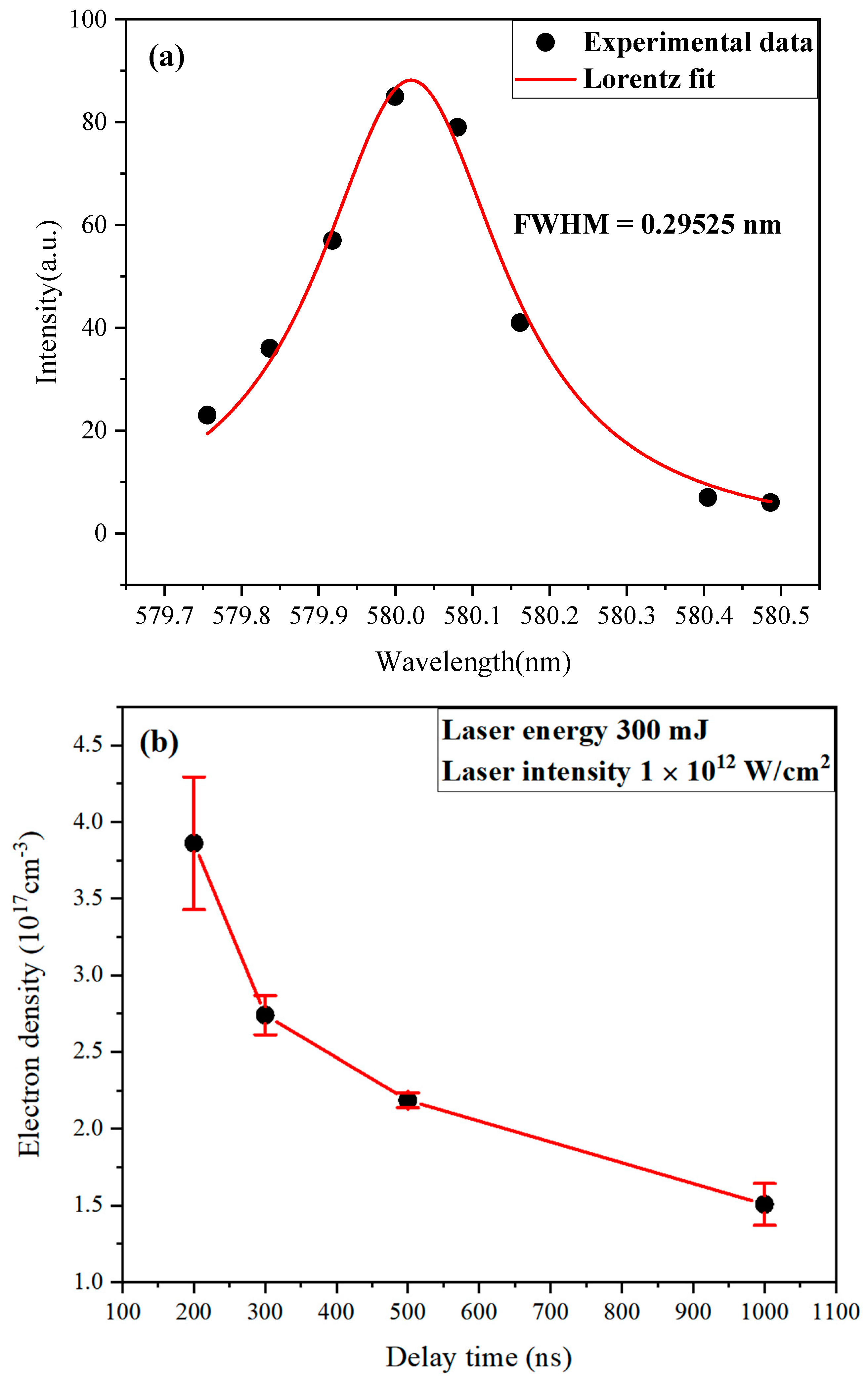
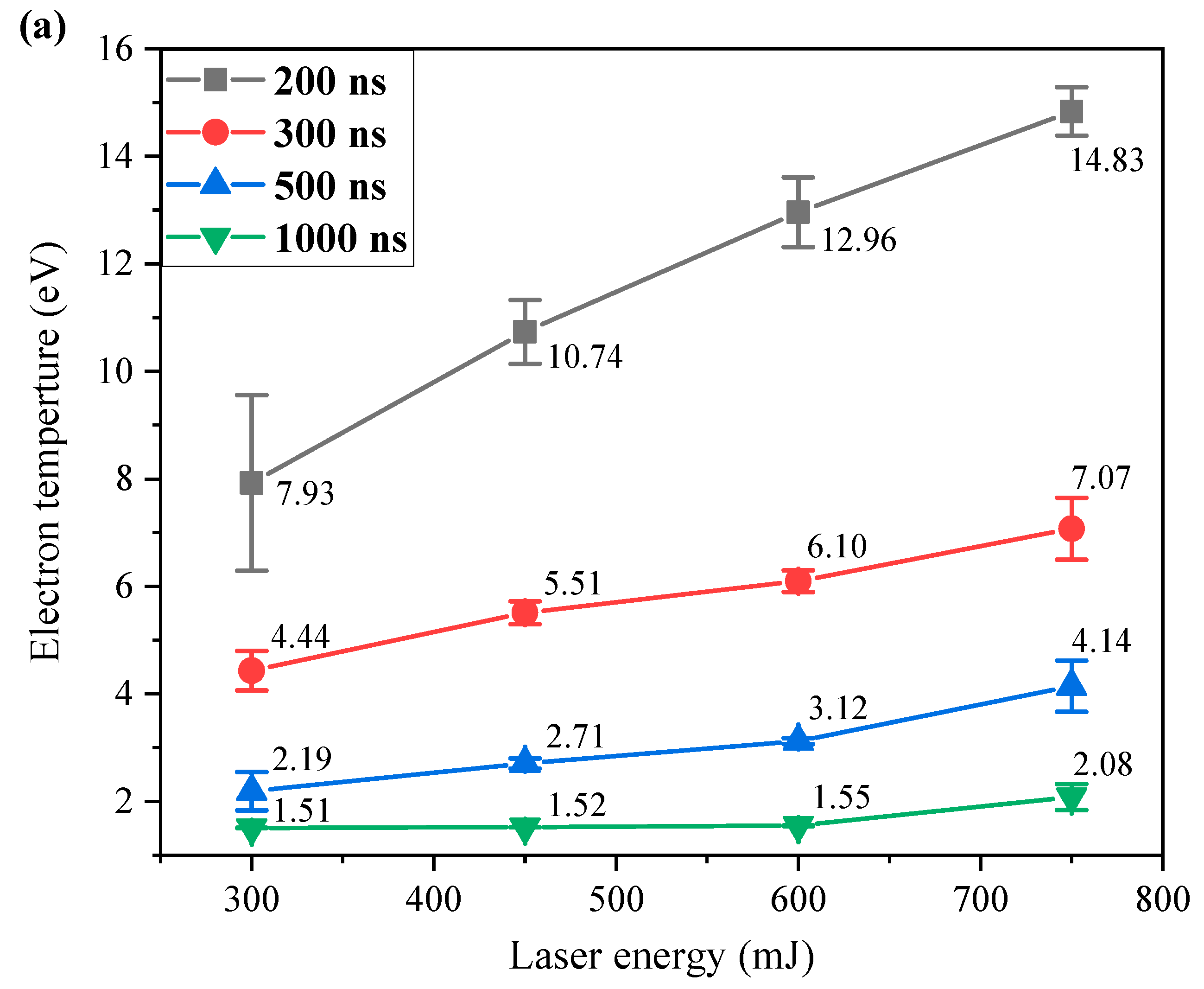
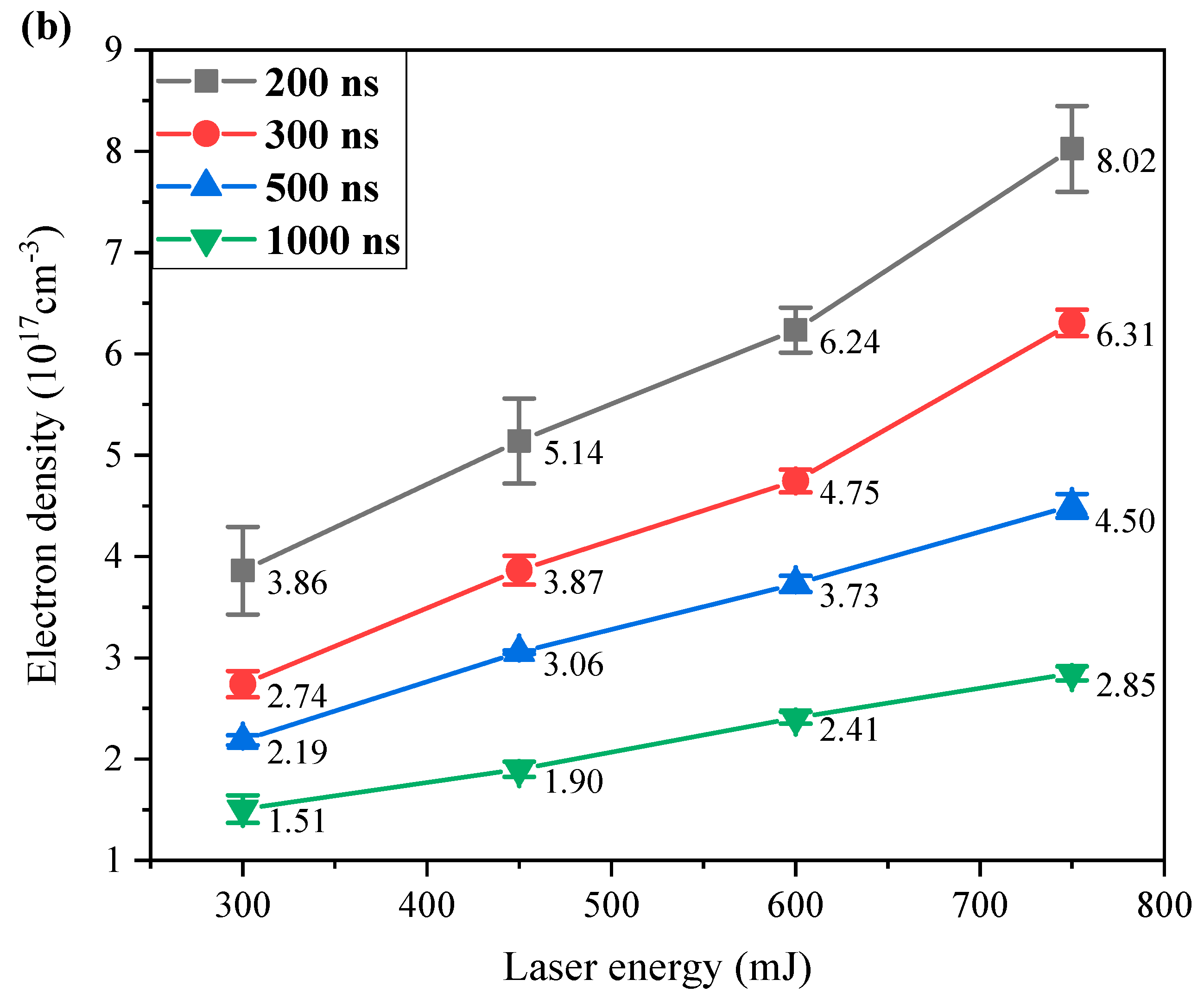
| Species | Wavelength/nm | gkAki/s−1 | Ei/eV | Ek/eV |
|---|---|---|---|---|
| Sn I | 452.60 | 7.8 × 107 | 2.128 | 4.867 |
| Sn II | 533.38 | 4.0 × 108 | 8.864 | 11.189 |
| Sn II | 556.35 | 6.78 × 108 | 8.974 | 11.202 |
| Sn II | 559.04 | 4.7 × 108 | 8.853 | 11.071 |
| Sn II | 580.05 | 6.2 × 108 | 8.933 | 11.070 |
| Sn II | 645.53 | 2.8 × 108 | 7.053 | 8.974 |
| Sn II | 684.61 | 1.2 × 108 | 7.053 | 8.864 |
| Species | Wavelength/nm | I |
|---|---|---|
| Sn I | 452.09 | 15 |
| Sn II | 533.24 | 60 |
| Sn II | 556.32 | 88 |
| Sn II | 559.09 | 75 |
| Sn II | 580.00 | 76 |
| Sn II | 645.40 | 78 |
| Sn II | 684.52 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhao, C.; Pan, Q.; Zhang, R.; Gao, Y.; Li, X.; Guo, J.; Chen, F. Experimental Study on the Temporal Evolution Parameters of Laser–Produced Tin Plasma under Different Laser Pulse Energies for LPP–EUV Source. Photonics 2023, 10, 1339. https://doi.org/10.3390/photonics10121339
Chen Y, Zhao C, Pan Q, Zhang R, Gao Y, Li X, Guo J, Chen F. Experimental Study on the Temporal Evolution Parameters of Laser–Produced Tin Plasma under Different Laser Pulse Energies for LPP–EUV Source. Photonics. 2023; 10(12):1339. https://doi.org/10.3390/photonics10121339
Chicago/Turabian StyleChen, Yiyi, Chongxiao Zhao, Qikun Pan, Ranran Zhang, Yang Gao, Xiaoxi Li, Jin Guo, and Fei Chen. 2023. "Experimental Study on the Temporal Evolution Parameters of Laser–Produced Tin Plasma under Different Laser Pulse Energies for LPP–EUV Source" Photonics 10, no. 12: 1339. https://doi.org/10.3390/photonics10121339
APA StyleChen, Y., Zhao, C., Pan, Q., Zhang, R., Gao, Y., Li, X., Guo, J., & Chen, F. (2023). Experimental Study on the Temporal Evolution Parameters of Laser–Produced Tin Plasma under Different Laser Pulse Energies for LPP–EUV Source. Photonics, 10(12), 1339. https://doi.org/10.3390/photonics10121339





