One-Step Implementation of Collective Anti-Blockade in a Rydberg Ring
Abstract
:1. Introduction
2. Model and Equations
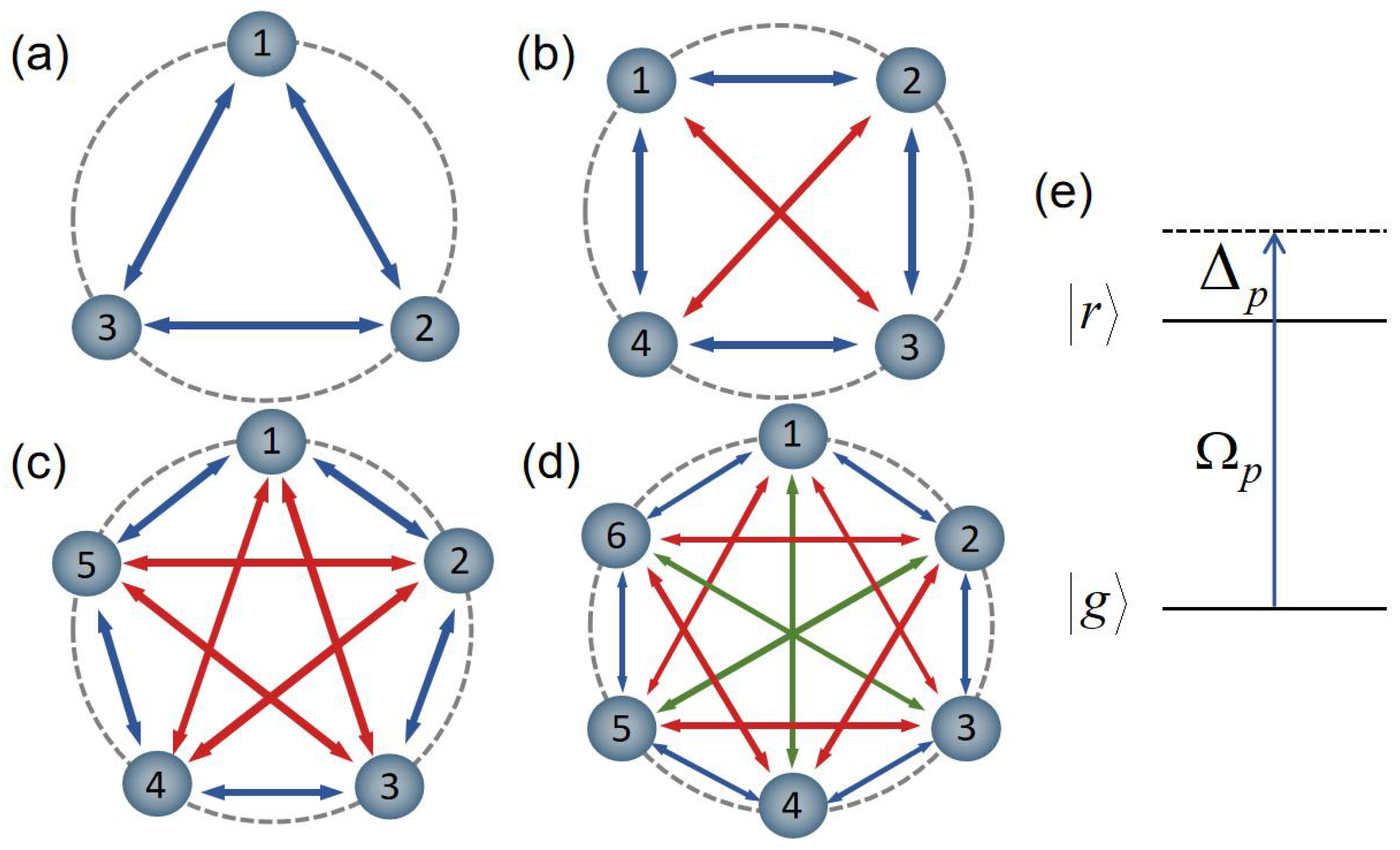
2.1. Level Configuration and Geometric Arrangement
2.2. Anti-Blockade Conditions of Rydberg Excitations
2.2.1. A Ring of Odd-Number Rydberg Atoms
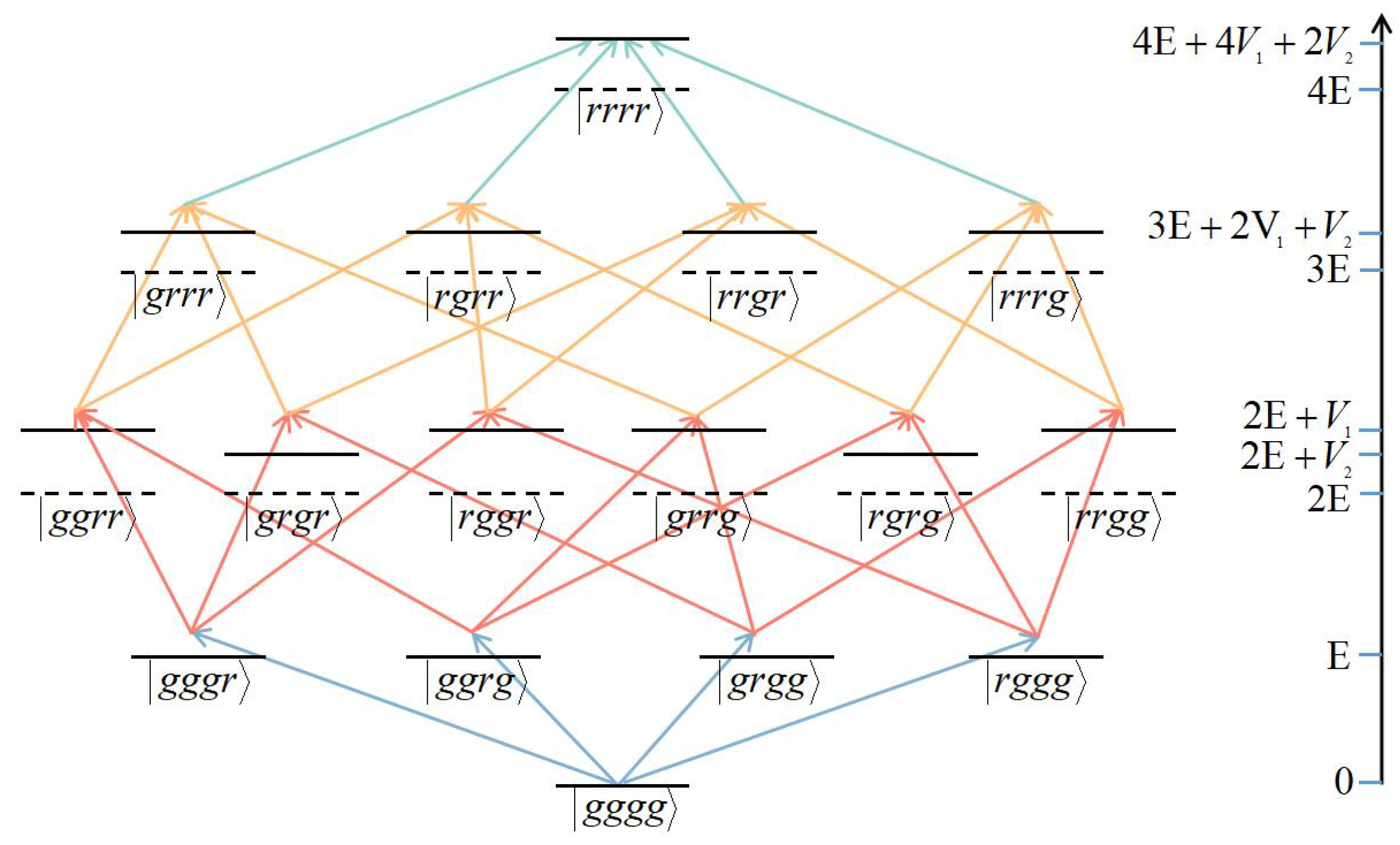
2.2.2. A Ring of Even-Number Rydberg Atoms
2.3. Effective Hamiltonians and Cutoff Times
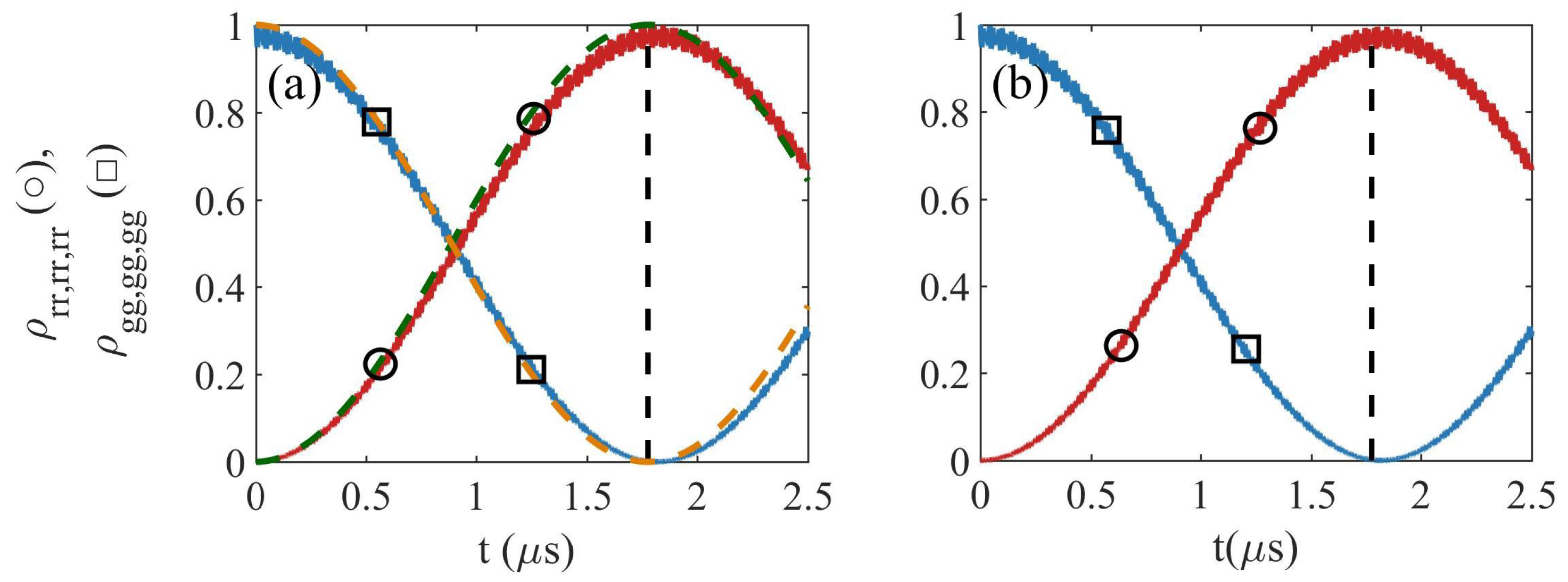
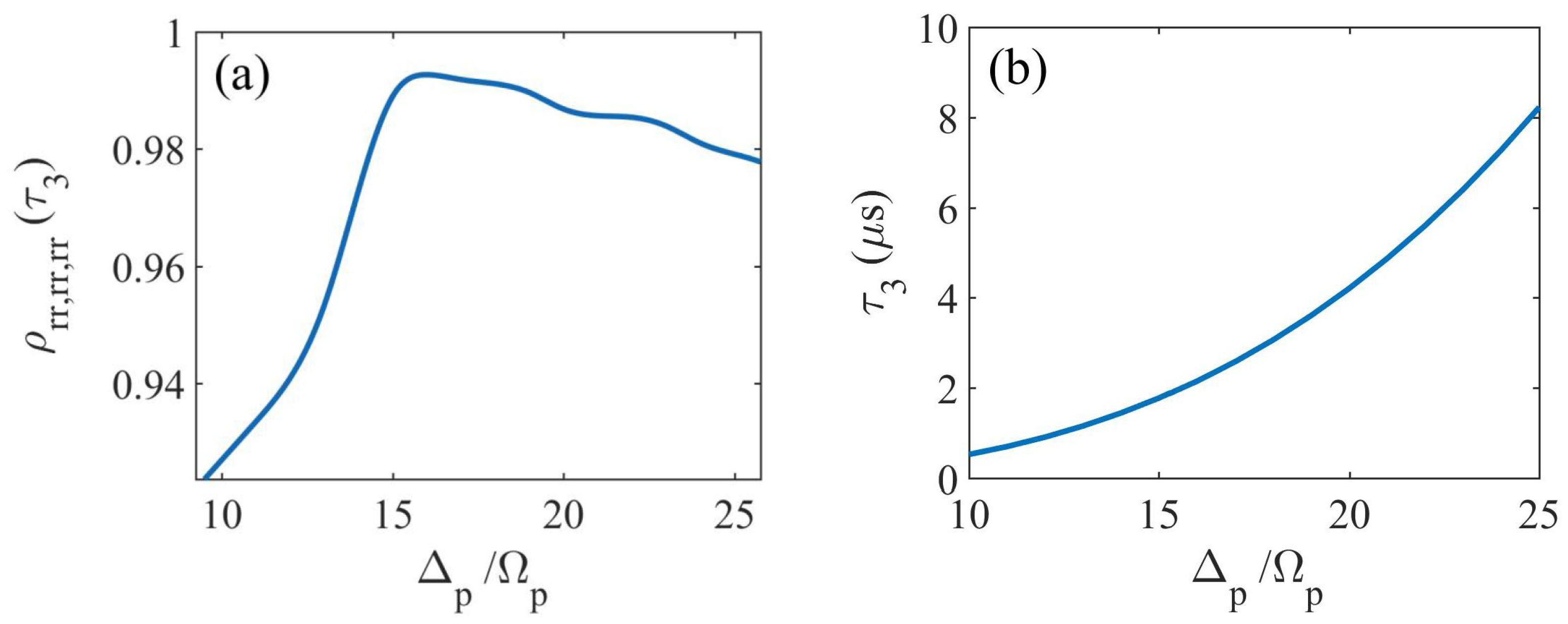
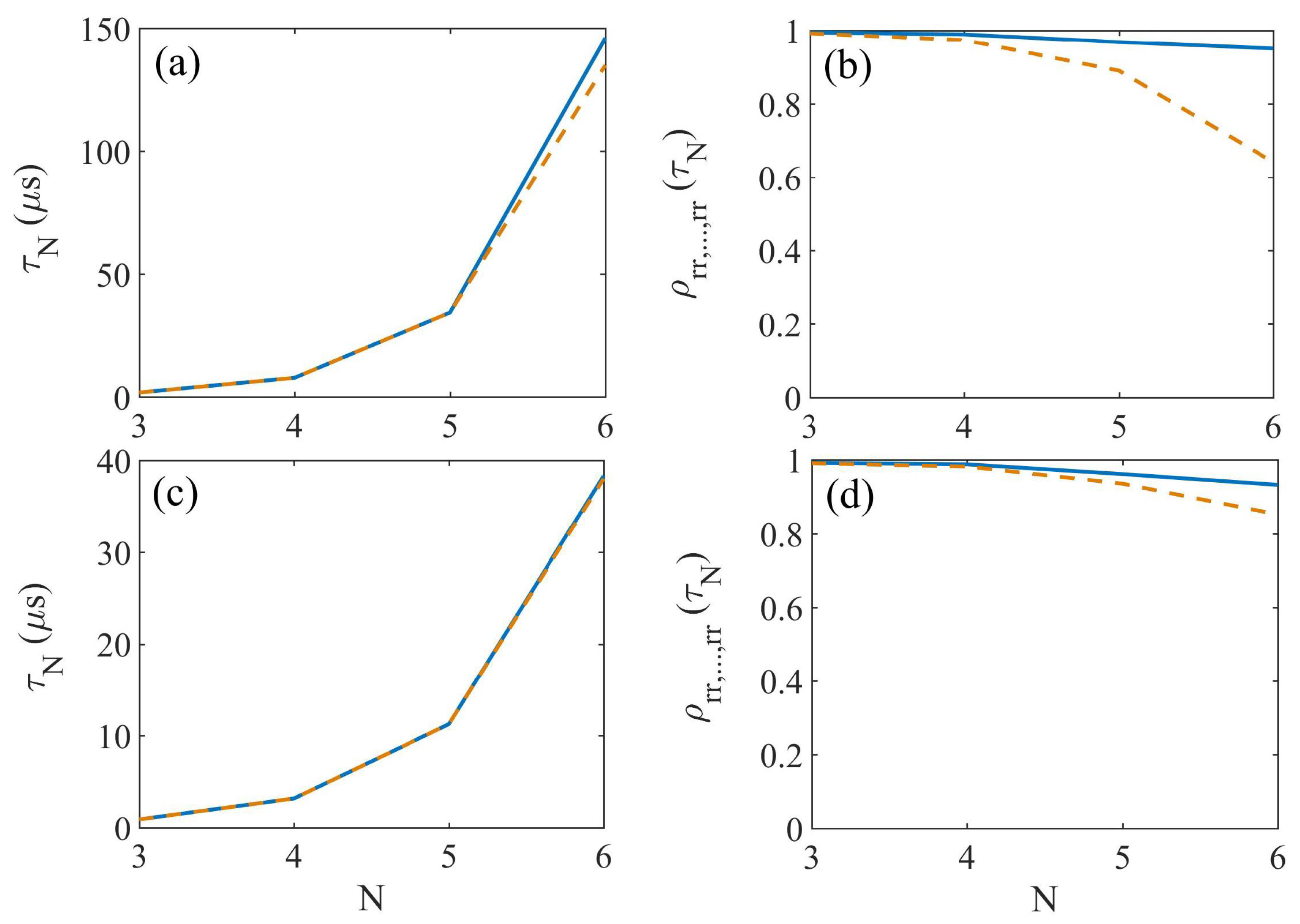
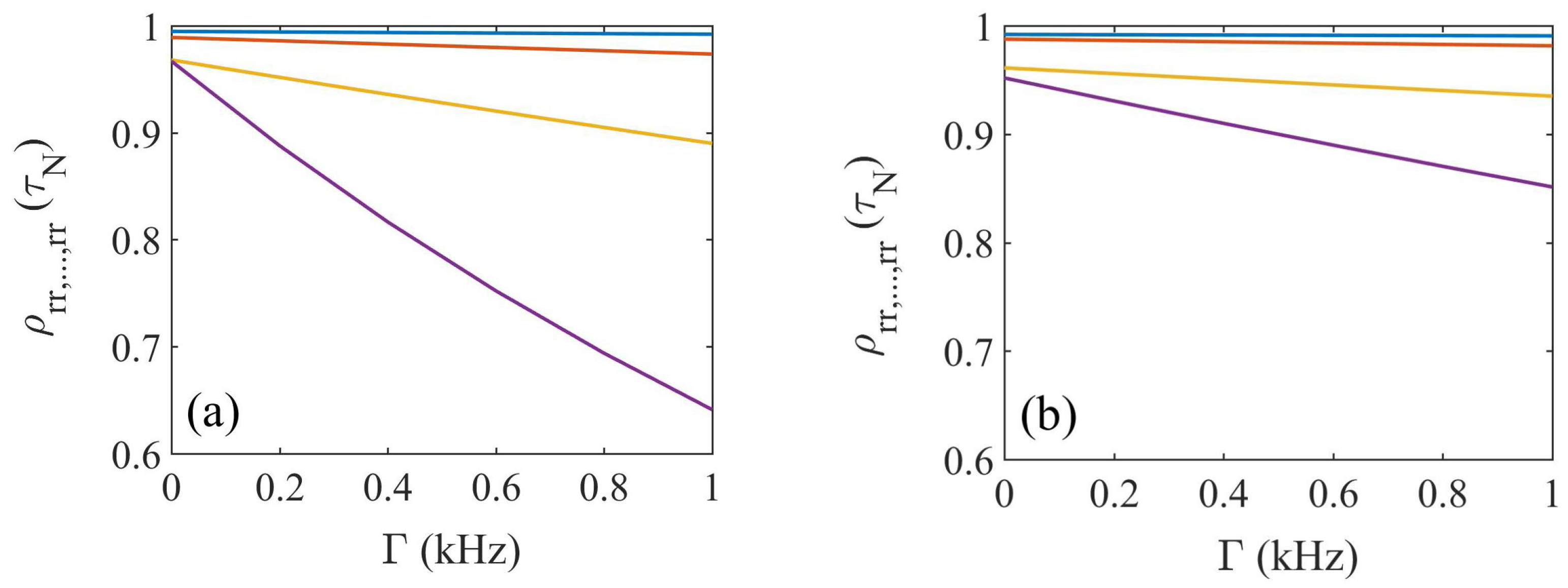
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Details on Deriving Anti-Blockade Conditions

Appendix B. Details on Deriving Effective Hamiltonians
References
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313–2363. [Google Scholar] [CrossRef]
- Sibalic, N. Rydberg Physics; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Vogt, T.; Viteau, M.; Chotia, A.; Zhao, J.; Comparat, D.; Pillet, P. Electric-field induced dipole blockade with Rydberg atoms. Phys. Rev. Lett. 2007, 99, 073002. [Google Scholar] [CrossRef] [PubMed]
- Lukin, M.D.; Fleischhauer, M.; Cote, R.; Duan, L.M.; Jaksch, D.; Cirac, J.I.; Zoller, P. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 2001, 87, 037901. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Wang, H.; Liu, J.M.; Su, S.L.; Qian, J.; Zhang, W.P. Multiqubit Toffoli gates and optimal geometry with Rydberg atoms. Phys. Rev. Lett. 2022, 18, 034072. [Google Scholar] [CrossRef]
- McDonnell, K.; Keary, L.F.; Pritchard, J.D. Demonstration of a quantum gate using electromagnetically induced transparency. Phys. Rev. Lett. 2022, 129, 200501. [Google Scholar] [CrossRef]
- Zheng, D.D.; Zhang, Y.; Liu, Y.M.; Zhang, X.J.; Wu, J.H. Spatial Kramers-Kronig relation and unidirectional light reflection induced by Rydberg interactions. Phys. Rev. A 2023, 107, 013704. [Google Scholar] [CrossRef]
- Wang, K.W.; Jin, H.; Lei, Y.B.; Zhao, Y.; Huang, K.Y.; Xu, S.L. Two-dimensional solitons in Bose–Einstein condensates with spin–orbit coupling and Rydberg–Rydberg interaction. Photonics 2022, 9, 283. [Google Scholar] [CrossRef]
- Ma, D.; Yu, D.; Zhao, X.-D.; Qian, J. Unidirectional and controllable higher-order diffraction by a Rydberg electromagnetically induced grating. Phys. Rev. A 2019, 99, 033826. [Google Scholar] [CrossRef]
- Young, J.T.; Bienias, P.; Belyansky, R.; Kaufman, A.M.; Gorshkov, A.V. Asymmetric blockade and multiqubit gates via dipole-dipole interactions. Phys. Rev. Lett. 2021, 127, 120501. [Google Scholar] [CrossRef]
- Shi, X.F. Quantum logic and entanglement by neutral Rydberg atoms: Methods and fidelity. Quantum Sci. Technol. 2022, 7, 023002. [Google Scholar] [CrossRef]
- Bai, W.J.; Yan, D.; Han, H.Y.; Hua, S.; Gu, K.H. Correlated dynamics of three-body Rydberg superatoms. Acta Phys. Sin. 2022, 71, 014202. [Google Scholar] [CrossRef]
- Heller, L.; Lowinski, J.; Theophilo, K.; Padron-Brito, A.; de Riedmatten, H. Raman storage of quasideterministic single photons generated by Rydberg collective excitations in a low-noise quantum memory. Phys. Rev. A 2022, 18, 024036. [Google Scholar] [CrossRef]
- Ripka, F.; Kubler, H.; Low, R.; Pfau, T. A room-temperature single-photon source based on strongly interacting Rydberg atoms. Science 2020, 367, 4382. [Google Scholar] [CrossRef] [PubMed]
- Bounds, A.D.; Jackson, N.C.; Hanley, R.K.; Bridge, E.M.; Huillery, P.; Jones, M.P.A. Coulomb anti-blockade in a Rydberg gas. New J. Phys. 2019, 21, 053026. [Google Scholar] [CrossRef]
- Ates, C.; Pohl, T.; Pattard, T.; Rost, J.M. Antiblockade in Rydberg excitation of an ultracold lattice gas. Phys. Rev. Lett. 2007, 98, 023002. [Google Scholar] [CrossRef]
- Amthor, T.; Giese, C.; Hofmann, C.S. Evidence of antiblockade in an ultracold Rydberg gas. Phys. Rev. Lett. 2010, 104, 013001. [Google Scholar] [CrossRef]
- Zuo, Z.; Nakagawa, K. Multiparticle entanglement in a one-dimensional optical lattice using Rydberg-atom interactions. Phys. Rev. A 2010, 82, 062328. [Google Scholar] [CrossRef]
- Lee, T.E.; Häffner, H.; Cross, M.C. Collective quantum jumps of Rydberg atoms. Phys. Rev. Lett. 2012, 108, 023602. [Google Scholar] [CrossRef]
- Su, S.L.; Gao, Y.; Liang, E.; Zhang, S. Fast Rydberg antiblockade regime and its applications in quantum logic gates. Phys. Rev. A 2017, 95, 022319. [Google Scholar] [CrossRef]
- Zheng, R.H.; Xiao, Y.; Su, S.L.; Chen, Y.H.; Shi, Z.C.; Song, J.; Xia, Y.; Zheng, S.B. Fast and dephasing-tolerant preparation of steady Knill-Laflamme-Milburn states via dissipative Rydberg pumping. Phys. Rev. A 2021, 103, 052402. [Google Scholar] [CrossRef]
- Su, S.L.; Liang, E.; Zhang, S.; Wen, J.J.; Sun, L.L.; Jin, Z.; Zhu, A.D. One-step implementation of the Rydberg-Rydberg-interaction gate. Phys. Rev. A 2016, 93, 012306. [Google Scholar] [CrossRef]
- Fan, C.H.; Zhang, H.X.; Wu, J.H. In-phase and antiphase dynamics of Rydberg atoms with distinguishable resonances. Phys. Rev. A 2019, 99, 033813. [Google Scholar] [CrossRef]
- Yan, D.; Bai, W.J.; Bai, J.N.; Chen, L.; Han, H.Y.; Wu, J.H. Dynamical collective excitations and entanglement of two strongly correlated Rydberg superatoms. Photonics 2022, 9, 242. [Google Scholar] [CrossRef]
- Su, S.L.; Tian, Y.; Shen, H.Z.; Zang, H.; Liang, E.; Zhang, S. Applications of the modified Rydberg antiblockade regime with simultaneous driving. Phys. Rev. A 2017, 96, 042335. [Google Scholar] [CrossRef]
- Jandura, S.; Pupillo, G. Time-optimal two- and three-qubit gates for Rydberg atoms. Quantum 2022, 6, 712. [Google Scholar] [CrossRef]
- Su, S.L.; Li, W. Dipole-dipole-interaction-driven antiblockade of two Rydberg atoms. Phys. Rev. A 2021, 104, 033716. [Google Scholar] [CrossRef]
- Chen, X.; Xie, H.; Lin, G.W.; Shang, X.; Ye, M.Y.; Lin, X.M. Dissipative generation of a steady three-atom singlet state based on Rydberg pumping. Phys. Rev. A 2017, 96, 042308. [Google Scholar] [CrossRef]
- Shao, X.Q.; Wu, J.H.; Yi, X.X. Dissipation-based entanglement via quantum Zeno dynamics and Rydberg antiblockade. Phys. Rev. A 2017, 95, 062339. [Google Scholar] [CrossRef]
- Jiao, Y.C.; Hao, L.P.; Fan, J.B.; Bai, J.X.; Zhao, J.M.; Jia, S.T. Autoionization of ultracold Cesium Rydberg atom in 37D5/2 state. Photonics 2022, 9, 352. [Google Scholar] [CrossRef]
- Jin, Z.; Li, R.; Gong, W.J.; Qi, Y.; Zhang, S.; Su, S.L. Implementation of the Rydberg double anti-blockade regime and the quantum logic gate based on resonant dipole-dipole interactions. Acta Phys. Sin. 2010, 70, 134202. [Google Scholar] [CrossRef]
- Endres, M.; Bernien, H.; Keesling, A.; Levine, H.; Anschuetz, E.R.; Krajenbrink, A.; Senko, C.; Vuletic, V.; Greiner, M.; Lukin, M.D. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 2016, 354, 1024–1027. [Google Scholar] [CrossRef] [PubMed]
- Barredo, D.; de Léséleuc, S.; Lienhard, V.; Lahaye, T.; Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 2016, 354, 1021–1023. [Google Scholar] [CrossRef]
- Yu, S.; He, X.; Xu, P.; Liu, M.; Wang, J.; Zhan, M. Single atoms in the ring lattice for quantum information processing and quantum simulation. Chin. Sci. Bull. 2012, 57, 1931–1945. [Google Scholar] [CrossRef]
- Barredo, D.; Lienhard, V.; de Léséleuc, S.; Lahaye, T.; Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature 2018, 561, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Sheng, C.; Hou, J.; He, X.; Wang, K.; Guo, R.; Zhuang, J.; Mamat, B.; Xu, P.; Liu, M.; Wang, J.; et al. Defect-free arbitrary-geometry assembly of mixed-species atom arrays. Phys. Rev. Lett. 2022, 128, 083202. [Google Scholar] [CrossRef]
- Wu, H.; Huang, X.R.; Hu, C.S.; Yang, Z.B.; Zheng, S.B. Rydberg-interaction gates via adiabatic passage and phase control of driving fields. Phys. Rev. A 2017, 96, 022321. [Google Scholar] [CrossRef]
- Petrosyan, D.; Motzoi, F.; Saffman, M.; Mølmer, K. High-fidelity Rydberg quantum gate via a two-atom dark state. Phys. Rev. A 2017, 96, 042306. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, P.; He, X.; Liu, Y.; Liu, M.; Wang, J.; Papoular, D.J.; Shlyapnikov, G.V.; Zhan, M. Entangling two individual atoms of different isotopes via Rydberg blockade. Phys. Rev. Lett. 2017, 119, 160502. [Google Scholar] [CrossRef]
- Beterov, I.I.; Ashkarin, I.N.; Yakshina, E.A.; Tretyakov, D.B.; Entin, V.M.; Ryabtsev, I.I.; Cheinet, P.; Pillet, P.; Saffman, M. Fast three-qubit Toffoli quantum gate based on three-body Förster resonances in Rydberg atoms. Phys. Rev. A 2018, 98, 042704. [Google Scholar] [CrossRef]
- Shi, X.F. Deutsch, Toffoli, and CNOT gates via Rydberg blockade of neutral atoms. Phys. Rev. A 2018, 9, 051001. [Google Scholar] [CrossRef]
- Labuhn, H.; Barredo, D.; Ravets, S.; de Léséleuc, S.; Macrì, T.; Lahaye, T.; Browaeys, A. Tunable two-dimensional arrays of single Rydberg atoms for realizing quantum Ising models. Nature 2016, 534, 667–670. [Google Scholar] [CrossRef] [PubMed]
- Bernien, H.; Schwartz, S.; Keesling, A.; Levine, H.; Omran, A.; Pichler, H.; Choi, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 2017, 551, 579–584. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Park, Y.; Kim, K.; Sim, H.S.; Ahn, J. Detailed balance of thermalization dynamics in Rydberg-atom quantum simulators. Phys. Rev. Lett. 2018, 120, 180502. [Google Scholar] [CrossRef] [PubMed]
- Barredo, D.; Labuhn, H.; Ravets, S.; Lahaye, T.; Browaeys, A.; Adams, C.S. Coherent excitation transfer in a spin chain of three Rydberg atoms. Phys. Rev. Lett. 2015, 114, 113002. [Google Scholar] [CrossRef] [PubMed]
- de Léséleuc, S.; Lienhard, V.; Scholl, P.; Barredo, D.; Weber, S.; Lang, N.; Büchler, H.P.; Lahaye, T.; Browaeys, A. Observation of a symmetry-protected topological phase of interacting bosons with Rydberg atoms. Science 2019, 365, 775–780. [Google Scholar] [CrossRef]
- Olmos, B.; González-Férez, R.; Lesanovsky, I. Creating collective many-body states with highly excited atoms. Phys. Rev. A 2010, 81, 023604. [Google Scholar] [CrossRef]
- Ebadi, S.; Wang, T.T.; Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Bluvstein, D.; Samajdar, R.; Pichler, H.; Ho, W.W.; et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 2021, 595, 227–232. [Google Scholar] [CrossRef]
- Scholl, P.; Schuler, M.; Williams, H.J.; Eberharter, A.A.; Barredo, D.; Schymik, K.N.; Lienhard, V.; Henry, L.P.; Lang, T.C.; Lahaye, T.; et al. Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 2021, 595, 233–238. [Google Scholar] [CrossRef]
- Šibalić, N.; Pritchard, J.D.; Adams, C.S.; Weatherill, K.J. An Introduction to Rydberg Atoms with ARC. Available online: https://arc-alkali-rydberg-calculator.readthedocs.io/en (accessed on 23 April 2023).
- Yang, H.; Yang, L.; Wang, X.C.; Cui, C.L.; Zhang, Y.; Wu, J.H. Dynamically controlled two-color photonic band gaps via balanced four-wave mixing in one-dimensional cold atomic lattices. Phys. Rev. A 2013, 88, 063832. [Google Scholar] [CrossRef]
- Schilke, A.; Zimmermann, C.; Courteille, P.W.; Guerin, W. Photonic band gaps in one-dimensionally ordered cold atomic vapors. Phys. Rev. Lett. 2011, 106, 223903. [Google Scholar] [CrossRef]
- Schilke, A.; Zimmermann, C.; Guerin, W. Photonic properties of one-dimensionally-ordered cold atomic vapors under conditions of electromagnetically induced transparency. Phys. Rev. A 2012, 86, 023809. [Google Scholar] [CrossRef]
- James, D.F.; Jerke, J. Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 2007, 85, 625–632. [Google Scholar] [CrossRef]
- Beterov, I.I.; Ryabtsev, I.I.; Tretyakov, D.B.; Entin, V.M. Erratum: Quasiclassical calculations of blackbody-radiation-induced depopulation rates and effective lifetimes of Rydberg nS, nP, and nDalkali-metal atoms with n ≤ 80. Phys. Rev. A 2009, 79, 052504. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Wu, J. One-Step Implementation of Collective Anti-Blockade in a Rydberg Ring. Photonics 2023, 10, 1172. https://doi.org/10.3390/photonics10101172
Fu Y, Wu J. One-Step Implementation of Collective Anti-Blockade in a Rydberg Ring. Photonics. 2023; 10(10):1172. https://doi.org/10.3390/photonics10101172
Chicago/Turabian StyleFu, Yijiao, and Jinhui Wu. 2023. "One-Step Implementation of Collective Anti-Blockade in a Rydberg Ring" Photonics 10, no. 10: 1172. https://doi.org/10.3390/photonics10101172
APA StyleFu, Y., & Wu, J. (2023). One-Step Implementation of Collective Anti-Blockade in a Rydberg Ring. Photonics, 10(10), 1172. https://doi.org/10.3390/photonics10101172




