Abstract
We report a novel photonic scheme to generate background-free phase-coded microwave pulses with elimination of power fading by cascading a dual-polarization dual-parallel Mach–Zehnder modulator (DP-DPMZM) and a polarization modulator (PolM). The DP-DPMZM is driven by a radio frequency (RF) signal to generate two first-order optical sidebands with an orthogonal polarization state, while the PolM is driven by a three-level electrical coding signal. By properly adjusting the polarization state, a series of background-free frequency-doubled phase-coded microwave pulses can be generated after optical-to-electrical conversion. Benefiting from the carrier-suppressed single-sideband (CS-SSB) modulation, the proposed signal generator can suppress the chromatic-dispersion-induced power-fading effect, which has excellent potential for long-distance fiber transmission. In addition, the system can directly generate phase-coded microwave signals in pulse mode by truncating continuous wave (CW) microwave signals. Moreover, the microwave signal generator has wideband tunability since no optical filter is involved in our scheme. The proposed method was theoretically analyzed and experimentally verified. Phase-coded microwave pulses centered at 14 GHz and 19.2 GHz with a bit rate of 0.5 Gb/s were successfully generated.
1. Introduction
Pulse compression techniques have been widely adopted in modern radar systems to attain high-range resolution and long detection distance in radar systems [1,2]. Conventionally, pulse compression signals are generated in the electrical domain. However, the requirement of high operating frequency, wideband tunability and large operating bandwidth are usually challenging to realize simultaneously with electrical approaches due to the electronic bottleneck. Compared with the traditional electrical methods, photonic-assisted microwave waveform generation has distinct advantages in terms of low loss, easy reconfiguration, large bandwidth and anti-electromagnetic interference [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Up to now, many photonic-assisted methods have been reported to generate phase-coded microwave signals, such as space-to-time mapping [3], frequency-to-time mapping [4] and optical heterodyning [5,6,7,8,9,10,11,12,13,14,15,17]. The method based on space-to-time mapping can generate phase-coded microwave signals with good flexibility. However, the system is relatively bulky, complicated and lossy on account of the use of spatial light modulators [3]. For the frequency-to-time mapping method, arbitrary waveforms can be generated using an optical waveshaper followed by a dispersive element. However, the spectral response of the spectrum shaper is usually fixed, which limits the time duration of the generated waveforms [4].
Furthermore, optical heterodyning is another promising phase-encoding scheme that can generate microwave signals with a large time-bandwidth product (TWBP). Various optical heterodyning approaches have been proposed and investigated with different configurations. In [8], a phase-coded microwave signal generator utilizing a dual-polarization dual-parallel Mach–Zehnder modulator (DP-DPMZM) and a polarization modulator (PolM) was reported. The photonic approach can realize frequency upconversion, but two microwave sources are involved, which increases power consumption and cost. In [9], frequency-multiplied phase-coded microwave signals were generated by cascading a polarization division multiplexing dual-polarization dual-parallel Mach–Zehnder modulator (PDM-DPMZM), a PolM and a fiber Bragg grating (FBG). The scheme based on a DP-DPMZM and a PolM to generate dual-band polyphase-coded microwave signals was proposed in [11]. Most of the above-mentioned phase-coded generators operate in continuous wave (CW) mode [5,6,7,8,9,10,11]. However, radar systems usually desire to send microwave signals in pulsed mode to further increase their range resolution [12]. In order to obtain the phase-coded microwave pulses, an additional intensity modulator is required to truncate the CW signals, which leads to background noise [13]. In [14], binary phase-coded microwave pulses could be generated directly based on a DP-DPMZM and a PolM. However, an electrical filter or a balanced photodetector (BPD) is required to remove the interference signal, which increases the complexity of the system. In [15], we addressed a scheme by cascading a PolM and a PM to generate phase-coded microwave signals in pulse mode without background noise. In contrast, the scheme in [14,15] suffers from fiber chromatic-dispersion-induced power fading due to the double-sideband (DSB) modulation [16]. A scheme based on two PolMs and an optical bandpass filter (OBPF) has the ability of anti-dispersion transmission [17]. Unfortunately, the center frequency tuning range is restricted because of the limited roll-off property of the OBPF.
In this paper, we demonstrate a photonic approach to generate binary phase-coded microwave signals. The key components of our scheme are a DP-DPMZM and a PolM. The DP-DPMZM is driven by a radio frequency (RF) signal to generate two first-order optical sidebands with orthogonal polarization, while the PolM is applied using a three-level electrical coding signal to change the polarization state of the two optical sidebands. The binary phase-coded microwave pulses can be recovered after the photodetector (PD). Compared with [8], the generated binary phase-coded microwave signals in our scheme are in pulsed mode rather than CW mode. More importantly, the precise π phase shift of the generated microwave pulses depends on the polarity of the coding signal rather than its amplitude. In addition, the generated phase-coded microwave pulses in our system are background-free. The interference caused by the background noise signals is effectively suppressed. It is worth noting that the proposed system has the ability to resist the periodic power-fading effect in long-distance transmission owing to the carrier-suppressed single-sideband (CS-SSB) modulation, which breaks the limitation in [14,15]. Another significance is that this scheme has wideband frequency tunability because no OBPF is involved in our scheme. In the proof-of-concept experiment, the binary phase-coded microwave pulses centered at 14 GHz and 19.2 GHz with a bit-rate of 0.5 Gb/s are successfully generated. The performances of pulse compression ratio (PCR) and peak-to-sidelobe ratio (PSR) are verified.
2. Principle and Methods
The schematic diagram of the proposed phase-coded microwave pulse generator is shown in Figure 1. The system contains a laser diode (LD), a DP-DPMZM, a PolM, two polarization controllers (PC), a polarizer (Pol.), an electrical coupler (EC), two 90° hybrid couplers (HC) and a PD. A linearly polarized lightwave from the LD is injected into the DP-DPMZM. The DP-DPMZM consists of a polarization beam splitter (PBS), two DPMZMs, a polarization rotator (PR) and a polarization beam combiner (PBC).
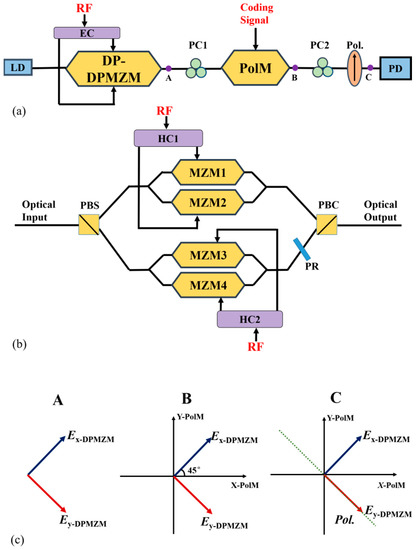
Figure 1.
(a) Schematic diagram of the binary phase-coded microwave pulse generator. (b) The layout of the DP-DPMZM. (c) Schematic illustration of the principle of the proposed scheme in the optical domain. LD: laser diode; EC: electrical coupler; HC: hybrid coupler; DP-DPMZM: dual-polarization dual-parallel Mach–Zehnder modulator; PC: polarization controller; Pol.: polarizer; PolM: polarization modulator; PD: photodetector.
An RF signal generated with a microwave signal generator (MSG) is divided into two parts through an EC. One is applied to the sub-MZM1 and sub-MZM2 through a 90° HC, and the other is applied to the sub-MZM3 and sub-MZM4 through another 90° HC. The optical field at the output of the x-DPMZM and y-DPMZM can be expressed as
where E0 and
are the amplitude and angular frequency of the input lightwave, respectively; β and
are the modulation index and the angular frequency of the RF signal, respectively; αn (n = 1, 2, 3, 4) represent the direct current (DC) phase shifts of the four sub-MZMs, which are all set at π to make the sub-MZMs worked at the minimum transmission point. φx and φy are the DC phase shifts of x-DPMZM and y-DPMZM, respectively, which are set at −π/2 and π/2, respectively. Considering the small signal modulation condition and utilizing Jacobi–Anger expansion, the output of the DP-DPMZM can be written as
where J1 is the 1-order Bessel function of the first kind. As seen from Equation (3), the two first-order optical sidebands have inherently orthogonal polarization, as shown in Figure 1a. Ex-DPMZM and Ey-DPMZM in Figure 1 represent the optical field of the +1st order optical sideband and the −1st order optical sideband from x-DPMZM and y-DPMZM. By properly adjusting the PC1, the principal axis of the DP-DPMZM is set at 45° to the X-axis of the PolM, as shown in Figure 1b. X-PolM and Y-PolM in Figure 1b represent the two principal axes at the orthogonal polarization of PolM.
where m is the modulation index of the PolM. The PolM includes two PMs with opposite phase modulation indices at transverse electric (TE) and transverse magnetic (TM) modes. By adjusting the PC2 and the Pol., the two orthogonally polarized optical signals are combined into the same polarization state, as depicted in Figure 1c. Therefore, the optical field after the Pol. can be shown as
where θ is the rotation angle. θ is set at π/4 in the proposed system. After optical-to-electrical conversion, the output photocurrent can be written as
where R is the responsivity of the PD. According to Equation (6), the photocurrent consists of direct current (DC) and alternating current (AC) parts. The DC part of the generated microwave signals is independent of the electrical driving signals and keeps constant, which means the proposed system is background-free. So, the interference caused by the baseband noise signal is successfully suppressed. For s(t) >0, the phase of the generated microwave signals is 0. For s(t) > 0, the output photocurrent in our scheme can be expressed as
For s(t) < 0, the output photocurrent can be written as
As seen from Equations (7) and (8), the generated microwave signals have π phase difference when the coding signals have an opposite sign. The precise π phase shift can be observed between the coding signal s(t) > 0 and s(t) < 0. For the coding signal s(t) = 0, no microwave signal is recovered after PD. Therefore, if a three-level coding signal (s(t) = 0, 1 and −1) is injected into the PolM, frequency-doubled binary phase-coded microwave pulses can be obtained. It is noted that the precise π phase shift of the generated microwave pulses depends on the polarity of the coding signal rather than its amplitude. Moreover, the generated phase-coded microwave signals are in pulse mode rather than CW mode, which can be transmitted via the radar antenna without additional intensity modulation.
When the optical signals propagate to a remote base station (BS), the dispersion of fiber will introduce a phase shift to the optical signal. The optical field after long-distance transmission can be given by
where θ+1 and θ−1 are the dispersion-induced phase shifts to the +1st order and −1st order sidebands of the microwave signals, respectively. The phase shift introduced by the dispersion of fiber can be described as θ = βz, where β is the propagation constant and z is the transmission distance. By expanding the propagation constant β in the Taylor series, we have
where β0(ω0), β1(ω0), β2(ω0) are the zeroth-, first-, and second-order derivatives of βd, respectively. After transmission, the generated phase-coded microwave pulses can be expressed as
As seen from Equation (11), the phase shift introduced by chromatic dispersion only affects the phase rather than the amplitude of the generated signals, which means the fiber dispersion has no impact on the signal power in our work. In this way, the chromatic-dispersion-induced power-fading effect for long-distance transmission is successfully eliminated in the scheme owing to the CS-SSB modulations.
3. Results
A proof-of-concept experiment was carried out to verify the proposed phase-coded microwave pulse generator. A continuous lightwave at 1550 nm from the LD was coupled to a DP-DPMZM (FTM7977HQA/331). A RF signal at 7 GHz generated by the MSG (ROHDE&SCHWARZ, SMW200A) was split into four paths to drive the four sub-MZMs. By properly setting the DC biases of the DP-DPMZM, CS-SSB modulation can be attained. The output optical spectrum from the DP-DPMZM was plotted in Figure 2. The blue line represents the +1st order optical sideband of the lower x-DPMZM and the red line represents the −1st order optical sideband of the upper y-DPMZM. As mentioned in Section 2, the polarization axis of the DP-DPMZM and the PolM were aligned by precisely controlling the PC1. A 0.5 Gb/s 32-bit coding signal with a pattern of “−1, −1, −1, −1, −1, 1, 1, −1, −1, 1, −1, 1, −1, 0, 0, 0, …, 0” (13-bit Barker code followed with 19-bit “0”) was generated using an arbitrary waveform generator (AWG, Tektronix AWG7001A) and applied to the PolM. By properly adjusting the PC2 and the Pol., the orthogonal optical sidebands were overlapped in the same polarization state.
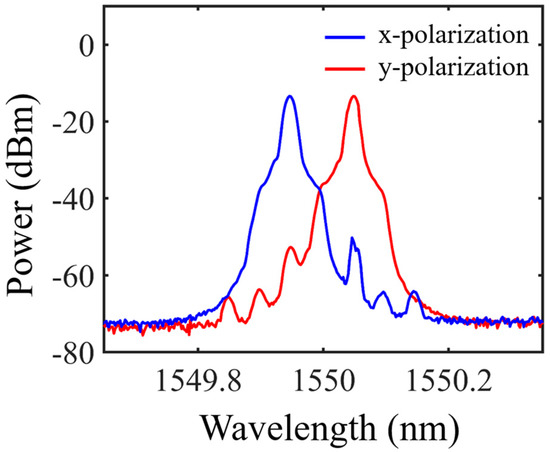
Figure 2.
Optical spectra of the output of the DP-DPMZM at x polarization state and y polarization state centered at 7 GHz.
Figure 3a,b exhibit the electrical spectrum and time-domain waveform of the generated background-free frequency-doubled binary phase-coded microwave pulses centered at 14 GHz. As seen from Figure 3a, no background noise exists in our proposed system. As seen from Figure 3b, the generated microwave signals are in pulse mode rather than CW mode. For s(t) = 0, no signal was recovered after the PD. The phase information was extracted from Figure 3c using Hilbert transformation. π phase shift can be observed between the coding signal s(t) = +1 and s(t) = −1, which coincided well with Equation (6). The pulse compression of the generated microwave pulses is shown in Figure 3d. The peak-to-sidelobe ratio (PSR) is 8.5 dB. The full width at half-maximum (FWHM) is 2.5 ns, and the corresponding pulse compression ratio (PCR) is 10.4.
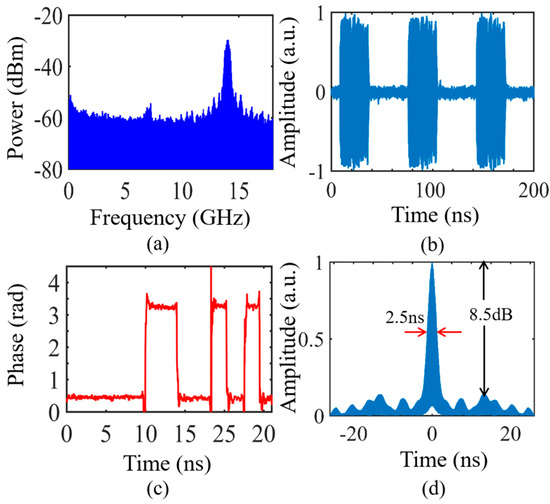
Figure 3.
(a) Electrical spectrum; (b) temporal waveform; (c) corresponding phase information using Hilbert transform and (d) autocorrelation of phase-coded microwave signal centered at 14 GHz with a bit rate of 0.5 Gb/s.
The proposed phase-coded microwave pulse generator also has the ability to suppress the chromatic-dispersion-induced power-fading effect. Figure 4 shows the experimental result of the power-fading effect after 10 km single-mode fiber (SMF) transmission with double sideband modulation. There is a significant power attenuation at the frequency of 19.2 GHz. In this case, the input RF signal was set at 9.6 GHz in order to indicate the property of anti-dispersion transmission in the proposed system. A 10 km SMF with 2 dB insertion loss was inserted into the link as an optical signal transmission path. Furthermore, a 2 dB optical attenuator was applied to the experiment as a contrast.
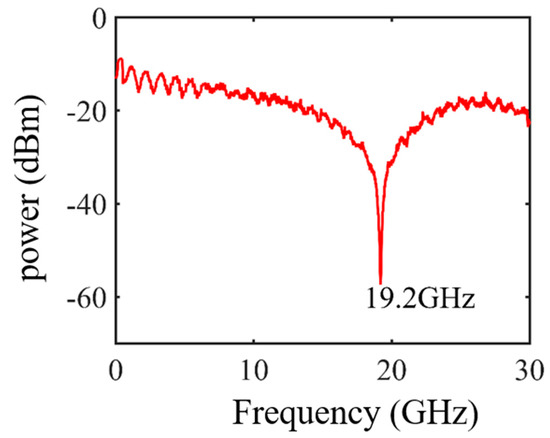
Figure 4.
Experimental result of the power-fading effect after 10 km SMF transmission with double sideband modulation.
Figure 5(a-i–c-i) illustrate the measured electrical spectra under the Back-to-Back (B-T-B) condition, transmitted over the 10 km SMF and after the 2 dB optical attenuator, respectively. The power of the generated microwave pulses after the 10 km SMF and the 2 dB optical attenuator transmission is −30 dBm, which is 2 dB lower than that under the B-T-B condition. As shown in Figure 5(a-i–c-i), the fiber dispersion has no impact on the optical power. Figure 5(a-ii–c-ii),(a-iii–c-iii) show the temporal waveforms and the corresponding phase information, respectively. The phase-coded microwave signals in pulse mode can be obtained. Moreover, π phase shift can be observed in Figure 5(a-iii–c-iii). It is noted that the π phase shift is determined by the polarity of the coding signal rather than its amplitude. In addition, Figure 5(a-iiii–c-iiii) display the pulse compression results of the generated 19.2 GHz phase-coded microwave pulses. The FWHMs of the generated microwave pulses are 2.34 ns, and the corresponding PCRs are 11.11. In addition, the PSRs are equal to 8.9 dB. Therefore, the proposed scheme can generate background-free phase-coded microwave signals in pulse mode, and has flexible tunability and good performance for long-distance optical fiber transmission.
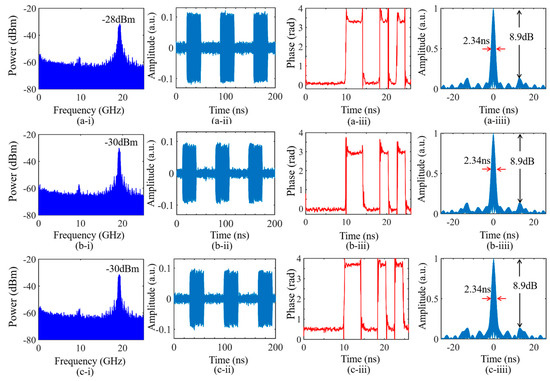
Figure 5.
(a-i–c-i) Electrical spectra; (a-ii–c-ii) temporal waveforms; (a-iii–c-iii) corresponding phase information using Hilbert transform and (a-iiii–c-iiii) autocorrelations of phase-coded microwave pulses centered at 19.2 GHz with a bit rate of 0.5 Gb/s under the Back-to-Back condition, transmitted over 10 km SMF and after 2 dB optical attenuator, respectively.
4. Discussion
We proposed a photonic scheme to generate background-free phase-coded microwave pulses with elimination of power fading based on a DP-DPMZM a PolM. Compared with the phase-coded signals in CW mode [8], the generated phase-coded microwave signals are in a pulsed mode, which can be directly transmitted to the free space by an antenna without additional intensity modulation. In addition, the center frequency of the phase-coded microwave signals is frequency-doubled. Since no OBPF or FBG is involved, the proposed scheme has wideband frequency tunability, which breaks the limitation in [9,11]. Compared with [14], the generated phase-coded microwave pulses in our system are background-free. The interference caused by the background noise signals is successfully eliminated. It is worth noting that the chromatic-dispersion-induced power-fading effect after long-distance transmission in [14,15] can be suppressed owing to the CS-SSB modulation.
5. Conclusions
In conclusion, we theoretically and experimentally demonstrated a novel photonic approach to generate binary phase-coded microwave pulses. In this paper, the proposed scheme can directly generate phase-coded signals in pulse mode. Thanks to the CS-SSB modulation, the proposed system has the ability to eliminate the periodic power-fading effect in long-distance transmission. Since no optical filter is involved, the proposed signal generator has flexible tunability. In addition, the generated frequency-doubled phase-coded microwave pulses are background-free. A proof-of-concept experiment was carried out. Binary phase-coded microwave pulses centered at 14 GHz and 19.2 GHz with a bit rate of 0.5 Gb/s were successfully generated. The performances of temporal waveform, phase information and pulse compression were also investigated.
Author Contributions
Conceptualization, M.G. and W.L.; methodology, M.G.; software, M.G., L.W and X.C.; validation, M.G., L.W. and F.L.; formal analysis, M.G.; investigation, M.G.; resources, M.L. and N.Z.; data curation, M.G.; writing—original draft preparation, M.G.; writing—review and editing, M.G. and W.L.; visualization, M.G.; supervision, W.L.; project administration, W.L.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Key Research and Development Program of China under Grant 2019YFB2203200, and in part by the National Natural Science Foundation of China (NSFC) under Grant 62075210, Grant 61835010.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Skolnik, M. Role of radar in microwaves. IEEE Trans. Microw. Theory Tech. 2002, 50, 625–632. [Google Scholar] [CrossRef]
- Ghelfi, P.; Laghezza, F.; Scotti, F. A fully photonics-based coherent radar system. Nature 2014, 507, 341–345. [Google Scholar] [CrossRef]
- McKinney, J.D.; Leaird, D.E.; Weiner, A.M. Millimeter-wave arbitrary waveform generation with a direct space-to-time pulse shaper. Opt. Lett. 2002, 27, 1345–1347. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Yan, L.; Chen, Z.; Pan, W.; Luo, B.; Zou, X.; Yi, A.; Yao, S. Photonic generation of microwave phase-coded signals based on frequency-to-time conversion. IEEE Photon. Technol. Lett. 2012, 24, 1527–1529. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, T.; Zhang, F.; Pan, S. Photonic generation of a phase-coded microwave signal based on a single dual-drive Mach–Zehnder modulator. Opt. Lett. 2013, 38, 5365–5368. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, L.; Li, M.; Wang, H.; Zhu, N. Photonic generation of binary phase-Coded microwave signals with large frequency tunability using a Dual-Parallel Mach–Zehnder Modulator. IEEE Photon. J. 2013, 38, 5365–5368. [Google Scholar]
- Chen, Y.; Pan, S. A frequency-tunable binary phase-coded microwave signal generator with a tunable frequency multiplication factor. IEEE Photon. J. 2017, 9, 1–15. [Google Scholar] [CrossRef]
- Zhu, S.; Shi, Z.; Li, M.; Zhu, N.; Li, W. Simultaneous frequency up-conversion and phase coding of a radio-frequency signal for photonic radars. Opt. Lett. 2018, 43, 583–586. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, F.; Pan, S. Generation of frequency-multiplied and phase-coded signal using an optical polarization division multiplexing modulator. IEEE Trans. Theory Tech. 2017, 65, 651–660. [Google Scholar] [CrossRef]
- Zhai, W.; Wen, A. Microwave photonic multifunctional phase coded signal generator. IEEE Photon. Technol. Lett. 2019, 31, 1377–1380. [Google Scholar] [CrossRef]
- Zhai, W.; Wen, A. Photonic generation of a dual-band polyphase-coded microwave signal with a tunable frequency multiplication factor. J. Light. Technol. 2019, 37, 4911–4920. [Google Scholar] [CrossRef]
- Chi, H.; Yao, J. An approach to photonic generation of high-frequency phase-coded RF pulses. IEEE Photon. Technol. Lett. 2007, 19, 768–770. [Google Scholar] [CrossRef]
- Chi, H.; Yao, J. Photonic Generation of Phase-Coded Millimeter-Wave Signal Using a Polarization Modulator. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 371–373. [Google Scholar] [CrossRef]
- Fan, X.; Cao, X.; Li, M.; Zhu, N.; Li, W. Photonic Generation of Multi-Band Phase-Coded Microwave Pulses by Polarization Manipulation of Optical Signals. J. Light. Technol. 2021, 40, 672–680. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Wang, H.; Zhu, N. Photonic generation of widely tunable and background-free binary phase-coded radio-frequency pulses. Opt. Lett. 2013, 38, 3441–3444. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Li, M.; Zhu, N.; Li, W. Transmission of dual-chirp microwave waveform over fiber with compensation of dispersion-induced power fading. Opt. Lett. 2018, 43, 2466–2469. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, W.; Wang, H.; Zheng, J.; Liu, J.; Zhu, N. Photonic generation of phase coded microwave pulses using cascaded polarization modulators. IEEE Photon. Technol. Lett. 2013, 25, 678–681. [Google Scholar] [CrossRef]
- Yao, J.; Zeng, F.; Wang, Q. Photonic generation of ultrawideband signals. J. Light. Technol. 2007, 25, 3219–3235. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).