Efficient Reconstruction of Low Photon Count Images from a High Speed Camera

Abstract

Challenging imaging applications requiring ultra-short exposure times or imaging in photon-starved environments can acquire extremely low numbers of photons per pixel, (<1 photon per pixel). Such photon-sparse images can require post-processing techniques to improve the retrieved image quality as defined quantitatively by metrics including the Structural Similarity Index Measure (SSIM) and Mean Squared Error (MSE) with respect to the ground truth. Bayesian retrodiction methods have been shown to improve estimation of the number of photons detected and spatial distributions in single-photon imaging applications. In this work, we demonstrate that at high frame rates (>1 MHz) and low incident photon flux (<1 photon per pixel), image post processing can provide better grayscale information and spatial fidelity of reconstructed images than simple frame averaging, with improvements in SSIM up to a factor of 3. Various other image post-processing techniques are also explored and some of which result in a similar quality of image reconstruction to Bayesian retrodiction, with lower computational load. Image reconstructions using Bayesian Retrodiction or bilateral filtering are of comparable quality to frame averaging, as measured by the Structural Similarity Index Measure, when using less than 40% of the photon flux.

1. Introduction

Advances in photon detection hardware are enabling optical image capture in extremely challenging scenarios. With detectors now capable of reliably recording single photons, the question of how many photons are needed to create an image is important for real-world applications [1]. New systems such as Single Photon Avalanche Diodes (SPADs) [2] and other advanced sensors [3], are key enabling technology for high-speed and low light level imaging. SPADs are now being incorporated into large pixel count arrays, where each pixel is capable of single photon sensitivity and picosecond detection timing. This combination of speed of acquisition and sensitivity, combined with the limitation of being able to detect only one photon per SPAD refresh cycle, means the task of reconstructing useful images quickly from these devices requires image post-processing techniques. Acquisition speed is a relative term and can be understood using the complementarity of scene brightness and frame exposure time. The methods we detail below are useful for sparse images, where the photon count per imaging frame is low, which may be generated either where photon flux is low, or at short exposure times.

Image reconstruction from relatively few photons is important in a number of fields. For example, in astronomy [4,5], where only a few photons may be gathered from distant objects, or in microscopy, where using bright light sources for illumination can be damaging to biological samples [6]. Further applications include ghost imaging and quantum interference measurements where the practical limits of imaging with few photons have been tested [7]. Typically in all of these applications, only a few photons are collected for a single image, and in some cases over a very long counting interval. New imaging technologies provide the potential for generating images with very few detected photons [3], such as SPAD camera arrays, with their ultra-short exposure times [8], and consequently generate low photon counts per frame. In this work we explore the question of how quickly can we generate images, with data from a SPAD camera array and only a few photons per frame.

The particular challenge faced in dealing with photon-sparse images is two-fold; firstly the spatial density of signal pixels is low, and secondly the discrete signals obtained from photon counting lead to grayscale values limited to the integer number of counts a SPAD can detect in a given time period. Although there are many denoising techniques used in image processing, there have been few applications to test them on images with the degree of photon sparsity achievable with SPAD arrays. One such technique claimed to address this need is the recent work on Bayesian Retrodictions, focused on treating few photon level, sparse images [9,10,11] using probabilistic methods. This technique performs two major functions: (1) Pixel-to-pixel discretisation noise is compensated for by processing spatially adjacent pixel regions and (2) expectation value calculation of photon detection probability at a single pixel increases the effective grayscale signal values available. In effect this method can spatially smooth the image and enhance grayscale level resolution. However, this is a computationally demanding technique compared to more conventional image processing techniques that tend to be optimised for classical applications.

In this work, we present the application of both Bayesian retrodiction image processing and also more conventional methods of image denoising, to sparse images collected using a SPAD array imager, verifying their utility for low light applications. The processed images are compared with long-exposure benchmark images and simple frame averaging. We show that Bayesian retrodiction not only improves the images, assessed using imaging comparison methods (such as Structural Similarity Index Measure [12]), but also produces images with improved grayscale and spatial properties with significantly less frames required than standard averaging methods. Using Bayesian retrodiction for low photon image reconstruction has the extra advantage of giving the full probability distribution for the detection of a photon at a given pixel [13], with the images reconstructed using the expectation value of this probability distribution. This amount of information is not always needed when reconstructing images at low photon levels. Several of the other image processing methods that we tested with the same data show a similar, or even slightly better, improvement to the quality of the reconstruction and perform significantly faster than the Bayesian Retrodiction, but without the probability distribution.

2. Experimental Setup and Image Processing Methods

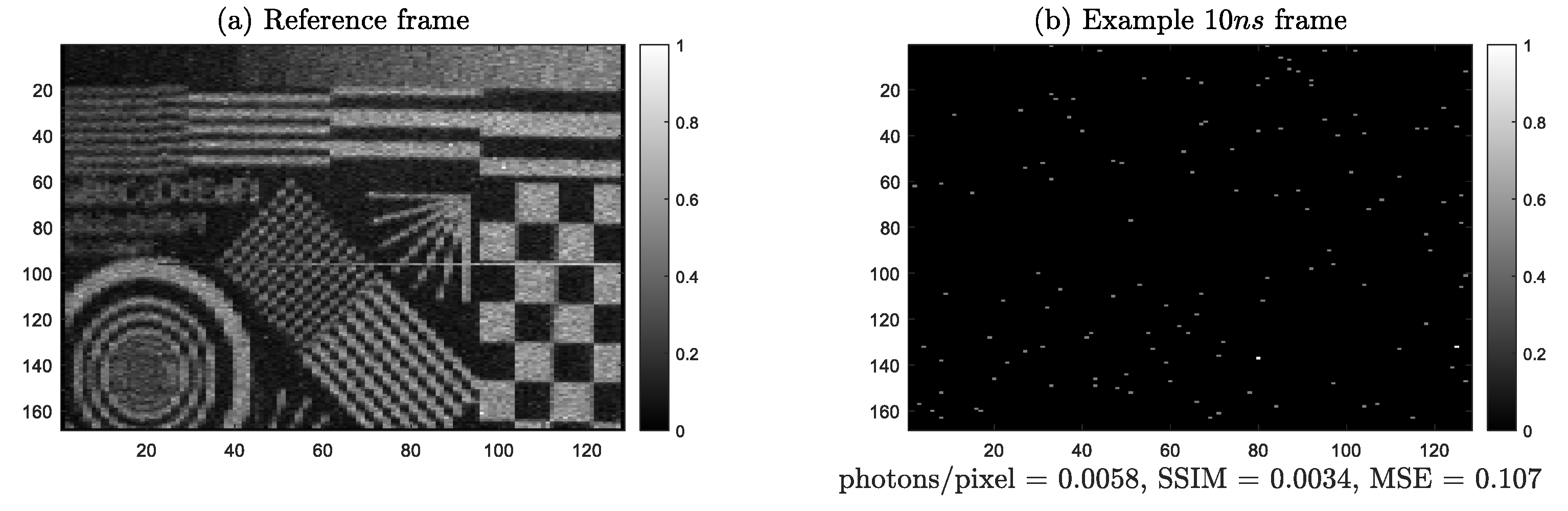
To produce a low photon flux image set, a test object with grayscale features of varying orientation and spatial frequencies was designed, an electronic version of which is shown in Figure 1a. The test object was printed onto white paper with outer frame dimensions of 8 × 8 mm${}^2$ and mounted onto a screen. The object was illuminated using non-directional room lighting, that together with short frame exposure times produces low photon flux images. The scene was imaged using a silicon SPAD array sensor with $192\times 128$ pixels [14], although this work was limited to a $168\times 128$ pixel region due to a malfunctioning part of the available device. The SPAD pixels in the imaging array are top side illuminated with a pixel fill-factor of $13\%$ and were not augmented with micro-lens optics. The system was run in a simple photon counting mode where the exposure time could be user defined. This array was imaged through a Thorlabs 8 mm Effective Focal Length, $f/1.4$, camera lens, positioned 80 cm from the test image. The experimental setup is shown in Figure 1b. The exposure time was set at its minimum of 10 ns, meaning each SPAD in the array could only be triggered a few times per exposure. This resulted in the maximum number of detected photons in any given pixel in a frame being one or two. The short exposure time also limited the number of dark counts that were detected. To produce a benchmark image the SPAD array was set to capture 5000 of these frames. The resultant image was the normalised sum of these frames and is shown in Figure 2a. In this image, and in all other images shown in this work, the lighting level in the room and the exposure time per frame were not changed. To vary the number of photons per pixel more individual frames are included (which is equivalent to changing the total exposure time). An alternative set of results could also have been produced by varying the brightness in the room, however, precise control over this was not available and therefore the change in exposure time is used to control the photons/per pixel in a given image.

In order to quantitatively assess the images presented here, we use both the Structural Similarity Index Measure (SSIM) and mean-squared error (MSE) as metrics to compare two images. SSIM is based on the grayscale intensity, contrast, variance and co-variance between the images and is normalised in the range of 0–1, with 1 being the best matching between images. MSE is the average squared difference between reconstructed image and the reference image with a lower number showing a better match. MSE is not presented for every result; however, it was observed to match well with SSIM across all of the testing. In our analysis, we compare the reconstructed images under test to the long exposure SPAD array image captured (our reference image), as shown in Figure 2a. All images are normalised to the maximum pixel intensity or photon count value of the image before comparing with either method to ensure an equivalent comparison for every image.

Two different image processing methods are initially applied to the SPAD array images captured. The first is a straightforward averaging method. Given a set of N captured frames, the value of each pixel is calculated as the average value of that pixel intensity, $I_{xy}$, over the full set of frames, $\frac{{\sum }_{n=1}^N\left[I_{xy,n}\right]}{N}$. The resultant image is then normalised to the maximum pixel value of the frame. The main advantage of averaging many frames together like this is that it is the simplest form of image processing, requiring very little computational load. The results of this averaging of frames is also used as the input for the various imaging filters that are explored in a later section.

The second method is the Bayesian Retrodiction process, presented in detail in [13]. In short, by considering the number of photon counts in pixels neighbouring the pixel of interest, a Bayesian estimate of the probability of photon arrival at that pixel can be calculated. One first assumes that the probability of a photon detected at a single pixel is related to the number of photons incident on that pixel and at the neighbouring pixels within a radius $R_0$ (for the case of $R_0=1$, these are the nearest neighbour pixels). A prior for the retrodiction is determined by looking at any pixels between a radius of $R_0$ and $R_0+1$ (again for the case of $R_0=1$, these are the next nearest neighbour pixels).

In the Bayesian retrodiction method, at each pixel j the intensity ${\lambda }_j$, is determined by calculating the expectation value of probability distribution of intensities,

$$\mathbb{E}\left({\lambda }_j\right|M_j,{\tilde{\lambda }}_j)=\frac{1}{\eta }\left[\frac{a}{b}+\frac{{\left(ϵb\right)}^a}{b}\frac{e^{-ϵb}}{\mathrm{\Gamma }(a,ϵb)}-ϵ\right].$$

(1)

This is evaluated separately at each pixel with regards to the number of photons detected at the pixel, $M_j$, and its neighbours within a radius $R_0$, and the local prior ${\tilde{\lambda }}_j$. We have used a pixel detection efficiency of $\eta =0.5$ and a dark count rate $ϵ=0.005$ for all of this work. The terms a and b are calculated from the detected photons and the calculated priors, with $a=M_j+1$ and $b=N_j+1/\left(\eta {\tilde{\lambda }}_j\right)$, where $N_j$ is the number of pixels contributing to $M_j$, shown in Figure 3. The term $\mathrm{\Gamma }(s,x)={\int }_x^{\infty }{t}^{s-1}{e}^{-t}dt$ is the upper incomplete gamma function. The local prior can be calculated with,

$${\tilde{\lambda }}_j=\frac{1}{\eta }\left[\frac{\mathrm{\Gamma }(\alpha +1,ϵ\beta )}{\beta \mathrm{\Gamma }(\alpha ,ϵ\beta )}-ϵ\right],$$

(2)

where $\alpha =M_j^{\circ }+1$ and $\beta =N_j^{\circ }+1/\left(\eta \widetilde{{\lambda }_j^{\circ }}\right)$, using data from the surrounding ring of pixel demonstrated in Figure 3 and $\widetilde{{\lambda }_j^{\circ }}\approx (\overline{m}-ϵ)/\eta$. For further details see [13]. In this work we have calculated the retrodiction based on a radius of interest for each pixel of $R_0=1$. Other values of $R_0$ were tested, however, none gave a better image reconstruction than $R_0=1$ for this experiment.

3. Bayesian Retrodiction Results

An example of a single captured frame with a $10ns$ exposure time is presented in Figure 2b. This frame has an average photon count of 0.0069 photons per pixel and as compared with the long exposure image has a $\mathrm{SSIM}=0.0058$. Qualitatively, it is clearly difficult to discern even major features of the test image. The sparsity of this image is beyond the limit where retrodiction can meaningfully operate, given that it is a method based on nearest neighbour calculation. Therefore, for the remainder of this work, we use a frame exposure time of at least 100 ns where there are approximately ten times as many photons per pixel.

Figure 4a shows a frame at 100 ns exposure time, with an average photon count of 0.072 photons per pixel and a SSIM of 0.033 to the reference image. The major features of the test pattern are now becoming visible, predominantly the low spatial frequency features. Figure 4b shows the Bayesian retrodiction of the 100 ns frame shown in Figure 4a. Clear smoothing of the image is apparent, with some improvement in effective dynamic range. The SSIM for this single frame has improved to 0.169. Although this is an improvement, this is still not a useful reconstruction, with only a few of the lower spatial frequency details visible in the reconstruction. In particular, the large chequerboard pattern in the lower right is discernible in both images as are the thicker stripes in the upper right of the reconstructed image.

By averaging over a number of retrodicted frames, the image quality can be improved. Figure 5 and Figure 6 show sample images using simple averaging (a) and averaging of retrodicted frames (b) for 5 and 20 frames respectively. Results are also included for comparison with median and bilateral filtering methods discussed in the following section. Sets of 5 and 20 frames correspond to a total exposure times of 0.5 $\mathsf{\mu }$s and 2 $\mathsf{\mu }$s, respectively, and have a total number of detected photons per pixel of 0.351 and 1.41. As expected, improvement in the qualitative image and the calculated SSIM is apparent for both the averaging and retrodiction cases with increasing total exposure time. The two exposure times selected here are both challenging cases where simple averaging performs poorly. Image extraction performance across most methods becomes challenging at photon flux around 1 photon per pixel and at levels less than 0.5 photons per pixel the reconstruction of images shows very different performance across the various methods, as characterised by the SSIM. The retrodiction performs markedly better for the 0.5 $\mathsf{\mu }$s image with a SSIM of 0.346 compared with 0.132 for the frame averaging. The averaging method provides a reasonable image for a 2 $\mathsf{\mu }$s effective exposure, although the SSIM of the retrodiction method is still higher for this case at 0.56, compared with 0.332 for the averaging. The averaging does, however, better preserve high spatial frequencies, with some blurring evident in the retrodiction case.

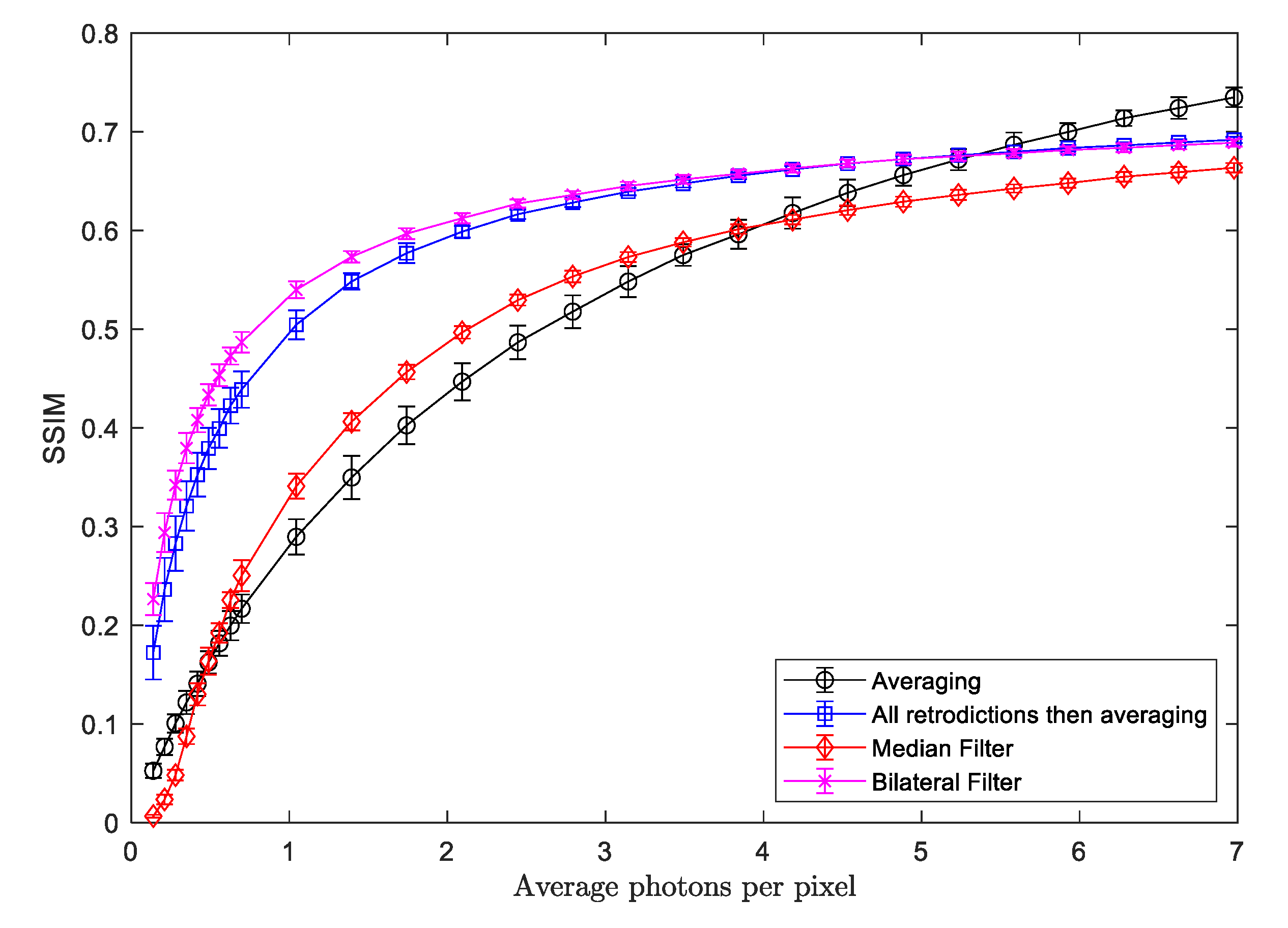
Figure 7 shows a comparison of the SSIM for different methods of image reconstruction and the variation of the quality of the reconstruction as the average number of photons per pixel is changed. This is altered by changing the exposure time for each point in the graph, with the stated photons per pixel being the average from 100 different measurements for a given exposure time. Frame averaging is shown with black circles and retrodiction for each separate 100 ns frame followed by averaging of these retrodicted frames is shown with blue squares. Values for the SSIM were calculated for 100 independent measurements for each method at each average photon count and the error bars represent the standard deviation of the SSIM for each data point.

As expected, with an increasing number photons per pixel, the image quality improves for each method. Retrodiction and averaging performs significantly better than simple averaging at low photon counts, where sparser image sets are being used. At around five photons/pixel, the averaging method and retrodiction and averaging method converge and above this value, averaging becomes the better technique. At this point, the images become less sparse and preservation of higher spatial frequencies in the averaging method leads to improvement in the calculated SSIMs compared with the retrodiction case which causes some unwanted smoothing. The averaging method also shows a larger standard deviation in the SSIM of independent measurements at low exposure times, illustrating its sensitivity to shot variations at low photon flux. The retrodiction based methods are more robust to these effects even at low numbers of photons per pixel.

4. Other Image Processing Techniques

The Bayesian retrodiction has unique properties when reconstructing images at low photon counts, most significantly the fact that an entire probability curve for photon detection can be determined at every pixel. However, this is not always necessary when one wants to reconstruct images quickly. Therefore, a number of more traditional image processing methods were tested for their effectiveness on this same very photon-sparse dataset. These methods tested are moving mean, median filtering, bilateral filtering, gaussian filtering, total variation denoising (TV denoising). All of these are well known and extensively studied for classical image reconstruction applications, but are not often used in photon-sparse situations. Comparisons of the key metrics (SSIM and MSE) for each of the methods considered are presented in Figure 8 and Figure 9. Example reconstructed images for each of the processing methods are provided in the Appendix A. Two different total exposure times are compared across the various methods, 0.5 $\mathsf{\mu }$s and 2.0 $\mathsf{\mu }$s, corresponding to about 0.35 and 1.4 photons per pixel, respectively. Some of the methods fail to work at the lower exposure time, but all function as intended at the higher value.

The results for Bayesian retrodiction with $R_0=2$ are always worse than the case of $R_0=1$ in this study, as increasing $R_0$ takes into account next nearest neighbour pixel in the retrodiction; this leads to more smoothing and a poorer reconstruction. However, there may be certain imaging cases where it is the better choice. Windowed averaging (also called moving mean), where each pixel is assigned the mean value of the surrounding pixels, results in good image reconstruction metrics; however, there are obvious artefacts added to the images (not shown, but this produces streak like feature in the reconstruction), demonstrating that metrics should not be relied on in isolation. Median filtering takes the median value of a 3 × 3 region around each pixel and this results in a very poor reconstruction at the lowest photon levels where the median is almost exclusively zero or one. Bilateral filtering [15,16] is specifically designed to preserve edges while also reducing noise and smoothing an image. It proved to be very effective at reconstructing the images when the degree of smoothing was set to be 100 (this is defined in the matlab function for bilateral filtering and is related to a Gaussian function that defines the range and the strength of the applied smoothing). Gaussian filtering proved to be almost as effective as bilateral filtering when using a value of two for the standard deviation (defining the width of the Gaussian). TV Denoising, similarly to bilateral filtering, is effective at preserving edges in images [17,18]. This functions by trying to reduce the total variation of an image, with the intention of removing spurious pixels that are very different from those around them. This minimisation was run over 100 iterations and the most effective results were with a regularisation parameter of 2, a factor that determines the strength of the noise removal in the TV denoising algorithm. This method again proved to be less effective in the most sparse images than bilateral filtering. A summary of the results for all of these methods can be seen in Figure 8 and Figure 9, showing the SSIM and MSE for the results of each method when compared with the reference image.

Of these methods, bilateral filtering proved to be particularly effective at reconstructing images even at very low numbers of photons per frame; therefore, it has been looked at more closely in order to compare it to averaging and the retrodiction and averaging methods. Median filtering has also been compared as it, like Bayesian retrodiction, is based on effects from the nearest neighbour pixels yet provides an example of how some filters do not function very well with sparse images. There are examples of reconstructions with these two techniques in both Figure 5c and Figure 6c showing the median filtering of the averaging (plot (a)) Figure 5d and Figure 6d showing the bilateral filtering of the averaging. In Figure 5c it is clear that the median filtering is failing to give a reasonable output due to the very low number of photon counts in the input. In Figure 5d, the bilateral filtering shows a qualitatively accurate reconstruction of the reference image and according to the metrics is similar in quality to the result from the Bayesian retrodiction. In Figure 6, both methods are seen to work now that there are more photons counts available and both show an improvement in the metrics compared to the previous figure.

Both the median filter and bilateral filter have their SSIM plotted for a variety of different average photon counts per pixel in Figure 7. Median filtering does not work at the lowest photon count levels, below about 0.5 photons per pixel it is not producing meaningful images. From about 0.5 to 3 photons per pixel, it does perform better than the simple frame averaging method, but above four photons per pixel the blurring effect from the median filter reduces the quality of the reconstruction. The bilateral filter functions very well down to the lowest photon counts that were tested, performing slightly better than the Bayesian retrodiction at all photon counts. At higher levels, about five photons per pixel in this case, it is also surpassed by averaging due to the blurring artefacts introduced by the filter being detrimental to the image reconstruction.

In addition to using the image comparison metrics, a few other aspects of the image denoising can be assessed for these reconstruction methods. One shortcoming of simply increasing counting time without any processing, as in the frame averaging case, is that there will only ever be a small number of possible grayscale values. This can be seen when comparing the histogram of the reference image to that of the averaging image, Figure 10a,b. The number of grayscale levels in averaging will always be limited to the maximum photon count and in this specific example, the maximum count for any pixel was 10. This limited grayscale reconstruction demonstrates the limitations of this method. By using Bayesian retrodiction or bilateral filtering (Figure 10c,d), a much more realistic histogram is produced, capturing at least some of the structure of the reference image histogram.

At the top of the test pattern, shown in Figure 1, there is a grayscale bar and comparing how well the different reconstruction methods resolve this feature highlights some aspects of the quality of each method. Two different cuts are looked at, a two pixel wide cut (thinner blue line) and a ten pixel wide cut (thicker red line) and these are shown in Figure 11 for (a) the reference image, (b) frame averaging, (c) retrodiction and averaging, and (d) bilateral filtering of frame averaging. The red line is smoother in all the of plots due to the increase in counting statistics across the cut. The averaging does a very poor job of reproducing the original image, there is a trend to higher intensity traced along the grayscale bar, but this is obscured by a lot of noise. Retrodiction and averaging and bilateral filtering are both much smoother, reducing the degree of granularity in the reconstructed image, and do a better job of reproducing the grayscale bar.

Table 1. Comparison of Image Reconstruction Methods (Ordering to match Figure 8 and Figure 9).

Method	Smoothing	Edge Preserving	Artifacts	Grayscale Levels	Proc. Time (ms) $\left[\mathit{N}\mathit{o}\mathit{r}\mathit{m}.\right]$
Frame Averaging	x	x	x	Photon #’s	0.25 [0.001]
Retrodiction + Averaging (R0 = 2)	over	√	blur	High	307.50 [1]
Median Filter	x	√	cut-out	Low	1.53 [0.005]
Bilateral Filter 10	√	√	x	High	3.80 [0.012]
Gaussian	over	x	blur	Medium	0.66 [0.002]
TV Denoise	x	√	cut-out	Low	53.15 [0.17]
Moving Mean 6	over	x	linear extension	Medium	0.57 [0.002]
Retrodiction + Averaging (R0 = 1)	√	√	x	High	298.87 [0.972]
Moving Mean 3	√	√	noise	Medium	0.54 [0.002]
Bilateral Filter 100	√	√	x	High	4.10 [0.013]

presents a summary of the major features of each processing method. Over-smoothing refers to significant blurring of the image. Cut-out artifacts are sections of the image below a threshold that are returned as dark areas, where they should be bright. The processing time quoted refers to a standardised test case where the same raw data are used for each method and are calculated as the operation time in Matlab on a laptop PC. The normalised processing time, compared with the longest case is also reported. The test image set used were five frames of 100 ns exposures with a photon flux of ≈0.35 photons/pixel. The Bayesian retrodiction processing times are dominated by calculation of the incomplete gamma function at each pixel, see Equation (1).

5. Discussion and Conclusions

The data collected for this work are only possible due to the significant advances in photon detection hardware over the last few years. As SPAD cameras are used in more applications, it will become necessary to find fast and effective methods of reconstructing useful images from the very low photon count, sparse images like the ones demonstrated here. This work experimentally verifies the use of Bayesian retrodictions for fast imaging with such sparse photon data, yet also highlights that more conventional image denoising techniques are useful for sparse photon count images.

Bayesian retrodiction has clear advantages in the ability to calculate a full probability distribution at each pixel for the reconstructed intensity, making it useful when extreme precision is required. However, this comes at the cost of being a more computationally challenging process than the simpler filters also shown in Figure 8 and Figure 9. For a quicker and slightly better reconstruction, bilateral filtering is very effective even with very few photons per pixel in the image. There is criticism that the nature of a bilateral filter, designed to preserve edges, may introduce artefacts to an image reconstruction, but no significant artefacts were observed in this study.

Referring to Figure 7, at around an average of one photon per pixel, the reconstructions using retrodiction and averaging or bilateral filtering, provide a similar image reconstruction to simple averaging with around 2.5 photons per pixel, both giving an $\mathrm{SSIM}\approx 0.5$. These techniques can therefore enable imaging approximately two and a half times faster than simple averaging in a very sparse photon count application. Combined with the lower computational time for filtering methods such as bilateral filtering, this could enable real-time video imaging in even very photon-sparse applications.

The increase in imaging speed is also matched by an increase in reliability of the reconstruction for a single shot measurement, as shown by the lower standard deviation in the relevant data point in Figure 7. Combined with the improved reconstruction of the range of possible values, demonstrated by the histograms, and the reduced sensitivity to granularity in the image, demonstrated by the grayscale bar, it is clear that these techniques are superior to averaging the counted frames when reconstructing a useful image from sparse, low-photon count data.