1. Introduction
Prior to the introduction of automated testing methods such as autorefraction, retinoscopy was the most practical objective method of measuring refractive status of an eye [
1,
2]. A classic spot retinoscope shines a spot of light into the patient’s eye at a working distance that is normally between 1/3 and 2/3 of a meter, and the pupil reflex is observed. When moving the illumination across the eye, three types of reflex motions are observed: with-, against-, and neutral- respectively indicating a hyperopic-, a myopic-, and a null-refraction relative to the reciprocal of the working distance (in diopter = 1/m). Trial lenses are placed in front of the eye in order to reach the “neutralization” where a very bright reflex appears at centered illumination and disappears with a slight eccentricity in any side. Although retinoscopy is generally practiced for refraction determination, experienced clinicians are aware of its sensitivity in observing a variety of ocular conditions including irregular astigmatism or high-order aberrations [
3,
4,
5]. One such example is the “scissor movement” or “split reflex” observation in keratoconus cornea dystrophy. However, drawbacks to the use of this versatile tool include the facts that first, its bright visible illumination in the extensive examination could be uncomfortable to examinees; it also causes the pupil to contract, and as a result, the use of eye drops for pupil dilation is often required; second, the broad-spectrum light source mixes chromatic signals that results in a decrease of image contrast and measurement sensitivity. Further, retinoscopic observations of unusual ocular conditions are not registered in digital form for future reference, discussion, sharing, or review, and their use for validation with theoretical analysis.
Photorefraction (PR) is also an objective refraction-measurement technique that was introduced in the early 1980s [
6,
7,
8,
9]. Eccentric photorefraction (EPR) is the most commonly practiced PR technique today. EPR uses a camera to photograph the retinal reflex that is induced by a light source located on the side of the camera lens. EPR shares the similarity in its optical illumination and detection paths with a traditional spot retinoscope. Because of EPR’s low demand on cooperation and eye alignment of the examinee, it has been widely used in screening preschool children for binocular refractive errors. Taking the advantages of PR’s friendly nature and digital registration and including additional modifications, an infrared retinoscope could overcome the difficulties of the traditional retinoscope.
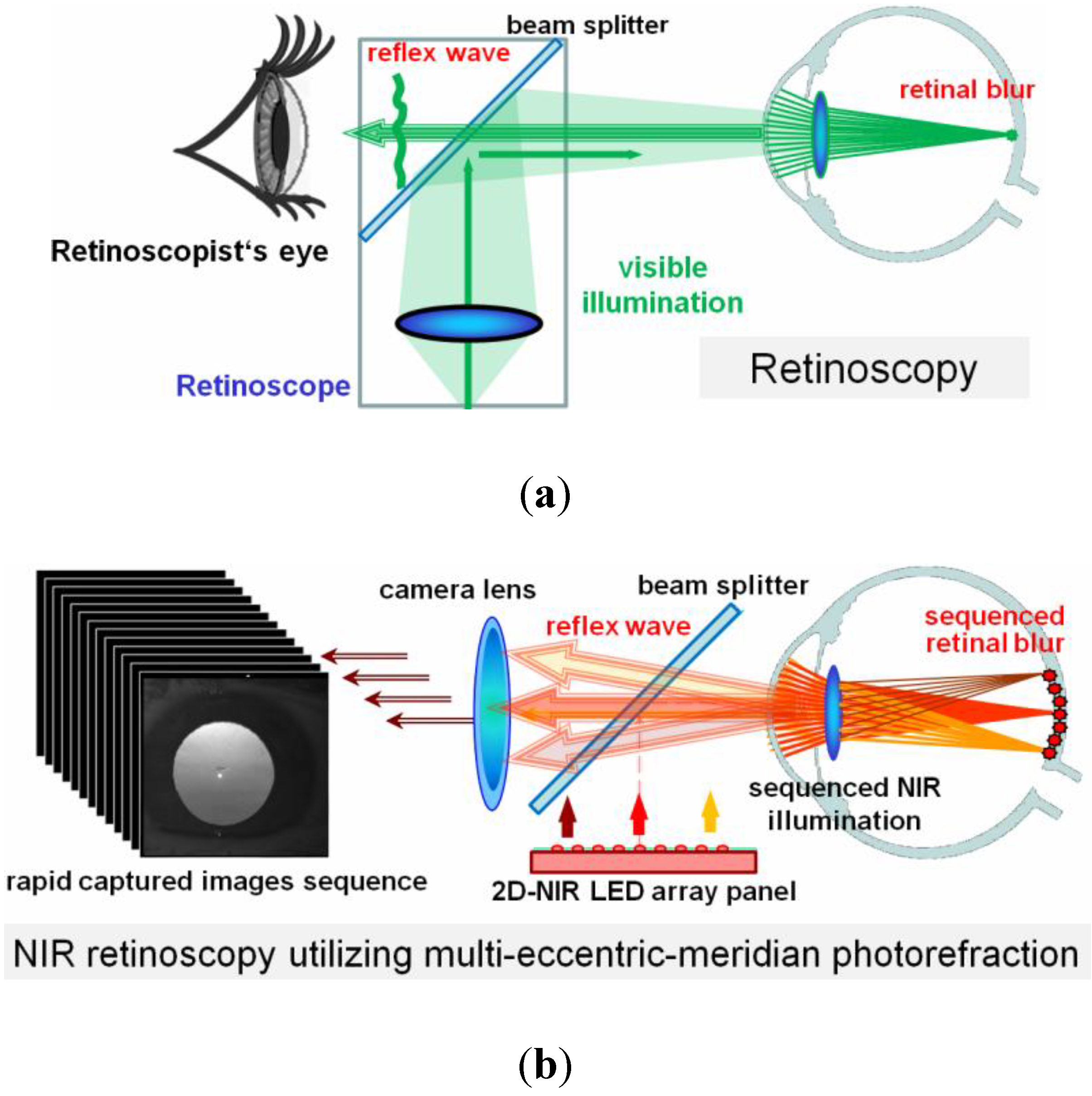
Illustrated in
Figure 1a is the simple diagram of a traditional spot retinoscope (not to scale).
Figure 1b shows the infrared retinoscope that is modified from EPR technique. The use of infrared sources and camera makes non-mydriatic measurements feasible for larger pupillary coverage and lessens the discomfort during measurement. The employment of a beam splitter and a 2-dimensional light source array that is aligned to the entrance pupil of the camera enables the detection of both coaxial and multiple eccentric and meridian reflex images just as the retinoscope does.
In this work, to test the sensitivity of observing abnormal ocular conditions we constructed a laboratory device with a simple 13-infrared LED array and used a near-working distance of 30 cm, which is a typical near-range that corresponds to a neutralization of −3.3 diopters. The experiment was performed as an additional test in a clinical setting where routine clinical diagnostics and treatments were given. The testing results were compared to the patients’ clinical diagnostics and history. To investigate how ocular aberrations and other ocular conditions could affect the reflex images, we used the existing clinical wavefront aberration data to construct simple eye models and used the geometric image analysis in ZEMAX to reproduce the measurements for comparison.
Figure 1.
Comparison of optical arrangements (not scaled) in (a) retinoscope, and (b) infrared retinoscope using multi-eccentric-meridian photorefraction design.
Figure 1.
Comparison of optical arrangements (not scaled) in (a) retinoscope, and (b) infrared retinoscope using multi-eccentric-meridian photorefraction design.
2. Theoretical Consideration
The intensity profiles of the reflex images in both photorefraction and retinoscopy are produced due to the fact that only a portion of the double-pass reflex at the pupil plane are detected by the PR camera or the peephole of the retinoscope. The portion of selection depends on how the returning reflex waves at the eye’s exit pupil propagate to the detection plane; specifically, divergent as in a hyperopic eye or convergent as in a myopic eye. The retinoscope involves multiple optical apertures in both the illumination and the returning path that results in an unexpected “edge” complication in the formation of the reflex patterns [
4,
5]. The theoretical consideration of EPR is more straightforward without the edge/vignetting problems.
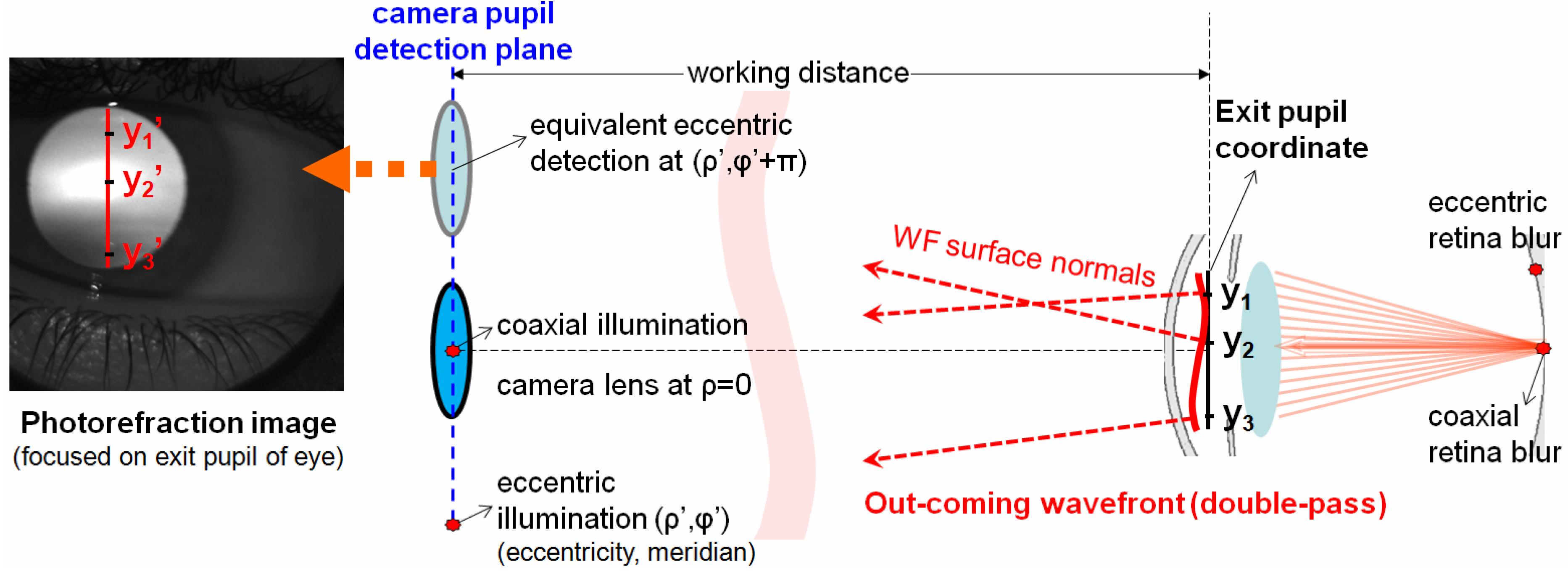
Figure 2 shows an illustration of an EPR setup. The system axis is aligned to the center of the camera’s entrance pupil, and the coaxial or eccentric light sources are placed at the detection pupil plane with eccentricities
and
from the axis. Under neutralization condition, the light source plane conjugates to the retinal surface of the examined eye. The out-going reflex rays return to the originating light source. Therefore, as observed in the retinoscopy neutralization condition, a coaxial PR reflex image is a pupil image at maximum brightness and an eccentric reflex image is all dark since the light source is outside the detection area. When defocus or any aberration is present, the reflex wavefront still propagates toward the originating light source, but at the detection plane, the wavefront surface will extend over the area of the originating light source. Assume that the double-pass wavefront of an eccentric-meridian illumination at the polar axis coordinate
is identical to that of a coaxial illumination at
except for the direction of propagation. In this case, the camera lens would capture the wavefront portion centered at
;
i.e., the opposite side of the light source. In
Figure 2, the coaxial detection of an eccentric illumination from the lower side of a camera pupil is equivalent to a coaxial illumination with the eccentric detection on the upper side. Since the reflex photograph is imaged with focus on the eye’s exit pupil plane, the intensity level at y’
1, y’
2, and y’
3 locations (photograph image at left of the figure) would be determined by the collected ray intensities toward this eccentric pupil at the upper location
, originating from y
1, y
2, and y
3 at the eye plane, which are maximized at their wavefront surface normals. This is similar to wave aberration’s first-order partial derivative that is used by Caballero to describe higher-order aberrations in PR [
10]. In the case of a hyperopic eye that produces a divergent out-going wavefront, the collected rays at the upper side of the axis are therefore attributed to the upper portion of wavefront at the eye’s exit pupil. This produces an upper crescent reflex image, which is opposite to the light source location at lower side. When moving the light source from the far lower side of the camera, passing the center, toward the upper side, the movement of the “crescent” reflex appears to be “against motion” in an hyperopic and “with motion” in a myopic eye, respectively, in the EPR-modified retinoscope.
The geometric theorems of EPR’s crescent reflex early on use only the eye’s pupil size, defocus, and the eccentricity measured from edge of light source to the edge of detector to determine their relationships to the reflex crescent boundary [
7,
8]. Other EPR approaches use slope-based analysis with the design of extended light sources [
11]. Our previous study shows that the crescent edge could not be clearly defined when considerations of normal ocular aberrations and the detection pupil’s size and shape are included [
12]. Further, the intraocular scattering and retinal reflectance, which vary with age, race, and among individuals, produce a significant background signal that demands individual calibration to yield reliable measurements. However, unaffected by individual ocular variables in the PR image is the maximization of reflex intensity when approaching the neutralization, which is the way the trial lens is used in the classic retinoscopy. By utilizing a beam splitter as shown in
Figure 1b and a Badal lens system, the optimal compensation power could be obtained to reach neutralization in one rapid PR imaging sequence. EPR image intensity also reduces with the increase of eccentricity. Along an arbitrary meridian, the reflex intensity produces a bell-shape curve peaked at the coaxial
location. The width of the bell curve increases with defocus. The 2-dimensional intensity surface
could be described with an elliptical surface fitting with three variables, the maximum and minimum widths on two perpendicular meridians and the rotation of the ellipse. The astigmatic meridians could be determined without influence from individual ocular intraocular scattering, retinal reflectance, and pupil variables.
In a particular example of a high-order aberration keratoconus case with the red curve wavefront and wavefront normals illustrated in the right side of the figure, representing a bulging “cone”, the reflex image on the left shows, respectively, the corresponding dark, bright, and deep dark at y’1, y’2, and y’3. By using a beam splitter and 2-dimensional array of light sources, the entrance pupil of camera becomes multiple spatial filters that sample the wavefront profile through the space—much like a cookie cutter sampling a piece of dough. The total double-pass wavefront normals at every pupillary location (x,y) could be determined from the related brightness in sampled multi-eccentric-meridian reflex images.
Figure 2.
Illustration of the eccentric photorefraction detection of double-pass wavefront.
Figure 2.
Illustration of the eccentric photorefraction detection of double-pass wavefront.
3. Experimental Section
3.1. Optical Components
The experimental prototype is the modified infrared photorefraction with a two-dimensional LED panel. The component arrangement is shown in
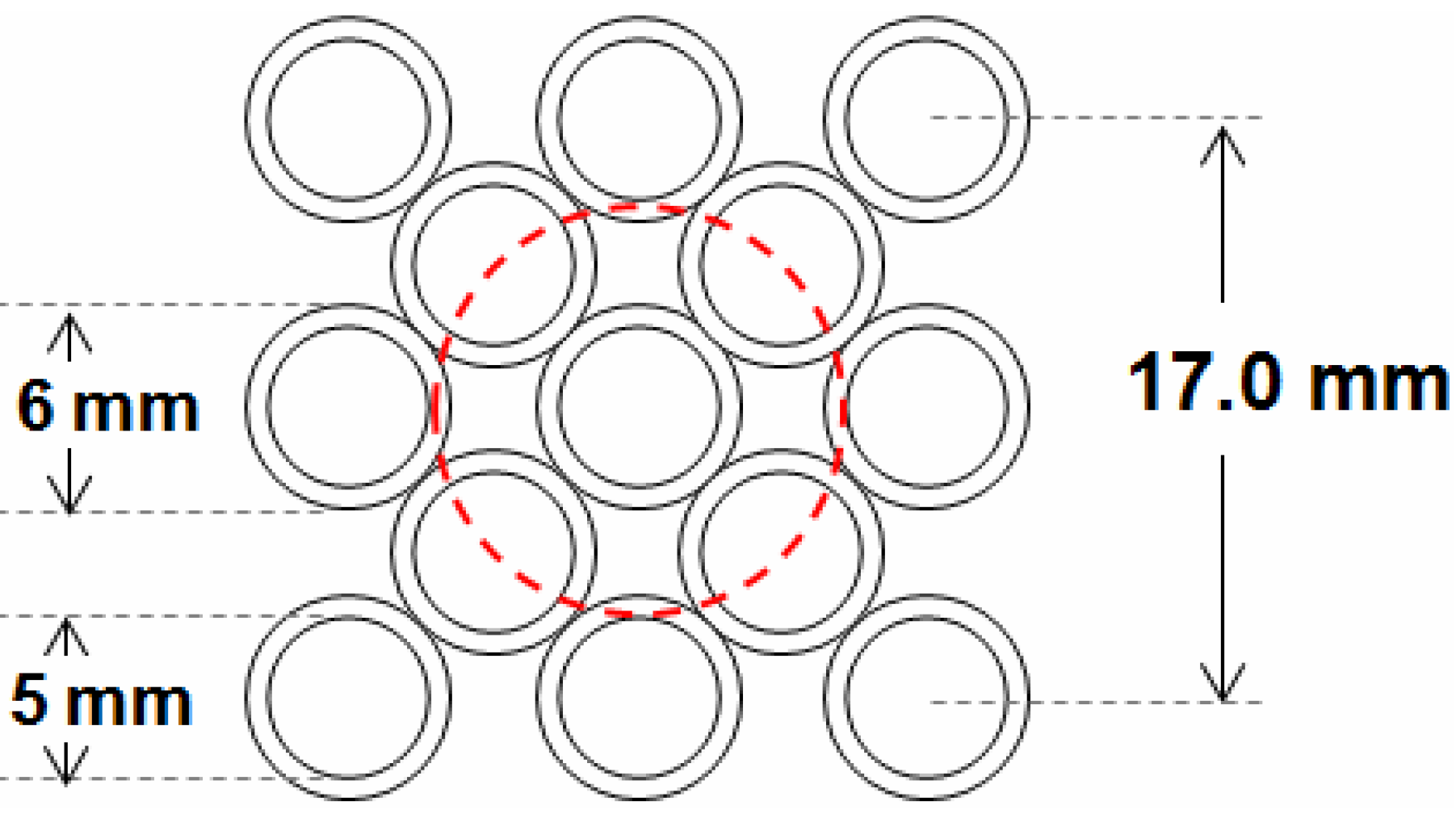
Figure 1b (not-to-scale). The working distance from the eye location to the entrance pupil of the camera is 30 cm. The infrared camera lens is focused on the pupil of the eye. The LED panel consists of 13 NIR LEDs that are arranged in four meridians as shown in
Figure 3. Each LED is about 6 mm with a 5 mm-diameter radiating field size. The light source at this size and working distance is considered as an extended source (~17 mradian). The LEDs radiate at wavelength 805+/−25 nm with maximum continuous output of 38 mW. During the measurements, the radiation of each LED pulse is limited between 10 and 50 ms. A feedback loop is programmed to control the LED’s radiation pulse duration and the camera gain to prevent saturation or under exposure. All 13 LEDs are pulsed on in a rapid sequence as the camera captures the pupil reflex images. The camera frame rate is 120 Hz, but the maximum acquisition rate is dominant by the required exposure time, which is equal to the radiation pulse. Each monocular image (10-bit gray level) is 350 by 350 pixel in size. A 25R/75T pellicle beam splitter is used to align the LED panel image to the camera entrance pupil plane. After reflected from the beam splitter, the maximum use of the light emission is considered as minimal risk at the maximum accessible emission of 0.041 j/cm
2/sr, less than 1% of the emission limit according to the federal regulation, e-CFR 1040. The entrance pupil radius of the camera is set at 6 mm as marked in red dashed lines in
Figure 3. With the intention to better observe various ocular abnormalities, this arrangement provides a coaxial illumination at the center, 4 knife-edge illumination at 0 and 90 degree meridians, and at 45 and 135 degree meridians with four EPR illuminations that are half-way overlapped by the detection, and four EPR illuminations that have no overlap area with the detection pupil. No mechanical or electronic approach for neutralization was constructed in this prototype.
Figure 3.
The spatial arrangement of two-dimensional LED panel that contains 13 LEDs: one coaxial LED at the center surrounded with 12 eccentric LEDs. The red dashed line indicates the location of the projected entrance pupil of the camera.
Figure 3.
The spatial arrangement of two-dimensional LED panel that contains 13 LEDs: one coaxial LED at the center surrounded with 12 eccentric LEDs. The red dashed line indicates the location of the projected entrance pupil of the camera.
3.2. Clinical Testing
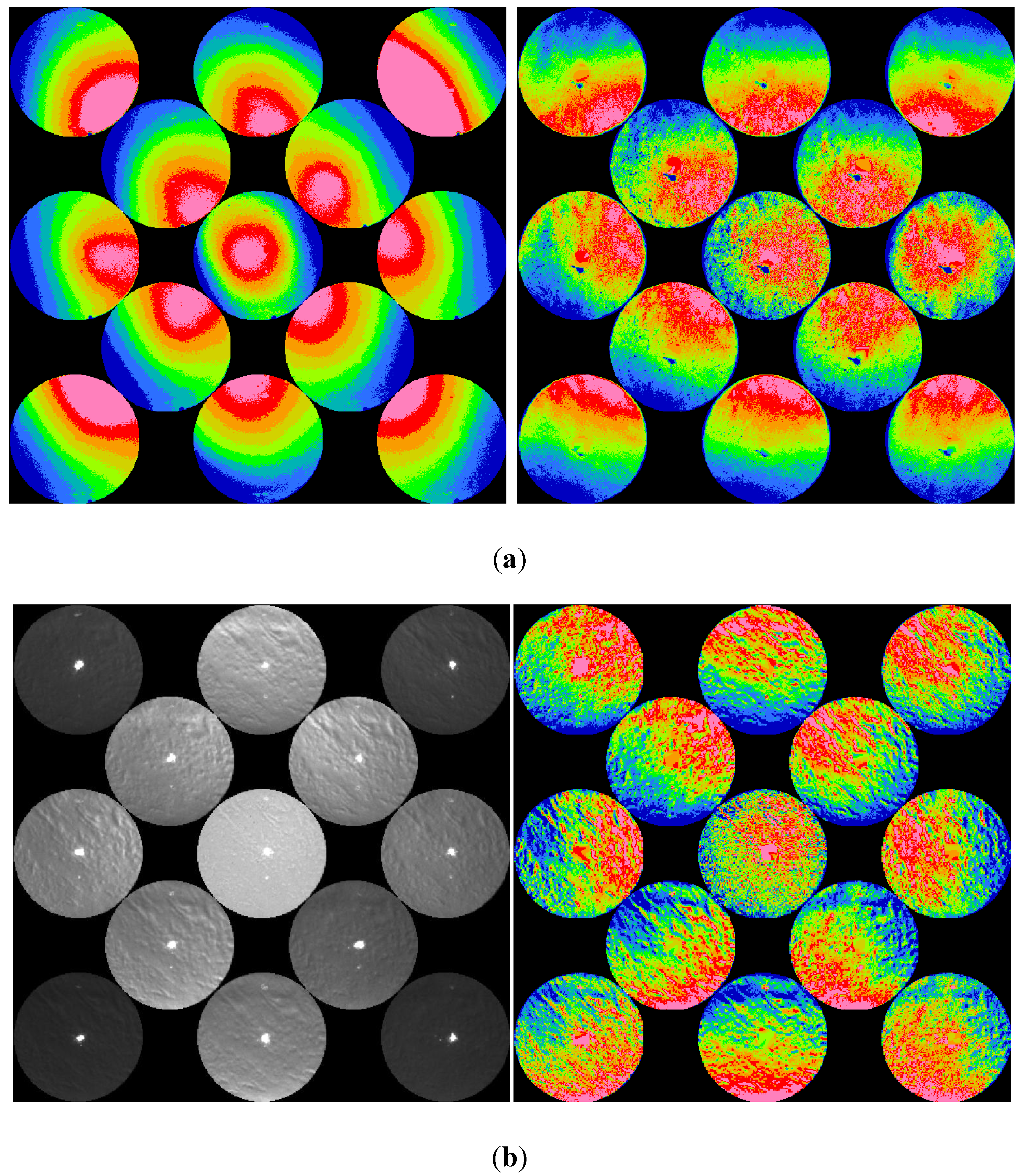
A total of 90 adult patients of Wang Vision Institute in Nashville participated in the experiment of the monocular infrared retinoscopic device during their visits for eye care. The experimental test was a voluntary addition that did not affect any clinical decision for their eye care. The IRB approval was obtained in the University of Tennessee at Knoxville. Prior to the tests the testing procedure, safety, and confidentiality were described to the participants and the signed consent forms were acquired. The measurements were performed when the room light was turned off. Once an eye was placed on the location and the camera detected the reflex, it automatically adjusted the radiation duration (10–50 ms) for optimal exposures and it acquired a sequence of images automatically. The patient only saw the blinking dim LED lights at 30 cm in front of the eye. The measurement for each eye took no longer than 3 s. All images were collected without difficulty. The clinicians who made the diagnosis and treatments were blinded to the IR retinoscopy findings.
For comparison, only the existing clinical data from the testing day and before were collected. The patients’ clinical diagnostics data were de-identified except for a number that linked to the corresponding images. Over half of the eye images were acquired from normal eyes of subjects seeking refraction corrections (i.e., spectacles, contact lens, or surgical corrections) or returning for follow-up examinations after treatments. Fifty-nine eyes in the 180 were clinically identified as keratoconus. The remaining non-infectious eyes presented with various ocular conditions. They included dry eyes, blepharitis, Fuch’s endothelium dystrophy, and corneal scars, etc.
3.3. Computation of the Measurement
Computational models are useful to validate theory, and to investigate and evaluate influential ocular properties in the measurements. Existing wavefront aberrometry data from some of the participating eyes were available. These wavefront data allowed us to perform a computational study of the aberration reflex profiles. Using the optical design program, Zemax (Radiant Zemax, Redmond, WA, USA), a simple paraxial ideal lens eye-model was constructed with a Zernike phase plate that characterizes the patient’s clinical wavefront aberration measurement. The optical components of the retinoscope prototype were constructed with the simple eye model. The geometric image analysis in Zemax was used to compute the retinal blur and to simulate the PR images. The Zernike phase plates were assumed for both inward and backward eye models. Spatial cares were taken to ensure the correct coordinate was obtained transferring between the two sequential computations, the Zernike coefficients’ sign change in the two coordinate systems, wavelength correction and input-order of the Zernike coefficients from clinical data in line with the Zemax convention.
5. Conclusions
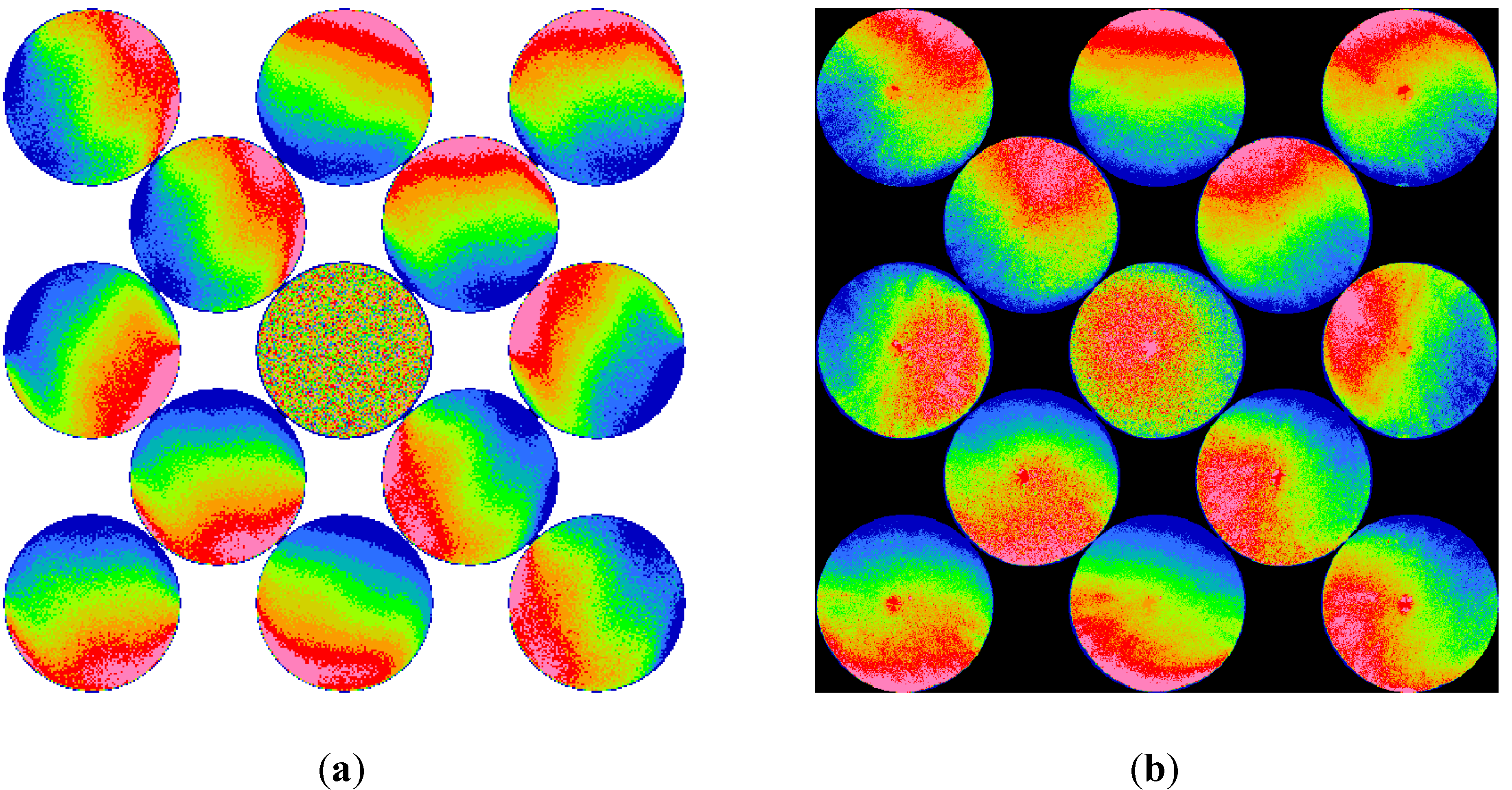
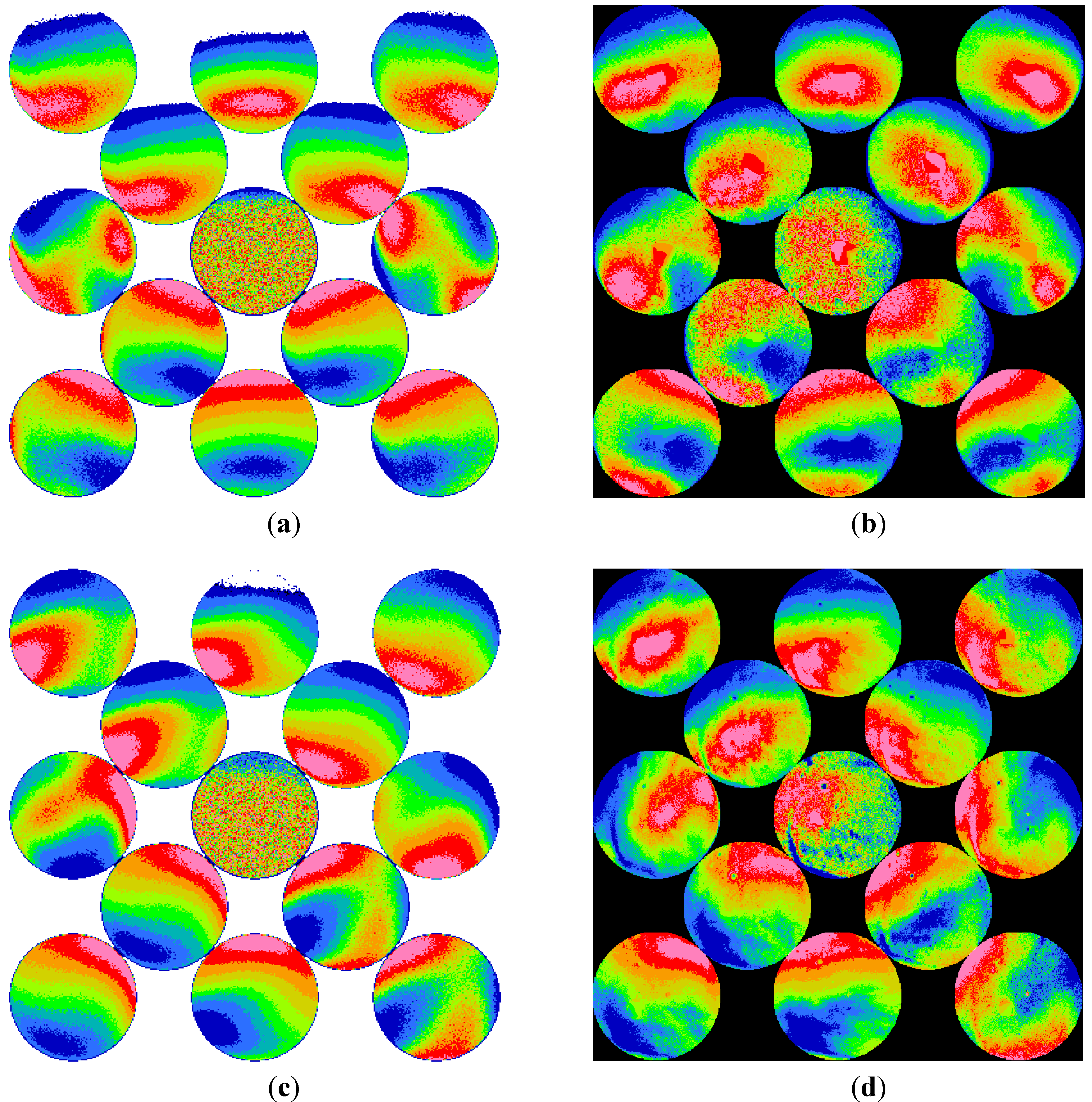
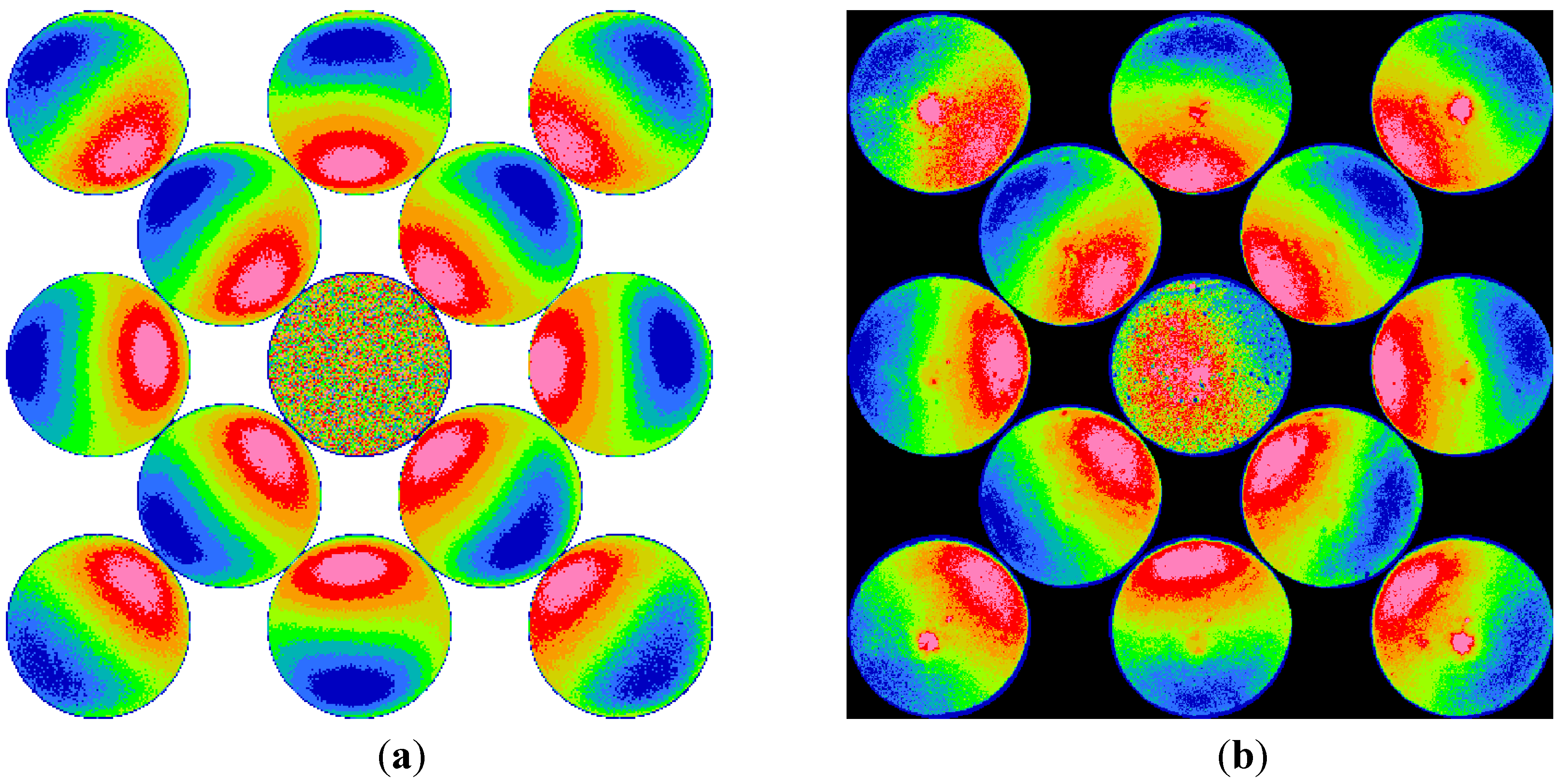
Through experiment and computation, this paper discusses and demonstrates the ophthalmic measurements with an infrared retinoscope. The retinoscopic pupil reflex images of several different conditions are presented in direct photographs and enhanced color images. Digitization of images and simple image analysis algorithms greatly improve the visualization. As the results show, small optical defects could be observed from the direct- or back-scattered light similar to the direct- and retro-illuminations of a slit lamp. Low- and high-order ocular aberrations appear as the background to the small optical defects. The type of aberration presents itself with shadows and intensity gradient variations of the pupil reflex. Defocus, astigmatism, and high-order aberrations in keratoconus and LASIK eyes show unique appearances of their own and can be identified easily.
Disregarding the possible discrepancy in pupil size, direction of gaze, and accommodations, the computation results show agreement with experiment results. Our computation indicates that the retinal stray light or intraocular scattering plays an important role for the far eccentric detection in retinoscopy. The simulations results from tested eyes suggest that the retinal stray light that is strongly linked to intraocular scattering extend the detection range of illuminating eccentricity in retinoscopy and make it more likely to observe ocular aberrations.