Comparison of Regularization Methods in Fluorescence Molecular Tomography
Abstract
:1. Introduction
2. Methodology
2.1. Forward Modeling
2.2. Non-Negative Regularized Least Squares
2.3. Optimization Transfer Algorithms
2.4. Regularization Parameter Selection and Image Quality Metrics
2.5. Numerical Simulations
2.6. Phantom Experiments
3. Results
3.1. Simulation Results for Small Targets
| RegType | Reg λ | VR | Dice | CNR | MSE |
|---|---|---|---|---|---|
| 5.0E-5 | 6.19 | 0.26 | 5.30 | 3.5E-3 | |
| 1.0E-11 | 6.05 | 0.27 | 5.36 | 3.5E-3 | |
| 5.9E-4 | 4.59 | 0.27 | 4.99 | 3.6E-3 | |
| 6E-4 | 1.25 | 0.31 | 4.42 | 3.6E-3 | |
| 1.0E-4 | 3.49 | 0.34 | 6.08 | 3.1E-3 | |
| 6.4E-5 | 2.61 | 0.33 | 5.72 | 3.1E-3 | |
| 3E-5 | 1.84 | 0.36 | 5.52 | 3.2E-3 | |
| 3.2E-6 | 2.13 | 0.36 | 5.38 | 3.3E-3 | |
| 1.3E-5 | 2.97 | 0.34 | 5.19 | 3.3E-3 |
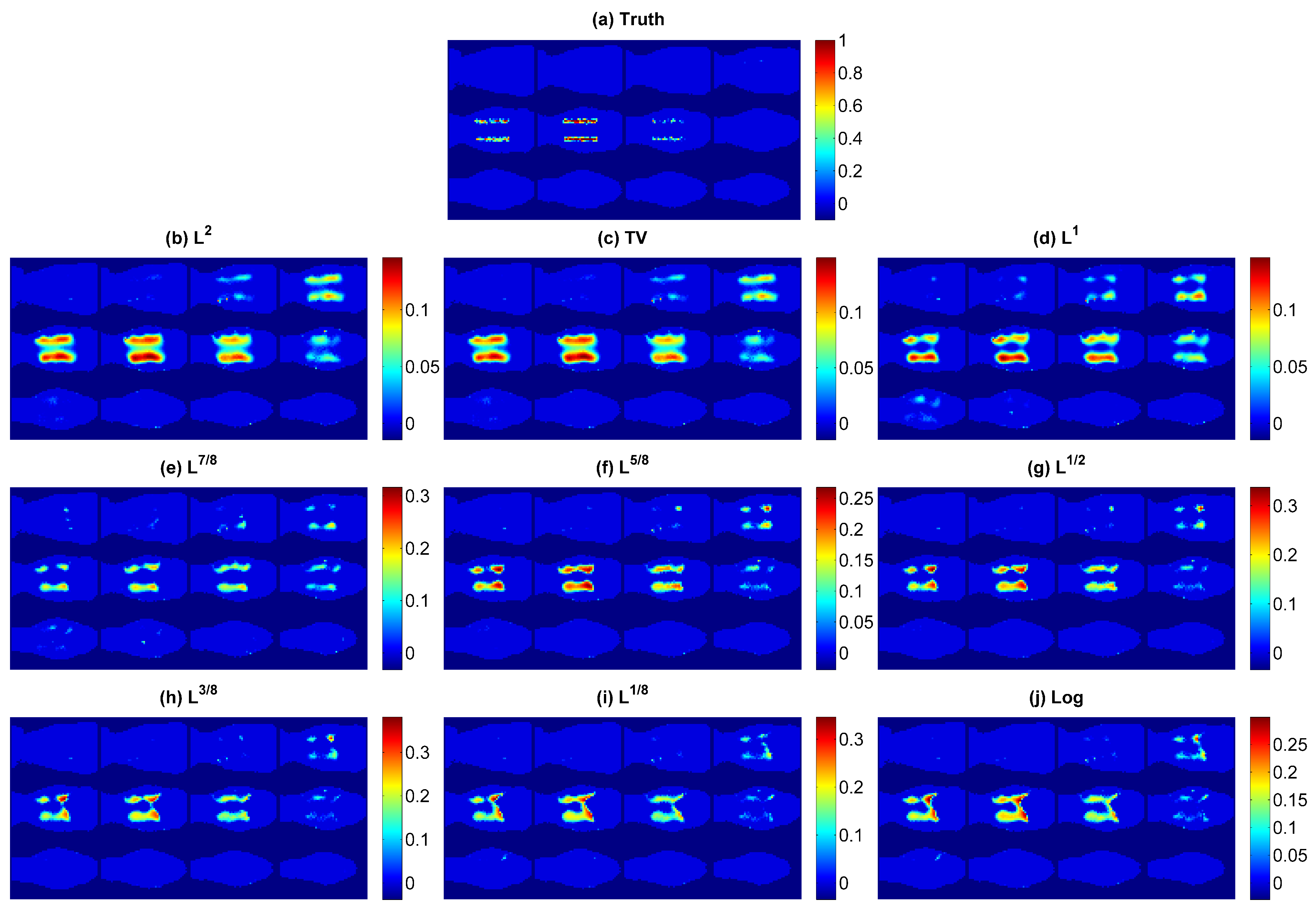
| Reg Type | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reg λ’s | VR | Dice | CNR | MSE | Reg λ’s | VR | Dice | CNR | MSE | ||
| 2.0E-11, 5.9E-4 | 4.60 | 0.27 | 4.99 | 3.6E-3 | 5.0E-5, 6.0E-10 | 4.63 | 0.26 | 4.94 | 3.6E-3 | ||
| 3.0E-11, 6.0E-4 | 1.16 | 0.30 | 4.41 | 3.6E-3 | 4.9E-5, 6.1E-4 | 1.16 | 0.29 | 4.36 | 3.6E-3 | ||
| 1.0E-11, 1.0E-4 | 3.45 | 0.34 | 6.07 | 3.1E-3 | 4.9E-5, 1.1E-4 | 3.61 | 0.33 | 6.04 | 3.1E-3 | ||
| 1.0E-11, 6.4E-5 | 2.61 | 0.33 | 5.72 | 3.1E-3 | 4.9E-5, 6.4E-5 | 2.71 | 0.32 | 5.7 | 3.1E-3 | ||
| 2.0E-11, 3.0E-5 | 1.84 | 0.36 | 5.52 | 3.2E-3 | 4.9E-5, 3.0E-5 | 1.99 | 0.35 | 5.51 | 3.2E-3 | ||
| 1.0E-11, 3.2E-6 | 2.13 | 0.36 | 5.38 | 3.3E-3 | 4.9E-5, 3.2E-6 | 2.26 | 0.37 | 5.35 | 3.3E-3 | ||
| 3.0E-11, 1.4E-5 | 2.46 | 0.34 | 5.04 | 3.4E-3 | 4.9E-5, 1.4E-5 | 2.63 | 0.34 | 5.03 | 3.4E-3 | ||
3.2. Simulation Results for Large Target
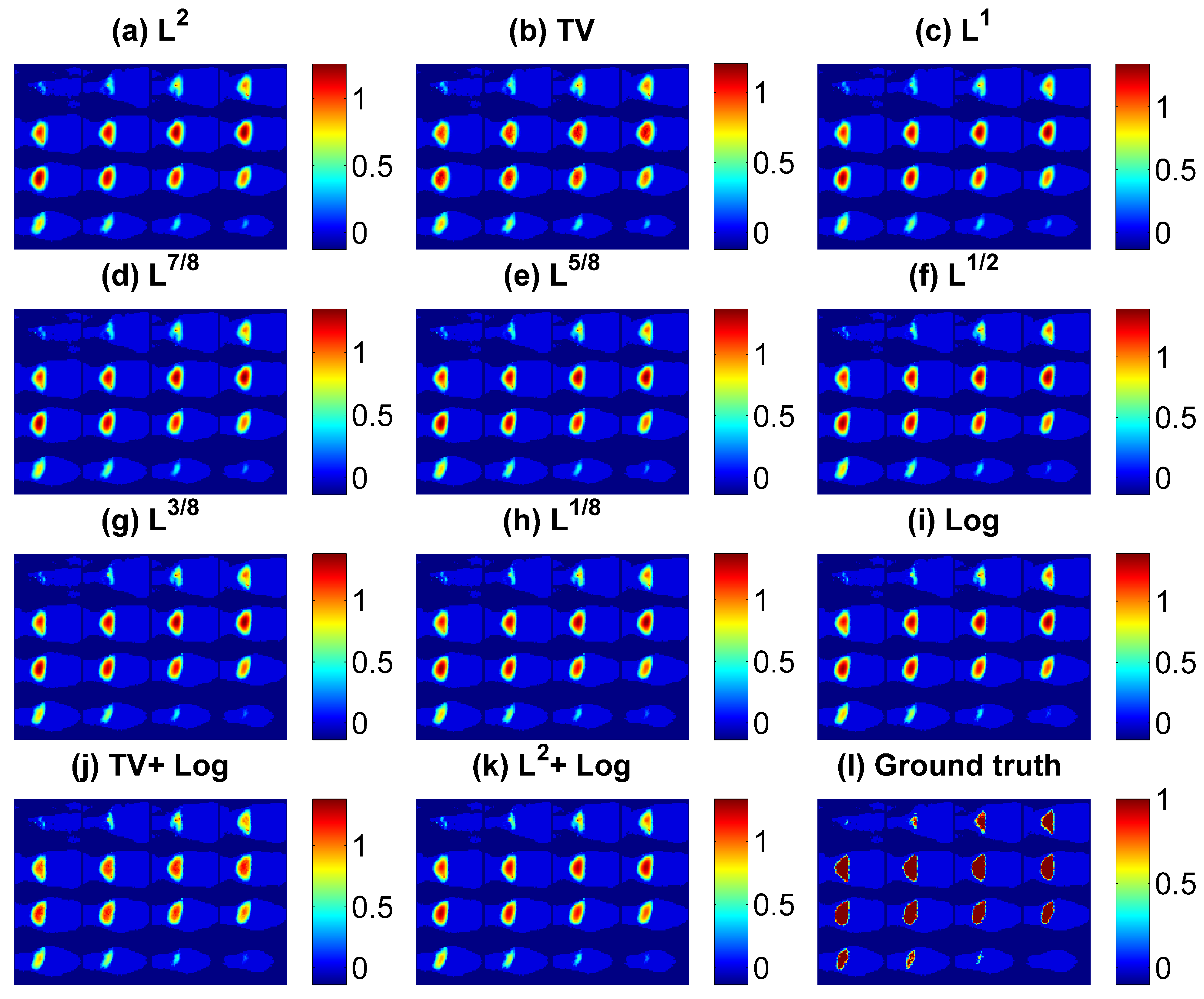
| Reg Type | Reg λ | VR | Dice | CNR | MSE |
|---|---|---|---|---|---|
| 1.0E-3 | 0.51 | 0.68 | 7.3 | 9.2E-3 | |
| 1.0E-6 | 0.50 | 0.67 | 7.3 | 8.9E-3 | |
| 1.0E-3 | 0.61 | 0.76 | 6.9 | 1.0E-2 | |
| 1.0E-3 | 0.62 | 0.76 | 7.0 | 1.0E-2 | |
| 1.0E-3 | 0.63 | 0.77 | 7.3 | 9.1E-3 | |
| 1.0E-3 | 0.64 | 0.78 | 7.6 | 8.3E-3 | |
| 5.0E-4 | 0.65 | 0.79 | 7.5 | 8.4E-3 | |
| 1.0E-4 | 0.67 | 0.79 | 7.5 | 8.4E-3 | |
| 1.0E-3 | 0.69 | 0.81 | 7.7 | 7.7E-3 |
| Reg Type | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reg λ’s | VR | Dice | CNR | MSE | Reg λ’s | VR | Dice | CNR | MSE | ||
| 1.0E-6, 1.0E-5 | 0.74 | 0.83 | 6.74 | 1.2E-2 | 1.0E-3, 1.0E-3 | 0.68 | 0.81 | 6.95 | 1.1E-2 | ||
| 5.0E-7, 1.0E-3 | 0.67 | 0.80 | 7.14 | 1.0E-2 | 1.0E-2, 1.0E-4 | 0.69 | 0.81 | 7.74 | 7.7E-3 | ||
| 1.0E-7, 1.0E-3 | 0.64 | 0.78 | 7.37 | 8.9E-4 | 1.0E-3, 1.0E-3 | 0.68 | 0.81 | 7.35 | 9.1E-3 | ||
| 5.0E-7, 5.0E-4 | 0.68 | 0.81 | 7.40 | 9.0E-3 | 1.0E-4, 1.0E-3 | 0.64 | 0.78 | 7.59 | 8.2E-3 | ||
| 1.0E-7, 5.0E-3 | 0.66 | 0.80 | 7.57 | 8.2E-3 | 1.0E-3, 1.0E-3 | 0.67 | 0.80 | 8.12 | 7.2E-3 | ||
| 5.0E-7, 1.0E-4 | 0.70 | 0.82 | 7.65 | 8.0E-3 | 1.0E-4, 1.0E-4 | 0.69 | 0.80 | 7.47 | 8.4E-3 | ||
| 5.0E-7, 1.0E-3 | 0.70 | 0.82 | 8.01 | 7.2E-3 | 1.0E-3, 1.0E-3 | 0.72 | 0.84 | 7.84 | 7.4E-3 | ||
3.3. Phantom Experimental Results
| Reg Type | Reg λ | VR | Dice | CNR |
|---|---|---|---|---|
| 1.0E-6 | 4.48 | 0.28 | 5.12 | |
| 3.0E-9 | 4.58 | 0.27 | 4.90 | |
| 9.0E+3 | 2.50 | 0.33 | 6.62 | |
| 1.0E+5 | 1.67 | 0.32 | 6.36 | |
| 4.0E+6 | 2.05 | 0.43 | 8.60 | |
| 5.0E+7 | 1.52 | 0.39 | 7.74 | |
| 6.0E+8 | 1.22 | 0.37 | 7.17 | |
| 1.0E+10 | 1.92 | 0.34 | 7.26 | |
| 9.0E+11 | 1.73 | 0.34 | 7.03 |
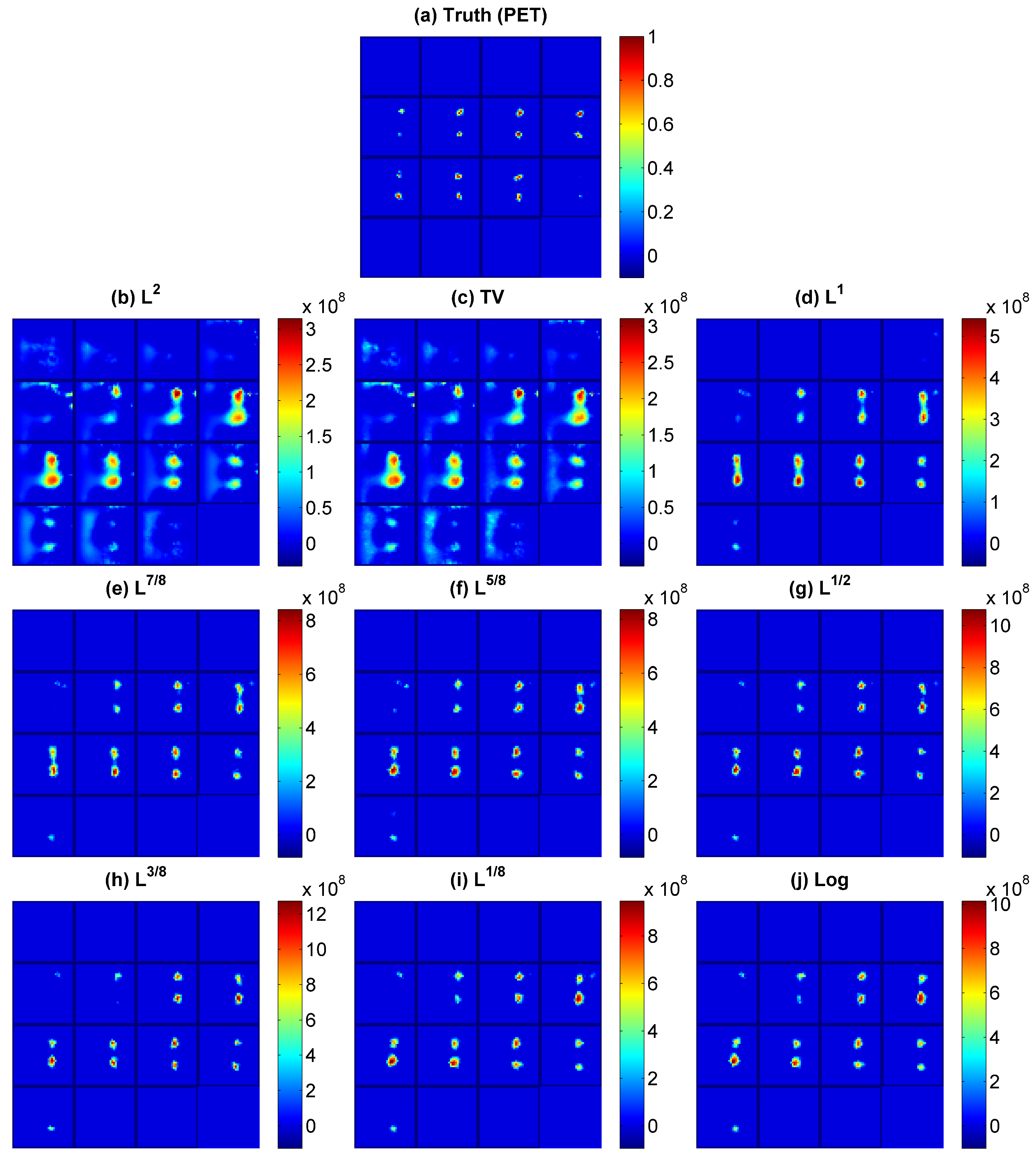
3.4. Regularization Parameter Selection
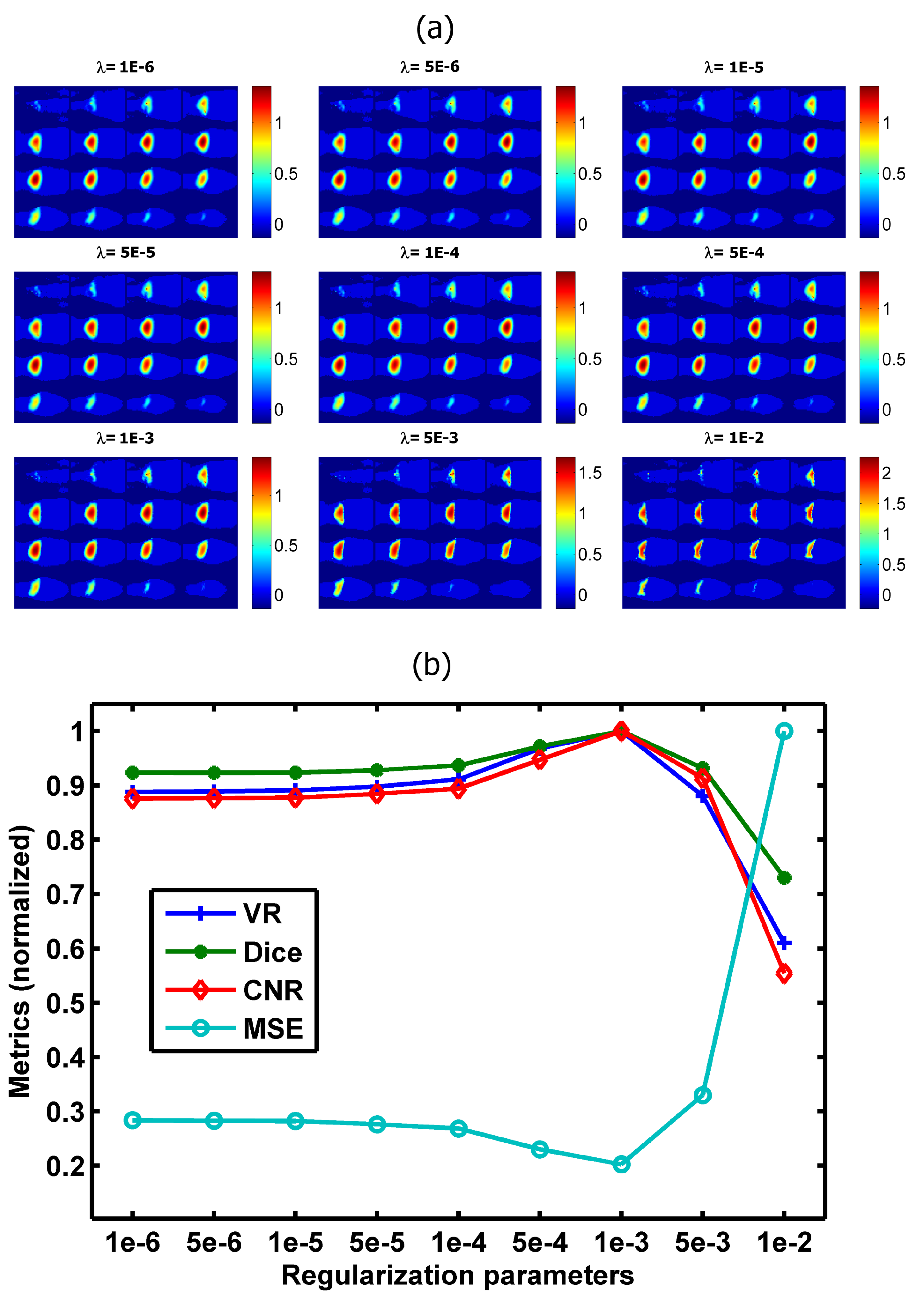
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cherry, S.R. In vivo molecular and genomic imaging: New challenges for imaging physics. Phys. Med. Biol. 2004, 49, R13–R48. [Google Scholar] [CrossRef] [PubMed]
- Ntziachristos, V.; Ripoll, J.; Wang, L.V.; Weissleder, R. Looking and listening to light: The evolution of whole-body photonic imaging. Nat. Biotechnol. 2005, 23, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A.; Arsenin, V.Y. Solutions of Ill-Posed Problems; WH Winston: Washington, DC, USA, 1977; p. 330. [Google Scholar]
- Hyde, D.; Miller, E.L.; Brooks, D.H.; Ntziachristos, V. Data specific spatially varying regularization for multimodal fluorescence molecular tomography. IEEE Trans. Med. Imaging 2010, 29, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Axelsson, J.; Svensson, J.; Andersson-Engels, S. Spatially varying regularization based on spectrally resolved fluorescence emission in fluorescence molecular tomography. Opt. Express 2007, 15, 574–13. [Google Scholar] [CrossRef]
- Pogue, B.W.; McBride, T.O.; Prewitt, J.; Österberg, U.L.; Paulsen, K.D. Spatially variant regularization improves diffuse optical tomography. Appl. Opt. 1999, 38, 2950–2961. [Google Scholar] [CrossRef] [PubMed]
- Bloch, S.; Lesage, F.; McIntosh, L.; Gandjbakhche, A.; Liang, K.; Achilefu, S. Whole-body fluorescence lifetime imaging of a tumor-targeted near-infrared molecular probe in mice. J. Biomed. Opt. 2005, 10, 054003–054003. [Google Scholar] [CrossRef] [PubMed]
- Weissleder, R.; Tung, C.H.; Mahmood, U.; Bogdanov, A. In vivo imaging of tumors with protease-activated near-infrared fluorescent probes. Nat. Biotechnol. 1999, 17, 375–378. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Zhang, B.; Liu, F.; Luo, J.; Bai, J. Efficient L1 regularization-based reconstruction for fluorescent molecular tomography using restarted nonlinear conjugate gradient. Opt. Lett. 2013, 38, 3696–3699. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; Tian, J.; Zhu, S.; Feng, J.; Qin, C.; Zhang, B.; Yang, X. A fast reconstruction algorithm for fluorescence molecular tomography with sparsity regularization. Opt. Express 2010, 18, 8630–8646. [Google Scholar] [CrossRef] [PubMed]
- Yi, H.; Chen, D.; Li, W.; Zhu, S.; Wang, X.; Liang, J.; Tian, J. Reconstruction algorithms based on L1-norm and L2-norm for two imaging models of fluorescence molecular tomography: A comparative study. J. Biomed. Opt. 2013, 18, 056013. [Google Scholar] [CrossRef] [PubMed]
- Behrooz, A.; Zhou, H.M.; Eftekhar, A.A.; Adibi, A. Total variation regularization for 3D reconstruction in fluorescence tomography: Experimental phantom studies. Appl. Opt. 2012, 51, 8216–8227. [Google Scholar] [CrossRef] [PubMed]
- Dutta, J.; Ahn, S.; Li, C.; Cherry, S.R.; Leahy, R.M. Joint L1 and total variation regularization for fluorescence molecular tomography. Phys. Med. Biol. 2012, 57, 1459–1476. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Li, C. Nonconvex regularizations in fluorescence molecular tomography for sparsity enhancement. Phys. Med. Biol. 2014, 59. (In Press.). [Google Scholar] [CrossRef] [PubMed]
- Prakash, J.; Shaw, C.; Manjappa, R.; Kanhirodan, R.; Yalavarthy, P.K. Sparse recovery methods hold promise for diffuse optical tomographic image reconstruction. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 6800609. [Google Scholar] [CrossRef]
- Okawa, S.; Hoshi, Y.; Yamada, Y. Improvement of image quality of time-domain diffuse optical tomography with Lq sparsity regularization. Biomed. Opt. Express 2011, 2, 3334–3348. [Google Scholar] [CrossRef] [PubMed]
- Weissleder, R.; Ntziachristos, V. Shedding light onto live molecular targets. Nat. Med. 2003, 9, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Shu, X.; Royant, A.; Lin, M.Z.; Aguilera, T.A.; Lev-Ram, V.; Steinbach, P.A.; Tsien, R.Y. Mammalian expression of infrared fluorescent proteins engineered from a bacterial phytochrome. Science 2009, 324, 804–807. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41–R93. [Google Scholar] [CrossRef]
- Li, C.; Mitchell, G.S.; Dutta, J.; Ahn, S.; Leahy, R.M.; Cherry, S.R. A three-dimensional multispectral fluorescence optical tomography imaging system for small animals based on a conical mirror design. Opt. Express 2009, 17, 7571–7585. [Google Scholar] [CrossRef] [PubMed]
- Correia, T.; Gibson, A.; Schweiger, M.; Hebden, J. Selection of regularization parameter for optical topography. J. Biomed. Opt. 2009, 14, 034044. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Alexandrakis, G.; Liu, H. Optimization of probe geometry for diffuse optical brain imaging based on measurement density and distribution. Appl. Opt. 2009, 48, 2496–2504. [Google Scholar] [CrossRef] [PubMed]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Song, X.; Pogue, B.W.; Jiang, S.; Doyley, M.M.; Dehghani, H.; Tosteson, T.D.; Paulsen, K.D. Automated region detection based on the contrast-to-noise ratio in near-infrared tomography. Appl. Opt. 2004, 43, 1053–1062. [Google Scholar] [CrossRef] [PubMed]
- Dogdas, B.; Stout, D.; Chatziioannou, A.F.; Leahy, R.M. Digimouse: A 3D whole body mouse atlas from CT and cryosection data. Phys. Med. Biol. 2007, 52, 577–587. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wang, G.; Qi, J.; Cherry, S.R. Three-dimensional fluorescence optical tomography in small-animal imaging using simultaneous positron-emission-tomography priors. Opt. Lett. 2009, 34, 2933–2935. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yang, Y.; Mitchell, G.S.; Cherry, S.R. Simultaneous PET and multispectral 3-dimensional fluorescence optical tomography imaging system. J. Nucl. Med. 2011, 52, 1268–1275. [Google Scholar] [CrossRef] [PubMed]
- Hunter, D.R.; Lange, K. A tutorial on MM algorithms. Am. Stat. 2004, 58, 30–37. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, D.; Zhao, Y.; Baikejiang, R.; Yuan, Z.; Li, C. Comparison of Regularization Methods in Fluorescence Molecular Tomography. Photonics 2014, 1, 95-109. https://doi.org/10.3390/photonics1020095
Zhu D, Zhao Y, Baikejiang R, Yuan Z, Li C. Comparison of Regularization Methods in Fluorescence Molecular Tomography. Photonics. 2014; 1(2):95-109. https://doi.org/10.3390/photonics1020095
Chicago/Turabian StyleZhu, Dianwen, Yue Zhao, Reheman Baikejiang, Zhen Yuan, and Changqing Li. 2014. "Comparison of Regularization Methods in Fluorescence Molecular Tomography" Photonics 1, no. 2: 95-109. https://doi.org/10.3390/photonics1020095
APA StyleZhu, D., Zhao, Y., Baikejiang, R., Yuan, Z., & Li, C. (2014). Comparison of Regularization Methods in Fluorescence Molecular Tomography. Photonics, 1(2), 95-109. https://doi.org/10.3390/photonics1020095






