A New Machine Learning Algorithm to Simulate the Outlet Flow in a Reservoir, Based on a Water Balance Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Database
- Compile the records from the HMP sheets of the Sunilla meteorological station, the inflow and outflow data, and the structural profile of the Cuchoquesera dam.
- Collect the historical data of the Sunilla station HMP: precipitation (Pp), evaporation (Ev), relative humidity (RH), and ambient temperature (Tamb).
- Obtain inflow (QE_obs) and outflow (QS_obs) data for the reservoir.
2.3. Data Analysis
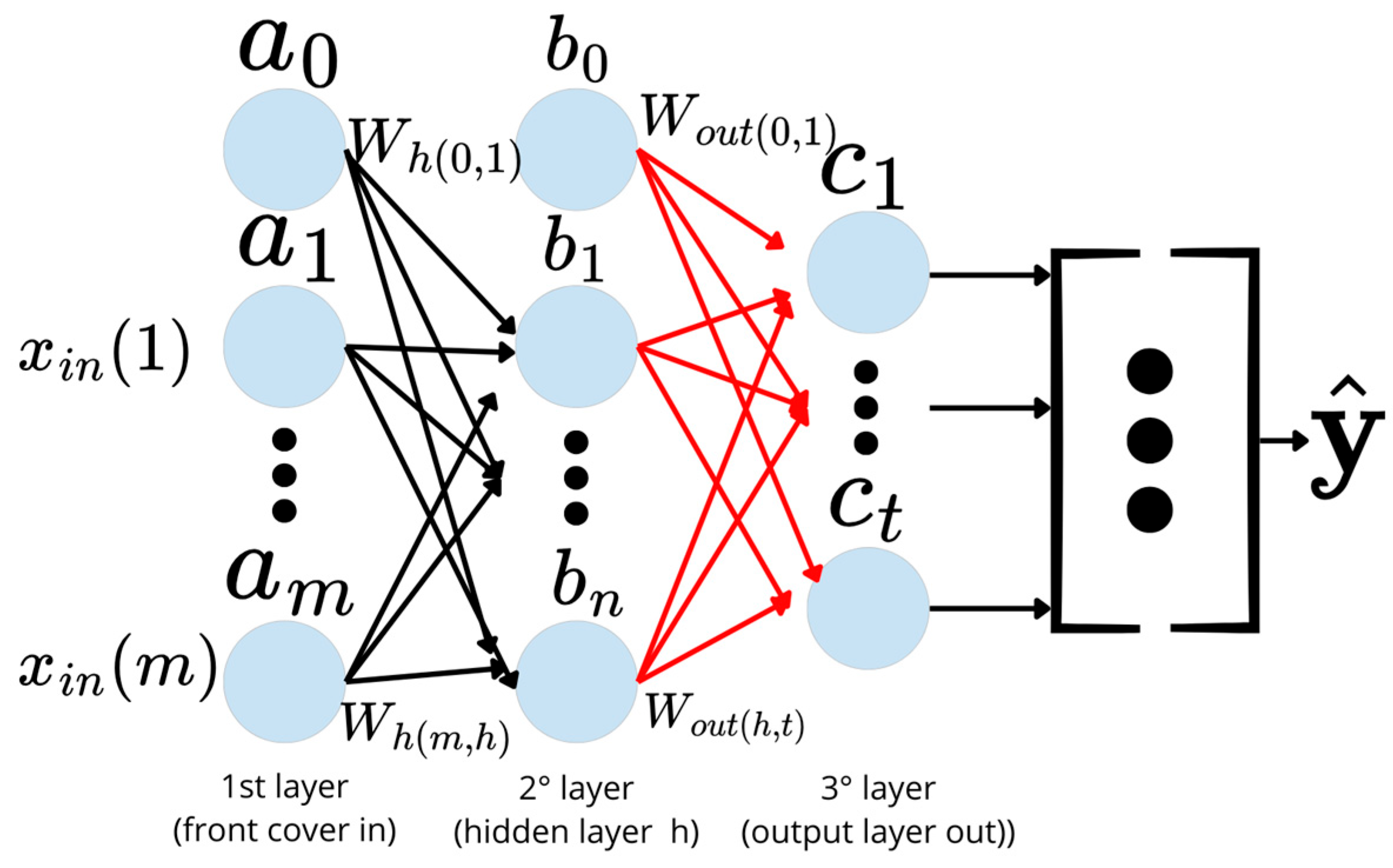
2.4. Artificial Neural Network (ANN)
- The input layer propagates forward to generate the network’s output.
- 2.
- The error between the predicted and actual output is computed by means of a cost function.
- 3.
- The error is backpropagated through the network, computing the derivatives with respect to the weights, and the model is updated accordingly. This process is repeated iteratively.
2.5. TensorFlow (TF)
2.6. Long Short-Term Memory (LSTM)
3. Water Balance Model and Simulation
- Hidden_layer_sizes (500,) asks to create a hidden layer of 500 neurons, for which each input will check Equation (3).
- Activation = ‘logistic’ is used to avoid linearity and model the input data, allowing it to learn the model according to Equation (4).
- Max_iter = 10,000 is the maximum number of iterations until the model converges.
- Random state = 50 is a pseudo-random number generator to initialize the weights and biases of the ANN.
4. Results
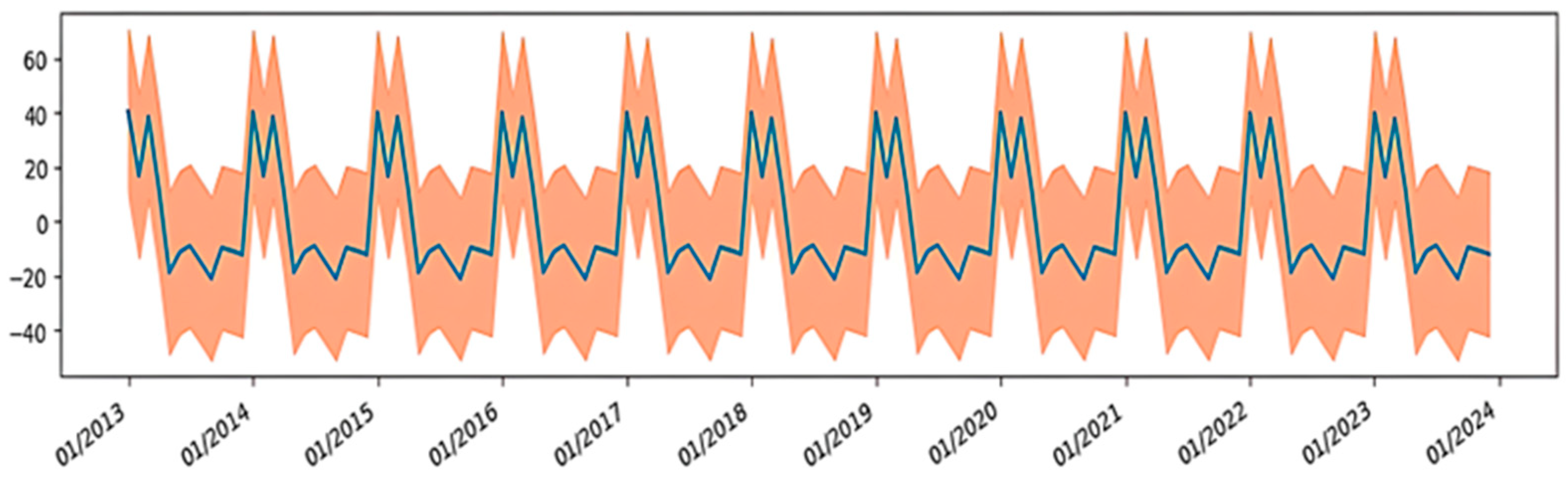
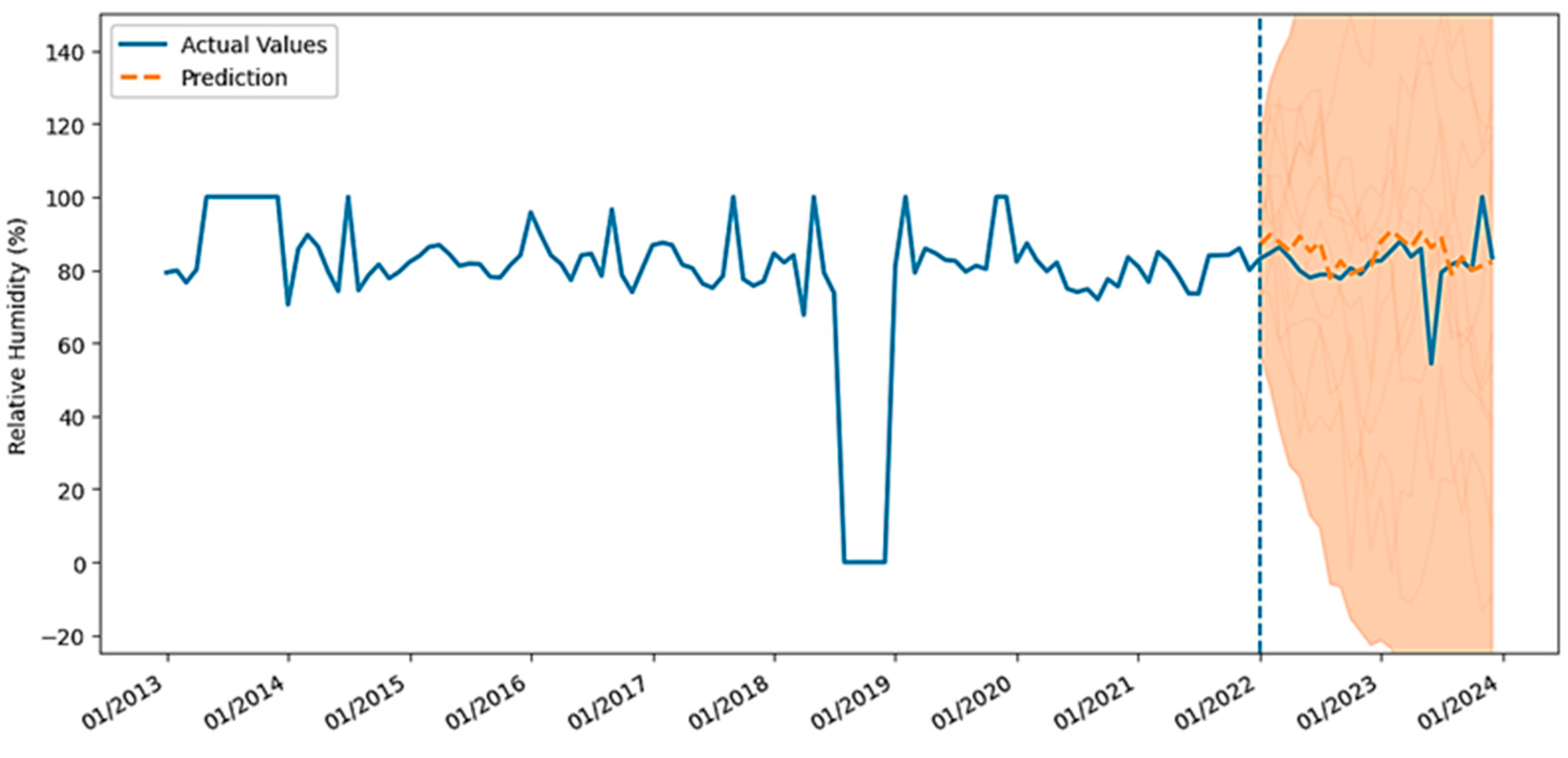
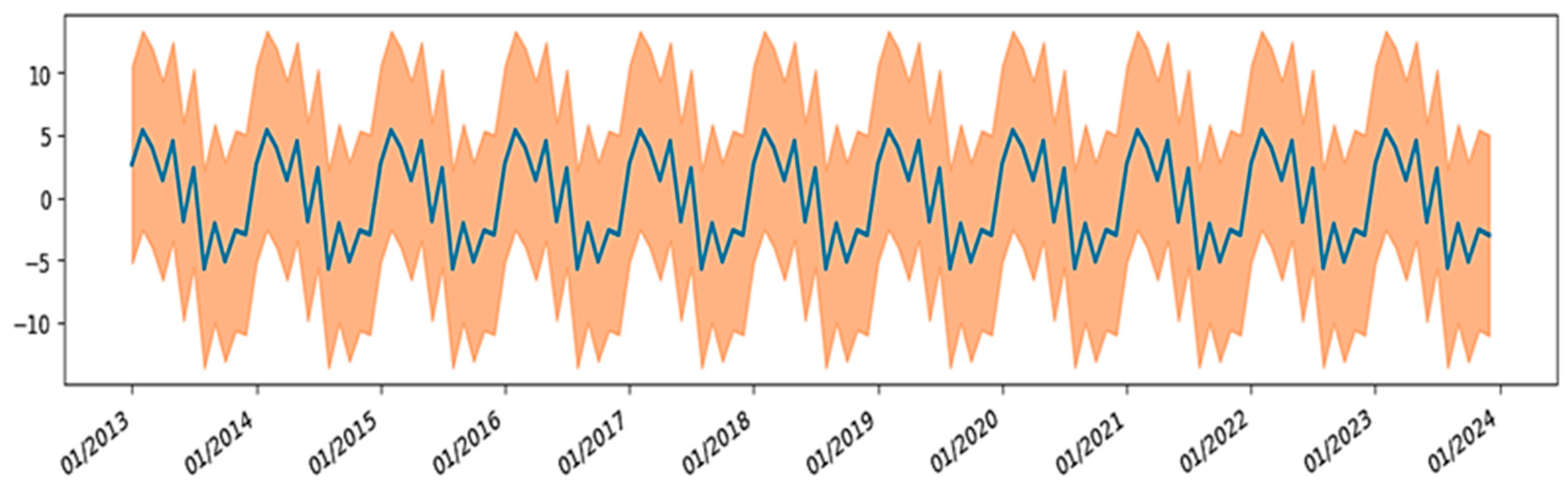
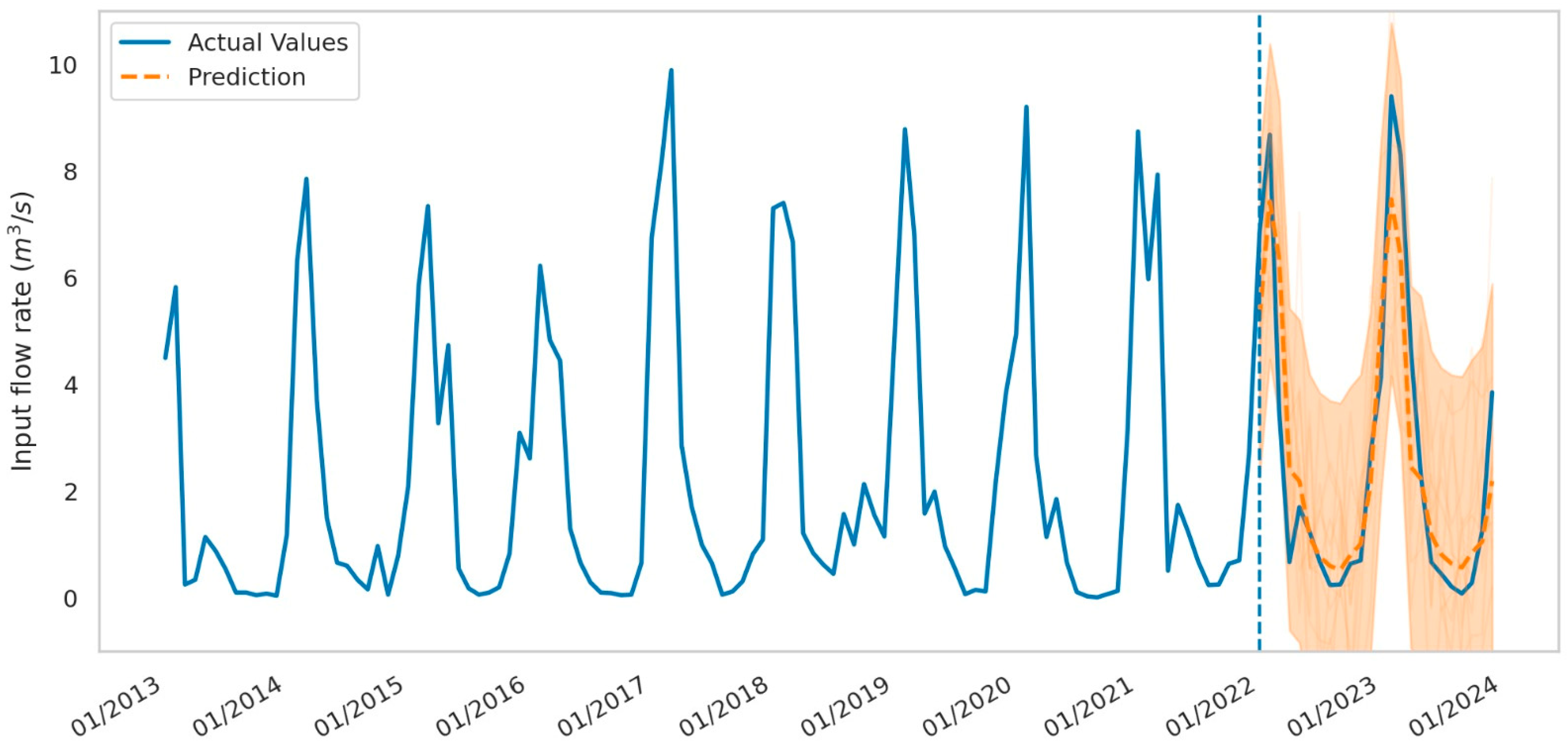
4.1. Time Series Projections of HMPs with TF
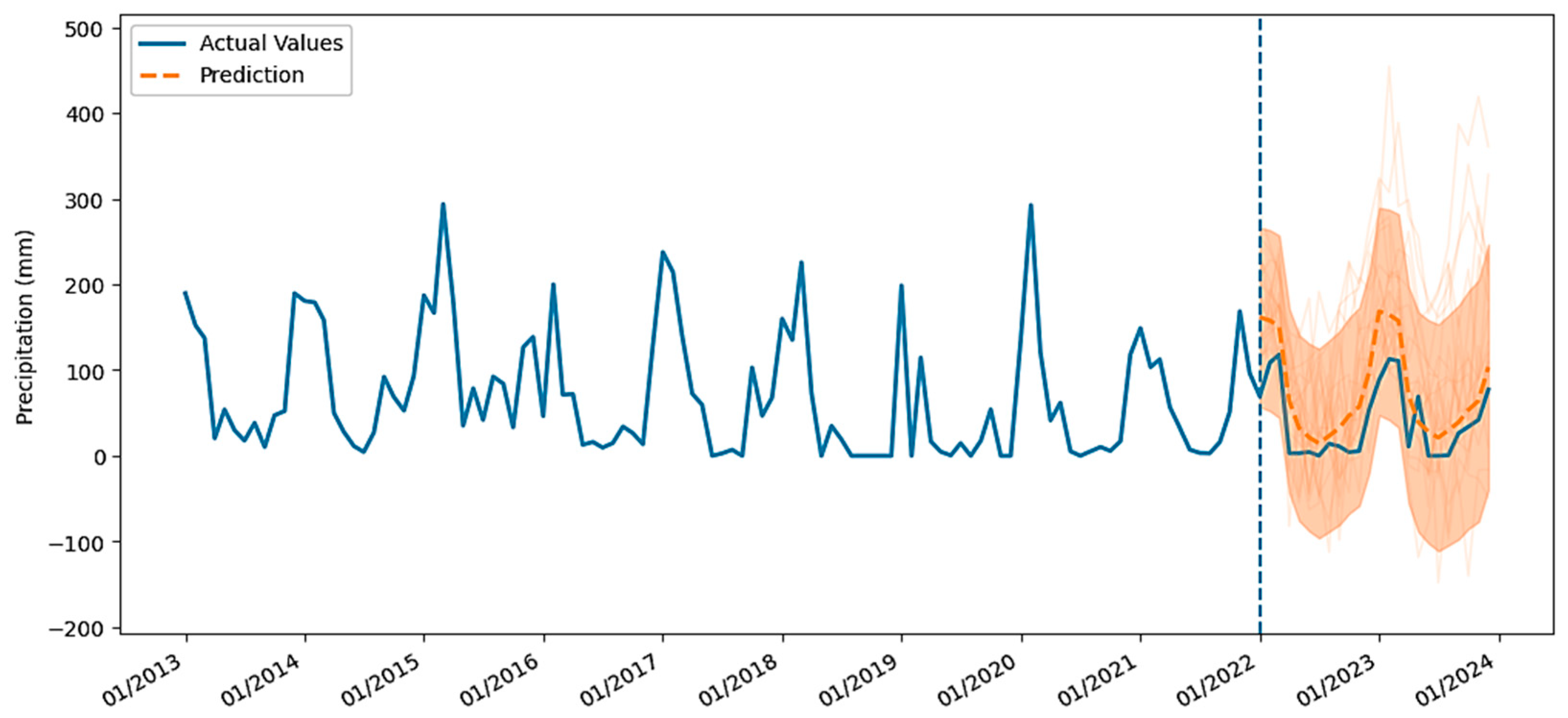
4.1.1. Precipitation (Pp)
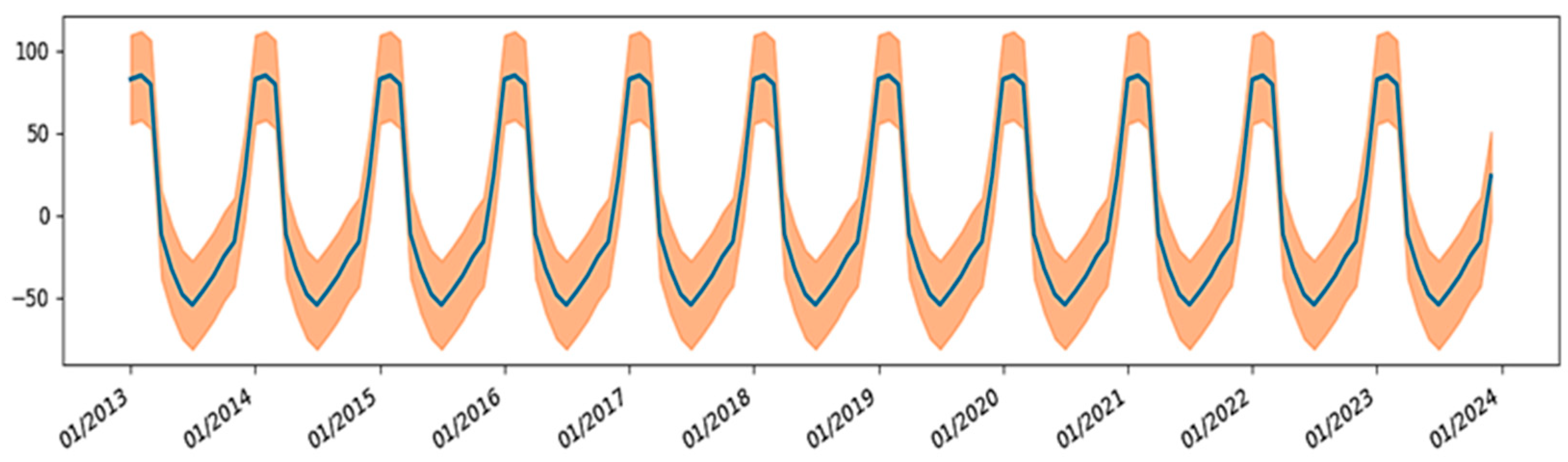
4.1.2. Evaporation (Ev)
4.1.3. Relative Humidity (RH)
4.1.4. Ambient Temperature (Tamb)
4.1.5. Observed Inflow (QE_obs)
4.1.6. Observed Outflow (QS_obs)
5. Discussion
- (i)
- Incomplete and missing data.
- (ii)
- Data errors resulting from the malfunctioning of sensors and instruments installed at the station.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OPEMAN | Operations and Maintenance Office. |
| TF | TensorFlow |
| ML | Machine Learning |
| ANN | Artificial Neural Network |
| Pp | Precipitation |
| Ev | Evaporation |
| RH | Relative humidity |
| Tamb | Ambient temperature |
| QE_obs | Observed inflow |
| QS | Outflow |
| QS_obs | Observed outflow |
| QS_sim | Simulated outflow |
| MCM | Meters per cubic million |
Appendix A
| Algorithm A1. Water Balance Code—Cuchoquesera Reservoir |
| import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.neural_network import MLPRegressor from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split # 1. Load data from a CSV data = pd.read_csv(‘datosBH.csv’) # 2. Prepare input and output data X = data[[‘Pp’, ‘Ev’, ‘Qi’,’Tamb’,’HR’]] y = data[‘Qs’] # 3. Splitting data into training and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 1000) # 4. Creating and training the RBF neural network model model = MLPRegressor(hidden_layer_sizes = (500,), activation = ‘logistic’, max_iter = 10,000, random_state = 50) model.fit(X_train, y_train) # 5. Predecir para todos los datos y calcular el error y_pred_all = model.predict(X) error = mean_squared_error(y, y_pred_all) print(f’Mean square error: {error}’) # 6. Calculate the dividing point between training and test. train_size = len(y_train) # Generate the graphic with the error includedplt.figure(figsize = (16, 8)) # Plotting actual and predicted lines plt.plot(y.values, label = ‘Real output flow rate’, color = ‘blue’, linewidth = 2, alpha = 0.8) # Línea real plt.plot(y_pred_all, label = ‘Simulated output flow rate’, color = ‘red’, linestyle = ‘--‘, linewidth = 2, alpha = 0.8) # Línea predicha # Vertical line to mark the end of training plt.axvline(x = train_size, color = ‘black’, linestyle = ‘-‘, linewidth = 2, label = ‘End of training’) # Adding points on the predicted curve plt.scatter(range(len(y_pred_all)), y_pred_all, color = ‘red’, s = 20, alpha = 0.6, label = ‘Puntos simulados’) # Add title and descriptive tags plt.xlabel(‘Number of samples’, fontsize = 14) plt.ylabel(‘Output flow rate (m3/s)’, fontsize = 14) # Add the error in a corner of the chart plt.text(0.3, 0.95, f’Mean square error (MSE): {error:.4f}’, fontsize = 12, transform = plt.gca().transAxes, verticalalignment = ‘top’, bbox = dict(facecolor = ‘white’, alpha = 0.8)) # Customize the legend plt.legend(fontsize = 12, loc = ‘upper left’, frameon = True, shadow = True) # Add grid for easy interpretation plt.grid(color = ‘gray’, linestyle = ‘--‘, linewidth = 0.5, alpha = 0.7) # Adjust the Y-axis limits to better display the data plt.ylim(min(y.min(), y_pred_all.min()) − 0.5, max(y.max(), y_pred_all.max()) + 0.5) # Adjust chart margins plt.tight_layout() # Show the graph plt.show() |
References
- Raphaëlle, O.; Núñez, A.; Cathala, C.; Ríos, A.R.; Nalesso, M. Water in the Time of Drought II: Lessons from Droughts Around the World; Ntercambiar—América un Desarrollo Prohib: Washington, DC, USA, 2021; p. 56. [Google Scholar] [CrossRef]
- Where Is Earth’s Water?|U.S. Geological Survey. Available online: https://www.usgs.gov/special-topics/water-science-school/science/where-earths-water (accessed on 29 April 2025).
- Wannasin, C.; Brauer, C.C.; Uijlenhoet, R.; Torfs, P.J.J.F.; Weerts, A.H. Machine Learning for Real-Time Reservoir Operation Simulation: Comparing Input Variables and Algorithms for the Sirikit Reservoir, Thailand. J. Hydroinformatics 2024, 26, 3151–3171. [Google Scholar] [CrossRef]
- Dashti Latif, S.; Najah Ahmed, A.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Reservoir Water Balance Simulation Model Utilizing Machine Learning Algorithm. Alex. Eng. J. 2021, 60, 1365–1378. [Google Scholar] [CrossRef]
- Hurtado Asto, J.J. Análisis Hidrológico y Estimación del Balance Hídrico Para la Presa de Relaves Pataz—La Libertad—2019. Master’s Thesis, Universidad Ricardo Palma, Lima, Peru, 2019. [Google Scholar]
- Wang, K.; Shi, H.; Chen, J.; Li, T. An Improved Operation-Based Reservoir Scheme Integrated with Variable Infiltration Capacity Model for Multiyear and Multipurpose Reservoirs. J. Hydrol. 2019, 571, 365–375. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, J.; Cheng, C.; Cao, H.; Yang, Y. Capacity Configuration of Hydropower-PV Complementary Station That Is Robust to the Inter-Annual Variability in Streamflow and PV Energy. Renew. Energy 2025, 248, 123163. [Google Scholar] [CrossRef]
- Fälth, H.E.; Hedenus, F.; Reichenberg, L.; Mattsson, N. Through Energy Droughts: Hydropower’s Ability to Sustain a High Output. Renew. Sustain. Energy Rev. 2025, 214, 115519. [Google Scholar] [CrossRef]
- Prado, I.G.; de Souza, M.A.; Coelho, F.F.; Pompeu, P.S. Dam Impact on Fish Assemblages Associated with Macrophytes in Natural and Regulated Floodplains of Pandeiros River Basin. Limnol. Rev. 2024, 24, 437–449. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Douglas, E.M.; Fekete, B.M.; Schumann, A.H.; Vörösmarty, C.J. The Significance of Local Water Resources Captured in Small Reservoirs for Crop Production—A Global-Scale Analysis. J. Hydrol. 2010, 384, 264–275. [Google Scholar] [CrossRef]
- Baalousha, H.M. Using Monte Carlo Simulation to Estimate Natural Groundwater Recharge in Qatar. Model. Earth Syst. Environ. 2016, 2, 87. [Google Scholar] [CrossRef]
- Chlost, I. Water Balance of Lake Gardno. Limnol. Rev. 2019, 19, 15–23. [Google Scholar] [CrossRef]
- Gurgiser, W.; Marzeion, B.; Nicholson, L.; Ortner, M.; Kaser, G. Modeling Energy and Mass Balance of Shallap Glacier, Peru. Cryosphere 2013, 7, 1787–1802. [Google Scholar] [CrossRef]
- Rabatel, A.; Francou, B.; Soruco, A.; Gomez, J.; Cáceres, B.; Ceballos, J.L.; Basantes, R.; Vuille, M.; Sicart, J.-E.; Huggel, C.; et al. Current State of Glaciers in the Tropical Andes: A Multi-Century Perspective on Glacier Evolution and Climate Change. Cryosphere 2013, 7, 81–102. [Google Scholar] [CrossRef]
- Sulca, J.; Vuille, M.; Dong, B. Interdecadal Variability of the Austral Summer Precipitation over the Central Andes. Front. Earth Sci. 2022, 10, 954954. [Google Scholar] [CrossRef]
- The Effect of El Niño on Weather in the Andes|GRID-Arendal. Available online: https://www.grida.no/resources/12828 (accessed on 26 April 2025).
- Krois, J.; Schulte, A.; Vigo, E.P.; Moreno, C.C. Temporal and spatial characteristics of rainfall patterns in the Northern Sierra of Peru—A case study for La Niña to El Niño transitions from 2005 to 2010. Espac. Desarro. 2013, 25, 23–48. [Google Scholar]
- Buytaert, W.; De Bièvre, B. Water for Cities: The Impact of Climate Change and Demographic Growth in the Tropical Andes. Water Resour. Res. 2012, 48, W08503. [Google Scholar] [CrossRef]
- Autoridad Administrativa del Agua Mantaro. Estudio de Prospección Batimétrica de la Represa Cuchoquesera; ANA-AAA X MANTARO; ANA—San Juan de Cuchoquesera-Ayacucho: Tokyo, Japan, 2016; p. 30. [Google Scholar]
- Soria-Lopez, A.; Sobrido-Pouso, C.; Mejuto, J.C.; Astray, G. Assessment of Different Machine Learning Methods for Reservoir Outflow Forecasting. Water 2023, 15, 3380. [Google Scholar] [CrossRef]
- Castro-Diaz, L.; García, M.A.; Villamayor-Tomas, S.; Lopez, M.C. Impacts of Hydropower Development on Locals’ Livelihoods in the Global South. World Dev. 2023, 169, 106285. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Sayed, S.; Abdoulhalik, A.; Moutari, S.; Oyedele, L. Applications of Machine Learning to Water Resources Management: A Review of Present Status and Future Opportunities. J. Clean. Prod. 2024, 441, 140715. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L.; Torres-Rua, A.; McKee, M. Assessment of Optimal Irrigation Water Allocation for Pressurized Irrigation System Using Water Balance Approach, Learning Machines, and Remotely Sensed Data. Agric. Water Manag. 2015, 153, 42–50. [Google Scholar] [CrossRef]
- Moncada, W.; Pereda, A.; Masías, M.; Lagos, M.; Portal-Quicaña, E.; Aldana, C.; Saavedra, Y.; Saavedra, E. Estimation of Soil Moisture of a High Andean Wetland Ecosystem (Bofedal) with Geo-Radar Data and In-Situ Measurements, Ayacucho—Peru. Int. Soil Water Conserv. Res. 2024, 13, 122–133. [Google Scholar] [CrossRef]
- Moncada, W.; Willems, B. Spatial and Temporal Analysis of Surface Temperature in the Apacheta Micro-Basin Using Landsat Thermal Data. Rev. Teledetección 2020, 57, 51–63. [Google Scholar] [CrossRef]
- Mathematical and Machine Learning Models for Groundwater Level Changes: A Systematic Review and Bibliographic Analysis. Available online: https://www.mdpi.com/1999-5903/14/9/259 (accessed on 28 April 2025).
- Osso Rodríguez, M.C.; Cabrales Arevalo, S.; Rosso Murillo, J.W. Diseño metodológico para la simulación del balance hídrico de una represa: Caso Tunja, Colombia. Rev. Científica 2017, 29, 230–248. [Google Scholar]
- Vargas Crispin, W.S.; Montes Raymundo, E.; Castrejón Valdez, M.; Hinojosa Benavides, R.A. Machine Learning como Herramienta para Determinar la Variación de los Recursos Hídricos. Sci. Res. J. CIDI 2021, 1, 56–69. [Google Scholar] [CrossRef]
- Fathian, F.; Mehdizadeh, S.; Kozekalani Sales, A.; Safari, M.J.S. Hybrid Models to Improve the Monthly River Flow Prediction: Integrating Artificial Intelligence and Non-Linear Time Series Models. J. Hydrol. 2019, 575, 1200–1213. [Google Scholar] [CrossRef]
- Marín Vilca, D.G.; Pineda Torres, I.A. Modelo predictivo Machine Learning Aplicado a Análisis de Datos Hidrometeorológicos Para un SAT en Represas. Mater’s Thesis, Universidad Tecnológica del Perú, Lima, Peru, 2019. [Google Scholar]
- Qian, X.; Qi, H.; Shang, S.; Wan, H.; Wang, R. Estimating Distributed Autumn Irrigation Water Use in a Large Irrigation District by Combining Machine Learning with Water Balance Models. Comput. Electron. Agric. 2024, 224, 109110. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Xie, J.F.; Wan, G.C.; Tong, M.S. Single-Step and Multi-Step Time Series Prediction for Urban Temperature Based on LSTM Model of TensorFlow. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 1531–1535. [Google Scholar]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward Improved Predictions in Ungauged Basins: Exploiting the Power of Machine Learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Sang, C.; Di Pierro, M. Improving Trading Technical Analysis with TensorFlow Long Short-Term Memory (LSTM) Neural Network. J. Financ. Data Sci. 2019, 5, 1–11. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Bellos, V. Machine Learning in Assessing the Performance of Hydrological Models. Hydrology 2022, 9, 5. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gobierno Regional de Ayacucho. Proyecto Especial “Rio Cachi”; GORE-Ayacucho: Ayacucho, Perú, 2006; p. 47. [Google Scholar]
- Mitchell, T.M. Machine Learning (McGraw-Hill International Editions Computer Science Series), 1st ed.; McGraw-Hill Education: New York, NY, USA, 1997; ISBN 978-0-07-115467-3. [Google Scholar]
- Raschka, S.; Mirjalilli, V. Aprendizaje Automático con Python; Segunda Edición; MARCOMBO: Barcelona, Spain, 2019; ISBN 978-84-267-2720-6. [Google Scholar]
- Corona, J.C.; Diez, H.G.; Morell, C. Un estudio empírico del modelo de red neuronal MLP para problemas de predicción con salidas múltiples. Ser. CientíFica La Univ. Las Cienc. Inf. Áticas 2020, 13, 1–14. [Google Scholar]
- Myllis, G.; Tsimpiris, A.; Aggelopoulos, S.; Vrana, V.G. High-Performance Computing and Parallel Algorithms for Urban Water Demand Forecasting. Algorithms 2025, 18, 182. [Google Scholar] [CrossRef]
- Torres, J.F.; Martínez-Álvarez, F.; Troncoso, A. A Deep LSTM Network for the Spanish Electricity Consumption Forecasting. Neural Comput. Appl. 2022, 34, 10533–10545. [Google Scholar] [CrossRef]
- Qin, J.; Liang, J.; Chen, T.; Lei, X.; Kang, A. Simulating and Predicting of Hydrological TimeSeries Based on TensorFlow Deep Learning. Pol. J. Environ. Stud. 2018, 28, 795–802. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Singh, V.P.; Cho, K.H. Tensorflow and Keras Programming for Deep Learning. In Deep Learning for Hydrometeorology and Environmental Science; Water Science and Technology Library; Springer International Publishing: Cham, Switzerland, 2021; Volume 99, pp. 151–162. ISBN 978-3-030-64776-6. [Google Scholar]
- Seo, J.Y.; Lee, S.-I. Predicting Changes in Spatiotemporal Groundwater Storage Through the Integration of Multi-Satellite Data and Deep Learning Models. IEEE Access 2021, 9, 157571–157583. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) Based Model for Predicting Water Table Depth in Agricultural Areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Campos Aranda, D.F. Procesos del Ciclo Hidrológico; Universidad Autónoma de San Luis Potosí: San Luis Potosí, Mexico, 1998; ISBN 978-968-6194-44-9. [Google Scholar]
- García-Feal, O.; González-Cao, J.; Fernández-Nóvoa, D.; Astray Dopazo, G.; Gómez-Gesteira, M. Comparison of Machine Learning Techniques for Reservoir Outflow Forecasting. Nat. Hazards Earth Syst. Sci. 2022, 22, 3859–3874. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Singh, V.P. Univariate Streamflow Forecasting Using Commonly Used Data-Driven Models: Literature Review and Case Study. Hydrol. Sci. J. 2018, 63, 1091–1111. [Google Scholar] [CrossRef]
- Ziyad Sami, B.F.; Latif, S.D.; Ahmed, A.N.; Chow, M.F.; Murti, M.A.; Suhendi, A.; Ziyad Sami, B.H.; Wong, J.K.; Birima, A.H.; El-Shafie, A. Machine Learning Algorithm as a Sustainable Tool for Dissolved Oxygen Prediction: A Case Study of Feitsui Reservoir, Taiwan. Sci. Rep. 2022, 12, 3649. [Google Scholar] [CrossRef]
- Workneh, H.A.; Jha, M.K. Utilizing Deep Learning Models to Predict Streamflow. Water 2025, 17, 756. [Google Scholar] [CrossRef]





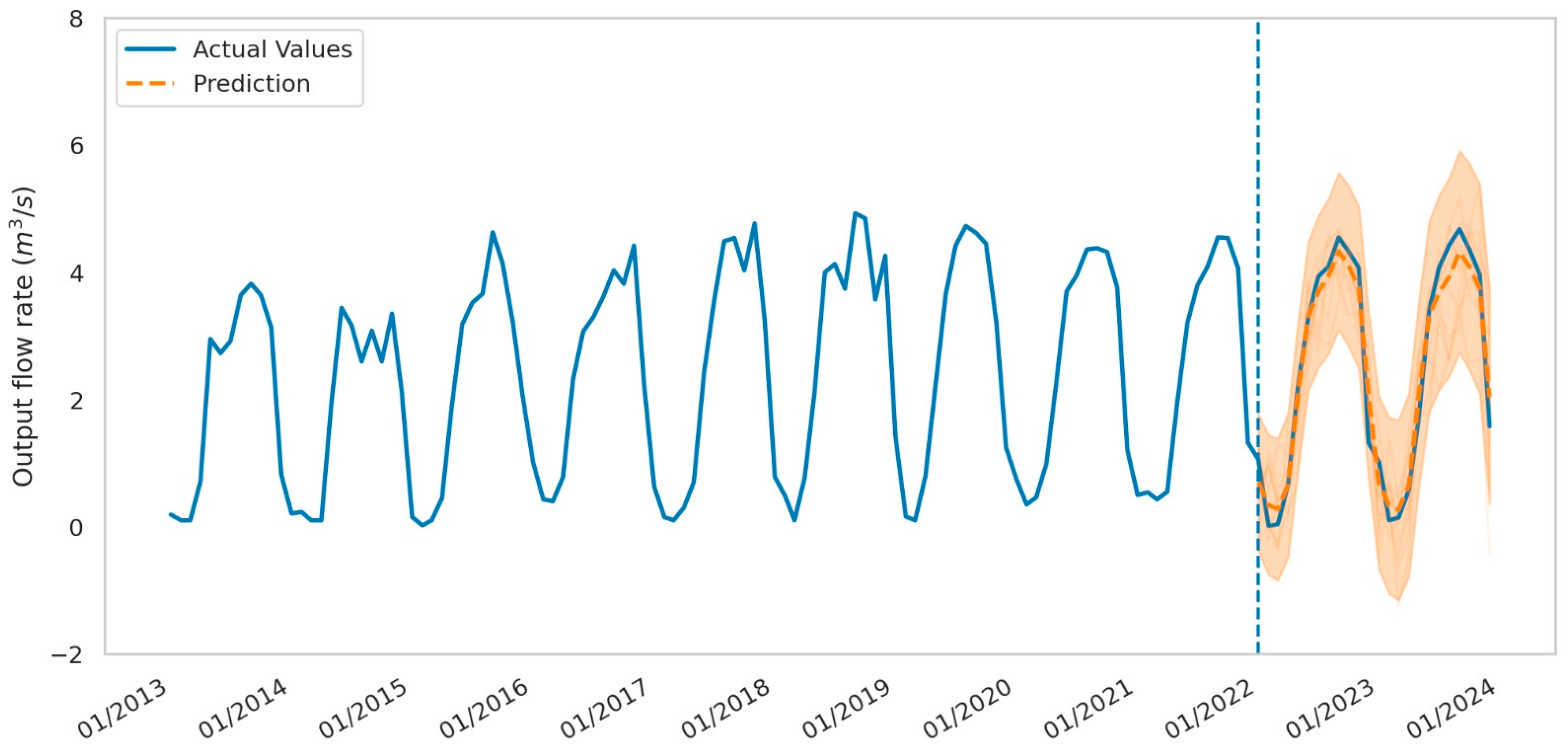
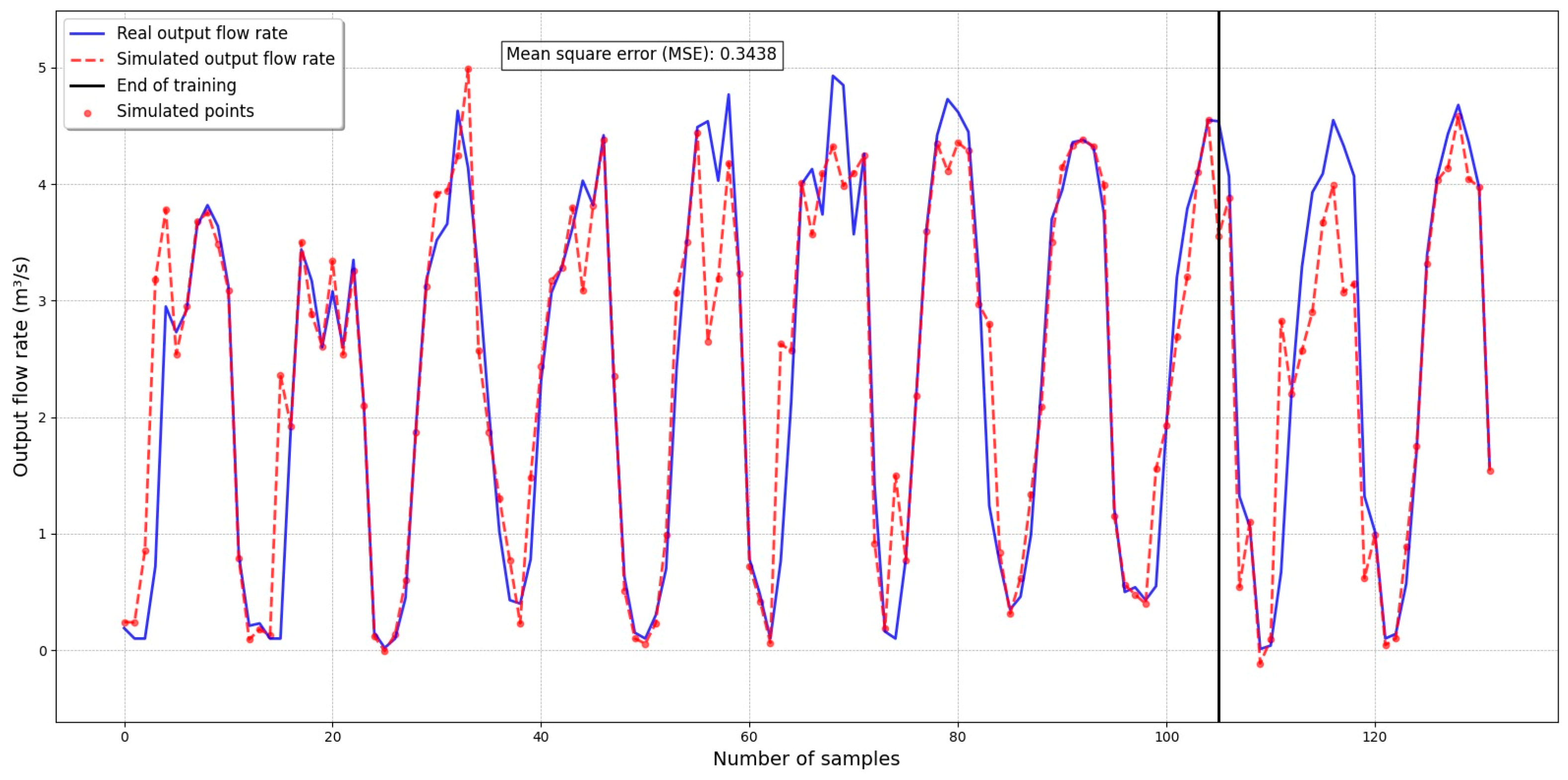

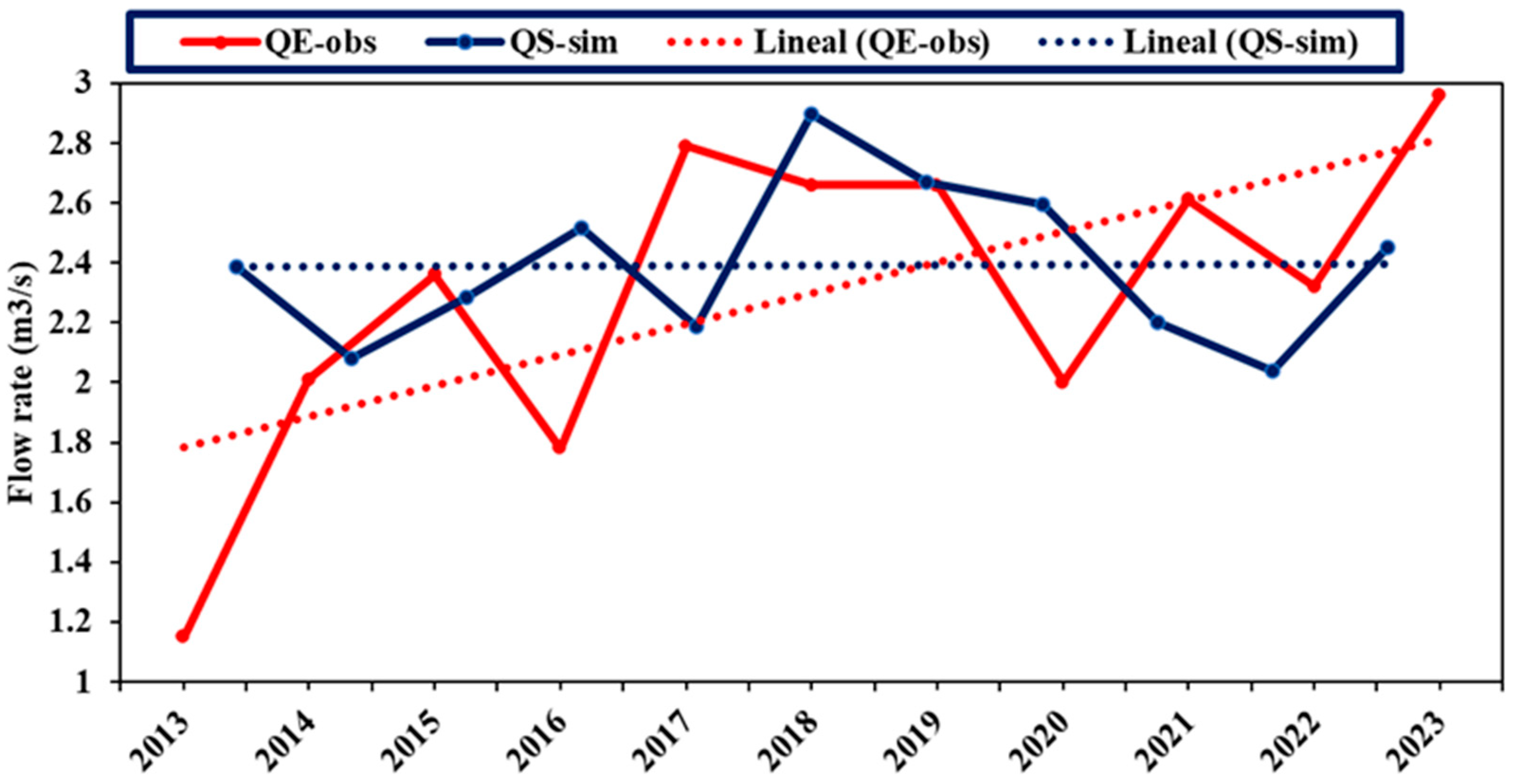
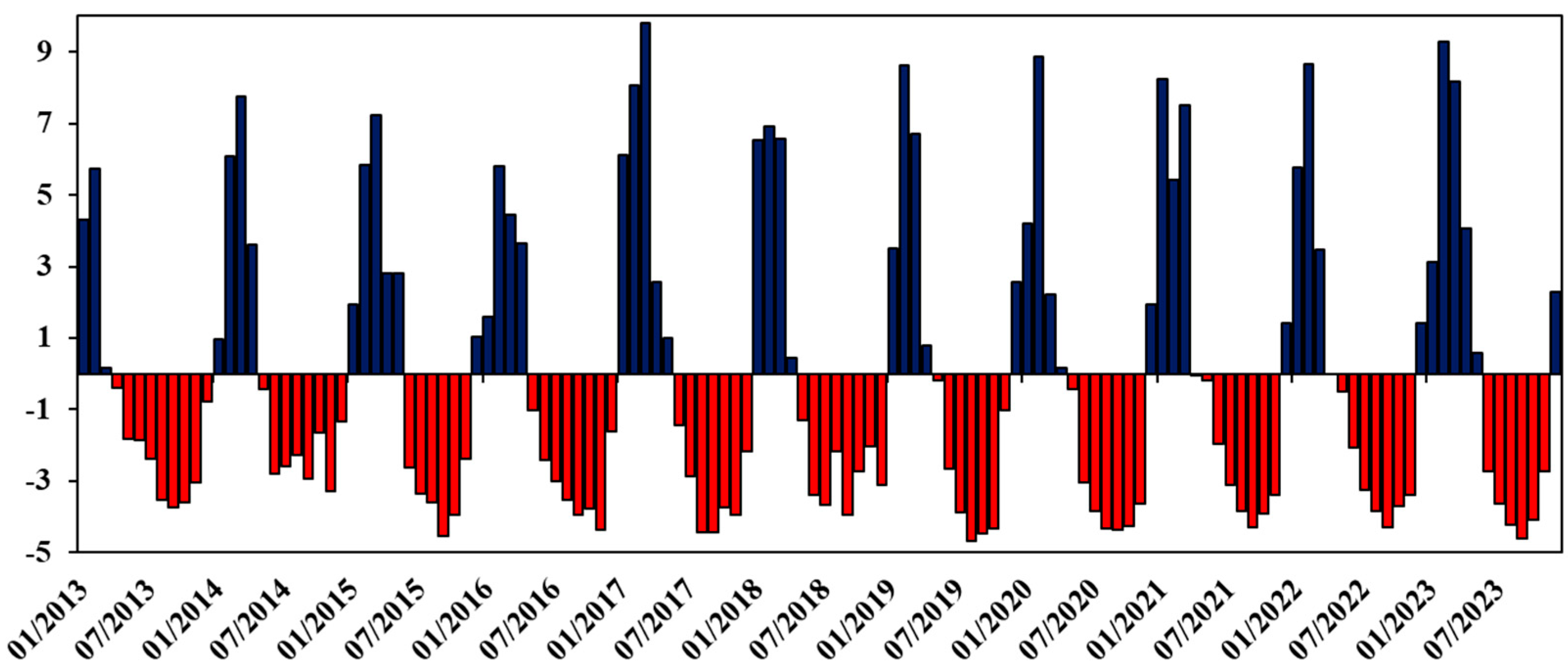

| Article | Description |
|---|---|
| Function | Water storage and supply managed by the Regional Government of Ayacucho, through the Sub-management of Works and the Operations and Maintenance Office (OPEMAN), for treatment and distribution of water for domestic and agricultural uses. |
| Altitude | 3730 m above sea level |
| Total Capacity | 80 million cubic meters |
| Water Use | 18 million cubic meters for drinking water and 42 million cubic meters for agriculture |
| Dam Structure | 42 m structural height and crest length of 390.72 m |
| Bottom outlet (main) | Capacity: 32 m3/s |
| Bottom outlet (auxiliary) | Capacity: 1–8.6 m3/s |
| Spillway capacity | Crest length: 247.70 m Discharge capacity: 9.32 m3/s |
| Parameter | Mean | Std | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|
| Pp (mm) | 65.06 | 68.50 | 0.00 | 9.00 | 41.97 | 109.10 | 293.70 |
| Ev (mm) | 68.39 | 60.40 | 0.00 | 0.00 | 89.30 | 107.10 | 306.90 |
| RH (%) | 79.92 | 17.72 | 0.00 | 78.31 | 81.53 | 85.01 | 100.00 |
| Tamb (°C) | 9.24 | 3.72 | 0.00 | 8.38 | 9.80 | 11.10 | 17.36 |
| QE_obs (m3/s) | 2.30 | 2.71 | 0.01 | 0.29 | 1.00 | 3.57 | 9.89 |
| QS_obs (m3/s) | 2.40 | 1.65 | 0.01 | 0.69 | 2.67 | 3.96 | 4.93 |
| Indicator | Result | Evaluation Range | Ideal Value |
|---|---|---|---|
| Nash–Sutcliffe Efficiency (NSE) | 0.871 | ||
| Nash–Sutcliffe-Ln Coefficient (NSE-Ln) | 0.830 | ||
| Pearson correlation coefficient | 0.935 | ||
| Coefficient of determination (R2) | 0.874 | ||
| Root Mean Squared Error (RMSE) | 0.244 | ||
| Bias-Score (Bs) | 0.999 | ||
| Relative Volume Error (RVB) | 0.005 | ||
| Normalized Peak Value Error (NPE) | 0.010 | ||
| Percentage of relative bias (PBIAS) | 0.143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordero Mancilla, M.A.; Moncada, W.; Silva Alvarado, V.L. A New Machine Learning Algorithm to Simulate the Outlet Flow in a Reservoir, Based on a Water Balance Model. Limnol. Rev. 2025, 25, 29. https://doi.org/10.3390/limnolrev25030029
Cordero Mancilla MA, Moncada W, Silva Alvarado VL. A New Machine Learning Algorithm to Simulate the Outlet Flow in a Reservoir, Based on a Water Balance Model. Limnological Review. 2025; 25(3):29. https://doi.org/10.3390/limnolrev25030029
Chicago/Turabian StyleCordero Mancilla, Marco Antonio, Wilmer Moncada, and Vinie Lee Silva Alvarado. 2025. "A New Machine Learning Algorithm to Simulate the Outlet Flow in a Reservoir, Based on a Water Balance Model" Limnological Review 25, no. 3: 29. https://doi.org/10.3390/limnolrev25030029
APA StyleCordero Mancilla, M. A., Moncada, W., & Silva Alvarado, V. L. (2025). A New Machine Learning Algorithm to Simulate the Outlet Flow in a Reservoir, Based on a Water Balance Model. Limnological Review, 25(3), 29. https://doi.org/10.3390/limnolrev25030029









