The Preference Selection Index (PSI) in Multi-Criteria Decision-Making: A Systematic and Critical Review of Applications, Integrations, and Future Directions
Abstract
1. Introduction
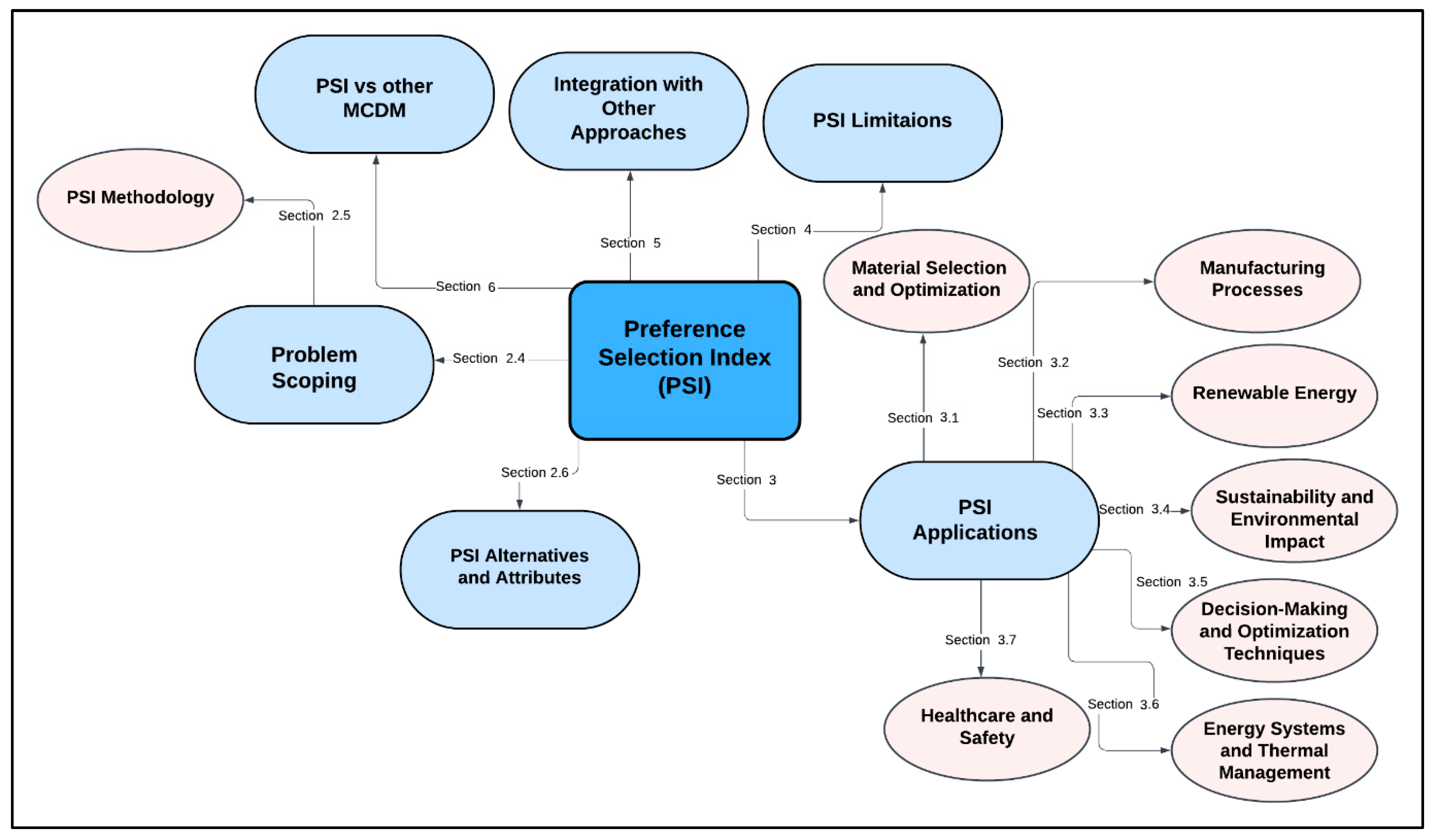
2. Research Methodology
2.1. Background and Objectives
- Defining the PSI applications: This is performed by mapping all areas where PSI has been utilized to help in evaluating different scenarios in various fields. Additionally, highlighting unique adaptations used across various industrial sectors.
- Comparing PSI with the other MCDM methods: This is performed through conducting a comparison between the PSI with other common approaches, aiming to identify situations where the PSI offers specific benefits, and where alternative methods may be more suitable. This will help guide future applications and research.
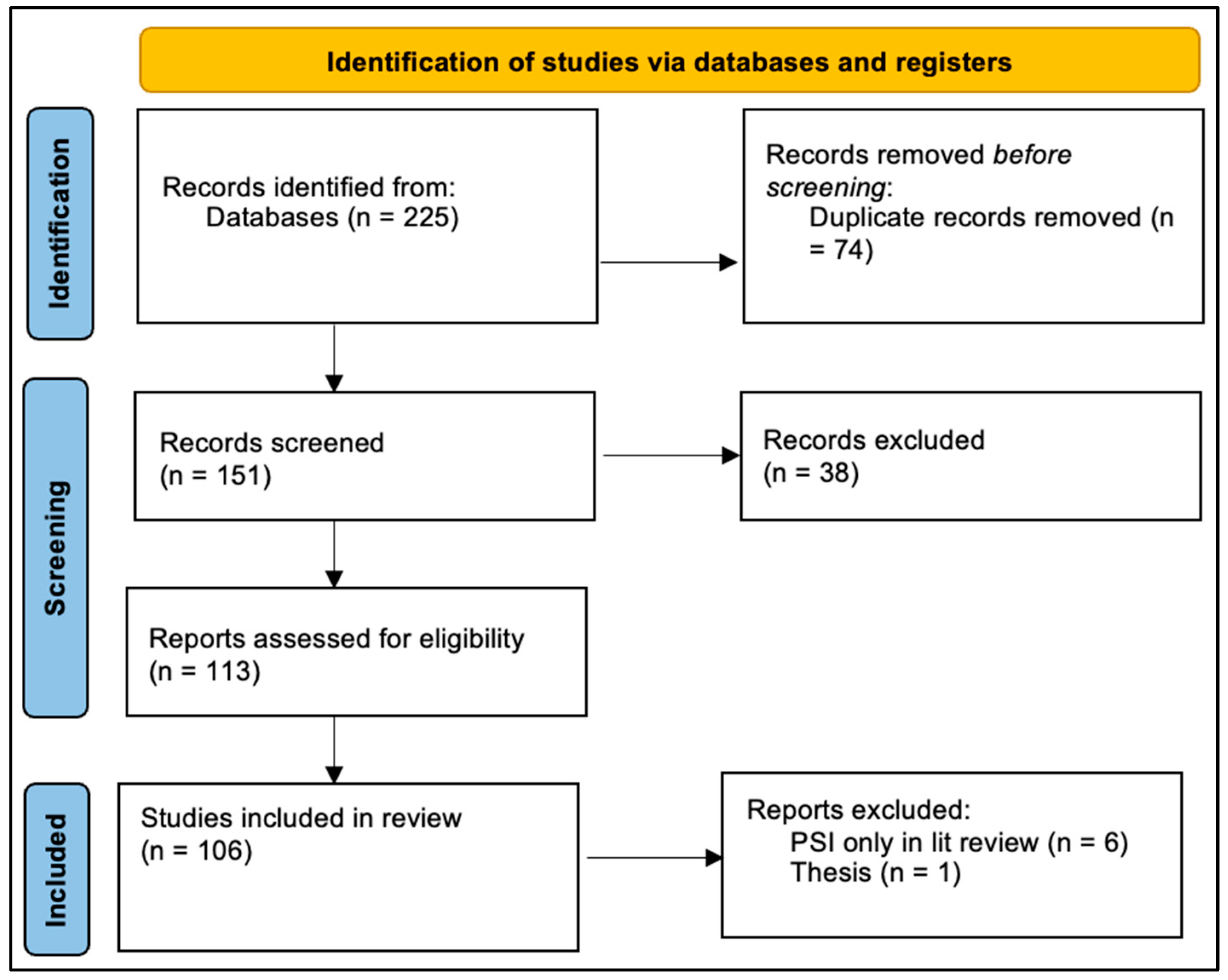
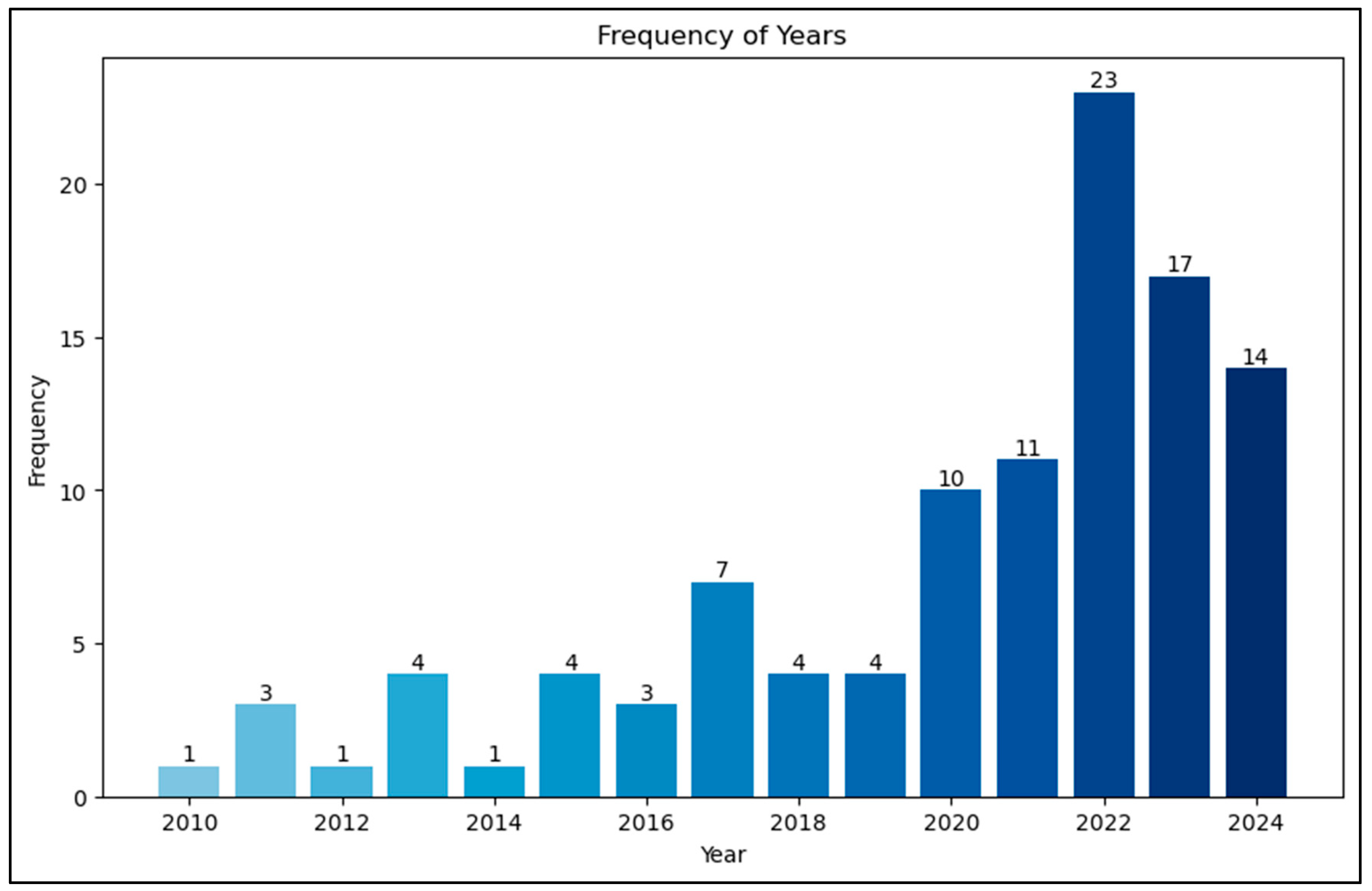
2.2. Bibliographic Search Process
2.3. Inclusion and Exclusion Criteria
- Exclusion Criterion: Chapters, theses, and reports.
2.4. Problem Scoping
- The PSI methodology: It focuses on theoretical and mathematical formulations, especially in steps where the weights of criteria are calculated and used to rank several alternatives.
- The PSI alternatives and attributes: It emphasizes the PSI adaptability for many alternatives and attributes, presenting several challenges in certain decision contexts.
- The PSI applications: It demonstrates the PSI efficiency across various sectors by categorizing the applications into industries, including healthcare, manufacturing, and renewable energy.
- The PSI limitations, integration and comparison with other MCDM techniques: These topics center on the performance of the PSI, starting with its limitations. This can open up opportunities for improvements in methodology or integrating it with other MCDM methods, leveraging the strength of all methods.
2.5. The PSI Methodology
- Step I: The objective is identified, and all related criteria and alternatives are determined for the purpose of deciding the given problem.
- Step II: The decision matrix Xij is constructed as shown in Table 2. For explaining the Xij, let C be a set of decision criteria, where C = {Cj for j = 1, 2, 3, …, m}, A is a set of alternatives, where A = {Ai for i = 1, 2, 3, …, n}, and Xij is representing the performance of alternative Ai under the effect of criterion Cj.
- Step III: The decision matrix data are then normalized; therefore, the values in the decision matrix are transformed into a 0–1 range. In the positive expectancy case (i.e., profit), the normalization is performed using Equation (1):However, in the negative expectancy case (i.e., cost), normalization is performed using Equation (2):where is the attribute measure in the decision matrix (i = 1, 2, 3, …, n and j = 1, 2, 3, …, m).
- Step IV: The preference variation value () is calculated using Equation (3):where is the meaning of the normalized j criteria and computed based on Equation (4):
- Step V: The preference value () deviation () is calculated for every criterion in the matrix using Equation (5):
- Step VI: The overall preference value () is calculated using Equation (6) for each criterion in the decision matrix:It is worth mentioning here that the overall summation of the preference value of all criteria must be one.
- Step VII: The value of the Preference Selection Index () is calculated using Equation (7):
- Step VIII: All the alternatives in the decision matrix are then ranked based on the value, where alternatives with the highest value must be selected first.
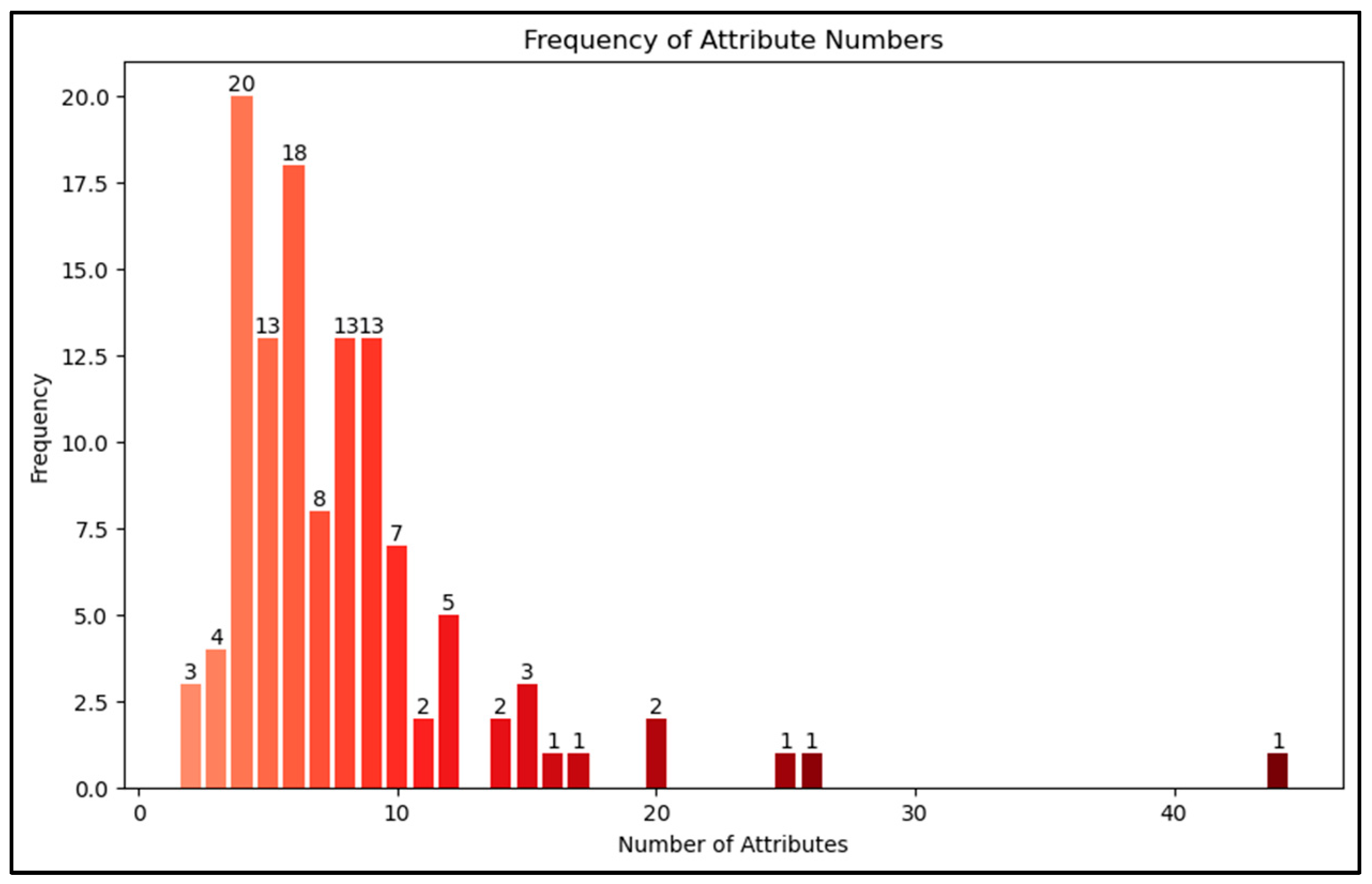
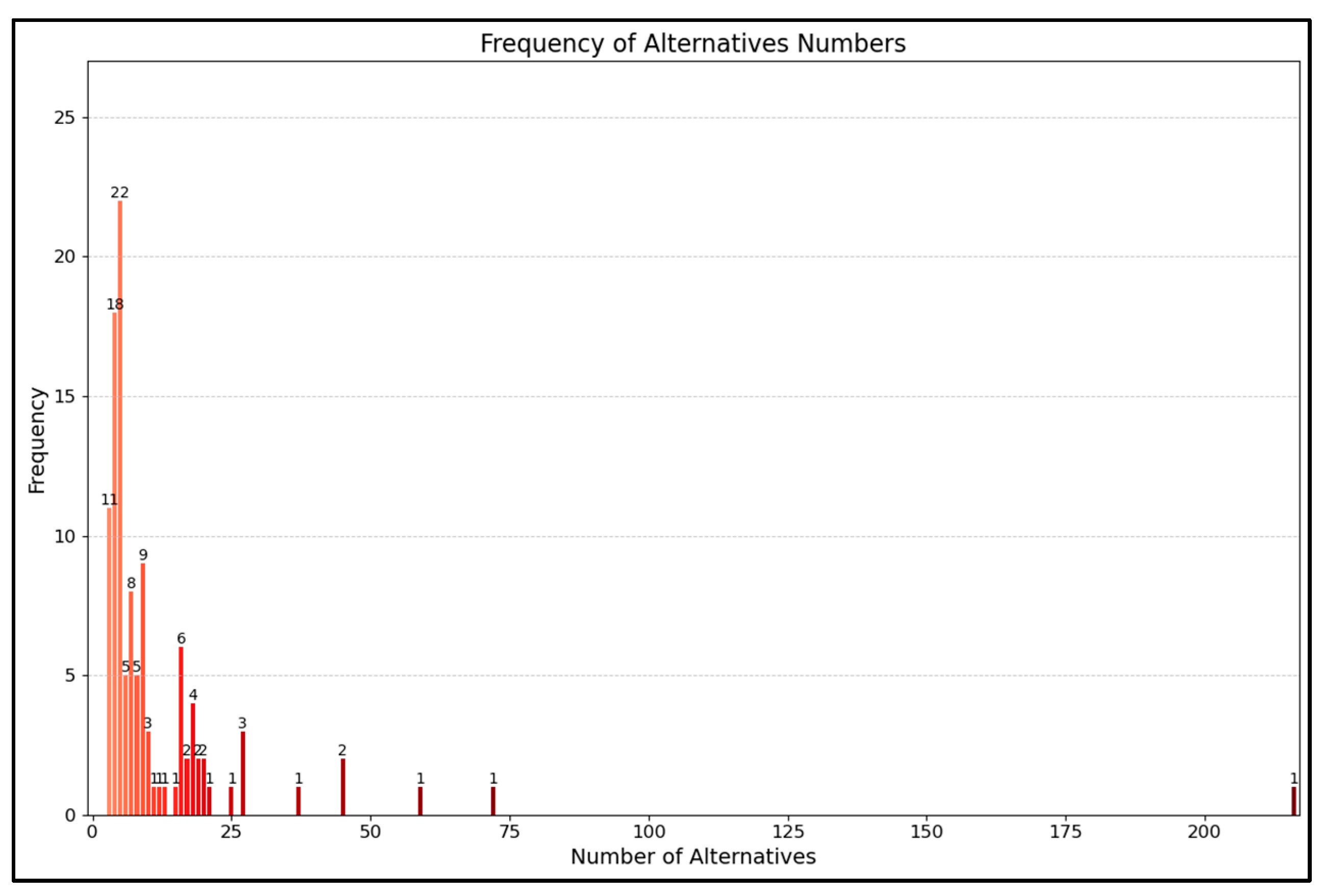
2.6. The PSI Alternatives and Attributes
3. Applications of the PSI
3.1. Material Selection and Optimization
3.2. Manufacturing Processes
3.3. Renewable Energy
3.4. Sustainability and Environmental Impact
3.5. Decision-Making and Optimization Techniques
3.6. Energy Systems and Thermal Management
3.7. Healthcare and Safety
| Article | Main Focus | Application Area |
|---|---|---|
| [5] | Selecting the appropriate material for engineering applications (structural components and wind turbine blades). | Material Selection and Optimization |
| [11] | Choosing the best alternative fuel buses utilizing unique fuzzy multi-criteria decision-making approaches. | Material Selection and Optimization |
| [6] | Using the PSI approach to select materials in engineering applications. | Material Selection and Optimization |
| [12] | Developing a sustainable material selection strategy for automobile bodies and including quantitative sustainability measures. | Material Selection and Optimization |
| [3] | Selecting materials that maximize strength and workability in Al/SiC composites. | Material Selection and Optimization |
| [36] | Optimizing nano-fillers to improve the three-dimensional performance of brake friction materials. | Material Selection and Optimization |
| [37] | Selection of 7075 aluminum alloy composites supplemented with alumina nanoparticles. | Material Selection and Optimization |
| [38] | Evaluating the impact of production procedures on the microstructure and mechanical characteristics of AZ80-0.5Ca-1.5Al203 nanocomposite. | Material Selection and Optimization |
| [39] | Characterizing biodegradable composites and optimizing phase combinations. | Material Selection and Optimization |
| [40] | Improving the selection of marine application materials based on physical, mechanical, and corrosive properties. | Material Selection and Optimization |
| [41] | Evaluating copper-based alloy composites supplemented with marble dust for applicability in bearing applications. | Material Selection and Optimization |
| [42] | Evaluating and optimizing the mechanical characteristics of waste marble dust-filled glass Fiber-Reinforced Polymer Composites. | Material Selection and Optimization |
| [43] | Optimizing nonwoven epoxy composites for better durability and wear resistance | Material Selection and Optimization |
| [44] | A performance-based ranking of ceramic particle-reinforced AA2024 alloy composite materials. | Material Selection and Optimization |
| [45] | Determining the ideal brake friction composite composition. | Material Selection and Optimization |
| [46] | Reviewing material selection for impact-resistant polymer matrix composites, focusing on natural fibers as suitable reinforcements. | Material Selection and Optimization |
| [47] | Optimizing the sliding and mechanical properties of a Ti/Ni metal powder particle-reinforced Al 6061 alloy composite. | Material Selection and Optimization |
| [48] | Focusing on the development and mechanical characterization of innovative polymer-based flexible composites and stacking sequence optimization. | Material Selection and Optimization |
| [49] | Optimizing material selection for ship bodies using manufactured zirconium dioxide and silicon carbide-filled aluminum hybrid metal alloy composites. | Material Selection and Optimization |
| [50] | Selecting the best material for suspension coil springs. | Material Selection and Optimization |
| [51] | Selecting the optimal formulation of various fillers for dental composites. | Material Selection and Optimization |
| [52] | Improving the selection of ceramic particulate-reinforced dental restorative composite materials. | Material Selection and Optimization |
| [53] | Focusing on the anti-fatigue lightweight design of heavy tractor frames. | Material Selection and Optimization |
| [54] | Examining the impact of various copper (Cu) and zinc (Zn) compositions in brass on the fade and recovery behavior of phenolic-based friction composites used in brakes. | Material Selection and Optimization |
| [55] | Optimizing material selection for Fiber-Reinforced Polymer Composites (FRPCs) in multi-layered armor systems. | Material Selection and Optimization |
| [56] | Selecting the best waste marble dust-filled sustainable polymer composite. | Material Selection and Optimization |
| [57] | Evaluating the tribological behavior of chemically modified Jatropha oils as bio-lubricants in a boundary lubrication regime. | Material Selection and Optimization |
| [58] | Investigating the influence of Ghatti gum content on the mechanical characteristics of epoxy composites. | Material Selection and Optimization |
| [59] | Evaluating the physical, mechanical, and sliding wear properties of ZA27-Gr alloy composites. | Material Selection and Optimization |
| [60] | Optimizing frame weight while retaining structural integrity and performance. | Material Selection and Optimization |
| [13] | Optimizing the wear characteristics of ceramic coatings, especially Cr2O3/TiAlN. | Material Selection and Optimization |
| [14] | Modeling and optimization of hybrid Kevlar/glass fabric-reinforced polymer composites to improve impact resistance in low-velocity applications. | Material Selection and Optimization |
| [61] | Optimizing and ranking the mechanical and tribological characteristics of the AA2024 alloy. | Material Selection and Optimization |
| [9] | Selecting the best facility layout design. | Manufacturing Processes |
| [15] | Selecting autonomous guided vehicles. | Manufacturing Processes |
| [16] | Enhancing the traditional SMED method to save setup time in manufacturing operations. | Manufacturing Processes |
| [62] | Evaluating the optimal production system design. | Manufacturing Processes |
| [63] | Evaluating layout options to improve an industry’s performance. | Manufacturing Processes |
| [17] | Optimizing process parameters for laser cutting stainless steel to improve multiple quality and productivity attributes simultaneously. | Manufacturing Processes |
| [64] | Analyzing facility layout alternatives. | Manufacturing Processes |
| [65] | Selecting optimal process settings for Polylactic Acid FDM, considering the influence on mechanical properties and surface roughness. | Manufacturing Processes |
| [66] | Ranking the performance factors in Flexible Manufacturing Systems (FMS). | Manufacturing Processes |
| [67] | Identifying appropriate three-dimensional scanning process settings to increase the overall quality of reverse-engineered models. | Manufacturing Processes |
| [68] | Evaluating the best 3D printer for producing automotive spoilers. | Manufacturing Processes |
| [69] | Focusing on the parametric analysis and multi-response optimization of laser surface texturing of titanium super alloy. | Manufacturing Processes |
| [70] | Focusing on the multi-objective optimization and experimental investigation of Electro-Discharge cutting (EDM) parameters. | Manufacturing Processes |
| [71] | Optimizing turning processes to produce the minimum surface roughness and maximum material removal rate (MRR). | Manufacturing Processes |
| [72] | Optimizing electrical discharge machining (EDM) process parameters for titanium alloy machining. | Manufacturing Processes |
| [73] | Selecting an appropriate setting for FDM printing techniques. | Manufacturing Processes |
| [74] | Selecting capacity expansion plans in manufacturing. | Manufacturing Processes |
| [75] | Focusing on the selection of the optimal electrical energy equipment. | Energy Systems and Thermal Management |
| [30] | Optimizing the V-down perforated baffled roughened rectangular channel. | Energy Systems and Thermal Management |
| [31] | Optimizing the characteristics of a solar thermal collector with impinging air jets. | Energy Systems and Thermal Management |
| [76] | Prioritizing energy performance in a rectangular channel with impinging air jets. | Energy Systems and Thermal Management |
| [77] | Optimizing the parameters of single arc protrusion ribs in a solar air heater | Energy Systems and Thermal Management |
| [78] | Developing novel heat transfer and pressure loss correlation for solar air heaters with internal conical ring obstacles. | Energy Systems and Thermal Management |
| [79] | Selecting the best cleaning procedure for solar panels (PVs). | Energy Systems and Thermal Management |
| [80] | Improving static voltage stability margin in power systems. | Energy Systems and Thermal Management |
| [81] | Ranking various water desalination systems. | Energy Systems and Thermal Management |
| [82] | Investigating the effect of novel elongated jet hole designs on the thermal efficiency of solar air heaters. | Energy Systems and Thermal Management |
| [83] | Focusing on the energy, economic, environmental, and climatic aspects of a solar combisystem for various consumption usages. | Energy Systems and Thermal Management |
| [84] | Selecting the best settings for a solar heat collector with a dimpled-V pattern roughened surface. | Energy Systems and Thermal Management |
| [85] | Selecting the appropriate phase change material (PCM) for solar adsorption cooling systems (SAC). | Energy Systems and Thermal Management |
| [10] | Designing a multi-stage optimization-based decision-making framework for sustainable hybrid energy systems in the residential sector. | Energy Systems and Thermal Management |
| [29] | Ranking water desalination methods to find the best method for different types of feed water. | Energy Systems and Thermal Management |
| [18] | Focusing on renewable energy policy selection. | Renewable Energy |
| [19] | Focusing on the selection of renewable energy policy. | Renewable Energy |
| [20] | Developing a decision support system to prioritize offshore wind farm sites. | Renewable Energy |
| [27] | Focusing on the influence of various criterion weight strategies in the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method of multi-criteria decision-making. | Decision-Making and Optimization Techniques |
| [86] | Focusing on the various criterion decision-making processes in hotel site selection and their relationship to post-purchase consumer feedback. | Decision-Making and Optimization Techniques |
| [87] | Evaluating product concepts using a hybrid approach. | Decision-Making and Optimization Techniques |
| [88] | Evaluating product concepts using a hybrid approach to select the best warehouse site using GPSI and GPIV methods. | Decision-Making and Optimization Techniques |
| [89] | Developing a new hesitant fuzzy ranking model to address the ranking challenge of non-traditional manufacturing processes. | Decision-Making and Optimization Techniques |
| [90] | Assessing students’ performance levels using the Moodle Learning Management System (LMS) based on usability criteria. | Decision-Making and Optimization Techniques |
| [91] | Evaluating traffic solutions in school zones to cut waiting time and increase safety levels. | Decision-Making and Optimization Techniques |
| [92] | Selecting third-party logistics providers. | Decision-Making and Optimization Techniques |
| [93] | Creating a novel multidimensional process type FMEA technique to optimize risk assessments. | Decision-Making and Optimization Techniques |
| [94] | Selecting support systems in underground mines. | Decision-Making and Optimization Techniques |
| [95] | Selecting magnets for permanent magnet synchronous machines (PMSMs). | Decision-Making and Optimization Techniques |
| [26] | Analyzing the potential benefits and applications of ChatGPT as a tool for increasing corporate efficiency and effectiveness. | Decision-Making and Optimization Techniques |
| [96] | Developing a novel technique for group decision-making to deal with data uncertainty and imprecision. | Decision-Making and Optimization Techniques |
| [97] | Developing a revolutionary multi-criteria decision-making and game theory-based framework for sentiment analysis and aspect ranking in customer reviews. | Decision-Making and Optimization Techniques |
| [28] | Evaluating and selecting third-party logistics (3PL) service providers for vehicle manufacturing firms. | Decision-Making and Optimization Techniques |
| [98] | Selecting the best vehicle routing software (VRS) for last-mile delivery companies. | Decision-Making and Optimization Techniques |
| [99] | Benchmarking the country’s supply chain performance. | Decision-Making and Optimization Techniques |
| [100] | Evaluating organization’s digital transformation capabilities (DTC). | Decision-Making and Optimization Techniques |
| [101] | Evaluating crowdfunding projects. | Decision-Making and Optimization Techniques |
| [102] | Ranking European nations using data from the Global Entrepreneurship Monitor (GEM). | Decision-Making and Optimization Techniques |
| [103] | Analyzing the performance and efficiency of European electric vehicles (EVs) in the European Union market. | Decision-Making and Optimization Techniques |
| [25] | Selecting a university for a doctoral program in industrial engineering in the United States. | Decision-Making and Optimization Techniques |
| [21] | Assessing sustainable mining contractor selection challenges. | Sustainability and Environmental Impact |
| [22] | Developing a Sustainable Performance Index (SPI) for self-compacting concretes that use supplementary cementitious materials (SCMs) such as fly ash and GGBS. | Sustainability and Environmental Impact |
| [23] | Investigating recovery options for electrical and electronic waste. | Sustainability and Environmental Impact |
| [104] | Comparing biomass pelleting techniques to determine the most efficient and cost-effective approach. | Sustainability and Environmental Impact |
| [105] | Identifying key challenges to green human resource management (GHRM) adoption in Ghana. | Sustainability and Environmental Impact |
| [106] | The feasibility and impact of employing marble dust as reinforcement in composites for various industrial applications. | Sustainability and Environmental Impact |
| [107] | Evaluating coalfields in Bangladesh for their potential to conduct underground coal gasification (UCG). | Sustainability and Environmental Impact |
| [108] | Identifying the most effective natural fiber for insulating products used in commercial buildings. | Sustainability and Environmental Impact |
| [109] | Evaluating the impact of the COVID-19 pandemic on medical waste disposal. | Sustainability and Environmental Impact |
| [110] | Addressing the hurdles to eliminating illegal gold mining (IGM) in Ghana to suggest sustainable mining practices. | Sustainability and Environmental Impact |
| [111] | Improving the green supplier selection process in the textile sector. | Sustainability and Environmental Impact |
| [24] | Evaluating energy-saving solutions to minimize energy usage and CO2 emissions in healthcare facilities. | Sustainability and Environmental Impact |
| [32] | Investigating the facilitators of resilience in the healthcare supply chain during the COVID-19 pandemic. | Healthcare and Safety |
| [33] | Assessing the possibility of establishing a natural disaster information management open-access repository (NDIM-OAR) in Iran. | Healthcare and Safety |
| [34] | MRI system selection for private hospitals. | Healthcare and Safety |
| [35] | Evaluating road safety performance in the EAS countries. | Healthcare and Safety |
4. PSI Limitations
5. Integration with the Other Decision-Making Approaches
5.1. The PSI Integration with the AHP
- Enhanced accuracy: The integration between both the AHP and PSI, as illustrated in [16,75], modifies the weakness of PSI in the case of evaluating complex scenarios through the facilitation of criteria weighing and prioritization. Therefore, the PSI–AHP integration provides more accuracy when making decisions.
- Robust decisions framework: Applying both the AHP and PSI techniques would enable a more resilient decision-making process, especially when selecting materials or in turbulent industrial applications and environments [54]
- Focused and efficient analysis: According to [25], the application of AHP was practical in managing many alternatives and attributes when PSI was used in the selection of a PhD program in industrial engineering at U.S. universities. This made the comprehensive AHP method less demanding, ultimately resulting in improvement in the overall reviews for decision-making.
5.2. The PSI Integration with the TOPSIS
- Enhanced decision accuracy: Integrating the PSI with the TOPSIS, as mentioned in [9,15], aims at reducing the PSI limitations when facing complex environments. This helps increase the accuracy of the decision-making process, as, on the one hand, there is the use of the TOPSIS capacity for determining the proximity of each option to the optimal solution, which complements the PSI approach.
- Comprehensive evaluation: Applying both the TOPSIS and PSI methods together leads to an even more comprehensive evaluation, which is particularly useful when the differentiation between criterion weights is crucial. As a result, the use of TOPSIS and PSI can be helpful when selecting materials for marine purposes, as, for instance, depicted in [40].
- Robustness in complex environments: Combining both the PSI and the TOPSIS is described by [16] for the utilization in industrial environments and minimizing the setup time in the processes. This methodology effectively performs a structured analysis considering multiple overlapping and interacting factors.
- Handling complexity and uncertainty: In their research, ref. [27] provided sufficient empirical evidence to show how the TOPSIS application with intuitionistic fuzzy data efficiently manages fuzzy data and enhances the decision-making results.
5.3. Integration of the PSI with the Fuzzy Set Theory
- Handling of uncertainties and vagueness: Modifications were introduced by [11] for improving the PSI under fuzzy environments, to augment its applicability in various decision-making scenarios. This improvement enables the PSI to address language complexities and noise data, which is often evident in real-world conditions.
- Robust decision framework: According to the study by [21], applying fuzzy techniques, including the Hesitant Fuzzy Preference Selection Index (HFPSI), improves the robustness and reliability of decision-making models. This technique is very useful, especially in fields such as mining, which require making decisions under conditions of risk and uncertainty.
- Comprehensive decision-making: In the study by [19], in which they integrated hesitant fuzzy sets to improve the accuracy of the decision-making process in conjunction with the PSI in the case of uncertainty. This allowed for a more comprehensive examination of multiple characteristics and viewpoints, which is beneficial, especially when working in complex scenarios such as energy policy.
5.4. Integration of the PSI with the Entropy Method
- Objective criteria weighting: The entropy method’s ability to establish weights based on criteria diversity is crucial for ensuring balanced and data-driven decision-making processes. Chauhan et al. [76] highlighted this in their study on energy systems optimizations.
- Systematic evaluation and risk management: As mentioned in [93], this integration between the PSI and the entropy method is helpful in cases where a detailed examination is required and risk assessment is critical, especially in the aerospace and military sectors. It also guarantees that all the relevant standards are expansively evaluated.
6. Comparing the PSI with Other Decision-Making Approaches
6.1. Comparing the PSI with Graph Theory and Matrix Approach (GTMA)
6.2. Comparing the PSI with the TOPSIS
6.3. The PSI Comparison with the AHP
6.4. The PSI Comparison with the Entropy Method
6.5. The PSI Comparison with the Fuzzy Set Theory
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Siksnelyte-Butkiene, I.; Zavadskas, E.K.; Streimikiene, D. Multi-criteria decision-making (MCDM) for the assessment of renewable energy technologies in a household: A review. Energies 2020, 13, 1164. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Khorshidi, R.; Hassani, A. Comparative analysis between TOPSIS and PSI methods of materials selection to achieve a desirable combination of strength and workability in Al/SiC composite. Mater. Des. 2013, 52, 999–1010. [Google Scholar] [CrossRef]
- Aruldoss, M.; Lakshmi, T.M.; Venkatesan, V.P. A Survey on Multi Criteria Decision Making Methods and Its Applications. Am. J. Inf. Syst. 2013, 1, 31–43. [Google Scholar]
- Maniya, K.; Bhatt, M. A selection of material using a novel type decision-making method: Preference selection index method. Mater. Des. 2010, 31, 1785–1789. [Google Scholar] [CrossRef]
- Chatterjee, P.; Chakraborty, S. Material selection using preferential ranking methods. Mater. Des. 2012, 35, 384–393. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Int. J. Surg. 2010, 8, 336–341. [Google Scholar] [CrossRef]
- Sarkis-Onofre, R.; Catalá-López, F.; Aromataris, E.; Lockwood, C. How to properly use the PRISMA Statement. Syst. Rev. 2021, 10, 117. [Google Scholar] [CrossRef]
- Maniya, K.; Bhatt, M. An alternative multiple attribute decision making methodology for solving optimal facility layout design selection problems. Comput. Ind. Eng. 2011, 61, 542–549. [Google Scholar] [CrossRef]
- Mehmood, A.; Zhang, L.; Ren, J. A multi-stage optimisation-based decision-making framework for sustainable hybrid energy system in the residential sector. Sustain. Futures 2023, 6, 100122. [Google Scholar] [CrossRef]
- Vahdani, B.; Zandieh, M.; Tavakkoli-Moghaddam, R. Two novel FMCDM methods for alternative-fuel buses selection. Appl. Math. Model. 2011, 35, 1396–1412. [Google Scholar] [CrossRef]
- Mayyas, A.T.; Qattawi, A.; Mayyas, A.R.; Omar, M. Quantifiable measures of sustainability: A case study of materials selection for eco-lightweight auto-bodies. J. Clean. Prod. 2013, 40, 177–189. [Google Scholar] [CrossRef]
- Kumar, S.; Maity, S.R.; Patnaik, L. Wear Parameter Optimization of Ceramic Coating Using the Fuzzy Integrated PSI-CODAS Decision-Making Framework. Arab. J. Sci. Eng. 2023, 48, 3819–3841. [Google Scholar] [CrossRef]
- Jambhulkar, T.; Sahu, R. Modelling and optimization of hybrid Kevlar/glass fabric reinforced polymer composites for low-velocity impact resistant applications. Forces Mech. 2024, 15, 100267. [Google Scholar] [CrossRef]
- Sawant, V.B.; Mohite, S.S.; Patil, R. CCIS 145-A Decision-Making Methodology for Automated Guided Vehicle Selection Problem Using a Preference Selection Index Method, Technology Systems and Management. In Technology Systems and Management; Shah, K., Lakshmi Gorty, V.R., Phirke, A., Eds.; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 145. [Google Scholar]
- Almomani, M.A.; Aladeemy, M.; Abdelhadi, A.; Mumani, A. A proposed approach for setup time reduction through integrating conventional SMED method with multiple criteria decision-making techniques. Comput. Ind. Eng. 2013, 66, 461–469. [Google Scholar] [CrossRef]
- Madić, M.; Antucheviciene, J.; Radovanović, M.; Petković, D. Determination of laser cutting process conditions using the preference selection index method. Opt. Laser Technol. 2017, 89, 214–220. [Google Scholar] [CrossRef]
- Vahdani, B.; Mousavi, S.M.; Ebrahimnejad, S. Soft computing-based preference selection index method for human resource management. J. Intell. Fuzzy Syst. 2014, 26, 393–403. [Google Scholar] [CrossRef]
- Mousavi, M.; Gitinavard, H.; Mousavi, S. A soft computing based-modified ELECTRE model for renewable energy policy selection with unknown information. Renew. Sustain. Energy Rev. 2017, 68, 774–787. [Google Scholar] [CrossRef]
- Rong, Y.; Yu, L. Decision Support System for Prioritization of Offshore Wind Farm Site by Utilizing Picture Fuzzy Combined Compromise Solution Group Decision Method. Entropy 2023, 25, 1081. [Google Scholar] [CrossRef] [PubMed]
- Borujeni, M.P.; Gitinavard, H. Evaluating the sustainable mining contractor selection problems: An imprecise last aggregation preference selection index method. J. Sustain. Min. 2017, 16, 207–218. [Google Scholar] [CrossRef]
- Reddy, A.S.; Kumar, P.R.; Raj, P.A. Development of Sustainable Performance Index (SPI) for Self-Compacting Concretes. J. Build. Eng. 2020, 27, 100974. [Google Scholar] [CrossRef]
- Sari, E.B. Recovery alternatives decision by using fuzzy based preference selection index method. Logforum 2020, 16, 171–181. [Google Scholar] [CrossRef]
- Kadric, D.; Blazevic, R.; Bajric, H.; Kadric, E. Evaluation of Energy Renovation Measures for Hospital Buildings using the PSI Method. Eng. Technol. Appl. Sci. Res. 2024, 14, 12753–12758. [Google Scholar] [CrossRef]
- Obeidat, M.S.; Ababneh, W.; Al Theeb, N. The preference selection index performance in large alternatives’ decisions to support the AHP: The case of a university selection. J. Appl. Res. Technol. 2023, 21, 56–72. [Google Scholar] [CrossRef]
- Raj, R.; Singh, A.; Kumar, V.; Verma, P. Analyzing the potential benefits and use cases of ChatGPT as a tool for improving the efficiency and effectiveness of business operations. BenchCouncil Trans. Benchmarks Stand. Eval. 2023, 3, 100140. [Google Scholar] [CrossRef]
- Dammak, F.; Baccour, L.; Alimi, A.M. The Impact of Criterion Weights Techniques in TOPSIS Method of Multi-Criteria Decision Making in Crisp and Intuitionistic Fuzzy Domains’. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Ulutaş, A.; Topal, A.; Görçün, Ö.F.; Ecer, F. Evaluation of third-party logistics service providers for car manufacturing firms using a novel integrated grey LOPCOW-PSI-MACONT model. Expert Syst. Appl. 2024, 241, 122680. [Google Scholar] [CrossRef]
- Obeidat, M.S.; Traini, H. Ranking of Water Desalination Technologies Based on the Preference Selection Index. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Dubai, United Arab Emirates, 10–12 March 2020. [Google Scholar]
- Chamoli, S. Preference selection index approach for optimization of V down perforated baffled roughened rectangular channel. Energy 2015, 93, 1418–1425. [Google Scholar] [CrossRef]
- Chauhan, R.; Singh, T.; Thakur, N.; Patnaik, A. Optimization of parameters in solar thermal collector provided with impinging air jets based upon preference selection index method. Renew. Energy 2016, 99, 118–126. [Google Scholar] [CrossRef]
- Zamiela, C.; Hossain, N.U.I.; Jaradat, R. Enablers of resilience in the healthcare supply chain: A case study of U.S healthcare industry during COVID-19 pandemic. Res. Transp. Econ. 2022, 93, 101174. [Google Scholar] [CrossRef]
- Rashidi, S.; Naghshineh, N.; Nia, F.F.; Izadkhah, Y.O.; Saghafi, F. How feasible is creating a natural disaster information management open-access repository (NDIM-OAR) in Iran? Libr. Inf. Sci. Res. 2022, 44, 101203. [Google Scholar] [CrossRef]
- Kundu, P.; Görçün, Ö.F.; Küçükönder, H. Medical device selection in private hospitals by integrated fuzzy MCGDM methods: A case study in choosing MRI (Magnetic Resonance Imaging) system. J. Oper. Res. Soc. 2022, 73, 2059–2079. [Google Scholar] [CrossRef]
- Chen, F.; Li, Y.; Feng, Q.; Dong, Z.; Qian, Y.; Yan, Y.; Ho, M.S.; Ma, Q.; Zhang, D.; Jin, Y. Road safety performance rating through PSI-PRIDIT: A planning tool for designing policies and identifying best practices for EAS countries. Socio-Econ. Plan. Sci. 2023, 85, 101438. [Google Scholar] [CrossRef]
- Singh, T.; Patnaik, A.; Gangil, B.; Chauhan, R. Optimization of tribo-performance of brake friction materials: Effect of nano filler. Wear 2015, 324-325, 10–16. [Google Scholar] [CrossRef]
- Ezatpour, H.; Parizi, M.T.; Sajjadi, S.; Ebrahimi, G.; Chaichi, A. Microstructure, mechanical analysis and optimal selection of 7075 aluminum alloy based composite reinforced with alumina nanoparticles. Mater. Chem. Phys. 2016, 178, 119–127. [Google Scholar] [CrossRef]
- Parizi, M.T.; Habibolahzadeh, A.; Ebrahimi, G. Optimizing and investigating influence of manufacturing techniques on the microstructure and mechanical properties of AZ80-0.5Ca-1.5Al2O3 nanocomposite. Mater. Chem. Phys. 2017, 199, 485–496. [Google Scholar] [CrossRef]
- Jha, K.; Chamoli, S.; Tyagi, Y.; Maurya, H.O. Characterization of Biodegradable Composites and Application of Preference Selection Index for Deciding Optimum Phase Combination. Mater. Today Proc. 2018, 5, 3353–3360. [Google Scholar] [CrossRef]
- Yadav, S.; Pathak, V.K.; Gangwar, S. A novel hybrid TOPSIS-PSI approach for material selection in marine applications. Sadhana 2019, 44, 58. [Google Scholar] [CrossRef]
- Rajak, S.K.; Aherwar, A.; Unune, D.R.; Mia, M.; Pruncu, C.I. Evaluation of copper-based alloy (C93200) composites reinforced with marble dust developed by stir casting under vacuum environment. Materials 2019, 12, 1574. [Google Scholar] [CrossRef]
- Choudhary, M.; Singh, T.; Sharma, A.; Dwivedi, M.; Patnaik, A. Evaluation of some mechanical characterization and optimization of waste marble dust filled glass fiber reinforced polymer composite. Mater. Res. Express 2019, 6, 105702. [Google Scholar] [CrossRef]
- Singh, T.; Tejyan, S.; Patnaik, A.; Chauhan, R.; Fekete, G. Optimal design of needlepunched nonwoven fiber reinforced epoxy composites using improved preference selection index approach. J. Mater. Res. Technol. 2020, 9, 7583–7591. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. Application of preference selection index method in performance based ranking of ceramic particulate (SiO2/SiC) reinforced AA2024 composite materials. Mater. Today Proc. 2019, 27, 2667–2672. [Google Scholar] [CrossRef]
- Singh, T.; Pattnaik, P.; Pruncu, C.I.; Tiwari, A.; Fekete, G. Selection of natural fibers based brake friction composites using hybrid ELECTRE-entropy optimization technique. Polym. Test. 2020, 89, 106614. [Google Scholar] [CrossRef]
- Mahesh, V.; Joladarashi, S.; Kulkarni, S.M. A comprehensive review on material selection for polymer matrix composites subjected to impact load. Def. Technol. 2021, 17, 257–277. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, M.; Patnaik, A.; Pawar, M.; Pandey, A.; Kumar, A.; Gautam, V. Optimization of sliding and mechanical performance Ti/NI metal powder particulate reinforced Al 6061 alloy composite using preference selection index method. Mater. Today Proc. 2020, 44, 4784–4788. [Google Scholar] [CrossRef]
- Mahesh, V.; Joladarashi, S.; Kulkarni, S.M. Development and mechanical characterization of novel polymer-based flexible composite and optimization of stacking sequences using VIKOR and PSI techniques. J. Thermoplast. Compos. Mater. 2021, 34, 1080–1102. [Google Scholar] [CrossRef]
- Gangwar, S.; Arya, P.; Pathak, V.K. Optimal Material Selection for Ship Body Based on Fabricated Zirconium Dioxide/ Silicon Carbide Filled Aluminium Hybrid Metal Alloy Composites Using Novel Fuzzy Based Preference Selection Index. Silicon 2021, 13, 2545–2562. [Google Scholar] [CrossRef]
- Samant, M.R.; Krisna, S.K.; Khishorre, K.R.; Sreeharan, B. A Systematic Way of using Preference Selection Index Methodology for Selecting Suspension Coil Spring Material. Mater. Today Proc. 2022, 68, 2249–2257. [Google Scholar] [CrossRef]
- Verma, R.; Azam, M.S.; Kumar, S.R. Performance evaluation of glass ionomer and alumina-silica nanoparticle reinforced dental composite using preference selection index. Polym. Compos. 2022, 43, 3745–3752. [Google Scholar] [CrossRef]
- Yadav, R. Fabrication, characterization, and optimization selection of ceramic particulate reinforced dental restorative composite materials. Polym. Polym. Compos. 2022, 30, 09673911211062755. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Kong, D.; Huang, B.; Zhang, Z.; He, Y. The anti-fatigue lightweight design of heavy tractor frame based on a modified decision method. Struct. Multidiscip. Optim. 2022, 65, 280. [Google Scholar] [CrossRef]
- Asrar Ahmed, K.; Rasool Mohideen, S.; Balachandran, S.R.; Sai Balaji, M.A. Varying Cu and Zn composition in brass and its effect on the fade and recovery behavior of the phenolic-based friction composites. Polym. Compos. 2022, 43, 4478–4494. [Google Scholar] [CrossRef]
- Gowda, D.; Bhat, R.; Rajole, S. An Optimization Study on Material Selection for FRPCs in Multi Layered Armour System Through Hybrid MCDM Approach and Numerical Simulation. Mater. Plast. 2022, 59, 205–223. [Google Scholar] [CrossRef]
- Singh, T.; Pattnaik, P.; Shekhawat, D.; Ranakoti, L.; Lendvai, L. Waste marble dust-filled sustainable polymer composite selection using a multi-criteria decision-making technique. Arab. J. Chem. 2023, 16, 104695. [Google Scholar] [CrossRef]
- Rajasozhaperumal, G.; Kannan, C. Comparative evaluation of chemically modified Jatropha oils as sustainable biolubricants in boundary lubrication regime. Tribol. Int. 2023, 186, 108594. [Google Scholar] [CrossRef]
- Nagamadhu, M.; Patil, S.; Kivade, S.; Gunge, A.; Kadhim, K.F. Effect of Ghatti gum content on mechanical properties of epoxy composite using multicriteria optimization techniques. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, M. Investigations on Physical, Mechanical and Sliding Wear Assessment of ZA27 -Gr Alloy Composites Using Preference Selection Index Method. Int. J. Met. 2023, 17, 2818–2835. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, X. Application of the preference selection index method in multi-objective lightweight design of heavy commercial vehicle frames. Eng. Optim. 2023, 55, 1020–1039. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, R.; Bhaskar, S.; Kumar, A. Parametric Optimization and Ranking Analysis of AA2024−Al2O3/AlN Alloy Composites Fabricated Via Stir Casting Route Under Dry Sliding Wear Investigation. Int. J. Met. 2024, 18, 667–687. [Google Scholar] [CrossRef]
- Attri, R.; Grover, S. Application of preference selection index method for decision making over the design stage of production system life cycle. J. King Saud Univ.-Eng. Sci. 2015, 27, 207–216. [Google Scholar] [CrossRef]
- Sharma, P.; Singhal, S. Design and evaluation of layout alternatives to enhance the performance of industry. Opsearch 2016, 53, 741–760. [Google Scholar] [CrossRef]
- Sharma, P.; Singhal, S. Analysis of facility layout alternatives using proposed integrated approach. Opsearch 2017, 54, 1–20. [Google Scholar] [CrossRef]
- Patel, P.B.; Patel, J.D.; Maniya, K.D. Application of PSI Methods to Select FDM Process Parameter for Polylactic Acid. Mater. Today Proc. 2018, 5, 4022–4028. [Google Scholar] [CrossRef]
- Jain, V. Application of combined MADM methods as MOORA and PSI for ranking of FMS performance factors. Benchmarking Int. J. 2018, 25, 1903–1920. [Google Scholar] [CrossRef]
- Pathak, V.K.; Singh, R.; Gangwar, S. Optimization of three-dimensional scanning process conditions using preference selection index and metaheuristic method. Measurement 2019, 146, 653–667. [Google Scholar] [CrossRef]
- Prabhu, S.R.; Ilangkumaran, M.; Mohanraj, T. 3D Printing of automobile spoilers using MCDM techniques. Mater. Test. 2020, 62, 1121–1125. [Google Scholar] [CrossRef]
- Shivakoti, I.; Kalita, K.; Kibria, G.; Sharma, A.; Pradhan, B.B.; Ghadai, R.K. Parametric analysis and multi response optimization of laser surface texturing of titanium super alloy. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 400. [Google Scholar] [CrossRef]
- Patnaik, P.K.; Mishra, S.K.; Swain, P.T.R.; Purohit, A.; Parija, S.K.; Panda, S.S. Multi-Objective optimization and experimental analysis of Electro-Discharge Machining parameters via Gray-Taguchi, TOPSIS-Taguchi and PSI-Taguchi methods. Mater. Today Proc. 2022, 62, 6189–6198. [Google Scholar] [CrossRef]
- Trung, D.D. Multi-criteria decision making of turning operation based on PEG, PSI and CURLI methods. Manuf. Rev. 2022, 9, 9. [Google Scholar] [CrossRef]
- Phan, N.H.; Vu, N.N.; Shirguppikar, S.; Ly, N.T.; Tam, N.C.; Tai, B.T.; Thanh, L.T.P. Multi-criteria decision making in electrical discharge machining with nickel coated aluminium electrode for titanium alloy using preferential selection index. Manuf. Rev. 2022, 9, 13. [Google Scholar] [CrossRef]
- Towaiq, A.; Obaidat, S.; Mumani, A.; Ziout, A. An application of the preference selection index decision making method for parameters selection of FDM printing process. J. Eng. Res. 2024, 13, 636–642. [Google Scholar] [CrossRef]
- Obaidat, S.; Mumani, A. A multiple objective decision analysis model for capacity expansion plans selection in manufacturing. J. Eng. Res. 2024, 13, 480–491. [Google Scholar] [CrossRef]
- Maniya, K.D.; Bhatt, M.G. A Selection of Optimal Electrical Energy Equipment Using Integrated Multi Criteria Decision Making Methodology. Int. J. Energy Optim. Eng. 2013, 2, 101–116. [Google Scholar] [CrossRef]
- Chauhan, R.; Singh, T.; Tiwari, A.; Patnaik, A.; Thakur, N. Hybrid entropy—TOPSIS approach for energy performance prioritization in a rectangular channel employing impinging air jets. Energy 2017, 134, 360–368. [Google Scholar] [CrossRef]
- Nadda, R.; Kumar, R.; Kumar, A.; Maithani, R. Optimization of single arc protrusion ribs parameters in solar air heater with impinging air jets based upon PSI approach. Therm. Sci. Eng. Prog. 2018, 7, 146–154. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, A.; Maithani, R. Development of new correlations for heat transfer and pressure loss due to internal conical ring obstacles in an impinging jet solar air heater passage. Therm. Sci. Eng. Prog. 2020, 17, 100493. [Google Scholar] [CrossRef]
- Obeidat, M.S.; Al Abed Alhalim, M.; Melhim, B.R. Systematic Approach for Selecting a Cleaning Method to Solar Panels Based on the Preference Selection Index Approach. Jordan J. Mech. Ind. Eng. 2020, 14, 279–287. [Google Scholar]
- Kyomugisha, R.; Muriithi, C.M.; Edimu, M. Multiobjective optimal power flow for static voltage stability margin improvement. Heliyon 2021, 7, e08631. [Google Scholar] [CrossRef]
- Obeidat, M.S.; Qasim, T.; Traini, H. The implementation of the preference selection index approach in ranking water desalination technologies. Desalination Water Treat. 2021, 238, 125–134. [Google Scholar] [CrossRef]
- Pazarlıoğlu, H.K.; Tepe, A.Ü.; Tekir, M.; Arslan, K. Effect of new design of elongated jet hole on thermal efficiency of solar air heater. Therm. Sci. Eng. Prog. 2022, 36, 101483. [Google Scholar] [CrossRef]
- Lotfabadi, A.K.; Hajinezhad, A.; Kasaeian, A.; Moosavian, S.F. Energetic, economic, environmental and climatic analysis of a solar combisystem for different consumption usages with PSI method ranking. Renew. Energy 2022, 197, 178–196. [Google Scholar] [CrossRef]
- Priyanka, S.; Kumar, S.; Kumar, A.; Maithani, R. Selection of optimal parameters using PSI approach of a dimpled-V pattern roughened solar heat collector. Mater. Today Proc. 2022, 64, 1229–1233. [Google Scholar] [CrossRef]
- Raj, V.K.; Baiju, V.; Junaid, F.P. Numerical investigations of thermal performance enhancement in phase change energy storage system effective for solar adsorption cooling systems. J. Energy Storage 2022, 45, 103696. [Google Scholar] [CrossRef]
- Aksoy, S.; Ozbuk, M.Y. Multiple criteria decision making in hotel location: Does it relate to postpurchase consumer evaluations? Tour. Manag. Perspect. 2017, 22, 73–81. [Google Scholar] [CrossRef]
- Chen, Z.; Zhong, P.; Liu, M.; Sun, H.; Shang, K. A novel hybrid approach for product concept evaluation based on rough numbers, shannon entropy and TOPSIS-PSI. J. Intell. Fuzzy Syst. 2021, 40, 12087–12099. [Google Scholar] [CrossRef]
- Ulutaş, A.; Balo, F.; Sua, L.; Demir, E.; Topal, A.; Jakovljević, V. A new integrated grey mcdm model: Case of warehouse location selection. Facta Univ. Series Mech. Eng. 2021, 19, 515–535. [Google Scholar] [CrossRef]
- Atalay, K.D.; İç, Y.T.; Keçeci, B.; Yurdakul, M.; Boran, M. Development of a new hesitant fuzzy ranking model for NTMP ranking problem. Soft Comput. 2021, 25, 14537–14548. [Google Scholar] [CrossRef]
- Yorulmaz, M.; Can, G.F. Evaluation of performance levels of students for moodle learning management system in terms of usability Criteria with PSI-Entropy-Marcos integration. Pamukkale Univ. J. Eng. Sci. 2022, 28, 588–603. [Google Scholar] [CrossRef]
- Maghableh, G.; Mumani, A. Simulation Based-MCDM Approach for Evaluating Traffic Solutions. Promet-Traffic Transp. 2022, 34, 117–133. [Google Scholar] [CrossRef]
- Ulutaş, A.; Topal, A. A new hybrid model based on rough step-wise weight assessment ratio analysis for third-party logistics selection. Soft Comput. 2022, 26, 2021–2032. [Google Scholar] [CrossRef]
- USLU, T.; Can, G.; Deli̇̇ce, E.K. A new multidimensional process type FMEA approach: Defense and aerospace industry application. J. Fac. Eng. Arch. Gazi Univ. 2022, 37, 1411–1426. [Google Scholar] [CrossRef]
- Gligorić, M.; Gligorić, Z.; Lutovac, S.; Negovanović, M.; Langović, Z. Novel Hybrid MPSI–MARA Decision-Making Model for Support System Selection in an Underground Mine. Systems 2022, 10, 248. [Google Scholar] [CrossRef]
- Jayaraman, T. Magnet selection for permanent magnet synchronous machines by decision science. Results Mater. 2023, 20, 100495. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, L.; Wan, B. NA Operator-Based Interval-Valued q-Rung Orthopair Fuzzy PSI-COPRAS Group Decision-Making Method. Int. J. Fuzzy Syst. 2023, 25, 198–221. [Google Scholar] [CrossRef]
- Punetha, N.; Jain, G. Aspect and orientation-based sentiment analysis of customer feedback using mathematical optimization models. Knowl. Inf. Syst. 2023, 65, 2731–2760. [Google Scholar] [CrossRef]
- Kara, K.; Yalçın, G.C.; Simic, V.; Gürol, P.; Pamucar, D. Vehicle routing software selection for last mile delivery companies using Fermatean fuzzy-based model. Eng. Appl. Artif. Intell. 2024, 131, 107813. [Google Scholar] [CrossRef]
- Kara, K.; Yalçın, G.C.; Simic, V.; Baysal, Z.; Pamucar, D. The alternative ranking using two-step logarithmic normalization method for benchmarking the supply chain performance of countries. Socio-Econ. Plan. Sci. 2024, 92, 101822. [Google Scholar] [CrossRef]
- Liu, T.; Gao, K.; Rong, Y. Multicriteria group decision-making based on Fermatean fuzzy fairly weighted and ordered weighted averaging operators. Granul. Comput. 2024, 9, 13. [Google Scholar] [CrossRef]
- Wu, M.; Song, J.; Fan, J. Crowdfunding project evaluation based on Fermatean fuzzy SAHARA three-way decision method. Appl. Intell. 2024, 54, 3566–3590. [Google Scholar] [CrossRef]
- Popovic, G.; Fedajev, A.; Mitic, P.; Meidute-Kavaliauskiene, I. An ADAM-based approach to unveiling entrepreneurial ecosystems in selected European countries. Manag. Decis. 2024, 63, 1262–1291. [Google Scholar] [CrossRef]
- Gökgöz, F.; Yalçın, E. Analyzing the Performances and Efficiencies of European Electric Vehicles in the European Union Market Using Decision Analysis Methods. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 1039–1056. [Google Scholar] [CrossRef]
- Tazzit, S.; Hossain, N.U.I.; Nur, F.; Elakramine, F.; Jaradat, R.; El Amrani, S. Selecting a biomass pelleting processing depot using a data driven decision-making approach. Systems 2021, 9, 32. [Google Scholar] [CrossRef]
- Kodua, L.T.; Xiao, Y.; Adjei, N.O.; Asante, D.; Ofosu, B.O.; Amankona, D. Barriers to green human resources management (GHRM) implementation in developing countries. Evidence from Ghana. J. Clean. Prod. 2022, 340, 130671. [Google Scholar] [CrossRef]
- Ror, C.K.; Tejyan, S.; Kumar, N. Effect of marble dust reinforcement in composites for different applications: A review. Mater. Today Proc. 2022, 60, 1120–1124. [Google Scholar] [CrossRef]
- Biswas, A.K.; Islam, R.; Habib, A. An analytical investigation of critical factors to prioritize coalfields for Underground Coal Gasification—Bangladesh case. Heliyon 2023, 9, e18416. [Google Scholar] [CrossRef]
- Ulutaş, A.; Balo, F.; Topal, A. Identifying the Most Efficient Natural Fibre for Common Commercial Building Insulation Materials with an Integrated PSI, MEREC, LOPCOW and MCRAT Model. Polymers 2023, 15, 1500. [Google Scholar] [CrossRef]
- Demir, A.T.; Moslem, S. Evaluating the effect of the COVID-19 pandemic on medical waste disposal using preference selection index with CRADIS in a fuzzy environment. Heliyon 2024, 10, e26997. [Google Scholar] [CrossRef]
- Ampaw, E.M.; Chai, J.; Jiang, Y.; Darko, A.P.; Ofori, K.S. Rethinking small-scale gold mining in Ghana: A holy grail for environmental stewardship and sustainability. J. Clean. Prod. 2024, 437, 140683. [Google Scholar] [CrossRef]
- Pamucar, D.; Ulutaş, A.; Topal, A.; Karamaşa, Ç.; Ecer, F. Fermatean fuzzy framework based on preference selection index and combined compromise solution methods for green supplier selection in textile industry. Int. J. Syst. Sci. Oper. Logist. 2024, 11, 2319786. [Google Scholar] [CrossRef]
- Darko, A.; Chan, A.P.C.; Ameyaw, E.E.; Owusu, E.K.; Pärn, E.; Edwards, D.J. Review of application of analytic hierarchy process (AHP) in construction. Int. J. Constr. Manag. 2019, 19, 436–452. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An in-depth review of theory of the TOPSIS method: An experimental analysis. J. Manag. Anal. 2020, 7, 281–300. [Google Scholar] [CrossRef]
- Maués, L.M.F.; Nascimento, B.D.M.O.D.; Lu, W.; Xue, F. Estimating construction waste generation in residential buildings: A fuzzy set theory approach in the Brazilian Amazon. J. Clean. Prod. 2020, 265, 121779. [Google Scholar] [CrossRef]
- Cui, X.; Zhao, T.; Wang, J. Allocation of carbon emission quotas in China’s provincial power sector based on entropy method and ZSG-DEA. J. Clean. Prod. 2021, 284, 124683. [Google Scholar] [CrossRef]
| Keywords Used for Searching | Science Direct | Web of Science |
|---|---|---|
| “Preference Selection Index” OR “PSI” | 140 | 85 |
| Total | 225 | |
| Alternatives (Ai) | Criteria (Cj) | ||||
|---|---|---|---|---|---|
| C1 | C2 | C3 | … | Cm | |
| A1 | X1×1 | X1×2 | X1×3 | … | X1×m |
| A2 | X2×1 | X2×2 | X2×3 | … | X2×m |
| A3 | X3×1 | X3×2 | X3×3 | … | X3×m |
| … | … | … | … | … | … |
| An | Xn×1 | Xn×2 | Xn×3 | … | Xn×m |
| Limitation | Definition/ Explanation | Studies |
|---|---|---|
| Lack of attribute weighting | The PSI often fails to account for the varying importance of different factors, assuming the same importance, which may not represent actual decision-making scenarios | [5,9,13,22,23,26,32,34,42,48,49,51,53,54,57,60,62,64,66,67,72,75,79,83,85,92,104,107] |
| Simplistic and inflexible approach | The PSI technique may oversimplify complicated decision-making scenarios, possibly missing accurate differences and interrelationships among criteria | [5,9,11,18,21,32,34,40,43,54,68,88,92] |
| Inadequacy in complex or detailed analyses | Although the PSI is valuable for quick assessments, it may not suffice for thorough evaluations in complex situations or accurately distinguishing between closely ranked options, which is crucial for precisely balanced decision-making contexts. | [17,40,78] |
| Inadequate integration with the other decision-making techniques | The PSI may need to integrate other approaches to enhance its analytical capabilities and effectively manage multidimensional data, especially in complex or fluctuating contexts | [35] |
| Oversimplification in multi-criteria decisions | The PSI may place excessive importance on some performance indicators, leading to biased decision results | [53] |
| Real-world applications challenges | Implementing the PSI technique may present specific challenges, particularly in real-life cases, where it is necessary to understand multiple, sometimes even conflicting, factors | [33,57,68] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obeidat, M.S.; Al Sliti, H.; Obeidat, A. The Preference Selection Index (PSI) in Multi-Criteria Decision-Making: A Systematic and Critical Review of Applications, Integrations, and Future Directions. Math. Comput. Appl. 2025, 30, 124. https://doi.org/10.3390/mca30060124
Obeidat MS, Al Sliti H, Obeidat A. The Preference Selection Index (PSI) in Multi-Criteria Decision-Making: A Systematic and Critical Review of Applications, Integrations, and Future Directions. Mathematical and Computational Applications. 2025; 30(6):124. https://doi.org/10.3390/mca30060124
Chicago/Turabian StyleObeidat, Mohammed Said, Hala Al Sliti, and Abdullah Obeidat. 2025. "The Preference Selection Index (PSI) in Multi-Criteria Decision-Making: A Systematic and Critical Review of Applications, Integrations, and Future Directions" Mathematical and Computational Applications 30, no. 6: 124. https://doi.org/10.3390/mca30060124
APA StyleObeidat, M. S., Al Sliti, H., & Obeidat, A. (2025). The Preference Selection Index (PSI) in Multi-Criteria Decision-Making: A Systematic and Critical Review of Applications, Integrations, and Future Directions. Mathematical and Computational Applications, 30(6), 124. https://doi.org/10.3390/mca30060124






