1. Introduction
Institutional corruption, understood as the abuse of public power for private benefit, represents a critical obstacle to socioeconomic development and a threat to democratic governance. In recent years, it has been recognized that stochastic mathematical models—particularly those inspired by epidemic dynamics (SIR-type models)—offer a promising framework to analyze the spread of corruption and to evaluate the impact of anti-corruption policies; see, for example [
1,
2,
3,
4]. These models often incorporate random factors (Brownian or Lévy noise) that capture intrinsic uncertainties, such as the random detection of offenses or variability in the effectiveness of sanctions. The stochastic formulation allows, among other things, the quantification of exit times (i.e., the first hitting times of acceptable corruption levels) via Kolmogorov/Fokker–Planck-type partial differential equations, which are essential to assess the temporal effectiveness of governmental interventions.
In this work, we introduce a novel stochastic model for institutional corruption aimed at evaluating public policies. We start from a framework that explicitly includes policy-related variables such as investment in transparency, ethical education, and legal sanctions. By incorporating Brownian noise into the transition rates, we capture unpredictable variability in the effectiveness of such measures and in the spread of corrupt behavior. Mathematically, this leads to a system of multivariate stochastic differential equations (SDEs). A distinctive feature of our model is the emphasis on exit times of corruption under different policy scenarios. We define a domain of interest D (for instance, high levels of corruption) and compute the first exit time to more acceptable levels. The distribution and density of are obtained analytically from the Kolmogorov/Fokker–Planck equation, whose numerical solution is computed using FreeFEM. This enables, for example, the evaluation of how changes in audit funding or educational campaigns affect the expected time to achieve a “reduction” in corruption.
The proposed formulation addresses several issues identified in the literature; see [
5]. First, it explicitly integrates public policy factors into stochastic dynamics, thereby connecting model parameters to real interventions. Second, by focusing on exit times, it provides a clear temporal metric (rather than purely population-based measures) to assess policy efficiency. Finally, it employs robust numerical methods to solve the PDEs associated with the exit time
.
A central theoretical result of this work arises from the study of the linearization of the system around the deterministic equilibrium. We show that bounds on the second-order moment (the mean square of perturbations) are governed by the spectral structure of the linearized matrix—that is, by its eigenvalues rather than by the magnitude of a single noise term. In particular, the presence of a dominant positive eigenvalue leads to an exponential growth of variability and limits the temporal validity of any linear approximation, rendering its conclusions essentially local in time. Conceptually, this explains why small variations in institutional reactivity parameters or in the effectiveness of sanctions can amplify uncertainty in non-intuitive ways, producing “overcorrection” effects. From a public policy perspective, this suggests that interventions must be designed with the collective interaction of parameters in mind (i.e., the system’s spectral structure), rather than focusing solely on reducing volatility in a single component.
We apply the proposed framework to the case of Mexico and compute exit times numerically for different policy calibrations. The results show that persistence in undesirable states does not depend on a single parameter in isolation but rather on the interaction between institutional laxity, punishment effectiveness, and governmental reactivity: certain combinations can significantly prolong high levels of corruption. Moreover, the volatility of institutional laxity affects exit speed in a non-monotone way: reducing policy uncertainty often accelerates recovery, but excessively reactive responses without effective sanctions may induce overcorrections and increase uncertainty. Based on our analysis for Mexico, we recommend prioritizing interventions that modify the system’s drift (e.g., strengthening the effectiveness of sanctions and implementing institutional reforms that reduce regulatory laxity), rather than relying on random fluctuations; in addition, institutional responses should be graduated to avoid overcorrections that exacerbate uncertainty. It is essential to incorporate time-based metrics derived from exit times to establish realistic policy horizons and evaluation criteria, thereby identifying high-risk parameter combinations. Such measures allow for faster and more robust improvements in reducing corruption while minimizing unpredictable effects stemming from complex interactions among laxity, sanction, and reactivity.
The organization of this paper is as follows. In
Section 2, we present the deterministic model introduced in [
5], which we then perturb randomly.
Section 3 introduces the stochastic dynamics and establishes global existence.
Section 4 studies a linear approximation of the stochastic system.
Section 5 and
Section 6 analyze the exit time through partial differential equations and their numerical solution. Finally, in
Section 7, we apply the model to the case of corruption in Mexico.
7. A Stochastic Model for Corruption in Mexico
In this section, we study the stochastic models developed earlier applied to a real-world problem, namely corruption in Mexico. Using data from the Transparency International and the Global Corruption Index, we compiled
Table 1, which contains information on the perception of corruption in Mexico (see also [
5], where some values are estimated).
As a starting point, we use the information from the year 2022, that is,
. We set
under the assumption that current anti-corruption policies are somewhat lax (see, for example, [
5]). On the other hand, we know that the parameter
in the deterministic case controls the speed of stabilization of the laxity of anti-corruption policies. In view of this, we propose (in concordance with [
5]) a relatively small value,
. The rationale is that policies and social practices generally require some time to be accepted and enforced by the population.
From the data in
Table 1, we also see that the normalized corruption perception index varies very little. Similarly, there is little variability in the proportion of corrupt acts that are reported and sanctioned. This suggests taking the population standard deviations for the parameters
and
; thus,
and
. Our interest lies in the behavior of the stochastic model near the unique asymptotically stable equilibrium of the deterministic system. As argued, this is reasonable for a political system, where stability is expected at least in the medium term, even though some random perturbations occur. Accordingly, we propose values for
considering the population standard deviation of
and
. Moreover, following [
5], we consider the values
and
for the parameter
, and
and
for
. The parameter values are summarized in
Table 2.
Using the initial condition
, Theorem 2 gives
where
The parameter values in
L and
U are provided in
Table 3 for rows 1, 2, and 3 of
Table 2. Row 4 is not considered since no equilibrium point exists for those parameters.
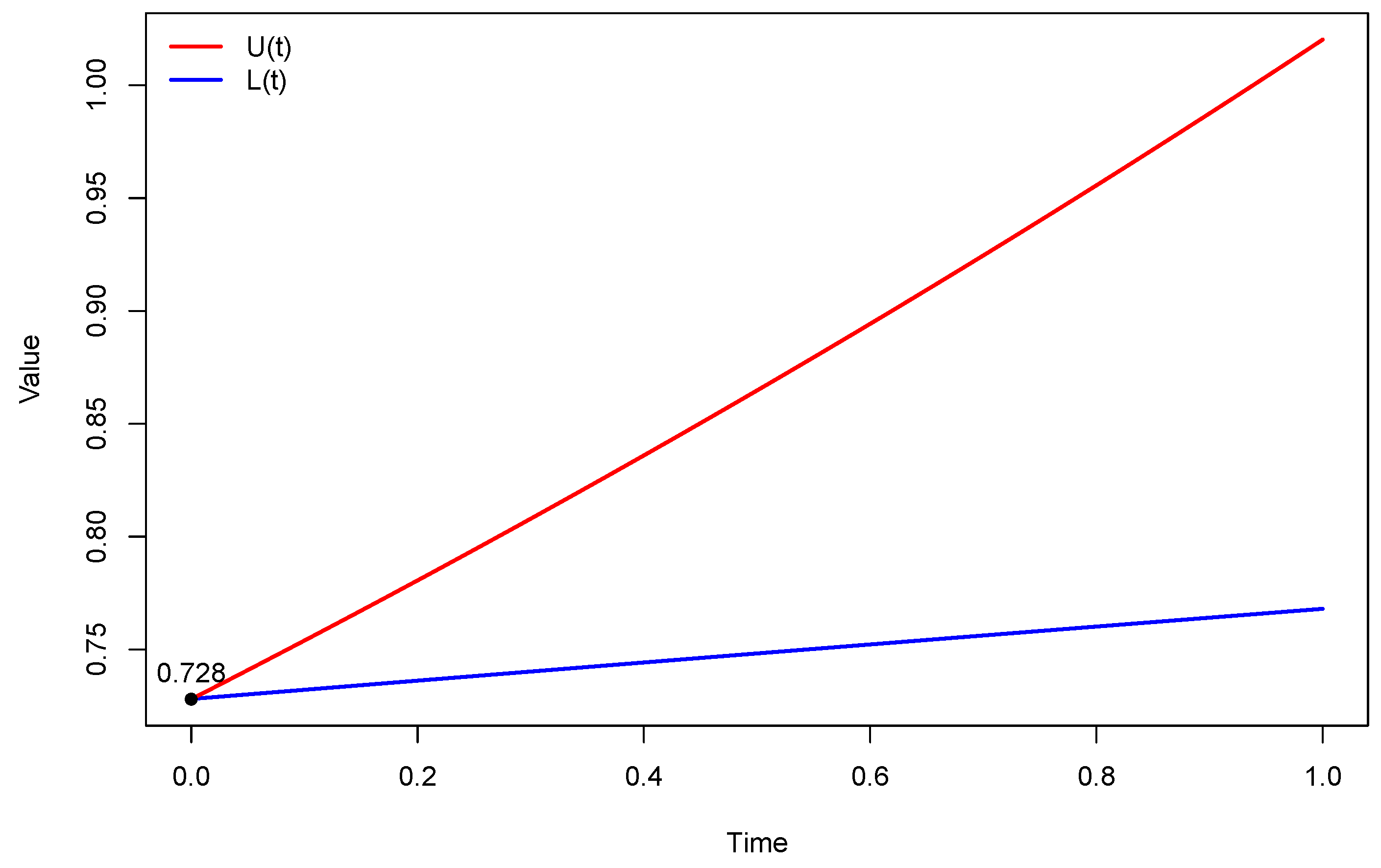
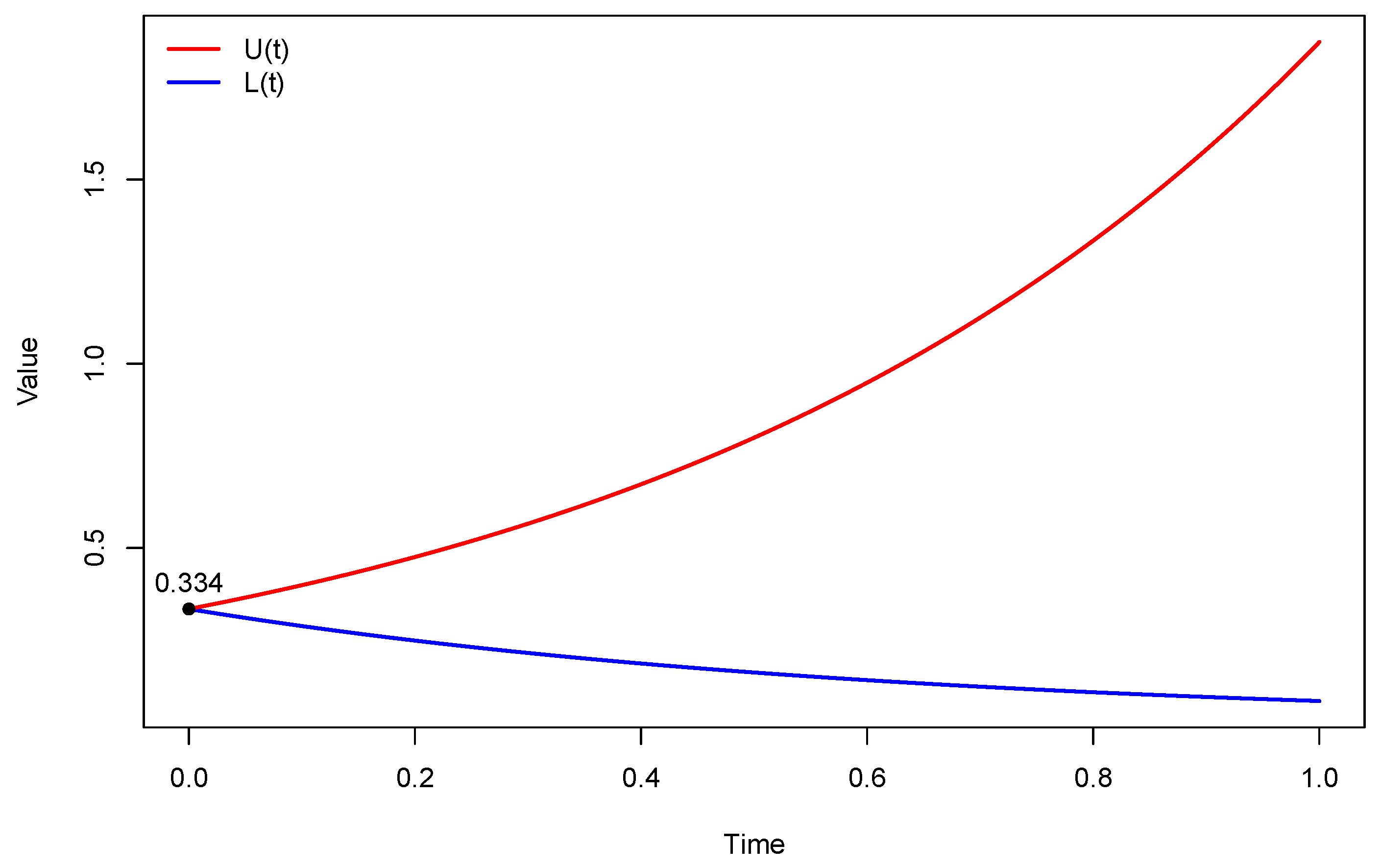
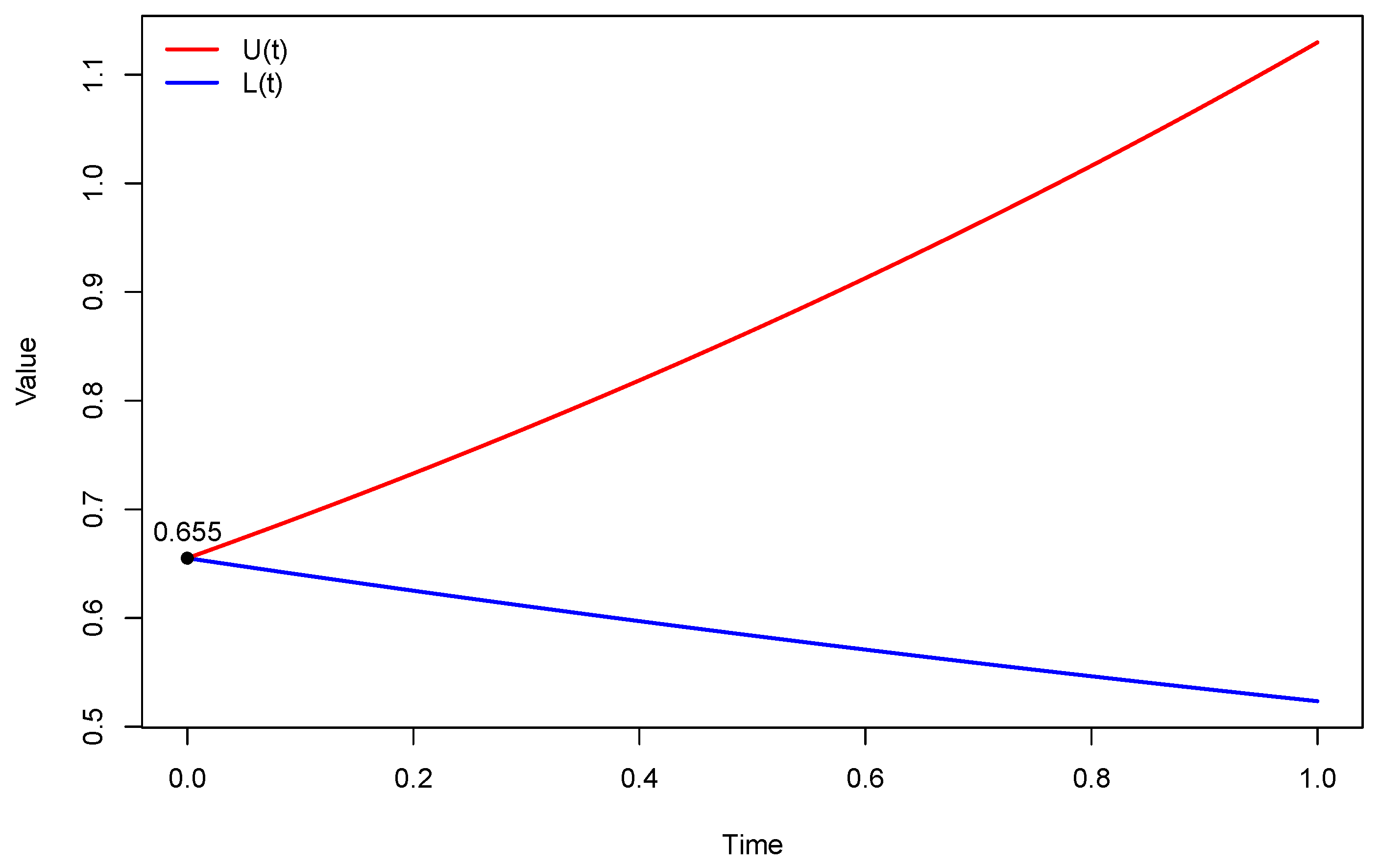
As is well known, linear approximations often provide only local information, but we aim to make the most of it. From
Figure 1,
Figure 2 and
Figure 3, we obtain
Table 4,
Table 5 and
Table 6, respectively. These show that in mean square, the linear approximation has greater dispersion when the parameters of Row 2 are used in the model. Conversely, we observe that the most stable model is obtained for the parameter values in Row 1. This behavior is not at all predictable. Indeed, the parameter values
and
are significantly smaller than
(see
Table 2); therefore, the stochastic behavior (and consequently the mean square error) would be expected to be driven mainly by this parameter. What actually occurs, however, is the opposite: the smaller
is, the larger the “error”.
The resolution of this apparent “paradox” lies in a deeper understanding of the dynamics of the linearized system. The key factor determining the exponential growth rate of the error is not the direct magnitude of the dispersion parameter , but rather the eigenvalues of the matrix M, which, besides , depends on other parameters. Thus, an increase in does not necessarily lead to a significant change in the eigenvalues of M. This result highlights a fundamental fact about complex dynamical systems: their behavior and stability are not linear functions of a single parameter. Instead, they are emergent, collective properties of the nonlinear interplay among all parameters. A small variation in one variable can significantly alter the eigenvalue structure of the system, generating effects that are not intuitively predictable, as in this case.
In what follows, we analyze row by row the parameter values from
Table 2:
- Row 1 (Stability):
With a relatively large
(0.7) and a small
(0.005), the government’s response to corruption is weak. This parameter combination yields an equilibrium point
, which reflects very strict policies. The associated matrix
M has a maximum eigenvalue (
) of 0.2563, the lowest among the three scenarios. As a result, the difference
grows very slowly and in a controlled manner, as shown in
Table 4. In other words, the linearized model remains valid only for a very short period of time.
- Row 3 (Moderate Stability):
Reducing the maximum permissiveness to
while keeping
small (0.005) yields a similarly low equilibrium level of laxity
. Although the volatility parameter
is smaller than in Row 1 (0.36520 vs. 0.38275), the corresponding matrix
M produces a maximum eigenvalue
, which is larger than in Row 1. Therefore, the error growth in
Table 6 is faster than in
Table 4, but still much slower than in Row 2.
- Row 2 (High Instability):
This is the most revealing scenario. With a large
(0.7) and a large
(0.025), the government’s response is much stronger than in the other cases. However, this combination of parameters leads to an equilibrium point with significantly higher laxity
(0.2637). Despite having the lowest value of
(0.26811), this particular equilibrium configuration produces a matrix
M with an exceptionally high maximum eigenvalue (
) of 1.6748. It is precisely this disproportionate eigenvalue that drives the exponential growth of the error, as shown in
Table 5, where the difference
grows explosively over time.
From a public policy perspective, this result suggests that merely intensifying the institutional response to perceived corruption is not sufficient: an overly aggressive response without effective sanctions may increase the observed uncertainty. Therefore, prioritizing the effectiveness of sanctions () and institutional robustness (), while designing graded responses (controlling ), is more effective in stabilizing the dynamics than simply increasing the reaction intensity. Finally, it should be emphasized that the above conclusions stem from the linear approximation around the equilibrium and are therefore valid only locally in time; it is recommended to complement these findings with sensitivity analyses (parameter sweeps in ) and nonlinear simulations to test the robustness of the policy recommendations outside the linear regime.
To study the global behavior of the stochastic system, we now examine the exit times from the following domain:
Since the function
cannot be easily plotted, and noting that the parameter that changes the least over time is
C, we fix
and consider the section
of
D to obtain information about the mean exit time.
Table 7 reports, for each row of parameters from
Table 2, the mean exit time
when starting at
. Moreover,
represents the point
where the expected exit time
attains its maximum in
.
From
Table 7, we observe that the mean exit time is greatest in Row 2, which exhibits the lowest volatility; in this case, the average exit time is
time units. Moreover, the maximum expected exit time is obtained at the point
. This is noteworthy, as it indicates that when the legal system
L tends to tolerate impunity and anti-corruption policies are relatively lax, the system takes longer to exit its boundaries, i.e., to leave
D; see (
22). The longest possible residence time is
time units.
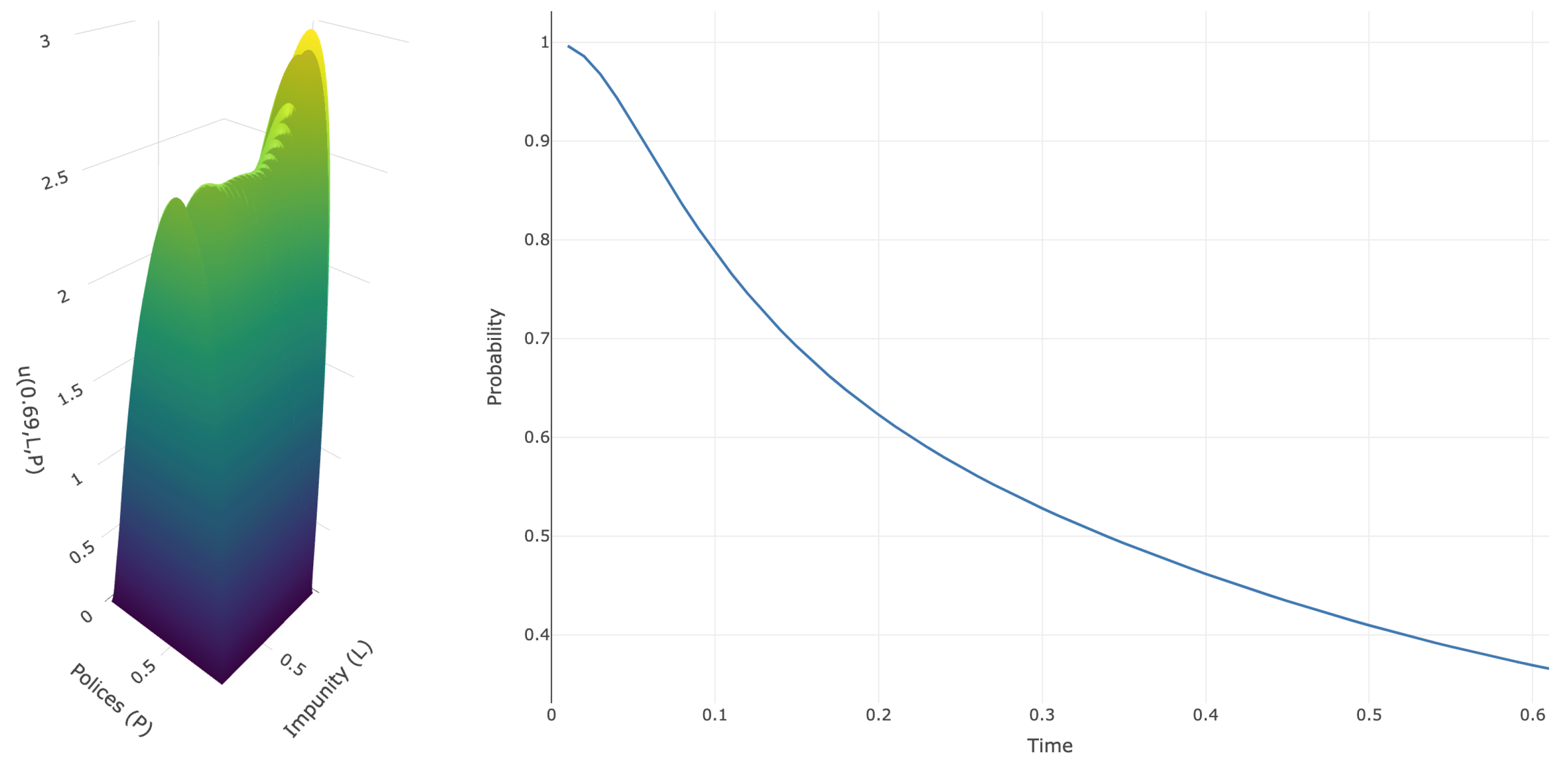
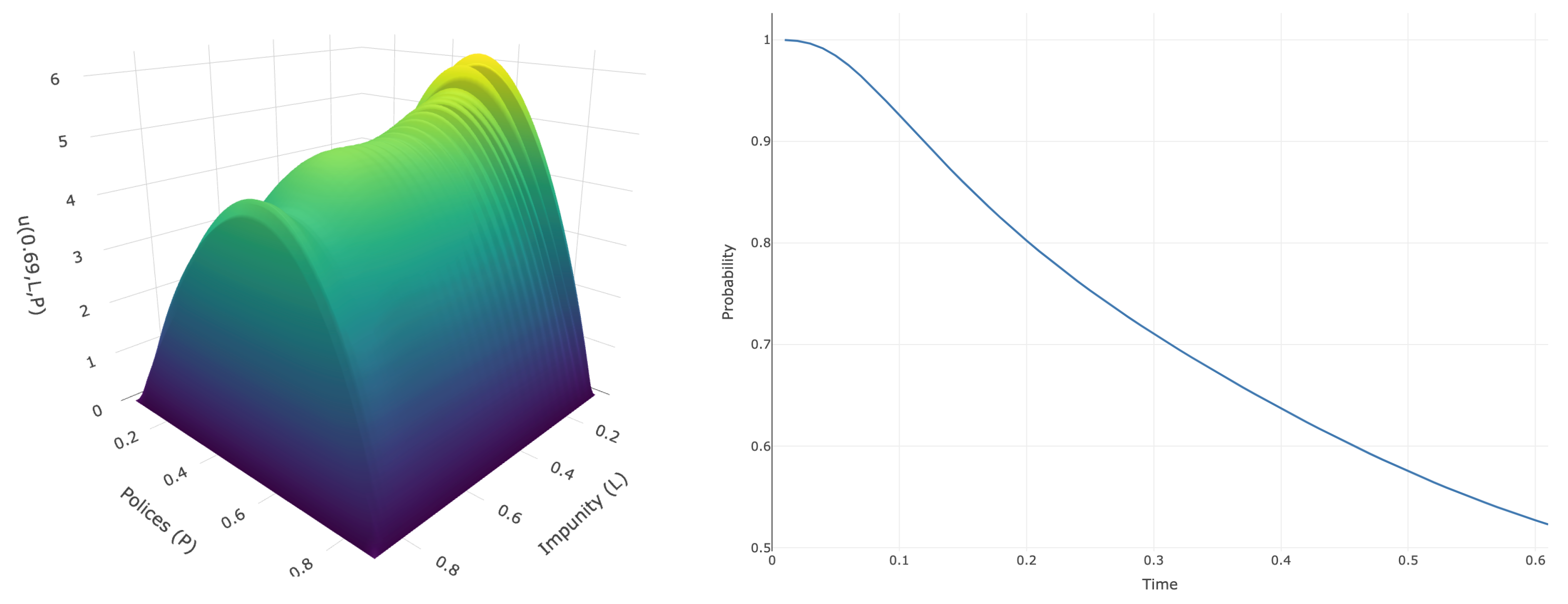
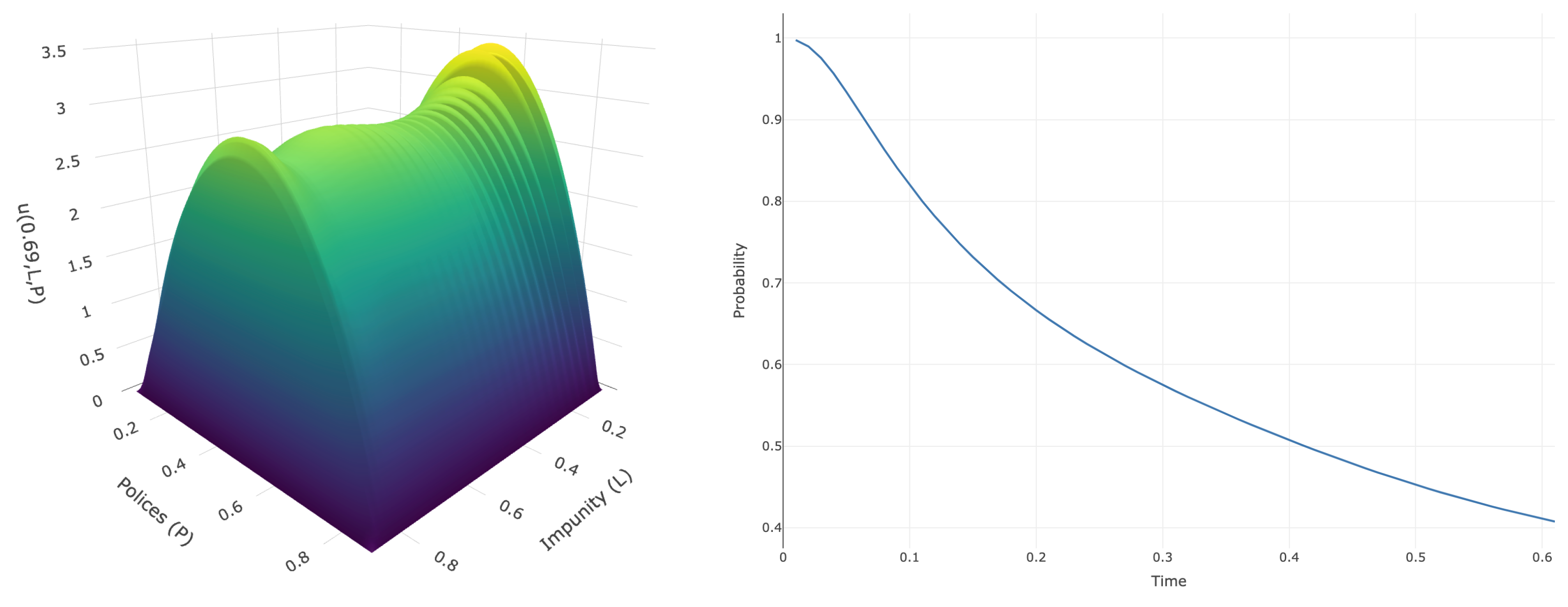
Figure 4,
Figure 5, and
Figure 6 display the plots of the functions
and
, respectively. Using this information, we fill
Table 8 with the values of
for different times and for the three parameter rows of
Table 2.
From
Table 8, we observe that, for short times, the most stable rate of change of
corresponds to Row 2, whereas the greatest variability occurs in Row 1, particularly for
. On the other hand, for longer times (
), there is no monotonic relation, as in the previous cases, with respect to
. Specifically, with lower uncertainty, it is more likely that the dynamics have already left the domain
D, i.e., the process exits faster (
). Conversely, under higher uncertainty—as in Row 1 (
)—the probability of remaining within the domain for a longer time increases.
The analysis carried out above depends only on the initial point
. However, from the first part of
Figure 4,
Figure 5 and
Figure 6, we observe the global behavior of
. Here, we see that the data from Row 1 exhibit a more dramatic behavior: near the boundaries, the function
u is almost 0, and then it increases rapidly. Moreover, we observe that along the
P-sections, the values of
u remain essentially constant in
L, meaning that the influence of
L is relatively marginal. This implies that the expected average exit time from
D is not significantly affected when the perception of corruption and the laxity of anti-corruption policies are fixed.
The evidence also shows that the variable that changes the least over time is the normalized index of corruption perception. Next comes the proportion of corrupt acts that have been prosecuted and sanctioned by law, and finally, the laxity of anti-corruption policies. To confirm this numerically, let us consider the following sets:
In sets
and
, we enlarge by
the margin of set
in the variables
L and
P, respectively. Recall that the initial point is
.
Table 9 shows several expected values of exit times
for the parameters of Row
i.
From
Table 9, we confirm that random perturbations are more pronounced in the variable
P: even a small change in the boundaries, from
to
, produces significant variations in the mean exit time, and this holds for all three parameter rows. Furthermore, the same table shows that this behavior is indeed related to the value of
: the smaller the value of
, the larger the expected exit time. For this model, this indicates that greater volatility leads to a faster exit from the domain of interest, which in this case agrees with intuition. In terms of the corruption model, we may conclude that the laxity of anti-corruption policies is strongly affected if the normalized index of corruption perception is modified.
It is worth noting that there is no contradiction with the observations from the linearized model, since both reflect different aspects of the dynamics. The linear approximation around evaluates local stability (growth of the mean squared error) and is dominated by the eigenvalues of matrix M, which depend on the interaction of all parameters. In contrast, the exit time analysis from D examines the global behavior under noise: greater volatility in induces stronger fluctuations that, on average, drive the system out of the domain more quickly. Hence, a larger accelerates the global exit without necessarily implying a proportional increase in the eigenvalues of M (and thus in local instability). In summary, local stability around (governed by the eigenvalues of M) and the global exit speed from D (influenced by ) are distinct but coherent aspects of the model.
From a public policy perspective, these findings highlight the importance of distinguishing between local stability and global resilience of the system. A context of high volatility in the laxity of anti-corruption policies ( large) implies that, although the system may appear locally stable around the equilibrium , in practice, it will exit the admissible domain D more quickly, leading to recurrent fluctuations in governance quality. Thus, effective policy design should not only aim at reducing immediate instability (through adjustments in or ) but also at containing long-term volatility by strengthening institutional capacity to sustain consistent enforcement. In other words, anti-corruption strategies should combine robust sanction mechanisms with mechanisms that minimize the dispersion in policy responses, thereby ensuring both local stability and global durability of the system’s dynamics.