Quantized Control of Switched Systems with Partly Unstabilizable Subsystems and Actuator Saturation

Abstract

This paper solves the stabilization problem of the continuous-time switched systems with partly unstabilizable subsystems subject to actuator saturation and data quantization. The static quantizer is designed by properly restraining the density of the finite partition. The relationship between an ellipse and a polyhedral is established and a suitable expression for the controller suffered by data quantization and actuator saturation is obtained. By defining the attraction domain and the invariant set based on the union or intersection of ellipses, we guarantee the decrement of the Lyapunov function in the optimal case if the state is within a given annular area. On this basis, if average dwell time and activation time of stabilizable subsystems meet some constraints, we derive that every trajectory whose initial state is within the given region will fall into a small ellipsoid and stay in a slightly larger ellipsoid. An illustrative example is given to verify the validity of the theoretical analysis.

1. Introduction

Switched systems have received extensive attention since many actual systems are essentially multi-modal, such as servo mechanism systems, manipulator robots, power electronics systems, flight control systems, etc. [1,2,3,4]. The research motivation of this paper stems from three key engineering challenges in the switched systems: (1) partially unstabilizable subsystems: practical switched systems often contain subsystems that cannot be stabilized inherently, necessitating specialized control approaches; (2) networked constraints: bandwidth limitations in networked systems require quantized control methods to handle data transmission efficiently [5]; (3) actuator saturation: widespread saturation nonlinearities due to physical constraints demand stability-preserving controller designs. By addressing the mode mismatch caused by sampling, the study aims to develop a unified control algorithm that ensures system stability despite quantization, sampling, and saturation in continuous-time switched systems with unstabilizable subsystems.

For the switched systems with unstabilizable subsystems, many studies exist. An et al. [6] proposed a dwell-time-based control algorithm for a class of switched positive systems with all unstabilizable subsystems. Li et al. [7] developed a sampled data stabilization scheme for switched nonlinear systems where every subsystem could be unstabilizable. For switched linear systems containing both stabilizable and unstabilizable subsystems under slow- and fast-switching constraints, Wang et al. [8] constructed a time-varying mode controller to guarantee the system stability. For continuous-time switched systems with partially unstabilizable subsystems experiencing quantization and denial-of-service (DoS) attacks, Yan et al. [9] designed a stability-guaranteeing framework. Li et al. [10] investigated the stability of switched linear systems with input saturation and time-varying delays, where delay-dependent switching combines stabilizable and unstabilizable subsystems.

The quantized control of the switched system is also worthy of our attention. Ahmadzadeh et al. [11] studied robust $H_{\infty }$ control and event-triggered sampling co-design for uncertain switched singular systems with output quantization. Parivallal et al. [12] investigated the guaranteed-cost consensus control problem for nonlinear systems under switching topologies considering data quantization effects. A quantized sliding mode controller for nonlinear stochastic switched systems was developed by Qi et al. [13]. In [14], Qi et al. proposed decentralized quantized control combined with two-terminal event-triggered communication to enhance resilience against network-induced attacks. The stability of switched linear systems under quantization and event-triggered communication was studied by Zhao et al. [15]. Ahmadzadeh et al. [16] investigated event-triggered variable structure control for nonlinear switched descriptor systems with matched and mismatched disturbances. An adaptive neural network observer utilizing quantized output data was designed by Chen et al. [17] for switched systems. Cheng et al. [18] presented a static output feedback strategy for fuzzy Markov switched singular perturbation systems with spoofing attacks and quantized measured outputs. Zou et al. [19] addressed finite-time bipartite synchronization of coupled competitive neural networks subject to switching parameters and delays. Cheng et al. [20,21] and Zhao et al. [22] further investigated non-stationary filtering switched systems and fuzzy Markov switched affinity systems under the combined effects of deception attacks and data quantization. In Maity et al. [23], the authors proposed the joint selection method of the quantizers and the controller. Yan et al. [24] proposed quantized controller designs for switched systems affected by delay and disturbance.

Actuator saturation is another key factor that can degrade performance and even compromise system stability. Chen et al. [25] studied the aperiodic sampled data control problem of the switched network affected by actuator saturation. Zhao et al. [26] addressed exponential stabilization for networked cascade control systems constrained by actuator saturation. In Ahmadzadeh et al. [27], a two-layer supervisory control scheme is proposed for discrete-time linear systems with state/input constraints. In Kumar et al. [28], the linear system affected by actuator saturation is experimentally studied. Wang et al. [29] developed a continuous dynamic gain scheduling control strategy for switched systems experiencing input saturation. Actuator failures including saturation, partial failure, interruption, and offset were considered in Yin et al. [30]. Through the application of a multi-time-varying Lyapunov function, sufficient conditions for exponential stabilization of the switched systems were established in Ma et al. [31]. This paper mainly refers to the method in [31] for handling saturated nonlinearity. Due to the lack of discussion of sampling and quantization issues in [31], how to describe the saturation controller as a linear combination of sampled states as in [31] is a difficult problem in this paper.

This paper integrates the influences of unstabilizable subsystems, data quantization, and actuator saturation into the analysis of switched systems. For switched systems subject to quantization and actuator saturation, an output feedback controller based on a sector-bounded quantizer was designed by Wu et al. [32]. In stability analysis, the attenuation of the quantization error plays a key role. Because of the advantages of simple design and easy implementation, this paper will adopt a static quantizer.

Table 1. Comparison between this paper and [32].

	Quantizer	Quantization Level	Sampling	Handling Saturation
this paper	memoryless quantizer	finite	with	linearization by Claim 1
[32]	sector-bounded quantizer	infinite	without	decoupling into two nonlinear functions by introducing a variable $\varpi$

provides a detailed comparison between the quantizer, quantization level, sampling situations, and saturation handling methods used in this paper and reference [32]. Considering that finite-level quantizers have more practical value and sampling is an indispensable key step in signal transmission, the linearized saturation function can simplify the system analysis process. Therefore, the results of this paper are superior to those in [32] both from a practical perspective and in terms of processing methods.

The key research challenges in this paper include (1) designing a static quantizer with fixed error bounds that accounts for the polyhedral constraints imposed by actuator saturation; (2) precisely defining the attraction domain and the invariant set under inherent quantization errors to ensure system performance analysis; and (3) guaranteeing that the Lyapunov function decreases in the optimal case under multiple factors (quantization, saturation, etc.) for stability verification.

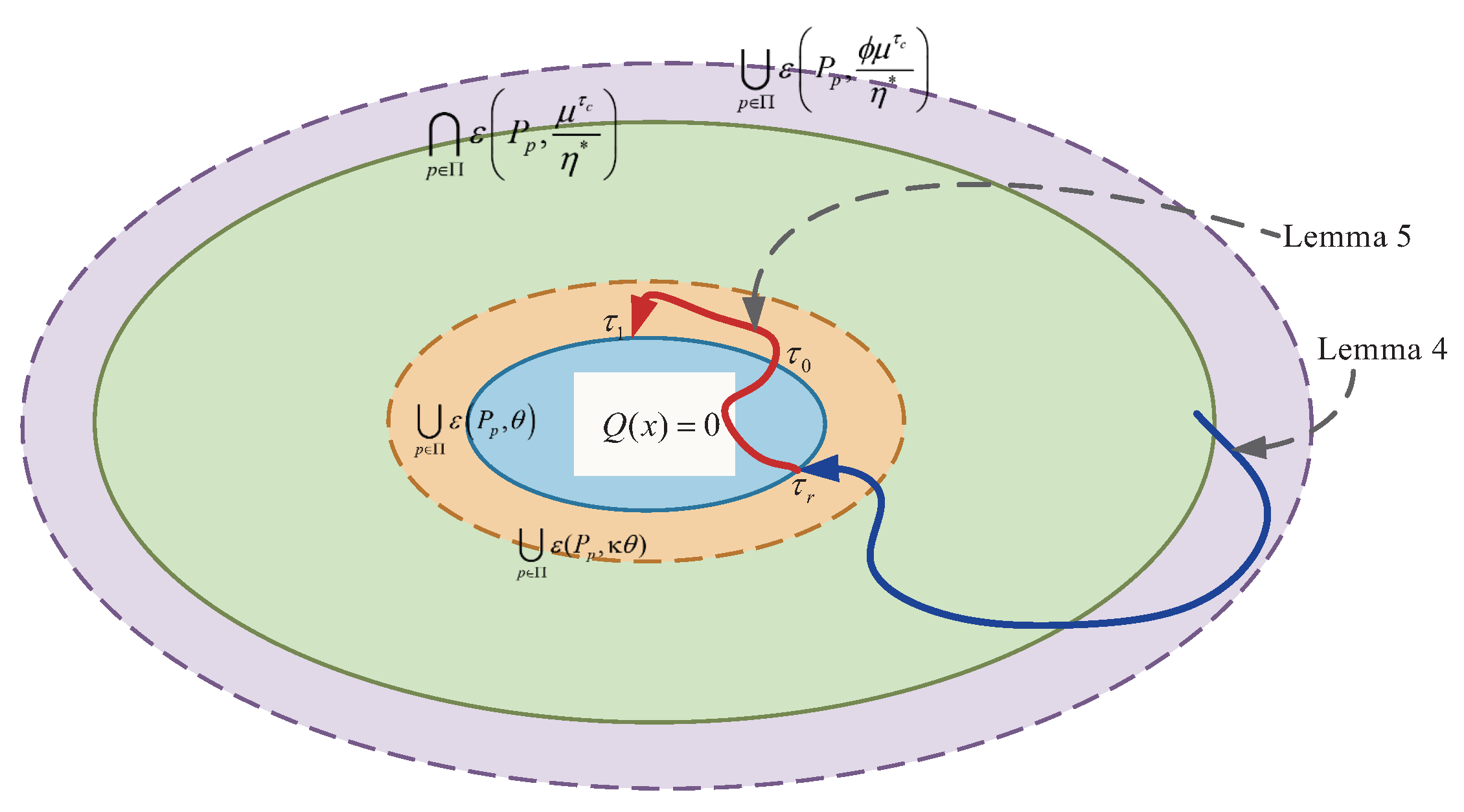
In light of the challenges discussed above, the following methodologies are introduced: (1) By restricting the initial state (see Condition 1) and the relationship between an ellipse and a polyhedral (see Condition 2), we claim that the system states at sampling times are always located within a polyhedron (see Claim 1, which is proven in Section 4.3). Then, the saturated controller can be expressed as a linear combination relating to sampled quantized states (see (5)). (2) For the designed quantization rules, if the state is within a given annular area $\mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, we can guarantee the decrement rate of the Lyapunov function in the optimal case (see (18)). (3) We pursue an attraction domain ${\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$ (see Condition 1, which is smaller than the outer ring of the annular area) and an invariant set ${\bigcup }_{p\in \Pi }\epsilon \left(P_p,\kappa \theta \right)$ (see Lemma 5, which is larger than the inner ring of the annular area) based on the union or intersection of ellipses to guarantee the system stability (see Theorem 1).

The remainder of this paper is structured as follows: In Section 2, we introduce the problem under consideration, including the plant definition, description of stabilizable and unstabilizable subintervals, quantization and control rules, and the primary objective of the study. By analyzing the rate of increase or decrease rate of the Lyapunov function in Section 3, the stability of the system can be established in Section 4. Furthermore, the controller design method and optimization problem for attractive regions are also discussed in Section 5 and Section 6, respectively. Section 7 presents simulation studies that validate the effectiveness of the obtained results. The conclusions in Section 8 summarize the results of this paper and directions for future research.

Notation: Let $\mathbb{R}$ denote the set of all real numbers, and ${\mathbb{R}}_{\ge 0}$ means $\mathbb{R}\bigcup \left\{0\right\}$. ${\mathbb{R}}^n$ represents the n-dimensional Euclidean space. The set of all positive integers is denoted by $\mathbb{N}$, and ${\mathbb{Z}}_{\ge 0}$ is defined as $\mathbb{N}\bigcup \left\{0\right\}$. The symbol “T” refers to the transposition of a matrix. Unless otherwise indicated, $\parallel ·\parallel$ denotes the Euclidean 2-norm, where $\parallel x\parallel ={\left({\sum }_{k=1}^n{x}_k^2\right)}^{{\displaystyle \frac{1}{2}}}$. The norm induced by the specified vector norm is adopted for matrices. The notation $x\left(t_k^{-}\right)$ stands for the left-hand limit of x at time $t_k$. The sampling period is denoted by ${\tau }_c$. For $\xi \ge 0$, we set ${\left[\xi \right]}^{-}:=k{\tau }_c$ and ${\left[\xi \right]}^{+}:=(k+1){\tau }_c$ whenever $k{\tau }_c\le \xi \le (k+1){\tau }_c$, $\forall k\in \mathbb{Z}\ge 0$. For a set $\mathcal{Q}\subset {\mathbb{R}}^{n\times n}$, the symbols Cl $\left(\mathcal{Q}\right)$, Int $\left(\mathcal{Q}\right)$, and $\partial \left(\mathcal{Q}\right)$ denote its closure, interior, and boundary, respectively. The maximum and minimum eigenvalues of a matrix P are denoted by ${\lambda }_{max}\left(P\right)$ and ${\lambda }_{min}\left(P\right)$, respectively.

2. Methodology

The system configuration discussed in this paper is presented in Figure 1. For a given sampling period ${\tau }_c>0$, the sensor acquires the plant state $x_k$ along with the mode information ${\sigma }_k$ at sampling times $t_k=k{\tau }_c,\forall k\in {\mathbb{Z}}_{\ge 0}$. Due to limited network bandwidth, the state $x_k$ is quantized as $Q\left(x_k\right)$ by the quantizer according to the special quantization rules (see Section 2.3). Subsequently, the encoder encodes $Q\left(x_k\right)$ into an integer $i_k\in \mathbb{N}$ and transmits $i_k$ and ${\sigma }_k$ to the controller through the network. We assume that the network is delay-free and transmission-reliable. Then, the controller can receive the transmitted signals at $t_k$ under the role of the decoder and updates the control algorithm $u\left(t\right),\forall t\in [t_k,t_{k+1})$ by using a zero-order holder (ZOH). Unless otherwise specified, we set $k\in {\mathbb{Z}}_{\ge 0}$.

2.1. Plant Definition

The plant shown in Figure 1 is modeled by the following switched systems:

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=A_{\sigma \left(t\right)}x\left(t\right)+B_{\sigma \left(t\right)}sat\left(u\left(t\right)\right),\end{array}$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^{n_x}$ is the system state and $u\left(t\right)\in {\mathbb{R}}^{n_u}$ is the control input. The signal $\sigma \left(t\right):[0,\infty )\to \Pi$ denotes the system mode at time t, where $\Pi$ is a finite index set. We call discontinuities of $\sigma$ “switching times” or “switches”. $N_{\sigma }(t,s)\in {\mathbb{Z}}_{\ge 0}$ denotes the total count of switches occurring over the time interval $(s,t]$, where $s<t,s,t\in {\mathbb{R}}_{\ge 0}$. The saturation function $sat\left(u\right)$ is defined as $sat\left(u\right)={[sat\left(u_1\right),sat\left(u_2\right),\dots ,sat\left(u_{n_u}\right)]}^T$ with $sat\left(u_m\right)=sgn\left(u_m\right)min\left\{\right|u_m|,1\}$, where $u_m,\forall m\in \{1,\dots ,n_u\}$ is the m-th component of u, and $sgn(·)$ denotes a generic symbolic function.

Assumption 1. 

The index set Π is partitioned into two subsets, ${\Pi }_s$ and ${\Pi }_u$, corresponding to stabilizable and unstabilizable index sets, respectively. That is, if the system mode $i\in {\Pi }_s$, there exists a feedback matrix $K_i\in {\mathbb{R}}^{n_x\times n_u}$ such that $A_i+B_i{K}_i$ is Hurwitz. Otherwise, if $j\in {\Pi }_u$, there is no feedback matrix $K_j$ to guarantee that $A_j+B_j{K}_j$ is Hurwitz.

Assumption 2 

(slow switching [6]).

1. 

There exists a dwell time ${\tau }_d>0$ satisfying $N_{\sigma }(t+{\tau }_d,t)\le 1,\forall t\ge 0$ and ${\tau }_d\ge {\tau }_c$.

2. 

For a constant $N_0\ge 1$, there exists an average dwell time ${\tau }_a>{\tau }_d$ satisfying $N_{\sigma }(t,s)\le N_0+(t-s)/{\tau }_a,\forall t>s\ge 0$.

2.2. Description of Stabilizable and Unstabilizable Subintervals

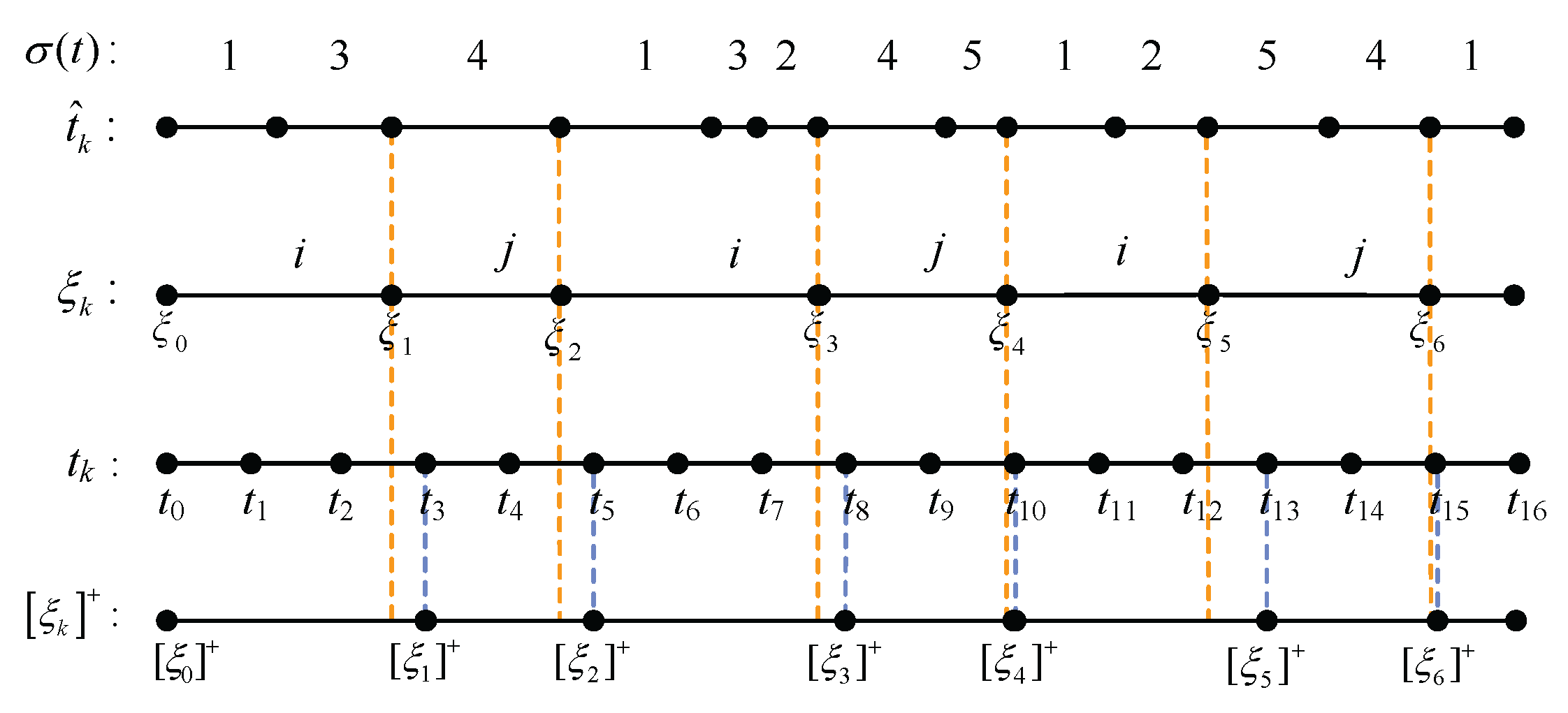
If we let ${\xi }_0=t_0=0$ and denote $[{\xi }_{2k},{\xi }_{2k+1})$ and $[{\xi }_{2k+1},{\xi }_{2k+2})$ as the intervals during which stabilizable and unstabilizable subsystems are, respectively, active, then the signal $T_k$ is adopted to represent the total time during which the stabilizable and unstabilizable subsystems are active in the interval $[{\xi }_{2k},{\xi }_{2k+2})$. Moreover, $T_k^{-}$ and $T_k^{+}$ denote, respectively, the activation times of the stabilizable and unstabilizable subsystems in $[{\xi }_{2k},{\xi }_{2k+2})$.

An illustration is provided in Figure 2 to aid in understanding the variables used in this paper, where modes $1,2,3\in {\Pi }_s$ and modes $4,5\in {\Pi }_u$. The signal ${\left[{\xi }_k\right]}^{+}$ is used to establish the global bound for sampling times in Section 3. Obviously, ${\xi }_k$ may not necessarily be a sampling time, while ${\left[{\xi }_k\right]}^{-}$ and ${\left[{\xi }_k\right]}^{+}$ are included in the set of sampling times, i.e., $\{{\left[{\xi }_k\right]}^{-},{\left[{\xi }_k\right]}^{+},\forall k\in {\mathbb{Z}}_{\ge 0}\}\subset \{t_k,\forall k\in {\mathbb{Z}}_{\ge 0}\}$.

2.3. Quantization and Control Rules

The memoryless quantizer proposed in Wakaiki et al. [33] is adopted here. Let ${\left\{{\mathcal{N}}_{\varrho }\right\}}_{\varrho \in \gamma }$ be the finite partition of ${\mathbb{R}}^n$. Given an arbitrary bounded region $\tilde{\Lambda }$, one can find a finite subset ${\gamma }_{\delta }$ of an index set $\gamma$ so that $\tilde{\Lambda }\subset {\cup }_{\varrho \in {\gamma }_{\delta }}{\mathcal{N}}_{\varrho }$. The quantizer is formulated as follows:

$$\begin{array}{cc}\hfill Q:{\mathbb{R}}^n& \to {\left\{c_{\varrho }\right\}}_{\varrho \in \gamma }\subset {\mathbb{R}}^n\hfill \\ \hfill x& \mapsto c_{\varrho }\mathrm{if}x\in {\mathcal{N}}_{\varrho }(\varrho \in \gamma ).\hfill \end{array}$$

(2)

Moreover, we assume that $Q\left(x\right)=0$ if Cl $\left({\mathcal{N}}_{\varrho }\right)$ contains the origin. Obviously, a sufficiently large constant $\theta$ can be found such that $\{x:Q\left(x\right)=0\}\subset {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, where ellipsoid $\epsilon (P_p,\theta )$ and matrix $P_p$ are defined in (4) and (6), respectively.

For the quantization function $Q(·)$ defined in (2), the control input is set as

$$\begin{array}{cc}\hfill u\left(t\right)& =K_{{\sigma }_k}Q\left(x_k\right),\forall t\in [t_k,t_{k+1})\hfill \end{array}$$

(3)

under the role of ZOH, where $K_{{\sigma }_k},\forall {\sigma }_k\in \Pi$ is the feedback matrix to be designed. Obviously, $A_{{\sigma }_k}+B_{{\sigma }_k}{K}_{{\sigma }_k}$ must not be Hurwitz if ${\sigma }_k\in {\Pi }_u$ by Assumption 1.

The following definition and conditions are useful to establish Claim 1, which is instrumental in proving the main results and will be verified in Section 4.3.

Definition 1. 

Considering a positive-definite matrix $P\in {\mathbb{R}}^{n_x\times n_x}$ and a matrix $G\in {\mathbb{R}}^{n_x\times n_u}$ that is designed, we respectively define an ellipsoid $\epsilon (P,\psi )$ and a polyhedron $\iota \left(G\right)$ as follows:

$$\begin{array}{cc}\hfill \epsilon (P,\psi )=& \{x\in {\mathbb{R}}^{n_x}:x^{T}Px\le \psi ,\psi >0\}\hfill \\ \hfill \iota \left(G\right)=& \{x\in {\mathbb{R}}^{n_x}:|f_l·Q\left(x\right)|\le 1,\forall l=1,2,\dots ,n_u\},\hfill \end{array}$$

(4)

where $f_l$ denotes the lth row of the matrix G.

Condition 1. 

For the given arbitrary constants $\mu >1$ and ${\eta }^{\ast }>0$, the initial state satisfies $x_0\in {\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$.

Condition 2. 

For the given μ and ${\eta }^{\ast }$, there exists a matrix $G_p$ such that $\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\subset \iota \left(G_p\right),\forall p\in \Pi$ with $\varphi :=\Gamma e^{\overline{\mu }{\tau }_c}$.

Claim 1. 

For the ellipsoid $\epsilon (P,\psi )$ and the polyhedron $\iota \left(G\right)$ defined in (4), if Conditions 1 and 2 hold, then $x_k\in \iota \left(G_{{\sigma }_k}\right)$.

Remark 1. 

Since μ and ${\eta }^{\ast }$ are arbitrary constants, if we set μ to be sufficiently large compared to ${\eta }^{\ast }$, then Condition 1 can always hold. Moreover, at the beginning of the proof of Theorem 2, we verified that if Condition 5 holds, then $\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\subset \iota \left(G_p\right)$ shown in Condition 2 is equivalent to (36). Therefore, we can obtain $h_{pl}$ and $X_p$ by solving (36) and then obtain the matrix $G_p$ that guarantees Condition 2 by $H_p=G_p{X}_p$.

Lemma 1 

([31]). For any $u\in R^{n_u}$ and $v\in R^{n_u}$ such that $|v_l|\le 1,\forall l\in [1,n_u]$, one has

$$\begin{array}{c}\hfill sat\left(u\left(t\right)\right)\in co\{E_{s}u+E_s^{-}v,s\in [1,2^{n_u}]\},\end{array}$$

where $co$ denotes the convex hull. $E_s\in R^{n_u\times n_u}$ is a diagonal matrix with 1 or 0 elements, and $E_s^{-}=I-E_s$.

If Claim 1 holds, the constrained control input $sat\left(u\right(t\left)\right)$ can be formulated as

$$\begin{array}{c}\hfill sat\left(u\left(t\right)\right)=\sum _{s=1}^{2^{n_u}}{\rho }_{\sigma s}\left(E_{\sigma s}{K}_{\sigma }+E_{\sigma s}^{-}{G}_{\sigma }\right)Q\left(x_k\right)\end{array}$$

(5)

where ${\rho }_{\sigma 1}\ge 0$, ${\rho }_{\sigma 2}\ge 0$,..., ${\rho }_{\sigma 2^{n_u}}\ge 0$ and ${\sum }_{s=1}^{2^{n_u}}{\rho }_{\sigma s}=1$. Hence, the closed-loop system formed by (1) and (5) is expressed as

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=\sum _{s=1}^{2^{n_u}}{\rho }_{\sigma s}[A_{\sigma }+B_{\sigma }(E_{\sigma s}{K}_{\sigma }+E_{\sigma s}^{-}{G}_{\sigma })]Q\left(x_k\right).\end{array}$$

Remark 2. 

From Lemma 1, it can be seen that the difficulty in obtaining the expression (5) lies in determining how to ensure that the moduli of all elements of $G_{\sigma }Q\left(x_k\right)$ are less than 1, that is, $x_k\in \iota \left(G_{{\sigma }_k}\right)$. To solve this problem, we introduce Claim 1 and prove it in Section 4.3.

The following lemma obviously holds by using the properties of the static quantizer proposed in Ma et al. [31].

Lemma 2. 

If $Q\left(x_k\right)\ne 0$, there exist positive numbers ${\alpha }_0$ and ${\varsigma }_0$ such that the quantizer defined in (2) satisfies

$$\begin{array}{cc}& \parallel B_p(E_{qs}{K}_q+E_{qs}^{-}{G}_q)Q\left(x_k\right)\parallel \le {\alpha }_0\parallel x_k\parallel \hfill \\ & \parallel P_q{B}_p(E_{qs}{K}_q+E_{qs}^{-}{G}_q)(Q\left(x_k\right)-x_k)\parallel \le {\varsigma }_0\parallel x_k\parallel \hfill \\ & \parallel P_q{B}_p(E_{qs}{K}_q+E_{qs}^{-}{G}_q)(Q\left(x_k\right)-x\left(t\right))\parallel <{\alpha }_1({\beta }_1\parallel P_q{B}_p(E_{qs}{K}_q+E_{qs}^{-}{G}_q)\parallel +{\varsigma }_0)\parallel x\left(t\right)\parallel \hfill \end{array}$$

for all $p,q\in \Pi$, $s\in \{1,\dots ,2^{n_u}\}$ and $x\in {\bigcup }_{p\in \Pi }\iota \left(G_p\right)\subset {\bigcup }_{\varrho \in {\gamma }_{\delta }}{\mathcal{N}}_{\varrho }$, in which

$$\begin{array}{cc}\hfill {\alpha }_0=& {\displaystyle \frac{{max}_{p,q\in \Pi }{max}_{\varrho \in {\gamma }_{\delta }}\parallel B_p(E_{qs}{K}_q+E_{qs}^{-}{G}_q)Q\left(x_k\right)\parallel }{{min}_{x\in {\mathcal{N}}_{\varrho }}\parallel x_k\parallel }}\hfill \\ \hfill {\varsigma }_0=& {\displaystyle \frac{{max}_{p,q\in \Pi }{max}_{\varrho \in {\gamma }_{\delta }\setminus {\gamma }_0}\parallel P_q{B}_p(E_{qs}{K}_q+E_{qs}^{-}{G}_q)\parallel }{{min}_{x\in {\mathcal{N}}_{\varrho }}\parallel x_k\parallel }}\underset{x\in {\mathcal{N}}_{\varrho }}{max}\parallel Q\left(x_k\right)-x_k\parallel \hfill \end{array}$$

and ${\gamma }_0=\left\{\varrho \in \gamma :0\in \mathit{Cl}\left({\mathcal{N}}_{\varrho }\right)\right\}$, ${\alpha }_1={\displaystyle \frac{e^{\Lambda {\tau }_c}}{1-\Phi }}$, and ${\beta }_1=(e^{\Lambda {\tau }_c}-1)\left(1+{\displaystyle \frac{{\alpha }_0}{\Lambda }}\right)$ with $\Phi ={\alpha }_0{\displaystyle \frac{e^{\Lambda {\tau }_c-1}}{\Lambda }}<1$ and $\Lambda ={max}_{p\in \Pi }\parallel A_p\parallel$.

2.4. Main Purpose

The purpose of this paper is to determine a switching condition (7) that guarantees that all trajectories of the switched system (5) enter a certain neighborhood ${\bigcup }_{p\in \Pi }\epsilon \left(P_p,\kappa \theta \right)$ around the origin and stay confined within a larger neighborhood $\mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$.

If we let ${\sigma }_k=p\in \Pi$, the stability results of the closed-loop system can be established by discussing the following four situations:

Case 1: $p\in {\Pi }_s$, and no switching occurs in $[t_k,t_{k+1})$.

Case 2: $p\in {\Pi }_s$, and a switch occurs in $[t_k,t_{k+1})$.

Case 3: $p\in {\Pi }_u$, and no switching occurs in $[t_k,t_{k+1})$.

Case 4: $p\in {\Pi }_u$, and a switch occurs in $[t_k,t_{k+1})$.

For the positive-definite matrix $P_p$ and the constants $\mu >1$ and ${\eta }^{\ast }>0$ given in Claim 1, we consider the Lyapunov function to be defined as

$$\begin{array}{c}\hfill V_p\left(t\right)={\psi }_p\left(t\right)x^T\left(t\right)P_{p}x\left(t\right),\end{array}$$

(6)

where the piecewise continuous function ${\psi }_p\left(t\right)$ satisfies $\dot{{\psi }_p}\left(t\right)=(ln\mu ){\psi }_p\left(t\right)$ and ${\psi }_p\left(t_k\right)={\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}$. It is obvious that ${\dot{\psi }}_p\left(t\right)\ge 0$. Thus, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}={\psi }_p\left(t_k\right)\le {\psi }_p\left(t\right)\le {\psi }_p\left(t_{k+1}^{-}\right)={\eta }^{\ast }.\end{array}$$

In the following, we will obtain the stability results (see Theorem 1 in Section 4.2) in four steps by using the Lyapunov function defined above. First, for any $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, we pursue the increasing/decreasing rate of the Lyapunov function for the four cases above. On this basis, the relationship between $V_{\sigma }\left(t\right)$ and $V_{\sigma }\left(t_0\right)$ is established (see Lemma 3). Second, we testify that all trajectories with an initial state in $\mathrm{Int}\left({\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$ fall into ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ (see Lemma 4). Next, it will show that the trajectory stays in a slightly larger ellipsoid, i.e., ${\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta )$, after it enters into ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ (see Lemma 5). Finally, we obtain Theorem 1 by using Lemmas 3–5.

3. Increasing/Decreasing Rate of the Lyapunov Function

To obtain the increasing/decreasing rate of the Lyapunov function, the parameters should meet the following conditions:

Condition 3. 

Sampling period ${\tau }_c$ is selected small enough such that

$$\begin{array}{c}\hfill {\tau }_a>{\displaystyle \frac{ln\widehat{\vartheta }-ln\widehat{\varpi }}{-ln\widehat{\varpi }}}{\tau }_c,\end{array}$$

(7)

where $\widehat{\vartheta }>1$ and $\widehat{\varpi }<1$ are defined in (21).

Condition 4. 

$T_k^{-}$ is sufficiently large compared with $T_k^{+}$ such that

$$\begin{array}{c}\hfill {\tau }_{c}ln(FJ\Omega /\Psi )+T_k^{+}ln\Omega +T_k^{-}ln\Psi \le {\tau }_{c}lnZ\end{array}$$

(8)

for a given constant $Z\in [\Psi ,1)$ with $J,\Psi$ and $F,\Omega$ defined in (21) and (22), respectively.

Condition 5. 

The partition ${\left\{{\mathcal{N}}_{\varrho }\right\}}_{\varrho \in \gamma }$ is dense enough such that the quantization error $e=Q\left(x\right)-x,\forall x\in {\mathcal{N}}_{\varrho }$ satisfies

$$\begin{array}{c}\hfill \parallel e\parallel \le \underset{x\in {\mathcal{N}}_{\varrho }}{max}\parallel Q\left(x\right)-x\parallel :=\tilde{\delta }\le {\displaystyle \frac{1-\sqrt{\zeta }}{\parallel f_{pl}\parallel }}\end{array}$$

(9)

for any $p\in \Pi$ and $l\in \{1,2,\dots ,n_u\}$, where $\zeta \in (0,1)$ and $f_{pl}$ is the lth row of matrix $G_p$ defined in Condition 2. Furthermore, it is assumed that ${\tau }_c$ is small enough and the partition ${\left\{{\mathcal{N}}_{\varrho }\right\}}_{\varrho \in \gamma }$ is dense enough so that

$$\begin{array}{cc}\hfill -\varpi :=& -\overline{\varpi }+2{\alpha }_1\left({\varsigma }_0+{\beta }_1\parallel P_i{B}_i[E_{is}{K}_i+E_{is}^{-}{G}_i]\parallel \right){\displaystyle \frac{1}{{\lambda }_{min}\left(P_i\right)}}<0\hfill \end{array}$$

(10)

holds for any $x\left(t\right)\in {\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\setminus {\bigcup }_{p\in \Pi }\epsilon \left(P_p,\theta \right)$, where $\overline{\varpi },P_i,K_i,G_i,\forall i\in {\Pi }_s$ are defined in (11), ${\alpha }_1,{\varsigma }_0$ and ${\beta }_1$ are given in Lemma 2, and the ellipsoids $\epsilon (P_p,\theta )$ and $\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right),\forall p\in \Pi$ are described by (4) with ϕ given in Condition 2.

Remark 3. 

For the given variables $\widehat{\vartheta },\widehat{\varpi }$ and ${\tau }_a$, sampling period ${\tau }_c$ meeting Condition 3 always exists. Considering $\Psi <1$, for the given ${\tau }_c,F,J,\Omega$ and Z, if $T_k^{-}$ is sufficiently large compared with $T_k^{+}$, then the left side of (8) is small enough such that Condition 4 holds. Condition 4 limits the length of the stabilizable interval, which is reasonable. In fact, when the system is unstabilizable, it must be divergent. So, the stability of the entire system can only be guaranteed if the stabilizable interval is long enough. Regarding Condition 5, if the partition is dense enough (at the cost of occupying more bandwidth), the quantization value $Q\left(x\right)$ and the state x can be arbitrarily close, so (9) can be satisfied. Moreover, if ${\tau }_c$ is selected to be small enough and the partition is dense enough, then ${\varsigma }_0$ and ${\beta }_1$ can be set arbitrarily small which guarantees (10).

Lemma 3. 

Let Assumptions 1–2 and Conditions 1–5 hold. For the given $\mu >1$, if there exist constants $\overline{\varpi }>0,\overline{\vartheta }>0,\overline{\omega }>\overline{\pi }>0$ and matrices $P_p>0$, $K_p,\forall p\in \Pi$ such that

$$\begin{array}{}\mathrm{(11)}& & (ln\mu )P_i+{(A_i+B_i(E_{is}{K}_i+E_{is}^{-}{G}_i))}^T{P}_i+P_i(A_i+B_i(E_{is}{K}_i+E_{is}^{-}{G}_i))+\overline{\varpi }{P}_i<0\hfill \mathrm{(12)}& & (ln\mu )P_i+{(A_p+B_p(E_{is}{K}_i+E_{is}^{-}{G}_i))}^T{P}_i+P_i(A_p+B_p(E_{is}{K}_i+E_{is}^{-}{G}_i))-\overline{\vartheta }{P}_i<0\hfill \mathrm{(13)}& & (ln\mu )P_j+{(A_j+B_j(E_{js}{K}_j+E_{js}^{-}{G}_j))}^T{P}_j+P_j(A_j+B_j(E_{js}{K}_j+E_{js}^{-}{G}_j))-\overline{\pi }{P}_j<0\hfill \mathrm{(14)}& & (ln\mu )P_j+{(A_p+B_p(E_{js}{K}_j+E_{js}^{-}{G}_j))}^T{P}_j+P_j(A_p+B_p(E_{js}{K}_j+E_{js}^{-}{G}_j))-\overline{\omega }{P}_j<0\hfill \mathrm{(15)}& & P_i\le {\mu }^{{\tau }_c}{P}_j,P_j\le {\mu }^{{\tau }_c}{P}_i\hfill \end{array}$$

hold for any $i\in {\Pi }_s$, $j\in {\Pi }_u$, and $s\in \{1,\dots ,2^{n_u}\}$, then Lyapunov function (6) satisfies

$$\begin{array}{c}\hfill V_{\sigma }\left(t\right)\le \Gamma e^{\overline{\mu }(t-t_k)}{e}^{-\phi (t_k-t_0)}{V}_{\sigma }\left(t_0\right),\forall t\in [t_k,t_{k+1})\end{array}$$

(16)

for all $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, where $\phi =-lnZ>0$, $\varphi =\Gamma e^{\overline{\mu }{\tau }_c}$, Γ, and $\overline{\mu }$ are defined in (23) and (25), respectively.

Proof.  

If we let ${\sigma }_k=p,{\sigma }_{k+1}=q,\forall p,q\in \Pi$, one gets

$$\begin{array}{cc}\hfill V_q\left(t_{k+1}\right)& ={\psi }_q\left(t_{k+1}\right)x_{k+1}^T{P}_q{x}_{k+1}={\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}{x}_{k+1}^T{P}_q{x}_{k+1}\hfill \\ & \le \left({\displaystyle \frac{{\eta }^{\ast }}{\mu }}\right)x_{k+1}^T\mu P_q{x}_{k+1})\le {\eta }^{\ast }{x}^T\left(t_{k+1}^{-}\right)P_{p}x\left(t_{k+1}^{-}\right)\hfill \\ & ={\psi }_p\left(t_{k+1}^{-}\right)x^T\left(t_{k+1}^{-}\right)P_{p}x\left(t_{k+1}^{-}\right)=V_p\left(t_{k+1}^{-}\right)\hfill \end{array}$$

(17)

due to the fact that $x\left(t_{k+1}^{-}\right)=x_{k+1}$.

Next, we will establish the upper bound of the Lyapunov function $V_{\sigma }\left(t\right),\forall t\in [t_k,t_{k+1})$ for four cases.

Case 1: In such a case, a mode $i\in {\Pi }_s$ exists such that $\sigma \left(t\right)=i,\forall t\in [t_k,t_{k+1})$. Then, the temporal derivative of $V_i\left(t\right)$ meets

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)=& {\dot{\psi }}_i\left(t\right)x^T\left(t\right)P_{i}x\left(t\right)+{\psi }_i\left(t\right){\dot{x}}^T\left(t\right)P_{i}x\left(t\right)+{\psi }_i\left(t\right)x^T\left(t\right)P_i\dot{x}\left(t\right)\hfill \\ \hfill =& (ln\mu ){\psi }_i\left(t\right)x^T\left(t\right)P_{i}x\left(t\right)+{\psi }_i\left(t\right)\sum _{s=1}^{2^{n_u}}{\rho }_{is}{[A_{i}x\left(t\right)+B_i(E_{is}{K}_i+E_{is}^{-}{G}_i)Q\left(x_k\right)]}^T{P}_{i}x\left(t\right)\hfill \\ & +{\psi }_i\left(t\right)x^T\left(t\right)P_i\sum _{s=1}^{2^{n_u}}{\rho }_{is}[A_{i}x\left(t\right)+B_i(E_{is}{K}_i+E_{is}^{-}{G}_i)Q\left(x_k\right)]\hfill \\ \hfill =& \sum _{s=1}^{2^{n_u}}{\rho }_{is}{\psi }_i\left(t\right)\{(ln\mu )x^T\left(t\right)P_{i}x\left(t\right)+x^T\left(t\right)[{(A_i+B_i(E_{is}{K}_i+E_{is}^{-}{G}_i))}^T{P}_i\hfill \\ & +P_i(A_i+B_i(E_{is}{K}_i+E_{is}^{-}{G}_i))]x\left(t\right)+2x^T\left(t\right)P_i{B}_i[E_{is}{K}_i+E_{is}^{-}{G}_i](Q\left(x_k\right)-x\left(t\right))\}\hfill \end{array}$$

due to ${\sum }_{s=1}^{2^{n_u}}{\rho }_{is}=1$. Then, (11) gives

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)\le & \sum _{s=1}^{2^{n_u}}{\rho }_{is}{\psi }_i\left(t\right)\{-\overline{\varpi }{x}^T\left(t\right)P_{i}x\left(t\right)+2x^T\left(t\right)P_i{B}_i[E_{is}{K}_i+E_{is}^{-}{G}_i](Q\left(x_k\right)-x\left(t\right))\}.\hfill \end{array}$$

If $x\left(t\right)\notin {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, then $Q\left(x_k\right)\ne 0$ must be true. According to Lemma 2 and (10), one has

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)\le & \sum _{s=1}^{2^{n_u}}{\rho }_{is}\{-\overline{\varpi }{V}_i\left(t\right)+2{\alpha }_1({\varsigma }_0+{\beta }_1\parallel P_i{B}_i[E_{is}{K}_i+E_{is}^{-}{G}_i]\parallel ){\displaystyle \frac{1}{{\lambda }_{min}\left(P_i\right)}}{V}_i\left(t\right)\}\le -\varpi V_i\left(t\right).\hfill \end{array}$$

Then, we get

$$\begin{array}{c}\hfill V_i\left(t_{k+1}^{-}\right)\le e^{-\varpi {\tau }_c}{V}_i\left(t_k\right).\end{array}$$

(18)

Remark 4. 

In order to ensure (16) with $\phi >0$, the Lyapunov function must monotonically decrease in the optimal case (that is, Case 1). To achieve this goal, we ensure that (10) holds by limiting the sampling interval ${\tau }_c$ and the density of the quantization partition, thus obtaining inequality (18), which guarantees the monotonic decreasing property.

Case 2: Let ${\sigma }_k=i\in {\Pi }_s$, ${\sigma }_{k+1}=p\in \Pi$, and the switching instant over the interval $[t_k,t_{k+1})$ be denoted by $t_k+\overline{t},\overline{t}\in (0,{\tau }_c)$. Based on the analysis of Case 1, it follows that $V_i(t_k+\overline{t})\le e^{-\varpi \overline{t}}{V}_i\left(t_k\right)$. If $t\in [t_k+\overline{t},t_{k+1})$, we have

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)=& (ln\mu ){\psi }_i\left(t\right)x^T\left(t\right)P_{i}x\left(t\right)+{\psi }_i\left(t\right)\sum _{s=1}^{2^{n_u}}{\rho }_{is}{[A_{p}x\left(t\right)+B_p(E_{is}{K}_i+E_{is}^{-}{G}_i)Q\left(x_k\right)]}^T{P}_{i}x\left(t\right)\hfill \\ & +{\psi }_i\left(t\right)x^T\left(t\right)P_i\sum _{s=1}^{2^{n_u}}{\rho }_{is}[A_{p}x\left(t\right)+B_p(E_{is}{K}_i+E_{is}^{-}{G}_i)Q\left(x_k\right)]\hfill \\ \hfill =& \sum _{s=1}^{2^{n_u}}{\rho }_{is}{\psi }_i\left(t\right)\{(ln\mu )x^T\left(t\right)P_{i}x\left(t\right)+x^T\left(t\right)[{(A_p+B_p(E_{is}{K}_i+E_{is}^{-}{G}_i))}^T{P}_i\hfill \\ & +P_i(A_p+B_p(E_{is}{K}_i+E_{is}^{-}{G}_i))]x\left(t\right)+2x^T\left(t\right)P_i{B}_p[E_{is}{K}_i+E_{is}^{-}{G}_i](Q\left(x_k\right)-x\left(t\right))\}\hfill \\ \hfill \le & \sum _{s=1}^{2^{n_u}}{\rho }_{is}\{\overline{\vartheta }{V}_i\left(t\right)+2{\alpha }_1({\varsigma }_0+{\beta }_1\parallel P_i{B}_p[E_{is}{K}_i+E_{is}^{-}{G}_i]\parallel ){\displaystyle \frac{1}{{\lambda }_{min}\left(P_i\right)}}{V}_i\left(t\right)\}\hfill \end{array}$$

by considering (12). Let

$$\begin{array}{cc}\hfill \vartheta :=& \underset{{\displaystyle \genfrac{}{}{0pt}{}{i\in {\Pi }_s,p\in \Pi ,}{s\in \{1,\dots ,2^{n_u}\}}}}{max}\{\overline{\vartheta }+2{\alpha }_1({\varsigma }_0+{\beta }_1\parallel P_i{B}_p[E_{is}{K}_i+E_{is}^{-}{G}_i]\parallel ){\displaystyle \frac{1}{{\lambda }_{min}\left(P_i\right)}}\}.\hfill \end{array}$$

This implies that ${\dot{V}}_i\left(t\right)\le \vartheta V_i\left(t\right)$. Therefore, one gets

$$\begin{array}{cc}\hfill V_i\left(t_{k+1}^{-}\right)\le & e^{\vartheta ({\tau }_c-\overline{t})}{V}_i(t_k+\overline{t})\le e^{\vartheta ({\tau }_c-\overline{t})}{e}^{-\varpi \overline{t}}{V}_i\left(t_k\right)\le e^{\vartheta {\tau }_c}{V}_i\left(t_k\right).\hfill \end{array}$$

(19)

Case 3: Let $\sigma \left(t\right)=j,\forall t\in [t_k,t_{k+1})$. By analogy with the analysis in Case 2, it follows that ${\dot{V}}_j\left(t\right)\le \pi V_j\left(t\right)$ by using (13), where

$$\begin{array}{cc}\hfill \pi :=& \underset{{\displaystyle \genfrac{}{}{0pt}{}{j\in {\Pi }_u,}{s\in \{1,\dots ,2^{n_u}\}}}}{max}\{\overline{\pi }+2{\alpha }_1\left({\varsigma }_0+{\beta }_1\parallel P_j{B}_j[E_{js}{K}_j+E_{js}^{-}{G}_j]\parallel \right){\displaystyle \frac{1}{{\lambda }_{min}\left(P_j\right)}}\}.\hfill \end{array}$$

Thus, it yields $V_j\left(t_{k+1}^{-}\right)\le e^{\pi {\tau }_c}{V}_j\left(t_k\right)$.

Case 4: Let ${\sigma }_k=j\in {\Pi }_u$, ${\sigma }_{k+1}=p\in \Pi$, and the switching instant in $[t_k,t_{k+1})$ be denoted by $t_k+\overline{t},\overline{t}\in (0,{\tau }_c)$. It is obvious that ${\dot{V}}_j\left(t\right)\le \omega V_j\left(t\right)$ by (14), where

$$\begin{array}{cc}\hfill \omega :=& \underset{{\displaystyle \genfrac{}{}{0pt}{}{j\in {\Pi }_u,p\in \Pi ,}{s\in \{1,\dots ,2^{n_u}\}}}}{max}\{\overline{\omega }+2{\alpha }_1\left({\varsigma }_0+{\beta }_1\parallel P_j{B}_p[E_{js}{K}_j+E_{js}^{-}{G}_j]\parallel \right){\displaystyle \frac{1}{{\lambda }_{min}\left(P_j\right)}}\}.\hfill \end{array}$$

This induces

$$\begin{array}{c}\hfill V_j\left(t_{k+1}^{-}\right)\le e^{\omega {\tau }_c}{V}_j\left(t_k\right)\end{array}$$

(20)

due to $\omega >\pi$.

$\widehat{\varpi }=e^{-\varpi {\tau }_c}<1,\widehat{\vartheta }=e^{\vartheta {\tau }_c},\widehat{\pi }=e^{\pi {\tau }_c}$ and $\widehat{\omega }=e^{\omega {\tau }_c}$ are denoted, and by considering (17), we now derive the upper bound of $V_{{\sigma }_k}\left(x\left(t\right)\right),\forall t\in [t_k,t_{k+1})$ based on (18)–(20).

(1) Stabilizable subintervals: The below analysis focuses on the increasing/decreasing rate of the Lyapunov function from ${\left[{\xi }_{2k}\right]}^{+}$ to ${\left[{\xi }_{2k+1}\right]}^{+}$ represented by ${\mathsf{ϝ}}_k$. If we recall that $\widehat{\vartheta }/\widehat{\varpi }>1$, then (18) and (19) yield

$$\begin{array}{cc}\hfill {\mathsf{ϝ}}_k\le & {\widehat{\vartheta }}^{N_{\sigma }({\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+})}{\widehat{\varpi }}^{{\displaystyle \frac{{\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_c}}-N_{\sigma }({\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+})}\hfill \\ \hfill \le & {(\widehat{\vartheta }/\widehat{\varpi })}^{N_0+{\displaystyle \frac{{\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_a}}}{\widehat{\varpi }}^{{\displaystyle \frac{{\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_c}}}\hfill \\ \hfill =& {\left(\widehat{\vartheta }/\widehat{\varpi }\right)}^{N_0}{\left\{{\left(\widehat{\vartheta }/\widehat{\varpi }\right)}^{{\displaystyle \frac{{\tau }_c}{{\tau }_a}}}\widehat{\varpi }\right\}}^{{\displaystyle \frac{{\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_c}}}\hfill \\ \hfill =& J{\Psi }^{{\displaystyle \frac{{\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_c}}}\hfill \end{array}$$

(21)

with $J={(\widehat{\vartheta }/\widehat{\varpi })}^{N_0}$ and $\Psi ={(\widehat{\vartheta }/\widehat{\varpi })}^{{\tau }_c/{\tau }_a}\widehat{\varpi }$. According to Condition 3, one has $\Psi <1$.

(2) Unstabilizable subintervals: $H_k$ is defined as the increasing/decreasing rate of the Lyapunov function between ${\left[{\xi }_{2k+1}\right]}^{+}$ and ${\left[{\xi }_{2k+2}\right]}^{+}$. Similar to the analysis of (21), we can easily get

$$\begin{array}{c}\hfill H_k\le F{\Omega }^{{\displaystyle \frac{{\left[{\xi }_{2k+2}\right]}^{+}-{\left[{\xi }_{2k+1}\right]}^{+}}{{\tau }_c}}}\end{array}$$

(22)

by using $\widehat{\omega }/\widehat{\pi }>1$, where $F={(\widehat{\omega }/\widehat{\pi })}^{N_0}$ and $\Omega ={(\widehat{\omega }/\widehat{\pi })}^{{\tau }_c/{\tau }_a}\widehat{\pi }>1$.

(3) Combined bound at sampling times: If $t_k$ lies within a stabilizable subinterval, i.e., $t_k\in [{\xi }_{2k},{\xi }_{2k+1})$ for some $k\in {\mathbb{Z}}_{\ge 0}$, we can obtain that

$$\begin{array}{cc}\hfill V_{\sigma }\left(t_k\right)\le & J{\Psi }^{{\displaystyle \frac{t_k-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_c}}}F{\Omega }^{{\displaystyle \frac{{\left[{\xi }_{2k}\right]}^{+}-{\left[{\xi }_{2k-1}\right]}^{+}}{{\tau }_c}}}J{\Psi }^{{\displaystyle \frac{{\left[{\xi }_{2k-1}\right]}^{+}-{\left[{\xi }_{2k-2}\right]}^{+}}{{\tau }_c}}}\times \hfill \\ & \dots \times F{\Omega }^{{\displaystyle \frac{{\left[{\xi }_2\right]}^{-}-{\left[{\xi }_1\right]}^{+}}{{\tau }_c}}}J{\Psi }^{{\displaystyle \frac{{\left[{\xi }_1\right]}^{+}-{\left[{\xi }_0\right]}^{+}}{{\tau }_c}}}{V}_{\sigma }\left(t_0\right)\hfill \\ \hfill \le & J{\Psi }^{k-1-{\displaystyle \frac{{\xi }_{2k}}{{\tau }_c}}}{(FJ\Omega /\Psi )}^k{\Omega }^{{\displaystyle \frac{k{T}_k^{+}}{{\tau }_c}}}{\Psi }^{{\displaystyle \frac{k{T}_k^{-}}{{\tau }_c}}}{V}_{\sigma }\left(t_0\right)\hfill \\ \hfill =& \Gamma {\Psi }^{k-{\displaystyle \frac{{\xi }_{2k}}{{\tau }_c}}}{\left\{{(FJ\Omega /\Psi )}^{{\tau }_c}{\Omega }^{T_k^{+}}{\Psi }^{T_k^{-}}\right\}}^{{\displaystyle \frac{k}{{\tau }_c}}}{V}_{\sigma }\left(t_0\right)\hfill \end{array}$$

(23)

by recalling $\Psi <1$ and $\Omega >1$, where $\Gamma =J/\Psi$. If Condition 4 holds, one gets

$$\begin{array}{c}\hfill V_{\sigma }\left(t_k\right)\le \Gamma {\Psi }^{k-{\displaystyle \frac{{\xi }_{2k}}{{\tau }_c}}}{Z}^{{\displaystyle \frac{{\xi }_{2k}}{{\tau }_c}}}{V}_{\sigma }\left(t_0\right)\le \Gamma Z^k{V}_{\sigma }\left(t_0\right)\end{array}$$

due to $1>Z>\Psi$ and $t_k\ge {\xi }_{2k}$.

Otherwise, if $t_k$ lies within an unstabilizable subinterval, i.e. $t_k\in [{\xi }_{2k+1},{\xi }_{2k+2})$ for some $k\in {\mathbb{Z}}_{\ge 0}$, we have

$$\begin{array}{cc}\hfill V_{\sigma }\left(t_k\right)\le & F{\Omega }^{{\displaystyle \frac{t_k-{\left[{\xi }_{2k+1}\right]}^{+}}{{\tau }_c}}}J{\Psi }^{{\displaystyle \frac{{\left[{\xi }_{2k+1}\right]}^{+}-{\left[{\xi }_{2k}\right]}^{+}}{{\tau }_c}}}F{\Omega }^{{\displaystyle \frac{{\left[{\xi }_{2k}\right]}^{+}-{\left[{\xi }_{2k-1}\right]}^{+}}{{\tau }_c}}}\times \hfill \\ & \dots \times F{\Omega }^{{\displaystyle \frac{{\left[{\xi }_2\right]}^{+}-{\left[{\xi }_1\right]}^{+}}{{\tau }_c}}}J{\Psi }^{{\displaystyle \frac{{\left[{\xi }_1\right]}^{+}-{\left[{\xi }_0\right]}^{+}}{{\tau }_c}}}{V}_{\sigma }\left(t_0\right)\hfill \\ \hfill \le & {\left\{{(FJ\Omega /\Psi )}^{{\tau }_c}{\Omega }^{T_k^{+}}{\Psi }^{T_k^{-}}\right\}}^{{\displaystyle \frac{k+1}{{\tau }_c}}}{V}_{\sigma }\left(t_0\right)\hfill \\ \hfill \le & Z^{k+1}{V}_{\sigma }\left(t_0\right)\le \Gamma Z^k{V}_{\sigma }\left(t_0\right)\hfill \end{array}$$

by recalling $Z<1<\Gamma$.

Summarized above, it is obvious that

$$\begin{array}{c}\hfill V_{\sigma }\left(t_k\right)\le \Gamma Z^k{V}_{\sigma }\left(t_0\right)\end{array}$$

(24)

always holds. If we let $\overline{\mu }=max\{\vartheta ,\pi ,\omega \}$ and $lnZ=-\phi <0$, one has

$$\begin{array}{c}\hfill V_{\sigma }\left(t\right)\le \Gamma e^{\overline{\mu }(t-t_k)}{e}^{-\phi (t_k-t_0)}{V}_{\sigma }\left(t_0\right),\forall t\in [t_k,t_{k+1})\end{array}$$

(25)

for all $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$. The lemma is proved. □

4. Stability Analysis

4.1. State Trajectory Analysis

First, we analyze the state behavior outside of ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$. The following lemma demonstrates that every trajectory with an initial state satisfying Condition 1 will never leave a larger intersection and fall into ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ at a finite time (see Figure 3). In such a figure, ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta ),{\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta )$, ${\bigcap }_{p\in \Pi }\epsilon (P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}})$ and ${\bigcup }_{p\in \Pi }\epsilon (P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}})$ are not necessarily ellipses, and $\{x:Q(x)=0\}$ is not necessarily a rectangle. Such a drawing is just for ease of understanding.

Remark 5. 

Under the influence of multiple factors (quantization, saturation, sampling, and unstabilizable subsystems), it is particularly important to define the attraction domain and the invariant set reasonably to analyze the evolution trend in the state trajectory. This paper defines an attractor domain ${\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$ and an invariant set ${\bigcup }_{p\in \Pi }\epsilon \left(P_p,\kappa \theta \right)$ based on the intersection and union of ellipses, respectively, which lays the foundation for system stability analysis.

Lemma 4. 

If we let Assumptions 1–2 and Conditions 1–5 hold, one can find a finite time ${\tau }_r\ge 0$ such that $x\left({\tau }_r\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ for any $\sigma \left(0\right)\in {\Pi }_s$. Moreover, it holds that $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right),\forall t\ge 0$.

Proof.  

Suppose that there exists a time instant $T_R$ such that $x\left(T_R\right)\in \partial \left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$, and furthermore

$$x\left(t\right)\in \mathrm{Int}\left(\bigcup _{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus \bigcup _{p\in \Pi }\epsilon (P_p,\theta ),\forall t\in [0,T_R).$$

This means that $x^T\left(T_R\right)P_{p}x\left(T_R\right)\ge {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}$ for any $p\in \Pi$. If we recall that ${\psi }_{\sigma }\left(t\right)\ge {\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}},\forall t\ge 0$, one gets $V_{\sigma }\left(T_R\right)\ge \varphi$.

However, due to

$$\begin{array}{cc}\hfill V_{\sigma }\left(t_0\right)=& {\psi }_{\sigma \left(t_0\right)}\left(t_0\right)x_0^T{P}_{\sigma \left(t_0\right)}{x}_0={\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}{x}_0^T{P}_{\sigma \left(t_0\right)}{x}_0\le {\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}·{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\le 1\hfill \end{array}$$

(26)

by considering Condition 1, (16) tells us that

$$\begin{array}{c}\hfill V_{\sigma }\left(T_R\right)\le \Gamma e^{\overline{\mu }(T_R-t_k)}{e}^{-\phi (t_k-t_0)}{V}_{\sigma }\left(t_0\right)<\varphi ,\forall T_R\in [t_k,t_{k+1}).\end{array}$$

Then, we have a contradiction. Hence, $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$ holds for any $t\ge 0$.

Now, let us prove $x\left({\tau }_r\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$. Assuming that $x\left(t\right)\notin {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta ),\forall t\ge 0$, one has

$$x\left(t\right)\in \mathrm{Int}\left(\bigcup _{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus \bigcup _{p\in \Pi }\epsilon (P_p,\theta ),\forall t\ge 0.$$

According to Lemma 3, (16) always holds for all $t\ge 0$. Hence, ${lim}_{t\to \infty }{V}_{\sigma }\left(x\left(t\right)\right)=0$. If we recall that ${\lambda }_{min}\left(P_{\sigma }\right){\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}{\parallel x\left(t\right)\parallel }^2\le V_{\sigma }\left(x\left(t\right)\right)$, it yields ${lim}_{t\to \infty }{\parallel x\left(t\right)\parallel }^2=0$. However, this contradicts $x\left(t\right)\notin {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, i.e., ${\lambda }_{max}\left(P_p\right){\parallel x\left(t\right)\parallel }^2\ge x^T\left(t\right)P_{p}x\left(t\right)\ge \theta ,\forall p\in \Pi$, which results in

$$\underset{t\to \infty }{lim}{\parallel x\left(t\right)\parallel }^2\ge {\displaystyle \frac{\theta }{{\lambda }_{max}\left(P_p\right)}}.$$

Thus, one can find ${\tau }_r\ge 0$ such that $x\left({\tau }_r\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$. This concludes the proof. □

The following lemma demonstrates that the state trajectory remains within an ellipsoid slightly larger than ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ after it enters into ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ (see Figure 3).

Lemma 5. 

Let Assumptions 1–2 and Conditions 1–2 hold. Assume that

$$\begin{array}{c}\hfill \kappa =\Gamma e^{2\overline{\mu }{\tau }_c}{\mu }^{{\tau }_c}\end{array}$$

(27)

satisfies $\epsilon (P,\kappa \theta )\subset {\bigcap }_{p\in \Pi }\epsilon (P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}})$. If we suppose that ${\tau }_0$ denotes a time instant at which $x\left(t\right)$ exits ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, then there exists ${\tau }_1>{\tau }_0$ such that $x\left({\tau }_1\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, and moreover, $x\left(t\right)\in {\bigcup }_{p\in \Pi }\left(\epsilon (P_p,\kappa \theta )\right)$ for any $t\in [{\tau }_0,{\tau }_1]$.

Proof.  

If trajectory $x\left(t\right)$ leaves ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ at time $t={\tau }_0$, it is obvious that $\sigma \left({\tau }_0\right)$ belongs to Cases 2, 3, or 4. Hence, $V_{\sigma }\left({\left[{\tau }_0\right]}^{+}\right)\le e^{\overline{\mu }({\left[{\tau }_0\right]}^{+}-{\tau }_0)}{V}_{\sigma }\left({\tau }_0\right)$ holds with $\overline{\mu }$ defined in (25). Combined with (16), this yields

$$\begin{array}{c}\hfill V_{\sigma }\left(t\right)\le \Gamma e^{\overline{\mu }(t-t_k)}{e}^{-\phi (t_k-{\left[{\tau }_0\right]}^{+})}{e}^{\overline{\mu }({\left[{\tau }_0\right]}^{+}-{\tau }_0)}{V}_{\sigma }\left({\tau }_0\right)\end{array}$$

(28)

for any $t\in [t_k,t_{k+1})$ satisfying $t>{\tau }_0$ and $x\left(t^{\prime }\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\setminus {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, $\forall t^{\prime }\in ({\tau }_0,t]$.

Considering that $x\left({\tau }_0\right)\in \partial {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ yields $x^T\left({\tau }_0\right)P_{\sigma \left({\left[{\tau }_0\right]}^{-}\right)}x\left({\tau }_0\right)\le \theta$, one has $V_{\sigma }\left({\tau }_0\right)\le {\eta }^{\ast }\theta$ by recalling that ${\psi }_p\left(t\right)\le {\eta }^{\ast },\forall t\ge 0$. Combined with (28), this induces

$$\begin{array}{cc}\hfill V_{\sigma }\left(t\right)\le & \Gamma e^{2\overline{\mu }{\tau }_c}{e}^{-\phi (t_k-{\left[{\tau }_0\right]}^{+})}{\eta }^{\ast }\theta \le \Gamma e^{2\overline{\mu }{\tau }_c}{\eta }^{\ast }\theta ,\forall t\in [t_k,t_{k+1}),\hfill \end{array}$$

indicating that

$$x^T\left(t\right)P_{{\sigma }_k}x\left(t\right)\le \Gamma e^{2\overline{\mu }{\tau }_c}{\eta }^{\ast }\theta {\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}=\kappa \theta .$$

This implies that $x\left(t\right)\in {\bigcup }_{p\in \Pi }\left(\epsilon (P_p,\kappa \theta )\right),\forall t\ge {\tau }_0.$ Similar to the analysis of Lemma 4, it must be a time ${\tau }_1$ such that $x\left({\tau }_1\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, which completes the proof. □

4.2. Main Results

Theorem 1. 

Provided that Assumptions 1–2 and Conditions 1–5 are fulfilled, for the constants Γ and $\overline{\mu }$ given in (23) and (25), respectively, if $\kappa >1$ in (27) satisfies ${\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta )\subset {\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$, then one can find a finite time ${\tau }_r>0$ ensuring that $x\left(t\right)\in {\bigcup }_{p\in \Pi }\epsilon \left(P_p,\kappa \theta \right),\forall t\ge {\tau }_r$, and furthermore, $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$, $\forall t\ge 0$ with $\varphi =\Gamma e^{\overline{\mu }{\tau }_c}$.

Proof.  

First, Lemma 4 guarantees that

$$x\left(t\right)\in \mathrm{Int}\left(\bigcup _{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right),\forall t\ge 0.$$

Second, Lemma 4 also induces that there is finite time ${\tau }_r>0$ such that $x\left({\tau }_r\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$. If $x\left(t\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta ),\forall t\ge {\tau }_r$, it is obvious that $x\left(t\right)\in {\bigcup }_{p\in \Pi }\left(\epsilon (P,\kappa \theta )\right),\forall t\ge {\tau }_r$ holds due to $\kappa >1$. Otherwise, if there exists a ${\tau }_0$ such that $x\left({\tau }_0\right)$ leaves ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, then Lemma 5 guarantees the existence of ${\tau }_1>{\tau }_0$ satisfying $x\left({\tau }_1\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ and $x\left(t\right)\in {\bigcup }_{p\in \Pi }\left(\epsilon (P_p,\kappa \theta )\right),\forall t\in [{\tau }_0,{\tau }_1]$. Therefore, no matter how many times the state escapes from the ellipse ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$, we can always get $x\left(t\right)\in {\bigcup }_{p\in \Pi }\left(\epsilon (P,\kappa \theta )\right),\forall t\ge {\tau }_0$. Then, Theorem 1 is established. □

4.3. Establishment of Claim 1

Based on Theorem 1, if Assumptions 1–2, Conditions 1–2, and ${\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta )\subset {\bigcap }_{p\in \Pi }\epsilon (P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}})$ hold, one has

$$x\left(t\right)\in \mathrm{Int}\left(\bigcup _{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)\subset \mathrm{Int}\left(\bigcup _{p\in \Pi }\iota \left(G_p\right)\right),\forall t\ge 0$$

by using Condition 2. But this does not mean that $x_k\in \iota \left(G_{{\sigma }_k}\right)$. Next, we will verify that Claim 1, i.e., $x_k\in \iota \left(G_{{\sigma }_k}\right)$, holds for two cases.

If $t_k\ge {\tau }_r$, by Theorem 1, one has

$$\begin{array}{cc}\hfill x_k& \in \bigcup _{p\in \Pi }\left(\epsilon (P_p,\kappa \theta )\right)\subset \bigcap _{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\subset \bigcap _{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\subset \bigcap _{p\in \Pi }\iota \left(G_p\right)\subset \iota \left(G_{{\sigma }_k}\right).\hfill \end{array}$$

(29)

Otherwise, if $t_k<{\tau }_r$, then (24) yields $V_{\sigma }\left(t_k\right)\le \Gamma Z^k{V}_{\sigma }\left(t_0\right)$. Due to $Z<1$ and $V_{\sigma }\left(t_0\right)\le 1$ given in (26), it is obvious that

$$\begin{array}{cc}\hfill V_{\sigma }\left(t_k\right)=& {\psi }_{{\sigma }_k}\left(t_k\right)x^T\left(t_k\right)P_{{\sigma }_k}{x}_k={\displaystyle \frac{{\eta }^{\ast }}{{\mu }^{{\tau }_c}}}{x}^T\left(t_k\right)P_{{\sigma }_k}{x}_k<\Gamma .\hfill \end{array}$$

Hence, $\varphi =\Gamma e^{\overline{\mu }{\tau }_c}\ge \Gamma$ implies that $x^T\left(t_k\right)P_{{\sigma }_k}{x}_k<{\displaystyle \frac{\Gamma {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\le {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}$, i.e., $x_k\in \epsilon (P_{{\sigma }_k},{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}})$. If we recall Condition 2, one has

$$\begin{array}{c}\hfill x_k\in \iota \left(G_{{\sigma }_k}\right),\forall t_k<{\tau }_r.\end{array}$$

(30)

By summarizing (29) and (30), the claim is established.

5. Controller Design

The design method of the controller (3) is formulated in the following theorem.

Theorem 2. 

Provided that Assumptions 1–2 and Conditions 1–1 are fulfilled, for the specified scalars $\mu >1,\overline{\varpi }>0,\overline{\vartheta }>0,\overline{\pi }>0,\overline{\omega }>0$ and $p\in \Pi$, there exist matrices $X_p>0$, $Y_p$, and $H_p$ such that

$$\begin{array}{}\mathrm{(31)}& & (ln\mu )X_i+A_i{X}_i+X_i{A}_i^T+B_i(E_{is}{Y}_i+E_{is}^{-}{H}_i)+{(E_{is}{Y}_i+E_{is}^{-}{H}_i)}^T{B}_i^T+\overline{\varpi }{X}_i<0\hfill \mathrm{(32)}& & (ln\mu )X_i+A_p{X}_i+X_i{A}_p^T+B_p(E_{is}{Y}_i+E_{is}^{-}{H}_i)+{(E_{is}{Y}_i+E_{is}^{-}{H}_i)}^T{B}_p^T-\overline{\vartheta }{X}_i<0\hfill \mathrm{(33)}& & (ln\mu )X_j+A_j{X}_j+X_j{A}_j^T+B_j(E_{js}{Y}_j+E_{js}^{-}{H}_j)+{(E_{js}{Y}_j+E_{js}^{-}{H}_j)}^T{B}_j^T-\overline{\pi }{X}_j<0\hfill \mathrm{(34)}& & (ln\mu )X_j+A_p{X}_j+X_j{A}_p^T+B_p(E_{js}{Y}_j+E_{js}^{-}{H}_j)+{(E_{js}{Y}_j+E_{js}^{-}{H}_j)}^T{B}_p^T-\overline{\omega }{X}_j<0\hfill \mathrm{(35)}& & \left[\begin{array}{cc}-{\mu }^{{\tau }_c}{X}_j& X_j\\ X_j& -X_i\end{array}\right]\le 0,\left[\begin{array}{cc}-{\mu }^{{\tau }_c}{X}_i& X_i\\ X_i& -X_j\end{array}\right]\le 0,\hfill \mathrm{(36)}& & \left[\begin{array}{cc}{\displaystyle \frac{\zeta {\eta }^{\ast }}{\varphi {\mu }^{{\tau }_c}}}& h_{pl}\\ h_{pl}^T& X_p\end{array}\right]\ge 0\hfill \end{array}$$

hold for any $i\in {\Pi }_s$, $j\in {\Pi }_u$, and $s\in \{1,\dots ,2^{n_u}\}$; then, the exponential stability of the switched systems (1) is ensured under the controller (3) with $K_p=Y_p{X}_p^{-1}$.

Proof.  

$P_p=X_p^{-1}$, $Y_p=K_p{X}_p$, and $H_p=G_p{X}_p$ are defined. Pre-multiplying and post-multiplying (31) and (32) by $P_i$ yield (11) and (12), respectively. Similarly, pre-multiplying and post-multiplying (33) and (34) by $P_j$ imply that (13) and (14) hold, respectively. Moreover, by using Schur complement, (35) is obviously equal to (15).

Next, the Lagrangian method is used to verify if Condition 5 holds; then, $\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\subset \iota \left(G_p\right)$ shown in Condition 2 is equivalent to (36).

It should be noted that $\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\subset \iota \left(G_p\right)$ if and only if all the hyperplanes $f_{pl}Q\left(x\right)=\pm 1$ lie completely outside of the ellipsoid

$$\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)=\left\{x\in {\mathbb{R}}^n:x^T{P}_{p}x\le {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right\}$$

For any $l\in \{1,2,\dots ,n_u\}$, i.e., at each point x on the hyperplanes $f_{pl}Q\left(x\right)=\pm 1$, we have $x^T{P}_{p}x\ge {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}$. Hence, $\epsilon (P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}})\subset \iota \left(G_p\right)$ is equivalent to

$$min\left\{x^T{P}_{p}x:f_{pl}Q\left(x\right)=1\right\}\ge {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}.$$

(37)

The solution of $min\left\{x^T{P}_{p}x:f_{pl}Q\left(x\right)=1\right\}$ can be regarded as a quadratic programming problem:

$$\left\{\begin{array}{c}min\left\{x^T{P}_{p}x\right\},\hfill \\ s.t.f_{pl}x=1-f_{pl}e,\hfill \end{array}\right.$$

where $e=Q\left(x\right)-x$. The Lagrangian function is defined as $L(x,\lambda )=x^T{P}_{p}x-{\lambda }^T(f_{pl}x-(1-f_{pl}e))$. If we let ${\nabla }_{x}L(x,\lambda )=0$ and ${\nabla }_{\lambda }L(x,\lambda )=0$, then we have

$$\left\{\begin{array}{c}2P_{p}x-f_{pl}^T\lambda =0\hfill \\ -f_{pl}x=-(1-f_{pl}e).\hfill \end{array}\right.$$

The above equations in matrix block form can be rewritten as follows:

$$\left[\begin{array}{cc}2P_p& -f_{pl}^T\\ -f_{pl}& 0\end{array}\right]\left[\begin{array}{c}x\\ \lambda \end{array}\right]=\left[\begin{array}{c}0\\ -(1-f_{pl}e)\end{array}\right],$$

We get the solution of $min\left\{x^T{P}_{p}x:f_{pl}Q\left(x\right)=1\right\}$ as

$$\left[\begin{array}{c}\overline{x}\\ \overline{\lambda }\end{array}\right]=\left[\begin{array}{cc}{\overline{F}}_p& -{\overline{B}}_p^T\\ -{\overline{B}}_p& {\overline{C}}_p\end{array}\right]\left[\begin{array}{c}0\\ -(1-f_{pl}e)\end{array}\right],$$

where

$$\begin{array}{cc}\hfill {\overline{F}}_p& ={\left(2P_p\right)}^{-1}-{\left(2P_p\right)}^{-1}{f}_{pl}^T{\left(f_{pl}{\left(2P_p\right)}^{-1}{f}_{pl}^T\right)}^{-1}{f}_{pl}{\left(2P_p\right)}^{-1},\hfill \\ \hfill {\overline{B}}_p& ={\left(f_{pl}{\left(2P_p\right)}^{-1}{f}_{pl}^T\right)}^{-1}{f}_{pl}{\left(2P_p\right)}^{-1},\hfill \\ \hfill {\overline{C}}_p& =-{\left(f_{pl}{\left(2P_p\right)}^{-1}{f}_{pl}^T\right)}^{-1}.\hfill \end{array}$$

Then, it is obvious that

$$\begin{array}{c}\hfill \overline{x}={\overline{B}}_p^T(1-f_{pl}e)={\left[{\left(f_{pl}{P}_p^{-1}{f}_p^T\right)}^{-1}{f}_{pl}{P}_p^{-1}\right]}^T(1-f_{pl}e),\end{array}$$

and thus, ${\overline{x}}^T{P}_p\overline{x}={(1-f_{pl}e)}^2{\left(f_{pl}{P}_p^{-1}{f}_{pl}^T\right)}^{-1}$. Hence, (37) is equal to

$$\begin{array}{c}\hfill {(1-f_{pl}e)}^2\ge {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\left(f_{pl}{P}_p^{-1}{f}_{pl}^T\right).\end{array}$$

(38)

Assuming that a constant $\zeta \in (0,1)$ exists, satisfying ${(1-f_{pl}e)}^2\ge \zeta$ and $\zeta \ge {\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\left(f_{pl}{P}_p^{-1}{f}_{pl}^T\right)$, then (38) is obviously guaranteed. On the one hand, ${(1-f_{pl}e)}^2\ge \zeta$ can be obtained by Condition 5. Furthermore, according to Schur complement, (36) can be rewritten as $h_{pl}{X}_p^{-1}{h}_{pl}^T\le {\displaystyle \frac{\zeta {\eta }^{\ast }}{\varphi {\mu }^{{\tau }_c}}}$, which is obviously equal to $f_{pl}{P}_p^{-1}{f}_{pl}^T\le {\displaystyle \frac{\zeta {\eta }^{\ast }}{\varphi {\mu }^{{\tau }_c}}}$. Therefore, if Condition 5 and (36) hold, then $\epsilon (P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}})\subset \iota \left(G_p\right)$ can be guaranteed, which completes the proof. □

6. Optimizing the Domain of Attraction

If the solutions of Theorem 2 exist, we subsequently discuss the amplification of the attraction domain ${\bigcap }_{p\in \Pi }\epsilon (P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}})$. In fact, such a problem can be transformed into the constrained optimization problems: minimizing z satisfies the inequalities $P_p\le zI$. If we recall that $P_p=X_p^{-}$, then $P_p\le zI$ can be rewritten as

$$\left[\begin{array}{cc}zI& I\\ I& X_p\end{array}\right]\ge 0$$

(39)

by using Schur complement. Hence, the optimization problem of the attractive region is given by

$$\begin{array}{cc}\hfill \underset{X_p,Y_p,G_p}{min}& z,\forall i\in {\Pi }_s,j\in {\Pi }_u,p\in \Pi ,s\in [1,2^{n_u}],l\in [1,n_u]\hfill \\ & \mathrm{s}.\mathrm{t}.\mathrm{LMIs}\left(31\right)–\left(35\right)\mathrm{and}\left(39\right)\mathrm{hold}.\hfill \end{array}$$

7. Simulation

The effectiveness of the proposed control strategy is validated by using a borrowed two-tank system, which can be modeled as system (1) with $\Pi =\{1,2\}$ and $A_1=A_2=[-1,1;1,-1]$ [33]. To analyze the effect of unstabilizable subsystems on closed-loop system performance, we set $B_1=[1;0]$ and $B_2=[1;1]$. Obviously, subsystems 1 and 2 belong to ${\Pi }_s$ and ${\Pi }_u$, respectively.

For any $n\in {\mathbb{Z}}_{\ge 0}$, the static quantizer is defined as $Q\left(x\right)={[Q_1\left(x_1\right),Q_2\left(x_2\right)]}^T$ with

$$\begin{array}{c}\hfill Q_i\left(x_i\right)=\left\{\begin{array}{cc}{\displaystyle \frac{-{\iota }_0({\chi }^n+{\chi }^{n+1})}{2}},& \mathrm{if}{x}_i\ge -{\iota }_0{\chi }^{n+1},x_i<-{\iota }_0{\chi }^n\hfill \\ 0,& \mathrm{if}{x}_i\ge -{\iota }_0,x_i\le {\iota }_0\hfill \\ {\displaystyle \frac{{\iota }_0({\chi }^n+{\chi }^{n+1})}{2}},& \mathrm{if}{x}_i>{\iota }_0{\chi }^n,x_i\ge {\iota }_0{\chi }^{n+1},\hfill \end{array}\right.\end{array}$$

(40)

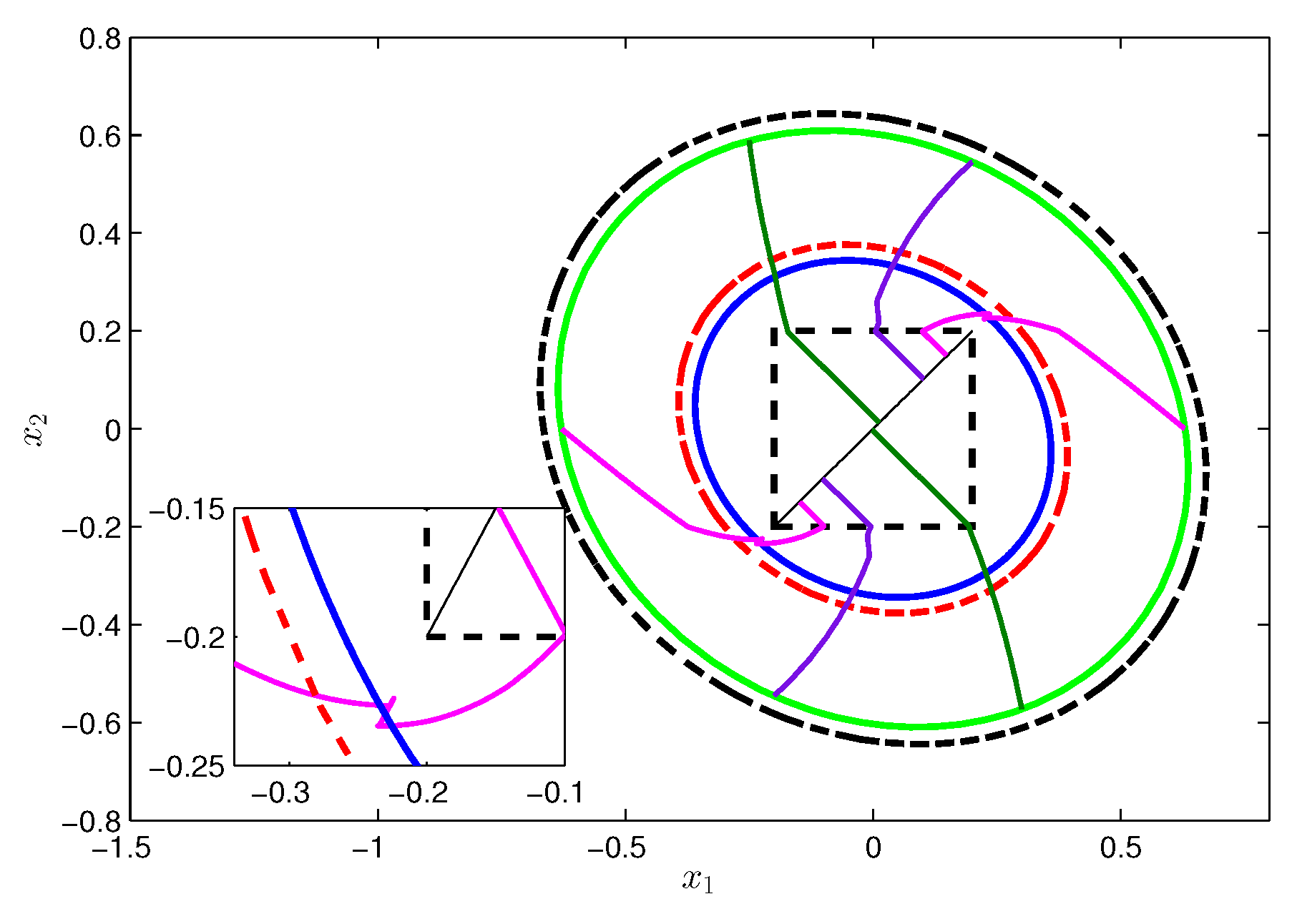
where ${\iota }_0=0.2$ and $\chi =1.1$. Obviously, the area $\{x:Q(x)=0\}$ is a square with the origin as the center and 0.4 as the side length, shown as the dotted square in Figure 4.

The variable design procedure is summarized as follows:

Step 1: Let ${\tau }_c=0.01,\mu =1.02$, z defined in (39) as $z=2$, and the variables in Lemma 3 as $\overline{\varpi }=0.5,\overline{\vartheta }=3.9,\overline{\pi }=3.5$ and $\overline{\omega }=6.6$.

Step 2: By solving the LMIs (31)–(35) and (39) by using matlab’s LMI toolbox, we get $X_1=X_2=[19.8568,2.7015;2.7015,18.2113]$, $Y_1=H_1=\left[-7.6301,-24.5729\right],Y_2=H_2=\left[23.4872,-10.7769\right]$. Then, we can easily get

$$\begin{array}{cc}& P_1=P_2=\left[\begin{array}{cc}0.0514& -0.0076\\ -0.0076& 0.0560\end{array}\right],\\ & K_1=\left[-0.2048,-1.3189\right],K_2=\left[1.2894,-0.7830\right].\end{array}$$

Step 3: By a simple calculation, one knows that ${\alpha }_0=2.24, {\varsigma }_0=0.0049, \Phi =0.0226,$${\alpha }_1=1.0438, {\beta }_1=0.0428$, and thus, $-\varpi =-0.1398<0$, which guarantees the establishment of (10). Similarly, we can get $\vartheta =4.0805,\pi =3.7027$ and $\omega =6.8027$, yielding $\overline{\mu }=6.8027$. Moreover, $\widehat{\varpi }=0.9986,\widehat{\vartheta }=1.0416,\widehat{\pi }=1.0014,$ and $\widehat{\omega }=1.0704$ hold. Assuming that $N_0=1$ and ${\tau }_a=100$, it is easy to see that $J=1.0431,\Psi =0.9986, F=1.0689$, and $\Omega =1.0014$, and thus, $\Gamma =1.0446$.

Step 4: To ensure (36), we need to pursue a suitable ${\eta }^{\ast }$. For the quantizer defined in (40), it is not hard to see that $\tilde{\delta }=0.0171$. Then, $\zeta$ in (9) can be chosen as $\zeta =0.96$. If we let ${\eta }^{\ast }=49$, we have $\kappa =1.1970$, and thus, (36) holds.

Step 5: If we let $\theta =0.0065$, by using the values of $\kappa ,\mu ,{\eta }^{\ast }$ and $\varphi$, then the ellipses ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ (blue solid line), ${\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta )$ (red dotted line), ${\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$ (green solid line), and ${\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\psi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$ (black dotted line) are shown in Figure 4.

Step 6: We set $T_k^{-}=9T_k^{+}$ to meet Condition 4. For the initial states located at $\partial \left({\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$ with ${\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}=0.0078$, the state trajectories of the closed-loop two-tank system are shown as colored polylines in Figure 4.

Analysis: From Figure 4, it can be observed that (1) $x\left(t\right)\in \mathrm{Int}\left({\bigcup }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{\varphi {\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$, $\forall t\ge 0$ if $x_0$ satisfies Condition 1 and that (2) one can find a finite time ${\tau }_r>0$ satisfying $x\left(t\right)\in {\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta ),\forall t\ge {\tau }_r$. Then, Theorem 1 is testified. Moreover, from the subfigure in Figure 4, we know that the state trajectories will never leave a slightly larger intersection ${\bigcup }_{p\in \Pi }\epsilon (P_p,\kappa \theta )$ rather than ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ upon entering ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$.

Since ${\dot{x}}_1+{\dot{x}}_2=0$ and ${\dot{x}}_1-{\dot{x}}_2=-2(x_1-x_2)$ when the control input $u\left(t\right)=0$, the state trajectories will eventually approach the dotted line $x_1=x_2$ instead of the origin once they reach the region $\{(x_1,x_2):-0.2\le x_1,x_2\le 0.2\}$, in which $Q\left(x\right)=0$, and thus, $u\left(t\right)=0$.

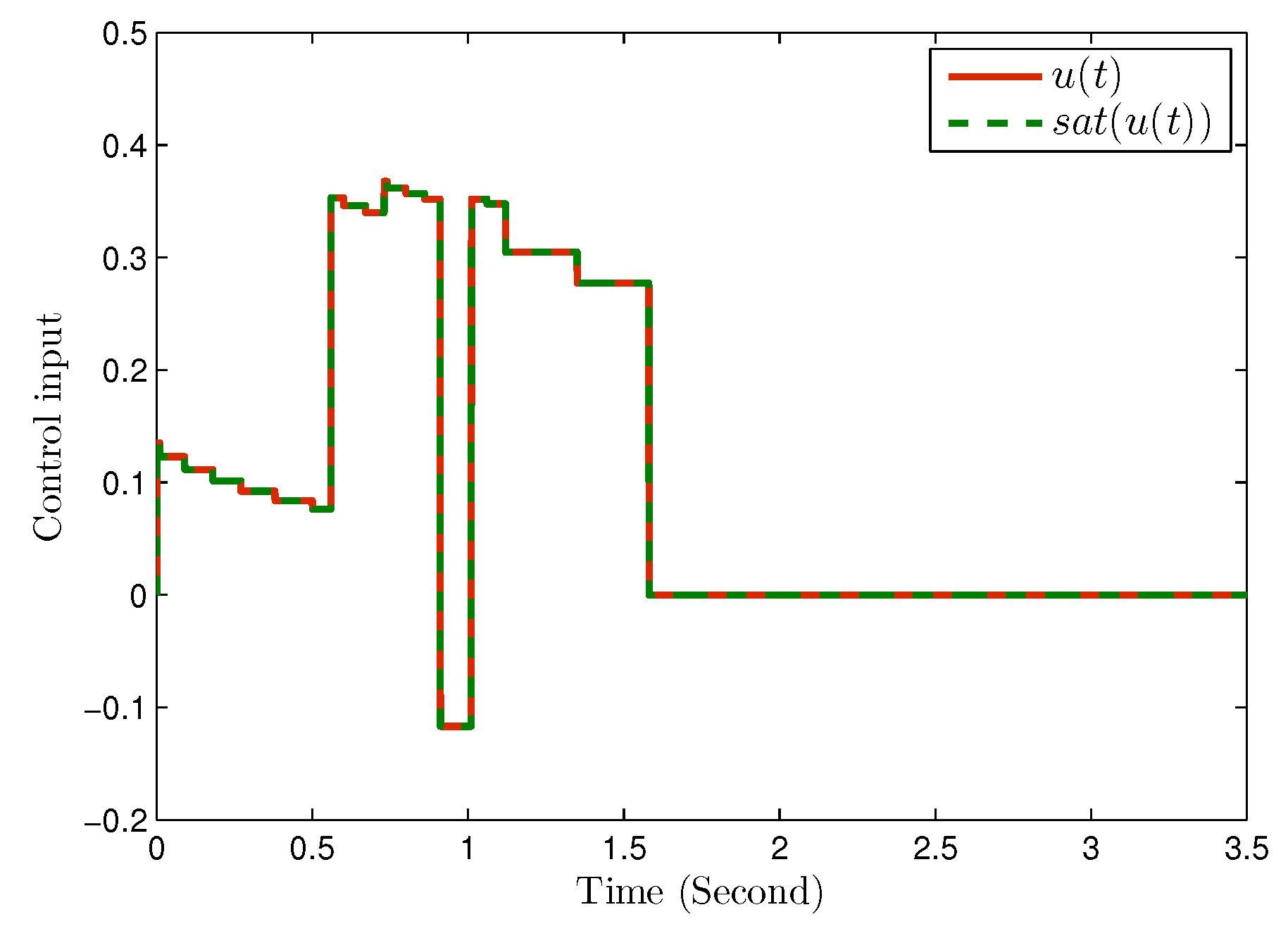
Step 7: Figure 5 presents the control input and the saturated control input. Obviously, saturation has no influence on the value of control input under the above variables, i.e., $u\left(t\right)\equiv sat\left(u\right(t\left)\right)$.

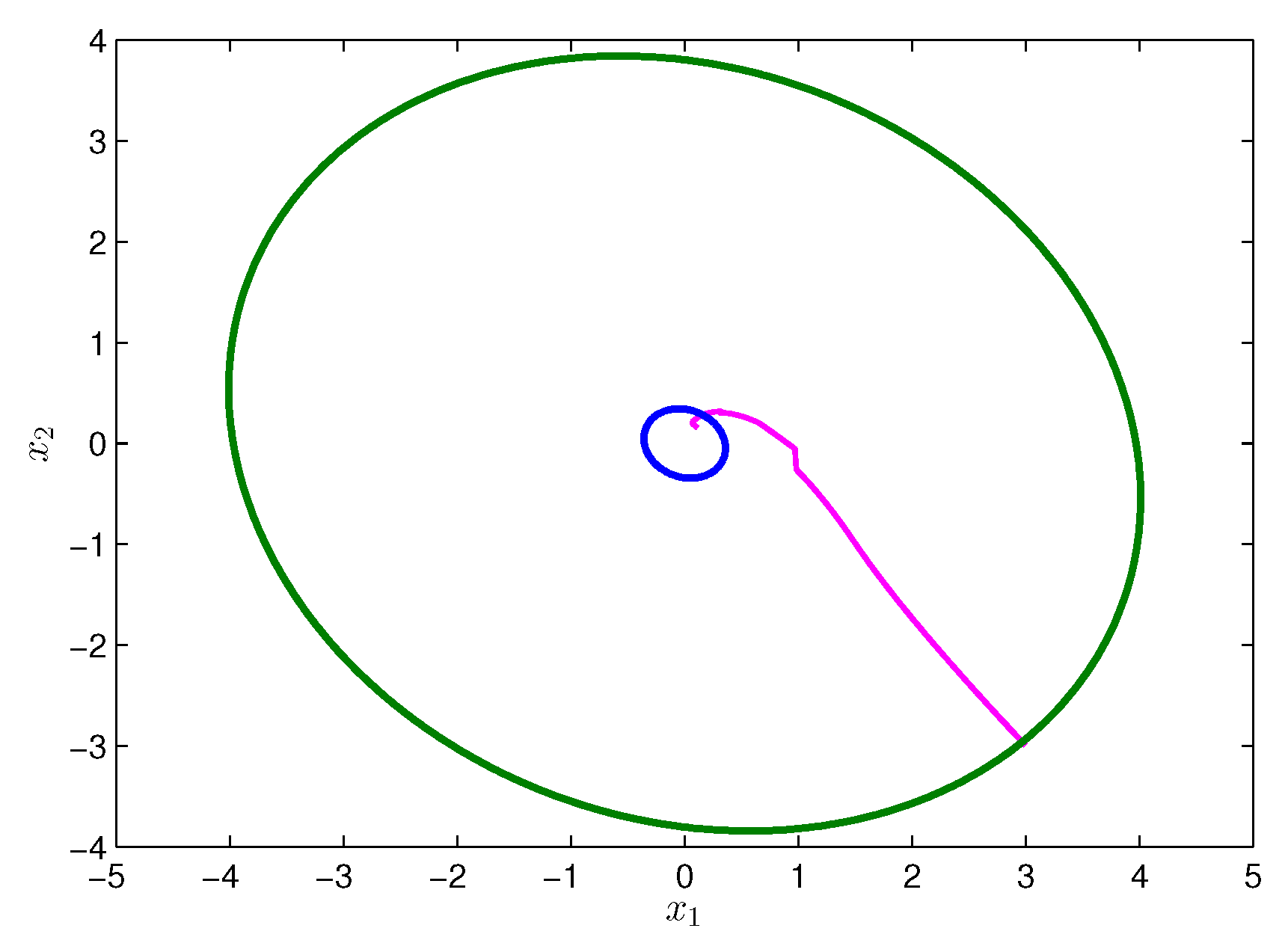
Step 8: To demonstrate the effect of saturation, for the initial state located at $\partial \left({\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)\right)$ with ${\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}=0.81$, the state trajectory of the closed-loop two-tank system is shown as a pink polyline in Figure 6, in which the ellipses ${\bigcup }_{p\in \Pi }\epsilon (P_p,\theta )$ are denoted by the blue solid line and ${\bigcap }_{p\in \Pi }\epsilon \left(P_p,{\displaystyle \frac{{\mu }^{{\tau }_c}}{{\eta }^{\ast }}}\right)$ is denoted by the green solid line. The corresponding control input and the saturated control input are shown in Figure 7. We can see that under the influence of saturation (i.e. $u\left(t\right)\ne sat\left(u\right(t\left)\right)$), the closed-loop system is still stable.

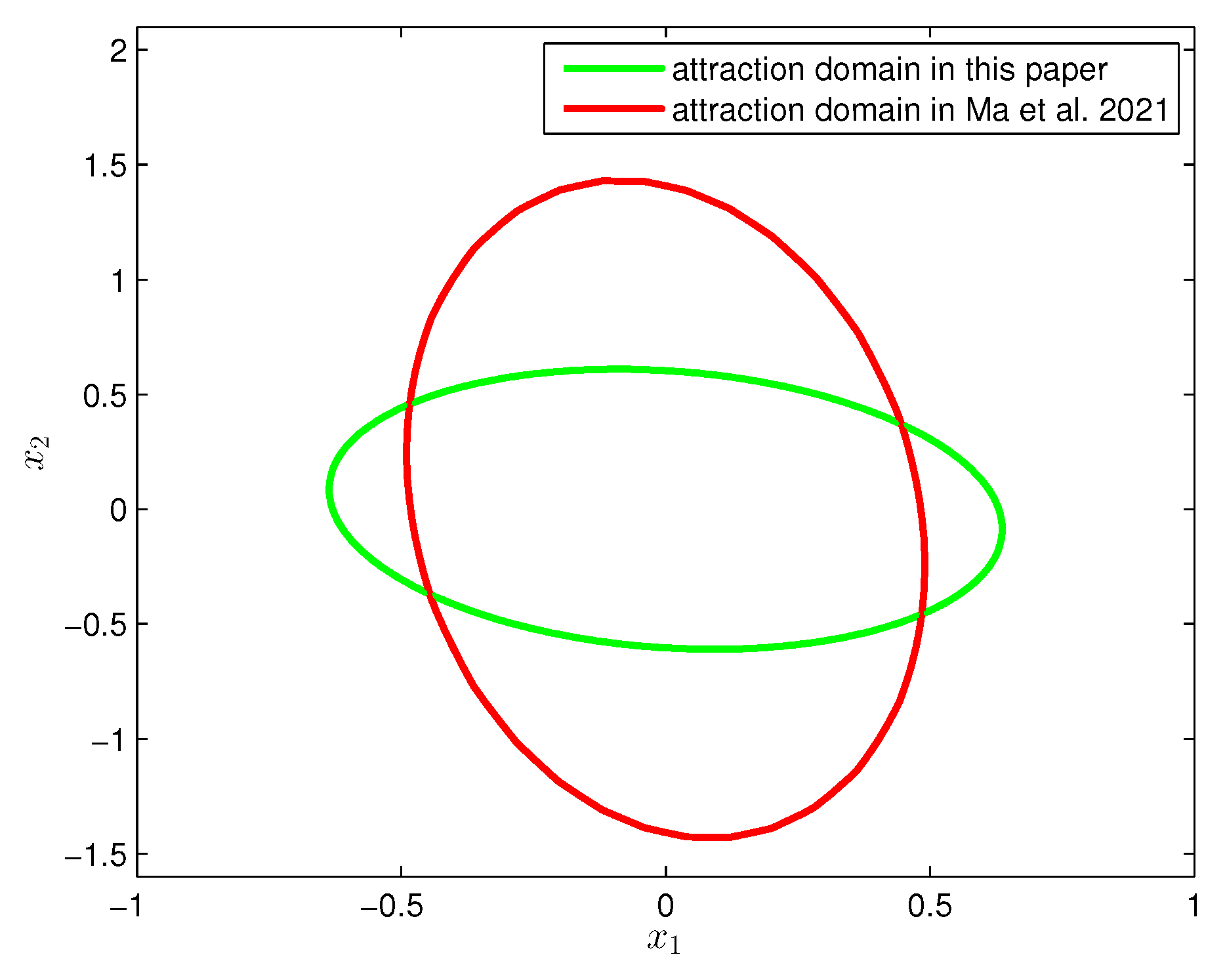
Comparison: To compare the results obtained in Ma et al. [31], the attraction domain obtained in our paper (green solid ellipse) and that (red dotted ellipse) obtained in Ma et al. [31] are given in Figure 8. From such a figure, we can see that the attraction domain obtained in this paper is smaller than the one in Ma et al. [31] due to the extra effects of sampling and data quantization. However, compared to the continuous data transmission adopted in Ma et al. [31], sampling can significantly reduce the volume of data transmission. In addition, the introduction of data quantization ensures that the algorithm proposed here can be used in the networked switched systems. It is worth mentioning that the domain attraction in this paper is not much smaller than the one in Ma et al. [31] due to the suitable design of quantization rules and ${\psi }_p\left(t\right)$ in the Lyapunov function.

8. Conclusions

The stabilization problem of the switched systems with partly unstabilizable subsystems with actuator saturation and data quantization was discussed in this paper. First, the saturated controller was rewritten as a linear combination of a sampling quantized feedback controller by setting a claim. Second, the increasing/decreasing rate of the Lyapunov function was obtained for different cases. On this basis, the sufficient conditions ensuring the stability of the closed-loop system were obtained, and the feedback matrices were designed by using the LMI method. Third, the predefined claim was established. Finally, the optimization problem for attractive regions was studied.

Future work may involve the joint design of controller and switching law to obtain better system performance. Some other network-induced factors, such as event-triggered transmission, packet loss, and time delay may be discussed. Moreover, given the underdeveloped experimental conditions, we were not able to experimentally verify the theoretical results obtained. We will strive to build relevant experimental platforms in the future and further conduct experimental verification on the basis of simulation.