Theory of Functional Connections Extended to Continuous Integral Constraints
Abstract
1. Introduction
2. Integral Invariant Functionals
2.1. Constrained Functionals for Initial Value Problems
Numerical Validation
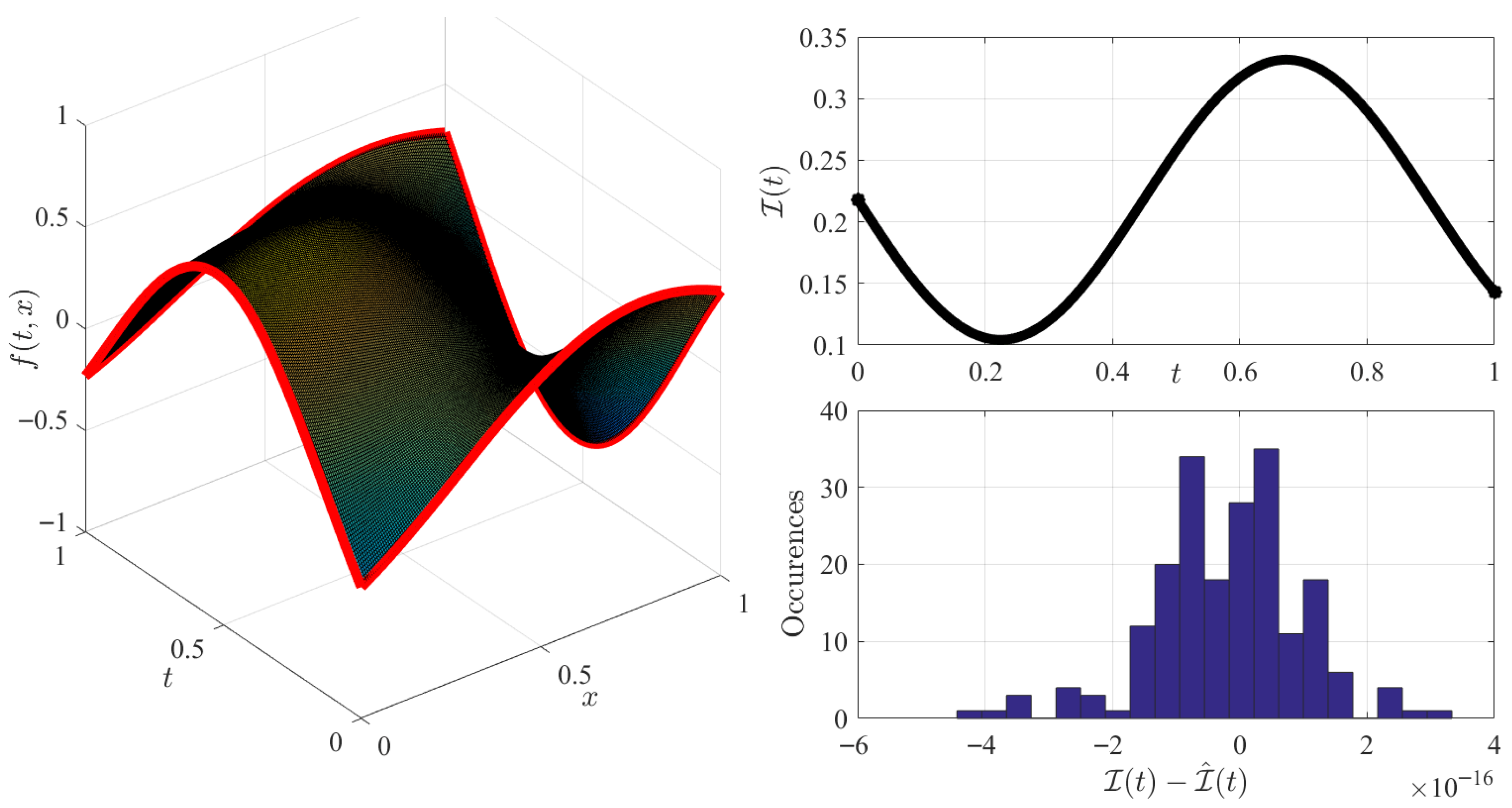
2.2. Constrained Functionals for Boundary Value Problems
Numerical Validation
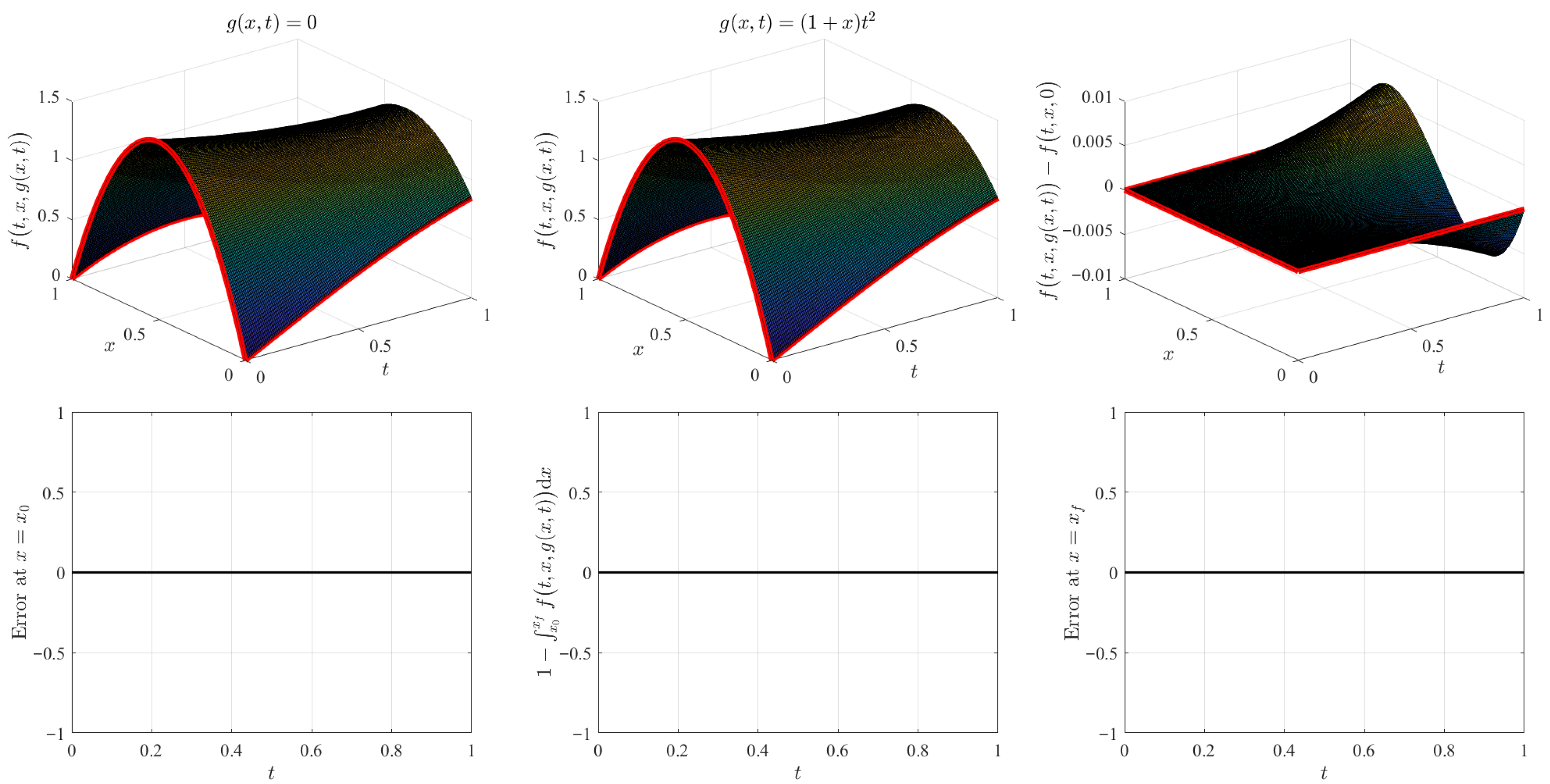
3. Time-Varying Integral Constrained Functionals
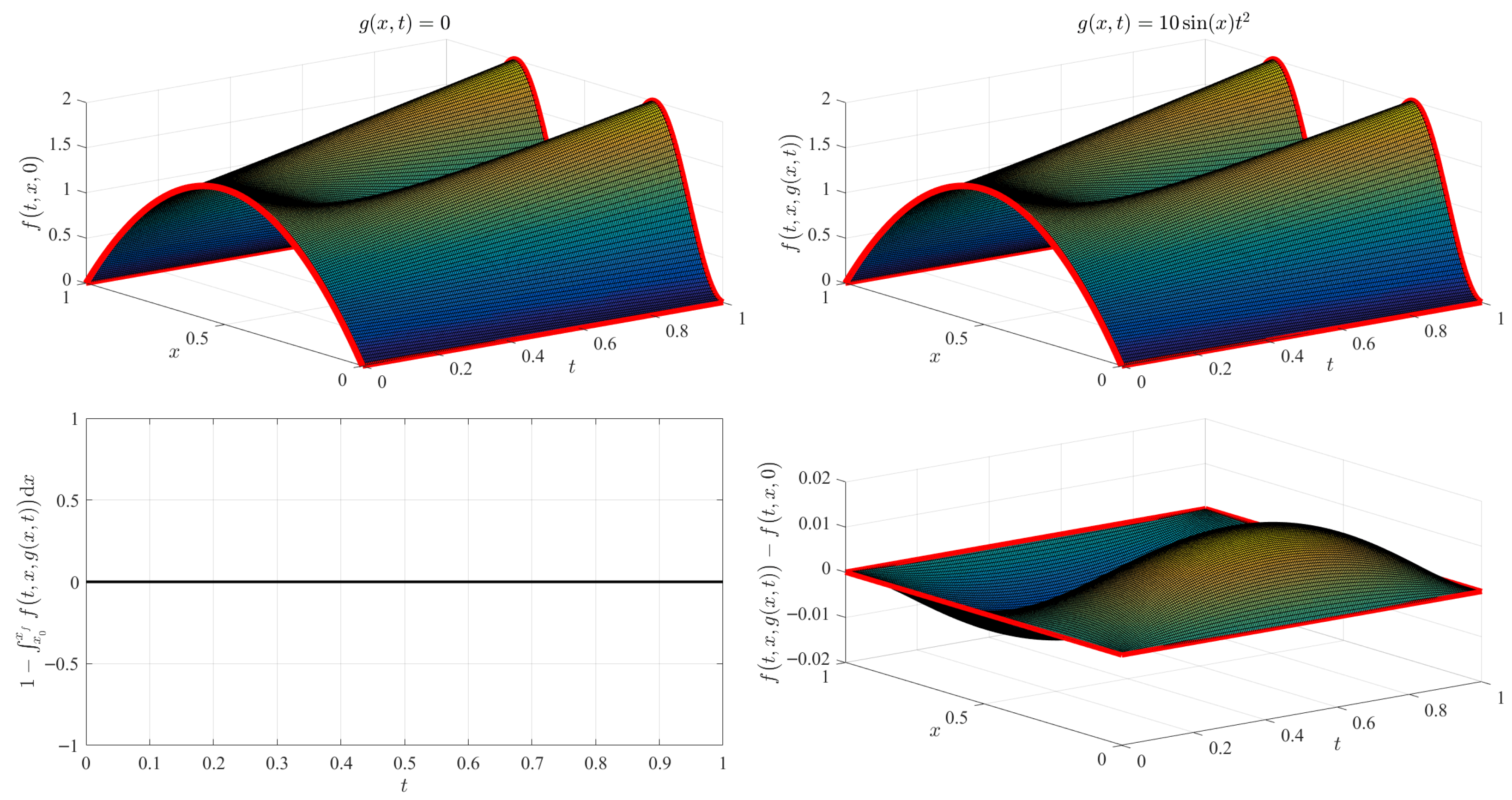
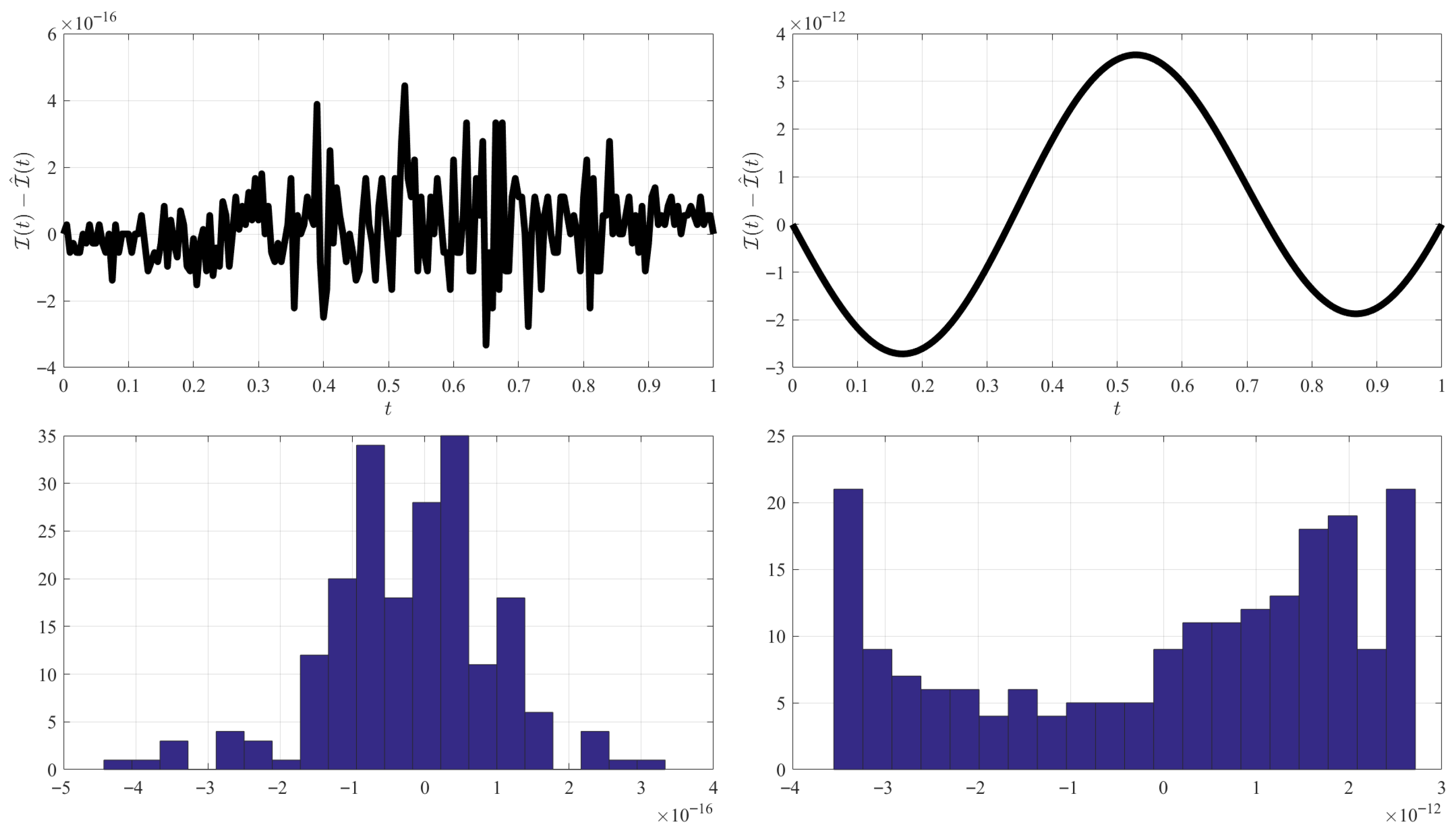
3.1. Numerical Validation
3.1.1. Interpolation Case
3.1.2. Functional Interpolation Case
- Note that, to obtain variations with functional interpolation, that is, using , the free function must be linearly independent of the support functions () used to derive the constrained functional in t. This means, for instance, that, using , the same surface would have been obtained as using (interpolation case).
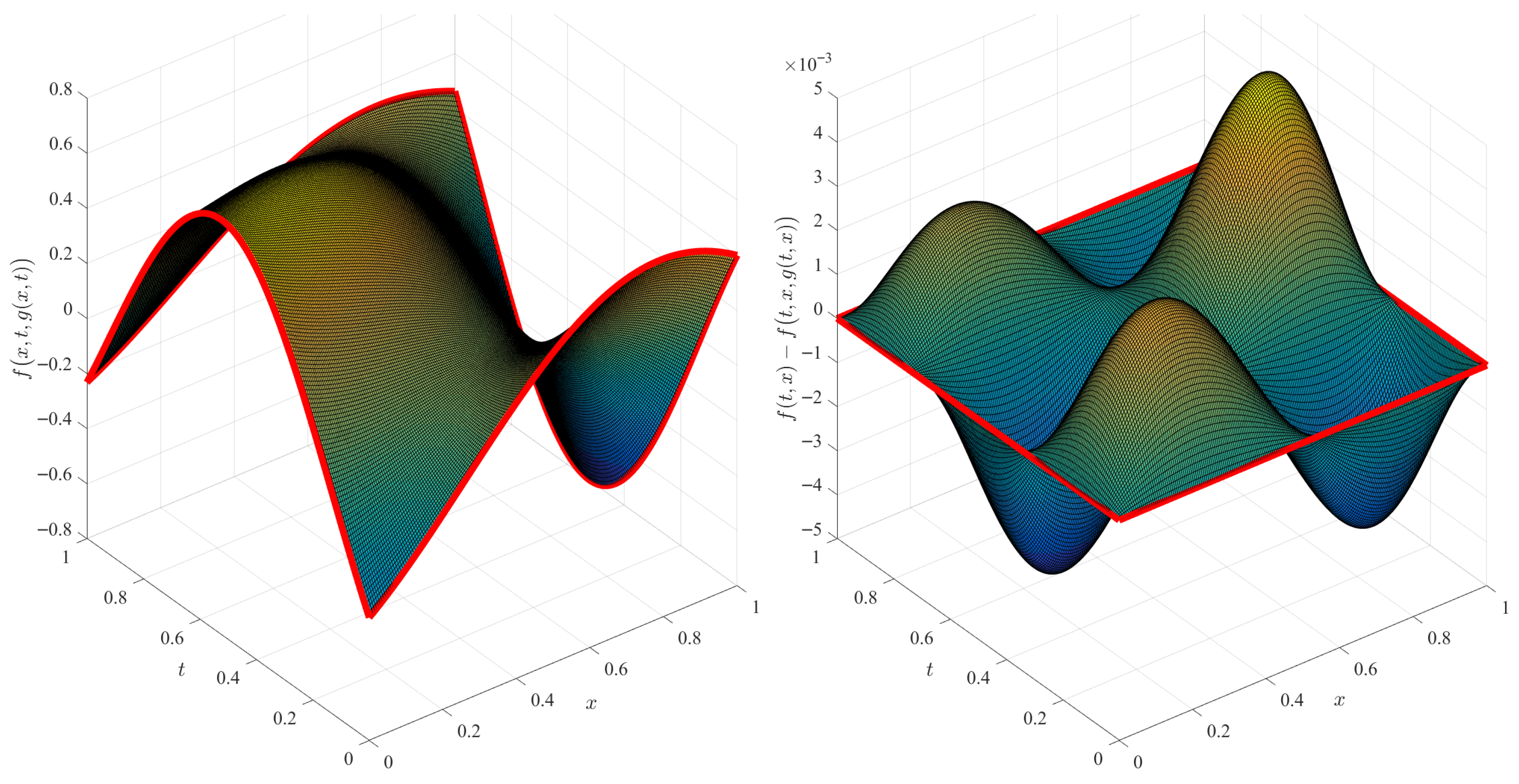
- Note that if the boundary constraints, and , and the integral constraint, , are all linear in t, then all and, consequently, all as well. The resulting interpolating surface will be a linear transformation from the initial to the final , and the prescribed integral would play no role.
4. Enforcing Positivity Constraint to Model Probability Density Functions
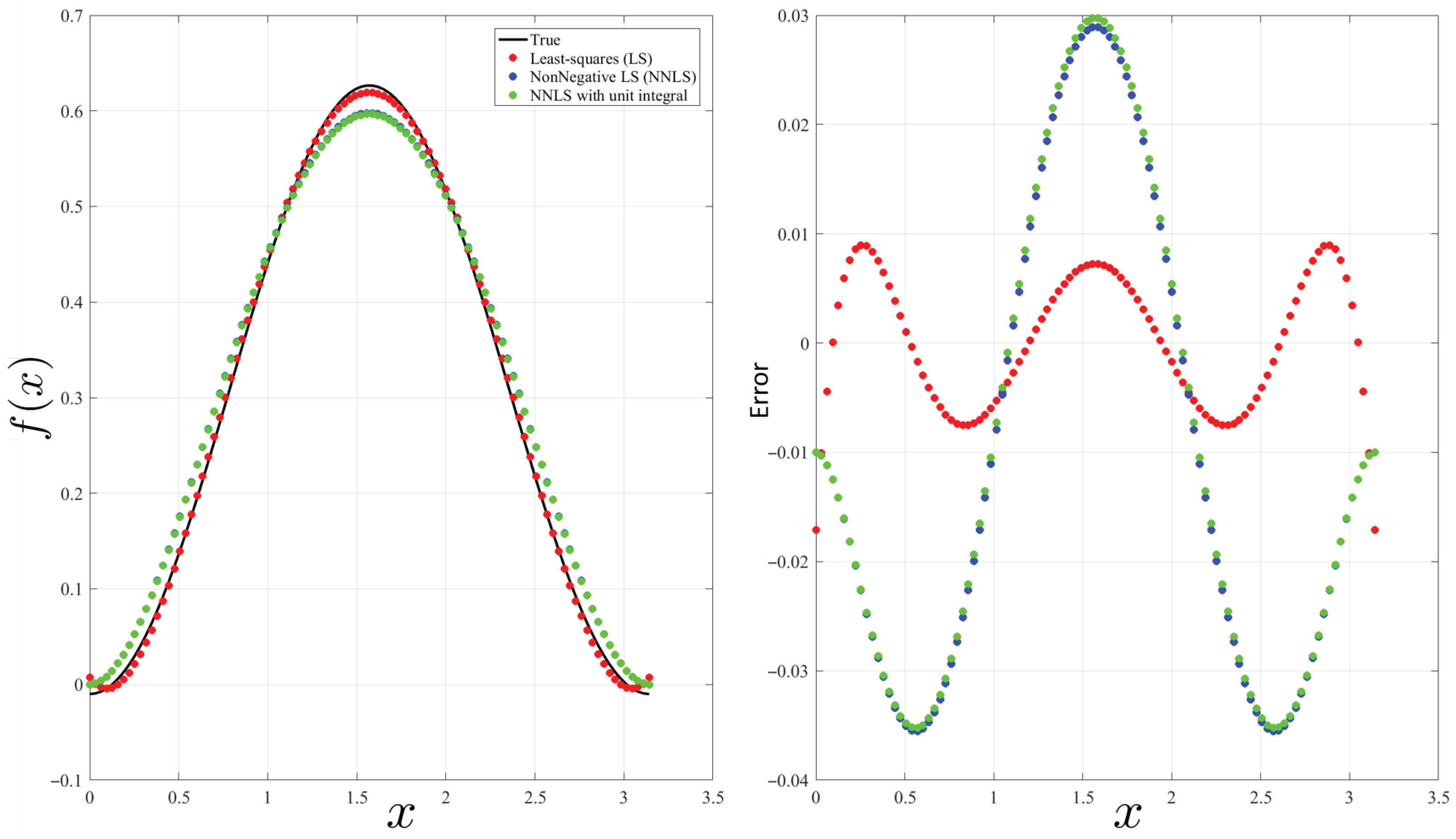
4.1. Non-Negative Least-Squares Methods
4.2. Univariate Procedure Example
5. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| TFC | Theory of Functional Connections |
| DE | Differential Equation |
Appendix A. Note on Negative Probability
References
- Mortari, D. The Theory of Connections: Connecting Points. Mathematics 2017, 5, 57. [Google Scholar] [CrossRef]
- Mortari, D. Least-Squares Solution of Linear Differential Equations. Mathematics 2017, 5, 48. [Google Scholar] [CrossRef]
- Leake, C.D. The Multivariate Theory of Functional Connections: An n-Dimensional Constraint Embedding Technique Applied to Partial Differential Equations. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Johnston, H.R. The Theory of Functional Connections: A Journey from Theory to Application. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Leake, C.; Johnston, H.; Mortari, D. The Theory of Functional Connections: A Functional Interpolation Framework with Applications; Lulu: Morrisville, NC, USA, 2022. [Google Scholar]
- Mortari, D. Theory of Functional Connections Subject to Shear-Type and Mixed Derivatives. Mathematics 2022, 10, 4692. [Google Scholar] [CrossRef]
- Mortari, D.; Garrappa, R.; Nicolò, L. Theory of Functional Connections Extended to Fractional Operators. Mathematics 2023, 11, 1721. [Google Scholar] [CrossRef]
- Mortari, D. Representation of Fractional Operators using the Theory of Functional Connections. Mathematics 2023, 11, 4772. [Google Scholar] [CrossRef]
- Mortari, D. Using the Theory of Functional Connections to Solve Boundary Value Geodesic Problems. Math. Comput. Appl. 2022, 27, 64. [Google Scholar] [CrossRef]
- Wang, Y.; Topputo, F. A TFC-based homotopy continuation algorithm with application to dynamics and control problems. J. Comput. Appl. Math. 2022, 401, 113777. [Google Scholar] [CrossRef]
- D’Ambrosio, A.; Schiassi, E.; Johnston, H.R.; Curti, F.; Mortari, D.; Furfaro, R. Time-energy optimal landing on planetary bodies via theory of functional connections. Adv. Space Res. 2022, 69, 4198–4220. [Google Scholar] [CrossRef]
- Schiassi, E.; D’Ambrosio, A.; Furfaro, R. An Overview of X-TFC Applications for Aerospace Optimal Control Problems. In The Use of Artificial Intelligence for Space Applications. Workshop at the 2022 International Conference on Applied Intelligence and Informatics; Springer Nature: Berlin/Heidelberg, Germany, 2023; Volume 1088, p. 199. [Google Scholar]
- De Florio, M.; Schiassi, E.; Furfaro, R. Physics-informed neural networks and functional interpolation for stiff chemical kinetics. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 063107. [Google Scholar] [CrossRef] [PubMed]
- Schiassi, E.; De Florio, M.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Physics-informed neural networks and functional interpolation for data-driven parameters discovery of epidemiological compartmental models. Mathematics 2021, 9, 2069. [Google Scholar] [CrossRef]
- Mai, T.; Mortari, D. Theory of Functional Connections Applied to Quadratic and Nonlinear Programming under Equality Constraints. J. Comput. Appl. Math. 2022, 406, 113912. [Google Scholar] [CrossRef]
- Yassopoulos, C.; Reddy, J.; Mortari, D. Analysis of Timoshenko-Ehrenfest Beam Problems using the Theory of Functional Connections. J. Eng. Anal. Bound. Elem. 2021, 132, 271–280. [Google Scholar] [CrossRef]
- Yassopoulos, C.; Reddy, J.; Mortari, D. Analysis of nonlinear Timoshenko–Ehrenfest Beam Problems with Von Kármán Nonlinearity using the Theory of Functional Connections. Math. Comput. Simul. 2023, 205, 709–744. [Google Scholar] [CrossRef]
- Leake, C.; Mortari, D. Deep theory of functional connections: A new method for estimating the solutions of partial differential equations. Mach. Learn. Knowl. Extr. 2020, 2, 37–55. [Google Scholar] [CrossRef] [PubMed]
- Schiassi, E.; Furfaro, R.; Leake, C.D.; Florio, M.D.; Johnston, H.R.; Mortari, D. Extreme Theory of Functional Connections: A Fast Physics-Informed Neural Network Method for Solving Ordinary and Partial Differential Equations. Neurocomputing 2021, 457, 334–356. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Wikipedia. Physics-Informed Neural Networks—Wikipedia, The Free Encyclopedia. 2024. Available online: http://en.wikipedia.org/w/index.php?title=Physics-informed%20neural%20networks&oldid=1251520404 (accessed on 26 October 2024).
- Mortari, D.; Johnston, H.R.; Smith, L. High Accuracy Least-squares Solutions of Nonlinear Differential Equations. J. Comput. Appl. Math. 2019, 352, 293–307. [Google Scholar] [CrossRef]
- Ding, J.; Eifler, L.; Rhee, N. Integral and nonnegativity preserving approximations of functions. J. Math. Anal. Appl. 2007, 325, 889. [Google Scholar] [CrossRef]
- Lorentz, G.G. Bernstein Polynomials; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Reynolds, D.A. Gaussian mixture models. Encycl. Biom. 2009, 741, 827–832. [Google Scholar]
- Wikipedia. Non-Negative Least Squares. 2004. Available online: https://en.wikipedia.org/wiki/Non-negative_least_squares (accessed on 24 November 2024).
- Kim, D.; Sra, S.; Dhillon, I.S. Fast Projection-Based Methods for the Least Squares Nonnegative Matrix Approximation Problem. Stat. Anal. Data Min. 2008, 1, 38–51. [Google Scholar] [CrossRef]
- Zhao, R.; Tan, V.Y. A unified convergence analysis of the multiplicative update algorithm for regularized nonnegative matrix factorization. IEEE Trans. Signal Process. 2017, 66, 129–138. [Google Scholar] [CrossRef]
- Hsieh, C.J.; Dhillon, I.S. Fast coordinate descent methods with variable selection for non-negative matrix factorization. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 1064–1072. [Google Scholar]
- Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Gong, P.; Zhang, C. Efficient nonnegative matrix factorization via projected Newton method. Pattern Recognit. 2012, 45, 3557–3565. [Google Scholar] [CrossRef]
- Zdunek, R. Alternating direction method for approximating smooth feature vectors in nonnegative matrix factorization. In Proceedings of the 2014 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), Reims, France, 21–24 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; SIAM: Bangkok, Thailand, 1995; Chapter 23; p. 161. [Google Scholar]
- Dirac, P.A.M. The physical interpretation of the quantum dynamics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 113, 621–641. [Google Scholar]
- Feynman, R.P. Negative Probability. 1984. Available online: https://cds.cern.ch/record/154856/files/pre-27827.pdf (accessed on 24 November 2024).
- Weinbub, J.; Ferry, D. Recent advances in Wigner function approaches. Appl. Phys. Rev. 2018, 5, 041104. [Google Scholar] [CrossRef]
- Blass, A.; Gurevich, Y. Negative probabilities: What they are and what they are for. arXiv 2020, arXiv:2009.10552. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortari, D. Theory of Functional Connections Extended to Continuous Integral Constraints. Math. Comput. Appl. 2025, 30, 105. https://doi.org/10.3390/mca30050105
Mortari D. Theory of Functional Connections Extended to Continuous Integral Constraints. Mathematical and Computational Applications. 2025; 30(5):105. https://doi.org/10.3390/mca30050105
Chicago/Turabian StyleMortari, Daniele. 2025. "Theory of Functional Connections Extended to Continuous Integral Constraints" Mathematical and Computational Applications 30, no. 5: 105. https://doi.org/10.3390/mca30050105
APA StyleMortari, D. (2025). Theory of Functional Connections Extended to Continuous Integral Constraints. Mathematical and Computational Applications, 30(5), 105. https://doi.org/10.3390/mca30050105




