Many-Objective Intelligent Scheduling Optimization Algorithm for Complex Integrated System

Abstract

Due to the increasing consumer demand for custom products, aluminum alloy component creep forming manufacturing has shifted towards production modes designed for multiple varieties and small batches, leading to problems such as complex production organization and low production efficiency. In the specific case of modern large-scale aluminum alloy aerospace components, the manufacturing requirements cannot be satisfied. According to the production characteristics and process requirements in this industry, a many-objective, whole-process production scheduling model was established, and a residual rectangle-based many-objective evolutionary algorithm (RTEA) was developed to solve it effectively. The RTEA uses the residual rectangle method in the decoding phase for autoclave filling, which improves the productivity of the autoclave. We further designed a three-stage environmental selection strategy to strengthen the balance of convergence and diversity and increase the selection pressure in the evolutionary process. Computational experiments were performed using industrial datasets relative to aerospace components and engineering production data. The advantages and competitiveness of the comprehensive production scheduling model and the RTEA were verified, as evidenced by an increase in production line efficiency of 20%. In conclusion, the proposed approach offers an effective solution to the many-objective production scheduling problem hindering aluminum alloy creep forming component production.

1. Introduction

Aluminum alloys are the predominant non-ferrous metal structural materials utilized in industry and specifically serve a crucial function in the production of aerospace equipment. With their excellent lightweight characteristics and high-strength performance, aluminum alloys have become the main structural materials for modern aircraft and spacecraft, effectively promoting the development of aerospace technology. In contemporary manufacturing, creep aging forming technology presents unique advantages that have led it to become a key manufacturing process for the integral forming of complex aerospace components [1].

Emerging technologies such as big data, the Internet of Things, and cloud computing are significantly reshaping the management frameworks and developmental strategies of traditional manufacturing industries, steering the sector toward increased automation, enhanced information utilization, and greater use of artificial intelligence. By tightly integrating new-generation information technology with manufacturing technology to build intelligent production systems and achieve optimal resource allocation throughout the product life cycle, companies can enhance manufacturing efficiency, ensure product quality, and increase production flexibility. In this context, intelligent production scheduling technology, which is the core of intelligent manufacturing decision making, presents both new challenges and opportunities [2].

With the accelerating process of economic globalization, consumer demand is increasingly diversified and individualized, and the traditional manufacturing industry is increasingly competitive. Aluminum alloy aerospace component creep forming production is gradually transitioning to the multi-category discrete production mode, leading to issues in production line management such as unreasonable scheduling, inefficient production processes, and elevated costs. In order to improve production efficiency, reduce production waste, and achieve load balance, it is very important to formulate reasonable and effective scheduling optimization schemes for aluminum alloy aerospace component creep forming production.

The creep forming-based production of aluminum alloy aerospace components has specific characteristics, i.e., the multi-variety small-batch production mode, complex process constraints, and high-precision quality requirements, which traditional scheduling methods cannot comply with due to three core problems: Firstly, the production constraints have multi-dimensional coupling characteristics, as they involve multiple factors, such as equipment capacity, process timing, and energy consumption constraints, resulting in a theoretical bottleneck in building an accurate scheduling model. Secondly, in scheduling optimization, many high-dimensional objectives need to be considered, requiring the synchronous optimization of five–eight key indicators, such as production efficiency, energy consumption, and equipment utilization, which is a significant challenge for traditional multi-objective optimization algorithms. Thirdly, due to frequent dynamic disturbance factors, including emergency order insertion and abnormal equipment shutdown, it is necessary to build an intelligent decision-making mechanism with adaptive capability. Aiming to address the above challenges, this study proposes a high-dimensional, many-objective, whole-process intelligent scheduling model and a decision optimization method. Our scheme can not only improve the production efficiency and resource utilization rate of manufacturing enterprises and reduce unit energy consumption but also promote the innovative development of intelligent manufacturing scheduling theory in complex manufacturing scenes and provide key technical support for high-end aerospace equipment manufacturing.

Currently, theoretical research on production process scheduling primarily concentrates on the steel and chemical sectors [3], with comparatively limited studies addressing the scheduling of non-ferrous metal processing and manufacturing [4]. Huang et al. [5] investigated the problem of aluminum alloy hot rolling production scheduling under conditions of uncertain demand, aiming to reduce furnace energy consumption and costs. They developed a multi-objective, mixed-integer linear programming model tailored for this sector and validated it by using a case study from an aluminum alloy manufacturing company, demonstrating both its feasibility and advantages. Additionally, Nishi et al. [6] examined the planning and scheduling of an aluminum rolling production line, introducing a distributed decision-making system designed for the collaborative optimization of production scheduling and distribution planning. Steinruecke et al. [7] studied the multi-stage production transportation and distribution scheduling problems in the aluminum industry with the aim of coordinating global production activities and material flows both in the long term (months in advance) and in the short term (nearest-day scale).

Production scheduling problems are NP-hard, i.e., do not allow the global optimal solution to be obtained in polynomial time; therefore, in recent decades, they have been extensively studied within the field of combinatorial optimization, as shown in Table 1. For small-scale job-shop scheduling problems, some accurate algorithms, such as integer linear programming, dynamic programming, and the branch-and-bound method, have been widely used to obtain the optimal solution. However, although these precise algorithms can guarantee the optimization of the solution, with an increase in the number of manufacturing tasks, they cannot quickly solve the job-shop scheduling problem due to the high computational costs.

The job-shop scheduling problem has two other kinds of solving algorithms, namely, regular methods and metaheuristic methods. Regarding the former, in recent decades, various scheduling rules have been proposed, including basic priority, compound, and heuristic rules. Jun et al. [8] proposed a random forest method for obtaining scheduling rules (RANFORS) in dynamic scheduling. Despite its simplicity, the regular method remains prevalent in certain scheduling contexts because of its extremely fast response times and robust applicability to various scheduling challenges. However, these scheduling rules are single rules designed based on specific knowledge of the job-shop scheduling problem. Therefore, the quality of scheduling schemes for different scheduling scenarios fluctuates greatly.

Table 1. Different types of methods and their advantages and disadvantages.

Algorithm Type		Advantages	Disadvantages	Representative Algorithms
Dispatching rule		Fast solution speed	The solution is unstable in terms of quality	[9]
Metaheuristic		Simple design	Quality cannot be guaranteed	[10]
Deep reinforcement learning	State characteristics	Fast network training	Complex states are difficult to represent	[11,12]
	Rules define actions	Controlled action space	Exploring the action space is limited	[13]

Table 1. Different types of methods and their advantages and disadvantages.

Algorithm Type		Advantages	Disadvantages	Representative Algorithms
Dispatching rule		Fast solution speed	The solution is unstable in terms of quality	[9]
Metaheuristic		Simple design	Quality cannot be guaranteed	[10]
Deep reinforcement learning	State characteristics	Fast network training	Complex states are difficult to represent	[11,12]
	Rules define actions	Controlled action space	Exploring the action space is limited	[13]

Metaheuristics can achieve a balance between solution quality and solution time, thus enabling a scheduling scheme with good performance to be obtained within reasonable solution time [14]. Gao et al. [15] leveraged the advantages of particle swarm optimization and the Tabu Search (TS) algorithm to develop a hybrid metaheuristic method, a balanced strategy to improve the exploration and development ability of particles. Nguyen et al. [16] proposed an iterative local search method for the automatic planning of scheduling rules, which can not only reduce the calculation cost but also improve the algorithm’s exploration ability. In order to solve the parameter sensitivity problem of metaheuristics, Lu et al. [17] proposed a knowledge-based, multi-objective memetic algorithm to guide individuals to effectively explore the search space based on domain knowledge.

With advancements in the Internet of Things and artificial intelligence technologies, manufacturing systems can now not only acquire real-time data regarding workshop environmental conditions but also make immediate decisions based on these data to facilitate dynamic scheduling. Reinforcement learning, as an important artificial intelligence technology, is widely used. At present, the field of deep reinforcement learning is still in a stage of rapid development, with various types of algorithms being frequently proposed [18]. Song et al. [19] proposed a scheduling method combining a graph neural network and deep reinforcement learning that integrates operation selection and machine allocation into a composite decision and uses a heterogeneous graph structure to represent the scheduling status; the results show that the method presents significantly improved efficiency and result quality in solving FJSPs in actual manufacturing systems. Liu et al. [20] introduced a dynamic flexible job-shop scheduling approach that utilizes deep reinforcement learning to facilitate real-time scheduling decision making in response to the continuous arrival of jobs in flexible workshops. Qin et al. [21] proposed a multi-agent-based deep reinforcement learning method to solve large-scale dynamic scheduling problems. There are still some challenges in applying deep reinforcement learning to engineering scheduling problems. Current job-shop scheduling algorithms are based on specific scheduling scenarios, so the generated adjustment scheme lacks universality. Moreover, existing single-layer deep reinforcement learning methods cannot effectively solve multi-objective optimization problems, which leads to a significant gap between theoretical research results and actual demand in production scheduling, as well as difficulty in solving practical engineering problems.

Currently, there is a lack of research regarding comprehensive production scheduling theoretical frameworks and their application to the creep aging forming production lines for aluminum alloy components. A scheduling model that encompasses the entire production process has not yet been developed, preventing the optimization of the scheduling problem from a global perspective.

Evolutionary algorithms based on the Pareto dominance relationship have significant limitations: the ability to distinguish solutions weakens as the target dimension increases, the efficiency of the diversity maintenance mechanism is low, and the computational cost is high. These deficiencies constrain the breadth and depth of application of many-objective evolutionary algorithms. Enhancing the optimization performance of these algorithms is essential to advancing research on theoretical frameworks for multi-objective optimization and fostering progress in engineering applications.

To address the many-objective scheduling problem in aluminum alloy component creep aging forming production, we first developed a many-objective production scheduling model based on the production characteristics, process flow, and constraints of creep forming. Subsequently, we designed a residual rectangle-based many-objective evolutionary algorithm (RTEA) to solve the established production scheduling model.

The main contributions of this study are as follows:

• A many-objective production scheduling model for aluminum alloy component creep forming production is developed, taking into account production characteristics, process flow, and constraints in accordance with the actual production requirements.
• A many-objective evolutionary method based on residual rectangles (RTEA) is proposed, and a three-stage environment selection method is designed. As a result of their implementation, the ability to distinguish non-dominated solutions is improved, and the balance between population convergence and diversity is strengthened.
• During the decoding phase of the RTEA method, the residual rectangle technique is employed for autoclave loading, ensuring both the feasibility and efficiency of the decision-making optimization process.
• The many-objective production scheduling problem relative to the entire aluminum alloy creep forming component production process is effectively addressed with the proposed scheme, resulting in enhanced production efficiency, improved management and operational capabilities for manufacturing enterprises, and an increase in the intelligent manufacturing level in this industry.

2. Introduction to Production Process and Model Description

2.1. The Production Process of Creep Forming

Creep aging forming technology combines the forming process with the heat treatment process and leverages the creep phenomenon in metals. Its basic principle is to use the creep stress relaxation and aging strengthening properties of metals to co-manufacture components in the same space–time environment (temperature and stress fields). The process of creep aging forming technology is shown in Figure 1.

Creep forming operation is mainly divided into three processes: (1) Load application process. The load on the integral component is increased according to the process requirements; the component is deformed by the applied load and shaped by the mold. (2) Creep aging forming process. The component is placed in an autoclave according to the process requirements, where the interior of the autoclave must meet the set temperature and pressure constraints; after a period of time, the internal structure of the component changes under high temperature and high pressure. (3) Unloading process. According to the process requirements, the load on the component is removed, and the component is cooled to room temperature in the natural environment. During this process, the component exhibits a certain degree of springback. The shape/property synergistic transformation of the component is completed by the creep aging forming method, which involves blanking, layup, creep forming, and dimension measurement. An autoclave is shown in Figure 2 and a blanking machine in Figure 3.

The scheduling problem in aluminum alloy creep forming component production can be expressed as follows: There are n independent workpieces that need to be processed through four operations, where each operation on each workpiece has a certain processing time. Each workpiece and its mold have certain length and width, and only workpieces with the same relevant parameters can be assembled in the same autoclave. When a workpiece is being processed in the machine, the operation cannot be interrupted. The purpose of creep aging forming whole-process intelligent scheduling is to determine when and on which piece of equipment each workpiece is processed under the condition that all constraints are met and to optimize the multiple scheduling objectives set.

2.2. The Proposed Whole-Process Scheduling Model for Creep Forming Production

The production scheduling model presented in this study concurrently optimizes five objective functions, representing a typical high-dimensional, many-objective optimization problem.

The nomenclature used is as follows:

$f_1$: Volume utilization rate of autoclave

$f_2$: Completion time

$f_3$: Delay time machine load

$f_4$: Equipment idle time

$f_5$: Number of autoclave brackets

$C_i$: Completion time of the i-th workpiece

$a_{ij}^k$: Whether operation $O_{ij}$ is processed on piece of equipment $M_k$

$t_{ij}^k$: Processing time of operation $O_{ij}$ on piece of equipment $M_k$

$D{D}_i$: Delivery date of the i-th workpiece

$n$: Number of autoclave brackets

$v_i$: Volume utilization rate of each bracket

The expression of the production scheduling model is as follows:

$$\min F=\left(-f_1,f_2,f_3,f_4,f_5\right),$$

(1)

where the following apply:

(1)

The volume utilization rate of the autoclave ($f_1$) is

$$f_1={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{v}_i}}{n},}$$

(2)

(2)

The completion time ($f_2$) is

$$f_2=\max \left(C_i\left|i=1,2,3,\cdots n\right.\right),$$

(3)

(3)

The delivery delay time ($f_3$) is

$$f_3={\displaystyle \sum _{i=1}^n\max \left(C_i-D{D}_i,0\right)},$$

(4)

(4)

The equipment idle time ($f_4$) is

$$f_4={\displaystyle \sum _{k=1}^m\left(T_k-{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{q_i}{a}_{ij}^k\times t_{ij}^k}}\right),}$$

(5)

(5)

The number of autoclave brackets ($f_5$) is

$$f_5=n,$$

(6)

The constraints are as follows:

$$\max (x_{i1}-x_{j3},x_{j1}-x_{i3},y_{i2}-y_{j4},y_{j2}-y_{i4})\ge 0,$$

(7)

$$0\le x_{ik}\le W,$$

(8)

$$0\le y_{ik}\le L,$$

(9)

$$0\le z_{ik}\le H,$$

(10)

Figure 4 shows the layout of the mold on the x-y plane of the support. Equation (7) states that the tooling positions of two components do not interfere with each other. Equations (8)–(10) define the boundary ranges of the tooling position in the width, height, and length of the support, respectively.

3. The Proposed RTEA Optimization Method

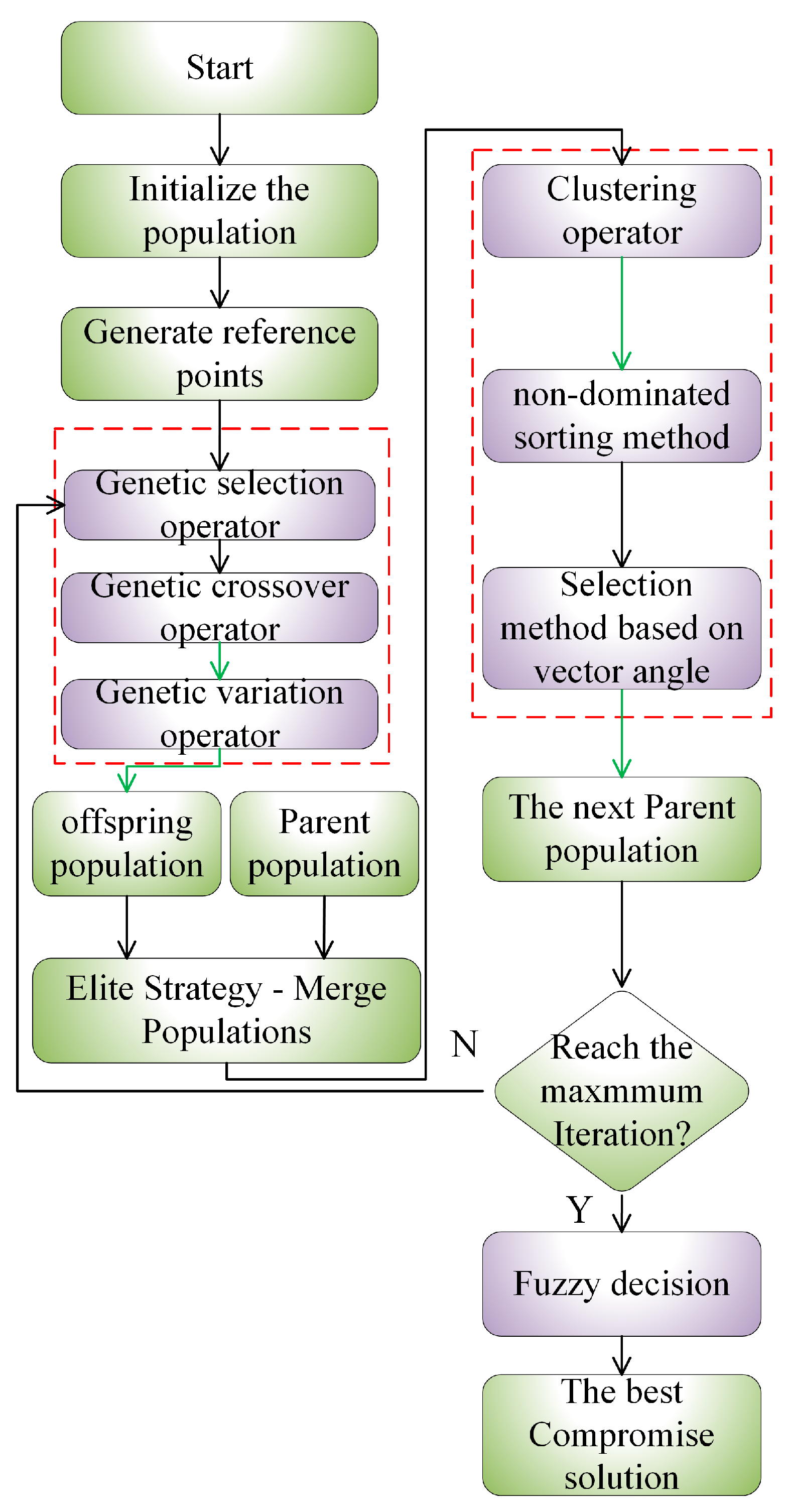
3.1. Overall Framework

Firstly, a set of uniformly distributed reference points is generated, with a scale defined by $H$. Genetic operators (selection, recombination, and mutation) are applied to the parent population with the initial scale of N to obtain an offspring population with the scale of N. A population $U_t$ with a size of 2N is obtained by mixing the parent and offspring populations. A three-stage environmental selection method was designed to select N individuals from population $U_t$: In the first stage, the first level of individual selection based on clustering is completed; in the second stage, non-dominated sorting is carried out, and different non-dominated levels $F_1$, $F_2$, … can be obtained through the non-dominated sorting of population $U_t$; the third stage involves individual selection based on vector angle, which ensures the coevolution of population convergence and diversity. This process is repeated until the iteration termination condition is met. Finally, a set of scheduling scheme solutions are obtained, and a high-quality production scheduling scheme is selected from the set by using the fuzzy decision method. The optimization flow chart of the RTEA method is shown in Figure 5.

3.2. The Method of Autoclave Bracket Filling

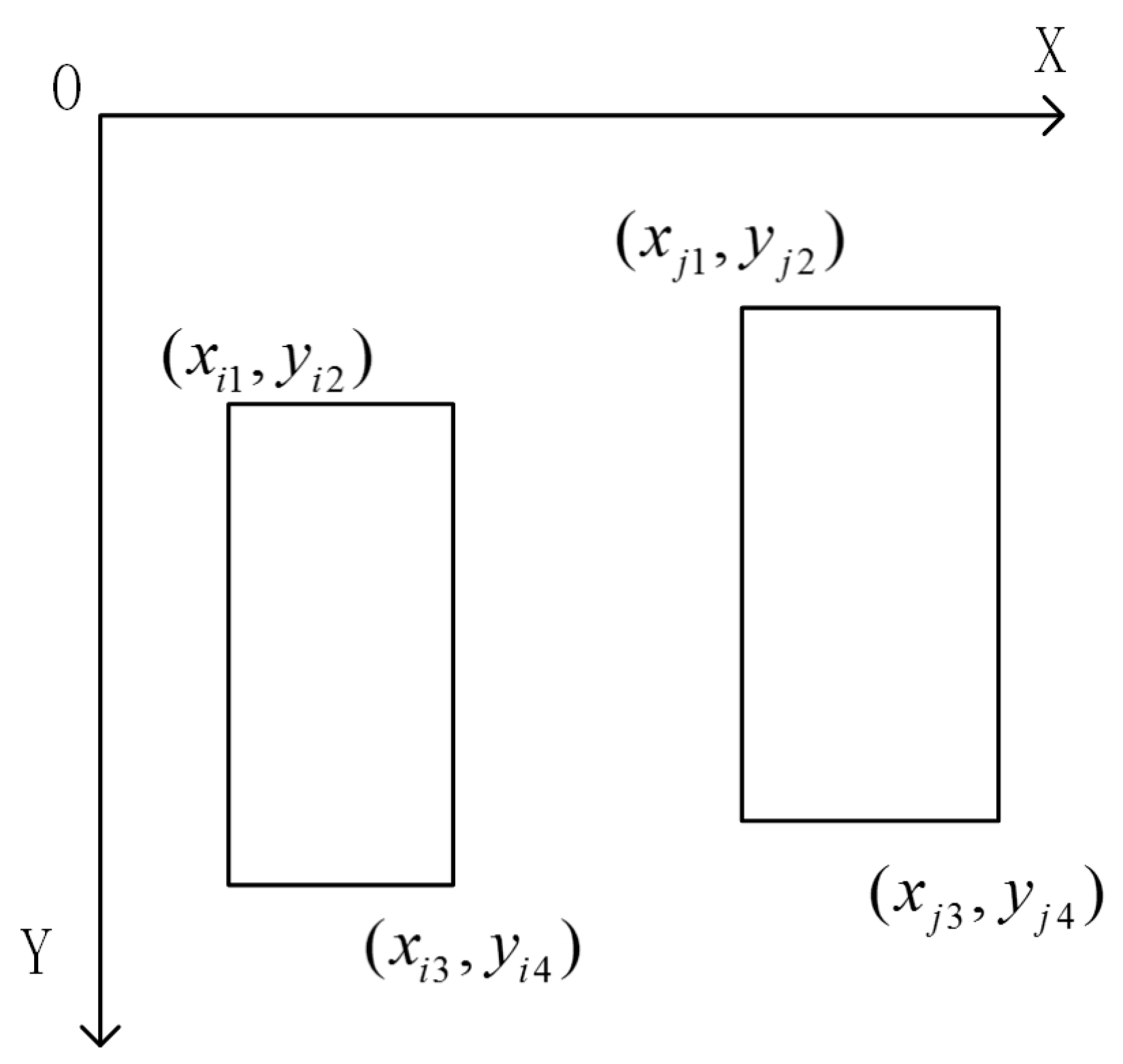
To effectively design a comprehensive scheduling model for aluminum alloy creep forming component production, it is essential to first determine the autoclave filling method. The workpieces within the autoclave are positioned on a support bracket, in this study, a double-layer structure, and the autoclave filling plan is determined by the components placed on this bracket. According to the known sequence of components entering the autoclave, the double-layer filling method needs to determine the position of each component on the bracket, as well as the number of autoclaves for the current order.

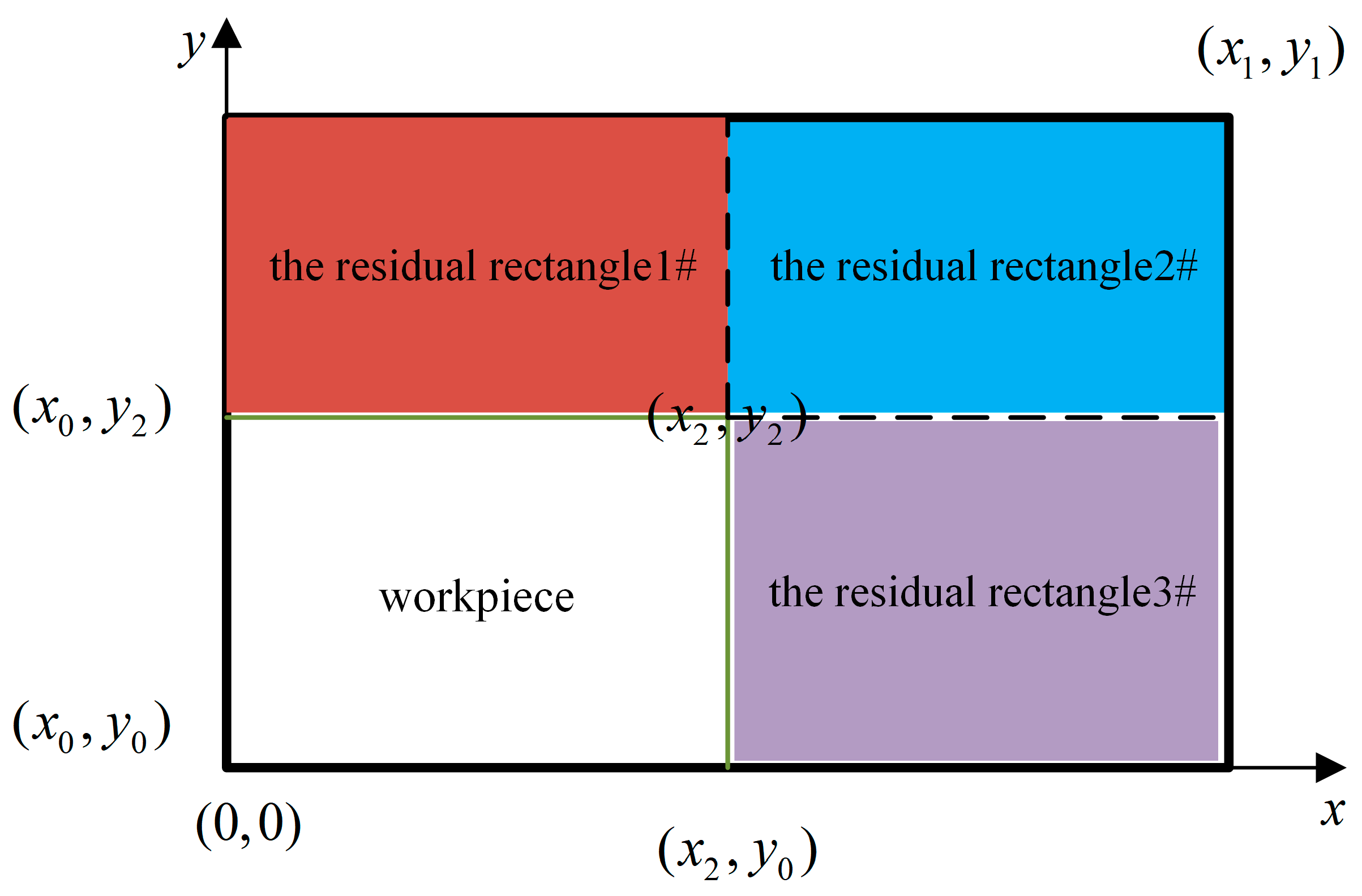
In this study, the residual rectangle method is used as the filling method. Before filling, the order of the components entering the autoclave and the orientation of each component (whether it is rotated by 90°) are determined. Assuming that there are n components, i is the serial number of the component. B1 = [0 0 L1 H1], where L1 and H1 are the length and width of the first-layer bracket in the autoclave, respectively, and B2 = [0 0 L2 H2] represents the size information of the second-layer support, as shown in Figure 6. Matrix A stores the placement coordinates and dimensions of each component.

The residual rectangle filling method optimally utilizes the available space on the autoclave bracket, which significantly enhances the volume utilization of the autoclave, thereby boosting its productivity. This approach is crucial to reducing costs and improving efficiency in the production process of aluminum alloy creep aging forming components.

3.3. The Encoding and Decoding Methods

To solve the scheduling problem in creep aging forming production, this study designed an optimization strategy based on two-layer gene coding in the RTEA method (Figure 7). The model has the following characteristics: (1) chromosome length strictly corresponds to the total number of workpieces; (2) the upper-layer code represents the time sequence of the workpiece entering the autoclave and enables path optimization through discrete permutation and combination; (3) the lower-layer code defines the spatial orientation parameters of the workpiece, and the binary variable set directly determines whether the components on the autoclave support need to perform a 90° rotation transformation.

The decoding mechanism converts genotypic data into executable process plans through topological mapping, and its core process includes three key steps: (1) Construction of process constraint matrix: Based on the autoclave entry sequence and spatial orientation parameters output by double-layer coding, a manufacturing constraint matrix containing process logic and sequence relationship is established. (2) Spatiotemporal resource allocation: The residual rectangle algorithm is used to analyze the three-dimensional space of the autoclave support, generate the tank drainage topology according to the component rotation transformation requirements, and accurately calculate the tank number (Batch), layer coordinates (Layer), and position vector (x, y, z) of each component. (3) Process chain scheduling: The decoding starts from the bottleneck process of creep forming and reversely deduces the processing sequence of each process along the process route. The timing priority principle (FCFS) and resource readiness priority principle (FAM) are used to realize the dynamic matching of pieces of equipment and workpieces; finally, a Gantt chart of production scheduling with spatiotemporal coupling characteristics is generated.

3.4. The Three-Stage Environment Selection Method

The niche preservation strategy selection mechanism primarily focuses on maintaining population diversity during execution; however, it overlooks the need for a balance between population convergence and diversity, which makes it an inadequate method for addressing the comprehensive production scheduling challenges in aluminum alloy aerospace components production. Therefore, a three-stage environment selection method is proposed.

(1) 

The first stage—Individual selection method based on clustering

(1) Normalization. The M-dimensional linear hyperplane defined by m extreme points allows intercept $a_i$ to be calculated. Thus, the objective function can be standardized as shown in Equation (11).

$$f_i^n\left(x\right)={\displaystyle \frac{f_i\left(x\right)-Z_i^{\min }}{a_i-Z_i^{\min }}}for\hspace{1em}i=1,2,\cdots M$$

(11)

where $Z_i^{\min }$ is the minimum value of the i-th target in the population.

(2) Clustering. The distance between individuals in the population and the reference line is determined using the PBI distance metric. Individuals are then linked to the reference vectors that exhibit the smallest PBI distance, and those associated with the same reference vector are categorized into the same class. Equations (12)–(14) represent the calculation formulas for PBI distance, convergence, and diversity, respectively.

$$d(x)=d_{j,1}(x)+\theta d_{j,2}(x),$$

(12)

$$d_{j,1}(x)=‖\left(f^n{\left(x\right)}^T{\omega }_{ji}\right)‖/‖{\omega }_{ji}‖,$$

(13)

$$d_{j,2}(x)=‖f^n\left(x\right)-d_{j,1}(x)\left({\omega }_{ji}/‖{\omega }_{ji}‖\right)‖,$$

(14)

(3) The selection method of the first layer. The function values of each solution are calculated based on the improved Chebyshev aggregation function method. The main feature of aggregate functions is to integrate multiple optimization objective values into a single objective function. The environment selection method in the first stage retains the individual with the highest function value in each class, while the remaining individuals in the population form the second layer. The selection method for the first layer enables not only the preservation of global diversity but also the convergence of the population when selecting individuals from each class.

$$\min g^{te}\left(x\left|\lambda ,z^{*}\right.\right)=\max \left\{{\displaystyle \frac{\left|f_j\left(x\right)-z_j^{*}\right|}{{\lambda }_j}}\right\},$$

(15)

(2) 

The second stage—Non-dominated sorting method

Following the non-dominated sorting of individuals in the second layer, various non-dominated levels $F_1$, $F_2$… are established. Individuals with non-dominated levels $F_1$, $F_2$… are added to the new population, $S_t$, in sequence until its size is greater than or equal to N, at which point individuals stop joining. Assuming that the most recent non-dominated level added is denoted by $F_l$, the individuals within $S_t/F_l$ are directly incorporated into the parent population for the next generation, $P_{t+1}$. The remaining individuals must be selected from $F_l$ based on the diversity maintenance strategy until the total number of individuals in $S_t$ reaches N.

(3) 

The third stage—Individual selection method based on vector angle

Based on the improved Chebyshev aggregation function, the fitness value of each individual is calculated, and the weight vector of each individual is determined with the clustering operation in the first stage. Further, the vector angles between each individual and other individuals within the population are calculated.

Firstly, m extreme solutions are selected in $F_l$. The extreme solutions in the solution set are defined as those with the smallest angle with m vectors (1, 0, …), (0, 1, …), …, (0, 0, …, 1) and are denoted by $e_i$, where i = 1, 2, …

Then, whether the number of individuals in A reaches N is calculated. If it is less than N, the maximum vector angle preservation strategy and the worst-individual deletion strategy are used to select individuals.

Maximum vector angle preservation strategy: Firstly, the vector angle between the individual to be selected and the individual in A is obtained, and the minimum value between them and individuals in population A is calculated. Then, the individual with the largest vector angle among the selected individuals is selected. The above operation is continuously executed until the number of individuals in A reaches N.

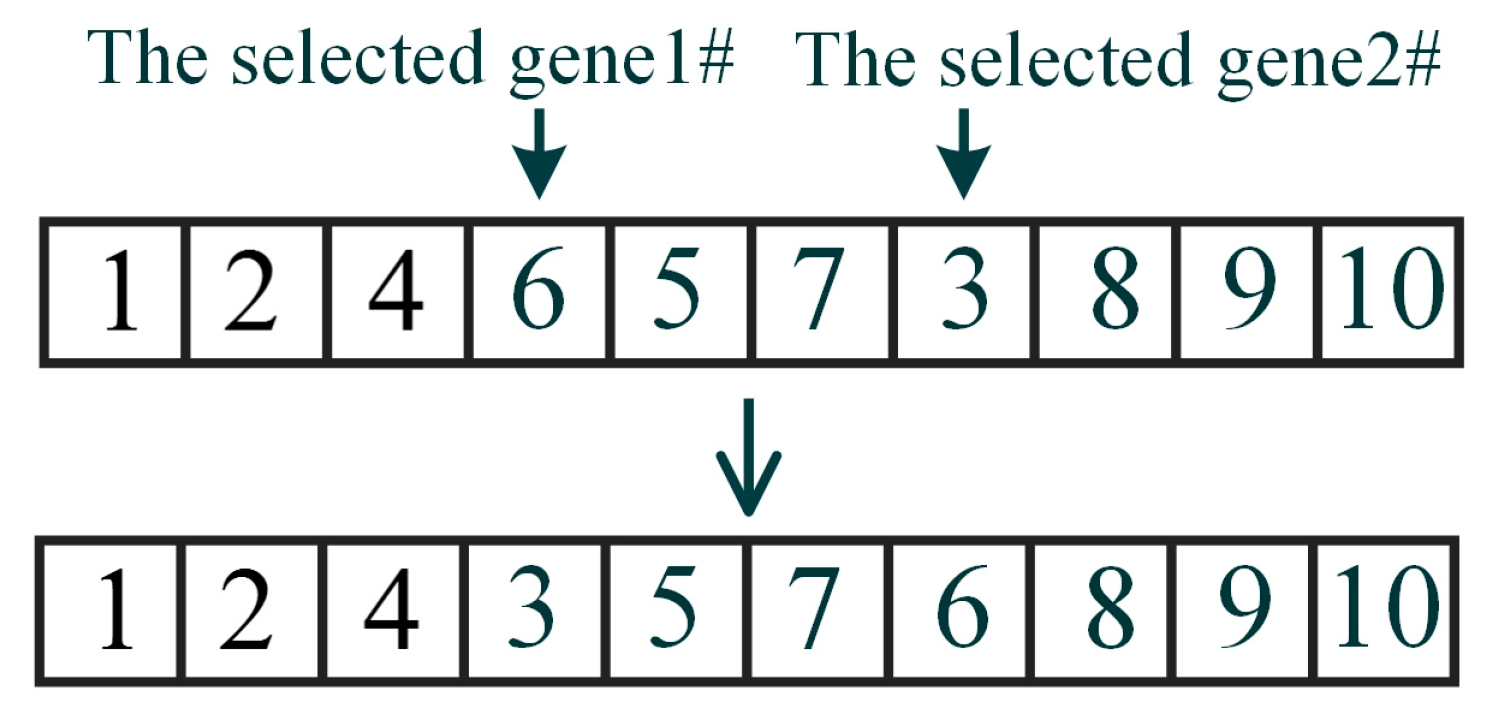
3.5. Genetic Operator

The RTEA method adopts a two-point crossover strategy for the crossover operation of its two-layer chromosome structure, detailed as follows: The parent individuals are randomly paired. If the generated random value is lower than the preset crossover probability, the crossover is executed: two cutting sites are randomly determined on the parent chromosome, and gene fragments are exchanged between them. Then, the chromosomes are scanned from the starting position, and any duplicate piece ID is removed. After the above steps are completed, two offspring chromosomes are obtained. In the mutation stage, the method uses a two-point exchange operator, which randomly selects two different gene loci on the chromosome and directly exchanges their positions to generate new mutant chromosomes, as shown in Figure 8.

4. Experimental Results and Discussion

In this section, we use a manufacturing system operation dataset and industrial production data to systematically verify the whole-process scheduling model and the high-dimensional, many-objective decision-making method (RTEA) developed for the creep forming production of aluminum alloy aerospace components.

4.1. Dataset Experiment

In view of the lack of standard test cases in the field of aluminum alloy aerospace component production whole-process scheduling, this study developed a test system (ACF01~ACF10) containing 10 groups of benchmark cases based on the actual production process parameters. The benchmark case information is shown in

Table 2. The constructed benchmarks.

	Benchmark	Total Number of Component Types	Total Number of Components
1	ACF01	4	230
2	ACF02	5	330
3	ACF03	6	420
4	ACF04	7	400
5	ACF05	4	200
6	ACF06	5	280
7	ACF07	6	380
8	ACF08	5	350
9	ACF09	6	300
10	ACF10	5	400

.

To assess the effectiveness of the proposed RTEA in optimizing production scheduling for aluminum alloy aerospace component creep forming, a comparative analysis was conducted using four established optimization algorithms: T-DEA, SPEA2+SDE, EFR_RR, and NSGA-III. The experimental design ensured methodological consistency by maintaining identical parameters across all algorithms, including population size, crossover-mutation operators, and their respective probabilities.

The termination criterion was set as follows: a uniform time limit was established for all comparative algorithms, while the RTEA-specific evaluation protocol involved five independent runs per benchmark case with a fixed 50-generation stopping condition, as shown in

Table 3. The average calculation time of each benchmark.

Benchmark	Average Time (s)
ACF01	83.6968
ACF02	96.3522
ACF03	121.2794
ACF04	135.0014
ACF05	146.3398
ACF06	156.1950
ACF07	169.8720
ACF08	178.5802
ACF09	83.9828
ACF10	186.6552

.

For comparison fairness, the mean computation time derived from the multiple runs of the RTEA was adopted as the standardized termination threshold for all algorithms, as shown in

Table 4. Parameter settings.

Parameter	Value
Population size	100
Number of iterations	50
Mating probability	0.7
Mutation probability	0.1

.

To evaluate the performance advantages of the RTEA, this study employed two comprehensive assessment metrics: Inverse Generation Distance (IGD) and Hypervolume (HV). The IGD is determined by calculating the average Euclidean distance from each point on the true Pareto front to the non-dominated solution set produced by the algorithm, with its value being inversely related to the algorithm’s performance; thus, a lower IGD indicates improved convergence and diversity of the solution set.

$$IGD\left(P^{*},P\right)={\displaystyle \frac{{\displaystyle {\sum }_{x\in P^{*}}\min dis\left(x,P\right)}}{\left|P^{*}\right|}},$$

(16)

The Hypervolume (HV) index assesses the quality of the solution set by quantifying the multi-dimensional volume encapsulated by the set within the objective space, thereby directly indicating the algorithm’s performance. A larger HV value signifies greater convergence accuracy and improved diversity coverage of the solution set.

$$HV=\delta \left({\cup }_{i=1}^{\left|S\right|}{v}_i\right),$$

(17)

where $\left|S\right|$ represents the number of individuals in the non-dominated solution set.

Table 5. Statistical values of IGD.

Problem	t-DEA	SPEA2+SDE	NSGA-III	EFR-RR	RTEA
	Mean	p-Value	Mean	p-Value	Mean	p-Value	Mean	p-Value	Mean
ACF01	15.8981	3.0199 × 10−11	12.6114	3.3384 × 10−11	14.6582	3.0199 × 10−11	13.4047	3.0199 × 10−11	5.3526
ACF02	31.7939	2.6098 × 10−10	23.6288	4.3106 × 10−8	22.6745	2.2273 × 10−9	30.4303	3.1589 × 10−10	12.5631
ACF03	111.8556	0.0056	99.2336	2.4327 × 10−5	98.7811	1.9963 × 10−5	120.3692	0.0215	140.1279
ACF04	106.0616	4.1997 × 10−10	70.6475	8.4848 × 10−9	89.0059	8.1014 × 10−10	103.4682	7.3803 × 10−10	20.2804
ACF05	7.9360 × 102	3.0199 × 10−11	648.1127	4.0772 × 10−11	7.2839 × 102	3.0199 × 10−11	7.6546 × 102	3.0199 × 10−11	1.0347 × 102
ACF06	2.7783 × 102	3.0199 × 10−11	224.4517	4.5043 × 10−11	247.1335	4.0771 × 10−11	2.7989 × 102	3.0199 × 10−11	59.1349
ACF07	169.5309	3.0199 × 10−11	130.3492	8.9934 × 10−11	151.1209	3.6897 × 10−11	164.1560	3.6897 × 10−11	42.3825
ACF08	371.8712	3.3384 × 10−11	294.8983	3.6897 × 10−11	297.1055	4.5043 × 10−11	3.3227 × 102	3.3384 × 10−11	42.2867
ACF09	17.0721	2.3715 × 10−10	14.2484	3.6897 × 10−11	16.6167	3.0199 × 10−11	16.0205	3.0199 × 10−11	6.0303
ACF10	3.1721 × 102	5.4941 × 10−11	2.7909 × 102	1.5465 × 10−9	3.0082 × 102	7.3891 × 10−11	326.9334	3.4742 × 10−10	150.7407

and

Table 6. Statistical values of HV.

Problem	t-DEA		SPEA2+SDE		NAGA-		EFR-RR		RTEA
	Mean	p-Value	Mean	p-Value	Mean	p-Value	Mean	p-Value	Mean
ACF01	0.1328	3.0199 × 10−11	0.1355	4.0772 × 10−11	0.1325	4.9752 × 10−11	0.1320	3.0199 × 10−11	0.1520
ACF02	0.1300	3.6897 × 10−11	0.1415	1.0666 × 10−7	0.1350	2.1544 × 10−10	0.1328	4.0772 × 10−11	0.1494
ACF03	0.0958	3.0199 × 10−11	0.1005	3.0199 × 10−11	0.0988	3.0199 × 10−11	0.0920	3.0199 × 10−11	0.1344
ACF04	0.0606	3.0199 × 10−11	0.0698	3.0199 × 10−11	0.0636	3.0199 × 10−11	0.0615	3.0199 × 10−11	0.1129
ACF05	0.0506	3.0199 × 10−11	0.0556	4.9752 × 10−11	0.0530	3.0199 × 10−11	0.0514	3.0199 × 10−11	0.0900
ACF06	0.0588	3.0199 × 10−11	0.0672	3.0199 × 10−11	0.0634	3.0199 × 10−11	0.0576	3.0199 × 10−11	0.1145
ACF07	0.0874	3.0199 × 10−11	0.0942	3.0199 × 10−11	0.0910	3.0199 × 10−11	0.0873	3.0199 × 10−11	0.1420
ACF08	0.0361	3.0199 × 10−11	0.0436	3.3384 × 10−11	0.0435	3.0199 × 10−11	0.0391	3.0199 × 10−11	0.1088
ACF09	0.1428	3.0199 × 10−11	0.1464	3.0199 × 10−11	0.1454	1.2057 × 10−10	0.1418	3.0199 × 10−11	0.1643
ACF10	0.0973	3.0199 × 10−11	0.1026	3.0199 × 10−11	0.0991	3.0199 × 10−11	0.0959	3.0199 × 10−11	0.1449

summarize the average IGD and HV indicators obtained for each algorithm following 30 independent operations on all benchmark cases. The P-value of the rank sum test is attached, where boldface indicates statistically significant results indicating superior performance. The analysis indicates that the RTEA method exhibits substantial advantages in terms of the IGD and HV metrics across the majority of test cases. This comprehensive evaluation verifies that both the overall process scheduling model for aluminum alloy aerospace component production and its RTEA optimization approach are efficient and practical. Therefore, the implementation of this method helps to generate better production scheduling schemes.

The three-stage environmental method introduced in the RTEA optimization framework enhances both the convergence and diversity of the population, thereby reinforcing the balance between these two aspects. The first-stage individual selection method, which is based on clustering, emphasizes not only the preservation of global diversity but also the convergence of the population when selecting individuals from each class. In contrast, the third-stage individual selection method, which utilizes vector angles, primarily aims to ensure population diversity while also considering convergence. Additionally, the RTEA optimization method introduces a sorting approach based on residual rectangles, enabling the optimal utilization of the remaining space in the hot press bracket, thereby enhancing its overall efficiency. This method significantly optimizes both the entering sequence and the placement orientation of components within the hot press. Consequently, the high-dimensional, multi-objective decision-making RTEA method effectively addresses the production scheduling problem associated with the creep forming process for aluminum alloy aerospace component production.

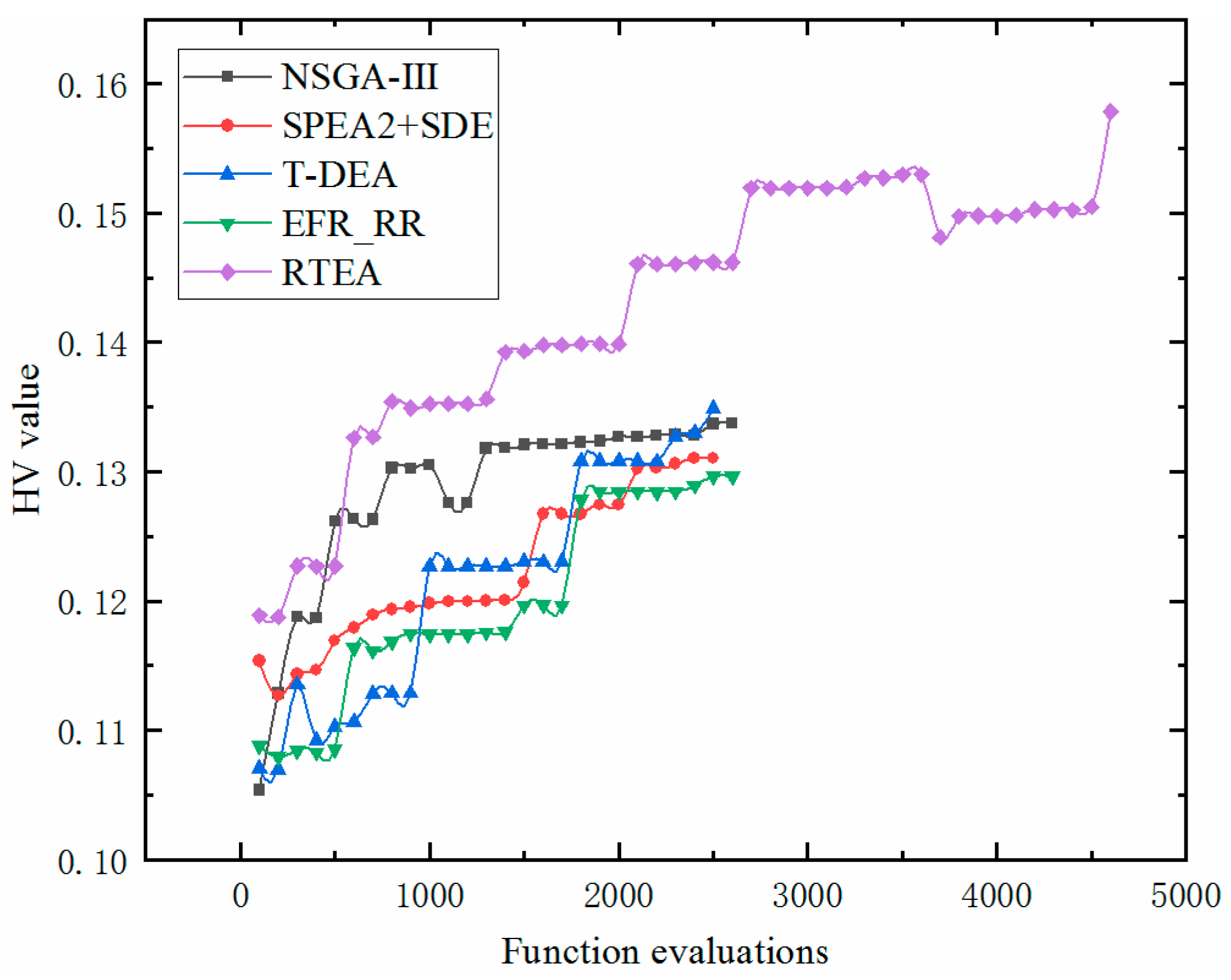
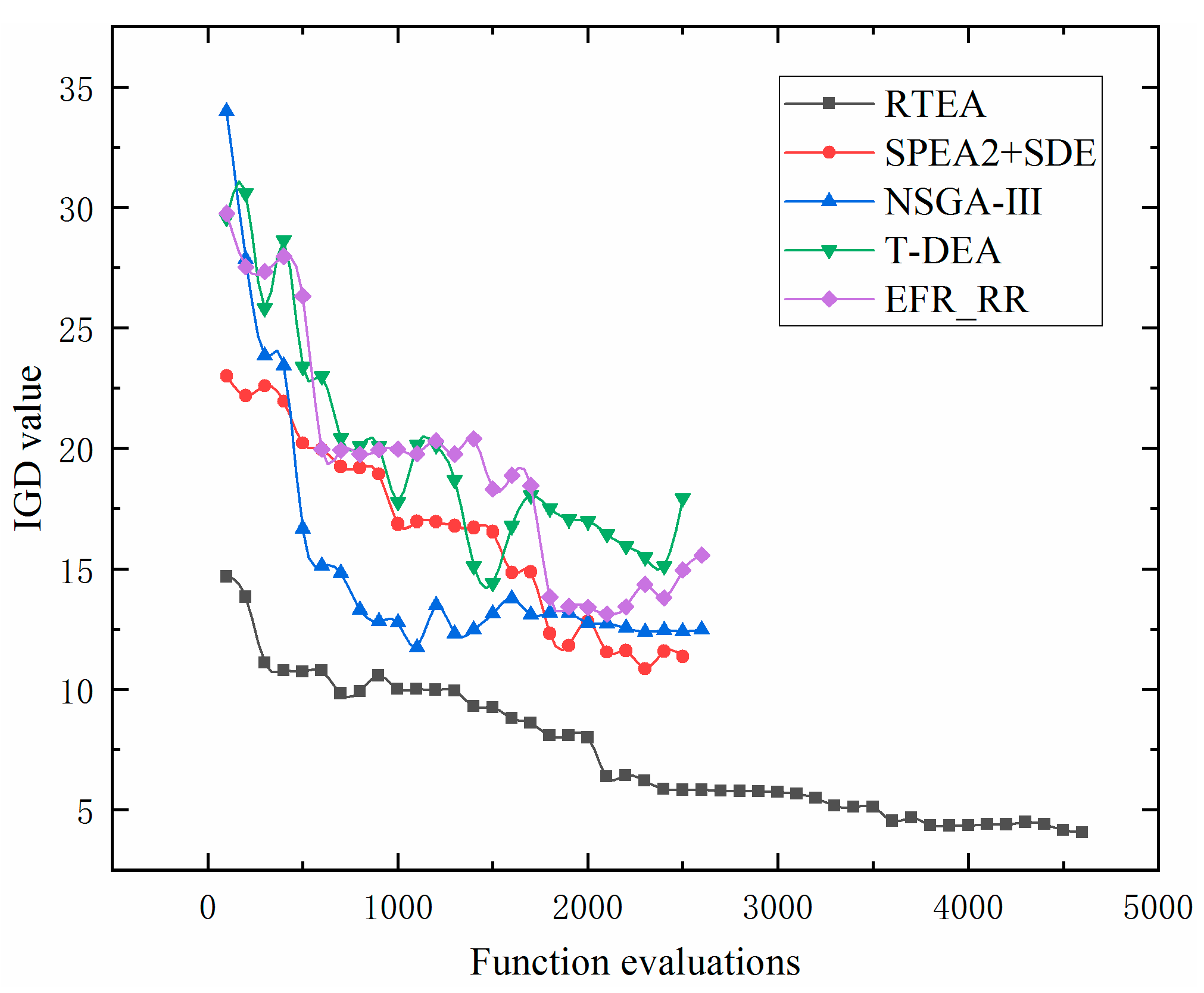
The ACF01 benchmark case was taken as the research object to verify in detail the engineering applicability and computational efficiency of the RTEA decision optimization method for the whole-process scheduling problem in aluminum alloy aerospace component creep forming production. Figure 7 and Figure 8 show the evolution laws of five intelligent optimization algorithms under the dual indicators of HV and IGD, respectively. The experimental data show that all algorithms exhibit stable convergence characteristics during the iteration process. In particular, the HV metric shows a continuous upward trend with the increase in the number of function evaluations, while the IGD metric shows a monotonically decreasing trend. It is worth noting that the RTEA exhibits significant advantages in computational performance. The evolution curve of the HV measurement value always stays in the range of about 15–22% above the other algorithms (Figure 9), while the IGD index is reduced by an average of 50% compared with the comparison algorithms (Figure 10). The comparative experimental results strongly confirm that the RTEA method has better optimization ability and convergence accuracy in solving the scheduling problem in the creep forming production of aluminum alloy aerospace components.

4.2. Experiments Based on Industrial Application

The industrial data in this section were derived from a large-scale aluminum alloy creep forming component production line.

The fuel tank of a launch vehicle serves as the storage unit for fuel and can constitute over 50% of the structural weight and volume of the rocket body. When fully fueled, the tank represents more than 90% of the rocket’s total weight; consequently, reducing the weight of the tank is crucial to enhancing the rocket’s payload capacity. Creep aging forming technology has emerged as a vital manufacturing process for complex integral components in aerospace applications. Specifically, the considered production line for large-scale aluminum alloy creep-formed components is capable of fabricating both the lids and the melon-shaped bottom parts of launch vehicle fuel tanks, and the production plan is to manufacture 40 pieces of each type.

The lid structure of the launch vehicle fuel tank is an ellipsoid component with the following specific structural dimensions: the long axis is 3338 mm, the ratio of the long axis to the short axis is 1.6, and the chord length is 1380 mm. After the top cover is unfolded, it takes on a ring shape.

The bottom part of the launch vehicle fuel tank is also an ellipsoid, and in some cases, it is melon-shaped. Based on the requirements, the size of the melon-shaped bottom part to be formed is determined to be a trapezoidal workpiece by expanding the curved surface and adding a certain machining allowance.

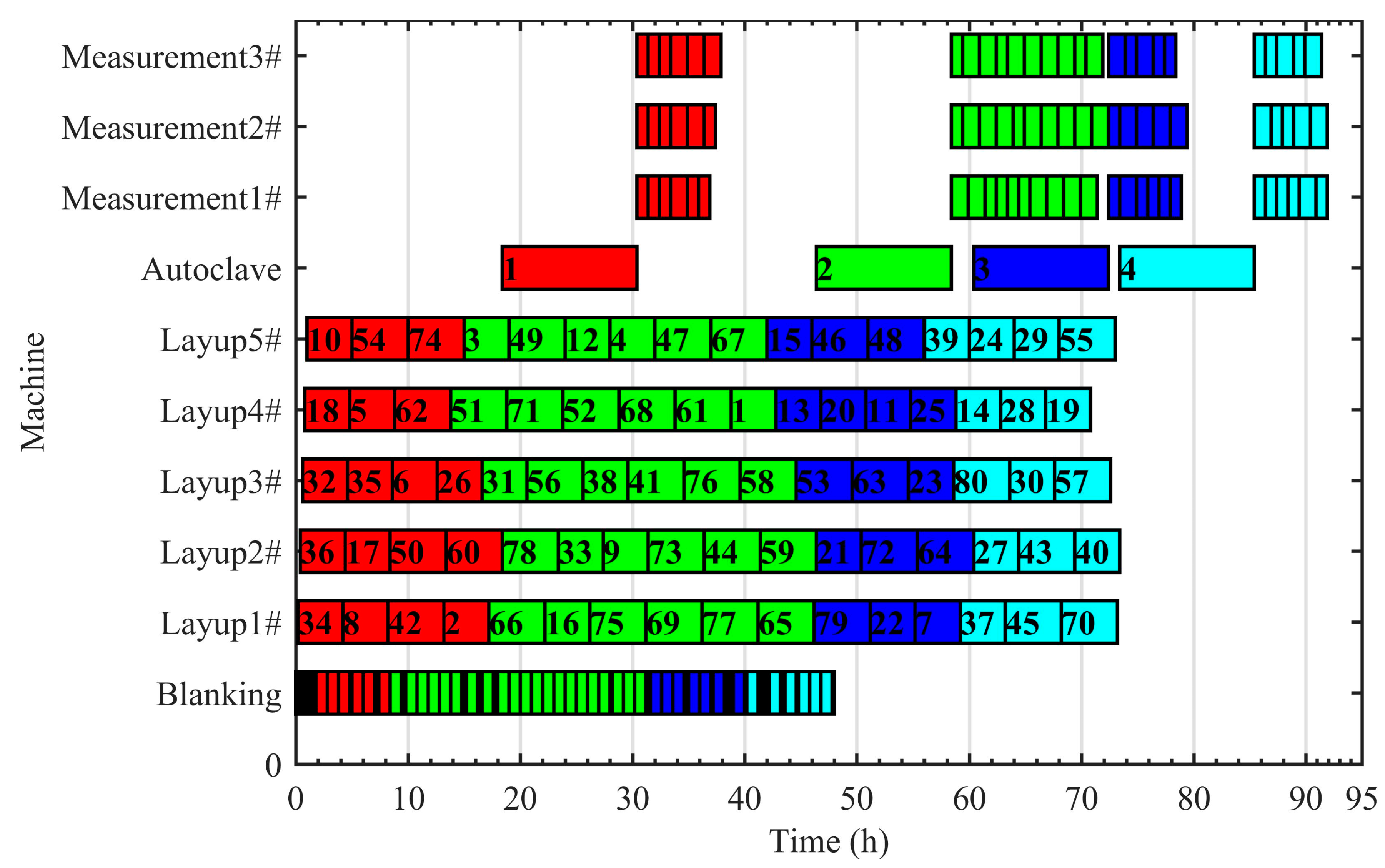
Based on the actual production data and the production scheduling model for the aluminum alloy creep forming component production line, the best compromise solution of the scheduling scheme comprises a completion time of 91.9 h, a delay time of 6.5 h, an idle time of 215.6 h, a volume utilization rate of the autoclave of 79.30%, and a total number of brackets of 8, as shown in

Table 7. The best compromise solution.

Optimization Objective	Makespan, h	Idle Time, h	Volume Utilization Rate	Delay Time, h	Total Number of Brackets
Value	91.9	215.6	79.30%	6.5	8

; this production scheduling scheme is also graphically reported in the Gantt chart in Figure 11 The scheduling scheme solved by the RTEA optimization method, which employs an autoclave filling technique based on residual rectangles, can improve production efficiency, equipment utilization rate, and autoclave volume utilization rate, as well as reducing production costs and better guiding production practice. The order sequence established in the scheduling scheme meets the technological specifications while enhancing the utilization of the autoclave volume, and the interconnections between the operations of each component ensure that the production capacity of the aluminum alloy creep forming component line is maintained. Therefore, the obtained scheduling scheme effectively addresses the production requirements for the considered line. Taken together, the experimental results demonstrate the efficacy of the proposed comprehensive production scheduling model and RTEA method for optimizing the aluminum alloy creep forming component production process.

5. Conclusions

The scheduling of aerospace component production is complex due to small-batch flexible manufacturing requirements. This study investigates the intelligent scheduling problem associated with the specific case of aluminum alloy creep aging forming production. Based on the analysis of production process characteristics, the coupling mechanism of “process flow–material flow–information flow” is deconstructed, and a high-dimensional, many-objective scheduling optimization model covering equipment utilization, energy consumption constraints, and delivery cycle is constructed. To enhance the performance of the scheduling model, we propose the RTEA method, an algorithm designed in accordance with the production characteristics of creep aging forming production that utilizes a matrix coding mechanism incorporating process correlation attributes to ensure the feasibility of the solution set. In order to improve the ability to distinguish non-dominated solutions and strengthen the balance between population convergence and diversity, a three-stage environmental selection strategy is designed within the RTEA optimization method. The feasibility and superiority of the whole-process production scheduling model and the RTEA method are verified with industrial data and dataset experiments, which show that production line efficiency can be increased by 20%. Our scheme offers an effective solution to the problem of many-objective collaborative scheduling in whole-process manufacturing and could effectively facilitate the transformation and upgrading of high-end manufacturing enterprises from the traditional experience-driven industry to intelligent manufacturing.

The production scheduling problem in aluminum alloy creep aging forming production considered in this study is categorized under static scheduling. During the actual production process, disturbance events (the insertion of urgent orders, equipment failures, etc.) often occur and disrupt the initial scheduling plan. The dynamic adjustment of the scheduling plan is complex but necessary to ensure the stability and efficiency of the production system. Therefore, future research will need to focus on high-dimensional, many-objective dynamic scheduling schemes that address various disturbance events in the production process quickly and dynamically.