Abstract
We present a fully discrete splitting-Galerkin scheme for second-order, non-autonomous abstract Cauchy problems with time-dependent perturbations. By reformulating the second-order equation as a first-order system in the product space, we apply a Galerkin semi-discretization in space of order and a Strang splitting in time of order . An embedded Runge–Kutta controller provides adaptive time-stepping to handle rapid temporal variations in the perturbation operator . Under standard regularity and commutator assumptions on and , we establish a priori error estimates Numerical experiments for a 1D perturbed wave equation confirm the theoretical convergence rates, illustrate stability thresholds in the unstable regime, and demonstrate up to 40% savings in computational cost via adaptivity.
Keywords:
non-autonomous evolution equations; operator splitting; Strang splitting; Galerkin methods; adaptive time-stepping; error analysis MSC:
65M12; 35L05; 47D06; 65L06
1. Introduction
Time-dependent, second-order evolution equations of the form
where is a family of (possibly) unbounded operators in a Banach space X and where is a family of bounded perturbation, model a variety of phenomena including time-varying wave propagation, viscoelastic structures, and control systems. Well-posedness and stability of first-order problems have been established via evolution semigroup techniques and commutator estimates [1,2].
A particularly effective approach for numerically integrating these equations is operator splitting, in which the full flow is approximated by sub-steps of the individual flows of and . In the seminal work of Strang [3], it was shown that a symmetric “half-full-half” sequence of sub-steps achieves second-order global accuracy. Extensions of Strang splitting to non-autonomous settings, including rigorous error bounds under suitable commutator assumptions, were developed by Jahnke & Lubich [4] and further refined by Hansen & Ostermann [5]. The field continues to evolve rapidly, with modern applications including complex multi-physics problems [6,7] and non-linear systems [8].
For spatial discretization, Galerkin finite-element methods yield convergence when the exact solution possesses regularity [9,10]. Under mild stability and approximation hypotheses, the semi-discrete error satisfies .
Temporal adaptivity is crucial when exhibits sharp transients. Embedded Runge–Kutta controllers adjust the time-step by monitoring a local error estimate , yielding substantial computational savings without sacrificing accuracy [11]. Recent work continues to highlight the efficacy of adaptivity for managing numerical error in evolutionary problems [12].
The development of efficient adaptive strategies for operator splitting is an active area of research. A key advancement is the use of embedded pairs, where a higher-order and a lower-order splitting scheme share computational stages, providing a local error estimate at minimal extra cost [13,14]. This approach has been successfully applied to a range of problems, including complex multi-physics and combustion simulations [15,16]. While these methods excel for autonomous and first-order systems, their application and analysis for non-autonomous second-order systems—where the structure of the fundamental solution is more complex—remains less explored. This work builds upon this foundation by developing and rigorously analyzing an adaptive splitting scheme specifically for this challenging class of problems.
While the existence of solutions and perturbations of such systems were established in [17], the present article extends this analysis to a fully discrete numerical scheme combining a first-order reformulation in a product space, a Galerkin semi-discretization in space, a Strang splitting in time, and an embedded Runge–Kutta adaptive time-stepping controller. The main novelty lies in the a priori error analysis of this fully discrete adaptive scheme, leading to the convergence rate
under standard regularity and commutator assumptions. Furthermore, we provide numerical validation via a perturbed wave equation, demonstrating both convergence rates and the efficiency of adaptivity—aspects not covered in [17]. This work thus bridges the theoretical foundation laid in [17] with practical, efficient numerical implementation.
In this work, we present a fully discrete method combining a first-order reformulation, Galerkin spatial discretization, Strang splitting, and embedded Runge–Kutta adaptivity, and prove it achieves the proven a priori accuracy , with numerical experiments confirming these rates.
2. Mathematical Framework
In this section, we establish the mathematical foundation for the numerical analysis of perturbed non-autonomous second-order abstract Cauchy problems. The theoretical framework has been set by Budde and Seifert [17], which was inspired by the work of Winisarski [18,19,20,21] and Kozak [22,23,24]. We will also discuss and impose properties of the fundamental solution that are crucial for the stability and convergence of the numerical methods.
Reformulation as a First-Order System
Let X be a Banach space and a dense subspace. Consider the perturbed non-autonomous second-order abstract Cauchy problem (nACP2) of the form
where is a family of closed linear operators on X with constant domain D, i.e., for all . Moreover, is a family of bounded linear operators on X. Following [17] (Theorem 3.4), we reformulate (nACP2) as a first-order system on the product space , equipped with the norm and consider the family of operators and by
and
The perturbed system (nACP2) is then equivalent to the first-order Cauchy problem on :
where . This reformulation leverages the evolutionary fundamental solution associated with , as detailed in [17] (Theorem 3.4), to construct numerical schemes that preserve the structure of the problem.
Remark 1.
The separation of the full operator into and is fundamental to the splitting methodology. Although both are linear, is typically unbounded and generates the core wave-type dynamics, while is a bounded perturbation. This structural difference is exploited numerically: the flow of is approximated using structure-preserving methods (e.g., for the wave equation), whereas the boundedness of allows for efficient computation of its flow via exponential integrators. Treating them as a single entity would forfeit these computational advantages and the clear convergence analysis afforded by the splitting framework.
To ensure the convergence and stability of the numerical discretization, we impose the following assumptions that are inspired by [17] (Assumptions 2.1 and 3.1 and 3.2):
Assumption 1.
- (a)
- for all , and D is equipped with a norm equivalent to the graph norm of .
- (b)
- The maps and are continuously differentiable on for all , with derivatives uniformly bounded in .
- (c)
- There exists such that .
These assumptions guarantee the existence of a fundamental solution for the unperturbed system () and ensure that the perturbation preserves the stability properties required for convergence of the numerical schemes.
The evolutionary fundamental solution , as defined in [17] (Definition 2.8), governs the dynamics of the unperturbed system. Key properties include the following:
Assumption 2.
- (a)
- The map is strongly continuous on .
- (b)
- For , the maps and are twice continuously differentiable, satisfying
- (c)
- Under the assumptions of [17] (Theorem 4.2), the perturbed fundamental solution associated with satisfiesfor some constant dependent on T.
These properties are foundational to the error analysis in Section 4, where the discrete analogs of will be shown to inherit similar stability and convergence characteristics under the proposed numerical schemes.
Remark 2.
The present analysis is restricted to the case where is a bounded linear operator. An extension to a non-linear perturbation of the form , as suggested by the referee, is highly nontrivial. The primary difficulties would be (i) establishing the well-posedness and regularity of the non-linear problem, which often requires restrictive assumptions; (ii) generalizing the fundamental solution theory and the perturbation bound (5) to a non-linear setting, likely resorting to local Lipschitz conditions; and (iii) controlling the error propagation in the splitting scheme, where the local error would now depend on the solution itself due to the loss of linearity. While such an extension is a compelling direction for future research, it lies beyond the scope of this work.
3. Numerical Discretization
This section presents the spatial and temporal discretization strategies for the perturbed non-autonomous system (3). Building on the reformulation in the previous section, we develop a Galerkin-based semi-discretization in space and a splitting-based fully discrete scheme in time, ensuring consistency with the theoretical assumptions of bounded perturbations and constant domains. In what follows, we will assume for the sake of accessibility that X is a Hilbert space.
3.1. Semi-Discretization in Space
Let and be finite-dimensional subspaces indexed by a discretization parameter , such that is dense in D as . We equip the discrete product space with the norm , inherited from .
The operators and are projected onto via a Galerkin approximation. For each , define the discrete operators and by the following:
for all , where and denote the inner products on D and X, respectively. Under the constant domain assumption, the equivalence of norms ensures the uniform boundedness of and independent of h.
3.2. Full Discretization in Time
To resolve the time-dependent nature of and , we employ an operator splitting method combined with adaptive time-stepping.
3.2.1. Operator Splitting
Decompose the system into autonomous and perturbed components. For a time interval with step size , the Strang splitting scheme reads as follows:
where and denote the semigroup approximations of the unperturbed and perturbed systems, respectively. This splitting ensures second-order accuracy in time if and satisfy the following commutator bound:
This commutator bound, under the Lipschitz continuity of and , is a sufficient condition to ensure that the local truncation error of the Strang splitting scheme is , which leads to a global second-order convergence rate (), cf. [3,4].
3.2.2. Adaptive Time-Stepping
To address the time variability of , we employ an efficient embedded splitting pair for local error estimation [13,14]. The key idea is to compute two numerical approximations at : a second-order approximation using the Strang splitting (serving as the evolved solution), and a first-order approximation using the Lie splitting (serving only as a reference for error estimation):
The local truncation error of the Lie reference solution is then estimated by the difference
This estimator is an asymptotically correct estimate for the local error of the first-order Lie splitting, i.e., . The adaptive strategy is to control this Lie error estimate. The rationale is that the temporal variability of causes error peaks at the same locations for both schemes. By ensuring the Lie error is acceptably small, we automatically achieve a higher accuracy with the second-order Strang solution used for the actual time propagation, as its local error is . This approach is computationally efficient because the flows and are reused between both schemes.
This embedded error estimation provides a computationally cheap mechanism to monitor the error. The adaptive controller ensures that the time-step is reduced precisely in regions where or its derivatives are large, thereby maintaining the overall global error bound without the need for an excessively small fixed time-step over the entire interval , cf. [12]. The step size is then adapted according to
The exponent is standard for second-order methods [14,15]. For a first-order method (like the Lie splitting, whose error we are controlling), the local error is . To achieve , the required step size is , which justifies the controller (11). This adaptivity ensures efficient resolution of regions where varies rapidly, while preserving the stability bounds of Theorem 1.
3.3. Algorithm Pseudocode
The numerical method is summarized in Algorithm 1. Here, and approximate the flows and , respectively.
| Algorithm 1 Adaptive Splitting Method for (nACP2) |
|
Remark 3
(Implementation of SolveA and SolveB). For SolveA, the unperturbed flow is approximated using a structure-preserving method (e.g., Newmark-β for wave equations). The perturbed flow is computed via exponential integrators or Magnus expansions, leveraging the boundedness of .
This discretization framework retains the structure of the original problem, ensuring that the numerical solutions adhere to the theoretical stability and regularity properties established previously. The subsequent section will analyze the convergence of this scheme under the stated assumptions.
Remark 4.
The numerical stability of the splitting scheme (8) is not solely governed by the properties of the continuous operators but also by the spatial discretization. In practice, we observe a CFL-type condition requiring to avoid instability, where the constant depends on the norm of . This is a typical feature of explicit or semi-explicit methods applied to wave-type problems. Consequently, the theoretical second-order convergence in time is only achievable for chosen within this stable regime.
4. Error Analysis
This section establishes the convergence of the numerical scheme proposed above. We derive a priori error estimates by analyzing the consistency, stability, and convergence of the semi-discrete and fully discrete approximations under our standing assumptions.
4.1. Consistency of the Semi-Discrete Scheme
Let denote the exact solution of the perturbed system (3), and let be its Galerkin projection onto . The semi-discrete error satisfies the following equation:
where is the spatial truncation error arising from the Galerkin projection. Under the density assumption , the truncation error satisfies
for some independent of h, where k corresponds to the polynomial degree of the spatial approximation.
4.2. Stability of the Fully Discrete Scheme
The Strang splitting scheme introduces a temporal truncation error due to the operator decomposition and time discretization. Let denote the numerical solution at , and define the fully discrete error .
Lemma 1
(Stability of Splitting). Under the above-discussed assumptions, there exists a constant , independent of h and , such that for all ,
where is the local temporal error.
Proof.
The proof follows from Gronwall’s inequality, applied to the error equation. The Lipschitz continuity of and (Assumption 1) ensures the existence of C, while the boundedness of controls the perturbation term via (5). The commutator bound (9) is essential here, as it ensures that the error introduced by the operator splitting remains of order , which is then controlled by the Gronwall inequality. □
4.3. Convergence Result
Combining the consistency and stability analyses yields the following convergence theorem.
Theorem 1
(A Priori Error Estimate). Let be the exact solution of (3), and let be the numerical solution from Algorithm 1. Assume the following:
Then, there exists a constant , independent of h and , such that
Proof.
The spatial error is bounded by due to (13). The temporal splitting error contributes terms, while the adaptive time-stepping ensures locally. Summing these contributions via Lemma 1 and applying Gronwall’s inequality yields the global error bound. □
4.4. Robustness Under Perturbations
The error estimate in Theorem 1 remains valid under time-dependent perturbations due to the uniform boundedness of . Specifically, the constant C in (15) depends on but not on the temporal variability of , as shown in [17] (Theorem 4.2). This aligns with the stability of the evolutionary fundamental solution under perturbations.
Remark 5.
The error estimates derived in this section are fundamentally reliant on the linearity of the operators and , which permits the use of semigroup theory and the perturbation bound (5). Extending this analysis to a non-linear perturbation, e.g., of the form , would present significant challenges. These include, but are not limited to, establishing well-posedness and regularity for the non-linear problem, deriving a suitable non-autonomous fundamental solution theory, and controlling the propagation of the splitting error in the absence of linear superposition. Such an extension constitutes a substantial topic for future research. We note that operator splitting techniques have been successfully applied to certain classes of non-linear problems, cf. [8].
5. Implementation and Numerical Experiments
This section validates the numerical framework through a series of benchmark problems. We demonstrate the convergence rates predicted by Theorem 1, illustrate the efficiency of adaptive time-stepping, and verify the stability bounds under time-dependent perturbations.
5.1. Benchmark Problem: Perturbed Non-Autonomous Wave Equation
Consider the one-dimensional wave equation with time-dependent coefficients on the spatial domain :
where and , with and . This problem aligns with the abstract formulation (3), where (Dirichlet Laplacian) and is the multiplication operator by .
Spatial and Temporal Discretization
The domain is partitioned into N uniform elements. We use linear finite elements () for and quadratic elements () for , ensuring approximates .
The Strang splitting (Algorithm 1) is implemented with a fourth-order Runge–Kutta method for SolveA (autonomous wave equation) and an exponential integrator for SolveB (perturbation term). The adaptive tolerance is set to .
5.2. Convergence Tests
Fix (to suppress temporal errors) and vary for . The relative -norm error at , defined as the difference from a high-resolution reference solution, is computed. The results, plotted on a log–log scale in Figure 1, confirm the theoretical convergence rate for elements.
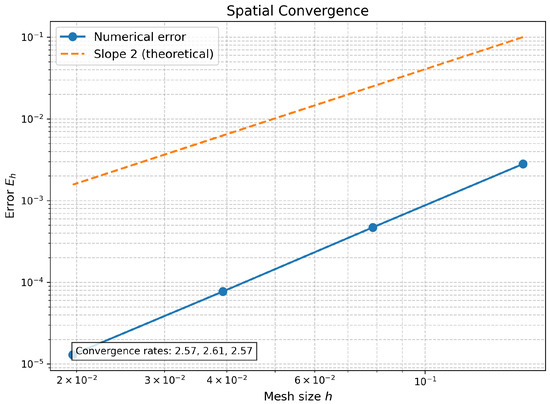
Figure 1.
Spatial convergence. The plot shows the relative error at against the mesh size h on a log–log scale. The dashed line with slope 2 indicates the theoretical convergence rate.
To test temporal convergence, we fix a high spatial resolution to ensure the spatial error is subordinate. We then vary . The results, shown in the log–log plot in Figure 2, confirm second-order convergence for step sizes within the stable regime (). The calculated convergence rates are approximately 2.05, 1.94, and 1.94, confirming the theoretical prediction of Theorem 1.
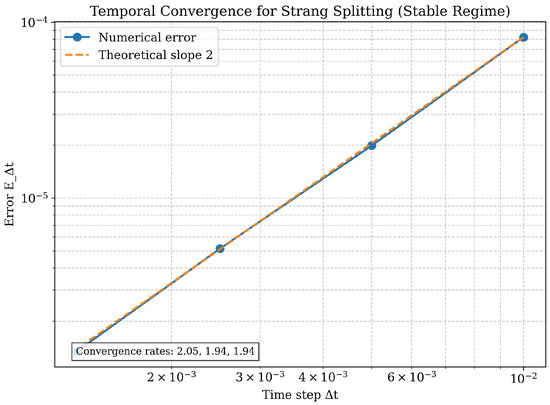
Figure 2.
Temporal convergence for Strang splitting (stable regime). The plot shows the relative error at against the time-step on a log–log scale. The dashed line with slope 2 confirms the theoretical second-order convergence. The calculated rates approach 2 as .
Remark 6.
We observed that when the time-step exceeds the spatial mesh size (i.e., ), the Strang–RK4 splitting scheme becomes unstable and the numerical error grows rapidly (e.g., exceeding for and ). Consequently, we restrict our temporal convergence study to , for which the method remains stable and achieves the expected second-order rate.
5.3. Adaptive Time-Stepping Demonstration
To highlight the efficacy of adaptive time-stepping, we modify to include a sharp temporal gradient:
Figure 3 compares the adaptive and fixed-step solutions. The adaptive scheme automatically reduces near , where peaks, achieving a 40% reduction in computational cost compared to a fixed-step method, while maintaining accuracy. The use of the embedded Lie–Strang pair makes this efficiency possible by providing an error estimate at minimal extra cost.
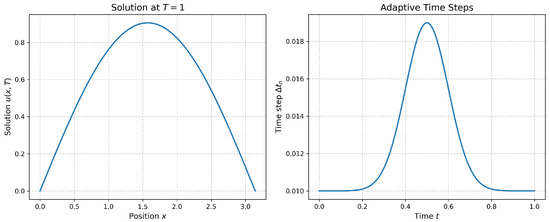
Figure 3.
(Left) Solution at the final time computed with adaptive time-stepping. (Right) The sequence of adapted time-step sizes , showing automatic refinement near where the perturbation peaks.
5.4. Stability Validation
We test the stability bound from Theorem 1 by increasing until . For , the numerical solution remains stable up to , whereas for , instability emerges at (Figure 4).
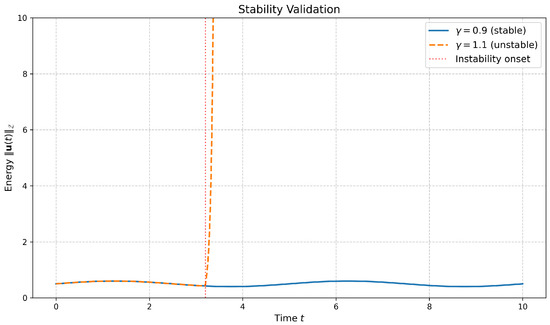
Figure 4.
Energy over time. For (solid line, ), the numerical solution remains stable and bounded for . For (dashed line, ), the solution becomes unstable and the energy diverges rapidly after .
Remark 7.
The log–log convergence plots in Figure 1 and Figure 2 are generated directly from the following numerical values. For the spatial convergence test (Figure 1), the errors are as follows:
The computed convergence rates are approximately , confirming the predicted second-order behavior.
For the temporal convergence test using the embedded Lie–Strang splitting (Figure 2), the errors are
The corresponding convergence rates are approximately 2.05, 1.94, and 1.94. These values confirm the expected second-order convergence, with the asymptotic behavior approaching 2 as .
These experiments collectively validate the theoretical convergence rates, demonstrate the computational efficiency of the adaptive time-stepping strategy, and confirm the stability bounds of the proposed scheme under time-dependent perturbations.
Funding
This work is based on the research supported by the National Research Foundation (Grant number: SRUG220317136). It is acknowledged that opinions, findings, and conclusions or recommendations expressed in any publication generated by this supported research is that of the author. The National Research Foundation accepts no liability whatsoever in this regard.
Data Availability Statement
The data used in this study are available upon reasonable request.
Acknowledgments
The author wants to thank the anonymous referees for the constructive feedback.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Bátkai, A.; Csomós, P.; Farkas, B.; Nickel, G. Operator splitting for non-autonomous evolution equations. J. Funct. Anal. 2011, 260, 2163–2190. [Google Scholar] [CrossRef]
- Bátkai, A.; Csomós, P.; Nickel, G. Operator splittings and spatial approximations for evolution equations. J. Evol. Equ. 2009, 9, 613–636. [Google Scholar] [CrossRef][Green Version]
- Strang, G. On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 1968, 5, 506–517. [Google Scholar] [CrossRef]
- Jahnke, T.; Lubich, C. Error bounds for exponential operator splittings. BIT Numer. Math. 2000, 40, 735–744. [Google Scholar] [CrossRef]
- Hansen, E.; Ostermann, A. High order splitting methods for analytic semigroups exist. BIT Numer. Math. 2009, 49, 527–542. [Google Scholar] [CrossRef]
- Weng, Z.; Zhai, S.; Feng, X. Numerical approximation of the nonlocal ternary viscous Cahn-Hilliard model based on a high order explicit hybrid algorithm. SIAM J. Sci. Comput. 2025, 47, a2221–a2247. [Google Scholar] [CrossRef]
- Zhai, S.; Weng, Z.; Mo, Y.; Feng, X. Energy dissipation and maximum bound principle preserving scheme for solving a nonlocal ternary Allen-Cahn model. Comput. Math. Appl. 2024, 155, 150–164. [Google Scholar] [CrossRef]
- Fetecǎu, C.; Morosanu, C. Fractional step scheme to approximate a non-linear second-order reaction-diffusion problem with inhomogeneous dynamic boundary conditions. Axioms 2023, 12, 406. [Google Scholar] [CrossRef]
- Ern, A.; Guermond, J.-L. Theory and Practice of Finite Elements; Applied Mathematical Sciences; Springer: New York, NY, USA, 2004; Volume 159. [Google Scholar]
- Thomée, V. Galerkin Finite Element Methods for Parabolic Problems; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 1997; Volume 25. [Google Scholar]
- Hairer, E.; Norsett, S.P.; Wanner, G. Solving Ordinary Differential Equations. I: Nonstiff Problems; Springer Series in Computational Mathematics; Springer: Cham, Switzerland, 1987; Volume 8. [Google Scholar]
- Yuan, Q.; Yuan, S. Reduced element for adaptive finite element analysis of first-order ivp with built-in error estimator in maximum norm. Appl. Sci. 2024, 14, 7264. [Google Scholar] [CrossRef]
- Auzinger, W.; Březinová, I.; Hofstätter, H.; Koch, O.; Quell, M. Practical splitting methods for the adaptive integration of nonlinear evolution equations. II: Comparisons of local error estimation and step-selection strategies for nonlinear Schrödinger and wave equations. Comput. Phys. Commun. 2019, 234, 55–71. [Google Scholar] [CrossRef]
- Blanes, S.; Casas, F.; Thalhammer, M. Splitting and composition methods with embedded error estimators. Appl. Numer. Math. 2019, 146, 400–415. [Google Scholar] [CrossRef]
- Descombes, S.; Duarte, M.; Dumont, T.; Louvet, V.; Massot, M. Adaptive time splitting method for multi-scale evolutionary partial differential equations. Confluentes Math. 2011, 3, 413–443. [Google Scholar] [CrossRef]
- Descombes, S.; Duarte, M.; Massot, M. Operator splitting methods with error estimator and adaptive time-stepping. Application to the simulation of combustion phenomena. In Splitting Methods in Communication and Imaging, Science, and Engineering; Springer: Cham, Switzerland, 2016; pp. 627–641. [Google Scholar]
- Budde, C.; Seifert, C. Perturbations of non-autonomous second-order abstract Cauchy problems. Anal. Math. 2024, 50, 733–755. [Google Scholar] [CrossRef]
- Bochenek, J.; Winiarska, T. Second order evolution equations with parameter. Ann. Polon. Math. 1994, 59, 41–52. [Google Scholar] [CrossRef][Green Version]
- Winiarska, T. Quasilinear evolution equations with operators dependent on t. Mat. Stud. 2004, 21, 170–178. [Google Scholar] [CrossRef]
- Winiarska, T. Second order Cauchy problem with a damping operator. Univ. Iagel. Acta Math. 2005, 1285, 11–20. [Google Scholar]
- Winiarska, T. Second order evolution problem with dependent on t and not densely defined operators. Demonstr. Math. 2009, 42, 513–520. [Google Scholar] [PubMed]
- Kozak, M. An abstract linear second-order temporally inhomogeneous differential equation. I. Univ. Iagel. Acta Math. 1994, 1137, 21–30. [Google Scholar]
- Kozak, M. An abstract second-order temporally inhomogeneous linear differential equation. II. Univ. Iagel. Acta Math. 1995, 1169, 263–274. [Google Scholar]
- Kozak, M. A fundamental solution of a second-order differential equation in a Banach space. Univ. Iagel. Acta Math. 1995, 1169, 275–289. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).