Modified Engel Algorithm and Applications in Absorbing/Non-Absorbing Markov Chains and Monopoly Game
Abstract
1. Introduction
2. From the Complete Graph to the Modified Graph
- Step 1:
- We begin with the state space of a non-absorbing Markov chain, denoted by S, then create another state space of an absorbing Markov chain with the same number of states as in the original chain of the transition diagram, denoted by . In this new absorbing chain, the state space is not fully connected. Then, we introduce the additional state space denoted by , which is also not fully connected. All states in are recurrent, meaning they eventually return to themselves. In general, a state is considered recurrent if, whenever we leave that state, we will return to it in the future with probability one. cannot go back to .
- Step 2:
- We introduce an artificial state s in S as a starting state. This state is not part of the original Markov chain but is added to the algorithm. The transition probabilities from S to each state in are set to specific probability distribution values (i.e., certain transitions). In contrast, the transition probabilities from S to each state in are all set to zeros (i.e., impossible transitions).
- Step 3:
- The stationary distribution of this modified Markov chain (including S, , and ) is equivalent to that of the original non-absorbing Markov chain. The proof of this equivalence is provided in Section 3.
3. Structure of the mEngel Algorithm
| Algorithm 1: Structure of the mEngel algorithm |
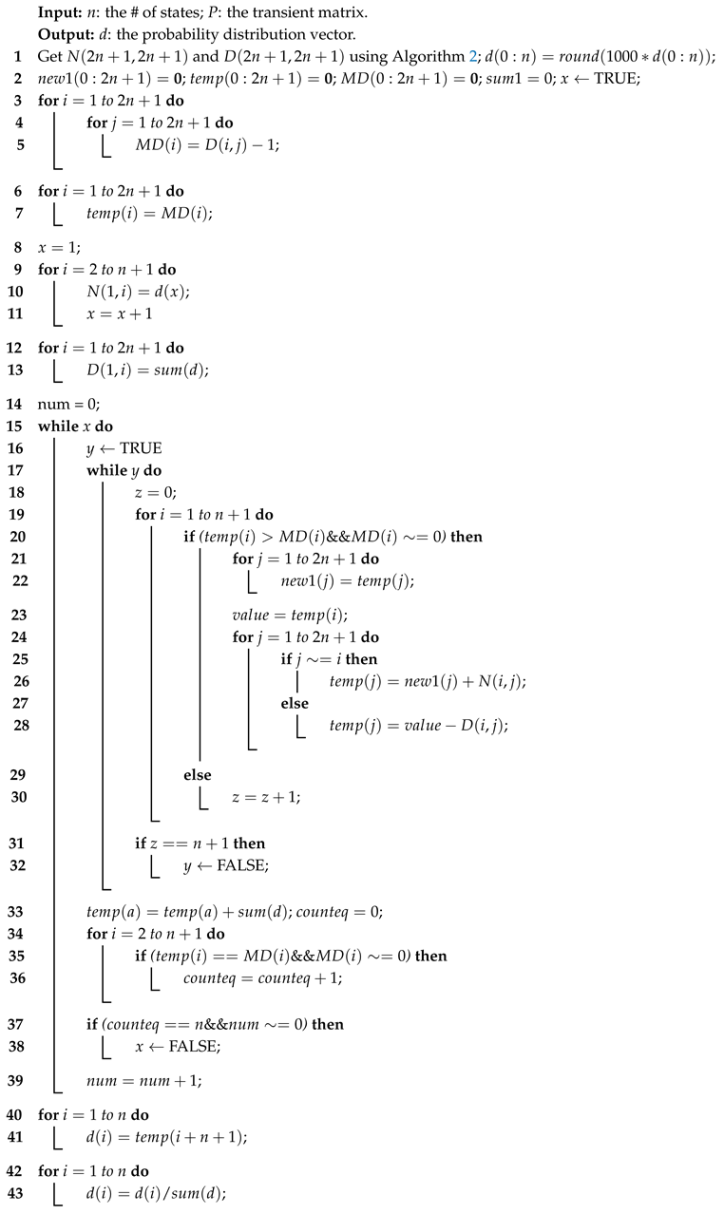 |
| Algorithm 2: Matrix formulations of N and D |
Input: P: the transition matrix; n: the # of states; . Output: N and D.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
- The ceil operation is used here to ensure that every element of the matrix is an integer since the distributing chips are in an integer process. For example, if an element of the transition matrix, P, for a non-absorbing Markov chain/absorbing chain, is 0.949 and , then the unrounded value will be . Thus, the rounded-up value is 95. Alternatively, one could choose c as 1000, thus avoiding the rounding-up procedure. Similarly, each corresponding entry of the ratio of and is equal to each position of the transition matrix P. Hence, is a matrix scaled by c.
- From S to , each arrow means a directed movement, where the number of chips being distributed is reshuffled and added. At the end of the iteration process, the number of configurations (chips) between the initial and final transient states remains the same.
- From to , the original transition matrix, P, is scaled by c. As a result of this rounding-up process, the chips in a vertex are distributed to its neighboring vertices based on the probabilities obtained from rounding up the values of to the nearest integers.
- From to , a set of transient states will be forced into a set of recurrent states, e.g., a state j is called an absorbing state if, with probability 1, the process will eventually return to j after it leaves Hence, this is crucial for transforming the transient state into the absorbing state. Typically, a self-loop at each state means that a state of a Markov chain is called absorbing if, once entered, it cannot be left. Chips are stored at each vertex.
- At the end of the iterative process, within the pre-assigned tolerance and the number of iterations, the stationary distribution for non-absorbing Markov chains is obtained by summing all chips from all vertices, i.e., , using the normalization procedure, i.e., for all i.
Implementation of the mEngel Algorithm
| Algorithm 3: Illustration of the nested mEngel algorithm |
 |
- In Lines 3–5, represents the capacity array of the states. An element in is equal to 0 when it is a recurrent state and not equal to zero when it is a transient state. This part is also called critical loading.
- In Lines 15–39, the while loop ends when the initial transient states’ chips are the same as the end states’ chips.
- In Lines 20–30, chips are firing if available. Otherwise, it simply counts the number of unavailable states.
- –
- In Lines 21–22, if the available chips are more than the capacity for chips, then the chips are stored in .
- –
- In Lines 24–28, , where j is the order of states that the chips move to, i is the order of states that the chips start from, and means that, in this round of the loop, the current state is not the starting state.
- In Lines 31–32, if the number of states that are not available is equal to the transient states, the while loop ends.
- In vector , the total of d is needed, i.e., , because the starting state needs chips to be available to be fired. We set , which is the number of unavailable transient states. The loop will stop when is equal to the number of transient states, n.
- In Lines 37–38, the number of the current transient state’s chips are checked to determine whether it is the same as that of the initial one, i.e., critical loading.
- In Lines 40–43, the probability distribution vector is updated and normalized.
4. Numerical Results
4.1. Torrence’s Problem
4.2. Monopoly
4.2.1. Construction of Monopoly Matrices
- Step 1:
- The probability of leaving from Jail is while the probability of staying in Jail is .
- Step 2:
- They have the same formation as the 1st–40th rows if ‘leaving Jail’. However, in states 41 and 42, the entries (where ), are ( because ‘if leaving’, from Step 1). Furthermore, (where ), is .
| Squares from Jail | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 11 | 11+1 | 11+2 | 11+3 | 11+4 | 11+5 | 11+6 | 11+7 | 11+8 | 11+9 | 11+10 | 11+11 | 11+12 | |
| Probability of | |||||||||||||
| Leaving after the | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 |
| First Turn in Jail | |||||||||||||
| Probability of | |||||||||||||
| Leaving after the | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 |
| Second Turn in Jail |
| Squares | 1 … 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 … 43 |
| Probability of | ||||||||||||||
| Leaving after the | 0 … 0 | 0 | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 | 0 … 0 |
| Third Turn in Jail |
- For Short Jail, the probability of staying in Jail for one more turn is 0 as opposed to Long Jail.
- They have the same formation as the 1st-40th rows if ‘leaving Jail’. (like )
- Starting with the 11st state (shared with “Just Visiting Jail”), the entries are the probabilities from rolling two dice, where , and .
- For the 31st, when players land in this state, they will go to Jail. So, when , when .
- For the 41st, 42nd, and 43rd, players who are already in Jail will stay in Jail. So, when , and when .
- For the first and last rows, as well as for all other rows except the 8th, 23rd, and 37th, there is no change. Therefore, for when .
- Moreover, when and .
- In the special case of the 8th, 23rd, and 37th rows, the probability depends on randomly drawn cards. Therefore, there are no specific formulations, and the probability is equal to the probability of the drawn cards as shown in Table 4.
4.2.2. Numerical Results for the Model (Long Jail) and for the Model (Short Jail)
4.3. The Model
4.4. The Return of Monopoly
- For , , , the number of the turns is calculated as .
- For 1 house, with and , .
- For 2 houses, with and , .
- For 3 houses, with and , .
- For 4 houses, with and , .
- For a hotel, with and , .
- , baseCost = 60 + 60 = 120, , the number of the turns is calculated as .
- For two houses, with , , .
5. Conclusions
- It can be applied to non-absorbing and absorbing Markov chains, whereas the original Engel algorithm is limited to absorbing cases.
- It provides process values, such as the passing frequency of intermediate states, which traditional methods cannot provide. This capability allowed us to identify which state had been firing, referred to as a firing state, and record this information for each configuration.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| mEngel | modified Engel algorithm |
| CFG | the chip-firing game |
| TR | transient |
| ABSs | absorbing states |
| M | movement |
| J | Jail |
| Chance | |
| Community Chest | |
| L | Long Jail |
| S | Short Jail |
| R | rent earnings |
Appendix A. Definitions of Transition Matrices
| 3/248 | 0 | 3/124 | 12/217 | 74/793 | 35/247 | 30/217 | 27/434 | 30/217 | 24/217 | 18/217 | 35/533 | 23/605 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 14/837 | 0 | 0 |
| 4/463 | 0 | 0 | 6/217 | 25/391 | 27/248 | 24/217 | 38/733 | 36/217 | 30/217 | 24/217 | 49/535 | 25/391 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 11/829 | 0 | 0 |
| 3/434 | 0 | 0 | 0 | 15/434 | 33/434 | 18/217 | 9/217 | 30/217 | 36/217 | 30/217 | 100/851 | 70/779 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 11/953 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 1/193 | 34/787 | 12/217 | 27/868 | 24/217 | 30/217 | 36/217 | 143/997 | 11/95 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 9/917 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 3/868 | 9/868 | 6/217 | 9/434 | 18/217 | 24/217 | 30/217 | 21/124 | 35/247 | 24/217 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 3/371 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 1/579 | 1/193 | 0 | 9/868 | 12/217 | 18/217 | 24/217 | 111/793 | 146/871 | 30/217 | 24/217 | 18/217 | 12/217 | 3/124 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 3/371 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 24/217 | 18/217 | 3/62 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/371 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 24/217 | 9/124 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/917 | 0 | 0 |
| 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 3/31 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11/953 | 0 | 0 |
| 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 15/124 | 24/217 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11/829 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 9/62 | 30/217 | 72/641 | 18/217 | 12/217 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 15/124 | 36/217 | 35/247 | 24/217 | 18/217 | 9/434 | 6/217 | 3/868 | 3/434 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 6/217 | 12/217 | 18/217 | 3/31 | 30/217 | 84/491 | 30/217 | 24/217 | 27/868 | 12/217 | 11/335 | 9/868 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 6/217 | 12/217 | 9/124 | 24/217 | 9/62 | 36/217 | 30/217 | 9/217 | 18/217 | 27/434 | 9/217 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 6/217 | 3/62 | 18/217 | 75/629 | 30/217 | 36/217 | 38/733 | 24/217 | 49/535 | 9/124 | 6/217 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 3/124 | 12/217 | 74/793 | 24/217 | 30/217 | 27/434 | 30/217 | 15/124 | 76/733 | 12/217 | 6/217 | 9/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 14/837 | 0 | 0 |
| 4/463 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 25/391 | 18/217 | 24/217 | 38/733 | 36/217 | 125/851 | 50/391 | 18/217 | 12/217 | 9/248 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 11/829 | 0 | 0 |
| 3/434 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15/434 | 12/217 | 18/217 | 9/217 | 30/217 | 136/787 | 33/217 | 24/217 | 18/217 | 27/434 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 11/953 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 6/217 | 12/217 | 27/868 | 24/217 | 143/997 | 150/851 | 30/217 | 24/217 | 75/851 | 12/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 13/347 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 6/217 | 9/434 | 18/217 | 56/491 | 9/62 | 36/217 | 30/217 | 56/491 | 18/217 | 0 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 9/142 | 0 | 0 |
| 1/579 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 9/868 | 12/217 | 21/248 | 56/491 | 30/217 | 36/217 | 111/793 | 24/217 | 0 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 81/907 | 0 | 0 |
| 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 0 | 18/217 | 12/217 | 3/124 | 0 | 0 | 0 | 0 | 0 | 0 | 20/171 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 0 | 24/217 | 18/217 | 3/62 | 6/217 | 0 | 0 | 0 | 0 | 0 | 6/41 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 0 | 30/217 | 24/217 | 9/124 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 68/387 | 0 | 0 |
| 4/463 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 6/217 | 12/217 | 21/248 | 24/217 | 0 | 36/217 | 30/217 | 46/467 | 18/217 | 50/851 | 9/868 | 0 | 0 | 1/579 | 5/33 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 6/217 | 50/851 | 18/217 | 0 | 30/217 | 36/217 | 27/217 | 24/217 | 70/779 | 9/434 | 6/217 | 0 | 3/868 | 48/377 | 0 | 0 |
| 10/643 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 11/335 | 12/217 | 0 | 24/217 | 30/217 | 66/439 | 30/217 | 15/124 | 27/868 | 12/217 | 6/217 | 1/193 | 56/543 | 0 | 0 |
| 10/643 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 3/434 | 6/217 | 0 | 18/217 | 24/217 | 50/391 | 36/217 | 33/217 | 9/217 | 18/217 | 12/217 | 15/434 | 4/53 | 0 | 0 |
| 34/787 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 4/463 | 0 | 0 | 12/217 | 18/217 | 37/351 | 30/217 | 135/737 | 38/733 | 24/217 | 18/217 | 25/391 | 43/899 | 0 | 0 |
| 35/494 | 6/217 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 9/868 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 100/629 | 27/434 | 30/217 | 24/217 | 74/793 | 20/991 | 0 | 0 |
| 3/31 | 12/217 | 3/124 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 6/217 | 28/491 | 18/217 | 50/391 | 38/733 | 36/217 | 30/217 | 75/629 | 16/867 | 0 | 0 |
| 113/921 | 18/217 | 3/62 | 6/217 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 27/868 | 12/217 | 3/31 | 9/217 | 30/217 | 36/217 | 9/62 | 14/837 | 0 | 0 |
| 59/397 | 24/217 | 9/124 | 12/217 | 6/217 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 1/193 | 6/217 | 35/533 | 27/868 | 24/217 | 30/217 | 84/491 | 3/200 | 0 | 0 |
| 150/851 | 30/217 | 3/31 | 18/217 | 12/217 | 27/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 3/868 | 0 | 15/434 | 9/434 | 18/217 | 24/217 | 35/247 | 3/200 | 0 | 0 |
| 59/397 | 36/217 | 15/124 | 24/217 | 18/217 | 28/491 | 6/217 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 1/579 | 0 | 3/868 | 9/868 | 12/217 | 18/217 | 72/641 | 3/200 | 0 | 0 |
| 113/921 | 30/217 | 9/62 | 30/217 | 72/641 | 75/851 | 12/217 | 9/868 | 0 | 0 | 0 | 1/579 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 21/248 | 14/837 | 0 | 0 |
| 23/242 | 24/217 | 15/124 | 36/217 | 35/247 | 15/124 | 18/217 | 9/434 | 6/217 | 0 | 0 | 3/868 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 50/851 | 14/837 | 0 | 0 |
| 37/549 | 18/217 | 3/31 | 30/217 | 84/491 | 2/13 | 24/217 | 27/868 | 12/217 | 6/217 | 0 | 1/193 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11/335 | 14/837 | 0 | 0 |
| 25/629 | 12/217 | 9/124 | 24/217 | 9/62 | 67/359 | 30/217 | 9/217 | 18/217 | 12/217 | 6/217 | 3/434 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 14/837 | 0 | 0 |
| 3/248 | 6/217 | 3/62 | 18/217 | 75/629 | 11/67 | 36/217 | 38/733 | 24/217 | 18/217 | 12/217 | 9/248 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 14/837 | 0 | 0 |
| 1/579 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 0 | 6/217 | 0 | 6/217 | 0 | 6/217 | 1/579 | 6/217 | 0 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 1/400 | 5/6 | 0 |
| 1/579 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 0 | 6/217 | 0 | 6/217 | 0 | 6/217 | 1/579 | 6/217 | 0 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 1/400 | 0 | 5/6 |
| 3/248 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 9/62 | 30/217 | 72/641 | 18/217 | 12/217 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 14/837 | 0 | 0 |
| 3/248 | 0 | 3/124 | 12/217 | 74/793 | 35/247 | 30/217 | 27/434 | 30/217 | 24/217 | 18/217 | 35/533 | 23/605 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 14/837 | 0 | 0 |
| 4/463 | 0 | 0 | 6/217 | 25/391 | 27/248 | 24/217 | 38/733 | 36/217 | 30/217 | 24/217 | 49/535 | 25/391 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 11/829 | 0 | 0 |
| 3/434 | 0 | 0 | 0 | 15/434 | 33/434 | 18/217 | 9/217 | 30/217 | 36/217 | 30/217 | 100/851 | 70/779 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 11/953 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 1/193 | 34/787 | 12/217 | 27/868 | 24/217 | 30/217 | 36/217 | 143/997 | 11/95 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 9/917 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 3/868 | 9/868 | 6/217 | 9/434 | 18/217 | 24/217 | 30/217 | 21/124 | 35/247 | 24/217 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 3/371 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 1/579 | 1/193 | 0 | 9/868 | 12/217 | 18/217 | 24/217 | 111/793 | 146/871 | 30/217 | 24/217 | 18/217 | 12/217 | 3/124 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 3/371 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 24/217 | 18/217 | 3/62 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/371 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 24/217 | 9/124 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/917 | 0 | 0 |
| 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 3/31 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11/953 | 0 | 0 |
| 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 15/124 | 24/217 | 18/217 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11/829 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 9/62 | 30/217 | 72/641 | 18/217 | 12/217 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 15/124 | 36/217 | 35/247 | 24/217 | 18/217 | 9/434 | 6/217 | 3/868 | 3/434 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 6/217 | 12/217 | 18/217 | 3/31 | 30/217 | 84/491 | 30/217 | 24/217 | 27/868 | 12/217 | 11/335 | 9/868 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 6/217 | 12/217 | 9/124 | 24/217 | 9/62 | 36/217 | 30/217 | 9/217 | 18/217 | 27/434 | 9/217 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 6/217 | 3/62 | 18/217 | 75/629 | 30/217 | 36/217 | 38/733 | 24/217 | 49/535 | 9/124 | 6/217 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 3/124 | 12/217 | 74/793 | 24/217 | 30/217 | 27/434 | 30/217 | 15/124 | 76/733 | 12/217 | 6/217 | 9/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 14/837 | 0 | 0 |
| 4/463 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 25/391 | 18/217 | 24/217 | 38/733 | 36/217 | 125/851 | 50/391 | 18/217 | 12/217 | 9/248 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 11/829 | 0 | 0 |
| 3/434 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15/434 | 12/217 | 18/217 | 9/217 | 30/217 | 136/787 | 33/217 | 24/217 | 18/217 | 27/434 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 11/953 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 6/217 | 12/217 | 27/868 | 24/217 | 143/997 | 150/851 | 30/217 | 24/217 | 75/851 | 12/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 13/347 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 6/217 | 9/434 | 18/217 | 56/491 | 9/62 | 36/217 | 30/217 | 56/491 | 18/217 | 0 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 9/142 | 0 | 0 |
| 1/579 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 9/868 | 12/217 | 21/248 | 56/491 | 30/217 | 36/217 | 111/793 | 24/217 | 0 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 81/907 | 0 | 0 |
| 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 30/217 | 0 | 18/217 | 12/217 | 3/124 | 0 | 0 | 0 | 0 | 0 | 0 | 20/171 | 0 | 0 |
| 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 36/217 | 0 | 24/217 | 18/217 | 3/62 | 6/217 | 0 | 0 | 0 | 0 | 0 | 6/41 | 0 | 0 |
| 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 0 | 30/217 | 24/217 | 9/124 | 12/217 | 6/217 | 0 | 0 | 0 | 0 | 68/387 | 0 | 0 |
| 4/463 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 6/217 | 12/217 | 21/248 | 24/217 | 0 | 36/217 | 30/217 | 46/467 | 18/217 | 50/851 | 9/868 | 0 | 0 | 1/579 | 5/33 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 6/217 | 50/851 | 18/217 | 0 | 30/217 | 36/217 | 27/217 | 24/217 | 70/779 | 9/434 | 6/217 | 0 | 3/868 | 48/377 | 0 | 0 |
| 10/643 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 11/335 | 12/217 | 0 | 24/217 | 30/217 | 66/439 | 30/217 | 15/124 | 27/868 | 12/217 | 6/217 | 1/193 | 56/543 | 0 | 0 |
| 10/643 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 3/434 | 6/217 | 0 | 18/217 | 24/217 | 50/391 | 36/217 | 33/217 | 9/217 | 18/217 | 12/217 | 15/434 | 4/53 | 0 | 0 |
| 34/787 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 4/463 | 0 | 0 | 12/217 | 18/217 | 37/351 | 30/217 | 135/737 | 38/733 | 24/217 | 18/217 | 25/391 | 43/899 | 0 | 0 |
| 35/494 | 6/217 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9/868 | 0 | 0 | 0 | 9/868 | 0 | 0 | 6/217 | 12/217 | 18/217 | 24/217 | 100/629 | 27/434 | 30/217 | 24/217 | 74/793 | 20/991 | 0 | 0 |
| 3/31 | 12/217 | 3/124 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 6/217 | 28/491 | 18/217 | 50/391 | 38/733 | 36/217 | 30/217 | 75/629 | 16/867 | 0 | 0 |
| 113/921 | 18/217 | 3/62 | 6/217 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 27/868 | 12/217 | 3/31 | 9/217 | 30/217 | 36/217 | 9/62 | 14/837 | 0 | 0 |
| 59/397 | 24/217 | 9/124 | 12/217 | 6/217 | 1/193 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 1/193 | 6/217 | 35/533 | 27/868 | 24/217 | 30/217 | 84/491 | 3/200 | 0 | 0 |
| 150/851 | 30/217 | 3/31 | 18/217 | 12/217 | 27/868 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 3/868 | 0 | 15/434 | 9/434 | 18/217 | 24/217 | 35/247 | 3/200 | 0 | 0 |
| 59/397 | 36/217 | 15/124 | 24/217 | 18/217 | 28/491 | 6/217 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 1/579 | 0 | 3/868 | 9/868 | 12/217 | 18/217 | 72/641 | 3/200 | 0 | 0 |
| 113/921 | 30/217 | 9/62 | 30/217 | 72/641 | 75/851 | 12/217 | 9/868 | 0 | 0 | 0 | 1/579 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 12/217 | 21/248 | 14/837 | 0 | 0 |
| 23/242 | 24/217 | 15/124 | 36/217 | 35/247 | 15/124 | 18/217 | 9/434 | 6/217 | 0 | 0 | 3/868 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/868 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6/217 | 50/851 | 14/837 | 0 | 0 |
| 37/549 | 18/217 | 3/31 | 30/217 | 84/491 | 2/13 | 24/217 | 27/868 | 12/217 | 6/217 | 0 | 1/193 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/193 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11/335 | 14/837 | 0 | 0 |
| 25/629 | 12/217 | 9/124 | 24/217 | 9/62 | 67/359 | 30/217 | 9/217 | 18/217 | 12/217 | 6/217 | 3/434 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3/434 | 14/837 | 0 | 0 |
| 3/248 | 6/217 | 3/62 | 18/217 | 75/629 | 11/67 | 36/217 | 38/733 | 24/217 | 18/217 | 12/217 | 9/248 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4/463 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 9/62 | 30/217 | 72/641 | 18/217 | 12/217 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 9/62 | 30/217 | 72/641 | 18/217 | 12/217 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 14/837 | 0 | 0 |
| 3/248 | 0 | 0 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 1/579 | 6/217 | 12/217 | 18/217 | 24/217 | 30/217 | 9/62 | 30/217 | 72/641 | 18/217 | 12/217 | 9/868 | 0 | 1/579 | 3/868 | 0 | 0 | 1/579 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/579 | 14/837 | 0 | 0 |
| 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 |
| 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 0 | 0 | 0 |
| 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 0 | 0 | 0 |
| 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 0 | 0 | 0 |
| 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 0 | 0 | 0 |
| 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 0 | 0 | 0 |
| 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 0 | 0 | 0 |
| 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 0 | 0 | 0 |
| 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 0 | 0 | 0 |
| 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 0 | 0 | 0 |
| 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 0 | 0 | 0 |
| 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5/6 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5/6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 |
| 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 0 | 0 | 0 |
| 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 0 | 0 | 0 |
| 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 0 | 0 | 0 |
| 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 0 | 0 | 0 |
| 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 0 | 0 | 0 |
| 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 0 | 0 | 0 |
| 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 0 | 0 | 0 |
| 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 0 | 0 | 0 |
| 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 0 | 0 | 0 |
| 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 0 | 0 | 0 |
| 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 0 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 215/216 | 1/216 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/16 | 0 | 0 | 0 | 1/16 | 3/16 | 0 | 3/8 | 0 | 0 | 0 | 1/16 | 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 1/16 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/16 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 3/8 | 0 | 1/16 | 1/8 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 1/16 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/16 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 1/16 | 0 | 0 | 0 | 0 | 1/16 | 0 | 1/8 | 3/8 | 0 | 0 | 1/16 | 1/16 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/16 | 0 | 7/8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7/8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1/16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7/8 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Appendix B. Turns in Monopoly for Each Property Using Different Strategies
| Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Go | 2.9220 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Mediterranean Avenue | 2.0355 × 10−2 | 2 | 60 | 1233.9140 | 10 | 10 | 699.2179 | 30 | 220 | 301.6234 | 90 | 270 | 123.3914 | 160 | 320 | 82.2609 | 250 | 370 | 60.8731 |
| Community Chest (South) | 1.8052 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Baltic Avenue | 2.0722 × 10−2 | 4 | 60 | 606.0323 | 20 | 20 | 343.4183 | 60 | 220 | 148.1412 | 180 | 270 | 60.6032 | 320 | 320 | 40.4022 | 450 | 370 | 33.2196 |
| Income Tax | 2.2233 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Reading Railroad | 2.8312 × 10−2 | 25 | 200 | 236.5666 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Oriental Avenue | 2.1544 × 10−2 | 6 | 100 | 647.6727 | 30 | 30 | 479.2778 | 90 | 420 | 181.3484 | 270 | 470 | 67.6458 | 400 | 520 | 50.5185 | 550 | 570 | 40.2735 |
| Chance (South) | 8.2430 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Vermont Avenue | 2.2046 × 10−2 | 6 | 100 | 632.9215 | 30 | 30 | 468.3619 | 90 | 420 | 177.2180 | 270 | 470 | 66.1051 | 400 | 520 | 49.3679 | 550 | 570 | 39.3562 |
| Connecticut Avenue | 2.1919 × 10−2 | 8 | 120 | 572.9275 | 40 | 40 | 353.3053 | 100 | 420 | 160.4197 | 300 | 470 | 59.8391 | 450 | 520 | 44.1366 | 600 | 570 | 36.2854 |
| Just Visiting | 2.1630 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Jail (First turn) | 3.7755 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Jail (Second turn) | 3.1430 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Jail (Third turn) | 2.6192 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. Charles Place | 2.5807 × 10−2 | 10 | 140 | 454.1722 | 50 | 50 | 350.3614 | 150 | 640 | 138.4144 | 450 | 740 | 53.3472 | 625 | 840 | 43.6005 | 750 | 940 | 40.6592 |
| Electric Company | 2.5050 × 10−2 | 28 | 150 | 179.0439 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| States Avenue | 2.1999 × 10−2 | 10 | 140 | 532.7875 | 50 | 50 | 411.0075 | 150 | 640 | 162.3733 | 450 | 740 | 62.5814 | 625 | 840 | 51.1476 | 750 | 940 | 47.6972 |
| Virginia Avenue | 2.4455 × 10−2 | 12 | 160 | 456.4690 | 60 | 60 | 308.1166 | 180 | 640 | 121.7251 | 500 | 740 | 50.6681 | 700 | 840 | 41.0822 | 900 | 940 | 35.7567 |
| Pennsylvania Railroad | 2.3798 × 10−2 | 25 | 200 | 281.4385 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. James Place | 2.6921 × 10−2 | 14 | 180 | 399.8397 | 70 | 70 | 293.2158 | 200 | 760 | 118.1748 | 550 | 860 | 48.6270 | 750 | 960 | 39.8063 | 950 | 1060 | 34.6995 |
| Community Chest (West) | 2.2957 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Tennessee Avenue | 2.8094 × 10−2 | 14 | 180 | 383.1519 | 70 | 70 | 280.9781 | 200 | 760 | 113.2427 | 550 | 860 | 46.5975 | 750 | 960 | 38.1449 | 950 | 1060 | 33.2513 |
| New York Avenue | 2.7827 × 10−2 | 16 | 200 | 376.0833 | 80 | 80 | 248.2150 | 220 | 760 | 103.9357 | 600 | 860 | 43.1242 | 800 | 960 | 36.1040 | 1000 | 1060 | 31.8919 |
| Free Parking | 2.7947 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Kentucky Avenue | 2.5740 × 10−2 | 18 | 220 | 397.5308 | 90 | 90 | 299.9551 | 250 | 980 | 127.4990 | 700 | 1130 | 52.5050 | 875 | 1280 | 47.5798 | 1050 | 1430 | 44.2963 |
| Chance (North) | 1.0270 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Indiana Avenue | 2.5216 × 10−2 | 18 | 220 | 405.7946 | 90 | 90 | 306.1905 | 250 | 980 | 130.1494 | 700 | 1130 | 53.5965 | 875 | 1280 | 48.5689 | 1100 | 1430 | 43.1618 |
| Illinois Avenue | 2.9513 × 10−2 | 20 | 240 | 340.4140 | 100 | 100 | 235.4530 | 300 | 980 | 92.6683 | 750 | 1130 | 42.7409 | 925 | 1280 | 39.2549 | 1150 | 1430 | 35.2748 |
| B&O Railroad | 2.8496 × 10−2 | 25 | 200 | 235.0391 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Atlantic Avenue | 2.5031 × 10−2 | 22 | 260 | 395.2774 | 110 | 110 | 288.8566 | 330 | 1100 | 111.4885 | 800 | 1250 | 52.2602 | 975 | 1400 | 48.0258 | 1200 | 1550 | 43.2018 |
| Ventnor Avenue | 2.4844 × 10−2 | 22 | 260 | 398.2623 | 110 | 110 | 291.0379 | 330 | 1100 | 112.3304 | 800 | 1250 | 52.6549 | 975 | 1400 | 48.3885 | 1275 | 1550 | 40.9676 |
| Water Works | 2.7545 × 10−2 | 28 | 150 | 162.8263 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Marvin Gardens | 2.4035 × 10−2 | 24 | 280 | 406.3789 | 120 | 120 | 275.7571 | 360 | 1100 | 106.4326 | 850 | 1250 | 51.2242 | 1025 | 1400 | 47.5761 | 1275 | 1550 | 42.3454 |
| Pacific Avenue | 2.4926 × 10−2 | 26 | 300 | 387.5449 | 130 | 130 | 289.3669 | 390 | 1320 | 113.6798 | 900 | 1520 | 56.7251 | 1100 | 1720 | 52.5182 | 1400 | 1920 | 46.0625 |
| North Carolina Avenue | 2.4466 × 10−2 | 26 | 300 | 394.8430 | 130 | 130 | 294.8161 | 390 | 1320 | 115.8206 | 900 | 1520 | 57.7933 | 1100 | 1720 | 53.5072 | 1100 | 1920 | 59.7290 |
| Community Chest (East) | 2.2259 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Pennsylvania Avenue | 2.3381 × 10−2 | 28 | 320 | 409.2178 | 150 | 150 | 267.3556 | 450 | 1320 | 105.0326 | 1000 | 1520 | 54.4260 | 1200 | 1720 | 51.3227 | 1400 | 1920 | 49.1061 |
| Short Line Railroad | 2.5533 × 10−2 | 25 | 200 | 262.3144 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Chance (East) | 8.1280 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Park Place | 2.0598 × 10−2 | 35 | 350 | 406.4567 | 175 | 175 | 220.6479 | 500 | 1150 | 93.4850 | 1100 | 1350 | 49.8833 | 1300 | 1550 | 48.4621 | 1500 | 1750 | 47.4200 |
| Luxury Tax | 2.0565 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Boardwalk | 2.4946 × 10−2 | 50 | 400 | 268.4822 | 200 | 200 | 159.4113 | 600 | 1150 | 64.3239 | 1400 | 1350 | 32.3617 | 1700 | 1550 | 30.5991 | 2000 | 1750 | 29.3652 |
| Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Go | 2.9160 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Mediterranean Avenue | 2.0362 × 10−2 | 2 | 60 | 1233.5090 | 10 | 170 | 698.9886 | 30 | 220 | 301.5245 | 90 | 270 | 123.3509 | 160 | 320 | 82.2340 | 250 | 370 | 60.8531 |
| Community Chest (South) | 1.8191 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Baltic Avenue | 2.1038 × 10−2 | 4 | 60 | 596.9153 | 20 | 170 | 338.2520 | 60 | 220 | 145.9126 | 180 | 270 | 59.6915 | 320 | 320 | 39.7944 | 450 | 370 | 32.7198 |
| Income Tax | 2.2788 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Reading Railroad | 2.9144 × 10−2 | 25 | 200 | 229.8131 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Oriental Avenue | 2.2373 × 10−2 | 6 | 100 | 623.6814 | 30 | 370 | 461.5242 | 90 | 420 | 174.6308 | 270 | 470 | 65.1401 | 400 | 520 | 48.6472 | 550 | 570 | 38.7816 |
| Chance (South) | 8.6140 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Vermont Avenue | 2.3168 × 10−2 | 6 | 100 | 602.2746 | 30 | 370 | 445.6832 | 90 | 420 | 168.6369 | 270 | 470 | 62.9042 | 400 | 520 | 46.9774 | 550 | 570 | 37.4505 |
| Connecticut Avenue | 2.3137 × 10−2 | 8 | 120 | 542.7636 | 40 | 370 | 334.7042 | 100 | 420 | 151.9738 | 300 | 470 | 56.6887 | 450 | 520 | 41.8129 | 600 | 570 | 34.3750 |
| Just Visiting | 2.2933 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Jail | 8.3424 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. Charles Place | 2.7218 × 10−2 | 10 | 140 | 430.6359 | 50 | 540 | 332.2049 | 150 | 640 | 131.2414 | 450 | 740 | 50.5826 | 625 | 840 | 41.3411 | 750 | 940 | 38.5522 |
| Electric Company | 2.6236 × 10−2 | 28 | 150 | 170.9502 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| States Avenue | 2.3298 × 10−2 | 10 | 140 | 503.0897 | 50 | 540 | 388.0978 | 150 | 640 | 153.3226 | 450 | 740 | 59.0931 | 625 | 840 | 48.2966 | 750 | 940 | 45.0385 |
| Virginia Avenue | 2.5452 × 10−2 | 12 | 160 | 438.5784 | 60 | 540 | 296.0404 | 180 | 640 | 116.9542 | 500 | 740 | 48.6822 | 700 | 840 | 39.4721 | 900 | 940 | 34.3553 |
| Pennsylvania Railroad | 2.4969 × 10−2 | 25 | 200 | 268.2396 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. James Place | 2.7770 × 10−2 | 14 | 180 | 387.6203 | 70 | 660 | 284.2549 | 200 | 760 | 114.5633 | 550 | 860 | 47.1409 | 750 | 960 | 38.5898 | 950 | 1060 | 33.6391 |
| Community Chest (West) | 2.3791 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Tennessee Avenue | 2.8775 × 10−2 | 14 | 180 | 374.0779 | 70 | 660 | 274.3238 | 200 | 760 | 110.5608 | 550 | 860 | 45.4939 | 750 | 960 | 37.2415 | 950 | 1060 | 32.4638 |
| New York Avenue | 2.8685 × 10−2 | 16 | 200 | 364.8294 | 80 | 660 | 240.7874 | 220 | 760 | 100.8256 | 600 | 860 | 41.8338 | 800 | 960 | 35.0236 | 1000 | 1060 | 30.9375 |
| Free Parking | 2.8474 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Kentucky Avenue | 2.6364 × 10−2 | 18 | 220 | 388.1295 | 90 | 830 | 292.8613 | 250 | 980 | 124.4837 | 700 | 1130 | 51.2633 | 875 | 1280 | 46.4546 | 1050 | 1430 | 43.2487 |
| Chance (North) | 1.0369 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Indiana Avenue | 2.5571 × 10−2 | 18 | 220 | 400.1630 | 90 | 830 | 301.9412 | 250 | 980 | 128.3432 | 700 | 1130 | 52.8527 | 875 | 1280 | 47.8948 | 1100 | 1430 | 42.5628 |
| Illinois Avenue | 2.9743 × 10−2 | 20 | 240 | 337.7788 | 100 | 830 | 233.6303 | 300 | 980 | 91.9509 | 750 | 1130 | 42.4100 | 925 | 1280 | 38.9511 | 1150 | 1430 | 35.0017 |
| B&O Railroad | 2.8552 × 10−2 | 25 | 200 | 234.5781 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Atlantic Avenue | 2.4905 × 10−2 | 22 | 260 | 397.2735 | 110 | 950 | 290.3153 | 330 | 1100 | 112.0515 | 800 | 1250 | 52.5241 | 975 | 1400 | 48.2683 | 1200 | 1550 | 43.4200 |
| Ventnor Avenue | 2.4582 × 10−2 | 22 | 260 | 402.4978 | 110 | 950 | 294.1330 | 330 | 1100 | 113.525 | 800 | 1250 | 53.2149 | 975 | 1400 | 48.9031 | 1275 | 1550 | 41.4032 |
| Water Works | 2.7150 × 10−2 | 28 | 150 | 165.1952 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Marvin Gardens | 2.3557 × 10−2 | 24 | 280 | 414.6250 | 120 | 950 | 281.3527 | 360 | 1100 | 108.5923 | 850 | 1250 | 52.2637 | 1025 | 1400 | 48.5415 | 1275 | 1550 | 43.2046 |
| Pacific Avenue | 2.4270 × 10−2 | 26 | 300 | 398.0252 | 130 | 1120 | 297.1922 | 390 | 1320 | 116.7541 | 900 | 1520 | 58.2591 | 1100 | 1720 | 53.9385 | 1400 | 1920 | 47.3081 |
| North Carolina Avenue | 2.3776 × 10−2 | 26 | 300 | 406.3009 | 130 | 1120 | 303.3713 | 390 | 1320 | 119.1816 | 900 | 1520 | 59.4704 | 1100 | 1720 | 55.0599 | 1100 | 1920 | 61.4622 |
| Community Chest (East) | 2.1616 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Pennsylvania Avenue | 2.2704 × 10−2 | 28 | 320 | 421.4250 | 150 | 1120 | 275.3310 | 450 | 1320 | 108.1657 | 1000 | 1520 | 56.0495 | 1200 | 1720 | 52.8537 | 1400 | 1920 | 50.5710 |
| Short Line Railroad | 2.4834 × 10−2 | 25 | 200 | 269.6978 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Chance (East) | 7.9220 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Park Place | 2.0149 × 10−2 | 35 | 350 | 415.5094 | 175 | 950 | 225.5623 | 500 | 1150 | 95.5672 | 1100 | 1350 | 50.9943 | 1300 | 1550 | 49.5415 | 1500 | 1750 | 48.4761 |
| Luxury Tax | 2.0201 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Boardwalk | 2.4734 × 10−2 | 50 | 400 | 270.7882 | 200 | 950 | 160.7805 | 600 | 1150 | 64.8764 | 1400 | 1350 | 32.6397 | 1700 | 1550 | 30.8619 | 2000 | 1750 | 29.6175 |
| Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Go | 3.1050 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Mediterranean Avenue | 2.1629 × 10−2 | 2 | 60 | 1161.2150 | 10 | 170 | 658.0216 | 30 | 220 | 283.8525 | 90 | 270 | 116.1215 | 160 | 320 | 77.4143 | 250 | 370 | 57.2866 |
| Community Chest (South) | 1.9181 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Baltic Avenue | 2.2016 × 10−2 | 4 | 60 | 570.4161 | 20 | 170 | 323.2358 | 60 | 220 | 139.4350 | 180 | 270 | 57.0416 | 320 | 320 | 38.0277 | 450 | 370 | 31.2673 |
| Income Tax | 2.3617 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Reading Railroad | 2.9964 × 10−2 | 25 | 200 | 223.5240 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Oriental Avenue | 2.2874 × 10−2 | 6 | 100 | 610.0102 | 30 | 370 | 451.4075 | 90 | 420 | 170.8028 | 270 | 470 | 63.7122 | 400 | 520 | 47.5808 | 550 | 570 | 37.9315 |
| Chance (South) | 8.7520 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Vermont Avenue | 2.3404 × 10−2 | 6 | 100 | 596.1970 | 30 | 370 | 441.1858 | 90 | 420 | 166.9352 | 270 | 470 | 62.2695 | 400 | 520 | 46.5034 | 550 | 570 | 37.0726 |
| Connecticut Avenue | 2.3266 × 10−2 | 8 | 120 | 539.7602 | 40 | 370 | 332.8521 | 100 | 420 | 151.1329 | 300 | 470 | 56.3750 | 450 | 520 | 41.5815 | 600 | 570 | 34.1848 |
| Just Visiting | 2.2954 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Jail | 4.0069 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. Charles Place | 2.7281 × 10−2 | 10 | 140 | 429.6315 | 50 | 540 | 331.43 | 150 | 640 | 130.9353 | 450 | 740 | 50.4647 | 625 | 840 | 41.2446 | 750 | 940 | 38.4623 |
| Electric Company | 2.4882 × 10−2 | 28 | 150 | 180.2528 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| States Avenue | 2.4003 × 10−2 | 10 | 140 | 488.3084 | 50 | 540 | 376.6950 | 150 | 640 | 148.8178 | 450 | 740 | 57.3569 | 625 | 840 | 46.8776 | 750 | 940 | 43.7152 |
| Virginia Avenue | 2.4864 × 10−2 | 12 | 160 | 448.9480 | 60 | 540 | 303.0399 | 180 | 640 | 119.7195 | 500 | 740 | 49.8332 | 700 | 840 | 40.4053 | 900 | 940 | 35.1676 |
| Pennsylvania Railroad | 2.6501 × 10−2 | 25 | 200 | 252.7329 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. James Place | 2.8063 × 10−2 | 14 | 180 | 383.5635 | 70 | 660 | 281.2799 | 200 | 760 | 113.3643 | 550 | 860 | 46.6475 | 750 | 960 | 38.1859 | 950 | 1060 | 33.2870 |
| Community Chest (West) | 2.5970 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Tennessee Avenue | 2.9245 × 10−2 | 14 | 180 | 368.0689 | 70 | 660 | 269.9172 | 200 | 760 | 108.7848 | 550 | 860 | 44.7631 | 750 | 960 | 36.6433 | 950 | 1060 | 31.9424 |
| New York Avenue | 3.0561 × 10−2 | 16 | 200 | 342.4284 | 80 | 660 | 226.0027 | 220 | 760 | 94.6348 | 600 | 860 | 39.2651 | 800 | 960 | 32.8731 | 1000 | 1060 | 29.0379 |
| Free Parking | 2.8516 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Kentucky Avenue | 2.7948 × 10−2 | 18 | 220 | 366.1346 | 90 | 830 | 276.2652 | 250 | 980 | 117.4294 | 700 | 1130 | 48.3583 | 875 | 1280 | 43.8220 | 1050 | 1430 | 40.7979 |
| Chance (North) | 1.0290 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Indiana Avenue | 2.6885 × 10−2 | 18 | 220 | 380.6071 | 90 | 830 | 287.1854 | 250 | 980 | 122.0711 | 700 | 1130 | 50.2698 | 875 | 1280 | 45.5542 | 1100 | 1430 | 40.4828 |
| Illinois Avenue | 3.1416 × 10−2 | 20 | 240 | 319.7852 | 100 | 830 | 221.1847 | 300 | 980 | 87.0526 | 750 | 1130 | 40.1508 | 925 | 1280 | 36.8761 | 1150 | 1430 | 33.1372 |
| B&O Railroad | 3.0215 × 10−2 | 25 | 200 | 221.6672 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Atlantic Avenue | 2.6705 × 10−2 | 22 | 260 | 370.4976 | 110 | 950 | 270.7482 | 330 | 1100 | 104.4993 | 800 | 1250 | 48.9841 | 975 | 1400 | 45.0151 | 1200 | 1550 | 40.4935 |
| Ventnor Avenue | 2.6435 × 10−2 | 22 | 260 | 374.2888 | 110 | 950 | 273.5187 | 330 | 1100 | 105.5686 | 800 | 1250 | 49.4853 | 975 | 1400 | 45.4757 | 1275 | 1550 | 38.5015 |
| Water Works | 2.9165 × 10−2 | 28 | 150 | 153.7819 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Marvin Gardens | 2.5507 × 10−2 | 24 | 280 | 382.9248 | 120 | 950 | 259.8418 | 360 | 1100 | 100.2898 | 850 | 1250 | 48.2678 | 1025 | 1400 | 44.8302 | 1275 | 1550 | 39.9014 |
| Pacific Avenue | 2.6460 × 10−2 | 26 | 300 | 365.0868 | 130 | 1120 | 272.5981 | 390 | 1320 | 107.0921 | 900 | 1520 | 53.4379 | 1100 | 1720 | 49.4748 | 1400 | 1920 | 43.3932 |
| North Carolina Avenue | 2.5974 × 10−2 | 26 | 300 | 371.9152 | 130 | 1120 | 277.6967 | 390 | 1320 | 109.0951 | 900 | 1520 | 54.4374 | 1100 | 1720 | 50.4002 | 1100 | 1920 | 56.2606 |
| Community Chest (East) | 2.3655 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Pennsylvania Avenue | 2.4837 × 10−2 | 28 | 320 | 385.2402 | 150 | 1120 | 251.6903 | 450 | 1320 | 98.8783 | 1000 | 1520 | 51.2370 | 1200 | 1720 | 48.3155 | 1400 | 1920 | 46.2288 |
| Short Line Railroad | 2.7122 × 10−2 | 25 | 200 | 246.9462 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Chance (East) | 8.6310 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Park Place | 2.1869 × 10−2 | 35 | 350 | 382.8212 | 175 | 950 | 207.8172 | 500 | 1150 | 88.0489 | 1100 | 1350 | 46.9826 | 1300 | 1550 | 45.6441 | 1500 | 1750 | 44.6625 |
| Luxury Tax | 2.1834 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Boardwalk | 2.6387 × 10−2 | 50 | 400 | 253.8248 | 200 | 950 | 150.7085 | 600 | 1150 | 60.8122 | 1400 | 1350 | 30.5950 | 1700 | 1550 | 28.9286 | 2000 | 1750 | 27.7621 |
| Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Go | 3.1326 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Mediterranean Avenue | 2.1925 × 10−2 | 2 | 60 | 1145.5540 | 10 | 170 | 649.1470 | 30 | 220 | 280.0242 | 90 | 270 | 114.5554 | 160 | 320 | 76.3702 | 250 | 370 | 56.5140 |
| Community Chest (South) | 1.9492 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Baltic Avenue | 2.2425 × 10−2 | 4 | 60 | 560.0061 | 20 | 170 | 317.3368 | 60 | 220 | 136.8904 | 180 | 270 | 56.0006 | 320 | 320 | 37.3337 | 450 | 370 | 30.6966 |
| Income Tax | 2.4130 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Reading Railroad | 3.0606 × 10−2 | 25 | 200 | 218.8353 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Oriental Avenue | 2.3464 × 10−2 | 6 | 100 | 594.6796 | 30 | 370 | 440.0629 | 90 | 420 | 166.5103 | 270 | 470 | 62.1110 | 400 | 520 | 46.3850 | 550 | 570 | 36.9783 |
| Chance (South) | 8.9930 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Vermont Avenue | 2.4088 × 10−2 | 6 | 100 | 579.2758 | 30 | 370 | 428.6641 | 90 | 420 | 162.1972 | 270 | 470 | 60.5021 | 400 | 520 | 45.1835 | 550 | 570 | 36.0204 |
| Connecticut Avenue | 2.3972 × 10−2 | 8 | 120 | 523.8757 | 40 | 370 | 323.0567 | 100 | 420 | 146.6852 | 300 | 470 | 54.7159 | 450 | 520 | 40.3578 | 600 | 570 | 33.1788 |
| Just Visiting | 2.3671 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Jail | 3.5222 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. Charles Place | 2.8034 × 10−2 | 10 | 140 | 418.0931 | 50 | 540 | 322.5290 | 150 | 640 | 127.4189 | 450 | 740 | 49.1094 | 625 | 840 | 40.1369 | 750 | 940 | 37.4293 |
| Electric Company | 2.5514 × 10−2 | 28 | 150 | 175.7878 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| States Avenue | 2.4455 × 10−2 | 10 | 140 | 479.2794 | 50 | 540 | 369.7298 | 150 | 640 | 146.0661 | 450 | 740 | 56.2963 | 625 | 840 | 46.0108 | 750 | 940 | 42.9069 |
| Virginia Avenue | 2.5165 × 10−2 | 12 | 160 | 443.5865 | 60 | 540 | 299.4209 | 180 | 640 | 118.2897 | 500 | 740 | 49.2381 | 700 | 840 | 39.9228 | 900 | 940 | 34.7476 |
| Pennsylvania Railroad | 2.6662 × 10−2 | 25 | 200 | 251.2068 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| St. James Place | 2.8065 × 10−2 | 14 | 180 | 383.5388 | 70 | 660 | 281.2618 | 200 | 760 | 113.3570 | 550 | 860 | 46.6445 | 750 | 960 | 38.1834 | 950 | 1060 | 33.2849 |
| Community Chest (West) | 2.5814 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Tennessee Avenue | 2.9115 × 10−2 | 14 | 180 | 369.7133 | 70 | 660 | 271.1231 | 200 | 760 | 109.2708 | 550 | 860 | 44.9631 | 750 | 960 | 36.8070 | 950 | 1060 | 32.0851 |
| New York Avenue | 3.0448 × 10−2 | 16 | 200 | 343.7042 | 80 | 660 | 226.8448 | 220 | 760 | 94.9874 | 600 | 860 | 39.4114 | 800 | 960 | 32.9956 | 1000 | 1060 | 29.1461 |
| Free Parking | 2.8416 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Kentucky Avenue | 2.7836 × 10−2 | 18 | 220 | 367.6007 | 90 | 830 | 277.3715 | 250 | 980 | 117.8996 | 700 | 1130 | 48.5519 | 875 | 1280 | 43.9975 | 1050 | 1430 | 40.9612 |
| Chance (North) | 1.0243 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Indiana Avenue | 2.6761 × 10−2 | 18 | 220 | 382.3616 | 90 | 830 | 288.5092 | 250 | 980 | 122.6338 | 700 | 1130 | 50.5015 | 875 | 1280 | 45.7642 | 1100 | 1430 | 40.6694 |
| Illinois Avenue | 3.1233 × 10−2 | 20 | 240 | 321.6596 | 100 | 830 | 222.4812 | 300 | 980 | 87.5629 | 750 | 1130 | 40.3862 | 925 | 1280 | 37.0923 | 1150 | 1430 | 33.3314 |
| B&O Railroad | 2.9929 × 10−2 | 25 | 200 | 223.7854 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Atlantic Avenue | 2.6411 × 10−2 | 22 | 260 | 374.6289 | 110 | 950 | 273.7673 | 330 | 1100 | 105.6646 | 800 | 1250 | 49.5303 | 975 | 1400 | 45.5170 | 1200 | 1550 | 40.9450 |
| Ventnor Avenue | 2.6132 × 10−2 | 22 | 260 | 378.6304 | 110 | 950 | 276.6915 | 330 | 1100 | 106.7932 | 800 | 1250 | 50.0593 | 975 | 1400 | 46.0032 | 1275 | 1550 | 38.9481 |
| Water Works | 2.8870 × 10−2 | 28 | 150 | 155.3534 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Marvin Gardens | 2.5245 × 10−2 | 24 | 280 | 386.9068 | 120 | 950 | 262.5439 | 360 | 1100 | 101.3327 | 850 | 1250 | 48.7698 | 1025 | 1400 | 45.2964 | 1275 | 1550 | 40.3163 |
| Pacific Avenue | 2.6226 × 10−2 | 26 | 300 | 368.3453 | 130 | 1120 | 275.0312 | 390 | 1320 | 108.0480 | 900 | 1520 | 53.9148 | 1100 | 1720 | 49.9164 | 1400 | 1920 | 43.7805 |
| North Carolina Avenue | 2.5762 × 10−2 | 26 | 300 | 374.9787 | 130 | 1120 | 279.9841 | 390 | 1320 | 109.9938 | 900 | 1520 | 54.8858 | 1100 | 1720 | 50.8153 | 1100 | 1920 | 56.7241 |
| Community Chest (East) | 2.3498 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Pennsylvania Avenue | 2.4701 × 10−2 | 28 | 320 | 387.3535 | 150 | 1120 | 253.0710 | 450 | 1320 | 99.4207 | 1000 | 1520 | 51.5180 | 1200 | 1720 | 48.5806 | 1400 | 1920 | 46.4824 |
| Short Line Railroad | 2.7040 × 10−2 | 25 | 200 | 247.6951 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Chance (East) | 8.6250 × 10−3 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Park Place | 2.1925 × 10−2 | 35 | 350 | 381.8509 | 175 | 950 | 207.2905 | 500 | 1150 | 87.8257 | 1100 | 1350 | 46.8635 | 1300 | 1550 | 45.5284 | 1500 | 1750 | 44.5493 |
| Luxury Tax | 2.1955 × 10−2 | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA | 0 | 0 | NA |
| Boardwalk | 2.6606 × 10−2 | 50 | 400 | 251.7395 | 200 | 950 | 149.4703 | 600 | 1150 | 60.3126 | 1400 | 1350 | 30.3436 | 1700 | 1550 | 28.6909 | 2000 | 1750 | 27.5340 |
References
- Engel, A. The probabilistic abacus. Educ. Stud. Math. 1975, 6, 1–2. [Google Scholar] [CrossRef]
- Engel, A. Why does the probabilistic abacus work? Educ. Stud. Math. 1976, 7, 59–69. [Google Scholar] [CrossRef]
- Snell, J.L. The Engel Algorithm for Absorbing Markov Chains. 1979. Available online: https://arxiv.org/abs/0904.1413v1 (accessed on 2 July 2025).
- Kaushal, N.; Tiwari, M.; Singh, V.; Parihar, C.L. Generalized Engel’s Algorithm for Minimizing Playing Time to Stabilize the Initial Configuration and for finding Absorbing Probability. Int. J. Comput. Appl. 2014, 107, 32–35. [Google Scholar]
- Kaushal, N.; Tiwari, M.; Parihar, C.L. Chip-Firing Game as Probability Abacus by Characterization of ULD Lattice. Asian J. Math. Appl. 2014, 2014, ama0167. [Google Scholar]
- Kaushal, N. A Study of Distributive Lattices and Related Computer Programming. Ph.D. Thesis, Government Model Autonomous Holkar Science College, Indore, India, 2014. [Google Scholar]
- Snell, J.L. Finite Markov Chains and their Applications. Am. Mon. 1959, 66, 99–104. [Google Scholar] [CrossRef]
- Ash, R.; Bishop, R. Monopoly as a Markov process. Coll. Math. J. 1972, 45, 26–29. [Google Scholar] [CrossRef]
- Tan, B. Markov Chains and the RISK Board Game. Math. Mag. 1997, 70, 349–357. [Google Scholar] [CrossRef]
- Abbott, S.D.; Richey, M. Take a walk on the boardwalk. Coll. Math. J. 1997, 28, 162–171. [Google Scholar] [CrossRef]
- Wu, D.W.; Baeth, N. How often does a monopoly player go to ‘JAIL’? Int. J. Math. Educ. Sci. Technol. 2010, 32, 774–778. [Google Scholar] [CrossRef]
- Johnson, R.W. Using games to teach Markov chains. PRIMUS Probl. Resour. Issues Math. Undergrad. Stud. 2003, 13, 37–348. [Google Scholar] [CrossRef]
- Osborne, J.A. Markov Chains for the RISK Board Game Revisited. Math. Mag. 2003, 76, 129–135. [Google Scholar] [CrossRef]
- Friedman, E.; Henderson, S.; Byuen, T.; Gallardo, G. Estimating the probability that the game of Monopoly never ends. In Proceedings of the 2009 Winter Simulation Conference, Austin, TX, USA, 13–16 December 2009; Schools of Operations Research and Information Engineering, Cornell University: New York, NY, USA, 2009. [Google Scholar]
- Bilisoly, R. Using Board Games and Mathematica to Teach the Fundamentals of Finite Stationary Markov Chains. Section on Statistical Education. 2014. Available online: https://arxiv.org/abs/1410.1107 (accessed on 2 July 2025).
- Shrestha, S.R.; Lewin, R.A.; Seitzer, J. Analyzing Real Estate Implications of Monopoly, Mega Edition through Simulation. AEF Pap. Proc. 2015, 39, 37–39. [Google Scholar]
- Bewersdorff, J. Luck, Logic, and White Lies: The Mathematics of Games; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Eithun; Lamb, M.; Young, M. A Long-term vs. short-term strategy in the game of Monopoly. UMAP J. 2017, 38, 35–57. [Google Scholar]
- Betz, K. Go Directly To Jail: The Mathematics Behind Family Game Night. Ph.D. Thesis, Department of Mathematics, Albright College, Reading, PA, USA, 2019. [Google Scholar]
- Nilsson, A. Exploring strategies in Monopoly using Markov chains and simulation, 2020. U.U.D.M. Project Report 2020:42. Available online: https://uu.diva-portal.org/smash/get/diva2:1471765/FULLTEXT01.pdf (accessed on 2 July 2025).
- Taylor, D.G. Games, Gambling, and Probability—An Introduction to Mathematics; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Carbonaro, B.; Menale, M. Kinetic Theory and Markov Chains with Stochastically Varying Transition Matrices. Mathematics 2025, 13, 1994. [Google Scholar] [CrossRef]
- Roeder, O. Who Keeps The Money You Found On The Floor? Available online: https://fivethirtyeight.com/features/who-keeps-the-money-you-found-on-the-floor/ (accessed on 9 July 2016).
- Propp, J. Engel’s Marvelously Improbable Machines. Math Horiz. 2018, 26, 5–9. [Google Scholar] [CrossRef]
- Collins, T. Probabilities in the Game of Monopoly. 1997. Available online: http://www.tkcs-collins.com/truman/monopoly/monopoly.shtml (accessed on 2 July 2025).
- Li, B. Markov Chains in the Game of Monopoly, Lecture note. 2013; unpublished. [Google Scholar]
- Murrell, P.R. The Statistics of Monopoly. Chance 1999, 12, 36–40. [Google Scholar] [CrossRef]
- Yasumura, Y.; Oguchi, K.; Nitta, K. Negotiation strategy of agents in the Monopoly game. In Proceedings of the 2001 IEEE International Symposium on Computational Intelligence in Robotics and Automation, Banff, AB, Canada, 29 July–1 August 2001; pp. 277–281. [Google Scholar]
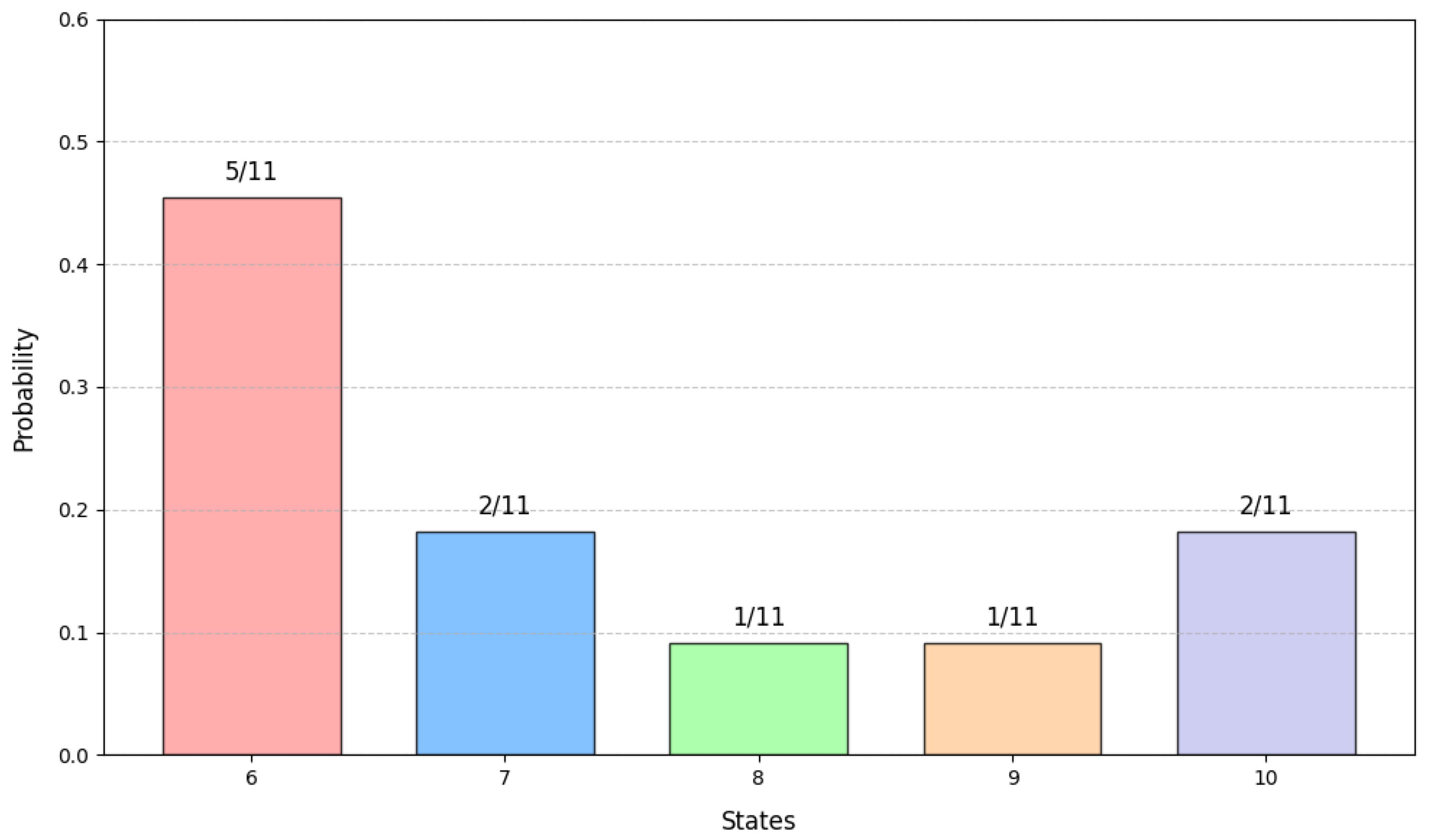
| State | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | A Firing State | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Configuration | ||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 2 | 2 | 0 | |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 1 | |
| 3 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 3 | 2 | 3 | 2 | |
| 4 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 3 | 3 | 3 | |
| 5 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 4 | 4 | |
| 6 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 5 | |
| 7 | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 1 | 0 | |
| 8 | 2 | 1 | 1 | 1 | 1 | 0 | 2 | 1 | 1 | 2 | 1 | |
| 9 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 0 | |
| 10 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 0 | |
| 11 | 2 | 1 | 1 | 1 | 1 | 3 | 2 | 1 | 1 | 2 | 0 | |
| 12 | 3 | 1 | 1 | 1 | 1 | 0 | 3 | 1 | 1 | 3 | 1 | |
| 13 | 3 | 2 | 1 | 1 | 1 | 1 | 0 | 2 | 1 | 3 | 2 | |
| 14 | 3 | 2 | 1 | 1 | 2 | 2 | 0 | 2 | 2 | 0 | 5 | |
| 15 | 3 | 2 | 1 | 1 | 2 | 3 | 0 | 2 | 2 | 0 | 0 | |
| 16 | 4 | 2 | 1 | 1 | 2 | 0 | 1 | 2 | 2 | 1 | 1 | |
| 17 | 4 | 2 | 1 | 1 | 2 | 1 | 1 | 2 | 2 | 1 | 0 | |
| 18 | 4 | 2 | 1 | 1 | 2 | 2 | 1 | 2 | 2 | 1 | 0 | |
| 19 | 4 | 2 | 1 | 1 | 2 | 3 | 1 | 2 | 2 | 1 | 0 | |
| 20 | 5 | 2 | 1 | 1 | 2 | 0 | 2 | 2 | 2 | 2 | 1 | |
| 21 | 5 | 2 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 0 | |
| 22 | 5 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | |
| Sum of Two Dice | Probability |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 |
| Card | Probability |
|---|---|
| Stay | 14/16 |
| Advance to Go | 1/16 |
| Go to Jail | 1/16 |
| Card | Probability |
|---|---|
| Take a Trip to Reading Railroad | 1/16 |
| Advance to the nearest Railroad | 2/16 |
| Advance to St. Charles Place | 1/16 |
| Advance to the Nearest Utility | 1/16 |
| Advance to Illinois Avenue | 1/16 |
| Advance to Boardwalk | 1/16 |
| Advance to Go | 1/16 |
| Go Directly to Jail | 1/16 |
| Go back three spaces | 1/16 |
| Stay | 6/16 |
| mEngel | Power | Canonical Form | ||||
|---|---|---|---|---|---|---|
| States | Long Jail | Short Jail | Long Jail | Short Jail | Long Jail | Short Jail |
| Go | 2.9220 × 10−2 | 3.1050 × 10−2 | 2.9225 × 10−2 | 3.1048 × 10−2 | 2.9225 × 10−2 | 3.1048 × 10−2 |
| Mediterranean Avenue | 2.0355 × 10−2 | 2.1629 × 10−2 | 2.0360 × 10−2 | 2.1622 × 10−2 | 2.0360 × 10−2 | 2.1622 × 10−2 |
| Community Chest (South) | 1.8052 × 10−2 | 1.9184 × 10−2 | 1.8056 × 10−2 | 1.9172 × 10−2 | 1.8056 × 10−2 | 1.9172 × 10−2 |
| Baltic Avenue | 2.0722 × 10−2 | 2.2016 × 10−2 | 2.0725 × 10−2 | 2.2004 × 10−2 | 2.0725 × 10−2 | 2.2004 × 10−2 |
| Income Tax | 2.2233 × 10−2 | 2.3617 × 10−2 | 2.2238 × 10−2 | 2.3607 × 10−2 | 2.2238 × 10−2 | 2.3607 × 10−2 |
| Reading Railroad | 2.8312 × 10−2 | 2.9964 × 10−2 | 2.8316 × 10−2 | 2.9953 × 10−2 | 2.8316 × 10−2 | 2.9953 × 10−2 |
| Oriental Avenue | 2.1544 × 10−2 | 2.2874 × 10−2 | 2.1544 × 10−2 | 2.2863 × 10−2 | 2.1544 × 10−2 | 2.2863 × 10−2 |
| Chance (South) | 8.2434 × 10−3 | 8.7516 × 10−3 | 8.2425 × 10−3 | 8.7468 × 10−3 | 8.2425 × 10−3 | 8.7468 × 10−3 |
| Vermont Avenue | 2.2046 × 10−2 | 2.3404 × 10−2 | 2.2042 × 10−2 | 2.3388 × 10−2 | 2.2042 × 10−2 | 2.3388 × 10−2 |
| Connecticut Avenue | 2.1919 × 10−2 | 2.3266 × 10−2 | 2.1911 × 10−2 | 2.3248 × 10−2 | 2.1911 × 10−2 | 2.3248 × 10−2 |
| Just Visiting | 2.1630 × 10−2 | 2.2954 × 10−2 | 2.1617 × 10−2 | 2.2934 × 10−2 | 2.1617 × 10−2 | 2.2934 × 10−2 |
| St. Charles Place | 2.5807 × 10−2 | 2.7281 × 10−2 | 2.5792 × 10−2 | 2.7262 × 10−2 | 2.5792 × 10−2 | 2.7262 × 10−2 |
| Electric Company | 2.5050 × 10−2 | 2.4882 × 10−2 | 2.5036 × 10−2 | 2.4864 × 10−2 | 2.5036 × 10−2 | 2.4864 × 10−2 |
| States Avenue | 2.2000 × 10−2 | 2.4003 × 10−2 | 2.1982 × 10−2 | 2.3990 × 10−2 | 2.1982 × 10−2 | 2.3990 × 10−2 |
| Virginia Avenue | 2.4455 × 10−2 | 2.4864 × 10−2 | 2.4438 × 10−2 | 2.4855 × 10−2 | 2.4438 × 10−2 | 2.4855 × 10−2 |
| Pennsylvania Railroad | 2.3798 × 10−2 | 2.6501 × 10−2 | 2.3781 × 10−2 | 2.6498 × 10−2 | 2.3781 × 10−2 | 2.6498 × 10−2 |
| St. James Place | 2.6921 × 10−2 | 2.8063 × 10−2 | 2.6909 × 10−2 | 2.8065 × 10−2 | 2.6909 × 10−2 | 2.8065 × 10−2 |
| Community Chest (West) | 2.2957 × 10−2 | 2.5970 × 10−2 | 2.2949 × 10−2 | 2.5976 × 10−2 | 2.2949 × 10−2 | 2.5976 × 10−2 |
| Tennessee Avenue | 2.8093 × 10−2 | 2.9245 × 10−2 | 2.8087 × 10−2 | 2.9254 × 10−2 | 2.8087 × 10−2 | 2.9254 × 10−2 |
| New York Avenue | 2.7827 × 10−2 | 3.0561 × 10−2 | 2.7822 × 10−2 | 3.0575 × 10−2 | 2.7822 × 10−2 | 3.0575 × 10−2 |
| Free Parking | 2.7947 × 10−2 | 2.8516 × 10−2 | 2.7949 × 10−2 | 2.8531 × 10−2 | 2.7949 × 10−2 | 2.8531 × 10−2 |
| Kentucky Avenue | 2.5740 × 10−2 | 2.7947 × 10−2 | 2.5742 × 10−2 | 2.7963 × 10−2 | 2.5742 × 10−2 | 2.7963 × 10−2 |
| Chance (North) | 1.0270 × 10−2 | 1.0290 × 10−2 | 1.0272 × 10−2 | 1.0296 × 10−2 | 1.0272 × 10−2 | 1.0296 × 10−2 |
| Indiana Avenue | 2.5216 × 10−2 | 2.6884 × 10−2 | 2.5219 × 10−2 | 2.6900 × 10−2 | 2.5219 × 10−2 | 2.6900 × 10−2 |
| Illinois Avenue | 2.9513 × 10−2 | 3.1416 × 10−2 | 2.9519 × 10−2 | 3.1432 × 10−2 | 2.9519 × 10−2 | 3.1432 × 10−2 |
| B&O Railroad | 2.8496 × 10−2 | 3.0215 × 10−2 | 2.8502 × 10−2 | 3.0231 × 10−2 | 2.8502 × 10−2 | 3.0231 × 10−2 |
| Atlantic Avenue | 2.5031 × 10−2 | 2.6705 × 10−2 | 2.5033 × 10−2 | 2.6717 × 10−2 | 2.5033 × 10−2 | 2.6717 × 10−2 |
| Ventnor Avenue | 2.4844 × 10−2 | 2.6434 × 10−2 | 2.4846 × 10−2 | 2.6444 × 10−2 | 2.4846 × 10−2 | 2.6444 × 10−2 |
| Water Works | 2.7545 × 10−2 | 2.9165 × 10−2 | 2.7547 × 10−2 | 2.9175 × 10−2 | 2.7547 × 10−2 | 2.9175 × 10−2 |
| Marvin Gardens | 2.4035 × 10−2 | 2.5507 × 10−2 | 2.4036 × 10−2 | 2.5512 × 10−2 | 2.4036 × 10−2 | 2.5512 × 10−2 |
| Go to Jail | 0 | 0 | 0 | 0 | 0 | 0 |
| Pacific Avenue | 2.4926 × 10−2 | 2.6460 × 10−2 | 2.4927 × 10−2 | 2.6461 × 10−2 | 2.4927 × 10−2 | 2.6461 × 10−2 |
| North Carolina Avenue | 2.4466 × 10−2 | 2.5974 × 10−2 | 2.4469 × 10−2 | 2.5974 × 10−2 | 2.4469 × 10−2 | 2.5974 × 10−2 |
| Community Chest (East) | 2.2259 × 10−2 | 2.3655 × 10−2 | 2.2262 × 10−2 | 2.3657 × 10−2 | 2.2262 × 10−2 | 2.3657 × 10−2 |
| Pennsylvania Avenue | 2.3381 × 10−2 | 2.4836 × 10−2 | 2.3384 × 10−2 | 2.4840 × 10−2 | 2.3384 × 10−2 | 2.4840 × 10−2 |
| Short Line Railroad | 2.5532 × 10−2 | 2.7122 × 10−2 | 2.5536 × 10−2 | 2.7130 × 10−2 | 2.5536 × 10−2 | 2.7130 × 10−2 |
| Chance (East) | 8.1276 × 10−3 | 8.6306 × 10−3 | 8.1287 × 10−3 | 8.6337 × 10−3 | 8.1287 × 10−3 | 8.6337 × 10−3 |
| Park Place | 2.0597 × 10−2 | 2.1869 × 10−2 | 2.0601 × 10−2 | 2.1877 × 10−2 | 2.0601 × 10−2 | 2.1877 × 10−2 |
| Luxury Tax | 2.0564 × 10−2 | 2.1834 × 10−2 | 2.0566 × 10−2 | 2.1839 × 10−2 | 2.0566 × 10−2 | 2.1839 × 10−2 |
| Boardwalk | 2.4946 × 10−2 | 2.6390 × 10−2 | 2.4951 × 10−2 | 2.6391 × 10−2 | 2.4951 × 10−2 | 2.6391 × 10−2 |
| Jail (First turn) | 3.7755 × 10−2 | 4.0069 × 10−2 | 3.7755 × 10−2 | 4.0073 × 10−2 | 3.7755 × 10−2 | 4.0073 × 10−2 |
| Jail (Second turn) | 3.1430 × 10−2 | 0 | 3.1462 × 10−2 | 0 | 3.1462 × 10−2 | 0 |
| Jail (Third turn) | 2.6192 × 10−2 | 0 | 2.6219 × 10−2 | 0 | 2.6219 × 10−2 | 0 |
| Number of Iterations | Long Jail | Short Jail | ||
|---|---|---|---|---|
| Tolerance | ||||
| 0.0001 | 1 | 1.2969 × 10−5 | 1.2969 × 10−5 | |
| 0.00001 | 2 | 8.2213 × 10−6 | 8.2733 × 10−6 | |
| 0.001 | 3 | 1.6723 × 10−4 | 1.7547 × 10−4 | |
| 0.001 | 4 | 6.2985 × 10−4 | 7.6839 × 10−4 | |
| 0.001 (0.01) | 5 | 9.8909 × 10−4 | 1.1038 × 10−3 | |
| 0.01 | 6 | 1.3026 × 10−3 | 1.5551 × 10−3 | |
| 0.01 | 7 | 1.4098 × 10−3 | 1.8264 × 10−3 | |
| 0.01 | 8 | 1.3658 × 10−3 | 1.8486 × 10−3 | |
| 0.01 | 9 | 1.3059 × 10−3 | 2.1228 × 10−3 | |
| 0.01 | 10 | 1.3650 × 10−3 | 2.3236 × 10−3 | |
| 0.001 (0.01) | 11 | 9.6764 × 10−4 | 2.1712 × 10−3 | |
| 0.001 (0.01) | 12 | 9.0800 × 10−4 | 1.8861 × 10−3 | |
| 0.001 (0.01) | 13 | 7.6921 × 10−4 | 1.6592 × 10−3 | |
| 0.001 (0.01) | 14 | 5.6854 × 10−4 | 1.4104 × 10−3 | |
| 0.001 (0.01) | 15 | 6.2546 × 10−4 | 1.3701 × 10−3 | |
| 0.001 (0.01) | 16 | 4.5819 × 10−4 | 1.4093 × 10−3 | |
| 0.001 (0.01) | 17 | 3.1808 × 10−4 | 1.2781 × 10−3 | |
| 0.001 | 18 | 2.4727 × 10−4 | 8.9537 × 10−4 | |
| 0.001 | 19 | 1.3592 × 10−4 | 6.5633 × 10−4 | |
| 0.001 | 20 | 1.1921 × 10−4 | 6.0545 × 10−4 | |
| 0.0001 (0.001) | 21 | 9.8218 × 10−5 | 4.3479 × 10−4 | |
| 0.001 | 22 | 1.0943 × 10−4 | 3.1397 × 10−4 | |
| 0.0001 (0.001) | 23 | 8.0613 × 10−5 | 2.4965 × 10−4 | |
| 0.0001 (0.001) | 24 | 5.5567 × 10−5 | 2.4997 × 10−4 | |
| 0.0001 (0.001) | 25 | 3.5889 × 10−5 | 1.5996 × 10−4 | |
| 0.0001 (0.001) | 26 | 5.0507 × 10−5 | 1.8358 × 10−4 | |
| 0.0001 (0.001) | 27 | 7.1482 × 10−5 | 2.5761 × 10−4 | |
| 0.0001 (0.001) | 28 | 7.8835 × 10−5 | 2.4739 × 10−4 | |
| 0.0001 (0.001) | 29 | 3.1048 × 10−5 | 1.7960 × 10−4 | |
| 0.0001 | 30 | 1.7391 × 10−5 | 8.6980 × 10−5 | |
| Rank | States | Long Jail | States | Short Jail |
|---|---|---|---|---|
| 1 | Jail (First turn) | 3.7755 × 10−2 | Jail (First turn) | 4.0069 × 10−2 |
| 2 | Jail (Second turn) | 3.1430 × 10−2 | Illinois Avenue | 3.1416 × 10−2 |
| 3 | Illinois Avenue | 2.9513 × 10−2 | Go | 3.1050 × 10−2 |
| 4 | Go | 2.9220 × 10−2 | New York Avenue | 3.0561 × 10−2 |
| 5 | B&O Railroad | 2.8496 × 10−2 | B&O Railroad | 3.0215 × 10−2 |
| 6 | Reading Railroad | 2.8312 × 10−2 | Reading Railroad | 2.9964 × 10−2 |
| 7 | Tennessee Avenue | 2.8094 × 10−2 | Tennessee Avenue | 2.9245 × 10−2 |
| 8 | Free Parking | 2.7947 × 10−2 | Water Works | 2.9165 × 10−2 |
| 9 | New York Avenue | 2.7827 × 10−2 | Free Parking | 2.8516 × 10−2 |
| 10 | Water Works | 2.7545 × 10−2 | St. James Place | 2.8063 × 10−2 |
| 11 | St. James Place | 2.6921 × 10−2 | Kentucky Avenue | 2.7948 × 10−2 |
| 12 | Jail (Third turn) | 2.6192 × 10−2 | St. Charles Place | 2.7281 × 10−2 |
| 13 | St. Charles Place | 2.5807 × 10−2 | Short Line Railroad | 2.7122 × 10−2 |
| 14 | Kentucky Avenue | 2.5740 × 10−2 | Indiana Avenue | 2.6885 × 10−2 |
| 15 | Short Line Railroad | 2.5533 × 10−2 | Atlantic Avenue | 2.6705 × 10−2 |
| 16 | Indiana Avenue | 2.5216 × 10−2 | Pennsylvania Railroad | 2.6501 × 10−2 |
| 17 | Electric Company | 2.5050 × 10−2 | Pacific Avenue | 2.6460 × 10−2 |
| 18 | Atlantic Avenue | 2.5031 × 10−2 | Ventnor Avenue | 2.6435 × 10−2 |
| 19 | Boardwalk | 2.4946 × 10−2 | Boardwalk | 2.6387 × 10−2 |
| 20 | Pacific Avenue | 2.4926 × 10−2 | North Carolina Avenue | 2.5974 × 10−2 |
| 21 | Ventnor Avenue | 2.4844 × 10−2 | Community Chest (West) | 2.5970 × 10−2 |
| 22 | North Carolina Avenue | 2.4466 × 10−2 | Marvin Gardens | 2.5507 × 10−2 |
| 23 | Virginia Avenue | 2.4455 × 10−2 | Electric Company | 2.4881 × 10−2 |
| 24 | Marvin Gardens | 2.4035 × 10−2 | Virginia Avenue | 2.4864 × 10−2 |
| 25 | Pennsylvania Railroad | 2.3798 × 10−2 | Pennsylvania Avenue | 2.4837 × 10−2 |
| 26 | Pennsylvania Avenue | 2.3381 × 10−2 | States Avenue | 2.4003 × 10−2 |
| 27 | Community Chest (West) | 2.2957 × 10−2 | Community Chest (East) | 2.3655 × 10−2 |
| 28 | Community Chest (East) | 2.2259 × 10−2 | Income Tax | 2.3618 × 10−2 |
| 29 | Income Tax | 2.2233 × 10−2 | Vermont Avenue | 2.3404 × 10−2 |
| 30 | Vermont Avenue | 2.2046 × 10−2 | Connecticut Avenue | 2.3266 × 10−2 |
| 31 | States Avenue | 2.1999 × 10−2 | Just Visiting | 2.2954 × 10−2 |
| 32 | Connecticut Avenue | 2.1919 × 10−2 | Oriental Avenue | 2.2874 × 10−2 |
| 33 | Just Visiting | 2.1630 × 10−2 | Baltic Avenue | 2.2016 × 10−2 |
| 34 | Oriental Avenue | 2.1544 × 10−2 | Park Place | 2.1869 × 10−2 |
| 35 | Baltic Avenue | 2.0722 × 10−2 | Luxury Tax | 2.1834 × 10−2 |
| 36 | Park Place | 2.0598 × 10−2 | Mediterranean Avenue | 2.1629 × 10−2 |
| 37 | Luxury Tax | 2.0564 × 10−2 | Community Chest (South) | 1.9181 × 10−2 |
| 38 | Mediterranean Avenue | 2.0355 × 10−2 | Chance (North) | 1.0290 × 10−2 |
| 39 | Community Chest (South) | 1.8052 × 10−2 | Chance (South) | 8.7516 × 10−3 |
| 40 | Chance (North) | 1.0270 × 10−2 | Chance (East) | 8.6306 × 10−3 |
| 41 | Chance (South) | 8.2434 × 10−3 | Go to Jail | 0 |
| 42 | Chance (East) | 8.1276 × 10−3 | Jail (Second turn) | 0 |
| 43 | Go to Jail | 0 | Jail (Third turn) | 0 |
| Rank | States | Long Jail | Rank | States | Short Jail |
|---|---|---|---|---|---|
| Model | Model | ||||
| 1 | Jail (First turn) | 3.7755 × 10−2 | 1 | Jail (First turn) | 4.0069 × 10−2 |
| 2 | Jail (Second turn) | 3.1430 × 10−2 | 31 | Just Visiting | 2.2954 × 10−2 |
| 12 | Jail (Third turn) | 2.6192 × 10−2 | 43 | Go to Jail | 0 |
| 33 | Just Visiting | 2.1630 × 10−2 | |||
| 43 | Go to Jail | 0 | |||
| 1.1701 × 10−1 | 6.3024 × 10−2 | ||||
| Rank | States | Long Jail | Rank | States | Short Jail |
| model | model | ||||
| 1 | Jail | 8.3424 × 10−2 | 1 | Jail | 3.5222 × 10−2 |
| 28 | Just Visiting | 2.2933 × 10−2 | 30 | Just Visiting | 2.3671 × 10−2 |
| 41 | Go to Jail | 0 | 41 | Go to Jail | 0 |
| 1.0636 × 10−1 | 5.8892 × 10−2 |
| Rank | States | Long Jail | States | Short Jail |
|---|---|---|---|---|
| 1 | Jail | 8.3424 × 10−2 | Jail | 3.5222 × 10−2 |
| 2 | Illinois Avenue | 2.9743 × 10−2 | Go | 3.1326 × 10−2 |
| 3 | Go | 2.9160 × 10−2 | Illinois Avenue | 3.1233 × 10−2 |
| 4 | Reading Railroad | 2.9144 × 10−2 | Reading Railroad | 3.0606 × 10−2 |
| 5 | Tennessee Avenue | 2.8775 × 10−2 | New York Avenue | 3.0448 × 10−2 |
| 6 | New York Avenue | 2.8685 × 10−2 | B&O Railroad | 2.9929 × 10−2 |
| 7 | B&O Railroad | 2.8552 × 10−2 | Tennessee Avenue | 2.9115 × 10−2 |
| 8 | Free Parking | 2.8474 × 10−2 | Water Works | 2.8870 × 10−2 |
| 9 | St. James Place | 2.7770 × 10−2 | Free Parking | 2.8416 × 10−2 |
| 10 | St. Charles Place | 2.7218 × 10−2 | St. James Place | 2.8065 × 10−2 |
| 11 | Water Works | 2.7150 × 10−2 | St. Charles Place | 2.8034 × 10−2 |
| 12 | Kentucky Avenue | 2.6364 × 10−2 | Kentucky Avenue | 2.7836 × 10−2 |
| 13 | Electric Company | 2.6236 × 10−2 | Short Line Railroad | 2.7040 × 10−2 |
| 14 | Indiana Avenue | 2.5571 × 10−2 | Indiana Avenue | 2.6761 × 10−2 |
| 15 | Virginia Avenue | 2.5452 × 10−2 | Pennsylvania Railroad | 2.6662 × 10−2 |
| 16 | Pennsylvania Railroad | 2.4969 × 10−2 | Boardwalk | 2.6606 × 10−2 |
| 17 | Atlantic Avenue | 2.4905 × 10−2 | Atlantic Avenue | 2.6411 × 10−2 |
| 18 | Short Line Railroad | 2.4834 × 10−2 | Pacific Avenue | 2.6226 × 10−2 |
| 19 | Boardwalk | 2.4734 × 10−2 | Ventnor Avenue | 2.6132 × 10−2 |
| 20 | Ventnor Avenue | 2.4582 × 10−2 | Community Chest (West) | 2.5814 × 10−2 |
| 21 | Pacific Avenue | 2.4270 × 10−2 | North Carolina Avenue | 2.5762 × 10−2 |
| 22 | Community Chest (West) | 2.3791 × 10−2 | Electric Company | 2.5514 × 10−2 |
| 23 | North Carolina Avenue | 2.3776 × 10−2 | Marvin Gardens | 2.5245 × 10−2 |
| 24 | Marvin Gardens | 2.3557 × 10−2 | Virginia Avenue | 2.5165 × 10−2 |
| 25 | States Avenue | 2.3298 × 10−2 | Pennsylvania Avenue | 2.4701 × 10−2 |
| 26 | Vermont Avenue | 2.3168 × 10−2 | States Avenue | 2.4455 × 10−2 |
| 27 | Connecticut Avenue | 2.3137 × 10−2 | Income Tax | 2.4130 × 10−2 |
| 28 | Just Visiting | 2.2933 × 10−2 | Vermont Avenue | 2.4088 × 10−2 |
| 29 | Income Tax | 2.2788 × 10−2 | Connecticut Avenue | 2.3972 × 10−2 |
| 30 | Pennsylvania Avenue | 2.2704 × 10−2 | Just Visiting | 2.3671 × 10−2 |
| 31 | Oriental Avenue | 2.2373 × 10−2 | Community Chest (East) | 2.3498 × 10−2 |
| 32 | Community Chest (East) | 2.1616 × 10−2 | Oriental Avenue | 2.3464 × 10−2 |
| 33 | Baltic Avenue | 2.1038 × 10−2 | Baltic Avenue | 2.2425 × 10−2 |
| 34 | Mediterranean Avenue | 2.0362 × 10−2 | Luxury Tax | 2.1955 × 10−2 |
| 35 | Luxury Tax | 2.0201 × 10−2 | Park Place | 2.1925 × 10−2 |
| 36 | Park Place | 2.0149 × 10−2 | Mediterranean Avenue | 2.1925 × 10−2 |
| 37 | Community Chest (South) | 1.8191 × 10−2 | Community Chest (South) | 1.9492 × 10−2 |
| 38 | Chance (North) | 1.0369 × 10−2 | Chance (North) | 1.0243 × 10−2 |
| 39 | Chance (South) | 8.6136 × 10−3 | Chance (South) | 8.9927 × 10−3 |
| 40 | Chance (East) | 7.9217 × 10−3 | Chance (East) | 8.6250 × 10−3 |
| 41 | Go to Jail | 0 | Go to Jail | 0 |
| Same Color Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Brown | 4.108 × 10−2 | 3 | 120 | 815.1989 | 15 | 220 | 298.9063 | 45 | 320 | 144.9243 | 135 | 420 | 63.4044 | 240 | 520 | 44.1566 | 350 | 620 | 36.1017 |
| Light Blue | 6.551 × 10−2 | 6.67 | 320 | 613.1272 | 33.33 | 470 | 180.2142 | 93.33 | 620 | 84.8979 | 280 | 770 | 35.1446 | 416.67 | 920 | 28.2177 | 566.67 | 1070 | 24.1313 |
| Light Purple | 7.226 × 10−2 | 10.67 | 440 | 477.7760 | 53.33 | 740 | 160.7667 | 160 | 1040 | 75.3094 | 466.67 | 1340 | 33.2683 | 650 | 1640 | 29.2325 | 800 | 1940 | 28.0962 |
| Orange | 8.284 × 10−2 | 14.67 | 560 | 385.7908 | 73.33 | 860 | 118.5252 | 206.67 | 1160 | 56.7250 | 566.67 | 1260 | 22.4716 | 766.67 | 1560 | 20.5641 | 966.67 | 1860 | 19.4459 |
| Red | 8.047 × 10−2 | 18.67 | 680 | 378.9349 | 93.33 | 1130 | 125.9671 | 266.67 | 1580 | 61.6429 | 716.67 | 2030 | 29.4698 | 891.67 | 2480 | 28.9366 | 1066.67 | 2930 | 28.5784 |
| Yellow | 7.391 × 10−2 | 22.66 | 800 | 399.9088 | 113.33 | 1250 | 124.9384 | 340 | 1700 | 56.6371 | 816.67 | 2150 | 29.8210 | 991.67 | 2600 | 29.6987 | 1166.67 | 3050 | 29.6130 |
| Green | 7.277 × 10−2 | 20 | 920 | 529.2240 | 136.67 | 1520 | 127.9535 | 410 | 2120 | 59.4886 | 933.33 | 2720 | 33.5286 | 1133.33 | 3320 | 33.7026 | 1316.67 | 3920 | 34.2524 |
| Dark Blue | 4.554 × 10−2 | 42.5 | 750 | 324.4243 | 187.5 | 1150 | 112.7555 | 550 | 1550 | 51.8096 | 1250 | 1950 | 28.6791 | 1500 | 2350 | 28.8017 | 1750 | 2750 | 28.8892 |
| Railroad | 1.061 × 10−1 | 200 | 800 | 31.5511 | |||||||||||||||
| Utility | 5.260 × 10−2 | 70 | 300 | 68.2137 | |||||||||||||||
| Same Color Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
| Brown | 4.140 × 10−2 | 3 | 120 | 808.8979 | 15 | 220 | 296.5959 | 45 | 320 | 143.8041 | 135 | 420 | 62.9143 | 240 | 520 | 43.8153 | 350 | 620 | 35.8226 |
| Light Blue | 6.868 × 10−2 | 6.67 | 320 | 584.8277 | 33.33 | 470 | 171.8962 | 93.33 | 620 | 80.9793 | 280 | 770 | 33.5225 | 416.67 | 920 | 26.9153 | 566.67 | 1070 | 23.0175 |
| Light Purple | 7.597 × 10−2 | 10.67 | 440 | 454.4438 | 53.33 | 740 | 152.9157 | 160 | 1040 | 71.6317 | 466.67 | 1340 | 31.6437 | 650 | 1640 | 27.8050 | 800 | 1940 | 26.7241 |
| Orange | 8.523 × 10−2 | 14.67 | 560 | 374.9725 | 73.33 | 860 | 115.2016 | 206.67 | 1160 | 55.1343 | 566.67 | 1260 | 21.8415 | 766.67 | 1560 | 19.9875 | 966.67 | 1860 | 18.9006 |
| Red | 8.168 × 10−2 | 18.67 | 680 | 373.3214 | 93.33 | 1130 | 124.1011 | 266.67 | 1580 | 60.7297 | 716.67 | 2030 | 29.0332 | 891.67 | 2480 | 28.5079 | 1066.67 | 2930 | 28.1550 |
| Yellow | 7.304 × 10−2 | 22.66 | 800 | 404.6722 | 113.33 | 1250 | 126.4266 | 340 | 1700 | 57.3117 | 816.67 | 2150 | 30.1762 | 991.67 | 2600 | 30.0524 | 1166.67 | 3050 | 29.9658 |
| Green | 7.075 × 10−2 | 20 | 920 | 544.3340 | 136.67 | 1520 | 131.6067 | 410 | 2120 | 61.1875 | 933.33 | 2720 | 34.4859 | 1133.33 | 3320 | 34.6649 | 1316.67 | 3920 | 35.2303 |
| Dark Blue | 4.488 × 10−2 | 42.5 | 750 | 329.1952 | 187.5 | 1150 | 114.4136 | 550 | 1550 | 52.5715 | 1250 | 1950 | 29.1009 | 1500 | 2350 | 29.2252 | 1750 | 2750 | 29.3141 |
| Railroad | 1.075 × 10−1 | 200 | 800 | 31.1520 | |||||||||||||||
| Utility | 5.339 × 10−2 | 70 | 300 | 67.2043 | |||||||||||||||
| Same Color Property | Probability | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn | Rent | Cost | Turn |
| Brown | 4.365 × 10−2 | 3 | 120 | 767.2021 | 15 | 220 | 281.3074 | 45 | 320 | 136.3915 | 135 | 420 | 59.6713 | 240 | 520 | 41.5568 | 350 | 620 | 33.9761 |
| Light Blue | 6.954 × 10−2 | 6.67 | 320 | 577.5951 | 33.33 | 470 | 169.7704 | 93.33 | 620 | 79.9779 | 280 | 770 | 33.1079 | 416.67 | 920 | 26.5825 | 566.67 | 1070 | 22.7328 |
| Light Purple | 7.615 × 10−2 | 10.67 | 440 | 453.3696 | 53.33 | 740 | 152.5542 | 160 | 1040 | 71.4624 | 466.67 | 1340 | 31.5689 | 650 | 1640 | 27.7392 | 800 | 1940 | 26.6610 |
| Orange | 8.787 × 10−2 | 14.67 | 560 | 363.7067 | 73.33 | 860 | 111.7404 | 206.67 | 1160 | 53.4779 | 566.67 | 1260 | 21.1853 | 766.67 | 1560 | 19.3870 | 966.67 | 1860 | 18.3328 |
| Red | 8.625 × 10−2 | 18.67 | 680 | 353.5408 | 93.33 | 1130 | 117.5255 | 266.67 | 1580 | 57.5119 | 716.67 | 2030 | 27.4949 | 891.67 | 2480 | 26.9974 | 1066.67 | 2930 | 26.6632 |
| Yellow | 7.865 × 10−2 | 22.66 | 800 | 375.8075 | 113.33 | 1250 | 117.4087 | 340 | 1700 | 53.2237 | 816.67 | 2150 | 28.0238 | 991.67 | 2600 | 27.9088 | 1166.67 | 3050 | 27.8283 |
| Green | 7.727 × 10−2 | 20 | 920 | 498.4034 | 136.67 | 1520 | 120.5018 | 410 | 2120 | 56.0241 | 933.33 | 2720 | 31.5760 | 1133.33 | 3320 | 31.7399 | 1316.67 | 3920 | 32.2576 |
| Dark Blue | 4.826 × 10−2 | 42.5 | 750 | 306.1393 | 187.5 | 1150 | 106.4004 | 550 | 1550 | 48.8895 | 1250 | 1950 | 27.0627 | 1500 | 2350 | 27.1784 | 1750 | 2750 | 27.2610 |
| Railroad | 1.138 × 10−1 | 200 | 800 | 29.4274 | |||||||||||||||
| Utility | 5.405 × 10−2 | 70 | 300 | 66.3837 | |||||||||||||||
| Brown | 4.435 × 10−2 | 3 | 120 | 755.0929 | 15 | 220 | 276.8674 | 45 | 320 | 134.2387 | 135 | 420 | 58.7295 | 240 | 520 | 40.9009 | 350 | 620 | 33.4398 |
| Light Blue | 7.152 × 10−2 | 6.67 | 320 | 561.6046 | 33.33 | 470 | 165.0704 | 93.33 | 620 | 77.7637 | 280 | 770 | 32.1914 | 416.67 | 920 | 25.8465 | 566.67 | 1070 | 22.1035 |
| Light Purple | 7.765 × 10−2 | 10.67 | 440 | 444.6117 | 53.33 | 740 | 149.6073 | 160 | 1040 | 70.0819 | 466.67 | 1340 | 30.9590 | 650 | 1640 | 27.2034 | 800 | 1940 | 26.1459 |
| Orange | 8.763 × 10−2 | 14.67 | 560 | 364.7028 | 73.33 | 860 | 112.0464 | 206.67 | 1160 | 53.6243 | 566.67 | 1260 | 21.2433 | 766.67 | 1560 | 19.4401 | 966.67 | 1860 | 18.3830 |
| Red | 8.583 × 10−2 | 18.67 | 680 | 355.2708 | 93.33 | 1130 | 118.1006 | 266.67 | 1580 | 57.7934 | 716.67 | 2030 | 27.6294 | 891.67 | 2480 | 27.1295 | 1066.67 | 2930 | 26.7937 |
| Yellow | 7.779 × 10−2 | 22.66 | 800 | 379.9622 | 113.33 | 1250 | 118.7067 | 340 | 1700 | 53.8121 | 816.67 | 2150 | 28.3336 | 991.67 | 2600 | 28.2174 | 1166.67 | 3050 | 28.1360 |
| Green | 7.600 × 10−2 | 20 | 920 | 506.7319 | 136.67 | 1520 | 122.5154 | 410 | 2120 | 56.9603 | 933.33 | 2720 | 32.1036 | 1133.33 | 3320 | 32.2702 | 1316.67 | 3920 | 32.7967 |
| Dark Blue | 4.853 × 10−2 | 42.5 | 750 | 304.4361 | 187.5 | 1150 | 105.8084 | 550 | 1550 | 48.6175 | 1250 | 1950 | 26.9122 | 1500 | 2350 | 27.0272 | 1750 | 2750 | 27.1093 |
| Railroad | 1.142 × 10−1 | 200 | 800 | 29.3141 | |||||||||||||||
| Utility | 5.438 × 10−2 | 70 | 300 | 66.1024 |
| Rank of Hotel Return | States | Long Jail Model | States | Short Jail Model |
|---|---|---|---|---|
| 1 | Brown | 36.10167 ≈ 36 | Brown | 33.97609 ≈ 34 |
| 2 | Green | 34.25238 ≈ 34 | Green | 32.25762 ≈ 32 |
| 3 | Yellow | 29.61302 ≈ 30 | Yellow | 27.82833 ≈ 28 |
| 4 | Dark Blue | 28.88921 ≈ 29 | Dark Blue | 27.26097 ≈ 27 |
| 5 | Red | 28.57838 ≈ 29 | Red | 26.66321 ≈ 27 |
| 6 | Light Purple | 28.09622 ≈ 28 | Light Purple | 26.66097 ≈ 27 |
| 7 | Light Blue | 24.13126 ≈ 24 | Light Blue | 22.7328 ≈ 23 |
| 8 | Orange | 19.44593 ≈ 19 | Orange | 18.33277 ≈ 18 |
| Rank of Hotel Return | States | Long Jail Model | States | Short Jail Model |
| 1 | Brown | 35.82262 ≈ 36 | Brown | 33.43983 ≈ 33 |
| 2 | Green | 35.23033 ≈ 35 | Green | 32.79666 ≈ 33 |
| 3 | Yellow | 29.96575 ≈ 30 | Yellow | 28.13598 ≈ 28 |
| 4 | Dark Blue | 29.31405 ≈ 29 | Dark Blue | 27.10931 ≈ 27 |
| 5 | Red | 28.15502 ≈ 28 | Red | 26.79369 ≈ 27 |
| 6 | Light Purple | 26.72414 ≈ 27 | Light Purple | 26.14594 ≈ 26 |
| 7 | Light Blue | 23.01746 ≈ 23 | Light Blue | 22.10345 ≈ 22 |
| 8 | Orange | 18.90063 ≈ 19 | Orange | 18.38298 ≈ 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wong, J.C.F. Modified Engel Algorithm and Applications in Absorbing/Non-Absorbing Markov Chains and Monopoly Game. Math. Comput. Appl. 2025, 30, 87. https://doi.org/10.3390/mca30040087
Liu C, Wong JCF. Modified Engel Algorithm and Applications in Absorbing/Non-Absorbing Markov Chains and Monopoly Game. Mathematical and Computational Applications. 2025; 30(4):87. https://doi.org/10.3390/mca30040087
Chicago/Turabian StyleLiu, Chunhe, and Jeff Chak Fu Wong. 2025. "Modified Engel Algorithm and Applications in Absorbing/Non-Absorbing Markov Chains and Monopoly Game" Mathematical and Computational Applications 30, no. 4: 87. https://doi.org/10.3390/mca30040087
APA StyleLiu, C., & Wong, J. C. F. (2025). Modified Engel Algorithm and Applications in Absorbing/Non-Absorbing Markov Chains and Monopoly Game. Mathematical and Computational Applications, 30(4), 87. https://doi.org/10.3390/mca30040087





