Computing Two Heuristic Shrinkage Penalized Deep Neural Network Approach
Abstract
1. Introduction
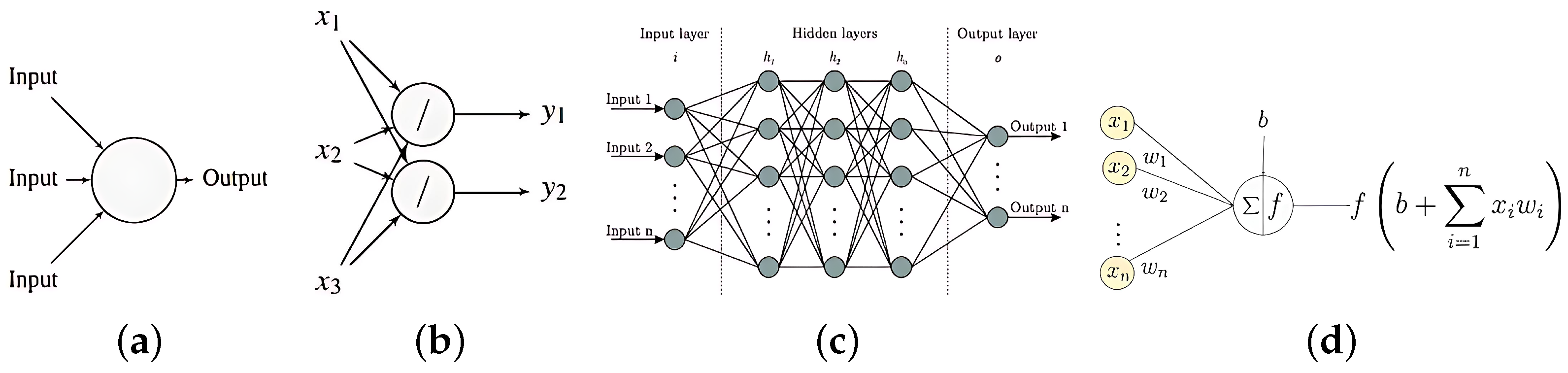
2. Regularization of DNN
2.1. Extending the Concept of Shrinkage Penalization in the GLMs to DNNs
- (a)
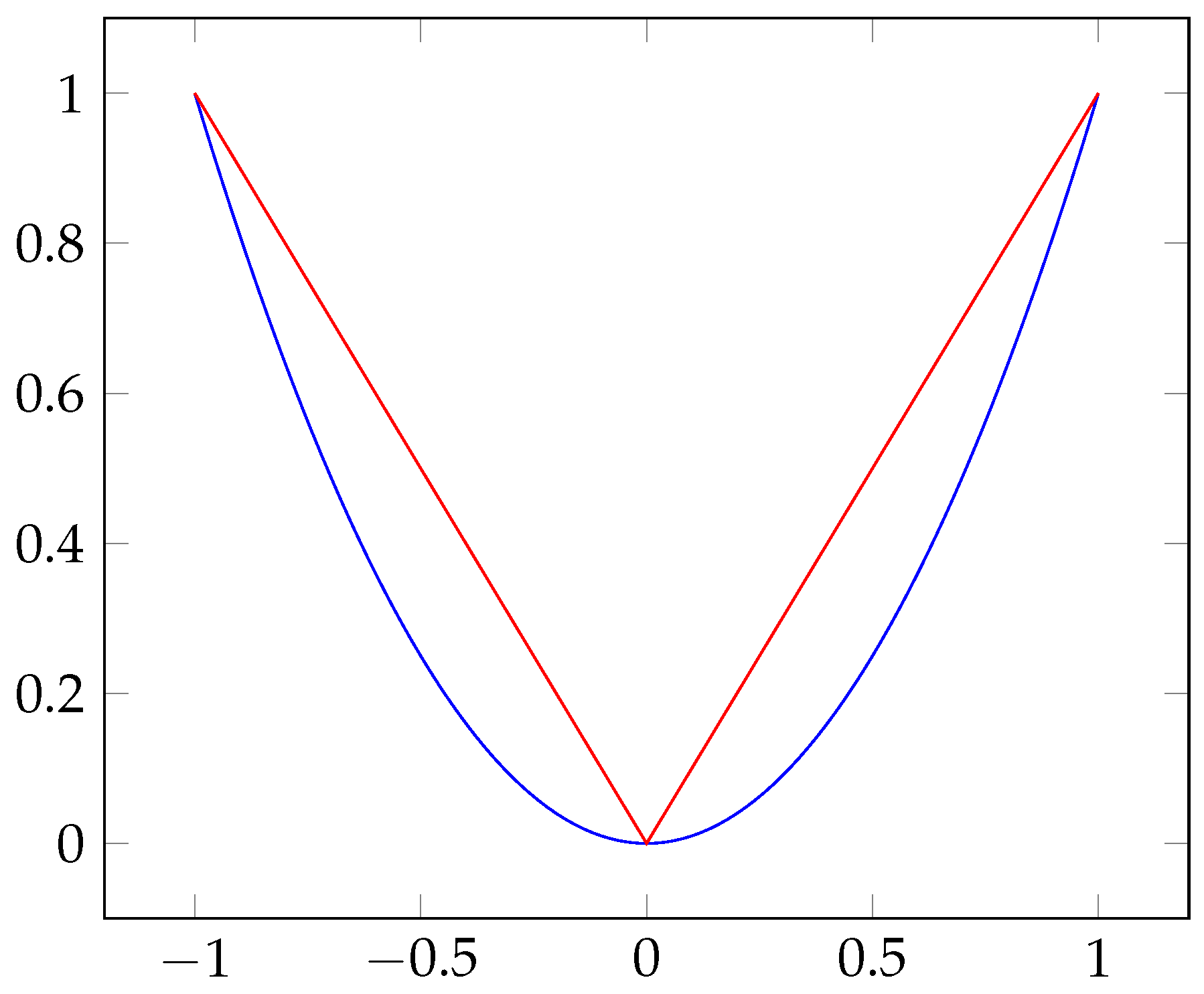
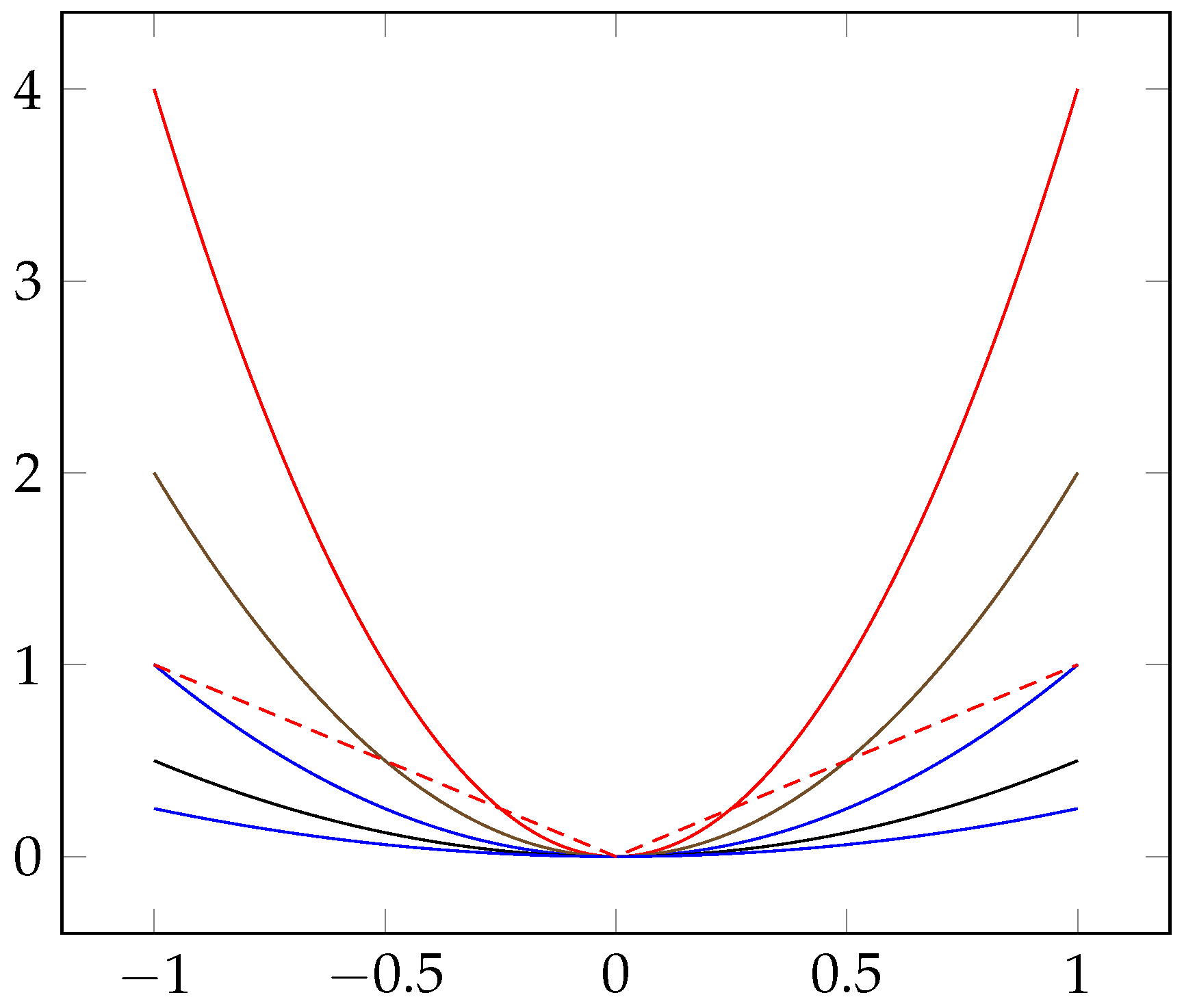
- In the case of , the Lasso selects at most n variables before it saturates, because of the nature of the convex optimization problem. It seems to be a limiting feature for a variable selection method. Moreover, the Lasso is not well defined unless the bound on the of the coefficients is smaller than a certain value.
- (b)
- If there is a group of variables among which the pairwise correlations are very high, then the Lasso tends to select only one variable from the group and does not care which one is selected.
- (c)
- For usual situations, if there are high correlations between predictors, it has been empirically observed that the prediction performance of the Lasso is dominated by ridge regression [29].
2.2. Empirical Extension of the Application of the Ratio Theory
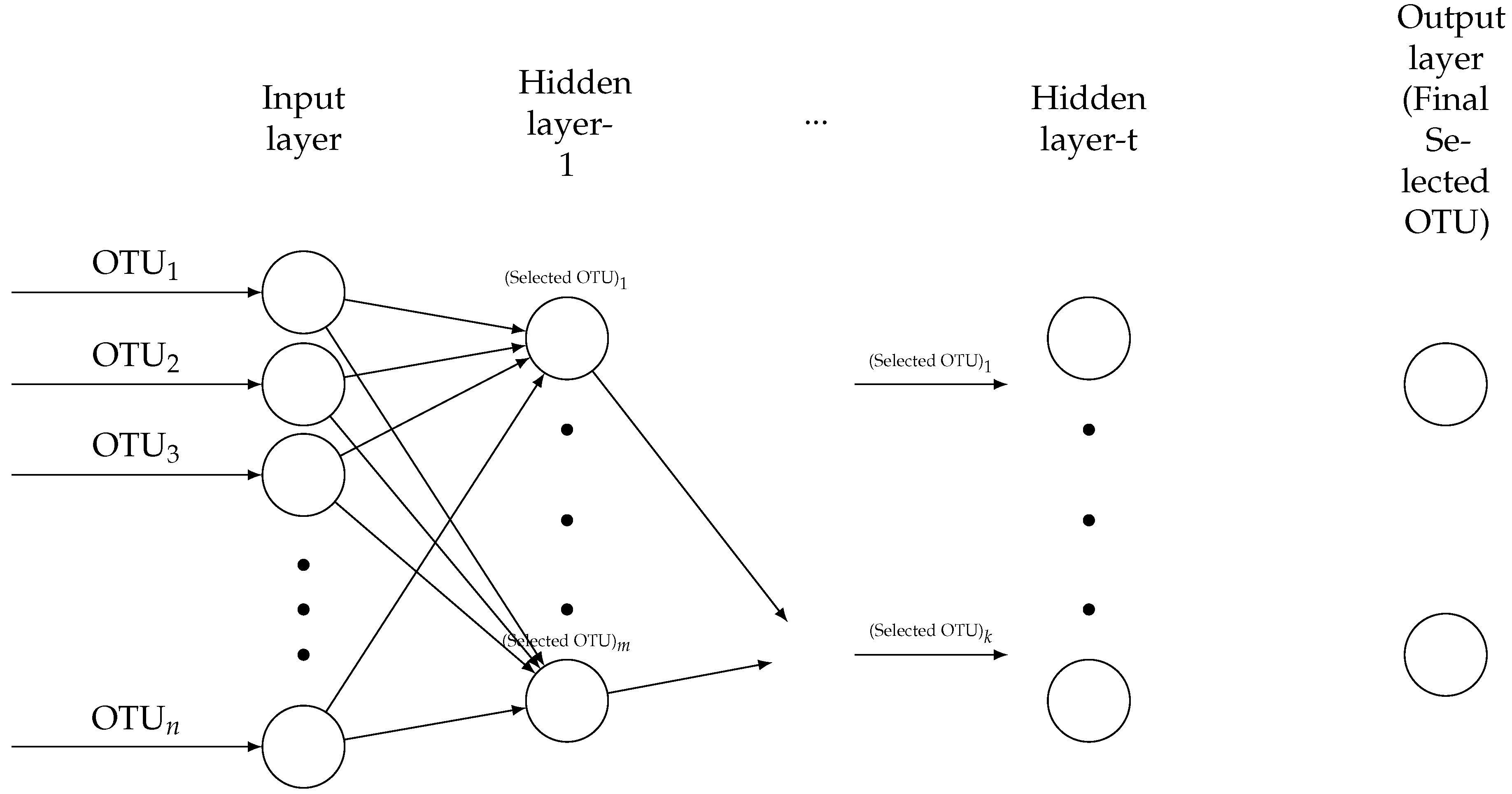
2.3. Constructing Two Heuristics DNN Approaches Based on the Shrinkage Penalized Methods
3. Microbiome Data
3.1. Simulation Study for Microbiome Data
| Algorithm 1 Extendable algorithm of the neural network. |
|
3.2. Classification of Simulated Microbiome Data Based on the Elastic-Net Penalization Using DNN
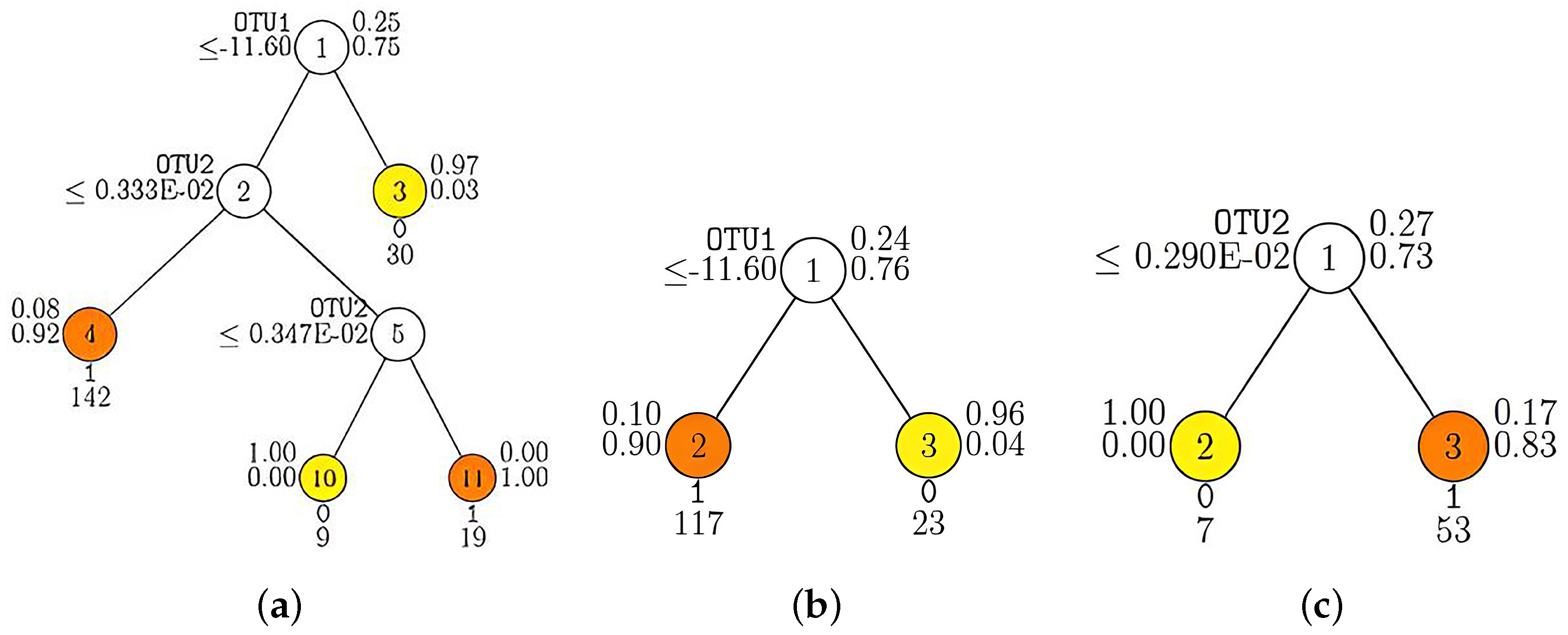
3.3. Classification of Simulated Microbiome Data with GUIDE
3.4. Classification of Real Microbiome Data Based on the Elastic-Net Penalization Using DNN
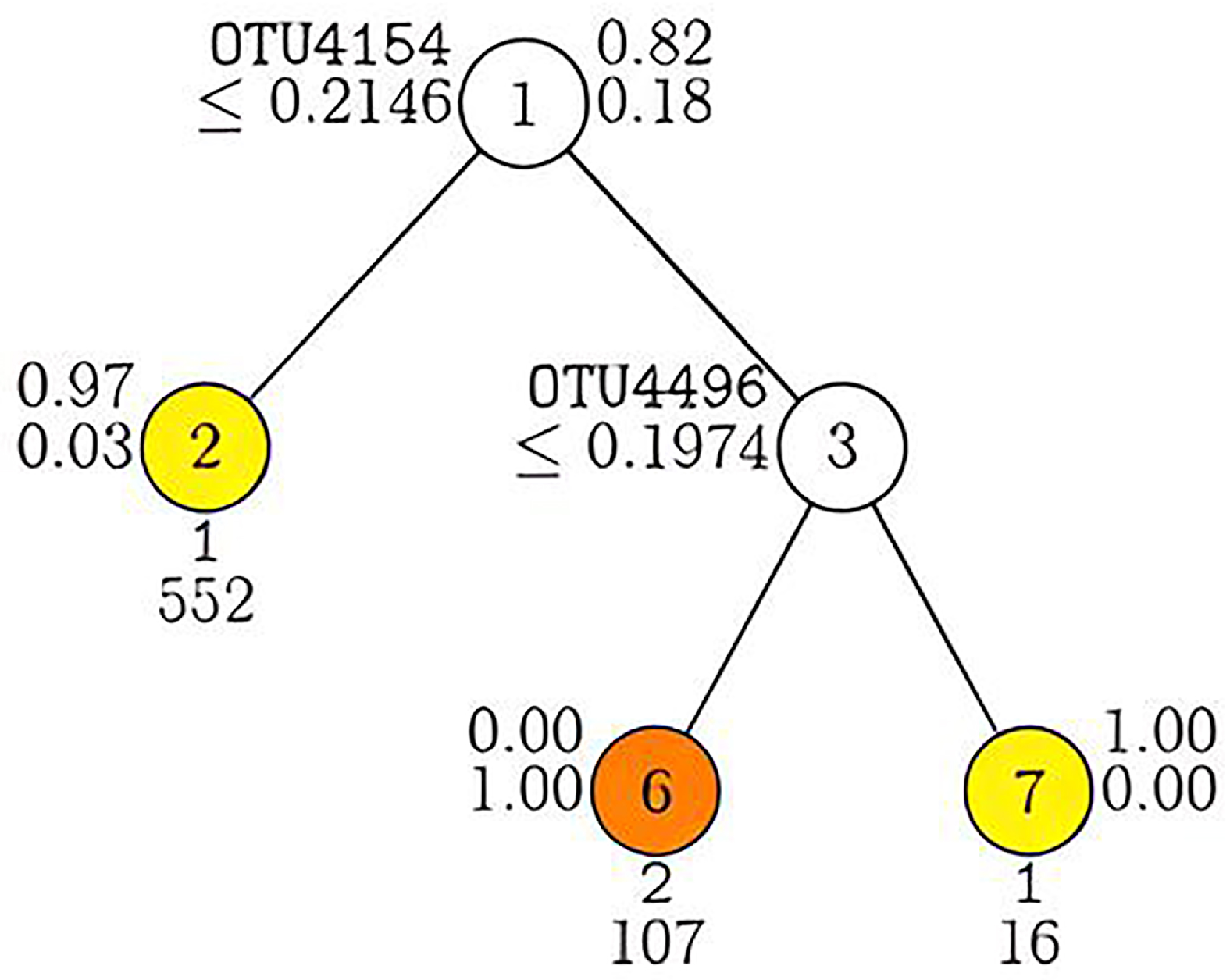
3.5. Classification of Real Microbiome Data with GUIDE
4. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Developing NN Algorithm to DDNs Algorithms

References
- Faraway, J.J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models; Chapman and Hall: New York, NY, USA, 2016. [Google Scholar]
- Penrose, R. The emperor’s new mind: Concerning computers, minds, and the laws of physics. Behav. Brain Sci. 1990, 13, 643–655. [Google Scholar] [CrossRef]
- Ciaburro, G.; Venkateswaran, B. Neural Networks with R: Smart Models Using CNN, RNN, Deep Learning, and Artificial Intelligence Principles; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Liu, Y.H.; Maldonado, P. R Deep Learning Projects: Master the Techniques to Design and Develop Neural Network Models in R; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Roozbeh, M.; Maanavi, M.; Mohamed, N.A. Penalized least squares optimization problem for high-dimensional data. Int. J. Nonlinear Anal. Appl. 2023, 14, 245–250. [Google Scholar]
- De-Julián-Ortiz, J.V.; Pogliani, L.; Besalú, E. Modeling properties with artificial neural networks and multilinear least-squares regression: Advantages and drawbacks of the two methods. Appl. Sci. 2018, 8, 1094. [Google Scholar] [CrossRef]
- Hammerstrom, D. Working with neural networks. IEEE Spectr. 1993, 30, 46–53. [Google Scholar] [CrossRef]
- Salehin, I.; Kang, D.K. A review on dropout regularization approaches for deep neural networks within the scholarly domain. Electronics 2023, 12, 3106. [Google Scholar] [CrossRef]
- Hertz, J.A. Introduction to the Theory of Neural Computation; Chapman and Hall: New York, NY, USA, 2018. [Google Scholar]
- Fan, J.; Li, R. Statistical challenges with high dimensionality: Feature selection in knowledge discovery. arXiv 2006, arXiv:math/0602133. [Google Scholar]
- Huang, J.; Breheny, P.; Lee, S.; Ma, S.; Zhang, C. The Mnet method for variable selection. Stat. Sin. 2016, 26, 903–923. [Google Scholar] [CrossRef]
- Farrell, M.; Liang, T.; Misra, S. Deep neural networks for estimation and inference. Econometrica 2021, 89, 181–213. [Google Scholar] [CrossRef]
- Kurisu, D.; Fukami, R.; Koike, Y. Adaptive deep learning for nonlinear time series models. Bernoulli 2025, 31, 240–270. [Google Scholar] [CrossRef]
- Bach, F. Breaking the curse of dimensionality with convex neural networks. J. Mach. Learn. Res. 2017, 18, 1–53. [Google Scholar]
- Celentano, L.; Basin, M.V. Optimal estimator design for LTI systems with bounded noises, disturbances, and nonlinearities. Circuits Syst. Signal Process. 2021, 40, 3266–3285. [Google Scholar] [CrossRef]
- Liu, F.; Dadi, L.; Cevher, V. Learning with norm constrained, over-parameterized, two-layer neural networks. J. Mach. Learn. Res. 2024, 25, 1–42. [Google Scholar]
- Shrestha, K.; Alsadoon, O.H.; Alsadoon, A.; Rashid, T.A.; Ali, R.S.; Prasad, P.W.C.; Jerew, O.D. A novel solution of an elastic net regularisation for dementia knowledge discovery using deep learning. J. Exp. Theor. Artif. Intell. 2023, 35, 807–829. [Google Scholar] [CrossRef]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. arXiv 2016, arXiv:1611.03530. [Google Scholar] [CrossRef]
- Mulenga, M.; Kareem, S.A.; Sabri, A.Q.; Seera, M.; Govind, S.; Samudi, C.; Saharuddin, M.B. Feature extension of gut microbiome data for deep neural network-based colorectal cancer classification. IEEE Access 2021, 9, 23565–23578. [Google Scholar] [CrossRef]
- Namkung, J. Machine learning methods for microbiome studies. J. Microbiol. 2020, 58, 206–216. [Google Scholar] [CrossRef]
- Topçuoğlu, B.D.; Lesniak, N.A.; Ruffin, M.T.; Wiens, J.; Schloss, P.D. A framework for effective application of machine learning to microbiome-based classification problems. mBio 2020, 11, 10-1128. [Google Scholar] [CrossRef]
- Anwar, S.M.; Majid, M.; Qayyum, A.; Awais, M.; Alnowami, M.; Khan, M.K. Medical image analysis using convolutional neural networks: A review. J. Med. Syst. 2018, 42, 226. [Google Scholar] [CrossRef]
- Lo, C.; Marculescu, R. MetaNN: Accurate classification of host phenotypes from metagenomic data using neural networks. BMC Bioinform. 2019, 20, 314. [Google Scholar] [CrossRef]
- Reiman, D.; Metwally, A.; Dai, Y. Using convolutional neural networks to explore the microbiome. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; pp. 4269–4272. [Google Scholar] [CrossRef]
- Arabameri, A.; Asemani, D.; Teymourpour, P. Detection of colorectal carcinoma based on microbiota analysis using generalized regression neural networks and nonlinear feature selection. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 17, 547–557. [Google Scholar] [CrossRef]
- Fiannaca, A.; La Paglia, L.; La Rosa, M.; Lo Bosco, G.; Renda, G.; Rizzo, R.; Gaglio, S.; Urso, A. Deep learning models for bacteria taxonomic classification of metagenomic data. BMC Bioinform. 2018, 19, 61–76. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and Regression Trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 4–23. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Segal, M.; Dahlquist, K.; Conklin, B. Regression approach for microarray data analysis. J. Comput. Biol. 2003, 10, 961–980. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Hastie, T.; Johnstone, I.R. Least angle regression. Ann. Statist. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Yin, P.; Esser, E.; Xin, J. Ratio and difference of L1 and L2 norms and sparse representation with coherent dictionaries. Commun. Inf. Syst. 2014, 14, 87–109. [Google Scholar] [CrossRef]
- Frank, L.E.; Friedman, J.H. A statistical view of some chemometrics regression tools. Technometrics 1993, 35, 109–135. [Google Scholar] [CrossRef]
- Fan, J.; Lv, J. A selective overview of variable selection in high dimensional feature space. Stat. Sin. 2010, 20, 101. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Tyler, A.D.; Smith, M.I.; Silverberg, M.S. Analyzing the human microbiome: A “How To” guide for physicians. Am. J. Gastroenterol. 2014, 109, 983–993. [Google Scholar] [CrossRef]
- Sender, R.; Fuchs, S.; Milo, R. Revised estimates for the number of human and bacteria cells in the body. PLoS Biol. 2016, 14, e1002533. [Google Scholar] [CrossRef] [PubMed]
- Bharti, R.; Grimm, D.G. Current challenges and best-practice protocols for microbiome analysis. Briefings Bioinform. 2021, 22, 178–193. [Google Scholar] [CrossRef]
- Qian, X.B.; Chen, T.; Xu, Y.P.; Chen, L.; Sun, F.X.; Lu, M.P.; Liu, Y.X. A guide to human microbiome research: Study design, sample collection, and bioinformatics analysis. Chin. Med. J. 2020, 133, 1844–1855. [Google Scholar] [CrossRef]
- Xia, Y.; Sun, J.; Chen, D.G. Statistical Analysis of Microbiome Data with R; Springer: Singapore, 2018. [Google Scholar]
- Wang, Q.Q.; Yu, S.C.; Qi, X.; Hu, Y.; Zheng, W.J.; Shi, J.X.; Yao, H.Y. Overview of logistic regression model analysis and application. Chin. J. Prev. Med. 2019, 53, 955–960. [Google Scholar]
- Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. Ser. Methodol. 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Aitchison, J.; Barceló-Vidal, C.; Martín-Fernández, J.A.; Pawlowsky-Glahn, V. Logratio Analysis and Compositional Distance. Math. Geol. 2000, 32, 271–275. [Google Scholar] [CrossRef]
- Martín-Fernández, J.A.; Barceló-Vidal, C.; Pawlowsky-Glahn, V. Dealing with zeros and missing values in compositional datasets using nonparametric imputation. Math. Geol. 2003, 35, 253–278. [Google Scholar] [CrossRef]
- Martín-Fernández, J.A.; Palarea-Albaladejo, J.; Olea, R.A. Dealing with Zeros, Compositional Data Analysis: Theory and Applications; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
- Martín-Fernández, J.A.; Hron, K.; Templ, M.; Filzmoser, P.; Palarea-Albaladejo, J. Model-based replacement of rounded zeros in compositional data: Classical and robust approaches. Comput. Stat. Data Anal. 2012, 56, 2688–2704. [Google Scholar] [CrossRef]
- Martín-Fernández, J.A.; Hron, K.; Templ, M.; Filzmoser, P.; Palarea-Albaladejo, J. Bayesian-multiplicative treatment of count zeros in compositional datasets. Stat. Model. 2015, 15, 134–158. [Google Scholar] [CrossRef]
- Loh, W.Y. Fifty years of classification and regression trees. Int. Stat. Rev. 2014, 82, 329–348. [Google Scholar] [CrossRef]
- Loh, W.Y.; Zhou, P. The GUIDE Approach to Subgroup Identification, Design and Analysis of Subgroups with Biopharmaceutical Applications; Springer: Cham, Switzerland, 2020; pp. 147–165. [Google Scholar]
- Turnbaugh, P.J.; Ridaura, V.K.; Faith, J.J.; Rey, F.E.; Knight, R.; Gordon, J. The effect of diet on the human gut microbiome: A metagenomic analysis in humanized gnotobiotic mice. Sci. Transl. Med. 2009, 1, 6ra14. [Google Scholar] [CrossRef] [PubMed]

| Type of the Deep Neural Network Model | Prediction Accuracy of Whole Dataset (%), Mean [CI 95%] | Sensitivity of Whole Dataset (%), Mean [CI 95%] | Prediction Accuracy of Training Dataset (%), Mean [CI 95%] | Sensitivity of Training Dataset (%), Mean [CI 95%] | Prediction Accuracy of Testing Dataset (%), Mean [CI 95%] | Sensitivity of Testing Dataset (%), Mean [CI 95%] |
|---|---|---|---|---|---|---|
| 80 | ||||||
| 82 | 80 | |||||
| 82 | ||||||
| 84 | ||||||
| GUIDE | 81 | 82 | ||||
| Type of the Deep Neural Network Model | Prediction Accuracy of Whole Dataset, % | Sensitivity of Whole Dataset, % | Prediction Accuracy of Training Dataset %, Mean [CI 95 %] | Sensitivity of Training Dataset %, Mean [CI 95 %] | Prediction Accuracy of Testing Dataset %, Mean [CI 95 %] | Sensitivity of Testing Dataset %, Mean [CI 95 %] |
|---|---|---|---|---|---|---|
| GUIDE | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behzadi, M.; Mohamad, S.B.; Roozbeh, M.; Yunus, R.M.; Hamzah, N.A. Computing Two Heuristic Shrinkage Penalized Deep Neural Network Approach. Math. Comput. Appl. 2025, 30, 86. https://doi.org/10.3390/mca30040086
Behzadi M, Mohamad SB, Roozbeh M, Yunus RM, Hamzah NA. Computing Two Heuristic Shrinkage Penalized Deep Neural Network Approach. Mathematical and Computational Applications. 2025; 30(4):86. https://doi.org/10.3390/mca30040086
Chicago/Turabian StyleBehzadi, Mostafa, Saharuddin Bin Mohamad, Mahdi Roozbeh, Rossita Mohamad Yunus, and Nor Aishah Hamzah. 2025. "Computing Two Heuristic Shrinkage Penalized Deep Neural Network Approach" Mathematical and Computational Applications 30, no. 4: 86. https://doi.org/10.3390/mca30040086
APA StyleBehzadi, M., Mohamad, S. B., Roozbeh, M., Yunus, R. M., & Hamzah, N. A. (2025). Computing Two Heuristic Shrinkage Penalized Deep Neural Network Approach. Mathematical and Computational Applications, 30(4), 86. https://doi.org/10.3390/mca30040086





