Enhanced BiCGSTAB with Restrictive Preconditioning for Nonlinear Systems: A Mean Curvature Image Deblurring Approach
Abstract
1. Introduction
- We introduce an innovative restrictive block preconditioner based on partitioning the five-by-five block structure of the MC-based image deblurring problem.
- We propose a robust RPBiCGSTAB algorithm for solving the MC-based image deblurring problem, which converges unconditionally.
- Spectral analysis indicates that the preconditioned matrix displays a favorable distribution of eigenvalues, thereby facilitating the rapid convergence of the proposed RPBiCGSTAB technique.
- We incorporate experimental data, subsequently comparing the results with those obtained from established methodologies.
2. Problem Description
Derivation of the Euler–Lagrange Equation for the Curvature Model
3. Cell Discretization
4. RPBiCGSTAB Method
| Algorithm 1: RPBiCGSTAB method |
|
| Algorithm 2: The preconditioning |
|
5. Spectral Analysis
6. Numerical Experiments
Remarks
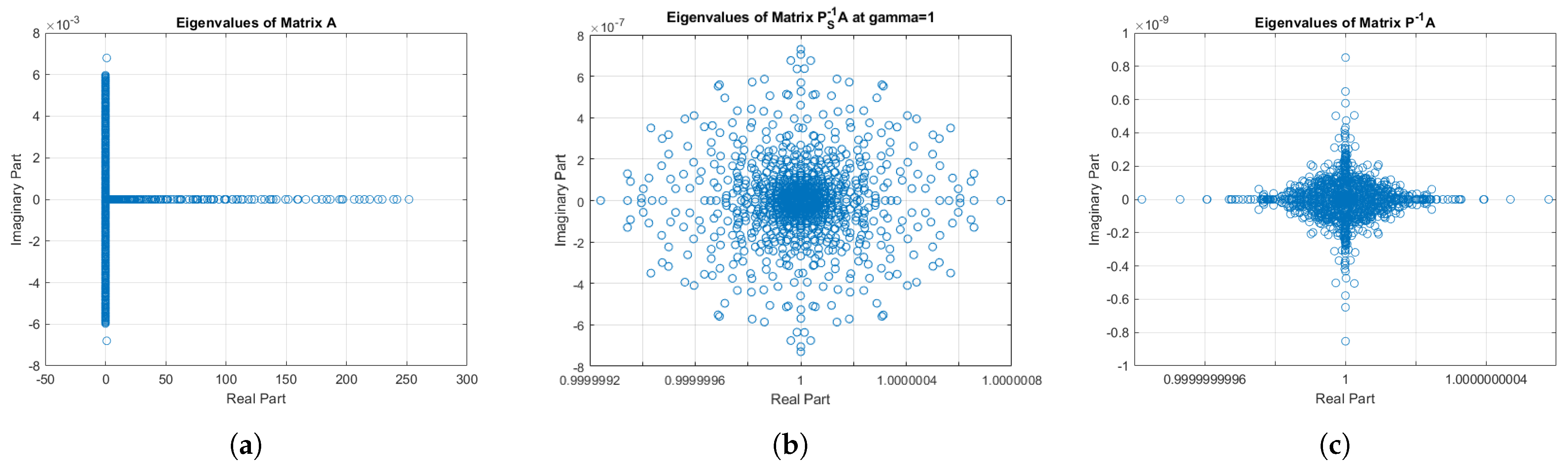
- Our computational analysis indicates that the optimal range for the eigenvalues is concentrated around 1. The most favorable spectrum of eigenvalues is depicted in Figure 4, which illustrates the distribution of eigenvalues across different scenarios. Clearly, our proposed preconditioner has a much better spectrum compared to the preconditioner [25] for the Goldhill image of size .
- The effect of preconditioning is clearly demonstrated in Figure 5. It is evident that the method attained the desired accuracy with substantially fewer iterations than other methods. In contrast, the method without preconditioning (GMRES and BICGSTAB) required over 50 iterations to reach convergence for the Goldhill image of size . Similar findings were observed for other image dimensions as well.
- All the Table 1, Table 2 and Table 3 demonstrate that the PSNR achieved by the method surpasses that of all other methods, including [25], and this was accomplished with a significantly reduced number of iterations. The implementation of the method resulted in a decrease of over in CPU time. Consequently, the method demonstrated superior performance compared to other methods.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ren, W.; Deng, S.; Zhang, K.; Song, F.; Cao, X.; Yang, M.-H. Fast ultra high-definition video deblurring via multi-scale separable network. Int. J. Comput. Vis. 2024, 132, 1817–1834. [Google Scholar] [CrossRef]
- Ren, W.; Wu, L.; Yan, Y.; Xu, S.; Huang, F.; Cao, X. INformer: Inertial-Based Fusion Transformer for Camera Shake Deblurring. IEEE Trans. Image Process. 2024, 33, 6045–6056. [Google Scholar] [CrossRef]
- Chen, K. Introduction to variational image-processing models and applications. Int. J. Comput. Math. 2013, 90, 1–8. [Google Scholar] [CrossRef]
- Sun, L.; Chen, K. A new iterative algorithm for mean curvature-based variational image denoising. BIT Numer. Math. 2014, 54, 523–553. [Google Scholar] [CrossRef]
- Yang, F.; Chen, K.; Yu, B.; Fang, D. A relaxed fixed point method for a mean curvature-based denoising model. Optim. Methods Softw. 2014, 29, 274–285. [Google Scholar] [CrossRef]
- Zhu, W.; Chan, T. Image denoising using mean curvature of image surface. SIAM J. Imaging Sci. 2012, 5, 1–32. [Google Scholar] [CrossRef]
- Zhu, W.; Tai, X.C.; Chan, T. Augmented Lagrangian method for a mean curvature based image denoising model. Inverse Probl. Imaging 2013, 7, 1409–1432. [Google Scholar] [CrossRef]
- Fairag, F.; Chen, K.; Ahmad, S. An effective algorithm for mean curvature-based image deblurring problem. Comput. Appl. Math. 2022, 41, 176. [Google Scholar] [CrossRef]
- Fairag, F.; Chen, K.; Ahmad, S. Analysis of the CCFD method for MC-based image denoising problems. Electron. Trans. Numer. Anal. 2021, 54, 108–127. [Google Scholar] [CrossRef]
- Mobeen, A.; Ahmad, S.; Fairag, F. Non-blind constraint image deblurring problem with mean curvature functional. Numer. Algorithms 2025, 98, 1703–1723. [Google Scholar] [CrossRef]
- Khalid, R.; Ahmad, S.; Medani, M.; Said, Y.; Ali, I. Efficient preconditioning strategies for accelerating GMRES in block-structured nonlinear systems for image deblurring. PLoS ONE 2025, 20, e0322146. [Google Scholar] [CrossRef]
- Fairag, F.; Chen, K.; Brito-Loeza, C.; Ahmad, S. A two-level method for image denoising and image deblurring models using mean curvature regularization. Int. J. Comput. Math. 2022, 99, 693–713. [Google Scholar] [CrossRef]
- Ahmad, S.; Fairag, F. Circulant preconditioners for mean curvature-based image deblurring problem. J. Algorithms Comput. Technol. 2021, 15, 17483026211055679. [Google Scholar] [CrossRef]
- Ahmad, S.; Al-Mahdi, A.M.; Ahmed, R. Two new preconditioners for mean curvature-based image deblurring problem. AIMS Math. 2021, 6, 13824–13844. [Google Scholar] [CrossRef]
- Beik, F.P.A.; Benzi, M. Preconditioning techniques for the coupled Stokes–Darcy problem: Spectral and field-of-values analysis. Numer. Math. 2022, 150, 257–298. [Google Scholar] [CrossRef]
- Kim, J.; Ahmad, S. On the preconditioning of the primal form of TFOV-based image deblurring model. Sci. Rep. 2023, 13, 17422. [Google Scholar] [CrossRef]
- Saad, Y. A flexible inner-outer preconditioned GMRES algorithm. SIAM J. Sci. Comput. 1993, 14, 461–469. [Google Scholar] [CrossRef]
- Cao, Y.; Jiang, M.Q.; Zheng, Y.L. A splitting preconditioner for saddle point problems. Numer. Linear Algebra Appl. 2011, 18, 875–895. [Google Scholar] [CrossRef]
- Knight, F.M.; Wathen, A.J.; Trefethen, L.N. The BiCGSTAB method for solving large sparse linear systems. SIAM J. Sci. Stat. Comput. 1994, 15, 237–248. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2003; pp. 1–462. [Google Scholar]
- Van der Vorst, H.A. BiCGSTAB: A fast and robust iterative solver for large, sparse, non-symmetric linear systems. Numer. Linear Algebra Appl. 2003, 10, 79–94. [Google Scholar]
- Chen, J.; Li, Y.; Zhang, Z. Efficient implementation of BiCGSTAB for large-scale sparse linear systems with preconditioning. J. Comput. Appl. Math. 2018, 334, 343–356. [Google Scholar]
- Bouyghf, A.; Abdessalem, M. An enhanced version of the BiCGSTAB method with global and block orthogonal projectors. Numer. Linear Algebra Appl. 2023, 30, 201–221. [Google Scholar]
- Tadano, Y.; Kuramoto, H. A block-wise updating method for BiCGSTAB with applications to multiple right-hand sides. J. Appl. Comput. Math. 2019, 6, 100–120. [Google Scholar]
- Ahmad, S. Optimized five-by-five block preconditioning for efficient GMRES convergence in curvature-based image deblurring. Comput. Math. Appl. 2024, 175, 174–183. [Google Scholar] [CrossRef]
- Lysaker, M.; Osher, S.; Tai, X.C. Noise removal using smoothed normals and surface fitting. IEEE Trans. Image Process. 2004, 13, 345–1457. [Google Scholar] [CrossRef]
- Brito, C.; Chen, K. Multigrid algorithm for high order denoising. SIAM J. Imaging Sci. 2010, 3, 363–389. [Google Scholar] [CrossRef]
- Rui, H.; Pan, H. A block-centered finite difference method for the DarcyForchheimer model. SIAM J. Numer. Anal. 2012, 5, 2612–2631. [Google Scholar] [CrossRef]
- Vogel, C.R.; Oman, M.E. Fast, robust total variation-based reconstruction of noisy, blurred images. IEEE Trans. Image Process. 1998, 7, 813–824. [Google Scholar] [CrossRef]
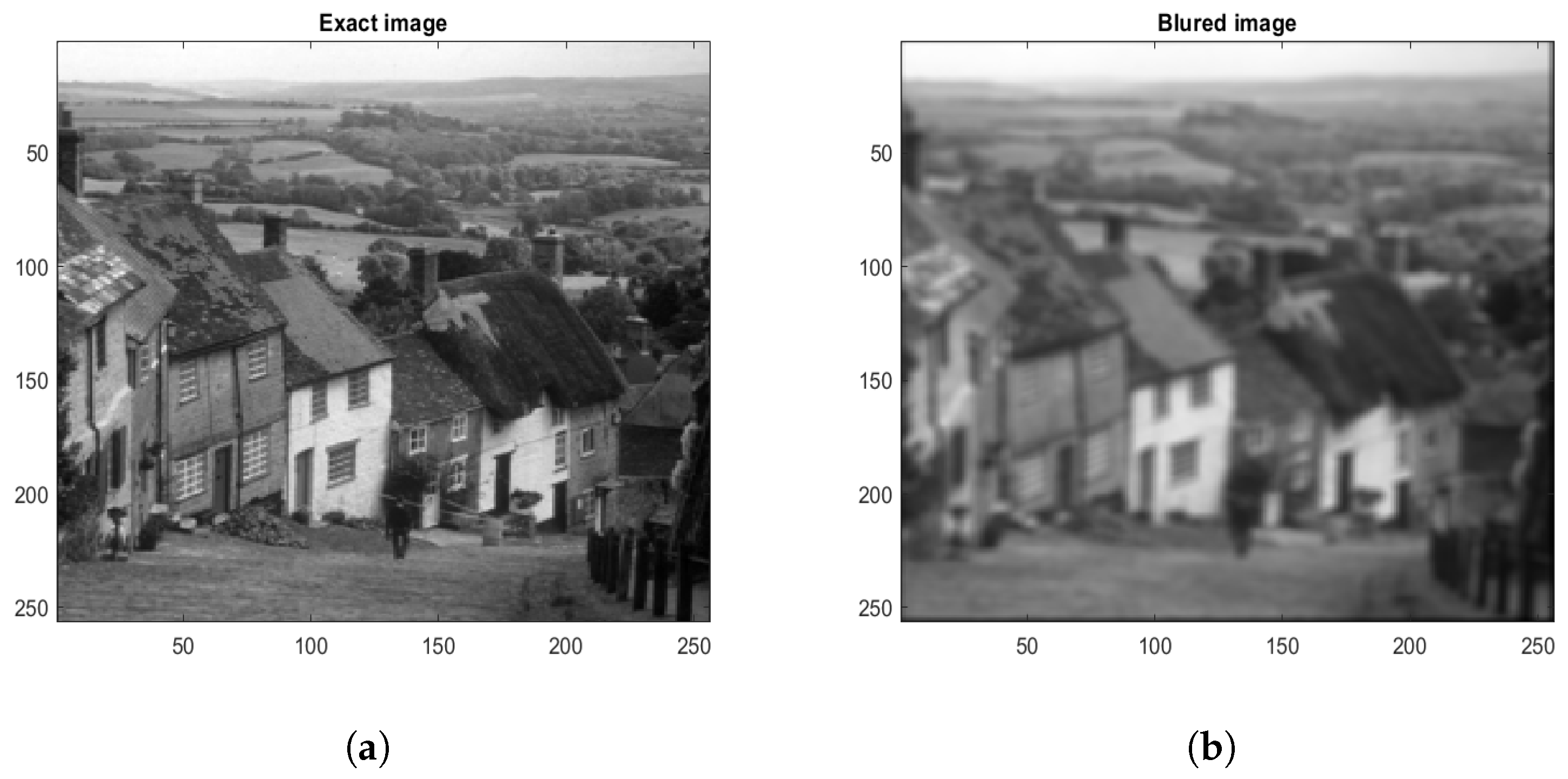






| Blurry PSNR | Method | Deblurred PSNR | Error | Iterations | CPU Time | |
|---|---|---|---|---|---|---|
| 128 | 24.7144 | GMRES | 48.0376 | 46 | 71.4365 | |
| BiCGSTAB | 48.4597 | 22 | 21.7596 | |||
| 49.7696 | 1(2) | 18.1246 | ||||
| RPBiCGSTAB | 49.8697 | 3 | 16.1349 | |||
| 256 | 24.5531 | GMRES | 47.9646 | 56 | 91.2974 | |
| BiCGSTAB | 47.4377 | 28 | 27.7834 | |||
| 48.7696 | 1(3) | 26.3425 | ||||
| RPBiCGSTAB | 48.9845 | 4 | 19.3124 | |||
| 512 | 24.6983 | GMRES | 44.2732 | 83 | 106.7548 | |
| BiCGSTAB | 44.5315 | 37 | 41.2586 | |||
| 46.7696 | 2(5) | 27.2659 | ||||
| RPBiCGSTAB | 46.9897 | 6 | 22.2791 |
| Blurry PSNR | Method | Deblurred PSNR | Error | Iterations | CPU Time | |
|---|---|---|---|---|---|---|
| 128 | 28.4896 | GMRES | 49.4596 | 48 | 81.5213 | |
| BiCGSTAB | 49.4789 | 24 | 31.8512 | |||
| 50.4578 | 1(3) | 19.5963 | ||||
| RPBiCGSTAB | 50.4586 | 3 | 16.1349 | |||
| 256 | 28.4596 | GMRES | 48.4786 | 58 | 95.4963 | |
| BiCGSTAB | 48.3125 | 29 | 29.1259 | |||
| 49.4369 | 1(4) | 28.1256 | ||||
| RPBiCGSTAB | 49.1425 | 5 | 19.1456 | |||
| 512 | 28.5429 | GMRES | 45.4963 | 85 | 109.8549 | |
| BiCGSTAB | 45.4236 | 41 | 45.2369 | |||
| 47.1236 | 2(6) | 29.5896 | ||||
| RPBiCGSTAB | 47.1456 | 7 | 21.1263 |
| Blurry PSNR | Method | Deblurred PSNR | Error | Iterations | CPU Time | |
|---|---|---|---|---|---|---|
| 128 | 23.2189 | GMRES | 47.1253 | 45 | 81.1258 | |
| BiCGSTAB | 47.8963 | 22 | 31.1149 | |||
| 48.2589 | 1(2) | 18.1858 | ||||
| RPBiCGSTAB | 48.1589 | 3 | 16.0012 | |||
| 256 | 23.1256 | GMRES | 46.1256 | 55 | 91.0025 | |
| BiCGSTAB | 46.4589 | 28 | 27.7034 | |||
| 47.7589 | 1(3) | 26.0421 | ||||
| RPBiCGSTAB | 47.1526 | 6 | 17.0125 | |||
| 512 | 23.1079 | GMRES | 43.5896 | 82 | 106.2109 | |
| BiCGSTAB | 43.8596 | 37 | 41.2586 | |||
| 45.5896 | 2(7) | 27.2307 | ||||
| RPBiCGSTAB | 45.1478 | 8 | 20.4839 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalid, R.; Ahmad, S.; Ali, I.; De la Sen, M. Enhanced BiCGSTAB with Restrictive Preconditioning for Nonlinear Systems: A Mean Curvature Image Deblurring Approach. Math. Comput. Appl. 2025, 30, 76. https://doi.org/10.3390/mca30040076
Khalid R, Ahmad S, Ali I, De la Sen M. Enhanced BiCGSTAB with Restrictive Preconditioning for Nonlinear Systems: A Mean Curvature Image Deblurring Approach. Mathematical and Computational Applications. 2025; 30(4):76. https://doi.org/10.3390/mca30040076
Chicago/Turabian StyleKhalid, Rizwan, Shahbaz Ahmad, Iftikhar Ali, and Manuel De la Sen. 2025. "Enhanced BiCGSTAB with Restrictive Preconditioning for Nonlinear Systems: A Mean Curvature Image Deblurring Approach" Mathematical and Computational Applications 30, no. 4: 76. https://doi.org/10.3390/mca30040076
APA StyleKhalid, R., Ahmad, S., Ali, I., & De la Sen, M. (2025). Enhanced BiCGSTAB with Restrictive Preconditioning for Nonlinear Systems: A Mean Curvature Image Deblurring Approach. Mathematical and Computational Applications, 30(4), 76. https://doi.org/10.3390/mca30040076







