1. Introduction
The Partially Linear Regression Model (PLRM), introduced by [
1], serves as a versatile tool for utilizing the advantage of both parametric linear models and nonparametric regression models. It allows for the modeling of complex relationships by incorporating both linear and nonlinear components, thereby offering greater flexibility and interpretability across various scientific disciplines, including social sciences, biology, and economics. Formally, the PLRM is defined as:
where
are the observations of the response variable,
and
are the values of the explanatory variable,
is an unknown
k-dimensional parameter vector to be estimated,
is an unknown smooth function, and
are assumed to be uncorrelated random variables with mean zero and a common variance
and independent of the explanatory variables. Note also that the observations of
depend linearly on the entries of
and nonlinearly on the values of a univariate variable
. The PLRM can be re-expressed in matrix and vector form:
where
,
is an (
) design matrix with
denoting the
i.th
dimensional row vector of the design matrix
X, and
and
are random error vectors with
and
. For more discussion on Model (1), see [
2,
3,
4], among others. Since it was initially presented in [
1], this model has been very popular and is frequently used in the social, biological, and economic sciences. The PLRM generalizes both the parametric linear regression model and nonparametric regression model. When the
, Model (1) reduces to the linear regression model
, when the
model (1) becomes a nonparametric regression model
with a univariate covariate. In addition, because PLRMs contain both linear and nonlinear components, they are more flexible than linear models. In this work, we are interested in estimating parameter vector
and function
.
Estimating the parameters and the smooth function in PLRM has been a focal point of research, with various methodologies proposed to enhance estimation accuracy and model interpretability. Early contributions [
4,
5] utilized kernel smoothing techniques for estimating the nonparametric component, laying the groundwork for subsequent advancements.
The advent of regularization methods introduced in [
6,
7] revolutionized parameter estimation by addressing issues such as multicollinearity and high-dimensionality through penalty functions. In particular, the authors of [
8,
9] explored penalized least squares in semiparametric models, emphasizing the integration of penalty functions with kernel smoothing to enhance estimator performance (see also [
10,
11,
12,
13]).
Adaptive methods, such as the Adaptive Lasso (aLasso) introduced in [
14], have been incorporated into PLRM frameworks to improve variable selection consistency. Moreover, SCAD [
15] and MCP [
16] penalties have been employed to mitigate the bias inherent in
penalties, providing more accurate parameter estimates in complex models. Recent studies [
17,
18] highlight the asymptotic properties of penalized estimators in semiparametric regression, emphasizing the significance of penalty strategies in PLRM. Challenges in balancing bias and variance persist, particularly in sparsity contexts with multicollinearity.
In regression problems, multicollinearity emerges when variables are highly correlated with each other and the dependent variable. This situation inflates confidence intervals, weakens parameter estimates, and leads to less reliable predictions. It also raises sampling variance, reducing accuracy for both inference and prediction. To counter these challenges in PLRMs, we integrate shrinkage estimation with penalty functions to bolster robustness and manage both multicollinearity and variable selection:
We tackle variable selection and multicollinearity in Model (1), which features strongly correlated covariates, using six penalty functions: Ridge, Lasso, aLasso, SCAD, Elastic Net, and MCP.
We then review and compare these methods, highlighting their strengths, limitations, and uses within PLRMs.
To further enhance parameter estimation, we incorporate shrinkage estimation techniques—both standard and positive shrinkage estimators—into the penalty-based framework.
Finally, kernel smoothing via penalized least squares is employed to estimate both the parametric (linear) and nonparametric (smooth) components of the model.
The remainder of this paper is structured as follows. At the end of this section, we summarized the background on penalty functions and partially linear models and their integration.
Section 2 describes the kernel smoothing method.
Section 3 introduces the kernel-type ridge estimator. In
Section 4, we discuss penalty functions and shrinkage estimators based on kernel smoothing.
Section 5 presents the evaluation metrics for both parametric and nonparametric components.
Section 6 outlines the estimators’ asymptotic properties.
Section 7 details the Monte Carlo simulations.
Section 8 compares the performance of our proposed estimators on real data. Finally,
Section 9 provides concluding remarks and includes supplementary technical materials.
Background
In this section, we present a relevant literature review of partially linear regression models (PLRMs) and show why penalty functions and shrinkage estimators are essential for handling challenges like multicollinearity, high-dimensional data, and complex nonlinearities. We also explain how kernel smoothing complements these approaches by capturing intricate patterns in the data based on the previous studies. Altogether, these methods offer a strong foundation for building reliable and flexible statistical models.
Partially Linear Regression Models (PLRMs) are a cornerstone of semiparametric statistics, offering a powerful way to model relationships that are not fully captured by purely parametric or nonparametric approaches. They blend the interpretability of linear models with the flexibility of nonparametric methods, making them ideal for data with both linear and nonlinear components. Their ability to isolate certain covariate effects while accommodating nonlinearities has led to widespread use in fields such as economics, biostatistics, and environmental science [
19]. Recent developments have expanded their scope to high-dimensional, longitudinal, and survival data [
20,
21].
Regularization methods, particularly those using penalty functions, have revolutionized regression analysis by tackling issues like multicollinearity, high dimensionality, and model selection. By constraining coefficient magnitudes, these methods shrink coefficients toward zero and improve model stability. Different penalty functions yield diverse estimators suited to various data characteristics and research goals.
Ridge regression, pioneered in [
22], is well-established, yet its application in high-dimensional contexts and its ties to Bayesian methods continue to be studied [
23]. Lasso has also evolved substantially [
6], with research on its consistency in variable selection, high-dimensional settings, and extensions to generalized linear models [
24]. Ahmed and colleagues contributed to Lasso’s development in PLRMs using Stein-type shrinkage estimators, especially under multicollinearity [
25].
Building on the adaptive Lasso (aLasso) [
26], researchers have explored data-driven weights for improving variable selection and estimation. For SCAD, recent work has focused on high-dimensional data, quantile regression, and robust estimation [
27]. The researchers applied SCAD along with the other penalty functions and with shrinkage estimators in PLRMs, showing its effectiveness in handling outliers [
10]. MCP, initially studied in [
16], has inspired efficient algorithms and further theoretical exploration [
25]. Elastic Net, proposed in [
26], has also gained traction in areas like genomics, imaging, and finance, where it handles correlated predictors well [
7]. Its benefits are used for balancing bias and variance in PLRMs [
11].
Beyond these penalty-based approaches, shrinkage estimation techniques—particularly Stein-type estimators—offer another route. The authors of [
28] investigated partially linear models by splitting the coefficient vector into main and nuisance effects and comparing shrinkage, pretest, and absolute penalty estimators. Their results show that a Stein-type shrinkage estimator uniformly outperforms the conventional least squares approach, especially when the nuisance parameter space is large, while the pretest estimator only offers benefits in a limited region. These methods shrink coefficients toward a chosen target, thereby reducing variance and mitigating noise [
29,
30,
31]. Further, Ahmed’s work demonstrates that these techniques can improve estimation accuracy and interpretability in partially linear regression models [
8,
32,
33]. Meanwhile, kernel smoothing remains central to nonparametric estimation for capturing nonlinear relationships, with advances such as adaptive bandwidth selection [
34] and its integration with penalty and shrinkage methods [
35]. The authors of [
36] showed via simulation that applying Stein-type shrinkage to the parametric components of the semi-nonparametric regression model [
37] enhanced accuracy. The authors of [
38] proposed a two-stage approach using LASSO/Elastic-Net for variable selection followed by post-selection shrinkage estimation to improve predictions in high-dimensional sparse linear regression models, while the authors of [
10] introduced shrinkage-type estimators for reliability and stress–strength parameters from progressively censored data that outperformed MLEs in simulations and industrial applications. Additional insights on shrinkage estimators are provided in [
31,
39,
40,
41,
42,
43,
44].
Combining penalty functions with kernel smoothing has become a potent strategy for complex data in PLRMs. This approach refines the parametric part through penalty-driven selection and shrinkage, while kernel smoothing captures nonlinearities. Recent studies highlight theoretical and practical benefits, including improved estimation accuracy and consistency in variable selection under multicollinearity or high dimensionality [
45]. The advanced penalized kernel smoothing in PLRMs using shrinkage estimators is shown in [
32], showing strong performance in simulations and real data. That work illustrates the advantages of using penalties like aLasso and shrinkage estimation alongside kernel smoothing, especially with high-dimensional covariates and intricate nonlinearities.
2. Estimation Based on Kernel Smoothing
Let us first consider the nonparametric estimation of the unknown regression function
in Model (1). For simplicity, we assume that
is known from Equation (1). The relationship between
and
in this instance may be represented as
The nonparametric part of the semiparametric model is equivalent to Equation (4). This results in the Nadaraya-Watson estimator, commonly known as the kernel estimator, which was proposed in [
46,
47], as mentioned in [
4]:
where
is a kernel smoothing matrix with
-th entries
and where
is a smoothing parameter (or bandwidth), as shown by:
To estimate
, kernel smoothing (regression) uses appropriate weights
, as shown in Equation (4). The kernel function
with a smoothing parameter
, which defines the size of the neighborhood around
, directs the weights assigned to the observations
[
48,
49]. The kernel or weight function
in Equation (6) has the properties of
and
. The kernel function is chosen to give the closest observations the most weight and the farthest from
the least weight.
The following partial residuals may be obtained via the matrix and vector forms of Model (2) in matrix form:
where
and
Hence, a transformed set of data based on kernel residuals is what we obtain as a result. The following weighted least squares (WLS) criterion is obtained by considering these partial residuals for the vector
:
The result for the criterion
provided in Equation (8) is easily demonstrated to be similar to the solution of ordinary least squares (OLS)
Additionally, revising the steps for
reduces Equation (5) to the form:
Another way to express Equation (10) in a matrix is as follows:
Thus, our estimation for
becomes:
for the hat (projection) matrix
3. Kernel Type Ridge Estimator in Semiparametric Model
For the sake of this paper, we limit our attention to kernel smoothing estimators of vector parameter
and unidentified smooth function
in a semiparametric model. The corresponding estimators
and
are based on Model (2) for a given bandwidth parameter
. By multiplying
on both sides of Model (2), we obtain the following model:
where
,
and
.
These considerations show that Model (13) is the optimal solution for obtaining vector
estimator, corresponding to the parametric part of the semiparametric Model (2). For the ridge regression problem, this model provides the following penalized least squares (PLS) criterion:
where
denotes a positive shrinkage parameter that regulates the severity of the penalty. The solution of the minimization problem (14) can be written as follows as a ridge-type kernel smoothing estimator (see [
18]), similar to [
22], but modified based on partial residuals obtained using smoothing matrix
The ridge-type kernel smoothing estimate simplifies to an ordinary least squares estimation problem when
on the basis of the local residuals specified in Equations (9) and (11). Additionally, to estimate the unknown function
, we imitate Equation (11) and define it.
Thus, in semiparametric Model (2), the estimator (16) is defined as the ridge type kernel estimator of unknown function .
4. Penalty Functions and Shrinkage Estimators
Many penalty functions for linear and generalized regression models have been studied [
11,
32]. Here, we consider the MCP, Lasso, SCAD, aLasso, and ElasticNet functions and shrinkage techniques additionally. Note that ElasticNet is a regularized regression technique that linearly combines the
and
penalties of the Lasso and ridge regression methods, respectively.
In this paper, we introduce the kernel smoothing estimators based on several penalties for the semiparametric regression model’s components. For a given penalty function and tuning parameter
, the general form of the penalty estimators is defined by the following penalized least squares
criterion:
where
denotes the penalty function based on the shrinkage (or tuning) parameter
This parameter needs to be selected with any selection criteria.
Note that the bridge estimator [
50] is the vector
that minimizes the Lasso and Ridge penalties in Model (17). However, SCAD, ElasticNet, aLasso, and MCP have different penalties, which are introduced later in this study. Note that
fulfills the
norm of the regression coefficients
because of the penalty functions used.
Hence, for various values of the shrinkage parameter , different penalty estimators that correspond to the parametric and nonparametric parts of the semiparametric model can be defined.
4.1. Estimation Procedure for the Parametric Component
According to Model (17), it is possible to obtain ridge estimates for the parametric component for
by minimizing the following penalized residual sum of squares.
where
is the
-th row of the matrix
, and
is the
i-th observation of
. Note that the regularization estimate in solution (18) matches that in (15). Alternative methods to ridge are described below.
Lasso: The authors of [
6] proposed Lasso, a regularization method that uses the
penalty for estimation and variable selection. The modified kernel smoothing estimators based on the Lasso penalty can be defined as
The absolute penalty term prevents Lasso from having an analytical solution, despite the apparent simplicity of Equation (19).
aLasso: The authors of [
14] proposed using adaptive weights on
penalties on the regression coefficients to modify the Lasso penalty. The term “aLasso” refers to this weighted Lasso with oracle properties. The kernel smoothing estimator
using aLasso penalty is defined as follows:
where
is a weight function given by
Notably, is an appropriate estimator of . In addition, an ordinary least squares (OLS) estimate can be used as a reference value. After the OLS estimate is obtained, is selected, and the weights are computed to obtain the adaptive-Lasso estimates in (20).
SCAD: The Lasso method’s penalty term increases linearly with the regression coefficient’s size, leading to highly biased estimates for coefficients with large values. To address this issue, the authors of [
15] proposed a
SCAD penalty that can be obtained by replacing
in (18) with
A modified kernel smoothing estimator
based on the
SCAD penalty can be expressed as
where
is the
SCAD penalty defined by
The penalty parameters in this case are and , where and is the indicator function. When , (22) is equivalent to the penalty.
ElasticNet: ElasticNet is a penalized least squares regression method proposed in
[26] that is widely used for regularization and automatic variable selection to choose groups of correlated variables. It combines the
and the
penalty term, where the
penalty term ensures sparsity, whereas the
penalty term selects correlated variable groups. Accordingly, the modified kernel-smoothing estimator
using an ElasticNet penalty is the solution to the following minimization problem:
In the expression above, the positive regularization parameters are and . Note that (23) ensures that the estimates correspond to the parametric part of the semiparametric regression Model (2).
MCP: The authors of [
16] introduced
MCP as a different method to obtain less biased estimates of nonzero regression coefficients in a sparse model. For given regularization parameters
and
, the kernel smoothing estimator
based on the
MCP penalty can be defined as
where
is the
MCP penalty expressed as
4.2. Shrinkage Estimators
Shrinkage estimation offers a robust method for parameter estimation, especially in sparse environments where traditional methods may face high variance or multicollinearity. This section introduces standard and positive shrinkage estimators to improve accuracy and stability. Shrinkage estimators balance full model estimators
, which use extensive predictors, with sub model estimators
, which focus on fewer, significant predictors using any of the introduced penalty functions (see [
32]). To better understand the shrinkage process, it is necessary to partition design matrix X into subsets that correspond to significant and less significant predictors. Let X represent the n × k design matrix, where n is the number of observations, and k is the total number of predictors. We partition X into two submatrices:
where
corresponds to the subset of significant nonzero predictors (
predictors) and
contains the remaining predictors (
) where
. This partitioning ensures that the shrinkage process selectively regularizes the coefficient associated with less significant predictors while preserving the interpretability of the model.
After optimizing
and
, we can define shrinkage estimator
and the positive part of the shrinkage estimator to avoid the over-shrinking of the regression coefficients
as follows:
where
,
represents the number of sparse parameters that are detected by the penalty functions to estimate
,
is the distance measure which can be defined as
with sparse subset of regression coefficients denoted by
, model variance
,
matrix of partial residuals of associated predictors with
and the projection matrix
where
is the partial residuals associated with the
significant coefficients. Finally,
is again the shrinkage parameter. Some of the advantages of using shrinkage estimators are as follows. Introducing the bias through the shrinkage, these estimators reduce variance and leading in the smaller Mean Squared Error (MSE) values, which means better prediction accuracy. In addition, shrinkage techniques shrink the coefficients in a controlled manner, which preserves interpretability.
Building upon the Shrinkage Estimation framework introduced above, we integrate both standard and Positive Shrinkage Estimators into the penalty estimation strategies. These estimators provide an additional layer of regularization, enhancing the estimation accuracy for sparse models. The estimation procedure involves the following.
Parametric Component Estimation: We utilize the respective penalty functions (Ridge, Lasso, aLasso, SCAD, ElasticNet, MCP) to estimate the parameter vector .
Shrinkage Application: We apply the shrinkage techniques to obtain ordinary stein-type shrinkage or positive shrinkage estimator to refine the parameter estimates.
Nonparametric Component Estimation: We estimate the smooth function
using the refined parameter estimates via kernel smoothing as described in Equation (25).
This comprehensive approach leverages the strengths of both penalty functions and shrinkage estimators, offering a robust estimation framework for PLRM. The incorporation of shrinkage estimators offers several advantages. By introducing a controlled bias, these estimators reduce the variance of parameter estimates, leading to more stable and reliable predictions. Additionally, they enhance model interpretability by focusing on significant predictors while mitigating the effects of multicollinearity. Moreover, the positive shrinkage estimator provides a practical safeguard against excessive regularization, striking a balance between bias and variance.
4.3. Estimation Procedure for the Nonparametric Component
For the parametric part of the semiparametric model in (2), modified kernel smoothing estimates based on various penalties are provided by Equations (18)–(24). Analogous to that of (16), the estimation of the nonparametric part of the same model can be constructed via the vector of estimated parametric coefficients
provided in (19). On the basis of the Lasso penalty of the unknown function, we obtain the transformed local estimates as follows:
as described in the previous section. Importantly, local estimates of the nonparametric component based on the adaptive-Lasso penalty are derived and are symbolically given as
in Equation (26), where
, defined in (20), is written in place of
. Similarly, for the nonparametric part of the semiparametric Model (2), the modified local kernel estimators
,
, and
based on the SCAD, ElasticNet, and MCP penalties, respectively, are obtained by replacing
in (26) with
,
, and
.
To better understand the adaptation of the penalty functions to the estimation process of the partially linear Model (1), a generic algorithm is introduced. As mentioned previously, to obtain a specific estimator on the basis of a determined penalty function, the corresponding penalty term is used in Algorithm 1. Therefore, the output estimators are denoted as
to generalize the algorithm. For example, if we obtain the Lasso estimator of the parametric components in Model (1), first,
is found to minimize (19), then
is obtained by using the vector of estimated parametric coefficients
. A similar path is followed for the remaining estimators. The algorithm describing their findings is as follows:
| Algorithm 1. Computation of penalty estimators. |
Input: Data matrix of parametric component , data vector , and response vector .
Output: Pair of estimates based on a certain penalty function
1: Select an appropriate bandwidth using a predetermined criterion and compute the smoother matrix , as defined in (6).
2: Compute the partial residuals and
3: To minimize determine the shrinkage parameter by a predetermined criterion.
4: Partition the partial residuals of in form , as defined in Section 4.2.
5: Apply shrinkage estimators , and based on used penalty functions
6: Find the estimate of parametric component associated with the contains and
7: Estimate the nonparametric smooth function as follows:
8: Return . |
5. Measuring the Quality of Estimators
This section describes several performance metrics that can be used to assess the performance of the modified semiparametric kernel smoothing estimators based on the penalty functions and shrinkage estimators defined in
Section 4. Note that the estimators are indicated by the acronyms in parentheses. Each estimator’s performance for the parametric component, nonparametric component, and overall estimated model is examined. Consequently, the performance metrics are explained in the following section.
5.1. Evaluation of the Parametric Component
The performance of a method is related to its ability to estimate the data. Note that the bias and variance of a penalty estimator are measured simultaneously via the mean squared error matrix. Some metrics are defined in the following section.
MSE: This value is calculated by adding the variance and squared bias, which is provided by
where
is the vector of the estimated regression coefficients determined by either of the methods. The key information regarding the quality standards for estimation is provided by Equation (19). To evaluate the risk more accurately via the MSE, a scalar variant of the MSE (SMSE) is utilized, which yields an estimator’s average quality score:
Additionally, the relative efficiencies of the methods for estimating can be easily obtained via (28). To do this, the relative efficiency (RE) is defined in Definition 1.
Definition 1. Let and denote the two distinct estimation methods for , and the estimators are shown as and , respectively. The formula for RE is as follows:
Here, means thatis more efficient than.
Root mean squared error (): The RMSE is simply the square root of the MSE. The formula for calculating the estimated regression coefficients
is as follows:
where
is the estimate of
obtained via one of the methods described in this paper, as defined in (28). To obtain the RMSE score for each estimator,
is replaced with
and
.
5.2. Evaluation of the Nonparametric Component
To evaluate the nonparametric part of Model (1),
can also be used. Suppose that
is any of the estimators of the nonparametric component in Model (1). That is, let us assume that it is equivalent to one of the estimators
and
defined in
Section 3. Therefore, the MSE is calculated as follows:
To compare how well each of the six methods estimates the nonparametric component, the relative
(
) is used. The formula for
is computed as follows:
6. Asymptotic Analysis
Suppose that
and
is the estimate of
, where
is any of the proposed estimators, which are Ridge, Lasso, aLasso, SCAD, ElasticNet, and MCP. This section defines the asymptotic distributional risk (ADR) of our full model and selected model estimators. Our primary objective is the performance of these estimators when
; for this reason, we consider a sequence
given by
Now, using a positive definite matrix (p.d.m.)
W, we define a quadratic loss function as follows:
Now, under
, we can define the asymptotic distribution function of
as
where
is nondegenerate. Hence, we can define the ADR of
as follows.
where
V is the dispersion matrix for the distribution
.
Assumption 1. We establish two regularity conditions as follows:
- (i).
where is the ith row of
- (ii).
where is a finite positive-definite matrix.
By Lemma 1, which is defined below, with assumed regularity conditions and local alternatives, the ADRs of the estimators under are given as:
Theorem 1. ADR () =ADR ) =+ .
Lemma 1 enables us to derive the result of Theorem 1 in this study.
Lemma 1.
where “
” denotes the convergence in the distribution. See the proof in [
2].
7. Simulation Studies
In this section, we conduct a thorough simulation study to assess the finite-sample performance of the aforementioned six semiparametric estimators proposed for a partially linear model. These estimators are compared to each other to evaluate their performance. R-software [
51] was used for all calculations. A description of the simulation design and data generation is as follows.
Design of the Simulation: The simulations are carried out as follows:
- i.
Samples of size
- ii.
Two numbers of parametric covariates and 40
- iii.
Two correlation levels
- iv.
The number of replications is 1000.
In addition, we generated zero and nonzero coefficients of the model to enable our absolute penalty functions to select significant variables. As mentioned above, each possible simulation design was repeated 1000 times to detect significant findings. Finally, the evaluation metrics mentioned in
Section 5 were used to assess the performance of the proposed estimators.
Data generation: We generated the explanatory variables
via the following equation:
where
are independent standard normal pseudorandom numbers and
represents the level of collinearity among the explanatory variables. The two levels of collinearity assumed in this study are 0.50 and 0.90, as denoted above. These variables are standardized so that
and
are in correlation forms. The
observations for the response variable
are generated by
where
, the nonparametric function
with
, and
. It is understood from this model that when
explanatory variables are considered, there are 6 nonzero
s to be estimated and
sparse coefficients. If
explanatory variables are considered, there will be 6 nonzero
s to be estimated and
sparse coefficients.
The Monte Carlo simulation approach involves repeatedly generating datasets according to the specified Partially Linear Regression Model (PLRM) under different conditions (sample size, correlation). For each generated dataset, all estimation strategies are applied, and their performance metrics are calculated. This process is replicated 1000 times with different random errors to ensure stable results, allowing us to assess the average performance and variability of the estimators under the controlled simulation settings.
In this study, to obtain the optimal value of
, we consider modified cross-validation (CV), which is generalized cross-validation (GCV). The main idea of the
criterion is to replace the factor
with the mean value, that is,
. In this case, the
value is obtained as follows:
where
represents the sum of the diagonal values of the matrix
, that is, its trace. Finally, to obtain the optimum shrinkage parameter
in the objective function given in (17), we use a five-fold cross-validation method.
In this simulation study, we analyze 12 different simulation configurations and attempt to display all of them. In this sense, the simulation study results are shown separately for the parametric and nonparametric components.
7.1. Analysis of the Parametric Component
This subsection examines the estimation of the parametric component of a semiparametric model, with the results shown in the following tables for all simulations. In addition to the estimation, the performance of the estimators is evaluated via the performance metrics mentioned in
Section 5. The results are presented in the following tables and figures.
Table 1,
Table 2 and
Table 3 detail the performance scores (MSE, RMSE, RE, SMSE) for the parametric component across different simulation setups.
In terms of general observations that can be concluded from the tables, as sample size (n) increases, the MSE and RMSE values generally decrease for all estimators, indicating improved accuracy. Higher multicollinearity ( = 0.9) tends to worsen the performance of all estimators compared to lower multicollinearity ( = 0.5). The MCP and SCAD penalty functions, along with the positive shrinkage estimator () and shrinkage estimator (), often demonstrate superior performance in terms of lower MSE and RMSE, especially in scenarios with high multicollinearity or smaller sample sizes.
In detail, Ridge () performs relatively poorly compared to other methods, particularly when multicollinearity is high. The Lasso () and aLasso () methods show moderate performance. aLasso tends to be slightly better than Lasso. ElasticNet () performs similarly to Lasso and aLasso. MCP () and SCAD () often exhibit the best performance among the penalty methods, with lower MSE and RMSE values, especially in challenging scenarios. Shrinkage estimators ( and ) consistently perform well, often outperforming the other methods, especially when the sample size is small and multicollinearity is high.
Figure 1 illustrates how the Mean Squared Error (MSE) of the parametric component estimators changes with varying levels of multicollinearity (
). Notably, as multicollinearity increases, so does the MSE for all estimators, which aligns with the data presented in
Table 1,
Table 2 and
Table 3. However,
,
, and the shrinkage estimators, particularly the
, consistently exhibit lower MSE values compared to
,
,
, and
. This trend is particularly pronounced when multicollinearity is high (ρ = 0.9). The superior performance of MCP, SCAD, and shrinkage estimators under these challenging conditions is further emphasized by the relatively flat lines they exhibit in
Figure A3 in
Appendix A.3, suggesting robustness to an increasing number of predictors.
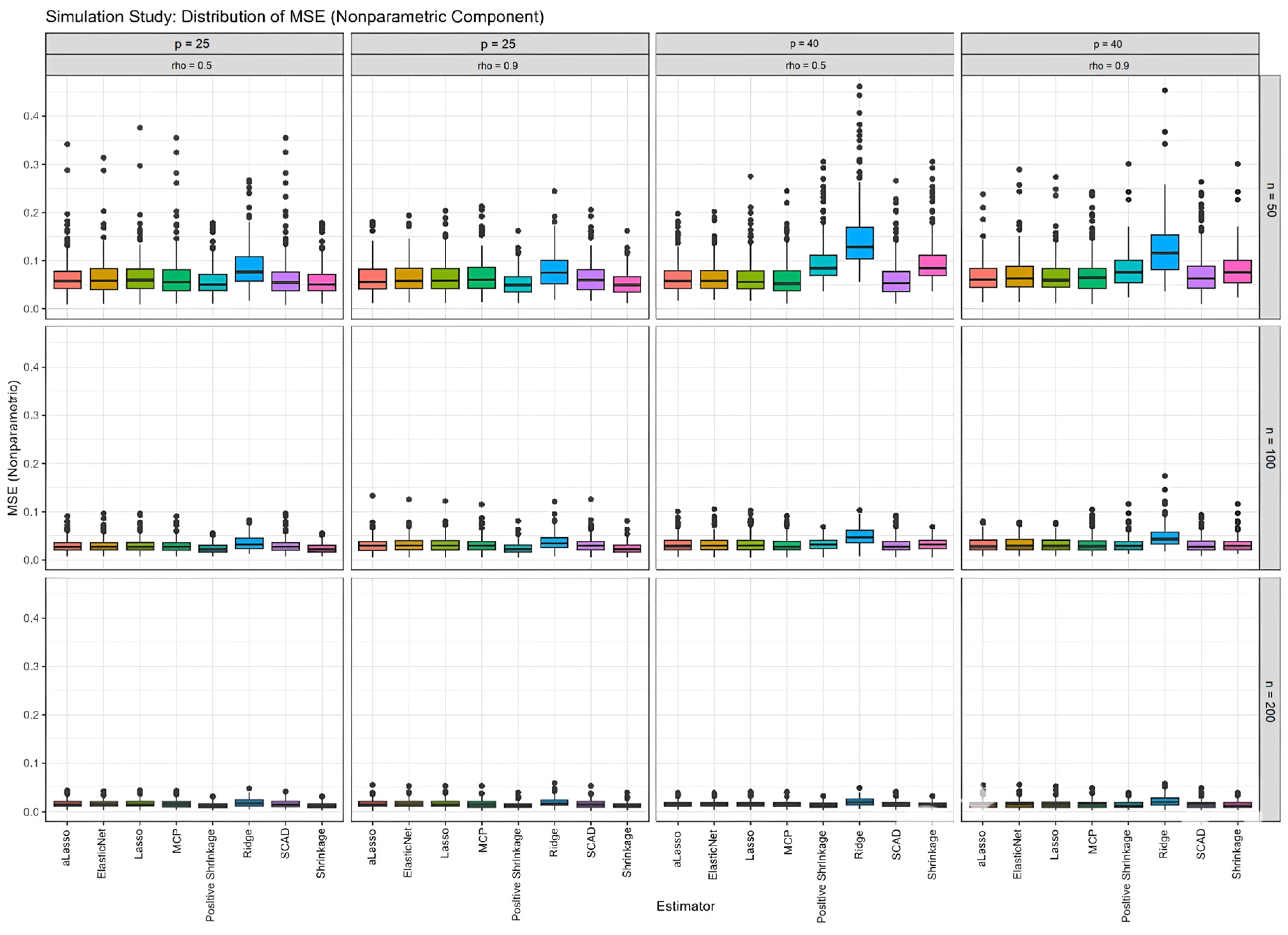
7.2. Analysis of the Nonparametric Component
This subsection examines the estimation of the nonparametric component of a semiparametric model, with the results shown in
Table 4 for all simulations. Furthermore, the performance scores of the proposed methods are measured via the MSE and RMSE metrics. In addition, the estimated curves obtained from all methods are examined using all the distinct configurations in
Figure 2 and
Figure 3.
Table 4 presents the performance scores for the nonparametric component estimators in a similar format to
Table 1,
Table 2 and
Table 3, which focuses on the parametric component. This table would quantify the accuracy and efficiency of each estimator in estimating the nonparametric function
under various simulation scenarios, varying sample size (
), number of predictors (
), and multicollinearity levels (
).
Based on the trends observed in
Figure 2,
Figure 3,
Figure A1 and
Figure A4, and the consistent findings in
Table 1,
Table 2 and
Table 3, it is highly probable that
Table 4 would further demonstrate the superior performance of
,
, and the shrinkage estimators (
and
), particularly in scenarios with high multicollinearity and smaller sample sizes. These estimators would likely exhibit lower MSE and RMSE values compared to others, indicating greater accuracy in estimating the nonparametric function and potentially higher RE values, suggesting greater efficiency relative to a reference estimator like
. The data in
Table 4 provide the numerical backbone to support the visual observations in
Figure 2 and the trends shown in
Figure 3,
Figure A1 and
Figure A4, solidifying the conclusion that
,
,
, and
offer significant advantages when estimating the nonparametric component of partially linear models.
Figure 2 provides a visual representation of how well each estimator captures the true nonparametric function,
When examining the fitted curves, especially under conditions of high multicollinearity (
) and small sample size (
), it becomes apparent that MCP (
), SCAD
, and the shrinkage estimators (
) produce curves that align more closely with the true function (represented by the black line) than those generated by Ridge (
), Lasso (
), aLasso (
), and ElasticNet (
). As the sample size increases, the differences become less visually striking, yet the advantage of
,
, and shrinkage estimators persists, particularly when multicollinearity is present. This visual observation is consistent with the quantitative data shown in
Figure 3, where these estimators consistently exhibit lower MSE values for the nonparametric component.
Figure 3 complements
Figure 2 by quantifying the MSE of the nonparametric component against varying levels of multicollinearity. The trend observed mirrors that of
Figure 1, i.e., MSE increases with multicollinearity for all estimators. However,
, consistently displays the highest MSE, while
,
, and the shrinkage estimators maintain lower MSE values across the board. This quantitative evidence corroborates the visual findings of
Figure 2, demonstrating that
,
, and shrinkage estimators (
and
,) provide more accurate estimates of the nonparametric function, especially when faced with correlated predictors. The relatively stable RMSE values of these better-performing estimators, even as the number of predictors increases, are shown in
Figure A4 and further support their robustness in
Appendix A.3.
8. Real Data
In this section, we implement our proposed six estimators, i.e., Ridge, Lasso, aLasso, SCAD, ElasticNet, and MCP, on real data. Our real data, Hitter’s dataset, can be obtained from the ISLR package in R. This dataset contains 322 rows and 20 variables. Three covariates, Division, League, and New League, which are not scalers, were deleted. The CN value obtained from this dataset is 5830, which indicates the presence of multicollinearity in the dataset. The remaining variables used for the estimation of a partially linear model are
,
,
,
,
and
. In addition, the performance of the estimators is compared, and the results are shown in
Table 5 and
Figure 4 and
Figure 5. Note that the logarithm of Salary is used as a response variable. From the visual inspection of the relationships between covariate and the response variable, the variable “
” has a significant nonlinear relationship with the response
. The remaining 15 predictor variables are added to the parametric component of the model. Hence, the partially linear model can be written as follows:
where
Therefore, there is an -dimensional covariate matrix for the parametric component of the model, and is the -dimensional vector of the regression coefficients to be estimated.
Table 5 quantifies the performance of each estimator on the Hitters dataset using RMSE, MSE, and RE, all based on the prediction of log(Salary). The Shrinkage and Positive Shrinkage estimators stand out with the lowest RMSE and MSE values of 0.413 and 0.171, and 0.405 and 0.164, respectively. This indicates that these two methods provide the most accurate predictions for log(Salary) on this dataset. Their superior performance is further underscored by their RE values, 1.950 and 2.025, respectively, which demonstrate that they are almost twice as efficient as the Ridge estimator, which has an RE of 1.000 and performs the worst on this metric.
aLasso also performs well, with an RMSE of 0.443, MSE of 0.196, and RE of 1.697, outperforming Lasso, SCAD, ElasticNet, and MCP. Lasso, SCAD, ElasticNet, and MCP exhibit moderate performance, with RMSE values ranging from 0.474 to 0.512 and RE values between 1.270 and 1.484. These results are consistent with the simulation study, which suggested that shrinkage estimators, particularly positive shrinkage, and aLasso are effective in handling multicollinearity and achieving good prediction accuracy.
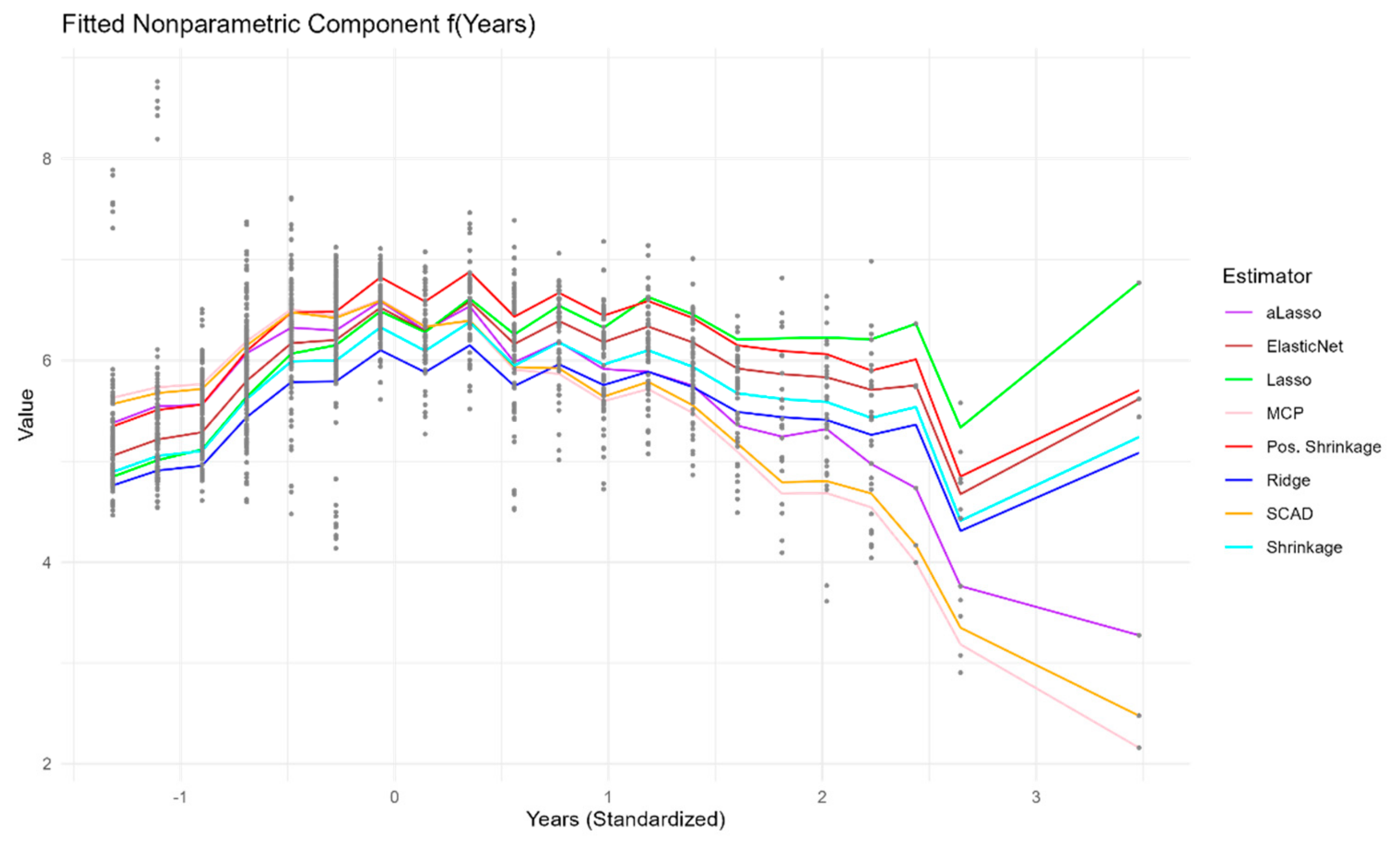
Figure 4 visually depicts the estimated nonparametric function f
for each estimator, revealing how they model the nonlinear relationship between a player’s standardized years of experience and their
. The curves generally capture an initial increase in log(Salary) as years of experience increase, followed by a plateau or a slight decrease for players with more years. Notably, the curves produced by Ridge, MCP, and the shrinkage estimators are relatively similar and smooth, suggesting a consistent estimation of the underlying nonlinear trend. Lasso, aLasso, and ElasticNet exhibit some deviations from this trend, particularly in the middle range of the “Years” variable, indicating potential sensitivity to noise or specific data points. SCAD produces a curve that is very different from the others. The black dots, representing the observed data points adjusted for the parametric component’s effect, provide a visual reference for assessing the fit of each curve. The variation in the shapes of the curves highlights the influence of the chosen estimation method on the estimated nonparametric relationship, emphasizing the importance of considering different estimators and their potential impact on the interpretation of the results.
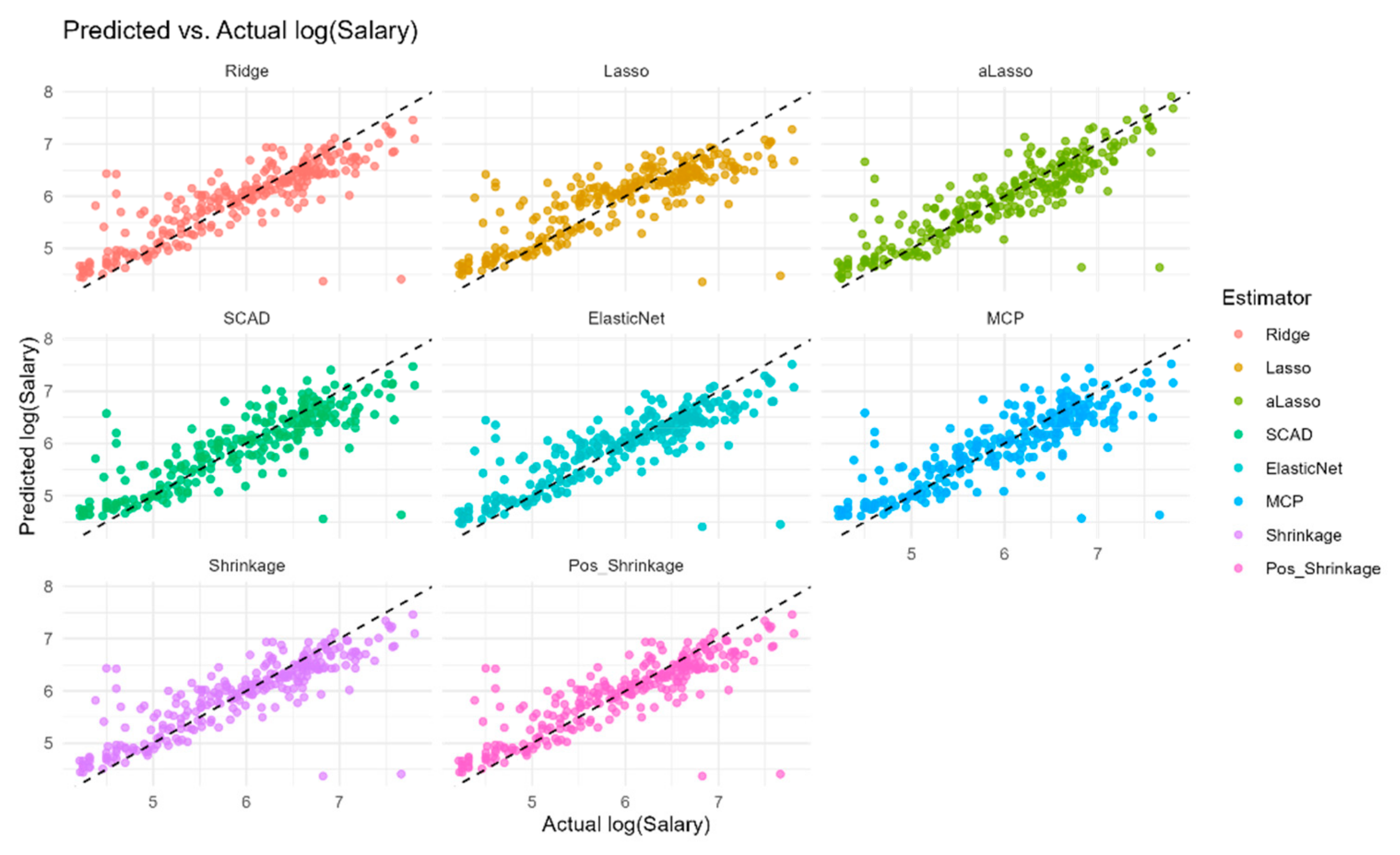
Figure 5 provides a visual comparison of the predicted log(Salary) values against the actual
values for each estimator, offering a direct assessment of their predictive accuracy. The points for Ridge, MCP, and the shrinkage estimators are more closely clustered around the diagonal line (
), indicating that their predictions are generally closer to the actual values. This observation aligns with the lower RMSE and MSE values reported for these estimators in
Table 5. Conversely, Lasso, aLasso, and ElasticNet exhibit a wider spread of points around the diagonal, suggesting greater prediction errors and confirming their higher RMSE and MSE values in the table. The plot for SCAD has a different pattern that does not align with the diagonal. Overall,
Figure 5 visually reinforces the quantitative findings in
Table 5, demonstrating that Ridge, MCP, and particularly the shrinkage estimators achieve better predictive performance on the Hitters dataset, while Lasso, aLasso, and ElasticNet show relatively weaker performance. This visualization underscores the practical implications of estimator selection for achieving accurate predictions in partially linear models.
9. Conclusions
This paper focuses on the realm of semiparametric regression, specifically focusing on Partially Linear Regression Models (PLRMs) that incorporate both linear and nonlinear components. It considers a comprehensive review of six penalty estimation strategies: Ridge, Lasso, aLasso, SCAD, ElasticNet, and MCP. Recognizing the challenges posed by multicollinearity and the need for robust estimation in sparse models, we further introduce Stein-type shrinkage estimation techniques. The core of the study lies in evaluating the performance of these methods through both theoretical analysis and empirical investigation. A kernel smoothing technique, grounded in penalized least squares, is employed to estimate the semiparametric regression models.
The theoretical contributions include a partly asymptotic analysis of the proposed estimators, providing insights into their long-term behavior and robustness. The empirical investigation encompasses a simulation study that examines the estimators’ performance under various conditions, including different sample sizes, numbers of predictors, and levels of multicollinearity. Finally, the practical applicability of these methods is demonstrated through a real data example using the Hitters dataset, where the estimators are used to model baseball players’ salaries based on their performance metrics. The paper concludes that aLasso and shrinkage estimators exhibit superior performance in terms of prediction accuracy and efficiency in the presence of multicollinearity, especially the positive shrinkage, performing even better than aLasso.
In detail, the following points can be emphasized in terms of theoretical inferences, simulation and real data studies:
The paper establishes the asymptotic properties of the proposed estimators, including Ridge, Lasso, aLasso, SCAD, ElasticNet, MCP, and the Stein-type shrinkage estimators, providing a theoretical foundation for their use in PLRMs.
The theoretical results highlight the advantages of aLasso and shrinkage estimation, particularly in scenarios with high multicollinearity and sparsity.
The simulation study demonstrates that aLasso and the shrinkage estimators, especially the positive shrinkage estimator, consistently outperform other methods in terms of lower Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) for both the parametric and nonparametric components of the PLRM.
The superior performance of aLasso and shrinkage estimators is more pronounced when the sample size is small and multicollinearity is high, confirming their robustness in challenging conditions.
MCP and SCAD also exhibit strong performance in the simulations, often outperforming Ridge, Lasso, and ElasticNet, particularly when multicollinearity is present.
The simulation results reveal that the choice of estimator can significantly impact the estimation of the nonparametric function, with aLasso and shrinkage estimators generally producing smoother and more accurate curves.
The analysis of the Hitters dataset confirms the practical advantages of aLasso and shrinkage estimation, particularly positive shrinkage, in a real-world scenario with multicollinearity, as indicated by the high condition number.
The shrinkage and aLasso estimators achieve the lowest RMSE and MSE values when predicting log(Salary), demonstrating their superior predictive accuracy compared to Ridge, Lasso, SCAD, ElasticNet, and MCP.
The fitted nonparametric curves for the “Years” variable reveal interesting differences in how each estimator captures the nonlinear relationship between experience and salary, with aLasso and shrinkage estimators providing a balance between flexibility and smoothness.
The real data results align with the findings of the simulation study, further supporting the use of aLasso and shrinkage estimation, especially positive shrinkage, in PLRMs when multicollinearity is a concern. Also, SCAD has unexpected results which needs more investigation.
While this study provides valuable theoretical and empirical insights into the performance of various penalty and shrinkage estimators for partially linear models, several limitations should be acknowledged. The simulation study uses a GCV for the bandwidth, which might not be the best choice. The analysis is also limited to a single real-world dataset (Hitters), and the simulation study, while comprehensive, does not cover all possible scenarios, such as different error distributions.
The computational cost of some estimators, particularly SCAD and MCP, is not explicitly addressed. Additionally, the choice of tuning parameters for the penalized estimators is obtained based on CV criterion, whereas in practice, these need to be carefully selected, potentially impacting the results. The paper’s theoretical results are based on regularity conditions that might not always hold in real-world applications. While shrinkage estimators are introduced and applied, a more in-depth investigation into their properties and performance would be beneficial. These limitations highlight the need for further research and careful consideration when applying these methods in practice.
Author Contributions
Conceptualization, S.E.A. and D.A.; methodology, S.E.A. and D.A.; software, A.J.A.; validation, A.J.A., D.A. and E.Y.; formal analysis, A.J.A.; investigation, A.J.A. and E.Y.; resources, S.E.A. and D.A.; data curation, A.J.A.; writing—original draft preparation, A.J.A. and E.Y.; writing—review and editing, A.J.A., E.Y., S.E.A. and D.A.; visualization, A.J.A.; supervision, S.E.A. and D.A.; project administration, S.E.A. and D.A.; funding acquisition, S.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available dataset has been used for the paper.
Acknowledgments
This paper is inspired by the Master’s Thesis of Ayuba Jack Alhassan. The research of S. Ejaz Ahmed was supported by the Natural Sciences and the Engineering Research Council (NSERC) of Canada.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Proof of Theorem 1
The most important step in obtaining the ridge penalty-based kernel smoothing estimator is to calculate the partial residuals and minimize (13). From that, as mentioned before,
and
are calculated, and the minimization of (13) is realized on the basis of response variable
as follows:
Appendix A.2. Proof of Lemma 1
can be defined as follows:
where
. According to [
52], it can be shown that
where
, with finite-dimensional convergence holding trivially. Hence,
Hence,
., because
is convex and
has a unique minimum, it yields
Appendix A.3. Additional Figures for Simulation and Real Data Studies
The boxplots in
Figure A1 provide a detailed distributional view of the MSE for the nonparametric component. Here, we see that MCP, SCAD, and the shrinkage estimators not only have lower median MSE values but also smaller interquartile ranges, indicating greater consistency and less susceptibility to extreme errors. This is in contrast to methods like Ridge, Lasso, aLasso, and ElasticNet, which exhibit more outliers, especially under challenging conditions. These observations align with the findings presented in
Figure 3 and further solidify the superior performance of MCP, SCAD, and shrinkage estimators in terms of both accuracy and precision when estimating the nonparametric part of the model.
Figure A1.
Boxplots of MSE values obtained for nonparametric component of the model for all simulation configurations and all introduced estimators.
Figure A1.
Boxplots of MSE values obtained for nonparametric component of the model for all simulation configurations and all introduced estimators.
Figure A2 shifts the focus to the relative efficiency (RE) of the estimators for the parametric component, comparing them to a reference estimator, likely Ridge. The plots reveal that MCP, SCAD, and the shrinkage estimators consistently demonstrate RE values greater than 1, often significantly so, particularly when the sample size is small and multicollinearity is high. This indicates that these methods are substantially more efficient than Ridge in estimating the parametric component under such conditions, a finding that resonates with the lower MSE values these estimators exhibit in
Figure 1 and
Table 1,
Table 2 and
Table 3.
Figure A2.
Plots of RE values for estimated parametric components of the model including all simulation configurations.
Figure A2.
Plots of RE values for estimated parametric components of the model including all simulation configurations.
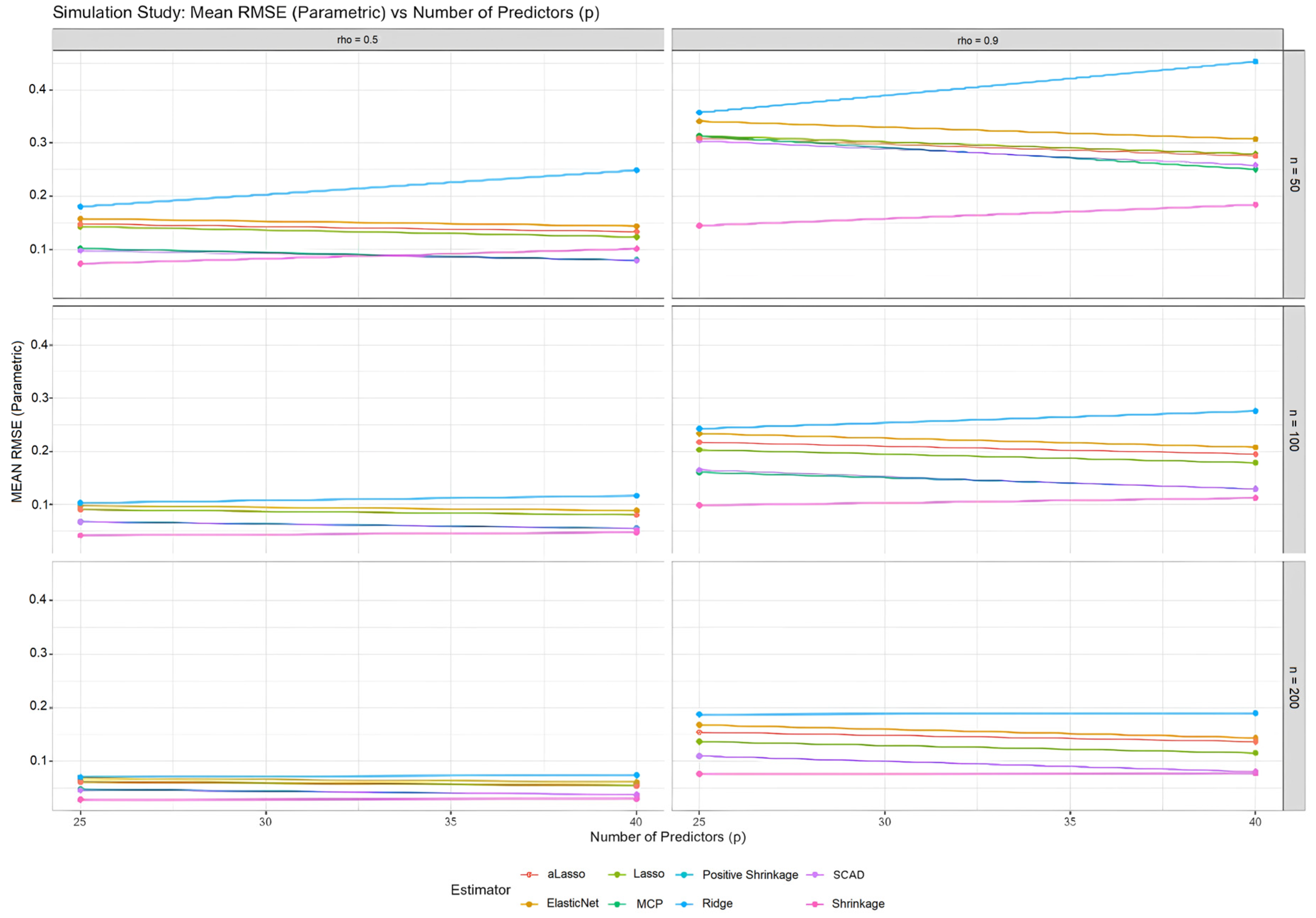
Figure A3 examines the impact of the number of predictors on the RMSE of the parametric component. Notably, the lines for MCP, SCAD, and the shrinkage estimators remain relatively flat as the number of predictors increases. This suggests that these methods are less sensitive to model complexity compared to Ridge, Lasso, aLasso, and ElasticNet, which show a more pronounced upward trend in RMSE, especially when multicollinearity is present. This observation reinforces the robustness of MCP, SCAD, and shrinkage estimators, aligning with their overall superior performance highlighted in previous figures and tables.
Figure A3.
RMSE values for estimated parametric component against the number of parameters (p) for all simulation configurations and introduced estimators.
Figure A3.
RMSE values for estimated parametric component against the number of parameters (p) for all simulation configurations and introduced estimators.
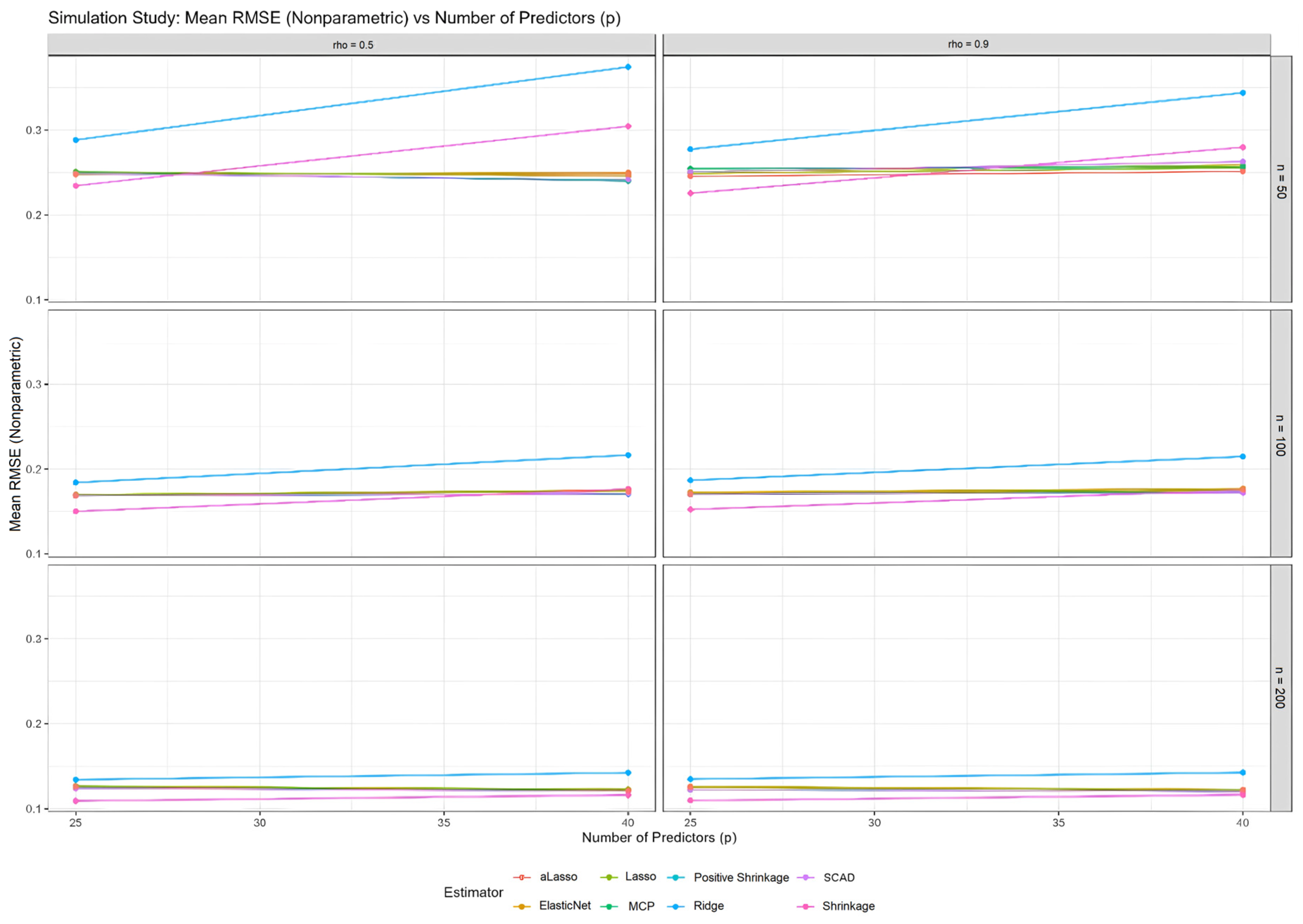
Figure A4.
RMSE values for estimated non-parametric component against the number of parameters (p) for all simulation configurations and introduced estimators.
Figure A4.
RMSE values for estimated non-parametric component against the number of parameters (p) for all simulation configurations and introduced estimators.
Finally,
Figure A4 investigates the relationship between RMSE and the number of predictors for the nonparametric component. Similar to
Figure A3, the plots show that MCP, SCAD, and the shrinkage estimators exhibit more stable RMSE values as the number of predictors increases, particularly compared to Ridge, Lasso, aLasso, and ElasticNet. This demonstrates the robustness of these estimators when estimating the nonparametric part of the model, even as the complexity of the parametric component grows. The findings in this figure are consistent with the lower MSE values for the nonparametric component observed for MCP, SCAD, and shrinkage estimators in
Figure 3 and visually confirmed in
Figure 2.
References
- Engle, R.F.; Granger, C.W.; Rice, J.; Weiss, A. Semiparametric Estimates of the Relation Between Weather and Electricity Sales. J. Am. Stat. Assoc. 1986, 81, 310–320. [Google Scholar] [CrossRef]
- Green, P.J.; Silverman, B.W. Nonparametric Regression and Generalized Linear Models, 1st ed.; Chapman and Hall/CRC: London, UK, 1994. [Google Scholar]
- Ruppert, D.; Wand, M.P.; Carroll, R.J. Semiparametric Regression, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Speckman, P. Kernel Smoothing in Partial Linear Models. J. R. Stat. Soc. B 1988, 50, 413–436. [Google Scholar] [CrossRef]
- Heckman, N.E. Spline Smoothing in a Partly Linear Model. J. R. Stat. Soc. B 1986, 48, 244–248. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, H.H. On the Adaptive Elastic-Net with a Diverging Number of Parameters. Ann. Stat. 2009, 37, 1733–1751. [Google Scholar] [CrossRef]
- Ahmed, S.E. Penalty, Shrinkage and Pretest Strategies: Variable Selection and Estimation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Wu, J.; Asar, Y. On Almost Unbiased Ridge Logistic Estimator for the Logistic Regression Model. Hacet. J. Math. Stat. 2016, 45, 989–998. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Belaghi, R.A.; Hussein, A.; Safariyan, A. New and Efficient Estimators of Reliability Characteristics for a Family of Lifetime Distributions Under Progressive Censoring. Mathematics 2024, 12, 1599. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Aydın, D.; Yılmaz, E. Penalty and Shrinkage Strategies Based on Local Polynomials for Right-Censored Partially Linear Regression. Entropy 2022, 24, 1833. [Google Scholar] [CrossRef]
- Yüzbaşı, B.; Arashi, M.; Ahmed, S.E. Big Data Analysis Using Shrinkage Strategies. arXiv 2017, arXiv:1704.05074. [Google Scholar]
- Yüzbaşı, B.; Ahmed, S.E.; Aydın, D. Ridge-Type Pretest and Shrinkage Estimations in Partially Linear Models. Stat. Pap. 2020, 61, 869–898. [Google Scholar] [CrossRef]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly Unbiased Variable Selection under Minimax Concave Penalty. arXiv 2010, arXiv:1002.4734. [Google Scholar] [CrossRef] [PubMed]
- Aydın, D.; Ahmed, S.E.; Yılmaz, E. Right-Censored Time Series Modeling by Modified Semi-Parametric A-Spline Estimator. Entropy 2021, 23, 1586. [Google Scholar] [CrossRef]
- Yilmaz, E.; Yuzbasi, B.; Aydin, D. Choice of Smoothing Parameter for Kernel-Type Ridge Estimators in Semiparametric Regression Models. REVSTAT-Stat. J. 2021, 19, 47–69. [Google Scholar]
- Li, T.; Kang, X. Variable Selection of Higher-Order Partially Linear Spatial Autoregressive Model with a Diverging Number of Parameters. Stat. Pap. 2022, 63, 243–285. [Google Scholar] [CrossRef]
- Sun, L.; Zhou, X.; Guo, S. Marginal Regression Models with Time-Varying Coefficients for Recurrent Event Data. Stat. Med. 2011, 30, 2265–2277. [Google Scholar] [CrossRef]
- Sun, Z.; Cao, H.; Chen, L. Regression Analysis of Additive Hazards Model with Sparse Longitudinal Covariates. Lifetime Data Anal. 2022, 28, 263–281. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Yang, S.P.; Emura, T. A Bayesian Approach with Generalized Ridge Estimation for High-Dimensional Regression and Testing. Commun. Stat. Simul. Comput. 2017, 46, 6083–6105. [Google Scholar] [CrossRef]
- Bühlmann, P.; van de Geer, S. Statistics for High-Dimensional Data: Methods, Theory and Applications; Springer Science & Business Media: Heidelberg, Germany, 2011. [Google Scholar]
- Breheny, P.; Huang, J. Coordinate Descent Algorithms for Nonconvex Penalized Regression, with Applications to Biological Feature Selection. Ann. Appl. Stat. 2011, 5, 232–253. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Liang, H.; Carroll, R.J. Estimation and Variable Selection for Generalized Additive Partial Linear Models. Ann. Stat. 2013, 41, 712–741. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Doksum, K.A.; Hossain, S.; You, J. Shrinkage, Pretest and Absolute Penalty Estimators in Partially Linear Models. Aust. N. Z. J. Stat. 2007, 49, 435–454. [Google Scholar] [CrossRef]
- Kubokawa, T. Highly-Efficient Quadratic Loss Estimation and Shrinkage to Minimize Mean Squared Error; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Piladaeng, J.; Ahmed, S.E.; Lisawadi, S. Penalised, Post-Pretest, and Post-Shrinkage Strategies in Nonlinear Growth Models. Aust. N. Z. J. Stat. 2022, 64, 381–405. [Google Scholar] [CrossRef]
- Piladaeng, J.; Lisawadi, S.; Ahmed, S.E. Improving the performance of least squares estimator in a nonlinear regression model. In Proceedings of the Fourteenth International Conference on Management Science and Engineering Management, Chisinau, Moldova, 30 July–2 August 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 492–502. [Google Scholar]
- Ahmed, S.E.; Ahmed, F.; Yüzbaşı, B. Post-Shrinkage Strategies in Statistical and Machine Learning for High Dimensional Data, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2023. [Google Scholar]
- Phukongtong, S.; Lisawadi, S.; Ahmed, S.E. Linear Shrinkage and Shrinkage Pretest Strategies in Partially Linear Models. E3S Web Conf. 2023, 409, 02009. [Google Scholar] [CrossRef]
- Li, D.; Racine, J. Nonparametric Econometrics: Theory and Practice. In Handbook of Research Methods and Applications in Empirical Macroeconomics; Edward Elgar Publishing: Northampton, MA, USA, 2013; pp. 3–28. [Google Scholar]
- Fan, J.; Gijbels, I. Local Polynomial Modelling and Its Applications: Monographs on Statistics and Applied Probability 66; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Zareamoghaddam, H.; Ahmed, S.E.; Provost, S.B. Shrinkage Estimation Applied to a Semi-Nonparametric Regression Model. Int. J. Biostat. 2020, 17, 23–38. [Google Scholar] [CrossRef]
- Ma, W.; Feng, Y.; Chen, K.; Ying, Z. Functional and Parametric Estimation in a Semi- and Nonparametric Model with Application to Mass-Spectrometry Data. Int. J. Biostat. 2013, 11, 285–303. [Google Scholar] [CrossRef]
- Asl, M.N.; Bevrani, H.; Belaghi, R.A.; Ahmed, S.E. Shrinkage and Sparse Estimation for High-Dimensional Linear Models. Adv. Intell. Syst. Comput. 2019, 1, 147–156. [Google Scholar]
- Aldeni, M.; Wagaman, J.C.; Amezziane, M.; Ahmed, S.E. Pretest and Shrinkage Estimators for Log-Normal Means. Comput. Stat. 2022, 38, 1555–1578. [Google Scholar] [CrossRef]
- Al-Momani, M.; Ahmed, S.E.; Hussein, A. Efficient Estimation Strategies for Spatial Moving Average Model. Adv. Intell. Syst. Comput. 2019, 1, 520–543. [Google Scholar]
- Reangsephet, O.; Lisawadi, S.; Ahmed, S.E. Post selection estimation and prediction in Poisson regression model. Thail. Stat. 2020, 18, 176–195. [Google Scholar]
- Reangsephet, O.; Lisawadi, S.; Ahmed, S.E. Weak signals in high-dimensional logistic regression models. In Proceedings of the Thirteenth International Conference on Management Science and Engineering Management, Ontario, ON, Canada, 5–8 August 2019; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 121–133. [Google Scholar]
- Reangsephet, O.; Lisawadi, S.; Ahmed, S.E. A Comparison of Pretest, Stein-Type and Penalty Estimators in Logistic Regression Model. In Proceedings of the Eleventh International Conference on Management Science and Engineering Management, Kanazawa, Japan, 28–31 July 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 19–34. [Google Scholar]
- Shah, M.K.; Zahra, N.; Ahmed, S.E. On the Simultaneous Estimation of Weibull Reliability Functions. In Proceedings of the Thirteenth International Conference on Management Science and Engineering Management, Ontario, ON, Canada, 5–8 August 2019. [Google Scholar]
- Antoniadis, A.; Gijbels, I.; Verhasselt, A. Variable Selection in Additive Models Using P-Splines with Nonconcave Penalties. Ann. Inst. Stat. Math. 2012, 64, 5–27. [Google Scholar]
- Nadaraya, E.A. On Estimating Regression. Theory Probab. Appl. 1964, 9, 141–142. [Google Scholar] [CrossRef]
- Watson, G.S. Smooth Regression Analysis. Sankhyā A 1964, 26, 359–372. [Google Scholar]
- Yüzbaşı, B.; Ahmed, S.E.; Arashi, M.; Norouzirad, M. LAD, LASSO and Related Strategies in Regression Models. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Staniswalis, J.G. The Kernel Estimate of a Regression Function in Likelihood-Based Models. J. Am. Stat. Assoc. 1989, 84, 276–283. [Google Scholar] [CrossRef]
- Frank, L.E.; Friedman, J.H. A Statistical View of Some Chemometrics Regression Tools. Technometrics 1993, 35, 109–135. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Fu, W.; Knight, K. Asymptotics for Lasso-type estimators. Ann. Stat. 2000, 28, 1356–1378. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).