RHADaMAnTe: An Astro Code to Estimate the Spectral Energy Distribution of a Curved Wall of a Gap Opened by a Forming Planet in a Protoplanetary Disk
Abstract
1. Introduction
1.1. Dust in Protoplanetary Disks
1.2. LkCa 15
2. Geometry of the Wall Projected on the Sky
2.1. Inclined Walls
2.2. Vertical Walls
3. The RHADaMAnTe Code
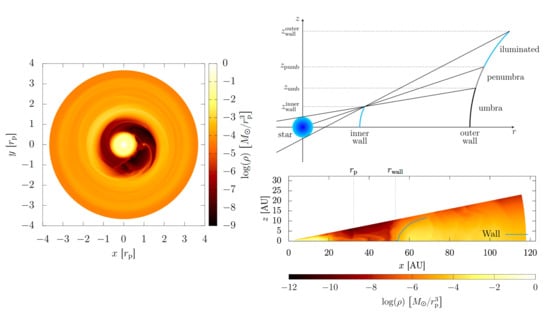
3.1. The Geometry of the Radiation Re-Emitted by the Wall
3.2. Discretization of the Two-Dimensional Wall
3.3. Curved Wall
Projection on the Plane of the Sky
3.4. Emission of the Wall
3.4.1. Rosseland Mean Opacity
4. Results: Implementation in the Stellar System LkCa 15
4.1. Simulation: Planet–Disk Interaction
4.2. Dust Grain
4.3. The Vertical Geometry of the Wall
4.4. SED of the Wall
4.5. SED of the System
5. Discussion: Vertical-Wall SED vs. Curved-Wall SED
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Mass of the Sun | |
| Mass of Jupiter |
Appendix A. Mathematical Tools
Appendix A.1. Construction of a Vertical Wall
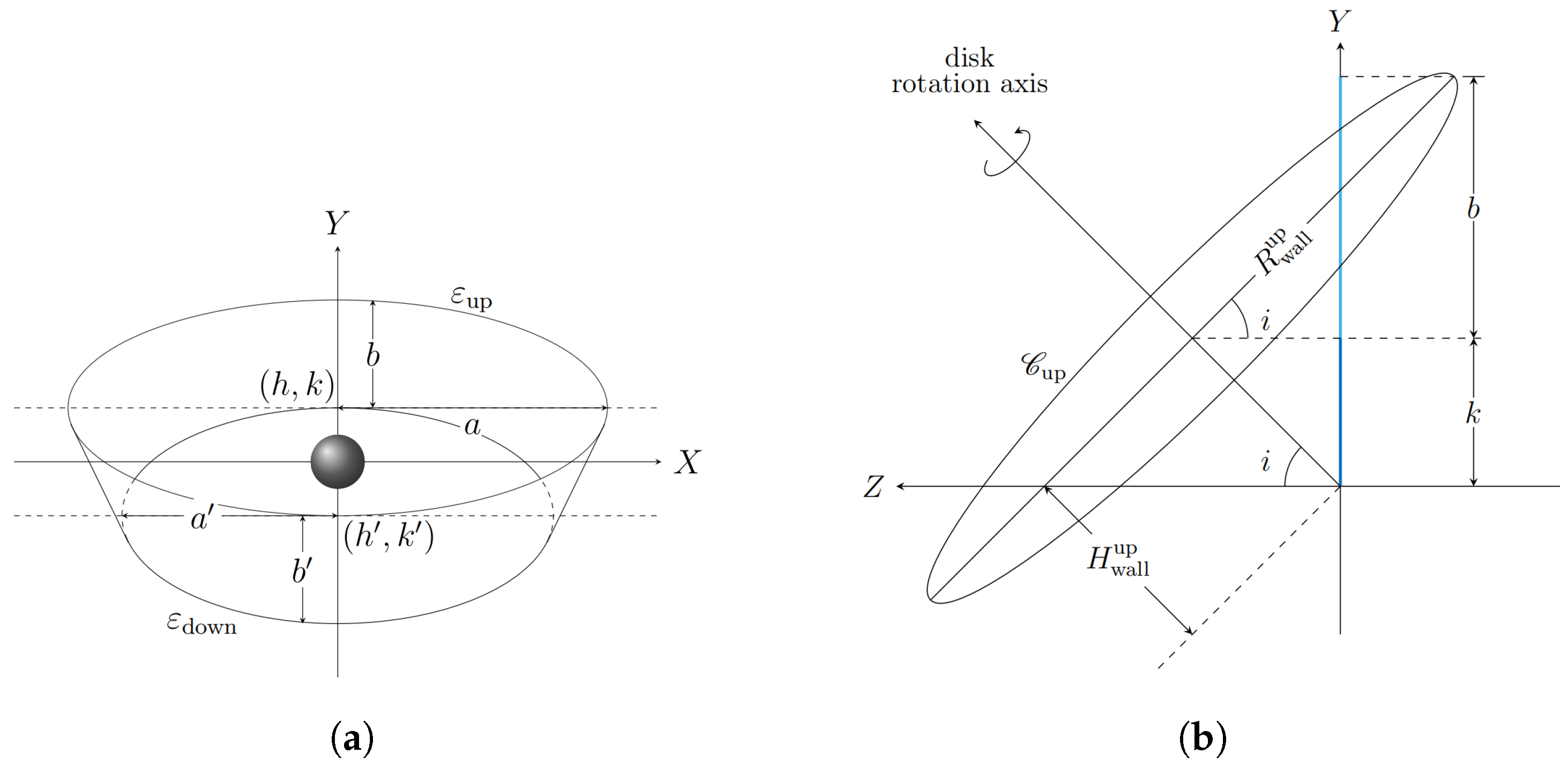
Appendix A.2. Area Between Two Curves
Appendix A.3. Theoretical Area of the Projected Vertical Wall: The Whole Wall

Appendix A.4. Theoretical Area of the Projected Vertical Wall: The Wall with Shadow

Appendix B. Testing RHADaMAnTe


References
- Calvet, N.; D’Alessio, P.; Hartmann, L.; Wilner, D.; Walsh, A.; Sitko, M. Evidence for a Developing Gap in a 10 Myr Old Protoplanetary Disk. Astrophys. J. 2002, 568, 1008–1016. [Google Scholar] [CrossRef]
- Espaillat, C.; Calvet, N.; D’Alessio, P.; Hernández, J.; Qi, C.; Hartmann, L.; Furlan, E.; Watson, D.M. On the Diversity of the Taurus Transitional Disks: UX Tauri A and LkCa 15. Astrophys. J. 2007, 670, L135–L138. [Google Scholar] [CrossRef]
- Espaillat, C.; Calvet, N.; D’Alessio, P.; Bergin, E.; Hartmann, L.; Watson, D.; Furlan, E.; Najita, J.; Forrest, W.; McClure, M.; et al. Probing the Dust and Gas in the Transitional Disk of CS Cha with Spitzer. Astrophys. J. 2007, 664, L111–L114. [Google Scholar] [CrossRef]
- Rendón, F. Modelación de la geometría de paredes de cavidades en discos protoplanetarios mediante el código ARTeMiSE. In Modelación Matemática V: Ingeniería, Ciencias Naturales y Ciencias Sociales; Reyes-Mora, S., Barragán-Mendoza, F., Eds.; Universidad Tecnológica de la Mixteca: Oaxaca, México, 2023; pp. 57–75. [Google Scholar]
- Muzerolle, J.; Calvet, N.; Hartmann, L.; D’Alessio, P. Unveiling the Inner Disk Structure of T Tauri Stars. Astrophys. J. 2003, 597, L149–L152. [Google Scholar] [CrossRef]
- Woitke, P.; Kamp, I.; Thi, W.-F. Radiation thermo-chemical models of protoplanetary disks. I. Hydrostatic disk structure and inner rim. Astron. Astrophys. 2009, 501, 383–406. [Google Scholar] [CrossRef]
- Bruderer, S. Survival of molecular gas in cavities of transition disks. I. CO. Astron. Astrophys. 2013, 559, A46. [Google Scholar] [CrossRef]
- Dullemond, C.P.; Juhasz, A.; Pohl, A.; Sereshti, F.; Shetty, R.; Peters, T.; Commercon, B.; Flock, M. RADMC-3D: A Multi-Purpose Radiative Transfer Tool; Astrophysics Source Code Library: Houghton, MI, USA, 2012; record ascl:1202.015. [Google Scholar]
- D’Alessio, P.; Hartmann, L.; Calvet, N.; Franco-Hernández, R.; Forrest, W.J.; Sargent, B.; Furlan, E.; Uchida, K.; Green, J.D.; Watson, D.M.; et al. The Truncated Disk of CoKu Tau/4. Astrophys. J. 2005, 621, 461–472. [Google Scholar] [CrossRef]
- Mathis, J.S.; Rumpl, W.; Nordsieck, K.H. The size distribution of interstellar grains. Astrophys. J. 1997, 217, 425–433. [Google Scholar] [CrossRef]
- Min, M.; Flynn, G. Dust Composition in Protoplanetary Disks. In Protoplanetary Dust: Astrophysical and Cosmochemical Perspectives; Apai, D.A., Lauretta, D.S., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 161–190. [Google Scholar]
- Jang, H.; Waters, R.; Kamp, I.; Dullemond, C.P. Spatial distribution of crystalline silicates in protoplanetary disks: How to interpret mid-infrared observations. Astron. Astrophys. 2024, 687, A275. [Google Scholar] [CrossRef]
- Jones, A.P. Nano-diamonds in proto-planetary discs. Astron. Astrophys. 2022, 665, A21. [Google Scholar] [CrossRef]
- Siebenmorgen, R.; Heymann, F. Polycyclic aromatic hydrocarbons in protoplanetary disks: Emission and X-ray destruction. Astron. Astrophys. 2012, 543, A25. [Google Scholar] [CrossRef]
- Acke, B.; van den Ancker, M.E. ISO spectroscopy of disks around Herbig Ae/Be stars. Astron. Astrophys. 2004, 426, 151–170. [Google Scholar] [CrossRef]
- Geers, V.C.; Augereau, J.-C.; Pontoppidan, K.M.; Dullemond, C.P.; Visser, R.; Kessler-Silacci, J.E.; Evans, N.J., II; van Dishoeck, E.F.; Blake, G.A.; Boogert, A.C.A.; et al. C2D Spitzer-IRS spectra of disks around T Tauri stars. II. PAH emission features. Astron. Astrophys. 2004, 459, 545–556. [Google Scholar] [CrossRef]
- Keller, L.P.; Hony, S.; Bradley, J.P.; Molster, F.J.; Waters, L.B.F.M.; Bouwman, J.; de Koter, A.; Brownlee, D.E.; Flynn, G.J.; Henning, T.; et al. Identification of iron sulphide grains in protoplanetary disks. Nature 2002, 417, 148–150. [Google Scholar] [CrossRef]
- Tazaki, R.; Murakawa, K.; Muto, T.; Honda, M.; Inoue, A.K. The Water-ice Feature in Near-infrared Disk-scattered Light around HD 142527: Micron-sized Icy Grains Lifted up to the Disk Surface? Astrophys. J. 2021, 921, 173. [Google Scholar] [CrossRef]
- Kim, M.; Wolf, S.; Potapov, A.; Mutschke, H.; Jäger, C. Constraining the detectability of water ice in debris disks. Astron. Astrophys. 2019, 629, A141. [Google Scholar] [CrossRef]
- Malfait, K.; Waelkens, C.; Bouwman, J.; de Koter, A.; Waters, L.B.F.M. The ISO spectrum of the young star HD 142527. Astron. Astrophys. 1999, 345, 181–186. [Google Scholar]
- McClure, M.K.; Manoj, P.; Calvet, N.; Adame, L.; Espaillat, C.; Watson, D.M.; Sargent, B.; Forrest, W.J.; D’Alessio, P. Probing Dynamical Processes in the Planet-forming Region with Dust Mineralogy. Astrophys. J. 2012, 759, L10–L16. [Google Scholar] [CrossRef]
- Simon, M.; Dutrey, A.; Guilloteau, S. Dynamical Masses of T Tauri Stars and Calibration of Pre-Main-Sequence Evolution. Astrophys. J. 2000, 545, 1034–1043. [Google Scholar] [CrossRef]
- Kenyon, S.J.; Hartmann, L. Pre-Main-Sequence Evolution in the Taurus-Auriga Molecular Cloud. Astrophys. J. Suppl. 1995, 101, 117–171. [Google Scholar] [CrossRef]
- Thalmann, C.; Mulders, G.D.; Hodapp, K.; Janson, M.; Grady, C.A.; Min, M.; de Juan Ovelar, M.; Carson, J.; Brandt, T.; Bonnefoy, M.; et al. The architecture of the LkCa 15 transitional disk revealed by high-contrast imaging. Astron. Astrophys. 2014, 556, A51–A74. [Google Scholar] [CrossRef]
- Espaillat, C.; D’Alessio, P.; Hernández, J.; Nagel, E.; Luhman, K.L.; Watson, D.M.; Calvet, N.; Muzerolle, J.; McClure, M. Unveiling the Structure of Pre-transitional Disks. Astrophys. J. 2010, 717, 441–457. [Google Scholar] [CrossRef]
- Kraus, A.L.; Ireland, M.J. LkCa 15: A Young Exoplanet Caught at Formation? Astrophys. J. 2012, 745, 5–17. [Google Scholar] [CrossRef]
- Sallum, S.; Follette, K.B.; Eisner, J.A.; Close, L.M.; Hinz, P.; Kratter, K.; Males, J.; Skemer, A.; Macintosh, B.; Tuthill, P.; et al. Accreting protoplanets in the LkCa 15 transition disk. Nature 2015, 527, 342–344. [Google Scholar] [CrossRef] [PubMed]
- Bergin, E.; Calvet, N.; Sitko, M.L.; Abgrall, H.; D’Alessio, P.; Herczeg, G.J.; Roueff, E.; Qi, C.; Lynch, D.K.; Russell, R.W.; et al. A New Probe of the Planet-forming Region in T Tauri Disks. Astrophys. J. 2004, 614, L133–L136. [Google Scholar] [CrossRef]
- Najita, J.R.; Strom, S.E.; Muzerolle, J. Demographics of transition objects. Mon. Not. R. Astron. Soc. 2007, 378, 369–378. [Google Scholar] [CrossRef]
- Espaillat, C.; Calvet, N.; Luhman, K.L.; Muzerolle, J.; D’Alessio, P. Confirmation of a Gapped Primordial Disk around LkCa 15. Astrophys. J. 2008, 682, L125–L128. [Google Scholar] [CrossRef]
- Piétu, V.; Dutrey, A.; Guilloteau, S.; Chapillon, E.; Pety, J. Resolving the inner dust disks surrounding LkCa 15 and MWC 480 at mm wavelengths. Astron. Astrophys. 2006, 378, L43–L47. [Google Scholar] [CrossRef]
- Andrews, S.M.; Williams, J.P. High-Resolution Submillimeter Constraints on Circumstellar Disk Structure. Astrophys. J. 2005, 659, 705–728. [Google Scholar] [CrossRef]
- Benítez-Llambay, P.; Masset, F.S. FARGO3D: A New GPU-oriented MHD Code. Astrophys. J. 2016, 223, 29. [Google Scholar] [CrossRef]
- Hui-Bon-Hoa, A. Stellar models with self-consistent Rosseland opacities-Consequences for stellar structure and evolution. Astron. Astrophys. 2021, 646, L6–L10. [Google Scholar] [CrossRef]
- D’Alessio, P.; Calvet, N.; Hartmann, L.; Franco-Hernández, R.; Servín, H. Effects of Dust Growth and Settling in T Tauri Disks. Astrophys. J. 2006, 638, 314–335. [Google Scholar] [CrossRef]
- Pollack, J.B.; Hollenbach, D.; Beckwith, S.; Simonelli, D.P.; Roush, T.; Fong, W. Composition and radiative properties of grains in molecular clouds and accretion disks. Astrophys. J. 1994, 421, 615–639. [Google Scholar] [CrossRef]
- Jaeger, C.; Mutschke, H.; Begemann, B.; Dorschner, J.; Henning, T. Steps toward interstellar silicate mineralogy. 1: Laboratory results of a silicate glass of mean cosmic composition. Astron. Astrophys. 1994, 292, 641–655. [Google Scholar]
- Dorschner, J.; Begemann, B.; Henning, T.; Jaeger, C.; Mutschke, H. Steps toward interstellar silicate mineralogy. II. Study of Mg-Fe-silicate glasses of variable composition. Astron. Astrophys. 1995, 300, 503–520. [Google Scholar]
- Draine, B.T. Interstellar Dust Grains. Annu. Rev. Astron. Astrophys. 2003, 41, 241–289. [Google Scholar] [CrossRef]
- Begemann, B.; Dorschner, J.; Henning, T.; Mutschke, H.; Thamm, E. A laboratory approach to the interstellar sulfide dust problem. Astrophys. J. 1994, 423, L71–L74. [Google Scholar] [CrossRef]
- Henning, T.; Il’In, V.B.; Krivova, N.A.; Michel, B.; Voshchinnikov, N.V. WWW database of optical constants for astronomy. Astron. Astrophys. Suppl. Ser. 1999, 136, 405–406. [Google Scholar] [CrossRef]
- Piétu, V.; Dutrey, A.; Guilloteau, S. Probing the structure of protoplanetary disks: A comparative study of DM Tau, LkCa 15, and MWC 480. Astron. Astrophys. 2007, 467, 163–178. [Google Scholar] [CrossRef]
- Andrews, S.M.; Rosenfeld, K.A.; Wilner, D.J.; Bremer, M. A Closer Look at the LkCa 15 Protoplanetary Disk. Astrophys. J. Lett. 2011, 745, L5–L10. [Google Scholar] [CrossRef]
- Nagel, E.; D’Alessio, P.; Calvet, N.; Espaillat, C.; Trinidad, M.A. The Effect of Sublimation Temperature Dependencies on Disk Walls Around T Tauri Stars. Rev. Mex. Astron. Astrofís. 2013, 49, 43–52. [Google Scholar]
- Mulders, G.D.; Dominik, C.; Min, M. Full two-dimensional radiative transfer modelling of the transitional disk LkCa 15. Astron. Astrophys. 2010, 512, A11. [Google Scholar] [CrossRef]
- Sturm, J.A.; Booth, A.S.; McClure, M.K.; Leemker, M.; van Dishoeck, E.F. Disentangling the protoplanetary disk gas mass and carbon depletion through combined atomic and molecular tracers. Astron. Astrophys. 2023, 670, A12. [Google Scholar] [CrossRef]




















| Parameter | Value | |
|---|---|---|
| Disk | Aspect ratio H | |
| Surface density | ||
| -viscosity | ||
| slope | 1.0 | |
| Flaring index | 0.0 | |
| Planet | (mass) | |
| (position) | 1 | |
| RocheSmoothing | 0.4 | |
| Acretion | No | |
| Mesh | Units | unitless |
| Dimension | 3D | |
| Geometry | spherical | |
| Timing | Orbits | 500 |
| silicate | [AU] | [AU] |
|---|---|---|
| pyroxene | ||
| 56.0 | 11.5 | |
| 49.8 | 12.3 | |
| 51.0 | 12.0 | |
| 50.0 | 13.2 | |
| olivine | ||
| 52.5 | 10.0 | |
| 53.0 | 12.0 | |
| parameter | value | |
|---|---|---|
| Star | ||
| 4370 K | ||
| Disk | Inclination | |
| Inner wall | ||
| Dust | - | silicates |
| - | graphite | |
| Outer wall | ||
| Dust | olivine | |
| - | organics | |
| - | troilite |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rendón, F. RHADaMAnTe: An Astro Code to Estimate the Spectral Energy Distribution of a Curved Wall of a Gap Opened by a Forming Planet in a Protoplanetary Disk. Math. Comput. Appl. 2025, 30, 48. https://doi.org/10.3390/mca30030048
Rendón F. RHADaMAnTe: An Astro Code to Estimate the Spectral Energy Distribution of a Curved Wall of a Gap Opened by a Forming Planet in a Protoplanetary Disk. Mathematical and Computational Applications. 2025; 30(3):48. https://doi.org/10.3390/mca30030048
Chicago/Turabian StyleRendón, Francisco. 2025. "RHADaMAnTe: An Astro Code to Estimate the Spectral Energy Distribution of a Curved Wall of a Gap Opened by a Forming Planet in a Protoplanetary Disk" Mathematical and Computational Applications 30, no. 3: 48. https://doi.org/10.3390/mca30030048
APA StyleRendón, F. (2025). RHADaMAnTe: An Astro Code to Estimate the Spectral Energy Distribution of a Curved Wall of a Gap Opened by a Forming Planet in a Protoplanetary Disk. Mathematical and Computational Applications, 30(3), 48. https://doi.org/10.3390/mca30030048