Abstract
A nonlinear finite element model for circular and annular micro-plates under thermal and mechanical loading was developed using a third-order shear deformation theory. In the kinematic assumptions, a change in plate thickness is allowed, and no transverse shear strains are considered on the top and bottom surfaces. A power-law distribution was utilized to account for variations in two constituents through the thickness of the plate. Three different types of porosity distributions are considered. The strain gradient effect in micro-scale structures is accounted for by using the modified couple stress theory. Hamilton’s principle is used to obtain the equations of motion, and conforming plate elements are used in the development of the finite element model. The developed finite element model was verified against the available literature and analytical solutions. The effects of the material and porosity distribution, microstructure-dependency, geometric nonlinearity, and various boundary conditions on the bending response of functionally graded and porous circular and annular micro-plates were studied using the developed nonlinear finite element model.
1. Introduction
Novel composite materials have recently been a subject of interest in the scientific community because of their many advantages over traditional materials. Functionally graded porous materials (FGPMs) represent one type of such materials, with potential applications in the aerospace sector and micro-electro-mechanical systems field. The concept of functionally graded materials first appeared [1] in Japan (1984) as a material for thermal barriers developed for aerospace missions that could reduce thermal stresses that occur predominantly at the interface of the metallic structure and the ceramic thermal shield during hypersonic flight. The review articles [2,3,4,5] provide context for the development of functionally graded materials.
Functionally graded materials (FGMs) are composite materials that have a gradual variation in their constituents instead of an abrupt change of composition, like in traditional laminated composite materials. This results in an inhomogeneous material that can be tailored to specific applications. A commonly studied type of FGM structure is plates with ceramic and metal as their constituents. Figure 1 shows a representation of an FGM under external thermal load. The ceramic provides excellent thermal characteristics to withstand extreme thermal environments, and the metal provides ductility and fracture resistance (since ceramics are commonly brittle). The current study focuses on FGM plates with a volumetric fraction variation along the thickness direction of the plates. The properties of the FGMs are given by
where is any material property, is the ceramic property, is the metallic property, z is the coordinate perpendicular to the plate, h is the height of the plate, and n is the power-law index. Figure 2 shows the variation in the volume fraction of the material on the top surface with different values for the power-law index n.
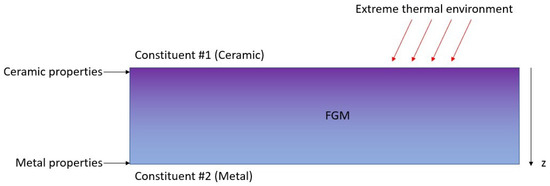
Figure 1.
Functionally graded material.
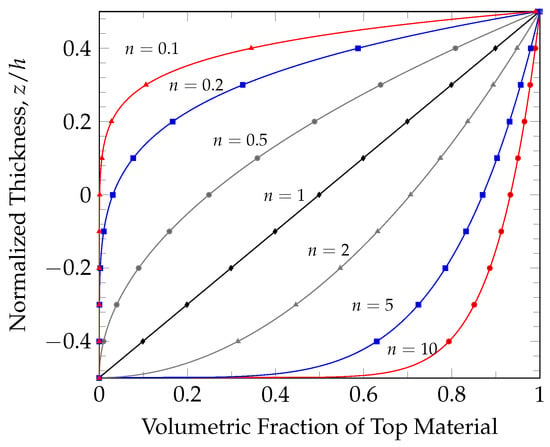
Figure 2.
Volumetric distribution of a functionally graded material.
Other potential fields of application for FGPMs are micro-electro-mechanical systems (MEMSs) [6] and nano-electro-mechanical systems (NEMSs). At their core, these systems depend on the behavior of micro-beams and micro-plates [7]. At such length scales, structures have been observed [8] to be size-dependent, which cannot be accounted for by conventional continuum mechanics [9]. To correctly model these length scale effects, couple stress theories [8,10,11], the Eringen nonlocal elasticity theory [12], and the strain gradient elasticity theories [13,14,15] have been developed. The modified couple stress theory by Yang [8] requires only one length scale parameter, which facilitates formulations and parametric studies.
To predict the behavior of FGM micro-plates, multiple finite element models (FEMs) that include size-dependent effects have been derived [16,17,18,19,20,21,22,23,24,25,26,27,28,29]. These FEMs require a plate theory, the simplest of which is classical plate theory (CPT). CPT neglects transverse shear deformation effects. This model is efficient and accurate for thin plates but becomes inaccurate for thick plates, where shear deformation is critical. Shear deformation theories have been developed to address these shortcomings.
First-order shear deformation theory (FSDT) has been used to model functionally graded plates in several studies [30,31,32,33]. FSDT requires a shear correction factor, which reduces its usefulness. Higher-order theories were developed in order to forego the correction factor and improve accuracy. The third-order shear deformation theory (TSDT) presented by Reddy [34] in 1984 considers the cubic variation of in-plane displacements and constant transverse displacement through thickness. It was used by Reddy [29] and, later on, by Najafizadeh et al. [35] on circular plates to investigate thermal buckling behavior. A general third-order plate theory (GTPT) was later presented by Reddy and Kim [36], which describes thickness stretch using a quadratic variation in order to obtain a parabolic variation in transverse shear strains. Kim and Reddy [37] presented the analytical solutions for the general third-order theory. Shear deformation theories have been used to study FGM plates [23,38,39,40,41,42,43]. Vinh [44] presented a comprehensive analysis of bending, free vibration, and buckling behaviors of functionally graded nanoplates using a modified nonlocal strain gradient theory. Wang et al. [45] studied the bending and buckling behavior of porous, functionally graded curved nano-beams using a size-dependent, quasi-3D beam model that accounts for a thickness-stretching effect.
Engineering structures commonly employ circular and annular plates. Although they are less common than rectangular plates [46], several studies have investigated the behavior of circular FG plates [20,33,46,47,48,49]. The analytical solutions for the full plate bending behavior of circular and annular plates under asymmetric loads were presented by Reddy [34] for several boundary conditions. The work by Duda [50] examined 3D heat transfer problems for annular plates using both Cartesian and polar finite element discretizations. The results demonstrate the advantages of using a cylindrical mesh to describe circular (or cylindrical) geometries. For the heat conduction problem to be solved, the relative error of the Cartesian finite element model was found to be , and for the cylindrical finite element model, it was only .
After a review of the available literature, it is evident that no existing nonlinear finite element model for porous circular/annular micro-plates incorporates higher-order shear deformations in cylindrical coordinates. This study makes a significant contribution by developing such a model, which not only solves circular/annular plate problems but also takes advantage of the increased accuracy provided by cylindrical formulations. Moreover, the model accounts for moderate rotations and stretches in the thickness direction, which is crucial for accurately capturing the behavior of thick plates under thermal and mechanical loads.
This study utilizes conforming elements, which are specifically employed to ensure the continuity condition in the context of strain gradient theory. These elements ensure that the displacement field and its gradients remain continuous across element boundaries, thereby improving the model’s accuracy in capturing the complex behavior of functionally graded porous materials. This approach allows for a more accurate representation of the plate’s bending response and thermal-mechanical behavior, which is essential for the design of advanced engineering structures.
Additionally, the study incorporates temperature-dependent behavior and porosity, which are critical factors in the typical applications of FGM plates. The temperature-dependent properties found in the literature [51] have been used in the work by Reddy and Chin [30]. Furthermore, this research considers the effect of porosity on material properties, as observed in numerous studies [42,52,53,54]. Three cosine functions have been used to prescribe the volumetric distribution of porosity on FGM plates to illustrate the effects of porosity distribution [17,23,55,56]. The expressions for the porosity distributions used in this study are
where is the porosity at a given location along the thickness of the plate, and is the maximum porosity value.
Since the variation in Poisson’s ratio with plate thickness is considered to have a minor impact on the behavior of the plate, many studies [17,20,33,36,37,49,57] consider it constant. Other studies consider its variation to be like any other FGM property [39,47,48,58,59]. In the current work, Poisson’s ratio is considered constant.
2. Model Development
2.1. Displacement Field and Strain Definition
Reddy and Kim [36] presented a general third-order displacement field by considering a cubic expansion of in-plane displacements and quadratic variation in transverse displacement. It can be written in the cylindrical coordinate system as
where , , and are the displacements at . , , and are the linear components of their respective displacements. , , and are the quadratic components. Similarly, and are the cubic components.
With zero transverse shear enforced on the upper and lower surfaces, we have (4)
the displacements in the radial direction, , and angular direction, , contain the cubic terms of the thickness coordinate, z, and the displacement along the thickness direction, , contains quadratic terms of z:
where the grouping was used to simplify the manipulation of the equations.
The proposed strain field is based on von Kármán strain definition in cylindrical coordinates:
Based on von Kármán strains (i.e., small strains and moderate rotation), equal to or higher than the square of the strains is neglected, and the following assumptions are made:
2.2. Hamilton’s Principle and Equations of Motion
The derivation of the equations of motion for the model begins with Hamilton’s principle, which is the dynamic form of the principle of virtual displacements:
where denotes virtual strain energy, denotes the virtual work carried out by external forces, and denotes virtual kinetic energy.
To account for size-dependent material behavior, the modified couple stress theory by Yang et al. [8] was included in the model. The theory starts with a definition for virtual strain energy:
where represents Cauchy stresses, represents strains, are the deviatoric part of the symmetric couple stress tensor, and represents the components of the curvature tensor.
The components of the curvature tensor, organized by the order of plate thickness direction and the notation in the work by Reddy and Kim [36], will take the form
where the terms are obtained using the displacement field in Equation (5) so that the curvature tensor can be expressed in terms of the generalized displacements.
The virtual strain energy can then be rewritten using the definitions in Equation (10):
where
Virtual kinetic energy is defined in cylindrical coordinates as
where is the mass density. By using the displacement field in Equation (5), virtual kinetic energy becomes
We use the following definition, which is nonzero for any value of i for functionally graded materials.
The virtual work carried out by external forces is defined by
where denotes body forces, is body couples, is surface tractions, and and denote distributed loads on the upper and lower surface, respectively, for . Figure 3 presents surfaces where external forces are applied, and the integration is carried out over the upper surface , lower surface , or lateral surface S to compute the virtual work carried out.
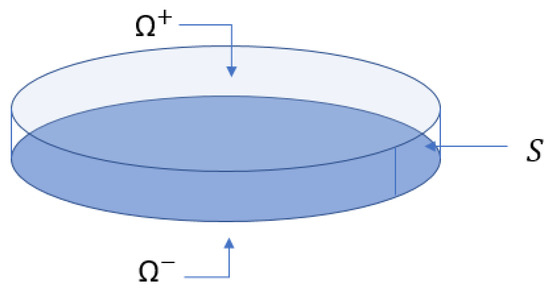
Figure 3.
Plate surfaces.
By using the displacement field in Equation (14), we obtain
with the following definitions:
By grouping all the terms in Equations (9), (12) and (15) using variational generalized displacements, we obtain the equations of motion:
2.3. Constitutive Relations
The functionally graded materials in this work are considered to have linearly elastic isotropic behavior, and therefore, the constitutive relations can be expressed as
where and are the lame parameters defined as
The porous functionally graded material properties are a function of the position in the transverse direction, the porosity, and the temperature. Therefore, the elastic modulus, E, and other material properties have the form of
where P indicates the material property of the functionally graded material, indicates the property of the ceramic constituent, indicates the material property of the metallic constituent, indicates the maximum porosity, the porosity distribution function, and n indicates the power-law index. The porosity distribution functions are defined in Equation (2).
2.4. Finite Element Model
A continuity conforming element was utilized to develop the finite element model. The utilized interpolation function of the conforming element was developed by Bogner et al. [60], with u, , , and being the degrees of freedom per node. Note that u and its derivatives are a nodal value and its derivatives. All seven generalized displacements were approximated with the same interpolation functions, with the form
where and nodal variables and their derivatives are in a four-node element and the interpolation functions. and are normalized coordinates with respect to the size of an element, where the interpolation functions are
where i is the number of degrees of freedom per generalized displacement in a four-node element. , , , and are interpolation functions associated with u, , , and , respectively.
The mesh was defined in polar coordinates, with a value for the radius and another for the angle, using four nodes at the vertices. If the modeled plate is circular, the elements at the center of the plate have a pair of nodes at the origin of the plate , which share physical position since their different angular coordinates () do not translate into a different position (given that the value of the radius is zero). The model behaved well given this mesh definition, and therefore, no three-node element was implemented.
The seven generalized displacements, then, are
where are the seven generalized displacements: , , , , , , and . The finite element equations will adopt the form
where U is a displacement vector (note that it should be distinct from the virtual strain energy in Equation (7)), the superscript e indicates an element, is the mechanical force vector, is the thermal force vector, and and are the stiffness and mass matrices. and are 112 by 112 matrices, the components of which are shown in Appendix A.1 and Appendix A.2, respectively. Note that a four-node element has seven generalized displacements per node and four degrees of freedom (nodal value and its derivatives) for each generalized displacement per node.
2.5. Computational Considerations
Newton iteration was selected as the iterative solution method, which obtains the solution increment for each iteration and adds it to the previous solution rather than finding the solution vector, U, itself. This is conducted through the following equation:
where r is the iteration number, and T is the tangent matrix. A large number of iterations were necessary to converge on a solution in the work by Reddy et al. [20], which used FSDT and a formulation made in the cylindrical coordinate system. Given that the current model is of a higher order, a large number of iterations to converge is expected.
The tangent matrix T is defined by
where represents the generalized displacements. After some manipulations, the expression in terms of the stiffness matrix elements can be obtained:
where represents the stiffness matrix elements. Since the second term of Equation (34) requires the stiffness matrix elements to be functions of the generalized displacements in order to be nonzero, the only components of T that are different from K are shown in Appendix A.3.
The numerical values of the matrices , , and were obtained via Gauss-Legendre quadrature formulas, which are of the form
where and are local normalized coordinates, and are Gauss weights, and F is a function, typically the stiffness matrix K, in terms of master element coordinates. The number of integration points was 2 × 2 for all nonlinear, couple stress, and transverse shear terms and 3 × 3 for all other terms in order to reduce shear-locking-like effects.
To accelerate the convergence of the iterative solver, acceleration parameters were implemented for static problems. This method uses a weighted average of the two previous solutions to obtain the solution increment instead of just using the last iteration’s solution. This weighted average adopts the form
where is the acceleration parameter, which must be a value from 0 to 1.
For the time approximation schemes, the Newmark constant average acceleration method was employed. Newmark’s method consists of approximating the solution and its first and second derivatives based on their previous values. This is achieved by using the approximation
where and are constants that depend on the method that is being implemented. For the constant-average acceleration method, the values are and .
The constrained generalized displacements for clamped and simply supported boundary conditions used in this work are defined in Table 1. The clamped outer edge boundary condition constrains the displacements, rotations, and thickness-wise stretch along the outer edge of the plate, and in the case of an annular plate, it leaves the inner edge free. For the clamped inner edge, the displacements, rotations, and thickness-wise stretch along the inner edge are constrained, and the outer edge is free. For the simply supported boundary condition, the outer edge displacements are stretched and constrained, but the rotations are released. In the case of annular plates, the simply supported case leaves the inner edge free.

Table 1.
Boundary condition definitions.
2.6. Steady State Heat Conduction
The steady-state heat conduction problem was solved using a 1D finite element model. The effective thermal conductivity, , was obtained using the Maxwell-Eucken model, as presented by Deng et al. [61].
where is the thermal conductivity of the solid, is the thermal conductivity of the fluid, and is the porosity. The thermal conductivity of the solid, , needs to be calculated using Equation (1). The finite element model approximation is
where represents the nodal temperatures of the element, and represents the quadratic Lagrange interpolation functions. Since thermal conductivity is considered a function of temperature, the Newton iteration method was used in order to model nonlinearity.
3. Model Validation
3.1. Static Load
The behavior of circular and annular plates under uniformly distributed mechanical loads was modeled using the first shear deformation theory by Reddy et al. [20]. The numerical results were compared with the current model. The following nondimensionalized parameters were used:
Figure 4 shows a mesh convergence study. The center deflection at associated with the load parameter is plotted.
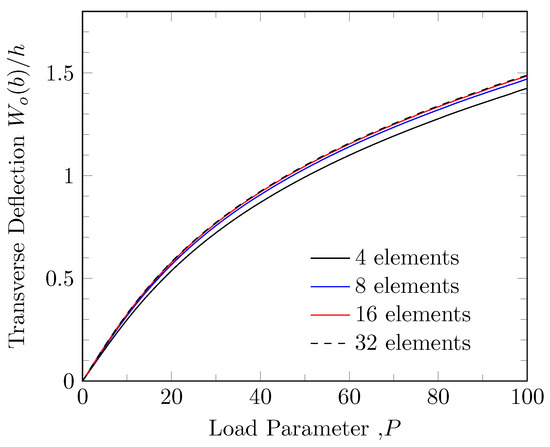
Figure 4.
Mesh convergence study.
A 16 by 1 mesh was used to model the circular and annular plates with a clamped outer edge. For the maximum deflection at , is plotted against the load parameter in Figure 5.
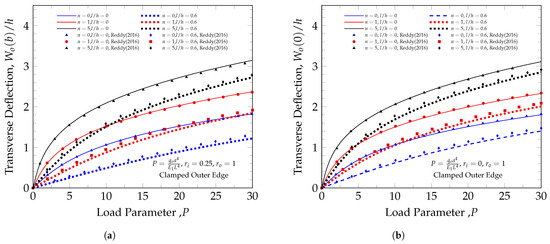
Figure 5.
Load deflection curves for clamped annular and circular plates. (a) Anular plate with clamped outer edge. (b) Circular plate with clamped outer edge.
There is good agreement between the current model and the one developed by Reddy et al. [20], both with and without length scale parameters. Clear nonlinear behavior is observed. The effect of a higher power-law index is to soften the material since the behavior becomes dominated by the softer material with elastic modulus, . Small discrepancies between the models can be attributed to the allowed change in thickness and the enforcement of zero traction at the upper and lower surfaces in the current model.
3.2. Asymmetric Load
The analytical solution for a circular plate under asymmetrical loads, as shown in Figure 6, was obtained by Reddy [34] using the infinitesimal strain definition. To validate the asymmetric behavior of the model, different loads were applied to a circular plate. Figure 7a,b show deflection along the load symmetry line. The linear and nonlinear solutions from the current model and the analytical solution from Reddy [34] are shown in the same plot.
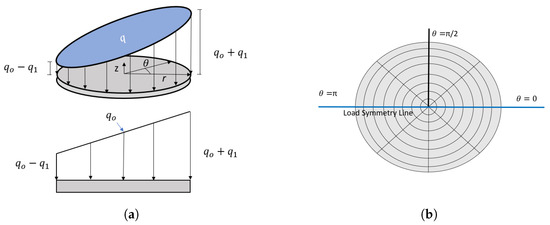
Figure 6.
Asymmetric load. (a) Asymmetric load form. (b) An 8 × 8 mesh.
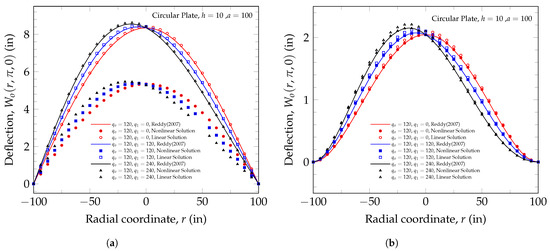
Figure 7.
Deflection along the symmetry line. (a) Simply supported. (b) Clamped.
The linear solution agrees very well with the analytical solution; this is expected given the strain definition used by Reddy [34]. The clamped case does not show much nonlinearity, and the linear, nonlinear, and analytical solutions all give virtually the same results.
3.3. Transient Response
The transient response of a circular plate clamped on the outer edge under a uniformly distributed load was analyzed by Reddy [62] using the first shear deformation theory (FSDT). The modeled plate has a radius of 100 in and a thickness of 2 in, and the numerical results for a uniformly distributed load of 1, 2, and 5 psi were obtained. A model verification study was conducted using the same geometry and loading cases as the current model. To ensure that the results are not mesh-dependent, a mesh convergence study was conducted using 6, 12, 24, 48, 96, and 192 elements in the radial direction and a single element in the angular direction, taking advantage of the polar coordinate formulation to establish symmetric boundary conditions.
Figure 8a shows that a mesh of 96 elements gives essentially the same results as a mesh of 192. The difference with respect to FSDT is less than at the peaks for 96 elements. The small stiffening effect may be attributed to zero traction enforcement and the higher-order model.
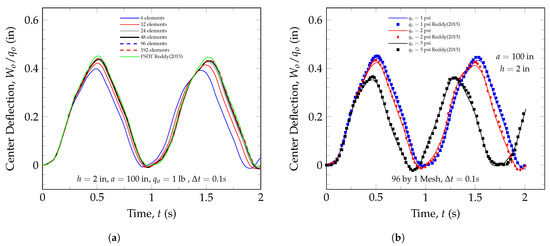
Figure 8.
Transient response validation. (a) Mesh convergence study of transient response for circular plate clamped in the outer edge. (b) Transient response for three different uniformly distributed loads for a clamped circular plate.
The transient response with 96 elements shows a clear match between the behavior of the plate using the present model and the behavior of the FSDT plate modeled by Reddy [62], as shown in Figure 8b. The increase in the uniformly distributed load affects both the amplitude and the frequency of the response, having a slightly smaller amplitude and higher frequency for higher loads.
3.4. Temperature Distribution
The temperature distribution of a functionally graded porous material was reported by Yapor et al. [17]. The constituents of the plate were zirconia and Ti-6Al-4 V, and their properties were considered to be temperature-dependent, adopting the polynomial presented by Reddy et al. [30]
Figure 9a shows the temperature distribution for the three porosity distributions considered and for no porosity. The plot shows remarkable agreement between the current model and the work of Yapor et al. [17]. The effect of different maximum porosity values with the symmetric porosity distribution (Type 1) is explored in Figure 9b, which also shows agreement between the models.
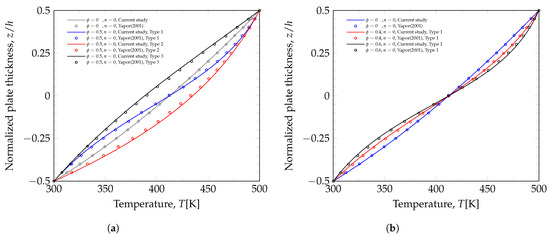
Figure 9.
Temperature distribution validation. (a) Temperature distribution for different porosity types. (b) Temperature distribution for Type 1 with different porosity values.
The small differences in the temperature distributions may be due to the use of different numbers of elements and element types since the current study used 100 linear elements, and the work carried out by Yapor et al. [17] used only 10 higher-order elements.
3.5. Thermo-Mechanical LOAD
The thermo-mechanical behavior of functionally graded plates was studied by Fallah et al. [48], and their results were validated against a previous study carried out by Ma et al. [33]. The same study was used to validate the work by Nosier et al. [47].
The materials chosen for this study were aluminum and zirconia, with the following material properties:
The mechanical load applied varied for different values of the load parameter, Q, from 0 to 300. The load parameter Q is defined as
where q is the mechanical, uniformly distributed load, b is the radius of the plate, is plate stiffness, and H is the thickness of the plate.
Thermal load was applied by holding the top and bottom surfaces at constant temperatures so that . The thermal and mechanical loads were applied gradually at the same time, as opposed to first applying the thermal load and then the mechanical load.
A mesh convergence test was conducted to ensure the results were not mesh-dependent. The displacement solutions were obtained using different numbers of elements. A 16 × 1 element mesh is enough for axisymmetric cases since a 32 × 1 version shows no significant improvement in the solution.
It was noted by Ma et al. [33] that pure thermal loading does not produce displacements in the case of clamped circular plates in a model, but it does produce displacements for simply supported plates. The current model predicts a very small displacement for pure thermal loading due to the allowed change in thickness, which the work by Ma [33] did not consider.
Good agreement between the models can be appreciated in Figure 10a. Slightly stiffer behavior by the current model may be explained by the higher-order model used, allowing for displacement along the thickness direction. As shown in the previous section, a higher power-law index corresponds to softer behavior, as the material properties become dominated by the metallic material.
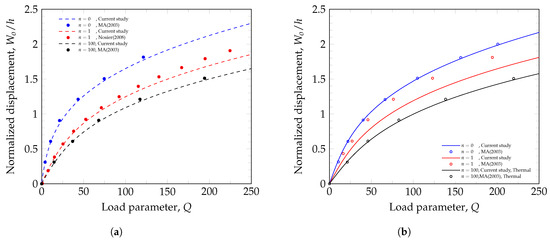
Figure 10.
Thermo-mechanical validation on circular clamped plates. (a) Thermo-mechanical load deflection curves. (b) Mechanical load deflection curves.
4. Numerical Examples
4.1. Dynamic Response
Dynamic response was studied using a thin plate of 100 inches in radius and 2 inches in thickness. The load applied was a uniformly distributed load of 1 psi, and no dampening was considered. Simply supported and clamped at the outer edge boundary conditions were used. The selected materials were zirconia and Ti-6Al-4V, the properties of which are shown in Table 2 and Table 3. A time step of 0.2 s and the constant-average acceleration method time scheme were used.

Table 2.
Temperature-dependent properties of zirconia.

Table 3.
Temperature-dependent properties of Ti-6Al-4V.
Figure 11a shows the expected behavior of a plate with and without length scale parameters. The effect of including the length scale parameter of the couple stress theory is to reduce amplitude and increase frequency across all power-law index numbers. The stiffening effect in micro-scale structures is clearly captured when utilizing the length scale parameter. The purely metallic plate at is the soft material configuration, and it shows a higher amplitude and lower frequency than the mostly ceramic plate at , which is mostly the stiffer material. The linearly varying material properties at represent a mixture of soft and stiff materials, showing behavior that is in between the previous two.
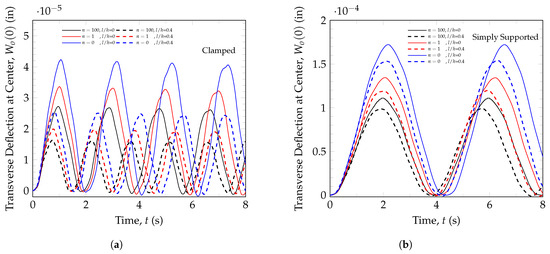
Figure 11.
Dynamic response for different material index numbers. (a) Clamped circular plate. (b) Simply supported circular plate.
When comparing Figure 11a and Figure 11b, it can be observed that boundary conditions play a big role in frequency and amplitude. The simply supported plate, which has a softer boundary condition than the clamped plate, shows a larger frequency than the case with the clamped boundary condition and a much larger amplitude. The trends regarding the index number and length scale parameters are similar in both cases. However, the clamped plates are more sensitive to material variations and the length scale parameters.
4.2. Static Response Under Symmetric Thermo-Mechanical Loads
For the static behavior under symmetric thermo-mechanical loads, a geometry of m, m, and m was used with the same FGM used in the dynamic study. The parameters a, b, and h are shown in Figure 12. The mechanical load was varied up to a load parameter of 30, as defined by Reddy et al. [20]. The thermal load was applied by holding the metallic surface at 300 degrees and the ceramic surface at 400 degrees. Cases of purely mechanical and thermo-mechanical loads were analyzed.
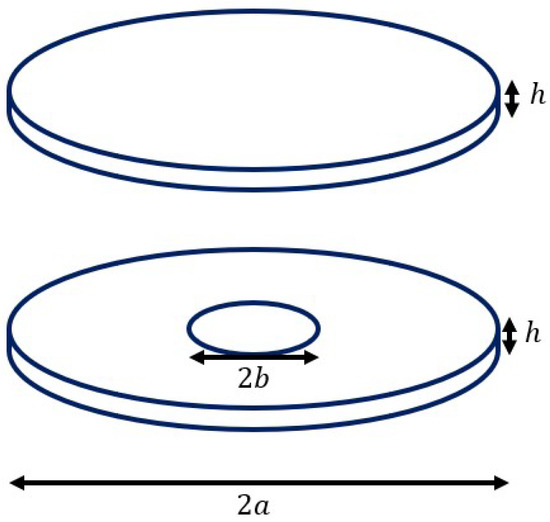
Figure 12.
Circular and annular plates.
The impact of thermal load on deflection diminishes as the load parameter increases, as shown in Figure 13a,b, where the thermo-mechanical case gives a very similar result to the purely mechanical load at load parameter 30; however, the curvature is higher in the thermo-mechanical case, and its effect is more noticeable at lower load parameter values. It can also be noted that the length scale parameters have a strong stiffening effect on both purely mechanical and thermo-mechanical cases. In the case of the thermo-mechanical load, the thermal load makes the plates stiffer, with compressive thermal stresses. This stiffening also noticeably reduces the nonlinear behavior of the plate. The stresses generated by the thermo-mechanical load close to the clamped edge of an annular plate clamped on the outer edge are shown in Figure 14a,b. The effect of the length scale parameter clearly results in a reduction in stress for all cases. Unlike homogeneous materials, the bending stress distribution of FGMs is not a linear variation. This shows that we can design the stress variation in FGM by controlling material variation.
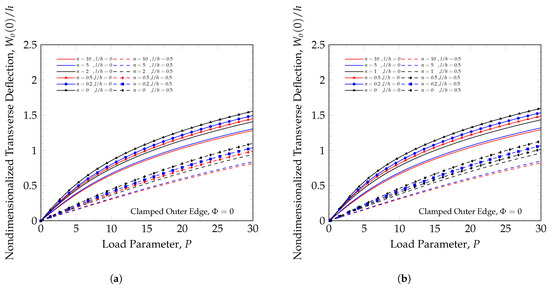
Figure 13.
Annular plate static response. (a) Mechanical load. (b) Thermo-mechanical load.
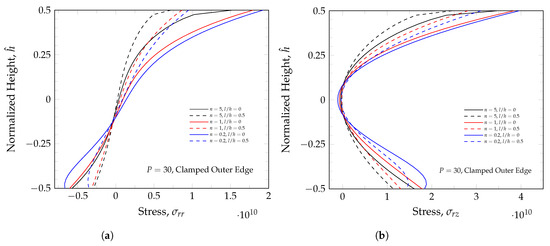
Figure 14.
Stresses for clamped circular plate under static thermo-mechanical load. (a) Radial stress. (b) Transverse shear stress.
4.3. Static Response Under Asymmetric Loads
Asymmetric cases were solved to assess the model’s full plate-modeling capabilities using the same geometry and loads as the asymmetric model verification cases, as well as the same FGM used in the other parametric study cases. Figure 15b shows the elastic curve for the same three FG plates under the same symmetric load and under two different asymmetric loads. The observed behavior corresponds with what was expected and the previous results. The stiffest behavior corresponds with the mostly ceramic plate, and the softest behavior is shown by the metallic plate, and the linear distribution () shows intermediate behavior. The different asymmetric loads change the magnitude of the maximum deflection of the plate but do not affect the deflection at the center, .
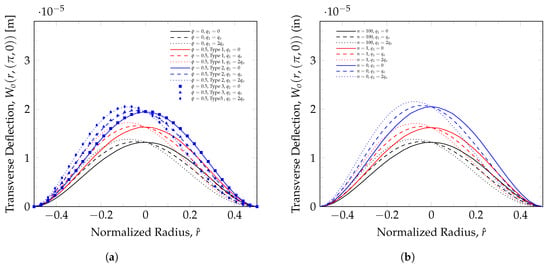
Figure 15.
Behavior at symmetry line for clamped circular plate. (a) Porosity effect under asymmetric loads. (b) Power-law index effect under asymmetric loads.
The porosity effect on full-plate behavior was explored using the three different porosity types and a maximum porosity of 0.5. Figure 15a shows the effect of the three different porosity distributions and compares this to the solid plate for a mostly ceramic plate (). The stiffest plate is the solid plate. Porosity distribution Type 1 is much stiffer than the Type 2 and 3 porosity distributions, as expected. In the considered examples, the Type 2 and Type 3 porosity distributions are symmetric to each other about the middle plane of plates, and the plate bending stiffness of homogeneous materials with these two porosity distributions are the same. As expected, the differences between porosity Types 2 and 3 are negligible. Therefore, distribution Type 3 can be omitted in the case of homogenous materials without loss of information.
5. Conclusions
A nonlinear finite element model for functionally graded porous micro-plates was developed for circular and annular micro-plates in cylindrical coordinates. In order to obtain a quadratic variation of transverse shear strains, the displacement field was expanded in the transverse direction with second-order transverse displacement and third-order in-plane displacements. Von Kármán strains were used to enable the model to capture moderate rotations. To account for length scale effects, the modified couple stress theory was implemented. The variation in material properties via the thickness of the plate was modeled using a power-law volumetric distribution. Three different porosity distributions were prescribed for the material.
The equations of motion for the proposed model were obtained using the principle of virtual displacements. The finite element model was obtained using a conforming four-node plate element with 112 degrees of freedom. The tangent matrix was derived to implement the Newton iteration method. Gauss-Legendre quadrature was utilized to numerically integrate the element matrices.
The model was validated against analytical solutions and numerical studies from the literature. The static response under a uniformly distributed load with and without length scale parameters was validated for various power-law index numbers. The temperature distribution matched the results available in the literature. Static response under an asymmetric load, dynamic response, and thermo-mechanical behavior all showed good agreement with the analytical solutions and available literature.
The numerical results for annular and circular plates under different loads and boundary conditions are presented; a parametric study was conducted. The study shows the following:
- A stiffening effect of the length scale parameter in the modified couple stress theory was observed for all boundary conditions and loads;
- Boundary conditions play an important role in the nonlinear behavior of the plate;
- The variation in the power-law index makes the plate softer or stiffer as it transitions from metallic- to ceramic-dominated properties;
- The model is able to capture nonlinear behavior and material variations in plate thickness. The proposed model was validated against other models in the literature, and it could be useful to study cases where these effects are expected to be significant;
- The proposed model has been found to be computationally expensive. This was expected due to the higher-order terms, and it is in line with the observations made by Reddy et al. [20] for their model, which also operates in cylindrical coordinates.
Author Contributions
Conceptualization, J.K.; Methodology, J.K.; Software, E.N.; Validation, J.K. and E.N.; Formal analysis, E.N.; Investigation, E.N.; Resources, J.K.; Writing—original draft, E.N.; Writing—review & editing, J.K.; Visualization, E.N.; Supervision, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Stiffness Matrix Elements
Appendix A.2. Mass Matrix Elements
Appendix A.3. Tangent Matrix Elements
References
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and Analysis of Functionally Graded Materials and Structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Mahamood, R.; Akinlabi, E.; Shukla, D.M.; Pityana, S. Functionally graded material: An overview. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2012; Volume III. [Google Scholar]
- Jha, D.; Kant, T.; Singh, R. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Swaminathan, K.; Sangeetha, D. Thermal analysis of FGM plates—A critical review of various modeling techniques and solution methods. Compos. Struct. 2017, 160, 43–60. [Google Scholar] [CrossRef]
- Judy, J.W. Microelectromechanical systems (MEMS): Fabrication, design and applications. Smart Mater. Struct. 2001, 10, 1115. [Google Scholar] [CrossRef]
- Tahani, M.; Askari, A.R.; Mohandes, Y.; Hassani, B. Size-dependent free vibration analysis of electrostatically pre-deformed rectangular micro-plates based on the modified couple stress theory. Int. J. Mech. Sci. 2015, 94–95, 185–198. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Ma, Q.; Clarke, D. Size dependent hardness of silver single crystals. J. Mater. Res. 1995, 10, 853–863. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Fleck, N.; Muller, G.; Ashby, M.; Hutchinson, J. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Lam, D.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Fleck, N.; Hutchinson, J. A Reformulation of Strain Gradient Plasticity. J. Mech. Phys. Solids 2001, 49, 2245–2271. [Google Scholar] [CrossRef]
- Shu, J.Y.; King, W.E.; Fleck, N.A. Finite elements for materials with strain gradient effects. Int. J. Numer. Methods Eng. 1999, 44, 373–391. [Google Scholar] [CrossRef]
- Yapor Genao, F.; Kim, J.; Żur, K.K. Nonlinear finite element analysis of temperature-dependent functionally graded porous micro-plates under thermal and mechanical loads. Compos. Struct. 2021, 256, 112931. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Ke, L.L.; Yang, J.; Kitipornchai, S.; Bradford, M.A. Bending, buckling and vibration of size-dependent functionally graded annular microplates. Compos. Struct. 2012, 94, 3250–3257. [Google Scholar] [CrossRef]
- Reddy, J.; Romanoff, J.; Loya, J.A. Nonlinear finite element analysis of functionally graded circular plates with modified couple stress theory. Eur. J. Mech.—A/Solids 2016, 56, 92–104. [Google Scholar] [CrossRef]
- Reddy, J.; Berry, J. Nonlinear theories of axisymmetric bending of functionally graded circular plates with modified couple stress. Compos. Struct. 2012, 94, 3664–3668. [Google Scholar] [CrossRef]
- Tadi Beni, Y.; Mehralian, F.; Razavi, H. Free vibration analysis of size-dependent shear deformable functionally graded cylindrical shell on the basis of modified couple stress theory. Compos. Struct. 2015, 120, 65–78. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Eshraghi, I.; Dag, S.; Soltani, N. Bending and free vibrations of functionally graded annular and circular micro-plates under thermal loading. Compos. Struct. 2016, 137, 196–207. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Bedroud, M.; Nazemnezhad, R. An exact analytical solution for free vibration of functionally graded circular/annular Mindlin nanoplates via nonlocal elasticity. Compos. Struct. 2013, 103, 108–118. [Google Scholar] [CrossRef]
- Chi, S.H.; Chung, Y.L. Mechanical behavior of functionally graded material plates under transverse load—Part I: Analysis. Int. J. Solids Struct. 2006, 43, 3657–3674. [Google Scholar] [CrossRef]
- Chi, S.H.; Chung, Y.L. Mechanical behavior of functionally graded material plates under transverse load—Part II: Numerical results. Int. J. Solids Struct. 2006, 43, 3675–3691. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Sab, K.; Bonnet, G. First-order shear deformation plate models for functionally graded materials. Compos. Struct. 2008, 83, 25–36. [Google Scholar] [CrossRef]
- Reddy, J. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar]
- Reddy, J.; Chin, C. Thermomechanical analysis of functionally graded cylinders and plates. J. Therm. Stress. 1998, 21, 593–626. [Google Scholar]
- Praveen, G.; Reddy, J. Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates. Int. J. Solids Struct. 1998, 35, 4457–4476. [Google Scholar] [CrossRef]
- Reddy, J.; Wang, C.; Kitipornchai, S. Axisymmetric bending of functionally graded circular and annular plates. Eur. J. Mech.–A/Solids 1999, 18, 185–199. [Google Scholar] [CrossRef]
- Ma, L.; Wang, T. Nonlinear bending and post-buckling of a functionally graded circular plate under mechanical and thermal loadings. Int. J. Solids Struct. 2003, 40, 3311–3330. [Google Scholar] [CrossRef]
- Reddy, J. Theory and analysis of Elastic Plates and Shells; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Najafizadeh, M.; Heydari, H. Thermal buckling of functionally graded circular plates based on higher order shear deformation plate theory. Eur. J. Mech.—A/Solids 2004, 23, 1085–1100. [Google Scholar] [CrossRef]
- Reddy, J.; Kim, J. A nonlinear modified couple stress-based third-order theory of functionally graded plates. Compos. Struct. 2012, 94, 1128–1143. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J. Analytical solutions for bending, vibration, and buckling of FGM plates using a couple stress-based third-order theory. Compos. Struct. 2013, 103, 86–98. [Google Scholar] [CrossRef]
- Prakash, T.; Ganapathi, M. Asymmetric flexural vibration and thermoelastic stability of FGM circular plates using finite element method. Compos. Part B Eng. 2006, 37, 642–649. [Google Scholar] [CrossRef]
- Efraim, E.; Eisenberger, M. Exact vibration analysis of variable thickness thick annular isotropic and FGM plates. J. Sound Vib. 2007, 299, 720–738. [Google Scholar] [CrossRef]
- Żur, K. Free vibration analysis of discrete-continuous functionally graded circular plates via Neumann series method. Appl. Math. Model. 2019, 73, 166–189. [Google Scholar] [CrossRef]
- Rahmat Talabi, M.; Saidi, A. An explicit exact analytical approach for free vibration of circular/annular functionally graded plates bonded to piezoelectric actuator/sensor layers based on Reddy’s plate theory. Appl. Math. Model. 2013, 37, 7664–7684. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, F.; Wang, A.; Shuai, C.; Tang, J.; Wang, Q. Dynamics analysis of functionally graded porous (FGP) circular, annular and sector plates with general elastic restraints. Compos. Part B Eng. 2019, 159, 20–43. [Google Scholar] [CrossRef]
- Talha, M.; Singh, B. Static response and free vibration analysis of FGM plates using higher order shear deformation theory. Appl. Math. Model. 2010, 34, 3991–4011. [Google Scholar] [CrossRef]
- Vinh, P.V. A novel modified nonlocal strain gradient theory for comprehensive analysis of functionally graded nanoplates. Acta Mech. 2025, 236, 173–204. [Google Scholar]
- Wang, S.; Ding, W.; Li, Z.; Xu, B.; Zhai, C.; Kang, W.; Yang, W.; Li, Y. A size-dependent quasi-3D model for bending and buckling of porous functionally graded curved nanobeam. Int. J. Eng. Sci. 2023, 193, 103962. [Google Scholar]
- Nosier, A.; Fallah, F. Non-linear analysis of functionally graded circular plates under asymmetric transverse loading. Int. J.-Non-Linear Mech. 2009, 44, 928–942. [Google Scholar] [CrossRef]
- Nosier, A.; Fallah, F. Reformulation of Mindlin–Reissner governing equations of functionally graded circular plates. Acta Mech. 2008, 198, 209–233. [Google Scholar]
- Fallah, F.; Nosier, A. Nonlinear behavior of functionally graded circular plates with various boundary supports under asymmetric thermo-mechanical loading. Compos. Struct. 2012, 94, 2834–2850. [Google Scholar] [CrossRef]
- Kim, J.; Nava, E.; Rakici, S. Nonlinear Finite Element Model for Bending Analysis of Functionally-Graded Porous Circular/Annular Micro-Plates under Thermomechanical Loads Using Quasi-3D Reddy Third-Order Plate Theory. Materials 2023, 16, 3505. [Google Scholar] [CrossRef] [PubMed]
- Piotr, D. Finite element method formulation in polar coordinates for transient heat conduction problems. J. Therm. Sci. 2016, 25, 188–194. [Google Scholar] [CrossRef]
- Touloukian, Y.S. Thermophysical Properties of High Temperature Solid Materials. Volume 4. Oxides and Their Solutions and Mixtures; Defense Technical Information Center: Fort Belvoir, VA, USA, 1966. [Google Scholar]
- Nguyen, L.B.; Thai, C.H.; Zenkour, A.; Nguyen-Xuan, H. An isogeometric Bézier finite element method for vibration analysis of functionally graded piezoelectric material porous plates. Int. J. Mech. Sci. 2019, 157–158, 165–183. [Google Scholar] [CrossRef]
- Carranza, J.C.; Pérez, L.; Ganesan, R.; Casas, B.Y.; Drew, R.A.L.; Ruiz-Aguilar, C.; Figueroa, I.A.; Alfonso, I. Effect of fractal distribution of the porosity on mechanical properties of Al foams manufactured by infiltration. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 379. [Google Scholar] [CrossRef]
- Gao, K.; Li, R.; Yang, J. Dynamic characteristics of functionally graded porous beams with interval material properties. Eng. Struct. 2019, 197, 109441. [Google Scholar]
- Coskun, S.; Kim, J.; Toutanji, H. Bending, Free Vibration, and Buckling Analysis of Functionally Graded Porous Micro-Plates Using a General Third-Order Plate Theory. J. Compos. Sci. 2019, 3, 15. [Google Scholar] [CrossRef]
- Mota, A.F.; Loja, M.A.R.; Barbosa, J.I.; Rodrigues, J.A. Porous Functionally Graded Plates: An Assessment of the Influence of Shear Correction Factor on Static Behavior. Math. Comput. Appl. 2020, 25, 25. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J. A general third-order theory of functionally graded plates with modified couple stress effect and the von Kármán nonlinearity: Theory and finite element analysis. Acta Mech. 2015, 226, 1973–2998. [Google Scholar] [CrossRef]
- Golmakani, M.; Kadkhodayan, M. Nonlinear bending analysis of annular FGM plates using higher-order shear deformation plate theories. Composite Structures 2011, 93, 973–982. [Google Scholar] [CrossRef]
- Mognhod Bezzie, Y.; Woldemichael, D. Effects of graded-index and Poisson’s ratio on elastic-solutions of a pressurized functionally graded material thick-walled cylinder. Forces Mech. 2021, 4, 100032. [Google Scholar] [CrossRef]
- Bogner, F. The generation of interelement compatible stiffness and mass matrices by the use of interpolation formulae. In Proceedings of the Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, Fairborn, OH, USA, 26–28 October 1965. [Google Scholar]
- Deng, Z.; Huang, Y.; Zhang, C.; Chen, Y. Heat Conduction in Porous Media Characterized by Fractal Geometry. Energies 2017, 10, 1230. [Google Scholar] [CrossRef]
- Reddy, J. An Introduction to Nonlinear Finite Element Analysis, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).