Scarce Sample-Based Reliability Estimation and Optimization Using Importance Sampling
Abstract
1. Introduction
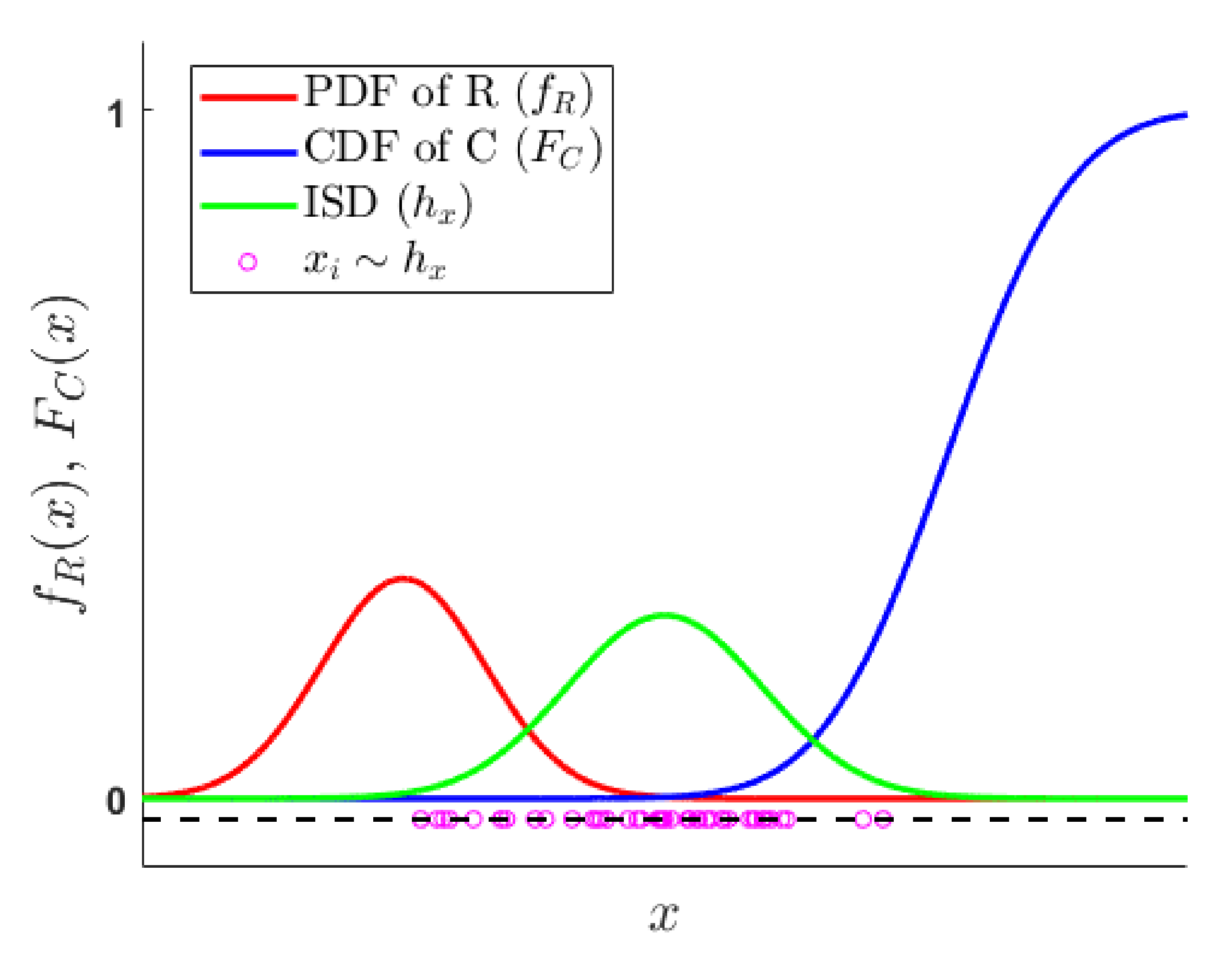
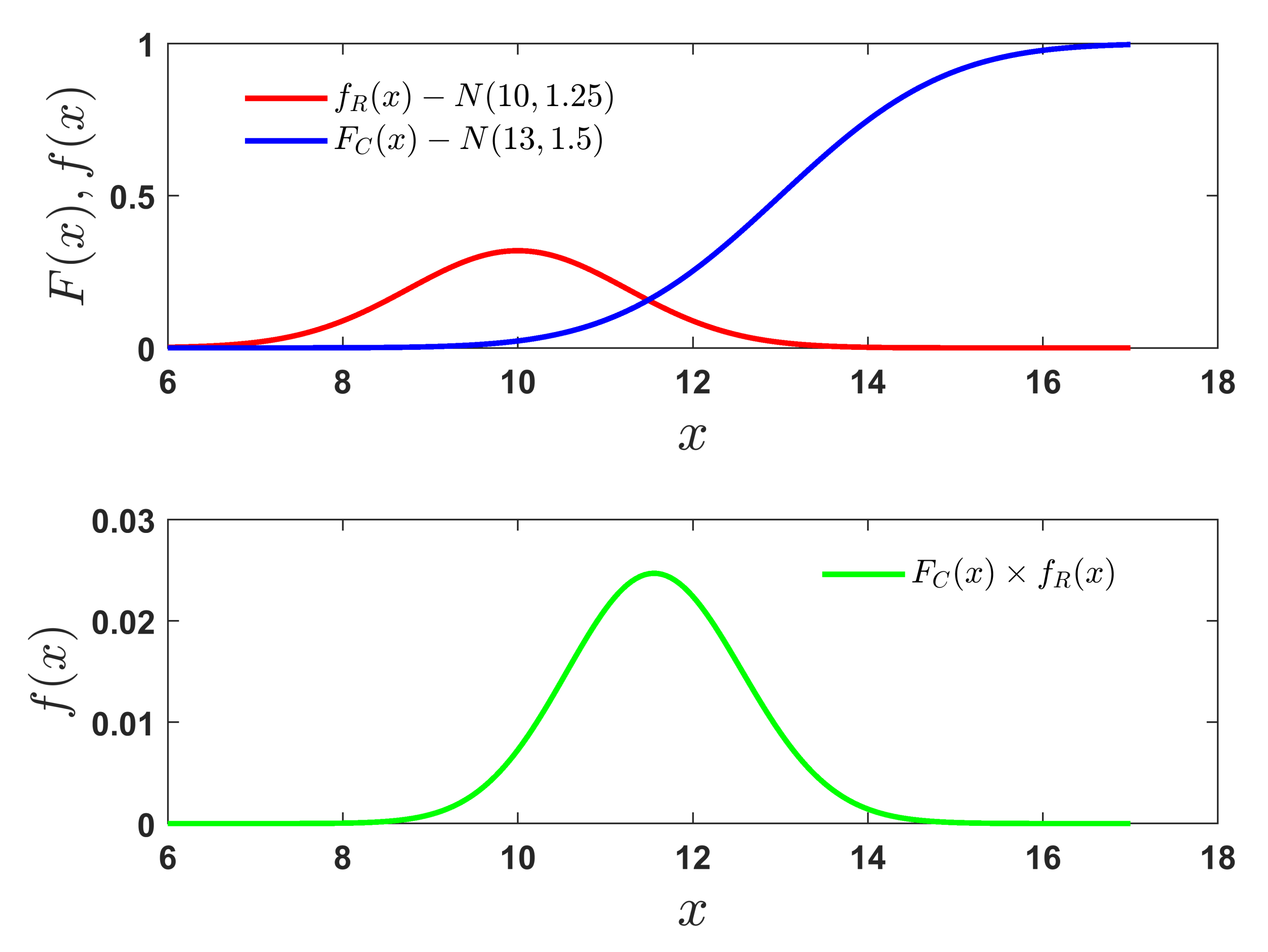
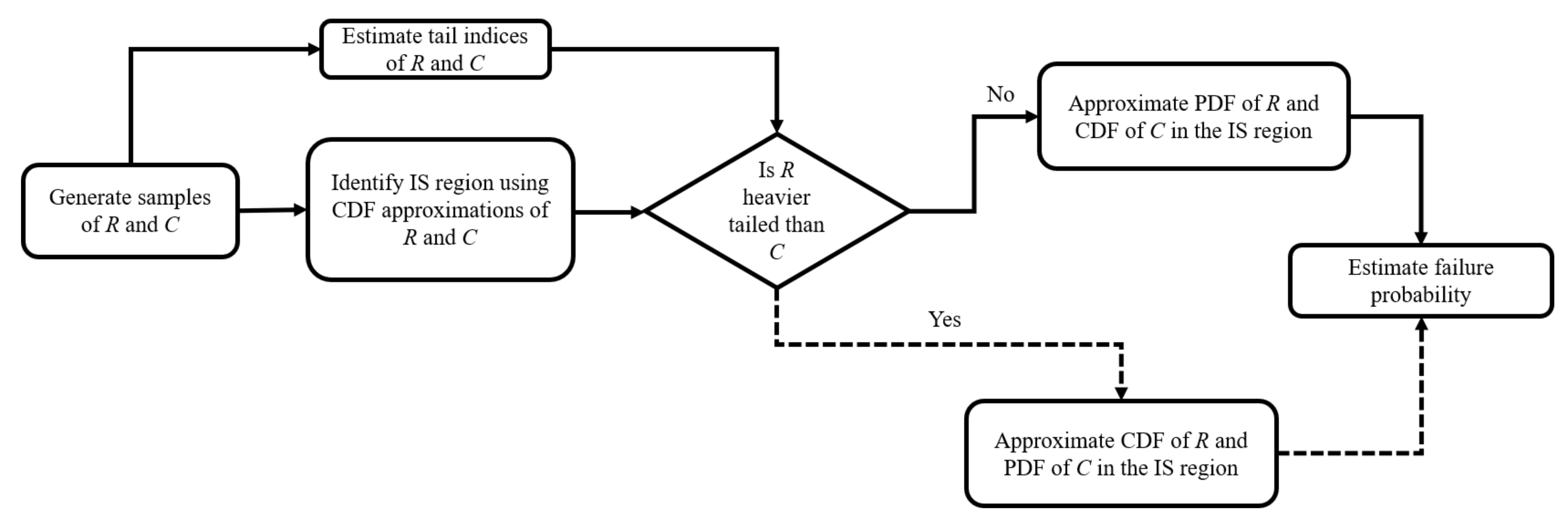
2. Reliability Estimation Using Importance Sampling for Separable Limit States
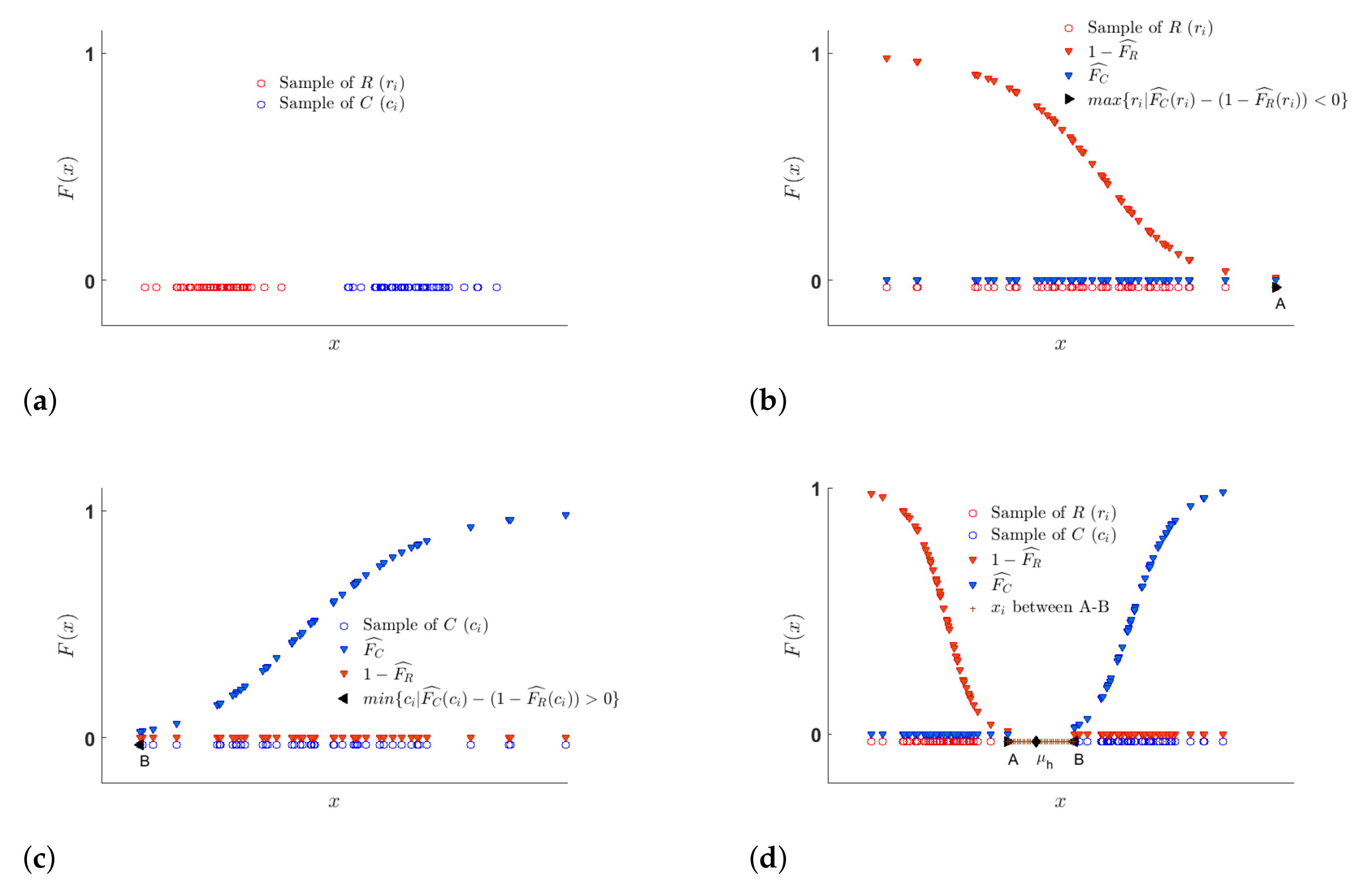
3. Identifying Parameters of Gaussian ISD
| Algorithm 1 Finding . |
|
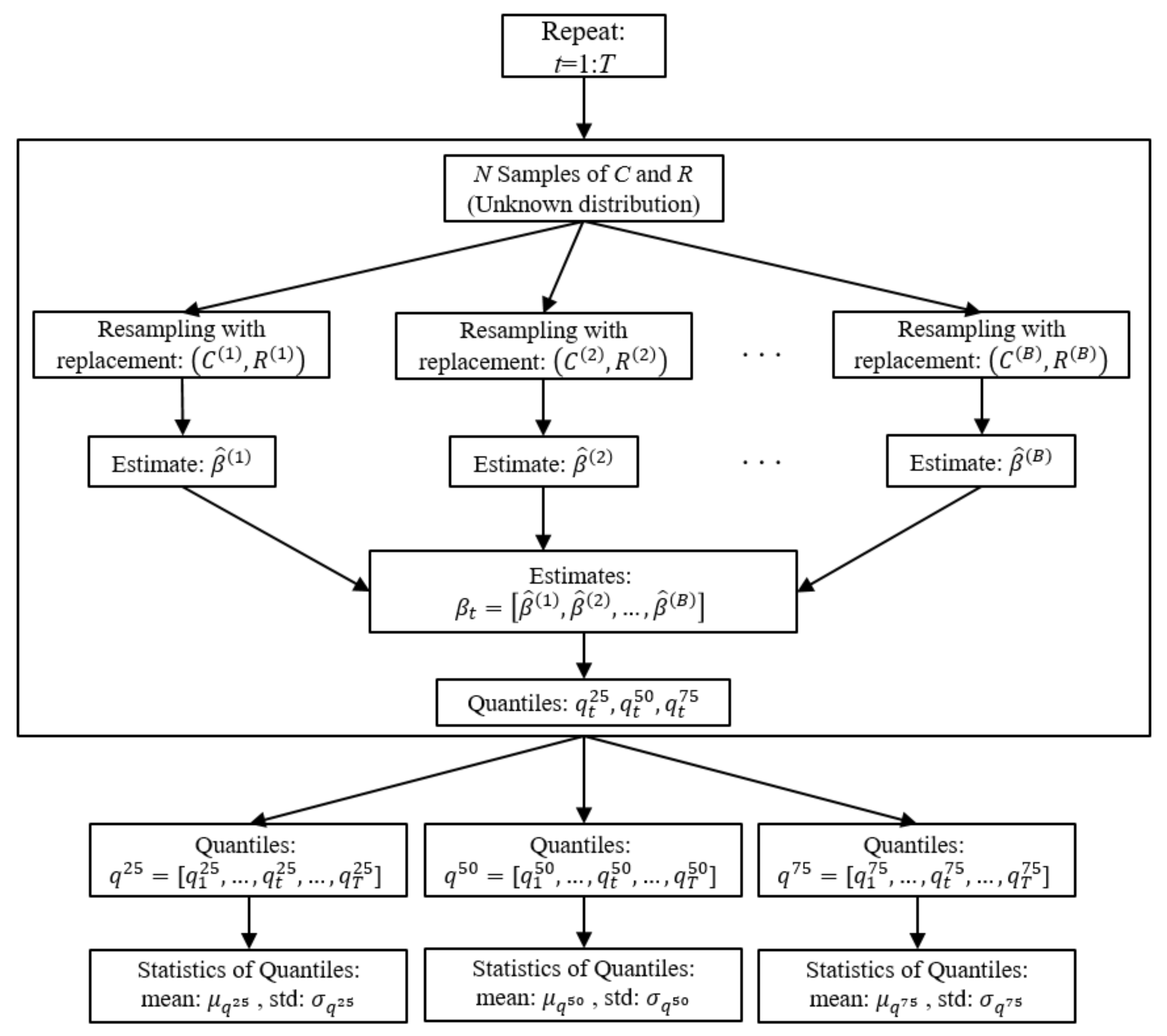
4. Estimation of Reliability and Its Confidence Bounds
| Algorithm 2 Confidence bounds using bootstrap. |
|
Tail-Index Estimation
5. Reliability Estimation Examples
5.1. Example 1: Concave Limit State 1
5.2. Example 2: Concave Limit State 2
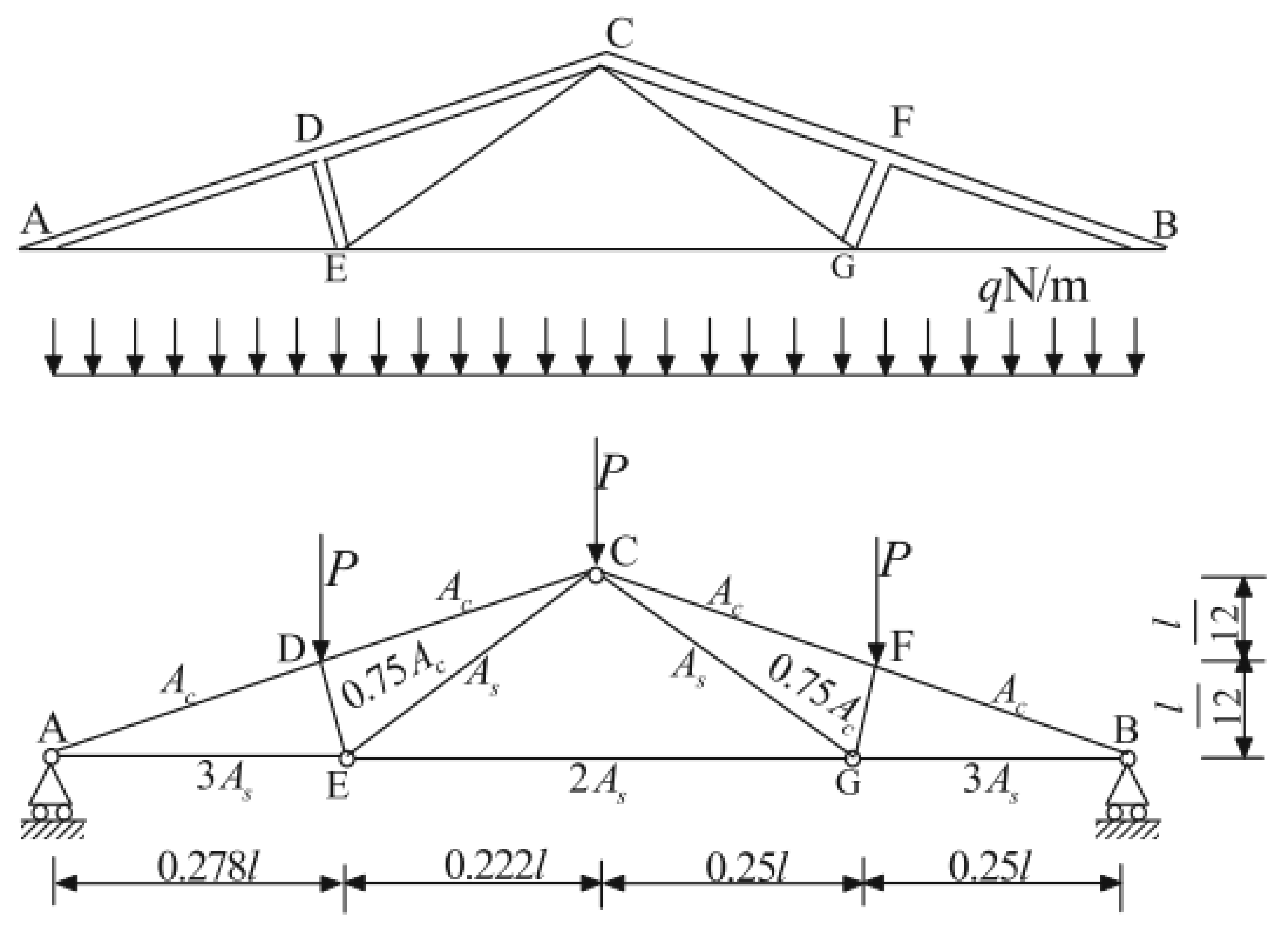
5.3. Example 3: Roof Truss Example
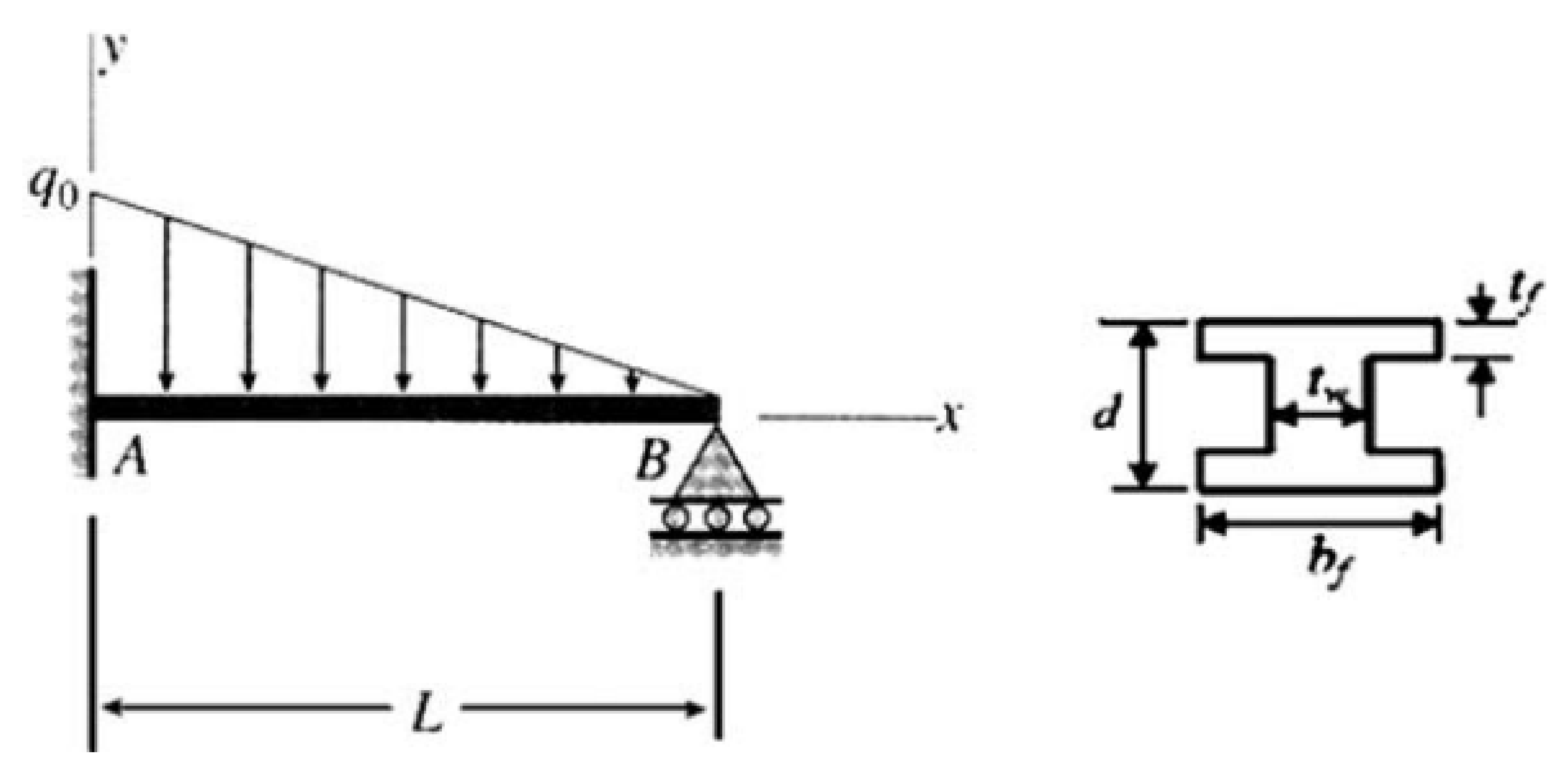
5.4. Example 4: Propped Cantilever Beam Example
6. Application to RBDO Examples
| Algorithm 3 RBDO using proposed importance sampling approach. |
|
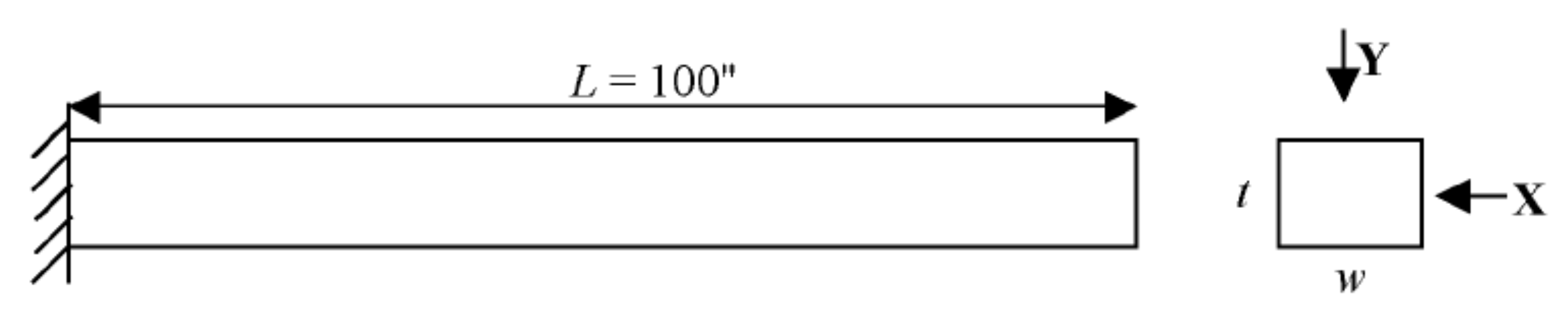
6.1. Cantilever Beam Example
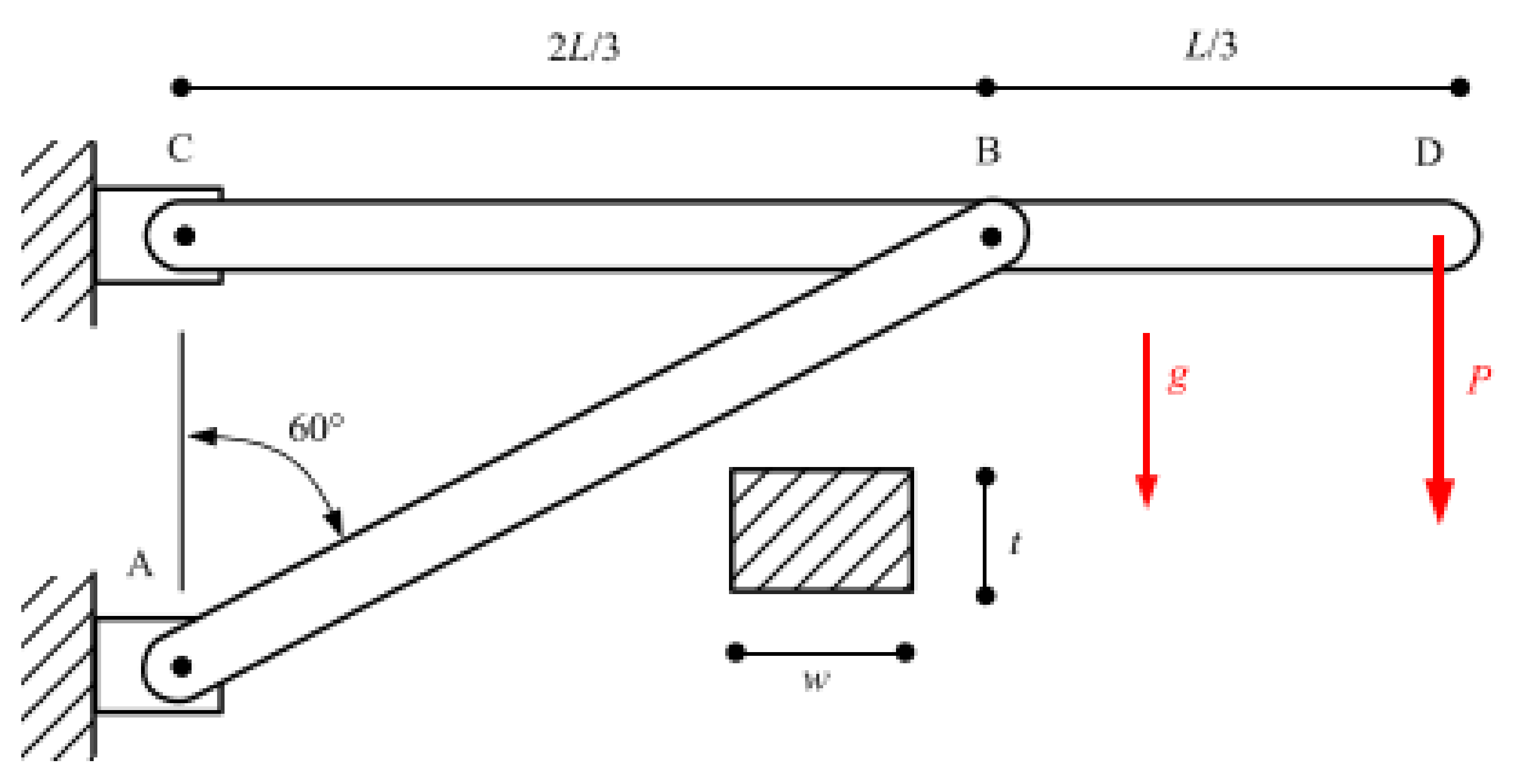
6.2. Bracket Structure Example
- (i)
- Maximum bending stress of beam CD at point B does not exceed its yield strength ,
- (ii)
- Maximum axial load on beam AB does not exceed the Euler critical buckling load .
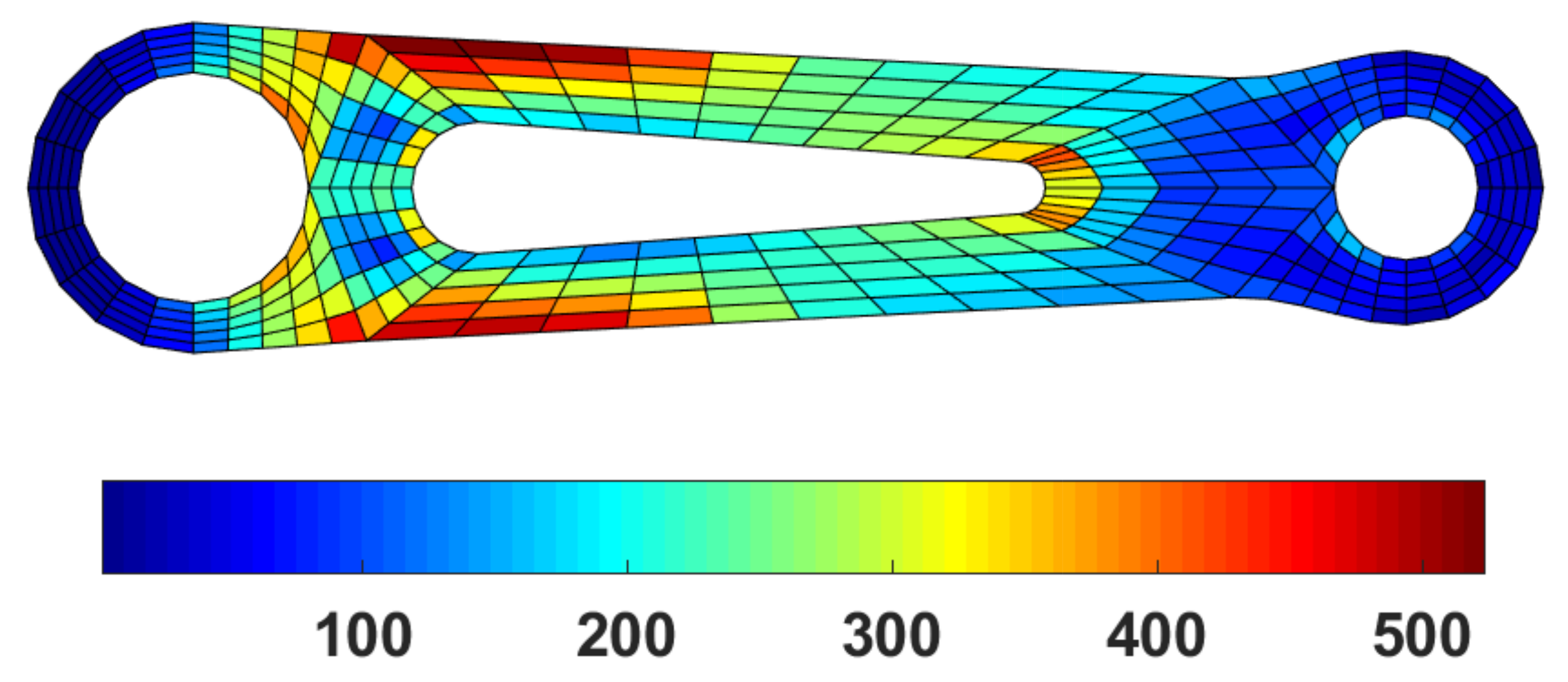
6.3. Torque Arm Example
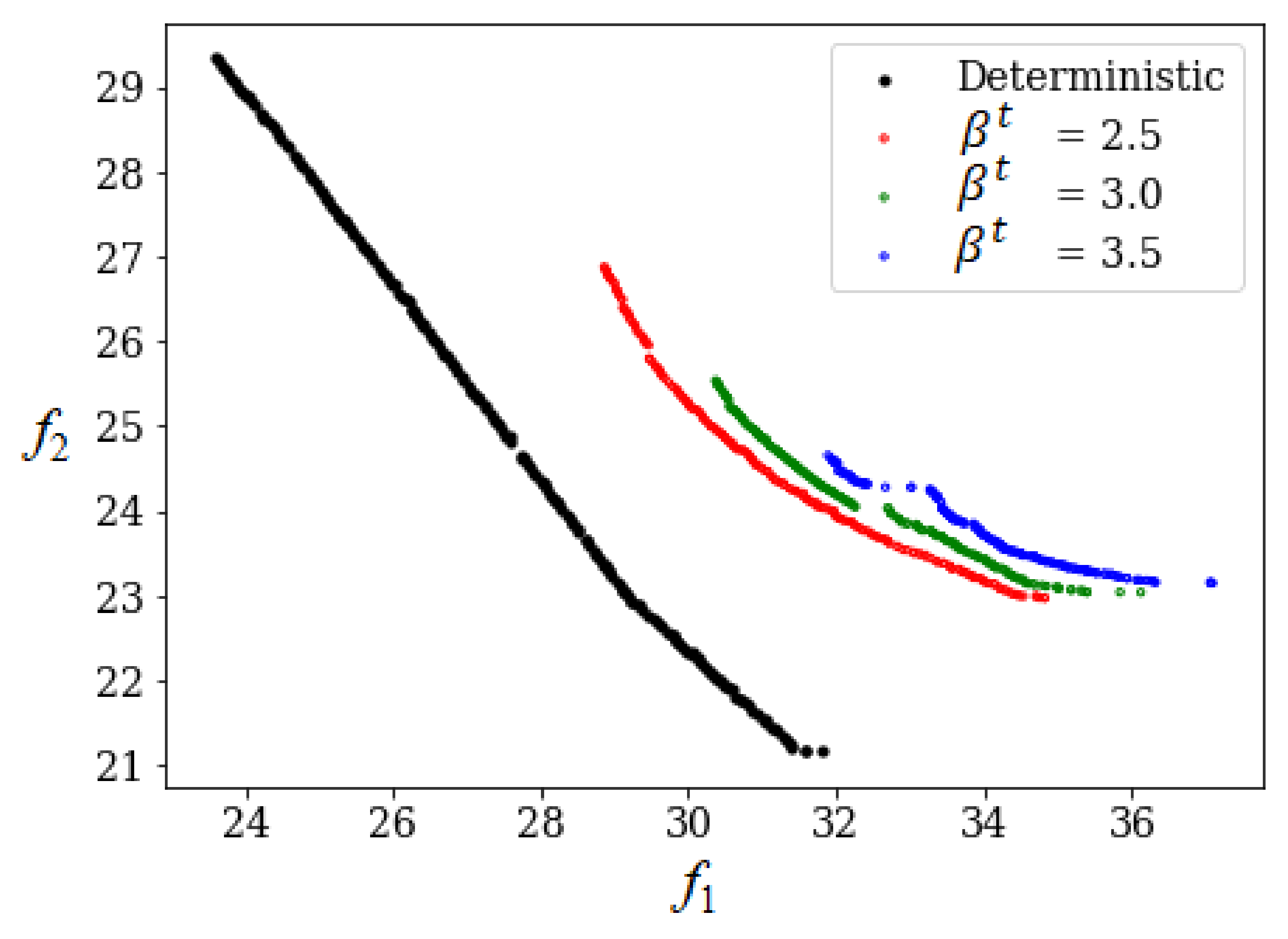
6.4. Car Side-Impact Problem—A Multi-Objective Reliability-Based Design Optimization (MORBDO) Example
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Kernel Density Estimation (KDE)
Appendix B. Third-Order Polynomial Normal Transformation Technique (TPNT)
Appendix C. Car Side-Impact Problem
References
- Au, S.K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Gollwitzer, S.; Kruse, W.; Rackwitz, R. New light on first- and second-order reliability methods. Struct. Saf. 1987, 4, 267–284. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Stix, R. A critical appraisal of methods to determine failure probabilities. Struct. Saf. 1987, 4, 293–309. [Google Scholar] [CrossRef]
- Rackwitz, R. Reliability analysis-a review and some perspective. Struct. Saf. 2001, 23, 365–395. [Google Scholar] [CrossRef]
- Engelund, S.; Rackwitz, R. A benchmark study on importance sampling techniques in structural reliability. Struct. Saf. 1993, 12, 255–276. [Google Scholar] [CrossRef]
- Zhi, P.; Yun, G.; Wang, Z.; Shi, P.; Guo, X.; Wu, J.; Ma, Z. A Novel Reliability Analysis Approach under Multiple Failure Modes Using an Adaptive MGRP Model. Appl. Sci. 2022, 12, 8961. [Google Scholar] [CrossRef]
- Tsompanakis, Y.; Papadrakakis, M. Large-scale reliability-based structural optimization. Struct. Multidiscip. Optim. 2004, 26, 429–440. [Google Scholar] [CrossRef]
- Chatterjee, T.; Chakraborty, S.; Chowdhury, R. A critical review of surrogate assisted robust design optimization. Arch. Comput. Methods Eng. 2019, 26, 245–274. [Google Scholar] [CrossRef]
- Li, J.; Xiu, D. Evaluation of failure probability via surrogate models. J. Comput. Phys. 2010, 229, 8966–8980. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, W.; Wang, W.; Cao, Z. An improved radial basis function network for structural reliability analysis. J. Mech. Sci. Technol. 2011, 25, 2151–2159. [Google Scholar] [CrossRef]
- Dubourg, V.; Sudret, B.; Deheeger, F. Metamodel-based importance sampling for structural reliability analysis. Probabilistic Eng. Mech. 2013, 33, 47–57. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Kramer, B.; Willcox, K.E. Information Reuse for Importance Sampling in Reliability-Based Design Optimization. Reliab. Eng. Syst. Saf. 2020, 201, 106853. [Google Scholar] [CrossRef]
- Foschi, R.; Li, H.; Zhang, J. Reliability and performance-based design: A computational approach and applications. Struct. Saf. 2002, 24, 205–218. [Google Scholar] [CrossRef]
- Qu, X.; Haftka, R.T. Reliability-based design optimization using probabilistic sufficiency factor. Struct. Multidiscip. Optim. 2004, 27, 314–325. [Google Scholar] [CrossRef]
- Moustapha, M.; Sudret, B. Surrogate-assisted reliability-based design optimization: A survey and a unified modular framework. Struct. Multidiscip. Optim. 2019, 60, 2157–2176. [Google Scholar] [CrossRef]
- Bichon, B.J. Efficient Surrogate Modeling for Reliability Analysis and Design. Ph.D. Thesis, Graduate School of Vanderbilt University, Nashville, TN, USA, 2010. [Google Scholar]
- Melchers, R.E. Importance sampling in structural systems. Struct. Saf. 1989, 6, 3–10. [Google Scholar] [CrossRef]
- Melchers, R.E. Search-based importance sampling. Struct. Saf. 1990, 9, 117–128. [Google Scholar] [CrossRef]
- West, N.; Swiler, L. Importance sampling: Promises and limitations. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 12–15 April 2010; pp. 1–14. [Google Scholar] [CrossRef][Green Version]
- Yin, C.; Kareem, A. Computation of failure probability via hierarchical clustering. Struct. Saf. 2016, 61, 67–77. [Google Scholar] [CrossRef]
- Smarslok, B.P.; Haftka, R.T.; Carraro, L.; Ginsbourger, D. Improving accuracy of failure probability estimates with separable Monte Carlo. Int. J. Reliab. Saf. 2010, 4, 393. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Haftka, R.T. Separable Monte Carlo combined with importance sampling for variance reduction. Int. J. Reliab. Saf. 2013, 7, 201. [Google Scholar] [CrossRef]
- Melchers, R.E. Structural Reliability Analysis and Prediction; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- De Boer, P.T.; Kroese, D.P.; Rubinstein, R.Y. A Tutorial on the Cross-Entropy Method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Kurtz, N.; Song, J. Cross-entropy-based adaptive importance sampling using Gaussian mixture. Struct. Saf. 2013, 42, 35–44. [Google Scholar] [CrossRef]
- Cao, Q.D.; Choe, Y. Cross-entropy based importance sampling for stochastic simulation models. Reliab. Eng. Syst. Saf. 2019, 191, 106526. [Google Scholar] [CrossRef]
- Geyer, S.; Papaioannou, I.; Straub, D. Cross entropy-based importance sampling using Gaussian densities revisited. Struct. Saf. 2019, 76, 15–27. [Google Scholar] [CrossRef]
- Ang, G.L.; Ang, A.H.; Tang, W.H. Optimal importance-sampling density estimator. J. Eng. Mech. 1992, 118, 1146–1163. [Google Scholar] [CrossRef]
- Zhang, P. Nonparametric Importance Sampling. J. Am. Stat. Assoc. 1996, 91, 1245–1253. [Google Scholar] [CrossRef]
- Au, S.; Beck, J. A new adaptive importance sampling scheme for reliability calculations. Struct. Saf. 1999, 21, 135–158. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, H.; Rasmussen, K.J.R.; Wang, W. Wavelet density-based adaptive importance sampling method. Struct. Saf. 2015, 52, 161–169. [Google Scholar] [CrossRef]
- Botev, Z.I.; L’Ecuyer, P.; Tuffin, B. Markov chain importance sampling with applications to rare event probability estimation. Stat. Comput. 2013, 23, 271–285. [Google Scholar] [CrossRef]
- Dalbey, K.; Swiler, L. Gaussian process adaptive importance sampling. Int. J. Uncertain. Quantif. 2014, 4, 133–149. [Google Scholar] [CrossRef]
- Zhao, H.; Yue, Z.; Liu, Y.; Gao, Z.; Zhang, Y. An efficient reliability method combining adaptive importance sampling and Kriging metamodel. Appl. Math. Model. 2015, 39, 1853–1866. [Google Scholar] [CrossRef]
- Wang, Z.; Song, J. Cross-entropy-based adaptive importance sampling using von Mises-Fisher mixture for high dimensional reliability analysis. Struct. Saf. 2016, 59, 42–52. [Google Scholar] [CrossRef]
- Lee, G.; Kim, W.; Oh, H.; Youn, B.D.; Kim, N.H. Review of statistical model calibration and validation—from the perspective of uncertainty structures. Struct. Multidiscip. Optim. 2019, 60, 1619–1644. [Google Scholar] [CrossRef]
- Acar, E. A reliability index extrapolation method for separable limit states. Struct. Multidiscip. Optim. 2016, 53, 1099–1111. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; John Wiley & Sons: Hoboken, NJ, USA, 2009; p. 345. [Google Scholar]
- Ramakrishnan, B.; Rao, S. A general loss function based optimization procedure for robust design. Eng. Optim. 1996, 25, 255–276. [Google Scholar] [CrossRef]
- Lee, D.; Rahman, S. Robust design optimization under dependent random variables by a generalized polynomial chaos expansion. Struct. Multidiscip. Optim. 2021, 63, 2425–2457. [Google Scholar] [CrossRef]
- Dymiotis, C.; Kappos, A.J.; Chryssanthopoulos, M.K. Seismic reliability of RC frames with uncertain drift and member capacity. J. Struct. Eng. 1999, 125, 1038–1047. [Google Scholar] [CrossRef]
- Li, D.; Dolezal, T.; Haimes, Y.Y. Capacity reliability of water distribution networks. Reliab. Eng. Syst. Saf. 1993, 42, 29–38. [Google Scholar] [CrossRef]
- Zhao, J.; Tang, J.; Wu, H.C. A generalized random variable approach for strain-based fatigue reliability analysis. J. Press. Vessel Technol. 2000, 122, 156–161. [Google Scholar] [CrossRef]
- Ramu, P.; Arul, S. Estimating probabilistic fatigue of Nitinol with scarce samples. Int. J. Fatigue 2016, 85, 31–39. [Google Scholar] [CrossRef]
- Yun, W.; Lu, Z.; Jiang, X. A modified importance sampling method for structural reliability and its global reliability sensitivity analysis. Struct. Multidiscip. Optim. 2018, 57, 1625–1641. [Google Scholar] [CrossRef]
- Cortés López, J.C.; Jornet Sanz, M. Improving kernel methods for density estimation in random differential equations problems. Math. Comput. Appl. 2020, 25, 33. [Google Scholar] [CrossRef]
- Coles, S. Classical extreme value theory and models. In An Introduction to Statistical Modeling of Extreme Values; Springer: Berlin/Heidelberg, Germany, 2001; pp. 45–73. [Google Scholar]
- Hill, B.M. A Simple General Approach to Inference About the Tail of a Distribution. Ann. Stat. 1975, 3, 1163–1174. [Google Scholar] [CrossRef]
- Aban, I.B.; Meerschaert, M.M. Shifted hill’s estimator for heavy tails. Commun. Stat. Part B Simul. Comput. 2001, 30, 949–962. [Google Scholar] [CrossRef]
- Nguyen, T.; Samorodnitsky, G. Tail inference: Where does the tail begin? Extremes 2012, 15, 437–461. [Google Scholar] [CrossRef]
- Yao, W.; Tang, G.; Wang, N.; Chen, X. An improved reliability analysis approach based on combined FORM and Beta-spherical importance sampling in critical region. Struct. Multidiscip. Optim. 2019, 60, 35–58. [Google Scholar] [CrossRef]
- Acar, E. Reliability prediction through guided tail modeling using support vector machines. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 2780–2794. [Google Scholar] [CrossRef]
- Wu, Y.T.; Shin, Y.; Sues, R.H.; Cesare, M.A. Safety-factor based approach for probability-based design optimization. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Baltimore, MD, USA, 23–25 September 1991. [Google Scholar] [CrossRef]
- Ravishankar, B.; Smarslok, B.; Haftka, R.; Sankar, B. Separable sampling of the limit state for accurate Monte Carlo Simulation. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 17th AIAA/ASME/AHS Adaptive Structures Conference, Palm Springs, CA, USA, 4–7 May 2009; p. 2266. [Google Scholar]
- Chateauneuf, A.; Aoues, Y. Advances in solution methods for reliability-based design optimization. In Structural Design Optimization Considering Uncertainties; CRC Press: Boca Raton, FL, USA, 2008; pp. 217–246. [Google Scholar] [CrossRef]
- Bennett, J.; Botkin, M. The Optimum Shape; Springer: New York, NY, USA, 1986. [Google Scholar] [CrossRef]
- Acar, E. Guided tail modelling for efficient and accurate reliability estimation of highly safe mechanical systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1237–1251. [Google Scholar] [CrossRef]
- Rahman, S.; Wei, D. Reliability-based design optimization by a univariate decomposition method. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference 2010, Fort Worth, TX, USA, 13–15 September 2010; pp. 1–14. [Google Scholar] [CrossRef]
- Picheny, V.; Kim, N.H.; Haftka, R.; Queipo, N. Conservative predictions using surrogate modeling. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, USA, 7–10 April 2008; p. 1716. [Google Scholar]
- Lindemann, J.; Persson, K. CALFEM, A finite element toolbox to MATLAB. 1999. Available online: http://www-amna.math.uni-wuppertal.de/~ehrhardt/TUB/NumPar/calfem/calfem.pdf (accessed on 14 September 2022).
- Deb, K.; Gupta, S.; Daum, D.; Branke, J.; Mall, A.K.; Padmanabhan, D. Reliability-based optimization using evolutionary algorithms. IEEE Trans. Evol. Comput. 2009, 13, 1054–1074. [Google Scholar] [CrossRef]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef]
- Botev, Z.I. Adaptive Kernel Density Estimation in One-Dimension—MATLAB Central File Exchange. 2016. Available online: https://www.mathworks.com/matlabcentral/fileexchange/58309-adaptive-kernel-density-estimation-in-one-dimension (accessed on 14 September 2022).
- Hong, H.P.; Lind, N.C. Approximate reliability analysis using normal polynomial and simulation results. Struct. Saf. 1996, 18, 329–339. [Google Scholar] [CrossRef]


| Response Tail | Capacity Tail | ||
|---|---|---|---|
| Heavy | () | ||
| Heavy | () | Medium | () |
| Light | () | ||
| Heavy | () | ||
| Medium | () | Medium | () |
| Light | () | ||
| Heavy | () | ||
| Light | () | Medium | () |
| Light | () |
| Heavy C | Medium C | Light C | |||||
|---|---|---|---|---|---|---|---|
| Percentile | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | |
| Heavy R | 0.96 | 1.10 (0.26) | 1.21 | 1.42 (0.29) | 1.79 | 2.08 (0.61) | |
| 1.06 | 1.17 (0.29) | 1.50 | 1.54 (0.32) | 2.13 | 2.46 (0.89) | ||
| 1.22 | 1.36 (0.31) | 1.76 | 1.77 (0.33) | 2.59 | 3.08 (1.31) | ||
| Medium R | 0.93 | 1.03 (0.20) | 0.85 | 0.95 (0.18) | 1.01 | 1.09 (0.21) | |
| 1.02 | 1.09 (0.21) | 0.97 | 1.01 (0.19) | 1.13 | 1.20 (0.25) | ||
| 1.18 | 1.25 (0.23) | 1.08 | 1.14 (0.22) | 1.30 | 1.40 (0.32) | ||
| Light R | 0.91 | 1.04 (0.23) | 0.78 | 0.85 (0.14) | 0.85 | 0.91 (0.12) | |
| 1.01 | 1.10 (0.25) | 0.88 | 0.91 (0.14) | 0.94 | 0.98 (0.13) | ||
| 1.18 | 1.28 (0.26) | 0.99 | 1.04 (0.17) | 1.03 | 1.09 (0.18) | ||
| Heavy C | Medium C | Light C | |||||
|---|---|---|---|---|---|---|---|
| Percentile | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | |
| Heavy R | 1.02 | 1.02 () | 1.67 | 1.71 (0.15) | 3.16 | 3.63 (0.66) | |
| 1.03 | 1.03 () | 1.78 | 1.72 (0.15) | 3.64 | 3.67 (0.67) | ||
| 1.04 | 1.04 () | 1.81 | 1.79 (0.06) | 4.00 | 4.09 (0.30) | ||
| Medium R | 0.99 | 0.99 () | 1.02 | 1.03 (0.06) | 1.25 | 1.32 (0.20) | |
| 1.00 | 1.00 () | 1.05 | 1.04 (0.05) | 1.37 | 1.34 (0.20) | ||
| 1.00 | 1.00 () | 1.08 | 1.07 (0.03) | 1.45 | 1.51 (0.14) | ||
| Light R | 0.99 | 0.99 () | 0.99 | 0.99 (0.02) | 0.98 | 1.03 (0.10) | |
| 1.00 | 1.00 () | 1.00 | 1.00 (0.02) | 1.07 | 1.06 (0.10) | ||
| 1.00 | 1.00 () | 1.02 | 1.01 (0.02) | 1.12 | 1.13 (0.07) | ||
| Heavy C | Medium C | Light C | |||||
|---|---|---|---|---|---|---|---|
| Percentile | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | |
| Heavy R | 0.96 | 0.98 (0.10) | 0.99 | 0.99 () | 1.00 | 1.00 () | |
| 1.03 | 1.00 (0.08) | 1.00 | 1.00 () | 1.00 | 1.00 () | ||
| 1.06 | 1.04 (0.05) | 1.00 | 1.00 () | 1.00 | 1.00 () | ||
| Medium R | 0.93 | 1.13 (0.31) | 0.87 | 0.92 (0.12) | 0.96 | 0.96 (0.05) | |
| 1.12 | 1.24 (0.35) | 0.96 | 0.96 (0.11) | 0.99 | 0.98 (0.04) | ||
| 1.42 | 1.52 (0.33) | 1.03 | 1.02 (0.07) | 1.00 | 1.00 (0.02) | ||
| Light R | 0.91 | 1.05 (0.23) | 0.82 | 0.90 (0.13) | 0.87 | 0.89 (0.09) | |
| 1.03 | 1.12 (0.25) | 0.93 | 0.95 (0.14) | 0.94 | 0.94 (0.09) | ||
| 1.20 | 1.29 (0.29) | 1.03 | 1.06 (0.14) | 1.00 | 0.99 (0.08) | ||
| Heavy C | Medium C | Light C | |||||
|---|---|---|---|---|---|---|---|
| Percentile | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | Original Sample | Bootstrap Mean (Std) | |
| Heavy R | 0.95 | 0.96 (0.09) | 0.95 | 1.14 (0.29) | 0.92 | 1.13 (0.31) | |
| 1.02 | 0.99 (0.07) | 1.13 | 1.22 (0.31) | 1.11 | 1.23 (0.35) | ||
| 1.03 | 1.03 (0.02) | 1.43 | 1.42 (0.30) | 1.38 | 1.51 (0.41) | ||
| Medium R | 0.99 | 0.99 (0.02) | 0.84 | 0.89 (0.12) | 0.77 | 0.89 (0.18) | |
| 0.99 | 0.99 (0.01) | 0.94 | 0.94 (0.11) | 0.93 | 0.96 (0.20) | ||
| 1.00 | 1.00 () | 1.02 | 1.01 (0.09) | 1.08 | 1.11 (0.21) | ||
| Light R | 0.99 | 0.99 () | 0.91 | 0.93 (0.07) | 0.79 | 0.84 (0.12) | |
| 1.00 | 1.00 () | 0.97 | 0.96 (0.06) | 0.87 | 0.90 (0.12) | ||
| 1.00 | 1.00 () | 1.00 | 0.99 (0.04) | 0.99 | 0.98 (0.12) | ||
| Percentile | Original Sample | Bootstrap Mean (Std) |
|---|---|---|
| 25th | 0.93 | 1.19 (0.39) |
| 50th | 1.12 | 1.32 (0.53) |
| 75th | 1.39 | 1.70 (1.02) |
| Percentile | Original Sample | Bootstrap Mean (Std) |
|---|---|---|
| 25th | 0.84 | 0.96 (0.20) |
| 50th | 0.96 | 1.03 (0.20) |
| 75th | 1.12 | 1.20 (0.22) |
| Percentile | Original Sample | Bootstrap Mean (Std) |
|---|---|---|
| 25th | 0.82 | 0.89 (0.16) |
| 50th | 0.90 | 0.95 (0.16) |
| 75th | 1.02 | 1.08 (0.19) |
| Random Variable | Mean (SD) |
|---|---|
| q (N/m) | 20,000 (1600) |
| l (m) | 12 (0.24) |
| 0.04 (0.008) | |
| Percentile | Original Sample | Bootstrap Mean (Std) |
|---|---|---|
| 25th | 0.84 | 0.94 (0.17) |
| 50th | 0.94 | 1.02 (0.20) |
| 75th | 1.07 | 1.18 (0.29) |
| Random Variable | Mean (SD) |
|---|---|
| (kN/m) | 20 (2) |
| L (m) | 6 (0.3) |
| E (GPa) | 210 (10) |
| d (cm) | 25 (0.5) |
| (cm) | 25 (0.5) |
| (cm) | 2 (0.2) |
| (cm) | 2 (0.2) |
| Percentile | Original | Bootstrap Mean (Std) | Original | Bootstrap Mean (Std) | Original | Bootstrap Mean (Std) |
|---|---|---|---|---|---|---|
| 25th | 0.84 | 1.03 (0.30) | 0.82 | 0.99 (0.27) | 0.81 | 0.99 (0.30) |
| 50th | 0.99 | 1.13 (0.36) | 0.99 | 1.09 (0.32) | 0.96 | 1.12 (0.39) |
| 75th | 1.29 | 1.31 (0.42) | 1.24 | 1.29 (0.44) | 1.26 | 1.35 (0.52) |
| Random Variable | Mean (SD) |
|---|---|
| 500 (100) | |
| (100) | |
| () | |
| () |
| Surrogate Model for Constraints | Reliability Estimation | Optima | Objective Function Value | at | at | |||
|---|---|---|---|---|---|---|---|---|
| (in) | (in) | (in) | ||||||
| WAS | IS | 2.59 | 3.74 | 9.69 | 3.00 | 3.64 | 3.25 | 3.69 |
| MCS | 2.59 | 3.66 | 9.50 | 3.00 | 3.44 | 2.95 | 3.39 | |
| Type | Variable | Distribution | Mean | C.o.V |
|---|---|---|---|---|
| Random | P (kN) | Gumbel | 100 | 15% |
| E (GPa) | Gumbel | 200 | 8% | |
| (MPa) | Lognormal | 225 | 8% | |
| Weibull | 7860 | 10% | ||
| L (m) | Gaussian | 5 | 5% | |
| Design | (mm) | Gaussian | 5% | |
| (mm) | Gaussian | 5% | ||
| t (mm) | Gaussian | 5% |
| Surrogate Model for Constraints | Reliability Estimation | Optima | Objective Function Value | at | at | ||||
|---|---|---|---|---|---|---|---|---|---|
| (kg) | |||||||||
| WAS | IS | 58 | 89 | 300 | 1576 | 2.00 | 2.00 | 2.59 | 2.87 |
| MCS | 62 | 77 | 300 | 1474 | 2.00 | 2.00 | 2.02 | 3.55 | |
| Random Variable | Distribution Type | Mean; SD |
|---|---|---|
| (N) | Normal | |
| (N) | Normal | |
| (MPa) | Lognormal |
| DV | (Optimum) | ||
|---|---|---|---|
| 1.80 | 3.20 | 2.15 | |
| 1.25 | 1.60 | 1.28 | |
| 1.20 | 4.60 | 1.59 | |
| −0.10 | 0.40 | −0.09 | |
| −0.30 | 0.30 | 0.30 | |
| −0.90 | 0.80 | 0.30 | |
| 0.40 | 1.80 | 0.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pannerselvam, K.; Yadav, D.; Ramu, P. Scarce Sample-Based Reliability Estimation and Optimization Using Importance Sampling. Math. Comput. Appl. 2022, 27, 99. https://doi.org/10.3390/mca27060099
Pannerselvam K, Yadav D, Ramu P. Scarce Sample-Based Reliability Estimation and Optimization Using Importance Sampling. Mathematical and Computational Applications. 2022; 27(6):99. https://doi.org/10.3390/mca27060099
Chicago/Turabian StylePannerselvam, Kiran, Deepanshu Yadav, and Palaniappan Ramu. 2022. "Scarce Sample-Based Reliability Estimation and Optimization Using Importance Sampling" Mathematical and Computational Applications 27, no. 6: 99. https://doi.org/10.3390/mca27060099
APA StylePannerselvam, K., Yadav, D., & Ramu, P. (2022). Scarce Sample-Based Reliability Estimation and Optimization Using Importance Sampling. Mathematical and Computational Applications, 27(6), 99. https://doi.org/10.3390/mca27060099










