An Efficient Two-Step Iterative Family Adaptive with Memory for Solving Nonlinear Equations and Their Applications
Abstract
1. Introduction
2. Iterative Method without Memory and Its Convergence Analysis
Convergence Analysis
3. Iterative Method with Memory and Its Convergence Analysis
Convergence Analysis
4. Numerical Results
- having one of the real zero .
- having one of the real zero 0.
- having one of the real zero 2.
- having one of the real zero .
- having one of the real zero .
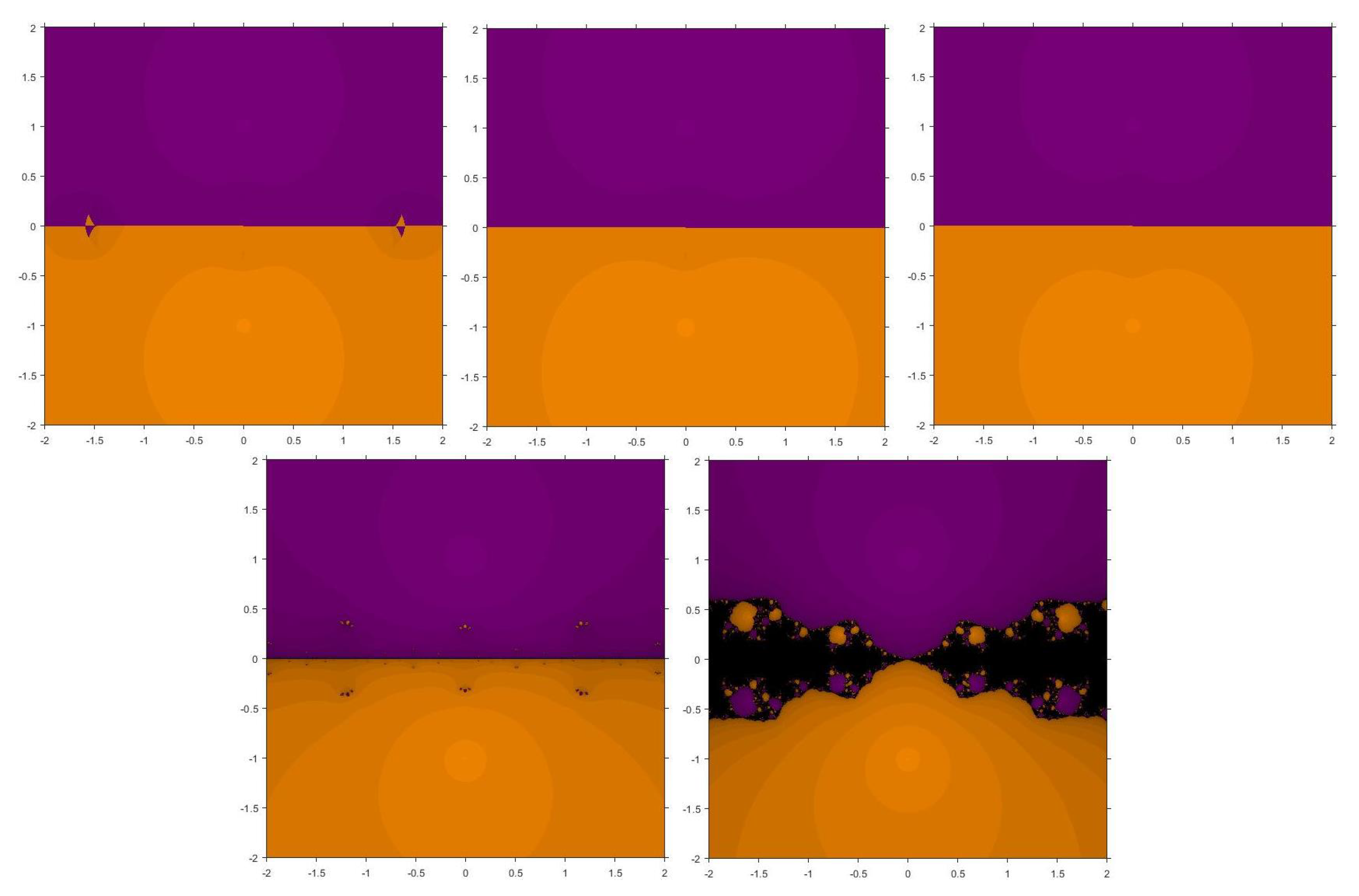
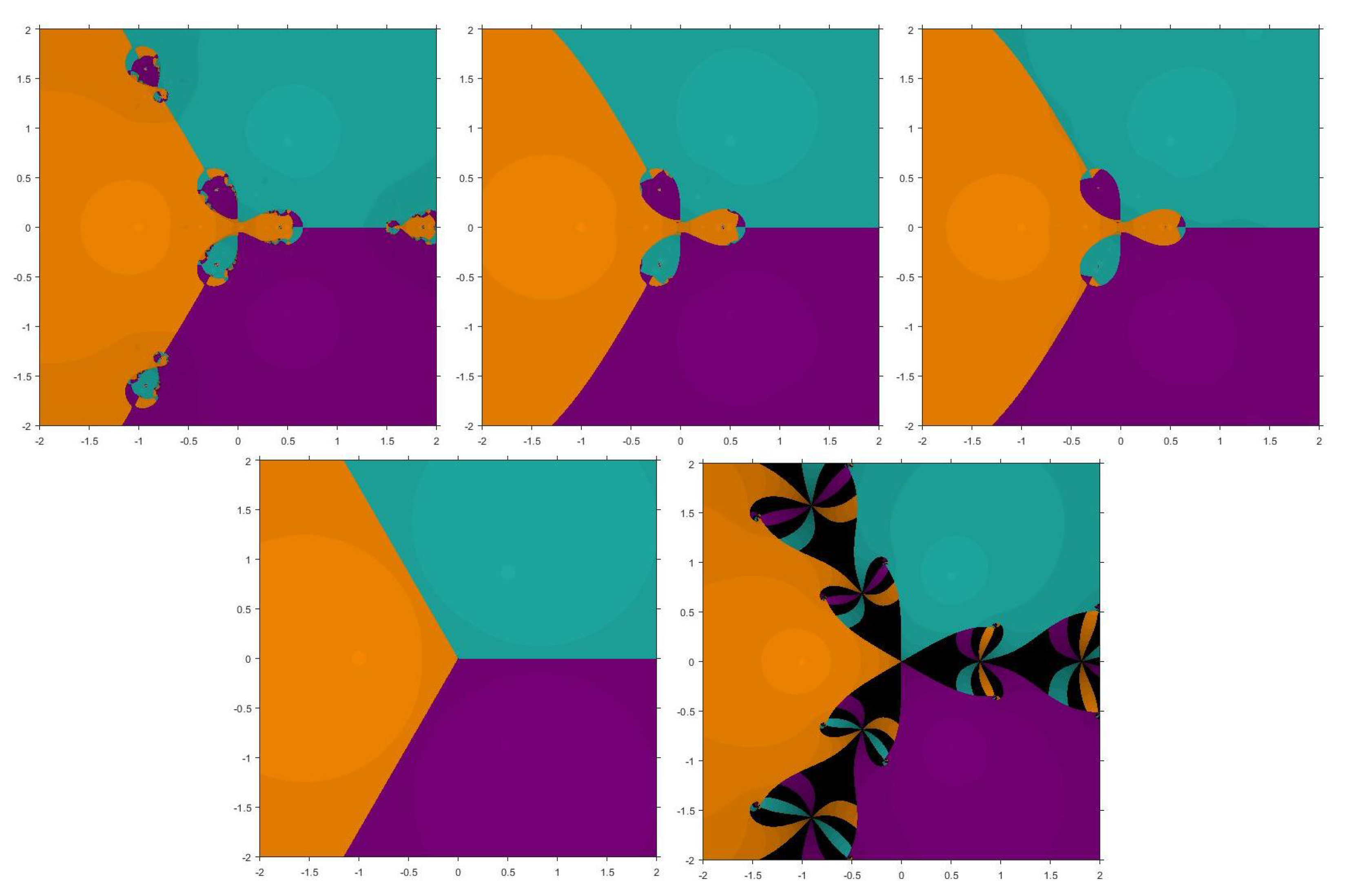
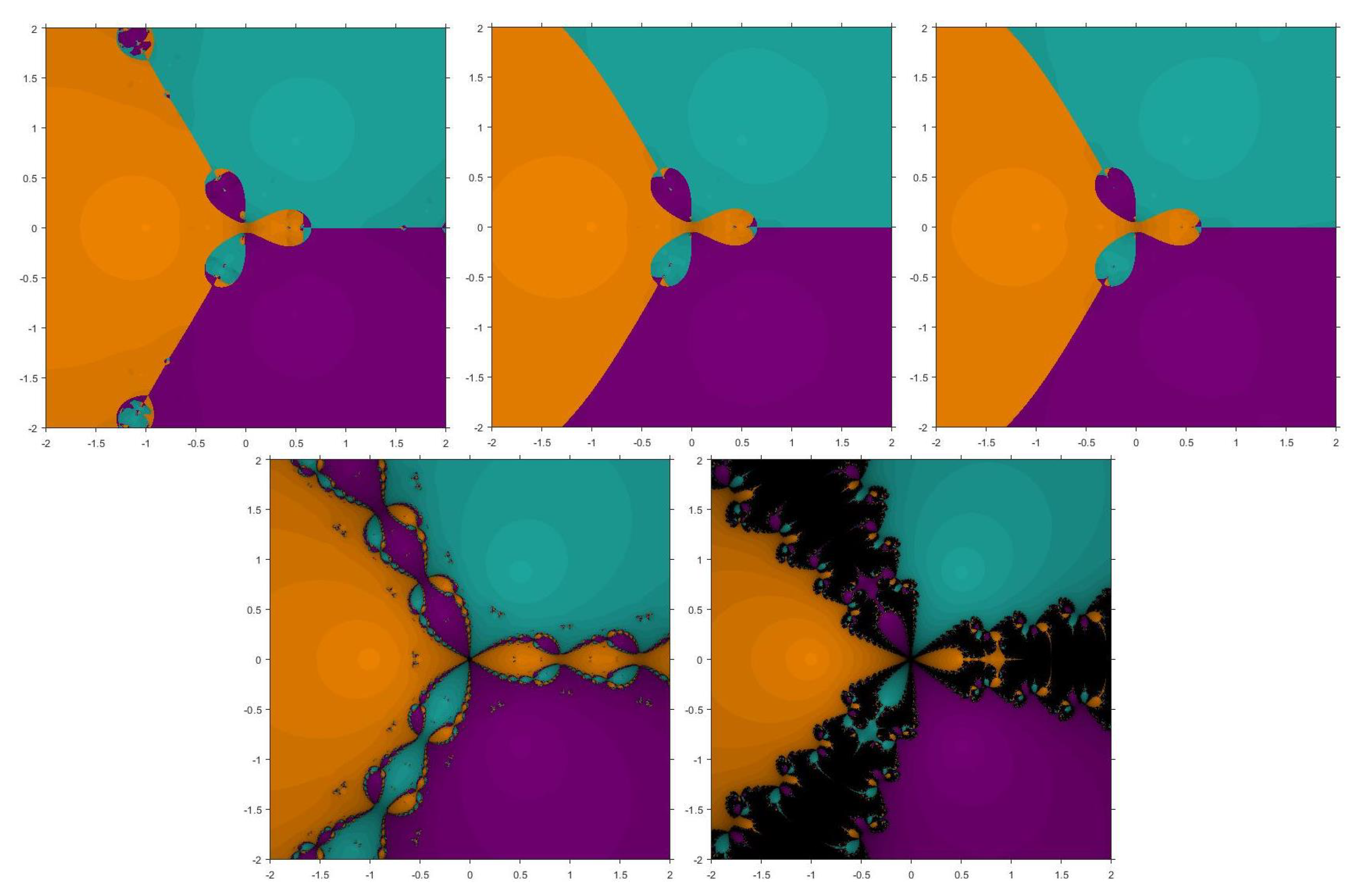
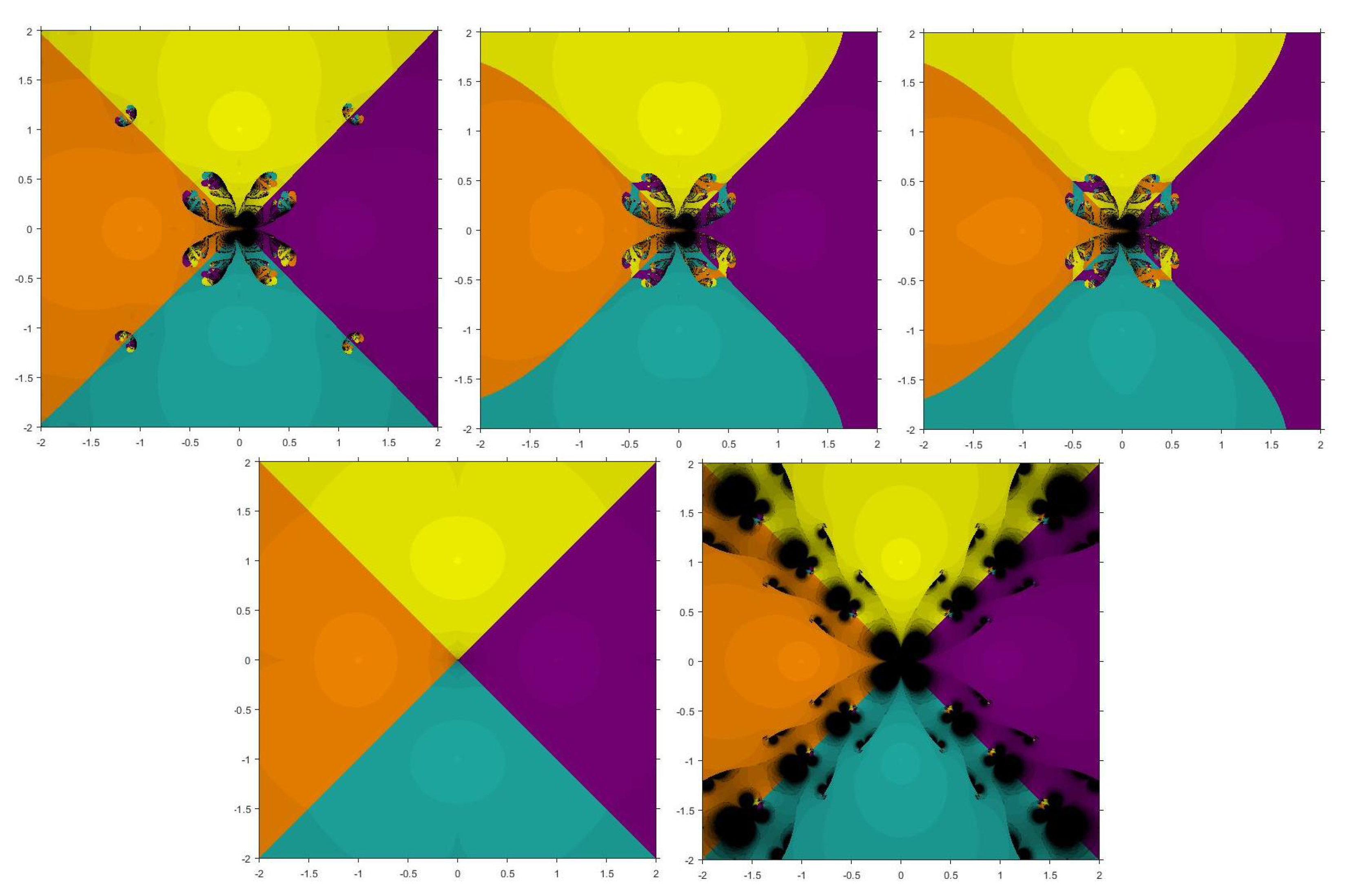
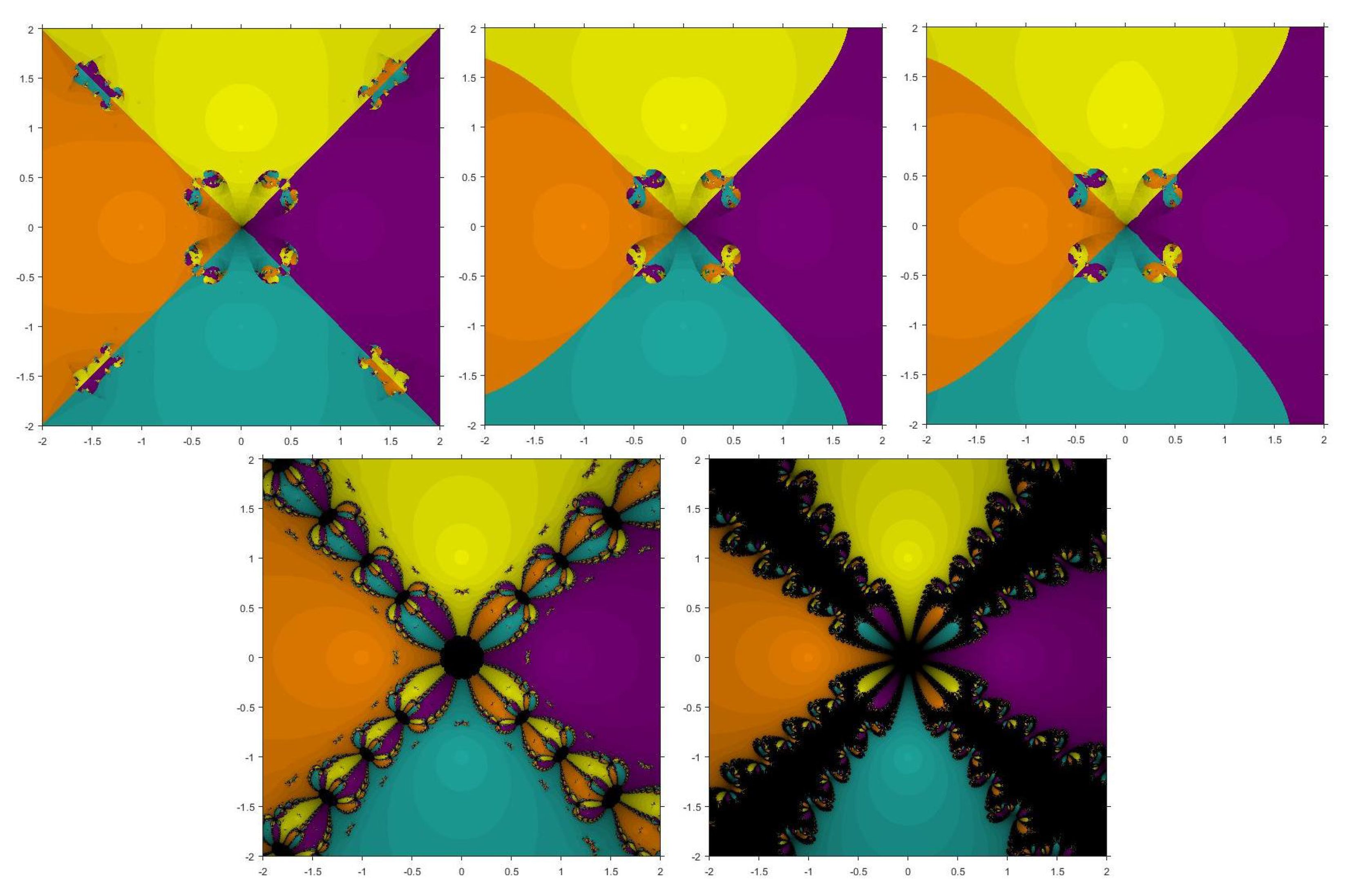
5. Basins of Attraction
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Amat, S.; Busquier, S.; Gutiérrez, J.M. Geometric constructions of iterative functions to solve nonlinear equations. J. Comput. Appl. Math. 2003, 157, 197–205. [Google Scholar] [CrossRef]
- Argyros, I.K. A note on the Halley method in Banach spaces. Appl. Math. Comput. 1993, 58, 215–224. [Google Scholar]
- Argyros, I.K.; Kansal, M.; Kanwar, V.; Bajaj, S. Higher-order derivative-free families of Chebyshev–Halley type methods with or without memory for solving nonlinear equations. Appl. Math. Comput. 2017, 315, 224–245. [Google Scholar] [CrossRef]
- Cordero, A.; Moscoso-Martinez, M.; Torregrosa, J.R. Chaos and stability in a new iterative family for solving nonlinear equations. Algorithms 2021, 14, 101. [Google Scholar] [CrossRef]
- Gutiérrez, J.M.; Hernández, M.A. A family of Chebyshev–Halley type methods in Banach spaces. Bull. Austral. Math. Soc. 1997, 55, 113–130. [Google Scholar] [CrossRef]
- Jain, P.; Chand, P.B. Derivative free iterative methods with memory having R-order of convergence. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 641–648. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Hansen, E.; Patrick, M. A family of root finding methods. Numer. Math. 1977, 27, 257–269. [Google Scholar] [CrossRef]
- Petković, M.S.; Neta, B.; Petković, L.D.; Dẑunić, J. Multipoint methods for solving nonlinear equations: A survey. Appl. Math. Comput. 2014, 226, 635–660. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. Some variants of Hansen–Patrick method with third and fourth order convergence. Appl. Math. Comput. 2009, 214, 171–177. [Google Scholar] [CrossRef]
- Kansal, M.; Kanwar, V.; Bhatia, S. New modifications of Hansen–Patrick’s family with optimal fourth and eighth orders of convergence. Appl. Math. Comput. 2015, 269, 507–519. [Google Scholar] [CrossRef]
- Zheng, Q.; Li, J.; Huang, F. An optimal Steffensen-type family for solving nonlinear equations. Appl. Math. Comput. 2011, 217, 9592–9597. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solutions of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Sihwail, R.; Solaiman, O.S.; Ariffin, K.A.Z. New robust hybrid Jarratt–Butterfly optimization algorithm for nonlinear models. J. King Saud Univ. Comput. Inform. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Sihwail, R.; Solaiman, O.S.; Omar, K.; Ariffin, K.A.Z.; Alswaitti, M.; Hashim, I. A hybrid approach for solving systems of nonlinear equations using harris hawks optimization and Newton’s method. IEEE Access 2021, 9, 95791–95807. [Google Scholar] [CrossRef]
- King, R.F. A family of fourth order methods for nonlinear equations. SIAM J. Numer. Anal. 1973, 10, 876–879. [Google Scholar] [CrossRef]
- Soleymani, F.; Lotfi, T.; Tavakoli, E.; Haghani, F.K. Several iterative methods with memory using self-accelerators. Appl. Math. Comput. 2015, 254, 452–458. [Google Scholar] [CrossRef]
- Campos, B.; Cordero, A.; Torregrosa, J.R.; Vindel, P. Stability of King’s family of iterative methods with memory. J. Comput. Appl. Math. 2017, 318, 504–514. [Google Scholar] [CrossRef]
- Jay, I.O. A note on Q-order of convergence. BIT Numer. Math. 2011, 41, 422–429. [Google Scholar] [CrossRef]
- Jain, D. Families of Newton-like method with fourth-order convergence. Int. J. Comput. Math. 2013, 90, 1072–1082. [Google Scholar] [CrossRef]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]
- Shacham, M. Numerical solution of constrained nonlinear algebraic equations. Int. J. Numer. Methods Eng. 1986, 23, 1455–1481. [Google Scholar] [CrossRef]
- Zachary, J.L. Introduction to Scientific Programming: Computational Problem Solving Using Maple and C; Springer: New York, NY, USA, 2012. [Google Scholar]



| Without Memory Methods | CPU Time | ||||
|---|---|---|---|---|---|
| () | 1.1717 | 3.0000 | 0.344 | ||
| () | 3.0000 | 0.312 | |||
| () | 3.0000 | 0.329 | |||
| () | 2.9993 | 0.343 | |||
| () | 3.0008 | 0.344 | |||
| () | 2.9990 | 0.281 | |||
| () | 2.9961 | 0.578 | |||
| () | 2.9946 | 0.656 | |||
| () | 2.9950 | 0.749 | |||
| () | 2.7546 | 0.594 | |||
| () | 2.7518 | 0.843 | |||
| () | 3.1314 | 0.751 | |||
| () | 3.0008 | 0.345 | |||
| () | 2.9971 | 0.344 | |||
| () | 3.0019 | 0.359 | |||
| () | 2.9994 | 0.358 | |||
| () | 3.0020 | 0.328 | |||
| () | 2.9993 | 0.390 | |||
| () | 2.8943 | 0.250 | |||
| () | 2.7963 | 0.266 | |||
| () | 2.7547 | 0.328 | |||
| () | F | F | F | # | - |
| () | F | F | F | # | - |
| () | F | F | F | # | - |
| () | 3.1821 | 0.422 | |||
| () | 3.5597 | 0.406 | |||
| () | 3.4779 | 0.328 | |||
| () | C | C | C | * | - |
| () | C | C | C | * | - |
| () | C | C | C | * | - |
| With Memory Methods | CPU Time | ||||
|---|---|---|---|---|---|
| () | 3.3435 | 0.407 | |||
| () | 3.3362 | 0.407 | |||
| () | 3.3434 | 0.344 | |||
| () | 2.4151 | 0.343 | |||
| () | 2.0037 | 0.312 | |||
| () | 3.6558 | 0.859 | |||
| () | 3.6119 | 0.875 | |||
| () | 3.6550 | 0.938 | |||
| () | 2.4624 | 0.672 | |||
| () | 1.9291 | 0.657 | |||
| () | 3.4661 | 0.516 | |||
| () | 3.4917 | 0.468 | |||
| () | 3.4628 | 0.422 | |||
| () | 2.4298 | 0.313 | |||
| () | 2.1886 | 0.297 | |||
| () | 3.4326 | 0.250 | |||
| () | 3.2771 | 0.250 | |||
| () | 3.2331 | 0.296 | |||
| () | 0.359 | ||||
| () | 0.282 | ||||
| () | 4.2117 | 0.360 | |||
| () | 6.8399 | 0.421 | |||
| () | 4.0907 | 0.485 | |||
| () | C | C | C | * | - |
| () | C | C | C | * | - |
| Without Memory Methods | CPU Time | ||||
|---|---|---|---|---|---|
| () | 3.0000 | 0.392 | |||
| () | 3.0000 | 0.390 | |||
| () | 3.0000 | 0.375 | |||
| () | 3.0000 | 0.313 | |||
| () | 3.0000 | 0.328 | |||
| () | 3.0000 | 0.329 | |||
| () | 2.9887 | 0.234 | |||
| () | 2.9976 | 0.218 | |||
| () | 2.9912 | 0.250 | |||
| () | 3.0008 | 0.282 | |||
| () | 2.9774 | 0.234 | |||
| () | 2.9830 | 0.234 | |||
| () | 3.0049 | 0.359 | |||
| () | 3.0056 | 0.360 | |||
| () | 3.0096 | 0.376 | |||
| () | 3.0000 | 0.344 | |||
| () | 3.0246 | 0.313 | |||
| () | 3.0000 | 0.296 | |||
| () | 2.9998 | 0.390 | |||
| () | 2.9999 | 0.375 | |||
| () | 2.9998 | 0.376 | |||
| () | 2.9994 | 0.328 | |||
| () | 2.9996 | 0.406 | |||
| () | 3.0001 | 0.375 | |||
| () | 3.0002 | 0.298 | |||
| () | 3.0001 | 0.327 | |||
| () | 3.0003 | 0.328 | |||
| () | 3.0000 | 0.313 | |||
| () | 3.0002 | 0.297 | |||
| () | 3.0003 | 0.234 |
| With Memory Methods | CPU Time | ||||
|---|---|---|---|---|---|
| () | 3.3297 | 0.359 | |||
| () | 3.3318 | 0.344 | |||
| () | 3.3293 | 0.297 | |||
| () | 2.4006 | 0.282 | |||
| () | 2.0001 | 0.297 | |||
| () | 3.2847 | 0.125 | |||
| () | 3.3337 | 0.187 | |||
| () | 3.3027 | 0.171 | |||
| () | 2.2611 | 0.157 | |||
| () | 1.7706 | 0.203 | |||
| () | 3.2477 | 0.390 | |||
| () | 3.2580 | 0.374 | |||
| () | 3.2322 | 0.297 | |||
| () | 2.7340 | 0.296 | |||
| () | 2.0345 | 0.344 | |||
| () | 3.3204 | 0.390 | |||
| () | 3.3363 | 0.391 | |||
| () | 3.3231 | 0.359 | |||
| () | 2.4205 | 0.328 | |||
| () | 1.9767 | 0.312 | |||
| () | 3.2964 | 0.218 | |||
| () | 3.3102 | 0.187 | |||
| () | 3.2930 | 0.234 | |||
| () | 2.5636 | 0.235 | |||
| () | 2.0023 | 0.220 |
| Without Memory Methods | Avg_Iter | CPU Time | |
|---|---|---|---|
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () | |||
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () | |||
| () | |||
| () | |||
| () | |||
| () | |||
| () | |||
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () |
| With Memory Methods | Avg_Iter | CPU Time | |
|---|---|---|---|
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () | |||
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () | |||
| () | |||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () | |||
| () | 0 | ||
| () | 0 | ||
| () | 0 | ||
| () | |||
| () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, H.; Kansal, M.; Behl, R. An Efficient Two-Step Iterative Family Adaptive with Memory for Solving Nonlinear Equations and Their Applications. Math. Comput. Appl. 2022, 27, 97. https://doi.org/10.3390/mca27060097
Sharma H, Kansal M, Behl R. An Efficient Two-Step Iterative Family Adaptive with Memory for Solving Nonlinear Equations and Their Applications. Mathematical and Computational Applications. 2022; 27(6):97. https://doi.org/10.3390/mca27060097
Chicago/Turabian StyleSharma, Himani, Munish Kansal, and Ramandeep Behl. 2022. "An Efficient Two-Step Iterative Family Adaptive with Memory for Solving Nonlinear Equations and Their Applications" Mathematical and Computational Applications 27, no. 6: 97. https://doi.org/10.3390/mca27060097
APA StyleSharma, H., Kansal, M., & Behl, R. (2022). An Efficient Two-Step Iterative Family Adaptive with Memory for Solving Nonlinear Equations and Their Applications. Mathematical and Computational Applications, 27(6), 97. https://doi.org/10.3390/mca27060097







