An Efficient Numerical Scheme Based on Radial Basis Functions and a Hybrid Quasi-Newton Method for a Nonlinear Shape Optimization Problem
Abstract
:1. Introduction
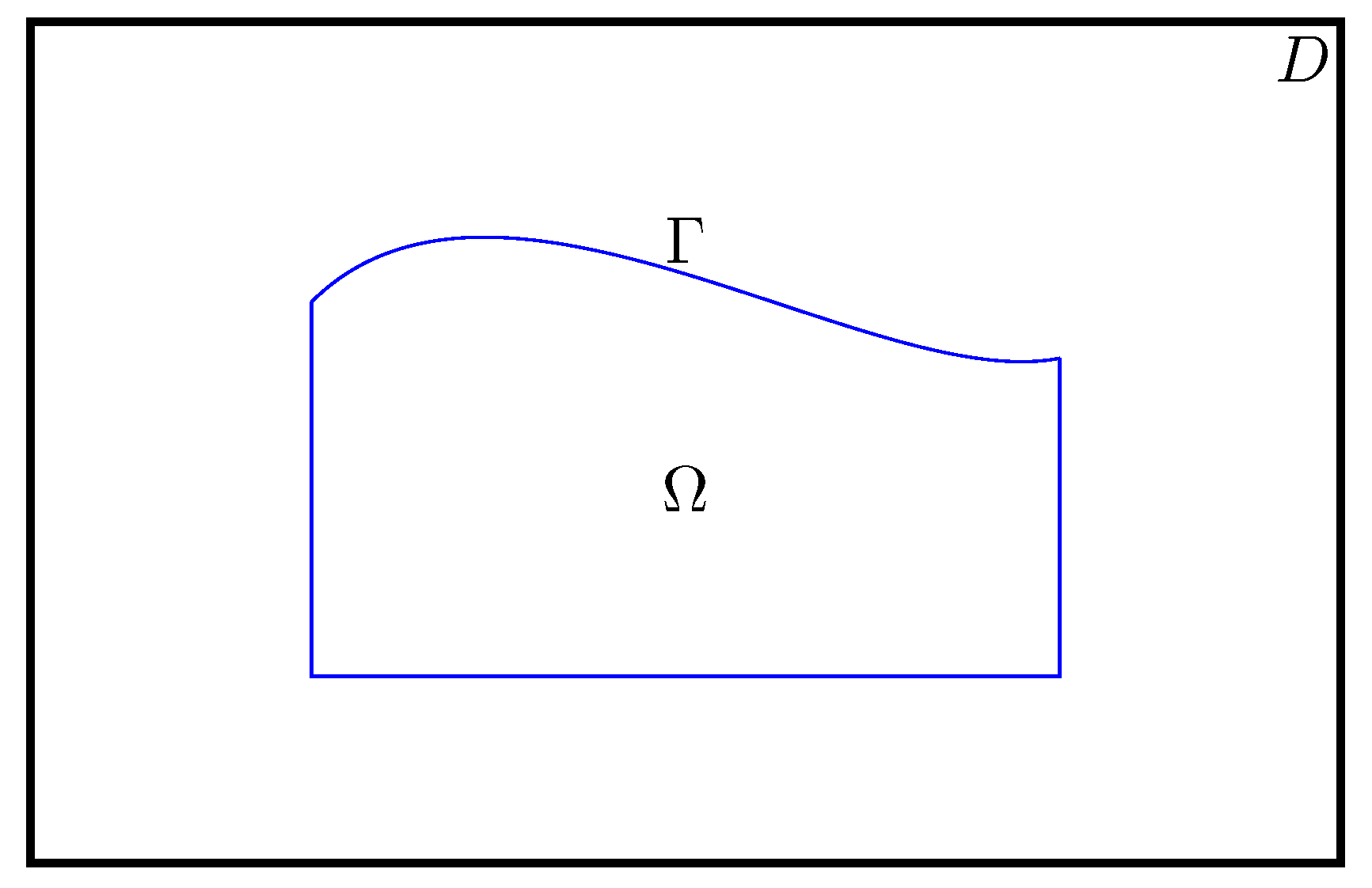
2. Analysis of the Shape Optimization Problem
2.1. Existence of the State Equation Solution
- H1
- Consider the regularity
- 1.
- and ,
- 2.
- and there exists such that a.e. in D.
- H2
- A is a Caratheodory function, such that:
- 1.
- is measurable for all ,
- 2.
- is continuous for almost every ,
- 3.
- for all ,
- 4.
- is differentiable for almost every .
- H3
- There exists a function that satisfies
- 1.
- continuous, nondecreasing and non negative function,
- 2.
- a.e., for ,
- 3.
- for any .
- (i)
- converges weakly to u in ,
- (ii)
- converges weakly to w in .
2.2. Existence of an Optimal Shape Design
3. Description of the Proposed Scheme
3.1. RBF Discretization

3.2. Computation of the Discrete Gradient
3.3. Differential Evolution Heuristic Method
3.4. Quasi-Newton Method

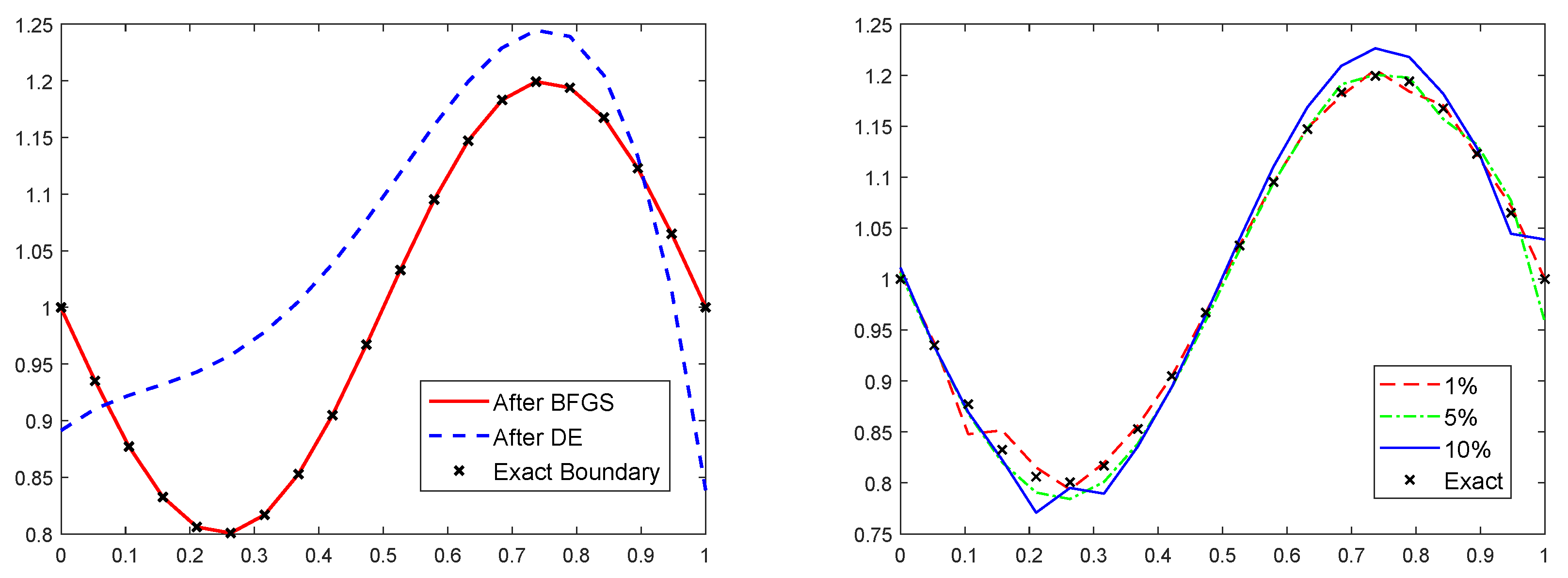
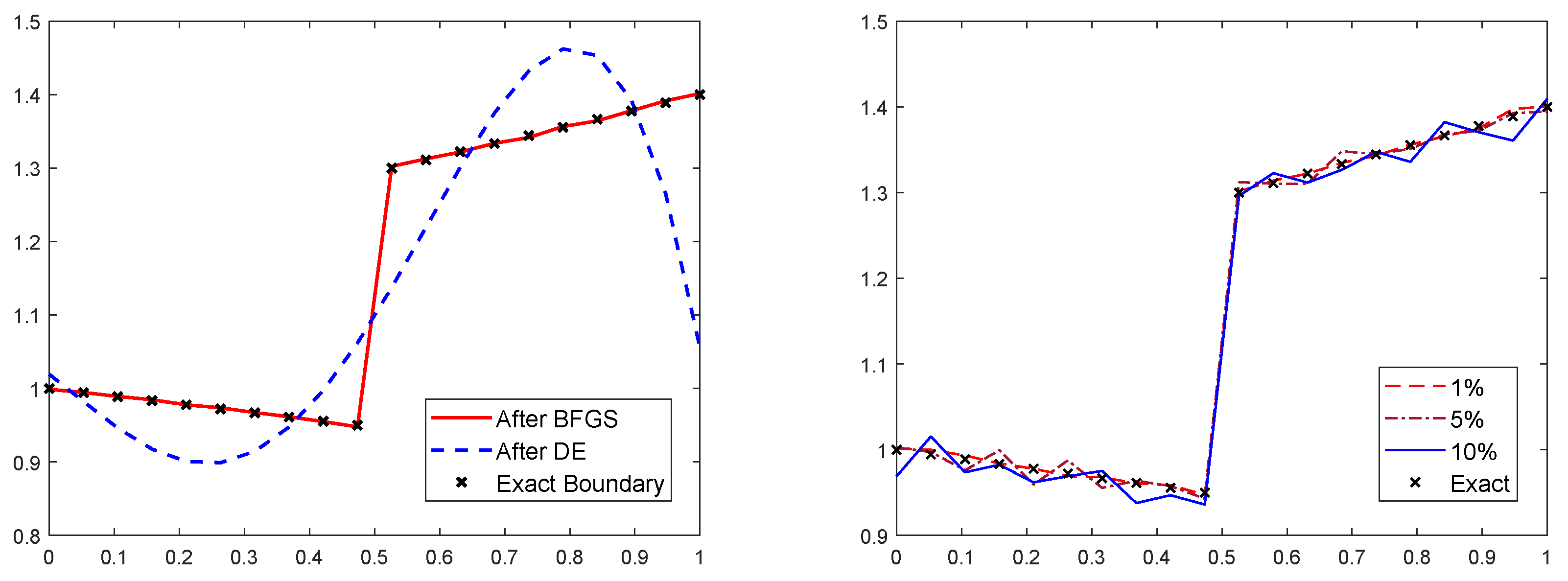
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cabarrubias, B.; Donato, P. Existence and uniqueness for a quasilinear elliptic problem with nonlinear Robin conditions. Carpathian J. Math. 2011, 27, 173–184. [Google Scholar] [CrossRef]
- Conca, C.; Diaz, J.; Linan, A.; Timofte, C. Homogenization in chemical reactive flows. Electron. J. Differ. Equ. 2004, 40, 1–22. [Google Scholar]
- Chipot, M. Elliptic Equations: An Introductory Course; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Wu, J. Analysis of a Nonlinear Necrotic Tumor Model with Two Free Boundaries. J. Dyn. Differ. Equ. 2021, 33, 511–524. [Google Scholar] [CrossRef]
- Zheng, J.; Cui, S. Analysis of a tumor model free boundary problem with action of an inhibitor and nonlinear boundary conditions. J. Math. Anal. Appl. 2021, 496, 124793. [Google Scholar] [CrossRef]
- Gangl, P.; Langer, U.; Laurain, A.; Meftahi, H.; Sturm, K. Shape Optimization of an Electric Motor Subject to Nonlinear Magnetostatics. SIAM J. Sci. Comput. 2015, 37, B1002–B1025. [Google Scholar] [CrossRef] [Green Version]
- Kolvenbach, P.; Lass, O.; Ulbrich, S. An approach for robust PDE-constrained optimization with application to shape optimization of electrical engines and of dynamic elastic structures under uncertainty. Optim. Eng. 2018, 19, 697–731. [Google Scholar] [CrossRef]
- El Yazidi, Y.; Ellabib, A. A new hybrid method for shape optimization with application to semiconductor equations. Numer. Algebra Control. Optim. 2021. [Google Scholar] [CrossRef]
- El Yazidi, Y.; Ellabib, A. An iterative method for optimal control of bilateral free boundaries problem. Math. Methods Appl. Sci. 2021, 44, 11664–11683. [Google Scholar] [CrossRef]
- Mozaffari, M.H.; Khodadad, M.; Dashti Ardakani, M. Simultaneous identification of multi-irregular interfacial boundary configurations in non-homogeneous body using surface displacement measurements. J. Mech. Eng. Sci. 2016, 231, 1–12. [Google Scholar] [CrossRef]
- Dashti Ardakani, M.; Khodadad, M. Shape estimation of a cavity by inverse application of the 2D elastostatics problem. Int. J. Comput. Methods 2013, 10, 1350042. [Google Scholar] [CrossRef]
- Sanyasiraju, Y.; Satyanarayana, C. On optimization of the RBF shape parameter in a grid-free local scheme for convection dominated problems over non-uniform centers. Appl. Math. Model. 2013, 37, 7245–7272. [Google Scholar] [CrossRef]
- Sarra, S. A local radial basis function method for advection-diffusion-reaction equations on complexly shaped domains. Appl. Math. Comput. 2012, 218, 9853–9865. [Google Scholar] [CrossRef] [Green Version]
- Jakobsson, S.; Amoignon, O. Mesh deformation using radial basis functions for gradient-based aerodynamic shape optimization. Comput. Fluids 2007, 36, 1119–1136. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Zhou, J. Optimization of a fan-shaped hole to improve film cooling performance by RBF neural network and genetic algorithm. Aerosp. Sci. Technol. 2016, 58, 18–25. [Google Scholar] [CrossRef]
- El Yazidi, Y.; Ellabib, A. Augmented Lagrangian approach for a bilateral free boundaries problem. J. Appl. Math. Comput. 2021, 67, 69–88. [Google Scholar] [CrossRef]
- Donato, P.; Cioranescu, D.; Zaki, R. Asymptotic behavior of elliptic problems in perforated domains with nonlinear boundary conditions in perforated domains. Asymptot. Anal. 2007, 53, 209–235. [Google Scholar]
- Boulkhemair, A.; Chakib, A. On the Uniform Poincaré Inequality. Commun. Partial Differ. Equ. 2007, 32, 1439–1447. [Google Scholar] [CrossRef]
- Boulkhemair, A.; Chakib, A.; Nachaoui, A. Uniform trace theorem and application to shape optimization. Appl. Comput. Math. 2008, 7, 192–205. [Google Scholar]
- Bendib, S. Homogénéisation dune Classe de Problèmes non Linéaires avec des Conditions de Fourier dans des ouverts Perforés. Ph.D. Thesis, Institut National Polytechnique de Lorraine, Vandœuvre-lès-Nancy, France, 2004. [Google Scholar]
- Boulkhemair, A.; Chakib, A.; Nachaoui, A. A shape optimization approach for a class of free boundary problems of Bernoulli type. Appl. Math. 2013, 58, 205–221. [Google Scholar] [CrossRef] [Green Version]
- Rudin, W. Functional Analysis; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Zolesio, J.; Sokolowski, J. Introduction to Shape Optimization Shape Sensitivity Analysis; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Schaback, R. Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]
- Fasshauer, G.; Zhang, J. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Hardy, R. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Buhmann, M. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; Volume 12. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Vogel, C. Computational Methods for Inverse Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002; p. 195. [Google Scholar] [CrossRef]


| Name | RBF |
|---|---|
| Multiquadric (MQ) | |
| Inverse Multiquadric (IMQ) | |
| Gaussian (GA) | |
| Thin plate spline (TPS) |
| Population Size | Max Iterations | |||
|---|---|---|---|---|
| 30 | 0.5 | 10 | 0.05 | 0.75 |
| RMS Error | Cost | CPU | Iterations | |
|---|---|---|---|---|
| Example 1 | 27 | |||
| Example 2 | 34 | |||
| Example 3 | 35 |
| Noise Level | Example 1 | Example 2 | Example 3 |
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Yazidi, Y.; Ellabib, A. An Efficient Numerical Scheme Based on Radial Basis Functions and a Hybrid Quasi-Newton Method for a Nonlinear Shape Optimization Problem. Math. Comput. Appl. 2022, 27, 67. https://doi.org/10.3390/mca27040067
El Yazidi Y, Ellabib A. An Efficient Numerical Scheme Based on Radial Basis Functions and a Hybrid Quasi-Newton Method for a Nonlinear Shape Optimization Problem. Mathematical and Computational Applications. 2022; 27(4):67. https://doi.org/10.3390/mca27040067
Chicago/Turabian StyleEl Yazidi, Youness, and Abdellatif Ellabib. 2022. "An Efficient Numerical Scheme Based on Radial Basis Functions and a Hybrid Quasi-Newton Method for a Nonlinear Shape Optimization Problem" Mathematical and Computational Applications 27, no. 4: 67. https://doi.org/10.3390/mca27040067
APA StyleEl Yazidi, Y., & Ellabib, A. (2022). An Efficient Numerical Scheme Based on Radial Basis Functions and a Hybrid Quasi-Newton Method for a Nonlinear Shape Optimization Problem. Mathematical and Computational Applications, 27(4), 67. https://doi.org/10.3390/mca27040067






