Magneto Mixed Convection of Williamson Nanofluid Flow through a Double Stratified Porous Medium in Attendance of Activation Energy
Abstract
:1. Introduction
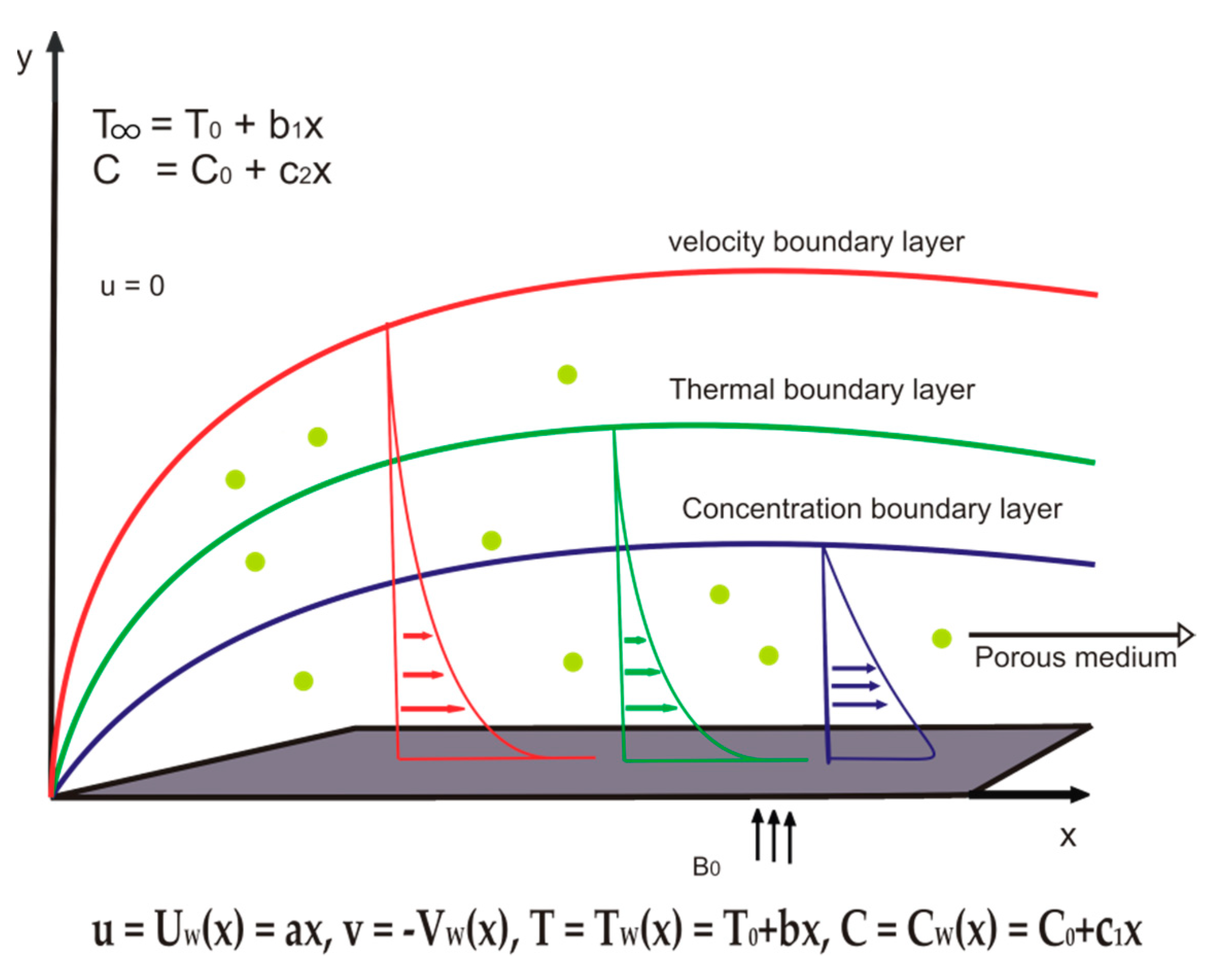
2. Development of the Flow Analysis
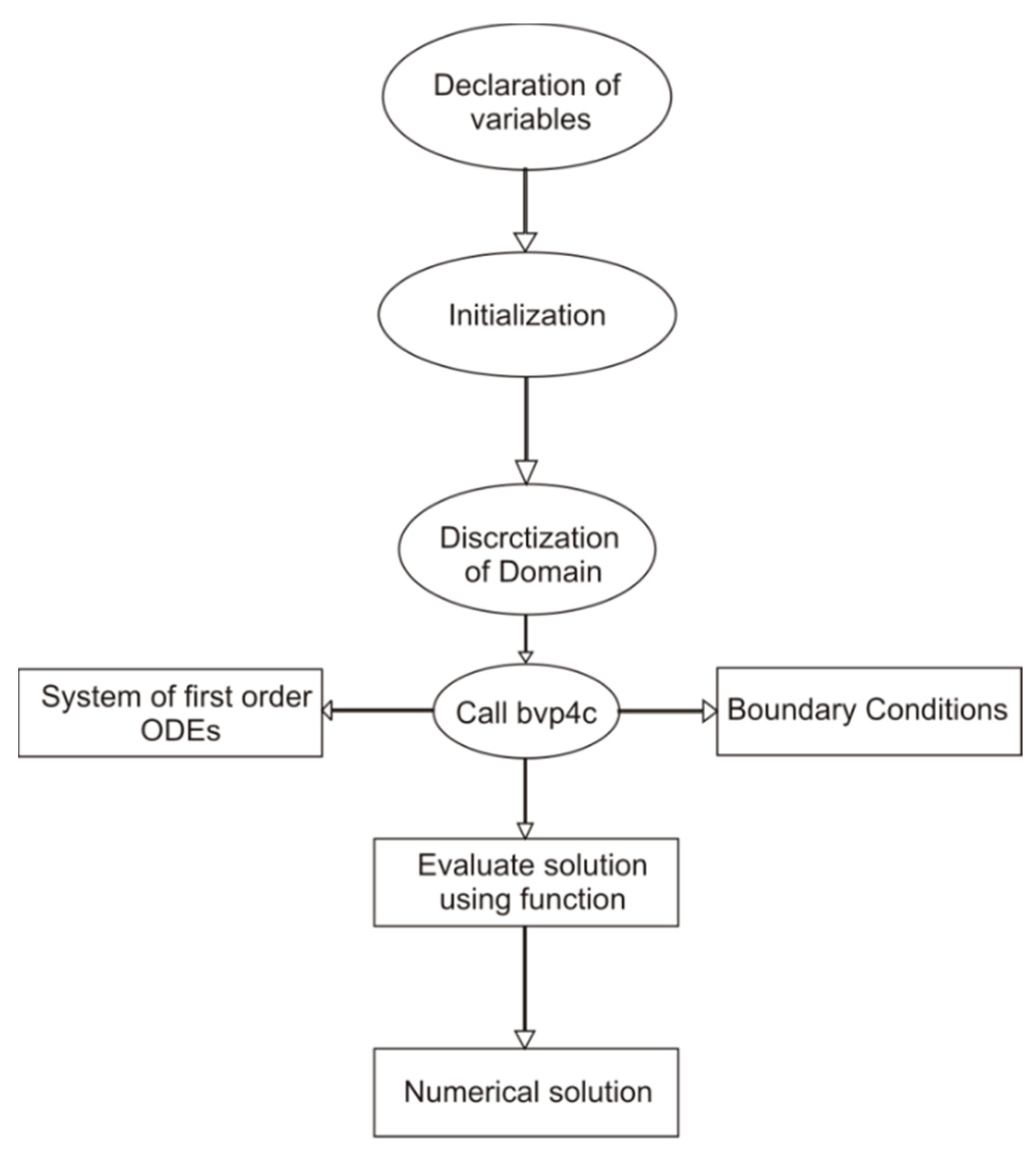
3. The Solution Methodology
4. Results and Discussion
5. Conclusions
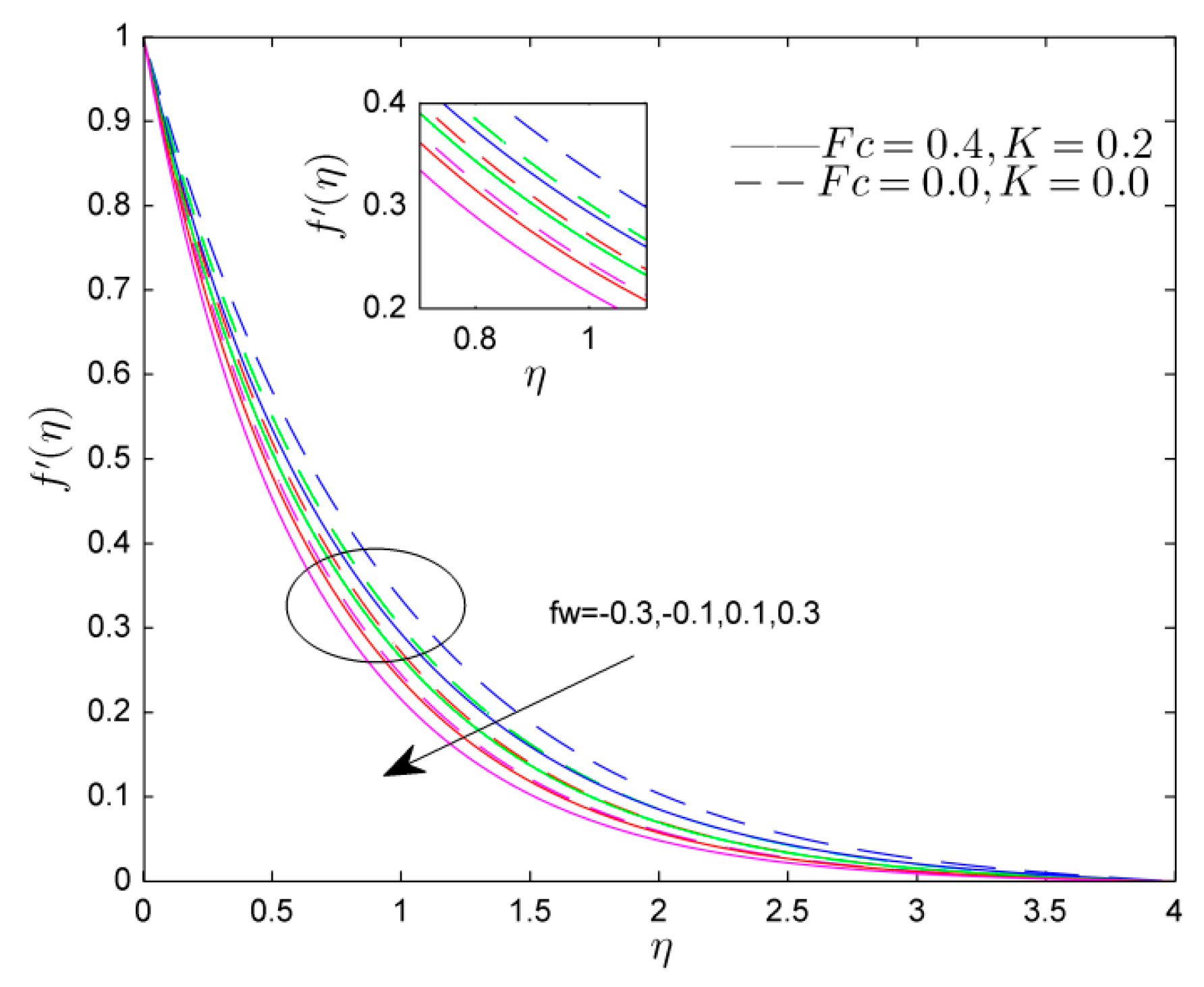
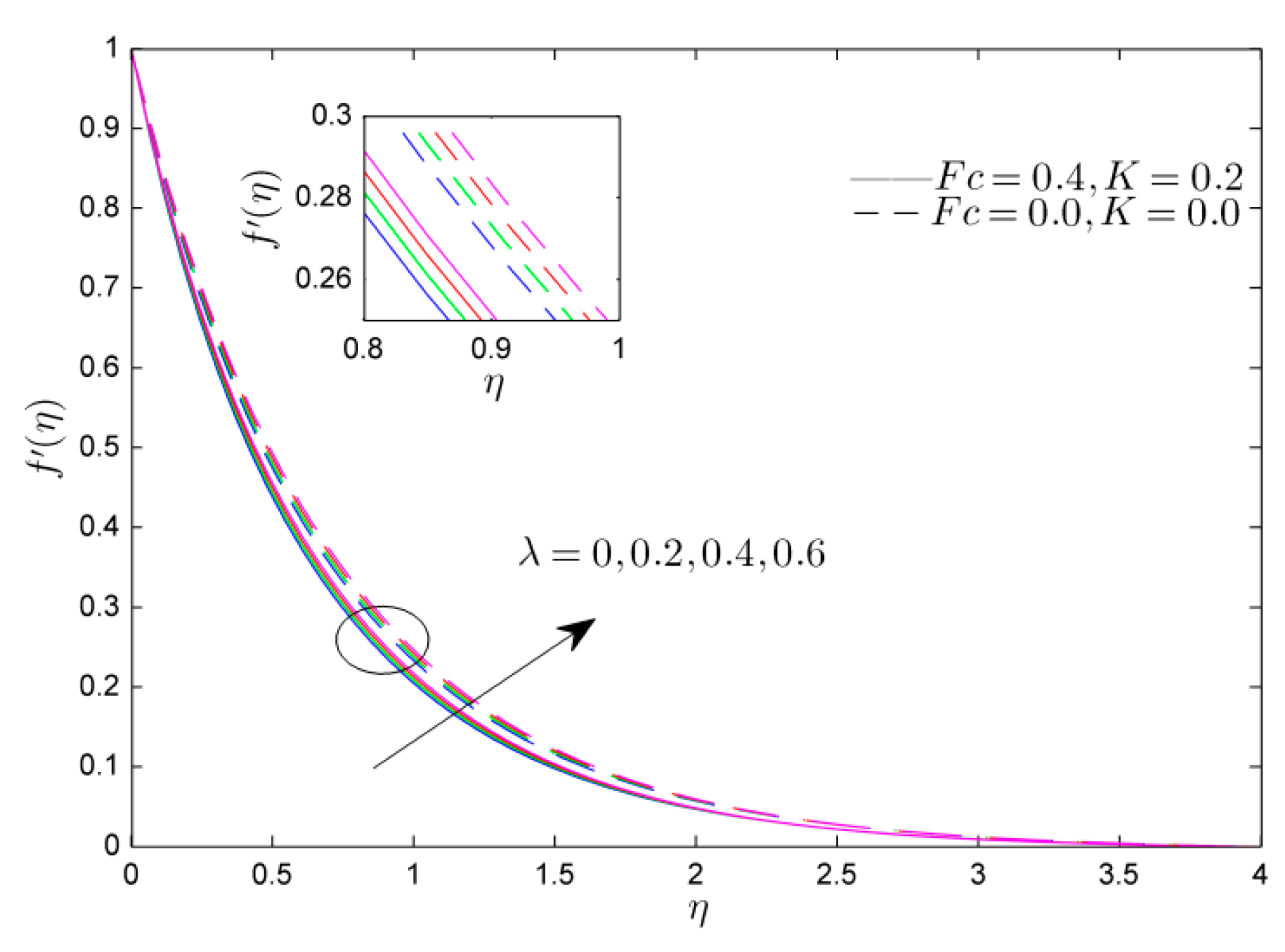
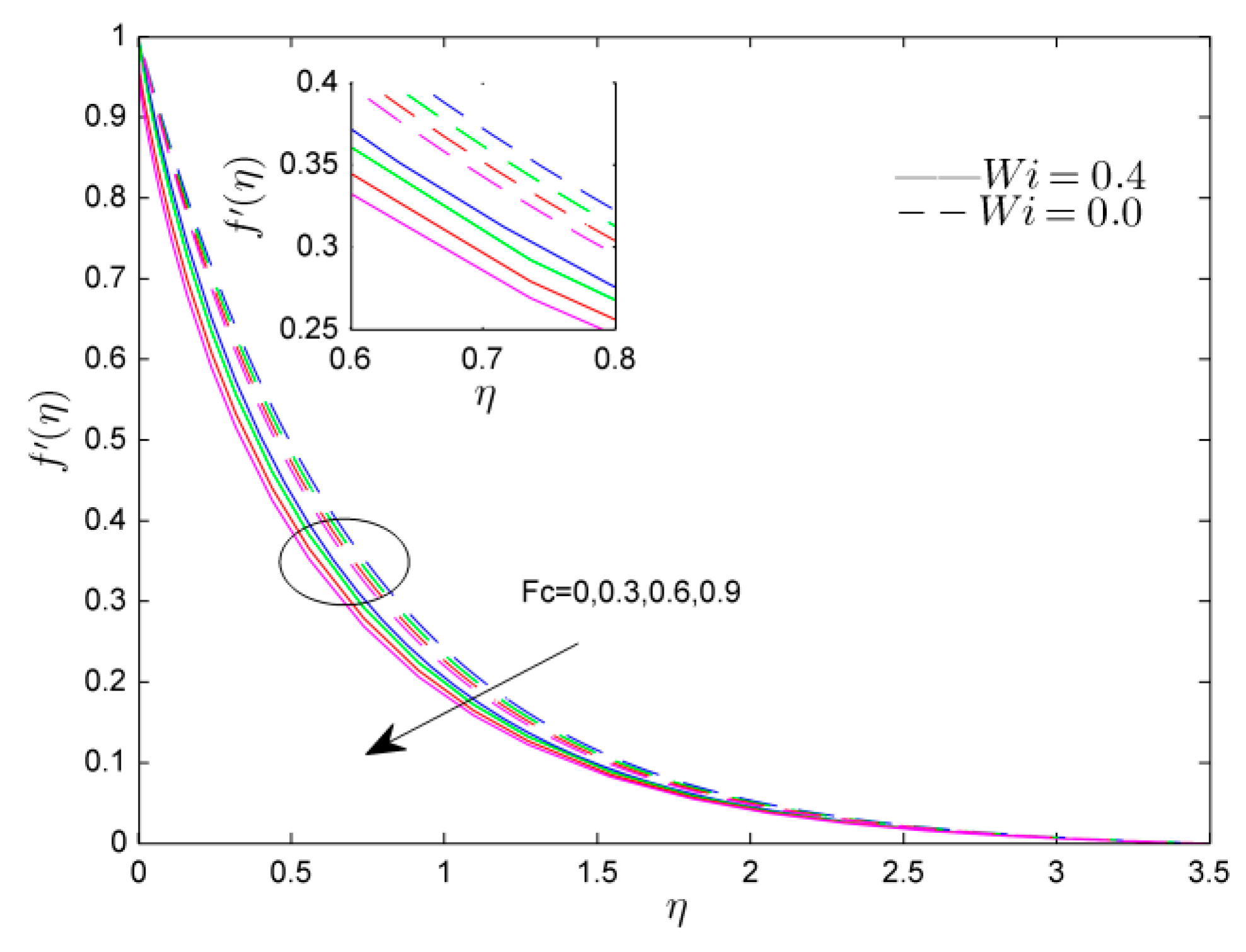
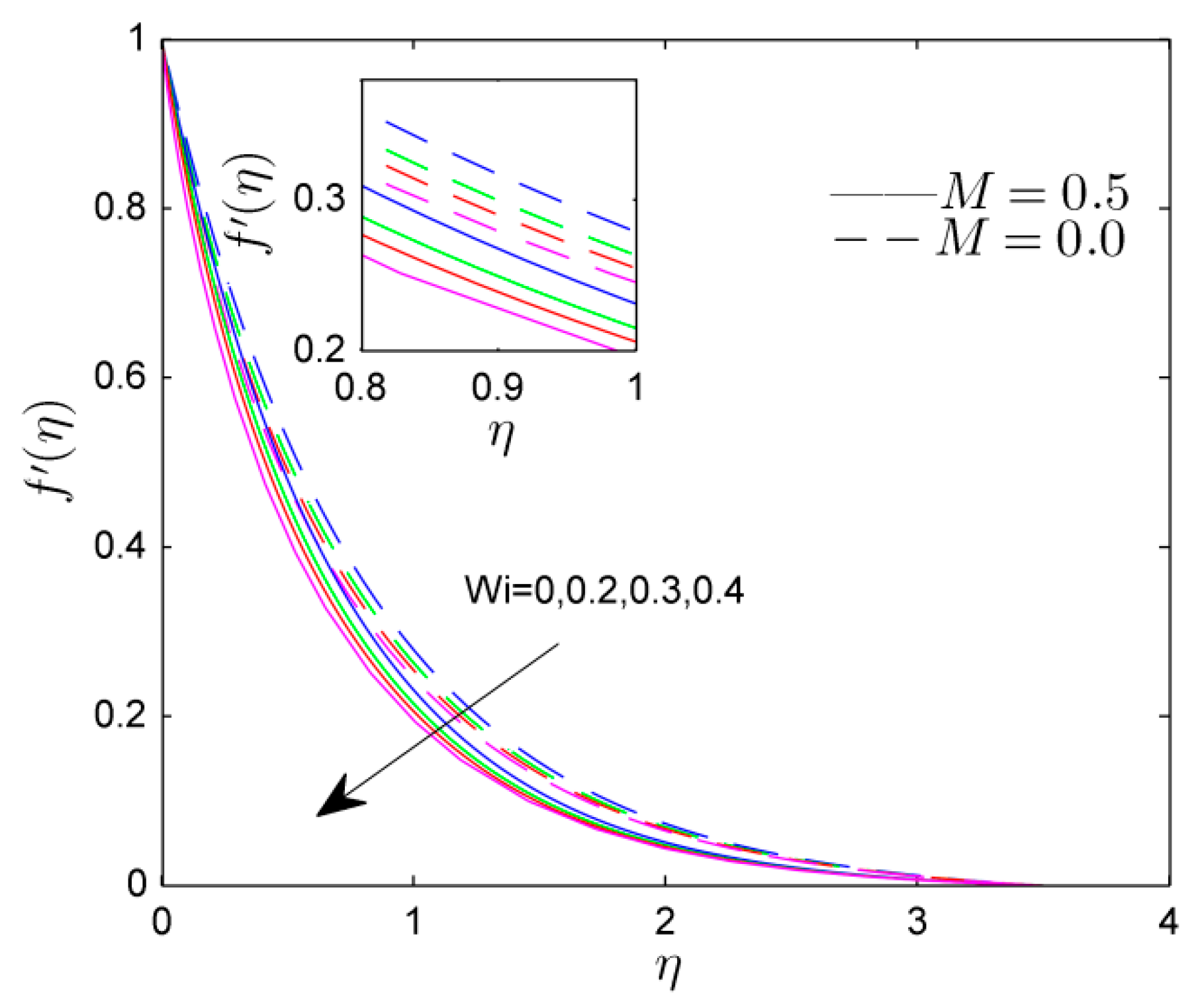
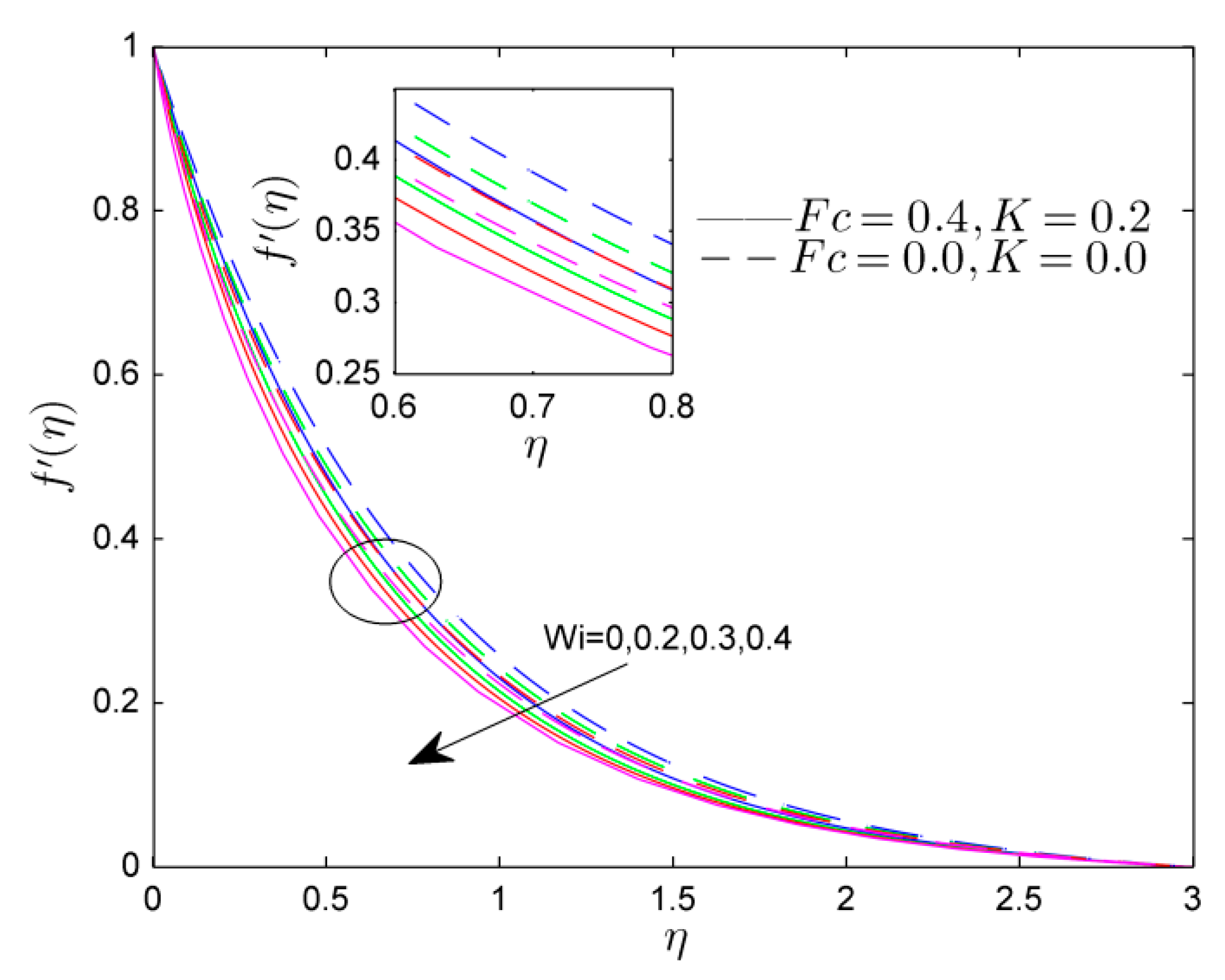
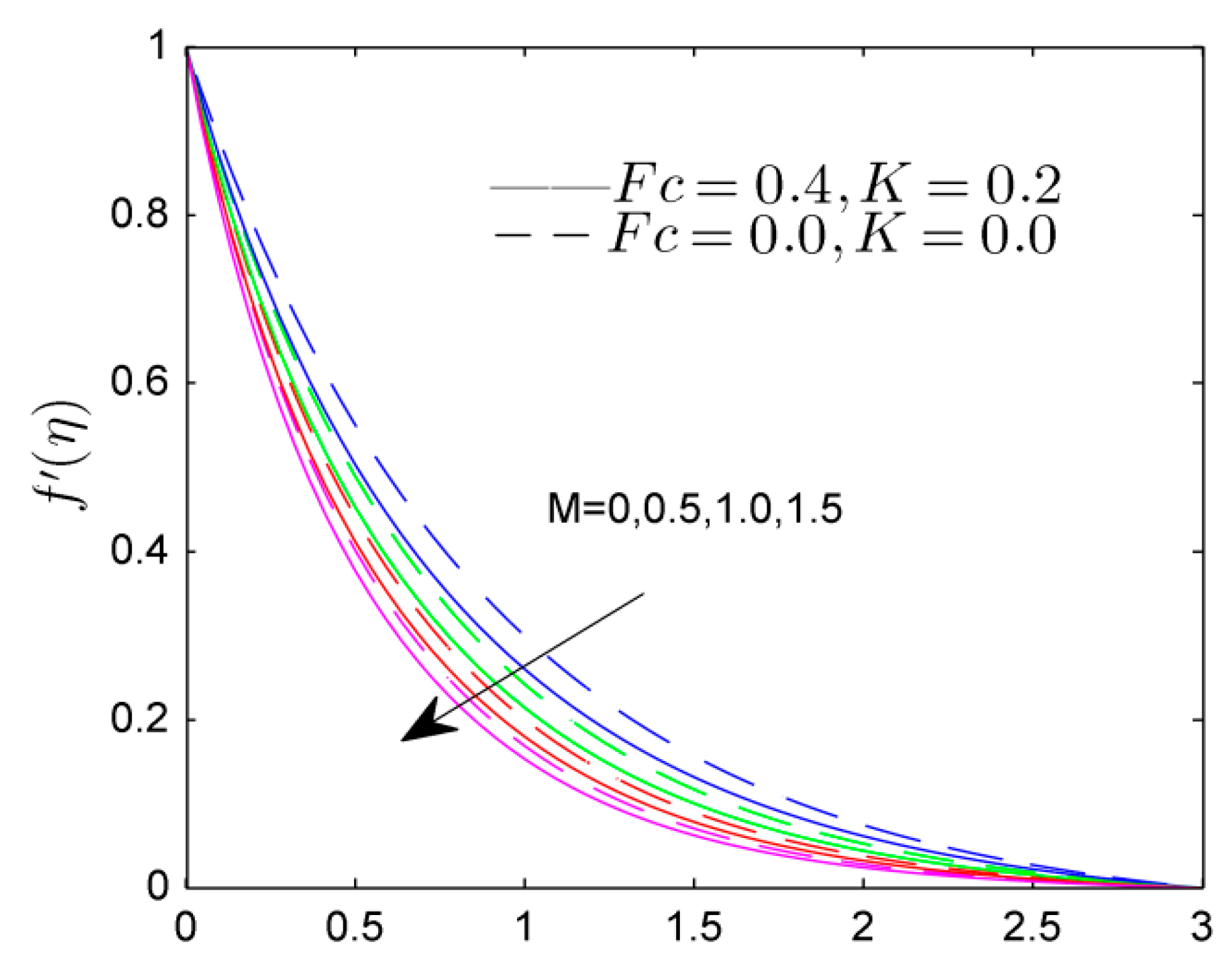
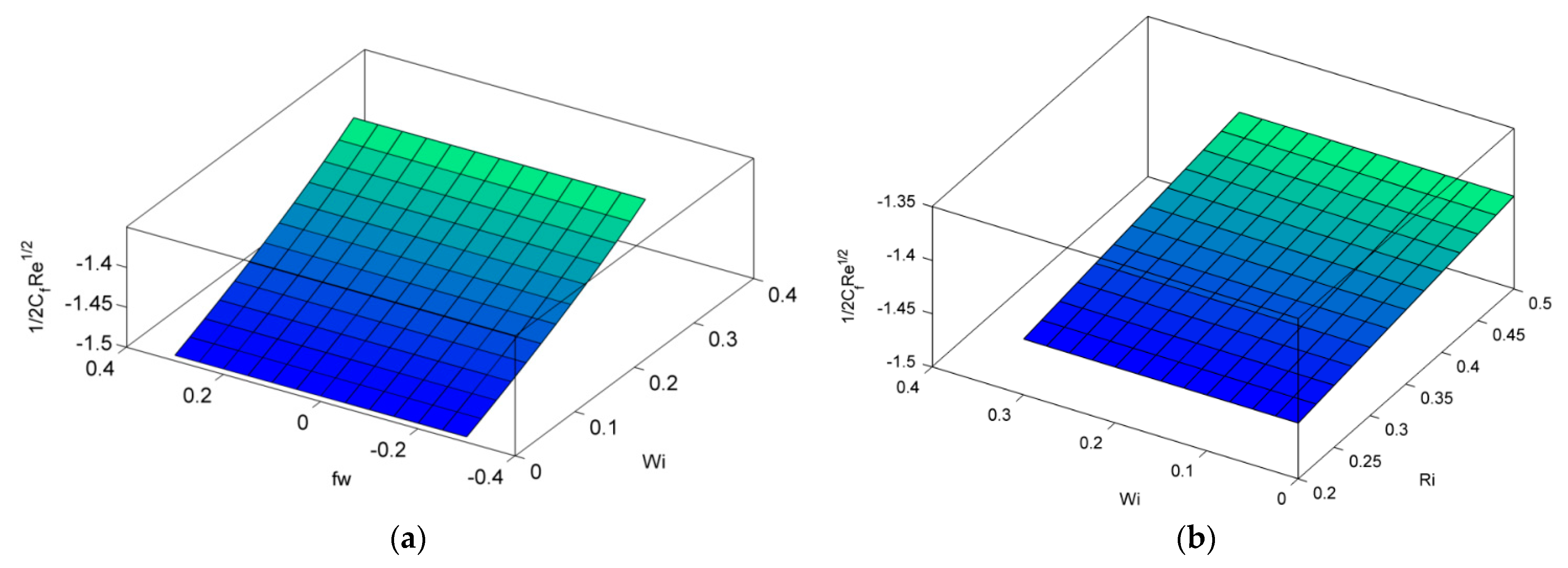
- The velocity profile was reduced by the Weissenberg number and Forchheimer number, while the mixed convective parameter shows the increasing tendency in velocity profile.
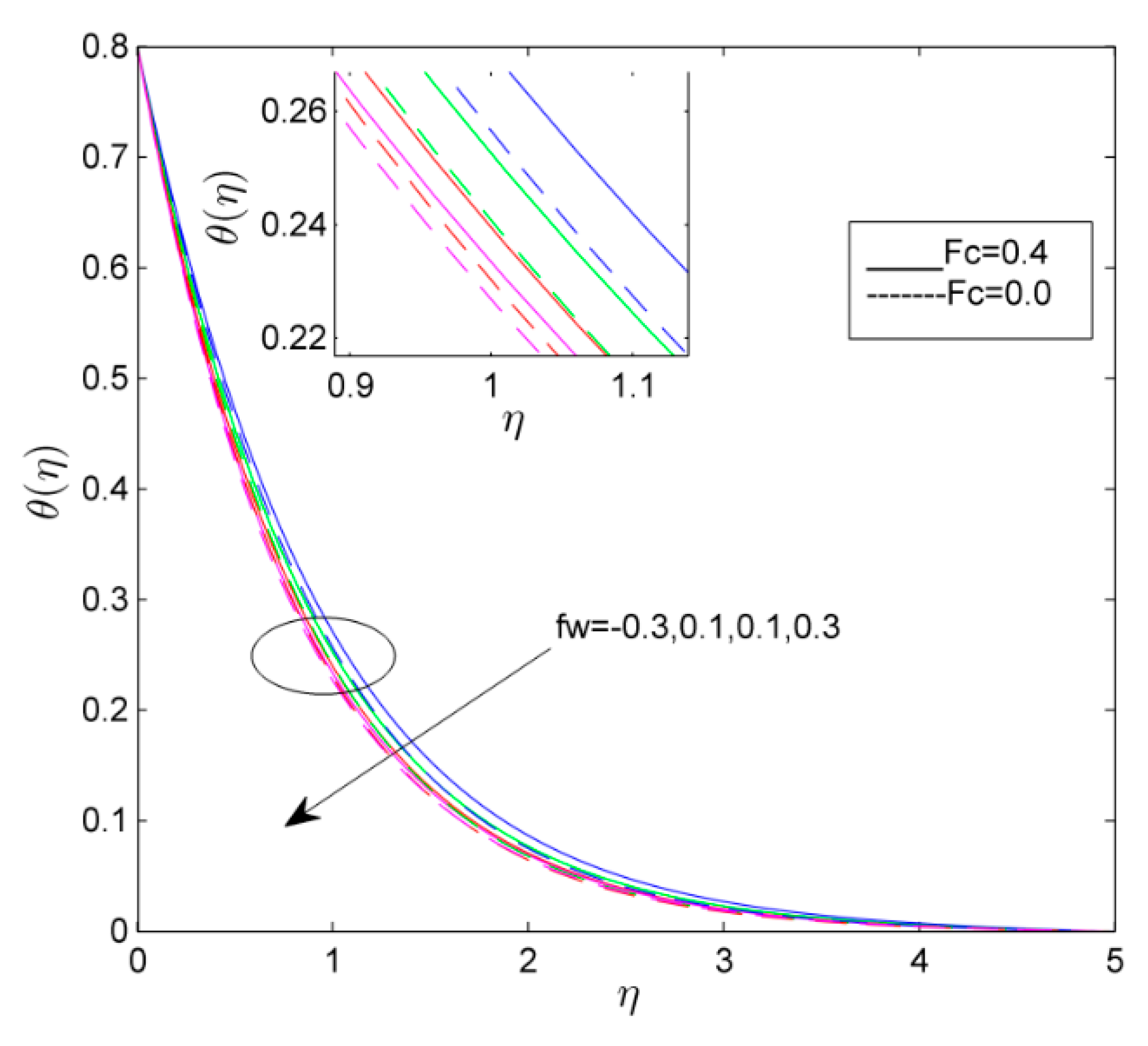
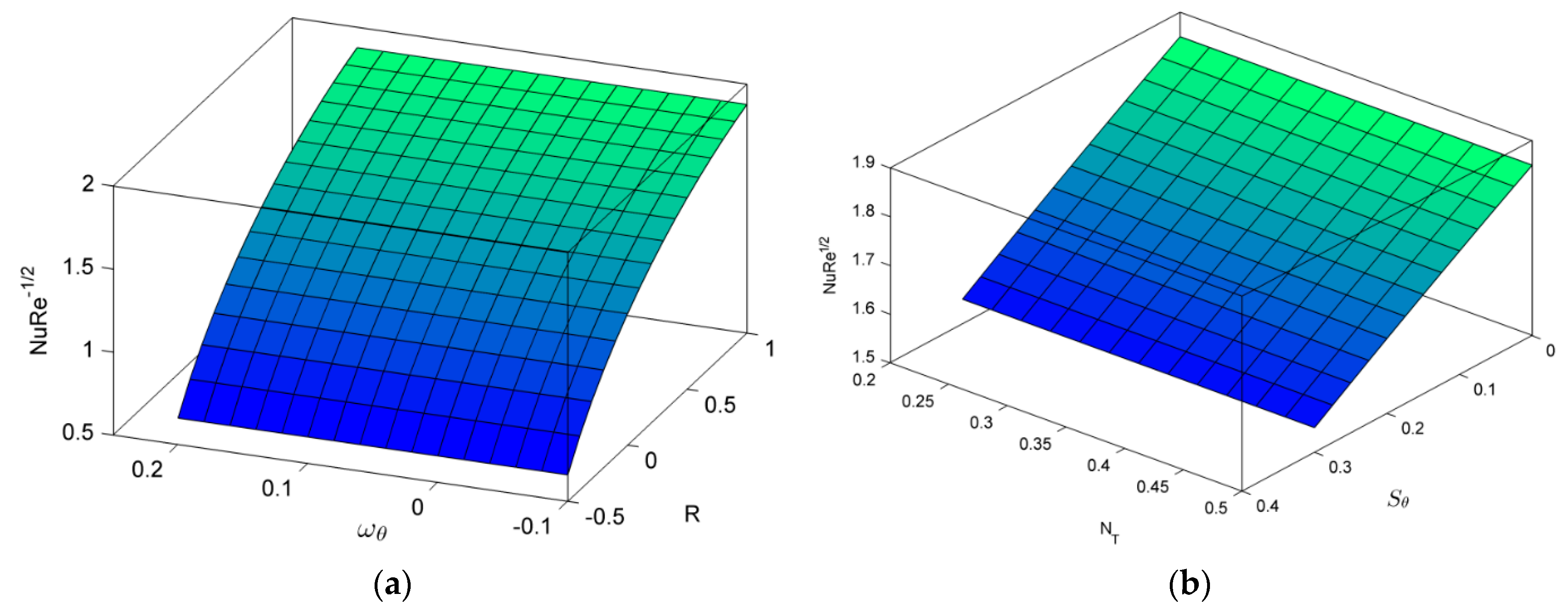
- The temperature distribution was raised with a high thermal relaxation time and radiation values.
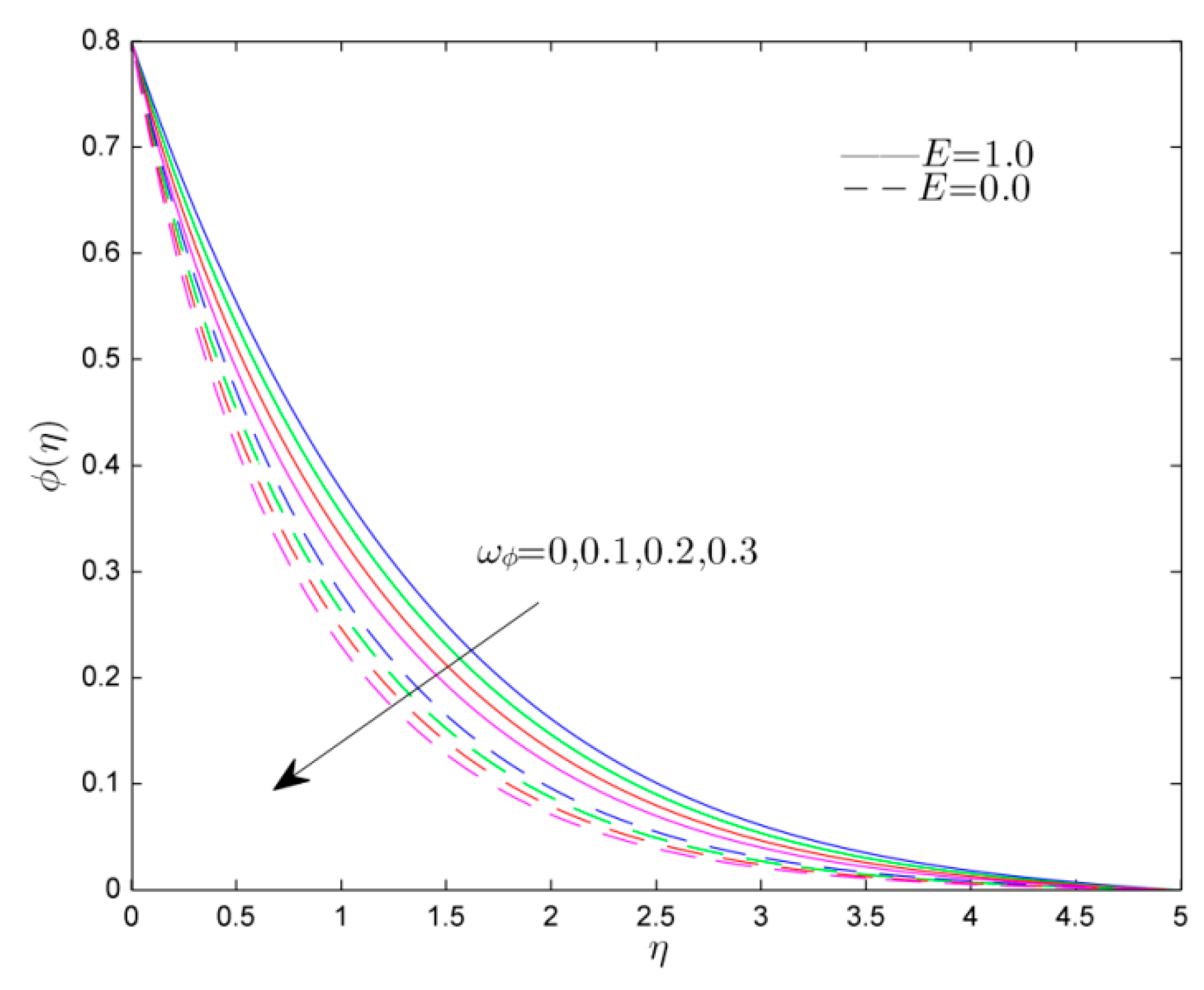
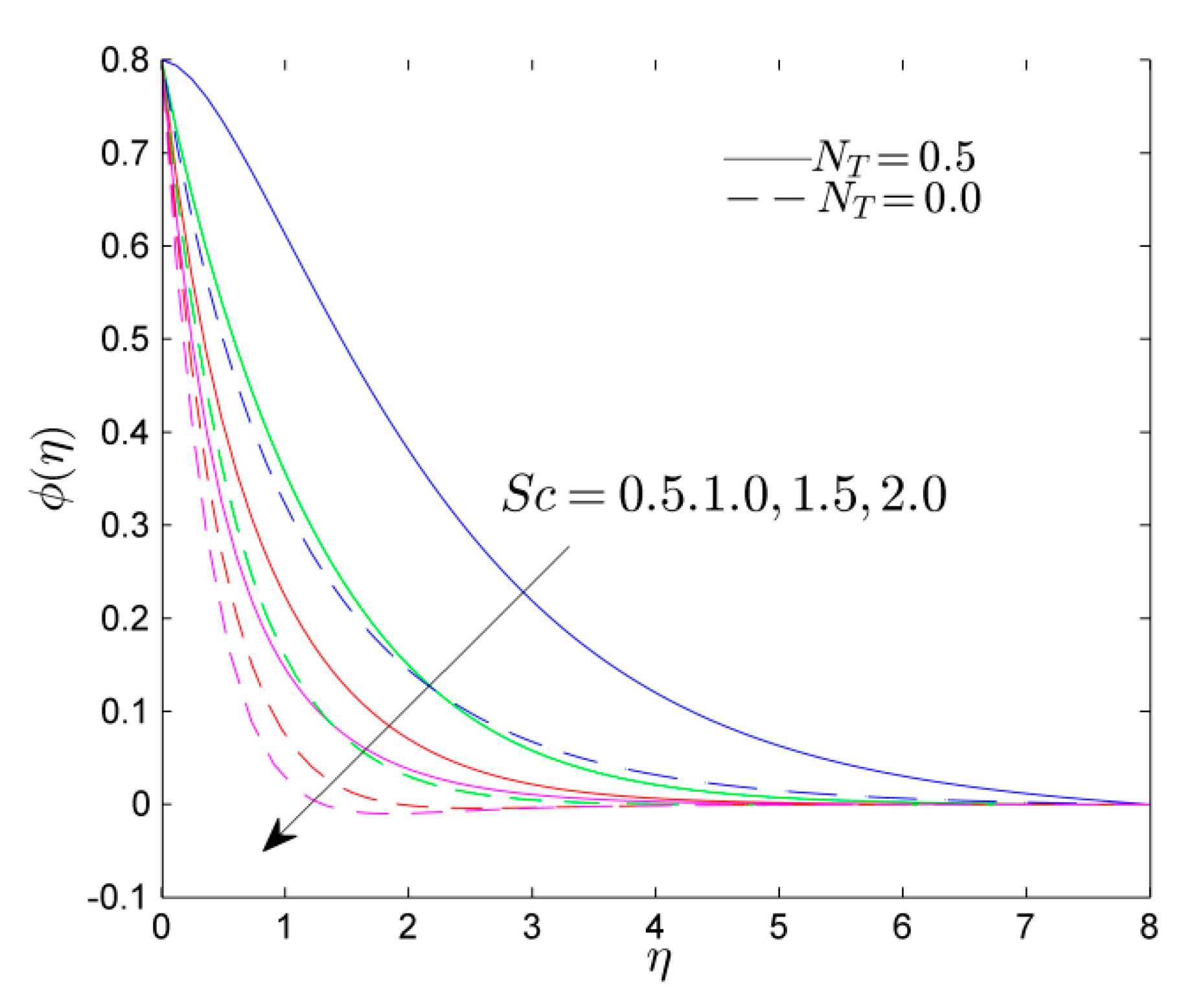
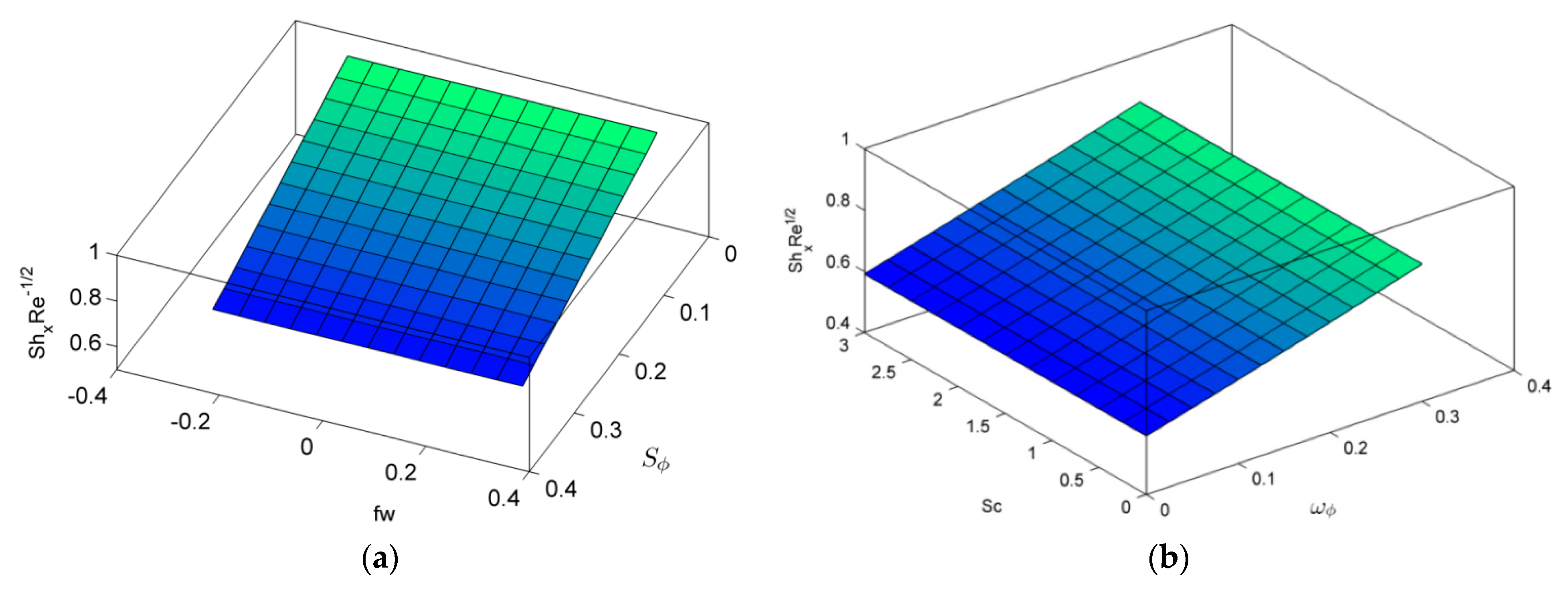
- For higher estimations of Schmidt number and mass relaxation time, the concentration profile diminished.
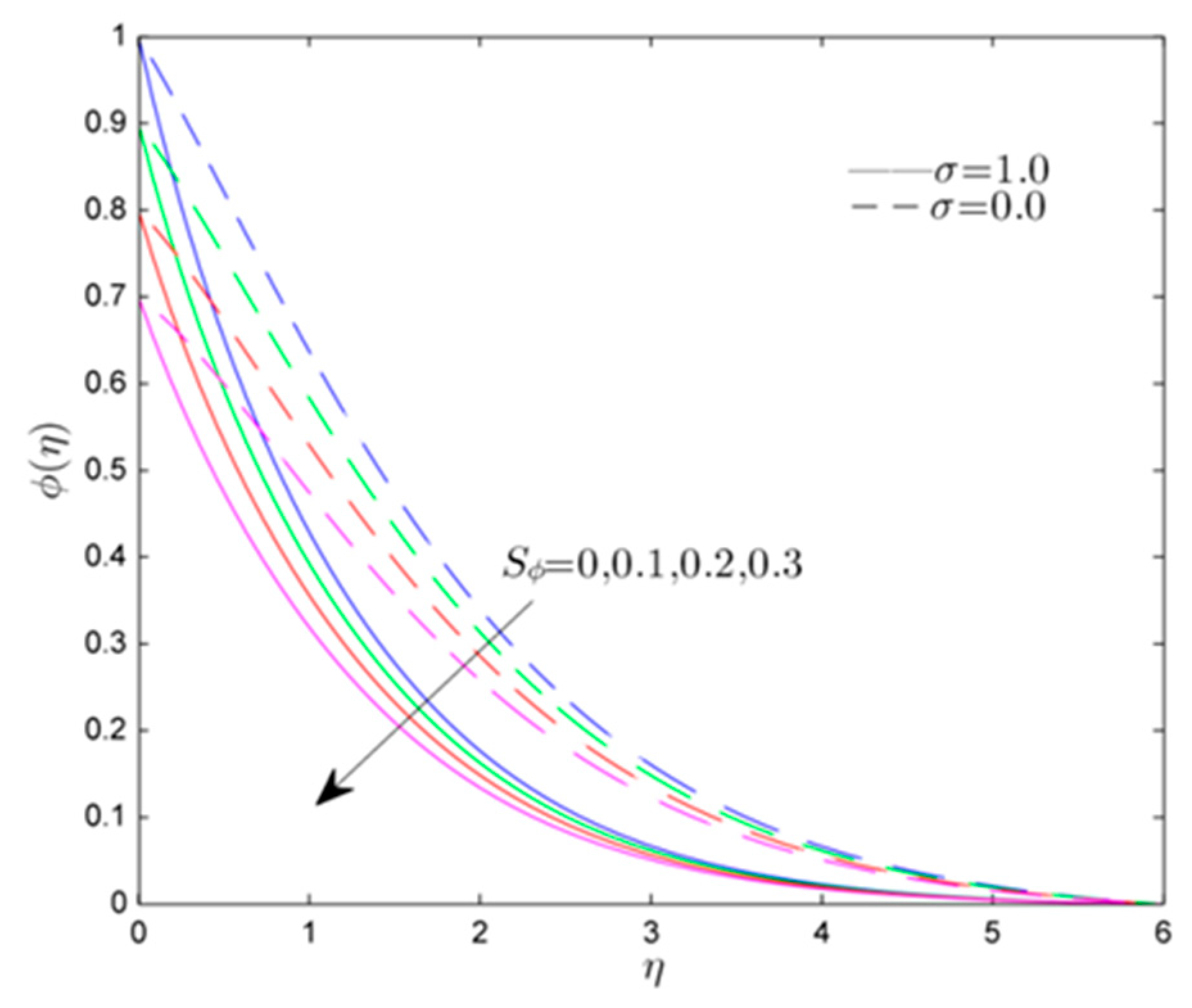
- Increases in the thermal and mass stratification parameters reduce the temperature and concentration profile.
- Heat and mass transfer rates were declined for large values of thermal radiation, thermal relaxation time, mass stratification, and suction parameter.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| List of Symbols | ||
| a | Stretching rate | |
| Drag coefficient | ||
| Specific heat | () | |
| Magnetic field | () | |
| Surface concentration | () | |
| Acceleration due to gravity | () | |
| Ambient fluid concentration | () | |
| Mass diffusivity | () | |
| C | Fluid concentration | () |
| Thermophoretic diffusion coefficient | () | |
| Activation energy | Dimensionless | |
| = | Forchheimer number | Dimensionless |
| Local Grashof number | Dimensionless | |
| Heat generation parameter | Dimensionless | |
| Thermal conductivity | ||
| Permeability of porous medium | Dimensionless | |
| = − | Suction/injection parameter | Dimensionless |
| Mean absorption coefficient | Dimensionless | |
| Reaction rate | Dimensionless | |
| M = | Magnetic parameter | Dimensionless |
| n | Fitted rate | Dimensionless |
| = | Brownian diffusion parameter | Dimensionless |
| Buoyancy ratio parameter | Dimensionless | |
| Prandtl number | Dimensionless | |
| Local Reynolds number | Dimensionless | |
| Richardson number | Dimensionless | |
| Schmidt number | Dimensionless | |
| Fluid temperature | (K) | |
| Weissenberg number | Dimensionless | |
| Ambient temperature | (K) | |
| Velocity components | () | |
| Stretching surface velocity | () | |
| Thermal stratification | Dimensionless | |
| Direction coordinates | (m) | |
| Solutal stratification | Dimensionless | |
| Wall temperature | (K) | |
| Thermophoresis parameter | Dimensionless | |
| Thermal Radiation | Dimensionless | |
| Heat capacity | ( | |
| Greek Symbols | ||
| Thermal relaxation time parameter | Dimensionless | |
| Temperature difference parameter | Dimensionless | |
| Mass relaxation parameter | Dimensionless | |
| Fluid density | ( | |
| Thermal diffusivity | ( | |
| Williamson parameter | Dimensionless | |
| Non dimensional temperature | Dimensionless | |
| Non dimensional concentration | Dimensionless | |
| Dimensionless reaction rate | Dimensionless | |
References
- Choi, S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995; pp. 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Williamson, R.V. The Flow of Pseudoplastic Materials. Ind. Eng. Chem. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, S.T.; Lee, C. Flow of a Williamson fluid over a stretching sheet. Braz. J. Chem. Eng. 2013, 30, 619–625. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Shafiq, A.; Alsaedi, A. Hydromagnetic boundary layer flow of Williamson fluid in the presence of thermal radiation and Ohmic dissipation. Alex. Eng. J. 2016, 55, 2229–2240. [Google Scholar] [CrossRef] [Green Version]
- Karthikeyan, S.; Bhuvaneswari, M.; Sivasankaran, S.; Rajan, S. Cross diffusion, radiation and chemical reaction effects on MHD combined convective flow towards a stagnation-point upon vertical plate with heat generation. IOP Conf. Ser. Mater. Sci. Eng. 2018, 390, 012088. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R. SS symmetry Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water- and Engine-Oil-Based Newtonian Fluids through Porous Media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Ahmed, K.; Akbar, T.; Muhammad, T. Physical Aspects of Homogeneous–Heterogeneous Reactions on MHD Williamson Fluid Flow across a Nonlinear Stretching Curved Surface Together with Convective Boundary Conditions. Math. Probl. Eng. 2021, 2021, 7016961. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Ali, S.; Hashim, K.; Marjan, M.A. Numerical analysis of dual variable of conductivity in bioconvection flow of Carreau–Yasuda nanofluid containing gyrotactic motile microorganisms over a porous medium. J. Therm. Anal. Calorim. 2021, 145, 2033–2044. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Shakeel, M.; Ellahi, R.; Sait, S.M. Effects of Magnetohydrodynamics Flow on Multilayer Coatings of Newtonian and Non-Newtonian Fluids through Porous Inclined Rotating Channel. Coatings 2022, 12, 430. [Google Scholar] [CrossRef]
- Loganathan, K.; Mohana, K.; Mohanraj, M.; Sakthivel, P.; Rajan, S. Impact of third-grade nanofluid flow across a convective surface in the presence of inclined Lorentz force: An approach to entropy optimization. J. Therm. Anal. Calorim. 2020, 144, 1935–1947. [Google Scholar] [CrossRef]
- Yusuf, T.A.; Mabood, F.; Prasannakumara, B.C.; Sarris, I.E. Magneto-bioconvection flow of Williamson nanofluid over an inclined plate with gyrotactic microorganisms and entropy generation. Fluids 2021, 6, 109. [Google Scholar] [CrossRef]
- Qureshi, M.A. Numerical simulation of heat transfer flow subject to MHD of Williamson nanofluid with thermal radiation. Symmetry 2021, 13, 10. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M. MHD flow of Cattaneo–Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: Using numerical approach. J. Magn. Magn. Mater. 2016, 401, 991–997. [Google Scholar] [CrossRef]
- Qayyum, S.; Khan, M.I.; Hayat, T.; Alsaedi, A.; Tamoor, M. Entropy generation in dissipative flow of Williamson fluid between two rotating disks. Int. J. Heat Mass Transf. 2018, 127, 933–942. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, A.; Alsaedi, A. Three-dimensional mixed convection squeezing flow. Appl. Math. Mech. 2015, 36, 47–60. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negara, M. Viscous dissipation effect on mixed convective heat transfer of MHD flow of Williamson nanofluid over a stretching cylinder in the presence of variable thermal conductivity and chemical reaction. Heat Transf. 2021, 50, 2427–2453. [Google Scholar] [CrossRef]
- Khan, W.A.; Khan, M.; Alshomrani, A.S.; Ahmad, L. Numerical investigation of generalized Fourier’s and Fick’s laws for Sisko fluid flow. J. Mol. Liq. 2016, 224, 1016–1021. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Loganathan, K.; Jain, R.; Gyeltshen, S. Darcy-Forchheimer 3D Flow of Glycerin-Based Carbon Nanotubes on a Riga Plate with Nonlinear Thermal Radiation and Cattaneo–Christov Heat Flux. J. Nanomater. 2022, 2022, 5286921. [Google Scholar] [CrossRef]
- Conduzionedelcalore, C.C.S. Atti del Seminario Matematico e Fisico dell'Universita di Modena e Reggio Emilia. Modena by Seminario matematico e fisico Università di Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Alessa, N.; Sangeethavaanee, M.; Namgyel, N. Numerical and Analytical Investigation for Darcy-Forchheimer Flow of a Williamson fluid over a Riga Plate with Double Stratification and Cattaneo–Christov Dual Flux. Adv. Math. Phys. 2021, 2021, 1867824. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqas, M.; Yasmeen, T. Impact of Cattaneo–Christov heat flux model inflow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Shankar, B. Goud Heat generation/absorption influence on steady stretched permeable surface on MHD flow of a micropolar fluid through a porous medium in the presence of variable suction/injection. Int. J. Thermofluids 2020, 7–8, 100044. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Hussain, S.; Manan, A.; Sadiq, M.T. Unsteady magneto-hydrodynamic transport of rotating Maxwell nanofluid flow on a stretching sheet with Cattaneo–Christov double diffusion and activation energy. Therm. Sci. Eng. Prog. 2020, 20, 100720. [Google Scholar] [CrossRef]
- Abu-Hamden, N.H.; Alsulami, R.A.; Rawa, M.J.H.; Alazwari, M.A.; Goodarzi, M.; Safaei, M.R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo–Christov Heat Flux Model. Mathematics 2021, 9, 669. [Google Scholar] [CrossRef]
- Rashid, S.; Khan, M.I.; Hayat, T.; Ayub, M.; Alsaedi, A. Darcy–Forchheimer flow of Maxwell fluid with activation energy and thermal radiation over an exponential surface. Appl. Nanosci. 2020, 10, 2965–2975. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Khalique, C.M. Significance of thermal slip and convective boundary conditions in three dimensional rotating darcy-forchheimer nanofluid flow. Symmetry 2020, 12, 741. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy generation and consequences of binary chemical reaction on mhd darcy-forchheimer Williamson nanofluid flow over non-linearly stretching surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Darcy–Forchheimer Three-Dimensional Flow of Williamson Nanofluid over a Convectively Heated Nonlinear Stretching Surface. Commun. Theor. Phys. 2017, 68, 387–394. [Google Scholar] [CrossRef]
- Bestman, A.R. Natural convection boundary layer with suction mass transfer in a porous medium. Int. J. Energy Res. 1990, 14, 389–396. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Islam, S. Mathematical modeling and study of MHD flow of Williamson nanofluid over a nonlinear stretching plate with activation energy. Heat Transf. 2021, 50, 2558–2570. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Hayat, T.; Khan, M.I.; Alsaadi, F.E. Heat transport and entropy optimization inflow of magneto-Williamson nanomaterial with Arrhenius activation energy. Comput. Methods Programs Biomed. 2020, 183, 105051. [Google Scholar] [CrossRef]
- Muhammad, R.; Khan, M.I.; Jameel, M.; Khan, N.B. Fully developed Darcy-Forchheimer mixed convective flow over a curved surface with activation energy and entropy generation. Comput. Methods Programs Biomed. 2020, 188, 105298. [Google Scholar] [CrossRef] [PubMed]
- Danook, S.H.; Jasim, Q.K.; Hussein, A.M. Nanofluid Convective Heat Transfer Enhancement Elliptical Tube inside Circular Tube under Turbulent Flow. Math. Comput. Appl. 2018, 23, 78. [Google Scholar] [CrossRef] [Green Version]
- Jamshed, W.; Goodarzi, M.; Prakash, M.; Nisar, K.S.; Zakarya, M.; Abdel-Aty, A.H. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud. Therm. Eng. 2021, 26, 101160. [Google Scholar] [CrossRef]
- Alghamdi, M.; Wakif, A.; Thumma, T.; Khan, U. Case Studies in Thermal Engineering Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a Darcy-Brinkman porous structure bounded vertically by an irregular slender surface. Case Stud. Therm. Eng. 2021, 28, 101428. [Google Scholar] [CrossRef]
- Loganathan, K.; Rajan, S. An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J. Therm. Anal. Calorim. 2020, 141, 2599–2612. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negara, M. The Investigation of MHD Williamson Nanofluid over Stretching Cylinder with the Effect of Activation Energy. Adv. Math. Phys. 2020, 2020, 9523630. [Google Scholar] [CrossRef]
- Sajid, T.; Tanveer, S.; Sabir, Z.; Guirao, J.L.G. Impact of Activation Energy and Temperature-Dependent Heat Source/Sink on Maxwell-Sutterby Fluid. Math. Probl. Eng. 2020, 2020, 5251804. [Google Scholar] [CrossRef]
- Zaib, A.; Abelman, S.; Chamkha, A.J.; Rashidi, M.M. Entropy Generation of Williamson Nanofluid near a Stagnation Point over a Moving Plate with Binary Chemical Reaction and Activation Energy. Heat Transf. Res. 2018, 49, 1131–1149. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Effects of binary chemical reaction and Arrhenius activation energy in Darcy–Forchheimer three-dimensional flow of nanofluid subject to rotating frame. J. Therm. Anal. Calorim. 2019, 136, 1769–1779. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negara, M. Viscous dissipation effect on Williamson nanofluid over stretching/ shrinking wedge with thermal radiation and chemical reaction. J. Phys. Commun. 2020, 4, 045015. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Kadry, S.; Chu, Y.M. Role of bioconvection in a three dimensional tangent hyperbolic partially ionized magnetized nanofluid flow with Cattaneo–Christov heat flux and activation energy. Int. Commun. Heat Mass Transf. 2021, 120, 104994. [Google Scholar] [CrossRef]
- Kumar, R.; Sood, S.; Shehzad, S.A.; Sheikholeslami, M. Radiative heat transfer study for flow of non-Newtonian nanofluid past a Riga plate with variable thickness. J. Mol. Liq. 2017, 248, 143–152. [Google Scholar] [CrossRef]
- Khan, W.A.; Khan, M.; Alshomrani, A.S. Impact of chemical processes on 3D Burgers fluid utilizing Cattaneo–Christov double-diffusion: Applications of non-Fourier’s heat and non-Fick’s mass flux models. J. Mol. Liq. 2016, 223, 1039–1047. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, K.; Farooq, M.; Alsaedi, A. Squeezed flow subject to Cattaneo–Christov heat flux and rotating frame. J. Mol. Liq. 2016, 220, 216–222. [Google Scholar] [CrossRef]
- Loganathan, K.; Alessa, N.; Kayikci, S. Heat Transfer Analysis of 3-D Viscoelastic Nano-fluid Flow Over a Convectively Heated Porous Riga Plate with Cattaneo–Christov Double Flux. Front. Phys. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Karthik, T.S.; Loganathan, K.; Shankar, A.N.; Carmichael, M.J.; Mohan, A.; Kaabar, M.K.A.; Kayikci, S. Zero and Nonzero Mass Flux Effects of Bioconvective Viscoelastic Nanofluid over a 3D Riga Surface with the Swimming of Gyrotactic Microorganisms. Adv. Math. Phys. 2021, 2021, 9914134. [Google Scholar] [CrossRef]
- Ahmad, A.G.; Kaabar, M.K.A.; Rashid, S.; Abid, M. A Novel Numerical Treatment of Nonlinear and Nonequilibrium Model of Gradient Elution Chromatography considering Core-Shell Particles in the Column. Math. Probl. Eng. 2022, 2022, 1619702. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N.; Yıldız, M. Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics. Mathematics 2022, 10, 1125. [Google Scholar] [CrossRef]
- Islam, T.; Yavuz, M.; Parveen, N.; Fayz-Al-Asad, M. Impact of Non-Uniform Periodic Magnetic Field on Unsteady Natural Convection Flow of Nanofluids in Square Enclosure. Fractal Fract. 2022, 6, 101. [Google Scholar] [CrossRef]
- Fayz-Al-Asad, M.; Yavuz, M.; Alam, M.; Sarker, M.; Alam, M.; Bazighifan, O. Influence of fin length on magneto-combined convection heat transfer performance in a lid-driven wavy cavity. Fractal Fract. 2021, 5, 107. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid with Newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms. Math. Model. Numer. Simul. Appl. 2022, 2, 13–25. [Google Scholar] [CrossRef]
- Khan, A.; Khan, A.; Sinan, M. Ion temperature gradient modes driven soliton and shock by reduction perturbation method for electron-ion magneto-plasma. Math. Model. Numer. Simul. Appl. 2022, 2, 1–12. [Google Scholar] [CrossRef]
- Sreelakshmi, K.; Sarojamma, G.; Makinde, O.D. Dual stratification on the Darcy–Forchheimer flow of a maxwell nanofluid over a stretching surface. In Defect and Diffusion Forum; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2018; Volume 387, pp. 207–217. [Google Scholar] [CrossRef]
- Hayat, T.; Shah, F.; Hussain, Z.; Alsaedi, A. Outcomes of double stratification in Darcy–Forchheimer MHD flow of viscoelastic nanofluid. J. Brazilian Soc. Mech. Sci. Eng. 2018, 40, 145. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Alessa, N.; Sangeethavaanee, M.; Kayikci, S.; Namgyel, N. Mixed Convection and Thermally Radiative Flow of MHD Williamson Nanofluid with Arrhenius Activation Energy and Cattaneo–Christov Heat-Mass Flux. J. Math. 2021, 2021, 2490524. [Google Scholar] [CrossRef]
- Ahmed, K.; Khan, W.A.; Akbar, T.; Rasool, G.; Alharbi, S.O.; Khan, I. Numerical Investigation of Mixed Convective Williamson Fluid Flow Over an Exponentially Stretching Permeable Curved Surface. Fluids 2021, 6, 260. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Darcy-Forchheimer, M.Z. 3D Williamson nanofluid flow with generalized Fourier and Fick’s laws in a stratified medium. Bull. Polish Acad. Sci. Technol. Sci. 2020, 68, 327–335. [Google Scholar] [CrossRef]
- Haider, F.; Hayat, T.; Alsaedi, A. Flow of hybrid nanofluid through Darcy-Forchheimer porous space with variable characteristics. Alex. Eng. J. 2021, 60, 3047–3056. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M. Simultaneous impact of nonlinear radiative heat flux and Arrhenius activation energy inflow of chemically reacting Carreau nanofluid. Appl. Nanosci. 2020, 10, 2977–2988. [Google Scholar] [CrossRef]
- Hayat, T.; Naz, S.; Waqas, M.; Alsaedi, A. Effectiveness of Darcy-Forchheimer and nonlinear mixed convection aspects in stratified Maxwell nanomaterial flow induced by convectively heated surface. Appl. Math. Mech. 2018, 39, 1373–1384. [Google Scholar] [CrossRef]
- Kumar, K.A.; Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. MHD Carreau fluid flow past a melting surface with Cattaneo–Christov heat flux. In Applied Mathematics and Scientific Computing; Trends in Mathematics; Birkhäuser: Cham, Switzerland, 2019; pp. 325–336. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A.; Al-Solamy, F. Radiative Three-Dimensional Flow with Chemical Reaction. Int. J. Chem. React. Eng. 2016, 14, 79–91. [Google Scholar] [CrossRef]
- Sahoo, A.; Nandkeolyar, R. Entropy generation in convective radiative flow of a Casson nanofluid in non-Darcy porous medium with Hall current and activation energy: The multiple regression model. Appl. Math. Comput. 2021, 402, 125923. [Google Scholar] [CrossRef]
- Chu, Y.M.; Nazeer, M.; Khan, M.I.; Ali, W.; Zafar, Z.; Kadry, S.; Abdelmalek, Z. Entropy analysis in the Rabinowitsch fluid model through inclined Wavy Channel: Constant and variable properties. Int. Commun. Heat Mass Transf. 2020, 119, 104980. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, M.; Imtiaz, M.; Alsaedi, A. Double stratification in the MHD flow of a nanofluid due to a rotating disk with variable thickness. Eur. Phys. J. Plus 2017, 132, 146. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Buoyancy Effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy. Int. J. Heat Mass Transf. 2017, 108, 1340–1346. [Google Scholar] [CrossRef]
- Loganathan, K.; Alessa, N.; Namgyel, N.; Karthik, T.S. MHD Flow of Thermally Radiative Maxwell Fluid Past a Heated Stretching Sheet with Cattaneo—Christov Dual Diffusion. J. Math. 2021, 2021, 5562667. [Google Scholar] [CrossRef]





| Pr | |||||||
|---|---|---|---|---|---|---|---|
| Mustafa et al. [69] | Present | ||||||
| 2 | 0.5 | 1 | 1 | 0.5 | 0.5 | 0.706605 | 0.706604 |
| 4 | 0.5 | 1 | 1 | 0.5 | 0.5 | 0.935952 | 0.935955 |
| 7 | 0.5 | 1 | 1 | 0.5 | 0.5 | 1.132787 | 1.132788 |
| 10 | 0.5 | 1 | 1 | 0.5 | 0.5 | 1.257476 | 1.257482 |
| 5 | 0.1 | 1 | 1 | 0.5 | 0.5 | 1.426267 | 1.426269 |
| 5 | 0.5 | 1 | 1 | 0.5 | 0.5 | 1.013939 | 1.013938 |
| 5 | 0.7 | 1 | 1 | 0.5 | 0.5 | 0.846943 | 0.846928 |
| 5 | 1.0 | 1 | 1 | 0.5 | 0.5 | 0.649940 | 0.649939 |
| 5 | 0.5 | 0 | 1 | 0.5 | 0.5 | 0.941201 | 0.941209 |
| 5 | 0.5 | 1 | 1 | 0.5 | 0.5 | 1.013939 | 1.013943 |
| 5 | 0.5 | 2 | 1 | 0.5 | 0.5 | 1.064551 | 1.064563 |
| 5 | 0.5 | 4 | 1 | 0.5 | 0.5 | 1.114549 | 1.114191 |
| 5 | 0.5 | 1 | 0 | 0.5 | 0.5 | 1.145304 | 1.145301 |
| 5 | 0.5 | 1 | 1 | 0.5 | 0.5 | 1.013939 | 1.013938 |
| 5 | 0.5 | 1 | 2 | 0.5 | 0.5 | 0.926282 | 0.926281 |
| 5 | 0.5 | 1 | 5 | 0.5 | 0.5 | 0.798671 | 0.798669 |
| 5 | 0.5 | 1 | 2 | −1 | 0.5 | 1.030805 | 1.030804 |
| 5 | 0.5 | 1 | 2 | −0.5 | 0.5 | 0.999470 | 0.999468 |
| 5 | 0.5 | 1 | 2 | 0 | 0.5 | 0.964286 | 0.964285 |
| 10 | 0.5 | 1 | 2 | 1 | 0.5 | 0.886830 | 0.886830 |
| 10 | 0.5 | 1 | 2 | 0.5 | 0 | 1.032281 | 1.032280 |
| 10 | 0.5 | 1 | 2 | 0.5 | 0.5 | 1.056704 | 1.056706 |
| 10 | 0.5 | 1 | 2 | 0.5 | 3 | 1.154539 | 1.154538 |
| 10 | 0.5 | 1 | 2 | 0.5 | 5 | 1.215937 | 1.215938 |
| Wi | Fc | λ | M | fw | |||
|---|---|---|---|---|---|---|---|
| 0 | 0.4 | 0.5 | 0.5 | 0.3 | −1.493123 | 1.667677 | 0.688683 |
| 0.1 | 0.4 | 0.5 | 0.5 | 0.3 | −1.455877 | 1.661396 | 0.681731 |
| 0.2 | 0.4 | 0.5 | 0.5 | 0.3 | −1.41351 | 1.653626 | 0.673835 |
| 0.3 | 0.4 | 0.5 | 0.5 | 0.3 | −1.362763 | 1.643289 | 0.664469 |
| 0.2 | 0 | 0.5 | 0.5 | 0.3 | −1.329383 | 1.662128 | 0.682787 |
| 0.2 | 0.2 | 0.5 | 0.5 | 0.3 | −1.372209 | 1.657807 | 0.678189 |
| 0.2 | 0.4 | 0.5 | 0.5 | 0.3 | −1.41351 | 1.653626 | 0.673835 |
| 0.2 | 0.6 | 0.5 | 0.5 | 0.3 | −1.45342 | 1.649575 | 0.669706 |
| 0.2 | 0.4 | 0 | 0.5 | 0.3 | −1.470747 | 1.646644 | 0.666783 |
| 0.2 | 0.4 | 0.2 | 0.5 | 0.3 | −1.44786 | 1.64946 | 0.669584 |
| 0.2 | 0.4 | 0.4 | 0.5 | 0.3 | −1.424968 | 1.652245 | 0.672411 |
| 0.2 | 0.4 | 0.6 | 0.5 | 0.3 | −1.402068 | 1.655 | 0.675269 |
| 0.2 | 0.4 | 0.5 | 0 | 0.3 | −1.167756 | 1.642785 | 0.789742 |
| 0.2 | 0.4 | 0.5 | 0.5 | 0.3 | −1.41351 | 1.653626 | 0.673835 |
| 0.2 | 0.4 | 0.5 | 1 | 0.3 | −1.56368 | 1.632112 | 0.646948 |
| 0.2 | 0.4 | 0.5 | 1.5 | 0.3 | −1.696232 | 1.612796 | 0.626083 |
| 0.2 | 0.4 | 0.5 | 0.5 | −0.3 | −1.13794 | 1.366538 | 0.605637 |
| 0.2 | 0.4 | 0.5 | 0.5 | −0.1 | −1.22469 | 1.476979 | 0.612521 |
| 0.2 | 0.4 | 0.5 | 0.5 | 0.1 | −1.316926 | 1.576889 | 0.632016 |
| 0.2 | 0.4 | 0.5 | 0.5 | 0.3 | −1.41351 | 1.653626 | 0.673835 |
| R | |||
|---|---|---|---|
| 0 | 0.1 | 0.2 | 1.292138 |
| 0.5 | 0.1 | 0.2 | 1.653626 |
| 1 | 0.1 | 0.2 | 1.877266 |
| 1.5 | 0.1 | 0.2 | 1.926091 |
| 0.5 | −0.1 | 0.2 | 1.64429 |
| 0.5 | 0 | 0.2 | 1.662016 |
| 0.5 | 0.1 | 0.2 | 1.653626 |
| 0.5 | 0.2 | 0.2 | 1.561214 |
| 0.5 | 0.1 | 0 | 1.849146 |
| 0.5 | 0.1 | 0.1 | 1.753203 |
| 0.5 | 0.1 | 0.2 | 1.653626 |
| 0.5 | 0.1 | 0.3 | 1.550338 |
| Sc | ||||
|---|---|---|---|---|
| 0.5 | 0.5 | 0.1 | 0.2 | 0.015548 |
| 1 | 0.5 | 0.1 | 0.2 | 0.673835 |
| 1.5 | 0.5 | 0.1 | 0.2 | 1.186802 |
| 2 | 0.5 | 0.1 | 0.2 | 1.628294 |
| 1 | 0.2 | 0.1 | 0.2 | 1.038076 |
| 1 | 0.3 | 0.1 | 0.2 | 0.911577 |
| 1 | 0.4 | 0.1 | 0.2 | 0.790267 |
| 1 | 0.5 | 0.1 | 0.2 | 0.673835 |
| 1 | 0.5 | 0 | 0.2 | 0.591323 |
| 1 | 0.5 | 0.1 | 0.2 | 0.673835 |
| 1 | 0.5 | 0.2 | 0.2 | 0.759523 |
| 1 | 0.5 | 0.3 | 0.2 | 0.848478 |
| 1 | 0.5 | 0.1 | 0 | 0.899109 |
| 1 | 0.5 | 0.1 | 0.1 | 0.786382 |
| 1 | 0.5 | 0.1 | 0.2 | 0.673835 |
| 1 | 0.5 | 0.1 | 0.3 | 0.561474 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamilzharasan, B.M.; Karthikeyan, S.; Kaabar, M.K.A.; Yavuz, M.; Özköse, F. Magneto Mixed Convection of Williamson Nanofluid Flow through a Double Stratified Porous Medium in Attendance of Activation Energy. Math. Comput. Appl. 2022, 27, 46. https://doi.org/10.3390/mca27030046
Tamilzharasan BM, Karthikeyan S, Kaabar MKA, Yavuz M, Özköse F. Magneto Mixed Convection of Williamson Nanofluid Flow through a Double Stratified Porous Medium in Attendance of Activation Energy. Mathematical and Computational Applications. 2022; 27(3):46. https://doi.org/10.3390/mca27030046
Chicago/Turabian StyleTamilzharasan, B. M., S. Karthikeyan, Mohammed K. A. Kaabar, Mehmet Yavuz, and Fatma Özköse. 2022. "Magneto Mixed Convection of Williamson Nanofluid Flow through a Double Stratified Porous Medium in Attendance of Activation Energy" Mathematical and Computational Applications 27, no. 3: 46. https://doi.org/10.3390/mca27030046
APA StyleTamilzharasan, B. M., Karthikeyan, S., Kaabar, M. K. A., Yavuz, M., & Özköse, F. (2022). Magneto Mixed Convection of Williamson Nanofluid Flow through a Double Stratified Porous Medium in Attendance of Activation Energy. Mathematical and Computational Applications, 27(3), 46. https://doi.org/10.3390/mca27030046








