New Modified Burr III Distribution, Properties and Applications
Abstract
1. Introduction
2. The New Modified BIII Model
3. Some Properties of NMBIII
3.1. Useful Expansion
3.2. Moments
3.3. Moment-Generating Function
3.4. Order Statistics
3.5. Stochastic Ordering
- Stochastic order () if for all x.
- Hazard rate order () if for all x.
- Mean residual order () if for all x.
- Likelihood ratio order () if for all x.
- Reversed hazard rate order () if is decreasing for all x.
4. Maximum Likelihood Estimation
5. Middle-Censoring
5.1. Estimation
5.2. Simulation Results
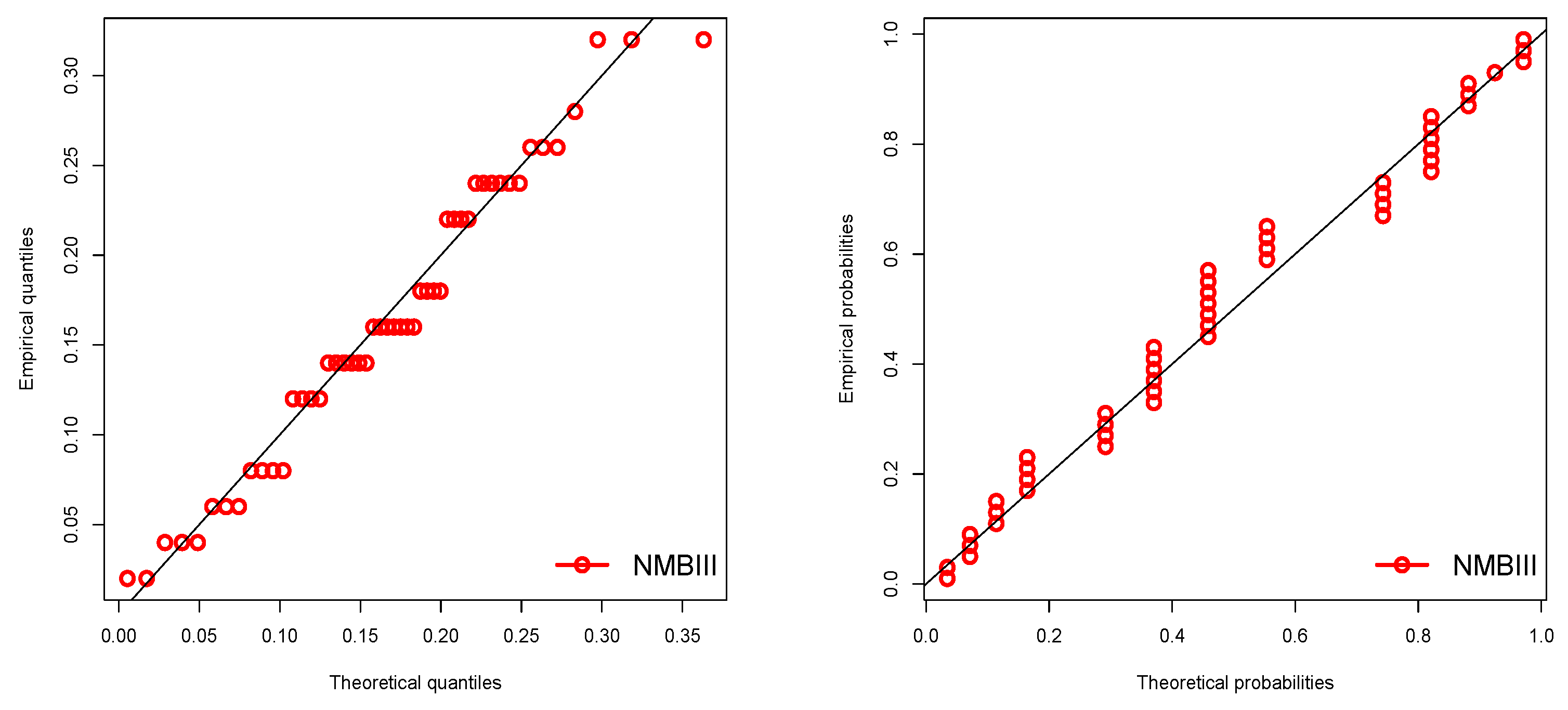
6. Applications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yousof, H.M.; Afify, A.Z.; Hamedani, G.G.; Aryal, G. The Burr X Generator of Distributions for Lifetime Data. J. Stat. Theory Appl. 2017, 16, 288–305. [Google Scholar] [CrossRef]
- Gove, J.H.; Ducey, M.J.; Leak, W.B.; Zhang, L. Rotated sigmoid structures in managed uneven-aged northern hardwood stands: A look at the Burr Type-III distribution. Forestry 2008, 81, 161–176. [Google Scholar] [CrossRef]
- Burr, I.W. Cumulative frequency distributions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Mielke, P.W. Another family of distributions for describing and analyzing precipitation data. J. Appl. Meterol. 1973, 12, 275–280. [Google Scholar] [CrossRef]
- Bebbington, M.S.; Lai, C.D.; Zitikis, R. A flexible Weibull extension. Reliab. Eng. Syst. Saf. 2007, 92, 719–726. [Google Scholar] [CrossRef]
- Zhang, T.; Xie, M. On the upper truncated Weibull distribution and its reliability implications. Reliab. Eng. Syst. Saf. 2011, 96, 194–200. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analysing bathtub failure rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Xie, M.; Tang, Y.; Goh, T.N. A modified Weibull extension with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 2002, 76, 279–285. [Google Scholar] [CrossRef]
- Almalki, S.J.; Yuan, J. A new modified Weibull distribution. Reliab. Eng. Syst. Saf. 2013, 111, 164–170. [Google Scholar] [CrossRef]
- Shao, Q.; Chen, Y.D.; Zhang, L. An extension of three-parameter Burr III distribution for low-flow frequency analysis. Comput. Stat. Data Anal. 2008, 52, 1304–1314. [Google Scholar] [CrossRef]
- Çankaya, M.N.; Yalçınkaya, A.; Altındaǧ, Ö.; Arslan, O. On the robustness of an epsilon skew extension for Burr III distribution on the real line. Comput. Stat. 2019, 34, 1247–1273. [Google Scholar] [CrossRef]
- Modi, K.; Gill, V. Unit Burr-III distribution with application. J. Stat. Manag. Syst. 2019, 23, 579–592. [Google Scholar] [CrossRef]
- Haq, M.A.U.; Hashmi, S.; Aidi, K.; Ramos, P.L.; Louzada, F. Unit modified Burr-III distribution: Estimation, characterizations and validation test. Ann. Data Sci. 2020, 1–26. [Google Scholar] [CrossRef]
- Ali, A.; Hasnain, S.A.; Ahmad, M. The modified Burr III distribution, properties and applications. Pak. J. Stat. 2015, 31, 697–708. [Google Scholar]
- Domma, F.; Condino, F. The Beta-Dagum Distribution: Definition and Properties. Commun. Stat. Theory Methods 2013, 42, 4070–4090. [Google Scholar] [CrossRef]
- Arifa, S.; Zafar Yab, M.; Ali, A. The Modified Burr III G Family of Distributions. J. Data Sci. 2017, 15, 41–60. [Google Scholar] [CrossRef]
- Bhatti, F.A.; Hamedani, G.G.; Korkmaz, M.C.; Cordeiro, G.M.; Yousof, H.M.; Ahmad, M. On Burr III Marshal Olkin family: Development, properties, characterizations and applications. J. Stat. Distrib. Appl. 2019, 6, 1–21. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Yousof, H.M.; Ramires, T.G.; Ortega, E.M.M. The Burr XII System of Densities: Properties, Regression Model and Applications. J. Stat. Comput. Simul. 2017, 87, 1–25. [Google Scholar] [CrossRef]
- Oluyede, B.O.; Huang, S.; Pararai, M. A New Class of Generalized Dagum Distribution with Applications to Income and Lifetime Data. J. Stat. Econom. Methods 2014, 3, 125–151. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: Hoboken, NJ, USA, 1995; Volume 2, pp. 140–142. [Google Scholar]
- Lai, C.D.; Xie, M.; Murthy, D.N.P. A modified Weibull distribution. IEEE Trans. Reliab. 2003, 52, 33–37. [Google Scholar] [CrossRef]
- Carrasco, M.; Ortega, E.M.; Cordeiro, G.M. A generalized modified Weibull distribution for lifetime modeling. Comput. Stat. Data Anal. 2008, 53, 450–462. [Google Scholar] [CrossRef]
- Aljouiee, A.; Elbatal, I.; Al-Mofleh, H. A New Five-Parameter Lifetime Model: Theory and Applications. Pak. J. Stat. Oper. Res. 2018, 14, 403–420. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders and Their Applications; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Jammalamadaka, S.R.; Mangalam, V. Non-parametric estimation for middle censored data. J. Nonparametr. Stat. 2003, 15, 253–265. [Google Scholar] [CrossRef]
- Iyer, S.K.; Jammalamadaka, S.R.; Kundu, D. Analysis of middle-censored data with exponential lifetime distributions. J. Stat. Plan. Inference 2008, 138, 3550–3560. [Google Scholar] [CrossRef][Green Version]
- Abuzaid, A.H. The estimation of the Burr-XII parameters with middle-censored data. SpringerPlus 2015, 4, 1–10. [Google Scholar] [CrossRef]
- Bennett, N.A. Some Contributions to Middle-Censoring. Ph.D. Thesis, Department of Statistics and Applied Probability, University of California Santa Barbara, Santa Barbara, CA, USA, 2011. [Google Scholar]
- Abuzaid, A.H.; Abu El-Qumsan, M.K.; El-Habil, A.M. On the robustness of right and middle censoring schemes in parametric survival models. Commun. Stat.-Simul. Comput. 2017, 46, 1771–1780. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. On the alternative to the Weibull function. Eng. Fract. Mech. 2007, 74, 451–456. [Google Scholar] [CrossRef]
- Dasgupta, R. On the distribution of Burr with applications. Sankhya 2011, B73, 1–19. [Google Scholar] [CrossRef]
- Feigl, P.; Zelen, M. Estimation of exponential probabilities with concomitant information. Biometrics 1965, 21, 826–838. [Google Scholar] [CrossRef]

| Model | c | k | Reference | ||
|---|---|---|---|---|---|
| Burr III | 0 | - | - | Standard | |
| Log-Logistic | 0 | - | 1 | Standard | |
| Modified Log-Logistic | - | - | 1 | New | |
| Logistic | - | 0 | 1 | Standard | |
| Modified skew logistic | - | 1 | - | New | |
| Generalized logistic Type-I or Burr II or skew logistic | 1 | 0 | - | Johnson et al. [22] and Aljouiee et al. [25] |
| 0.6754 | 2.0695 | 10.4250 | 72.6365 | 3.3418 | 20.5484 | |
| 0.6662 | 1.0760 | 3.1293 | 14.2983 | 3.1239 | 27.1548 | |
| 1.2849 | 2.6939 | 8.7612 | 41.8399 | 2.4599 | 23.6830 | |
| 0.8024 | 0.8745 | 1.2564 | 2.3394 | 1.6650 | 70.6890 | |
| 0.6814 | 0.9031 | 2.0319 | 7.3171 | 2.8155 | 31.7670 | |
| 1.3695 | 2.6073 | 7.0943 | 27.8595 | 2.4280 | 39.1836 | |
| 0.8041 | 0.7682 | 0.8775 | 1.2098 | 1.5101 | 226.2743 |
| Distribution | n | Un-Censored | Middle-Censored | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0.25, 0.25) | (1, 0.75) | (1.25, 0.5) | |||||||||||
| () | c | k | c | k | c | k | c | k | |||||
| (1, 2, 0.5) | 10 | 1.114 | 2.079 | 0.397 | 1.123 | 2.233 | 0.447 | 1.087 | 2.130 | 0.524 | 1.196 | 2.088 | 0.561 |
| (0.130) | (0.102) | (0.122) | (0.141) | (0.163) | (0.096) | (0.111) | (0.159) | (0.108) | (0.121) | (0.099) | (0.125) | ||
| 30 | 1.039 | 2.036 | 0.464 | 1.082 | 2.170 | 0.452 | 1.072 | 2.080 | 0.519 | 1.127 | 2.080 | 0.547 | |
| (0.034) | (0.039) | (0.080) | (0.096) | (0.072) | (0.043) | (0.036) | (0.082) | (0.046) | (0.052) | (0.093) | (0.037) | ||
| 50 | 1.036 | 2.032 | 0.484 | 1.071 | 2.096 | 0.536 | 1.066 | 2.071 | 0.508 | 1.103 | 2.022 | 0.529 | |
| (0.03) | (0.031) | (0.029) | (0.033) | (0.031) | (0.032) | (0.028) | (0.032) | (0.028) | (0.022) | (0.025) | (0.027) | ||
| 70 | 1.015 | 1.984 | 0.511 | 1.035 | 2.018 | 0.510 | 1.042 | 2.053 | 0.496 | 1.042 | 1.985 | 0.476 | |
| (0.016) | (0.015) | (0.019) | (0.017) | (0.021) | (0.022) | (0.015) | (0.021) | (0.020) | (0.021) | (0.016) | (0.017) | ||
| 100 | 1.001 | 1.991 | 0.502 | 1.019 | 1.998 | 0.495 | 0.980 | 2.020 | 0.498 | 0.981 | 1.907 | 0.491 | |
| (0.012) | (0.013) | (0.011) | (0.013) | (0.015) | (0.014) | (0.015) | (0.016) | (0.017) | (0.016) | (0.013) | (0.013) | ||
| (0.5, 2, 0.5) | 10 | 0.621 | 2.074 | 0.427 | 0.582 | 2.325 | 0.522 | 0.534 | 2.135 | 0.524 | 1.196 | 2.098 | 0.530 |
| (0.052) | (0.040) | (0.151) | (0.127) | (0.086) | (0.063) | (0.056) | (0.084) | (0.088) | (0.080) | (0.105) | (0.096) | ||
| 30 | 0.613 | 2.057 | 0.464 | 0.531 | 2.264 | 0.513 | 0.529 | 2.104 | 0.516 | 1.127 | 2.087 | 0.521 | |
| (0.034) | (0.036) | (0.032) | (0.038) | (0.039) | (0.040) | (0.034) | (0.033) | (0.037) | (0.030) | (0.033) | (0.037) | ||
| 50 | 0.538 | 2.010 | 0.484 | 0.519 | 2.125 | 0.489 | 0.518 | 2.014 | 0.505 | 1.103 | 2.054 | 0.518 | |
| (0.026) | (0.012) | (0.044) | (0.094) | (0.067) | (0.032) | (0.019) | (0.064) | (0.037) | (0.031) | (0.016) | (0.031) | ||
| 70 | 0.5017 | 1.928 | 0.511 | 0.491 | 2.020 | 0.490 | 0.506 | 1.982 | 0.501 | 1.042 | 2.010 | 0.509 | |
| (0.012) | (0.009) | (0.041) | (0.057) | (0.037) | (0.021) | (0.012) | (0.035) | (0.013) | (0.017) | (0.012) | (0.014) | ||
| 100 | 0.492 | 2.003 | 0.502 | 0.504 | 2.003 | 0.507 | 0.492 | 2.004 | 0.499 | 0.981 | 1.923 | 0.495 | |
| (0.002) | (0.001) | (0.027) | (0.046) | (0.027) | (0.007) | (0.006) | (0.026) | (0.005) | (0.011) | (0.010) | (0.012) | ||
| (2, 2, 2) | 10 | 2.212 | 2.452 | 2.517 | 2.298 | 2.571 | 2.322 | 2.331 | 2.280 | 2.371 | 2.102 | 2.493 | 2.256 |
| (0.063) | (0.127) | (0.096) | (0.105) | (0.056) | (0.151) | (0.040) | (0.088) | (0.052) | (0.086) | (0.084) | (0.080) | ||
| 30 | 2.176 | 2.420 | 2.161 | 2.179 | 2.552 | 2.291 | 2.238 | 2.222 | 2.328 | 2.045 | 2.258 | 2.173 | |
| (0.043) | (0.096) | (0.037) | (0.093) | (0.036) | (0.080) | (0.039) | (0.046) | (0.034) | (0.072) | (0.082) | (0.052) | ||
| 50 | 1.962 | 2.013 | 2.008 | 2.057 | 2.150 | 2.171 | 2.061 | 2.064 | 2.091 | 1.959 | 2.041 | 1.901 | |
| (0.032) | (0.094) | (0.031) | (0.016) | (0.019) | (0.044) | (0.012) | (0.037) | (0.026) | (0.067) | (0.064) | (0.031) | ||
| 70 | 1.953 | 1.875 | 1.949 | 1.809 | 1.823 | 1.956 | 1.864 | 2.054 | 1.903 | 1.953 | 2.004 | 1.825 | |
| (0.021) | (0.057) | (0.014) | (0.012) | (0.012) | (0.041) | (0.009) | (0.013) | (0.012) | (0.037) | (0.035) | (0.017) | ||
| 100 | 2.045 | 2.113 | 2.160 | 2.070 | 2.503 | 2.207 | 2.183 | 2.145 | 2.143 | 2.026 | 2.125 | 2.144 | |
| (0.007) | (0.046) | (0.012) | (0.010) | (0.006) | (0.027) | (0.001) | (0.005) | (0.002) | (0.027) | (0.026) | (0.011) | ||
| Model | Parameters | MLE | Standard Error | AIC | BIC | A* | W* |
|---|---|---|---|---|---|---|---|
| NMBII | c | 2.543 | 0.507 | 362.159 | 370.497 | 1.888 | 0.296 |
| k | 25.243 | 5.185 | |||||
| 1.703 | 0.179 | ||||||
| MBIII | c | 1111.230 | 461.820 | 379.380 | 387.718 | 3.515 | 0.583 |
| k | 4.943 | 0.281 | |||||
| 770.050 | 398.963 | ||||||
| BIII | c | 3.058 | 0.180 | 423.535 | 429.094 | 7.658 | 1.365 |
| k | 51.879 | 11.180 | |||||
| W | 0.002 | 0.0002 | 394.821 | 405.379 | 1.955 | 0.422 | |
| 3.984 | 0.0773 | ||||||
| Ga | 15.521 | 1.991 | 385.737 | 374.295 | 2.745 | 0.457 | |
| 3.588 | 0.468 | ||||||
| LN | 1.432 | 0.025 | 428.845 | 434.403 | 3.374 | 0.568 | |
| 0.269 | 0.0174 | ||||||
| EW | 0.0114 | 0.006 | 374.644 | 386.981 | 1.945 | 0.315 | |
| 3.2126 | 0.278 | ||||||
| 2.0077 | 0.388 | ||||||
| GEV-II | 48.447 | 10.816 | 425.796 | 431.354 | 7.875 | 1.408 | |
| 3.022 | 0.185 |
| Model | Parameters | MLE | Standard Error | AIC | BIC | A* | W* |
|---|---|---|---|---|---|---|---|
| NMBII | c | 2.802 | 1.620 | −106.358 | −100.622 | 0.524 | 0.090 |
| k | 0.317 | 0.219 | |||||
| 17.274 | 5.605 | ||||||
| MBIII | c | 0.0020 | 0.0002 | −99.778 | −94.042 | 0.988 | 0.159 |
| k | 3.466 | 0.205 | |||||
| 0.0039 | 0.0007 | ||||||
| BIII | c | 7.788 | 26.572 | −26.027 | −22.202 | 1.056 | 0.177 |
| k | 0.065 | 0.221 | |||||
| W | 36.141 | 14.390 | −101.784 | −93.960 | 0.644 | 0.105 | |
| 2.118 | 0.246 | ||||||
| Ga | 3.029 | 0.576 | −102.743 | −98.919 | 1.636 | 0.279 | |
| 18.561 | 3.836 | ||||||
| LN | 1.987 | 0.095 | 105.700 | 109.524 | 1.922 | 0.331 | |
| 0.670 | 0.067 | ||||||
| EW | 819.305 | 2409.321 | −106.069 | −100.333 | 0.535 | 0.093 | |
| 4.982 | 2.636 | ||||||
| 0.297 | 0.200 | ||||||
| GEV-II | 0.054 | 0.020 | −70.449 | −66.625 | 3.567 | 0.634 | |
| 1.236 | 0.118 |
| Model | Parameters | MLE | Standard Error | AIC | BIC | A* | W* |
|---|---|---|---|---|---|---|---|
| NMBII | c | 0.521 | 0.121 | 303.703 | 308.101 | 0.440 | 0.064 |
| k | 4.734 | 1.065 | |||||
| 0.012 | 0.005 | ||||||
| MBIII | c | 153.592 | 319.615 | 309.465 | 313.863 | 0.672 | 0.098 |
| k | 1.494 | 0.464 | |||||
| 0.201 | 796.017 | ||||||
| BIII | c | 0.755 | 0.092 | 309.714 | 312.645 | 0.919 | 0.151 |
| k | 5.705 | 1.228 | |||||
| W | 0.057 | 0.028 | 304.302 | 307.234 | 0.552 | 0.079 | |
| 0.792 | 0.112 | ||||||
| Ga | 0.706 | 0.150 | 304.357 | 309.288 | 0.459 | 0.085 | |
| 0.017 | 0.005 | ||||||
| LN | 2.884 | 0.266 | 320.9177 | 323.8491 | 0.648 | 0.102 | |
| 1.504 | 0.188 | ||||||
| EW | 0.0431 | 0.186 | 306.296 | 310.693 | 0.554 | 0.079 | |
| 0.844 | 0.794 | ||||||
| 0.901 | 1.352 | ||||||
| GEV-II | 4.259 | 0.933 | 310.463 | 313.395 | 0.983 | 0.160 | |
| 0.685 | 0.091 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamal, F.; Abuzaid, A.H.; Tahir, M.H.; Nasir, M.A.; Khan, S.; Mashwani, W.K. New Modified Burr III Distribution, Properties and Applications. Math. Comput. Appl. 2021, 26, 82. https://doi.org/10.3390/mca26040082
Jamal F, Abuzaid AH, Tahir MH, Nasir MA, Khan S, Mashwani WK. New Modified Burr III Distribution, Properties and Applications. Mathematical and Computational Applications. 2021; 26(4):82. https://doi.org/10.3390/mca26040082
Chicago/Turabian StyleJamal, Farrukh, Ali H. Abuzaid, Muhammad H. Tahir, Muhammad Arslan Nasir, Sadaf Khan, and Wali Khan Mashwani. 2021. "New Modified Burr III Distribution, Properties and Applications" Mathematical and Computational Applications 26, no. 4: 82. https://doi.org/10.3390/mca26040082
APA StyleJamal, F., Abuzaid, A. H., Tahir, M. H., Nasir, M. A., Khan, S., & Mashwani, W. K. (2021). New Modified Burr III Distribution, Properties and Applications. Mathematical and Computational Applications, 26(4), 82. https://doi.org/10.3390/mca26040082








