Dynamic and Interactive Tools to Support Teaching and Learning ^†

Abstract

The use of technological learning tools has been increasingly recognized as a useful tool to promote students’ motivation to deal with, and understand, mathematics concepts. Current digital technology allows students to work interactively with a large number and variety of graphics, complementing the theoretical results and often used paper and pencil calculations. The computer algebra system Mathematica is a very powerful software that allows the implementation of many interactive visual applications. The main goal of this work is to show how some new dynamic and interactive tools, created with Mathematica and available in the Computable Document Format (CDF), can be used as active learning tools to promote better student activity and engagement in the learning process. The CDF format allows anyone with a computer to use them, at no cost, even without an active Wolfram Mathematica license. Besides that, the presented tools are very intuitive to use which makes it suitable for less experienced users. Some tools applicable to several mathematics concepts taught in higher education will be presented. This kind of tools can be used either in a remote or classroom learning environment. The corresponding CDF files are made available as supplement of the online edition of this article.

1. Introduction

Mathematics is often perceived as difficult and many students leave disciplines in science, technology, engineering, and mathematics (STEM) as a result, closing doors to scientific, engineering, and technological careers [1]. However, the use of technological learning tools has been increasingly recognized as a useful tool to promote students’ motivation to deal with, and understand, new concepts in different study fields (see, for instance [2,3,4,5,6,7,8,9,10,11,12,13]). In fact, technological tools have a great potential of applicability, particularly at the higher education, where the knowledge of various areas by different careers is required [9].

Technology in STEM education can be defined as educational or instructional technology that is used to enhance teaching and learning [14]. In fact, current educational digital technology allows students to work with a large number and variety of graphics, in an interactive way, complementing the theoretical results and the so often used paper and pencil calculations. Obviously, calculations with this kind of support do not replace paper and pencil calculations, and they should be properly combined with other methods of calculation, including mental calculation [15]. Some studies conclude that students using computer algebra systems are at least as good in “pencil and paper” skills as their traditional counterparts [16]. This aspect is not of minor relevance. Although the “pencil and paper” work can be done by computers, students should learn how calculations are made and also should learn how the computer algebra systems work [17]. Furthermore, the use of technology in the classroom can lead to advances in conceptualization, contributing thereby to students’ engagements and motivation [18]. According to [19], one of the reasons for students to use computer algebra systems is their belief that these tools help their understanding of new concepts.

The computer algebra system Mathematica (Wolfram Mathematica is a symbolic mathematical computation program used in many scientific, engineering, and computing fields. It was conceived by Stephen Wolfram and is developed by Wolfram Research) is a very powerful software that allows the implementation of many dynamic and interactive visual applications. In fact, combining the power of a computer algebra system like Mathematica and the resolution and graphics engine now accessible in even relatively inexpensive laptop computers, makes possible a degree of visualization and helps to develop graphical reasoning and graphical intuition. More importantly, it takes the graphics out of the textbook and puts them under the control of the user, who can manipulate, investigate, and explore these characteristics. Graphics are always helpful in learning, but [19] states that it makes a difference whether the students interaction with graphic visualization is active or passive. Students who have used Mathematica at least for one year identified this kind of visualization as other of the significant benefits they found in the use of Mathematica. Conrad Wolfram, from Wolfram Research, described (Conrad Wolfram TED Talk: http://www.youtube.com/watch?v=60OVlfAUPJg, accessed on 21 December 2021) their vision of what a new mathematics curriculum could look like if the full power of the available technology was exploited. Mathematics is clearly important for an increasing number of technical jobs in a quantitative world. It also develops the ability to think logically. Neither of these aims is supported by an excessive focus on the mechanics of calculating. According to Conrad, the broader mathematics processes are:

1.

Posing the right questions;

2.

Real world ⟶ math formulation;

3.

Computation;

4.

Math formulation ⟶ real world, verification.

Unfortunately, mathematics education is often focused on the third of these stages even though this is the only one that computers can do better! Many examples have been used to show that the usage of technology to perform the calculations, manipulations, or to demonstrate results graphically could give the students enough time to concentrate on the other three processes.

This paper intends to show how some dynamic and interactive tools, created by the author with Mathematica and available in the Computable Document Format (CDF), can be used as active learning tools to promote better student activity and engagement in a remote or classroom learning environment. The CDF format allows anyone with a computer to use them, at no cost, even without an active Wolfram Mathematica license (additional information about how to work with CDF format can be found at http://www.wolfram.com/cdf-player/, accessed on 21 December 2021). Besides that, the presented tools are very intuitive to use which makes it suitable for less experienced users. All tools presented in this article were used in class (in the classroom and in online class), in autonomous work by students and in the assessment process. After this brief introduction section, Section 2 relates the concept of active learning and the difficulties of some higher education teachers facing students with such different scientific knowledge and different attitudes. Section 3 is dedicated to technological learning tools and how they can be used in higher education, at no cost and with great benefits. Section 4 is devoted to some comments and observations.

2. Materials and Methods

The higher education is attended by students with different motivations and levels of involvement, which may affect the teaching and learning process. There are students with a more active attitude, who, even in a more transmissive class, theorize, apply and relate, and there are those who exhibit a more passive behavior. Clearly, these students require different orientation and teaching methods so that they are able to fully engage in the classroom activities as agents of a truly active learning process. This type of learning denotes a style of teaching that provides classroom opportunities for students to talk, listen to, and reflect on as they participate in a variety of learning activities [20]. On the other hand, classes taught in higher education institutions are no longer compatible with traditional teaching methodologies. In fact, as reported by [21], the academics in a higher education institution should not only worry about the contents, but also give attention to the learning environment [2].

Active learning is generally defined as any instructional method that engages students in the learning process. However, teachers can expect that, in any classroom, some students will prefer to be receivers (observers or listeners), while others will prefer to be active participants. We also should note that teachers who employ active learning strategies in their classrooms are unlikely to please all students all the time [22], but neither is a teacher who relies regularly on traditional lectures.

The active learning also aims to improve the students’ performance and develop the skills they need, for example, to obtain a better classification in a specific curricular unit [23]. In many cases, active learning can be employed without increased costs and with only a modest change in current teaching practices. The risk is low and the return is high [22]. Unfortunately, there are some gaps in the practice of higher education including the gap between teaching and learning, the gap between teaching and testing, and the gap between educational research and practice [24]. A serious gap also exists between how faculty members typically teach (i.e., relying largely on the “lecture method”) and how they know they should teach (i.e., employing active learning to facilitate students’ mastery of subject matter, develop intellectual skills, and form personal attitudes and values). Moreover, teachers see few incentives to change for several common reasons. First and foremost is the pervasive belief that “we are all good teachers”. Besides that, any faculty member who has ever attempted to lead a true one hour class discussion where students talk and respond to one another knows how difficult it is to have control over the discussion. Furthermore, unfortunately, as long as teachers consider themselves enchanted listeners to their own lectures, students will not be able to share that same passion.

Notwithstanding the above, the importance of using educational software in mathematics, as an efficient tool to help students grasp with hard-to-understand concepts and to more quickly gain a deeper understanding of the materials being taught firsthand, is acknowledged (see, for instance [2,11,19,25,26] and thereby such software can help to promote an active learning environment inside the classroom.

The reader interested in active learning approaches can look into [27] for links and references to definitions and core elements of different strategies, examples of application of specific activities, reports on the impact of the use of these instructions strategies in students learning outcomes, recommendations to help the teacher prepare for embracing active learning approaches and many resources [28].

3. Results

According to [28], technological learning tools becoming more popular, readily available and accessible with multiple devices, these tools have increasingly been included into the instructional design of the courses to enhance learning (and also to assess student progress). Technological learning tools are in themselves a valuable resource but they are of most relevance when used in an active learning environment.

Nowadays several technological learning tools, that can be used in higher education, are available with no costs. Some of the used by the author, either in remote or classroom learning environment, are (several examples of the use of these technological learning tools in the classroom can be seen, for instance, in [25,26,29,30,31,32,33,34,35]):

• Computable Document Format files ↪ created by the author, using the computer algebra system Mathematica [25,26,29,33,35,36].
• Khan Academy ↪ non-profit educational organization, conceived by Sal Khany, that creates a set of online tools that help educate students. The organization produces short lessons in the form of videos and its website also includes supplementary practice exercises and materials for educators. All resources are available for free to users of the website and application;
• Photomath ↪ app for solving mathematical problems. The app instantly scans, accurately solves and intuitively explains math problems to users through step-by-step explanations;
• Wolfram|Alpha ↪ computational knowledge engine for computing answers and providing knowledge, developed by Wolfram Research and it was released in 2009. It works by using its vast store of expert-level knowledge and algorithms to automatically answer questions, do analysis and generate reports. Refs. [32,34] contain some examples of the possible use of Wolfram|Alpha as a technological learning tool;
• Wolfram Demonstrations Project ↪ open-code resource, conceived by Stephen Wolfram, as a way to bring computational exploration to the widest possible audience. Includes lots of computable document format files for various areas of knowledge;

When used appropriately, technological learning tools, can improve a better student activity and engagement in the learning process. So, in the author opinion, the use of dynamic and interactive tools can help students to have interesting active learning experiences. Unfortunately, many students are using technology as a tool for passive learning.

3.1. Dynamic and Interactive Tools

This subsection is dedicated to the description of some dynamic and interactive tools created by the author. All those tools were used by the author in the classroom (either in a remote or classroom environment) and by their students in autonomous work. In fact, these kind of technological learning tools can be used as active learning tools to promote better student activity and engagement in the learning process. This format allows anyone with a computer, to use them, at no cost, even without an active Wolfram Mathematica license. Besides that, the presented tools are very intuitive to use, which makes it suitable for less experienced users. All the dynamic and interactive tools presented in this section were created as an interactive Mathematica notebook and are available online, in the Computable Document Format, to the author’s students and as Supplementary Material of this article. Moreover, these tools have already been presented at various scientific and pedagogical practices sharing meetings.

3.1.1. Designing Dynamic and Interactive Tools with Mathematica

The use of the symbolic computation capabilities of Mathematica, and its own programming language (along with the pretty-print functionality that allows one to write mathematical expressions on the computer using the traditional notation, as on paper), enables us to implement on a computer, and in a rather straightforward manner, all the ideas associated to these kind of technological tools [26,29,35].

The tools present in this subsection were essentially created by a single Manipulate command (https://reference.wolfram.com/language/tutorial/IntroductionToManipulate.html, accessed on 21 December 2021) (Figure 1), whose output is not just a static result but a running program that we can interact with.

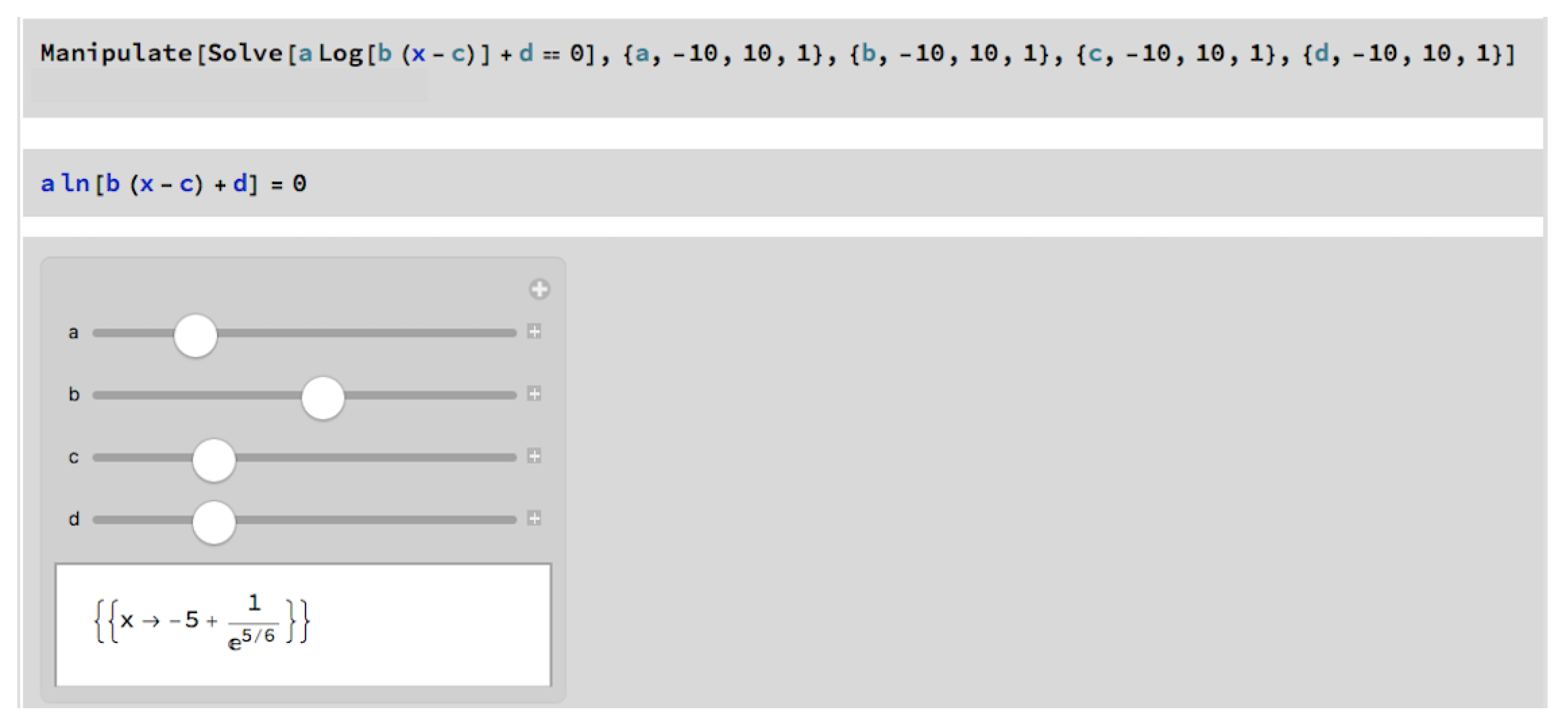
In Figure 2, in addition to the Manipulate command, it is possible to observe some of the Mathematica functions that allow solving the problem involving the analysis, and possible resolution, of an exact differential Equation (calculating the auxiliary primitives needed to obtain the desired output).

The code consists of some initial definitions, followed by the single command Manipulate. This command is responsible for creating an interactive object that contains one or more functional controls, such as the sliders for the parameters’ values (Figure 3) and checkboxes for the plots’ options. Through dynamic changes of the parameters’ values, it is possible to obtain static and non-static visual information [26]. It is through this kind of dynamic interaction that “computer algebra systems present new opportunities for teaching and learning” [37].

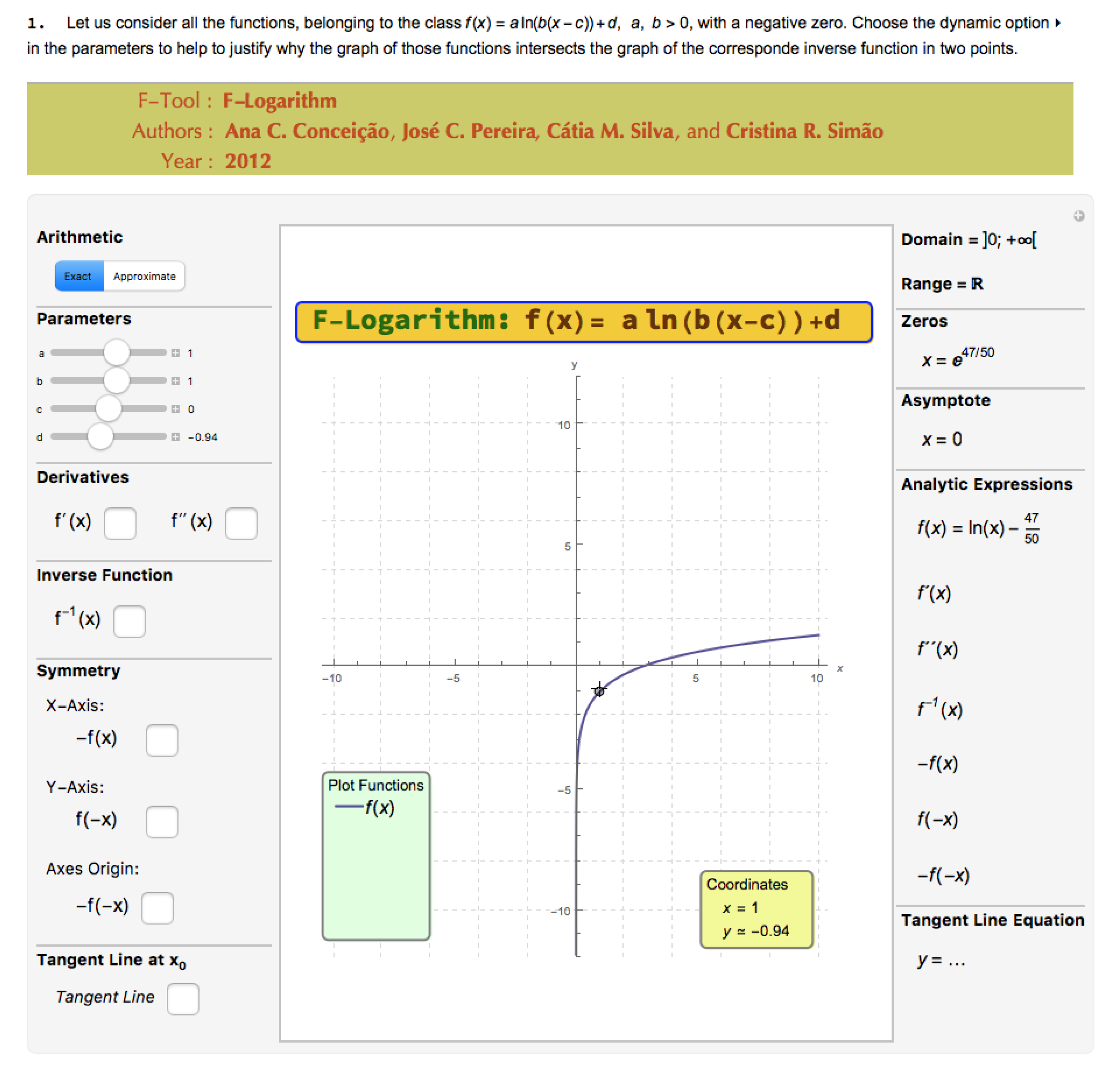
3.1.2. Precalculus, Differential Calculus and Integral Calculus

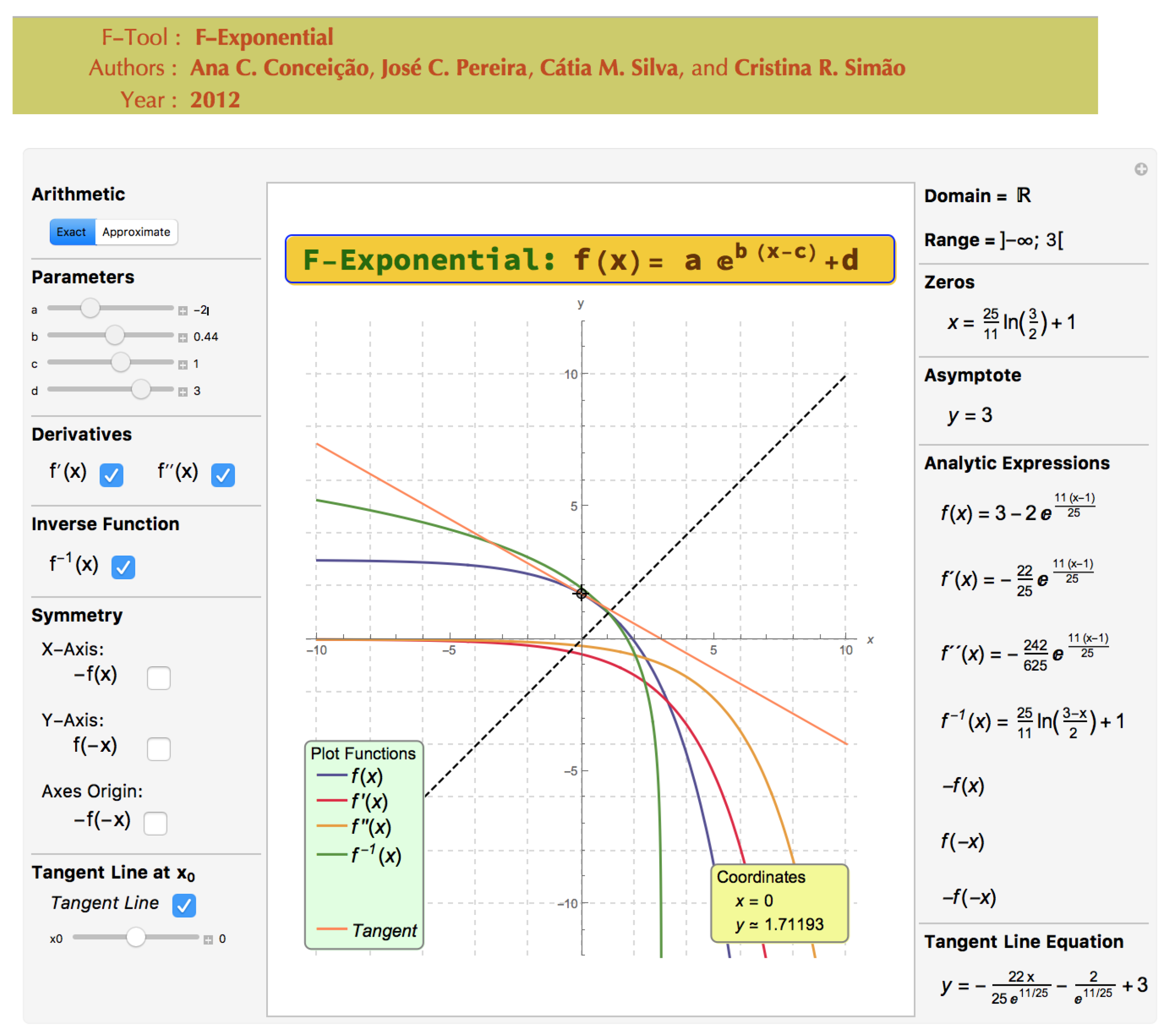
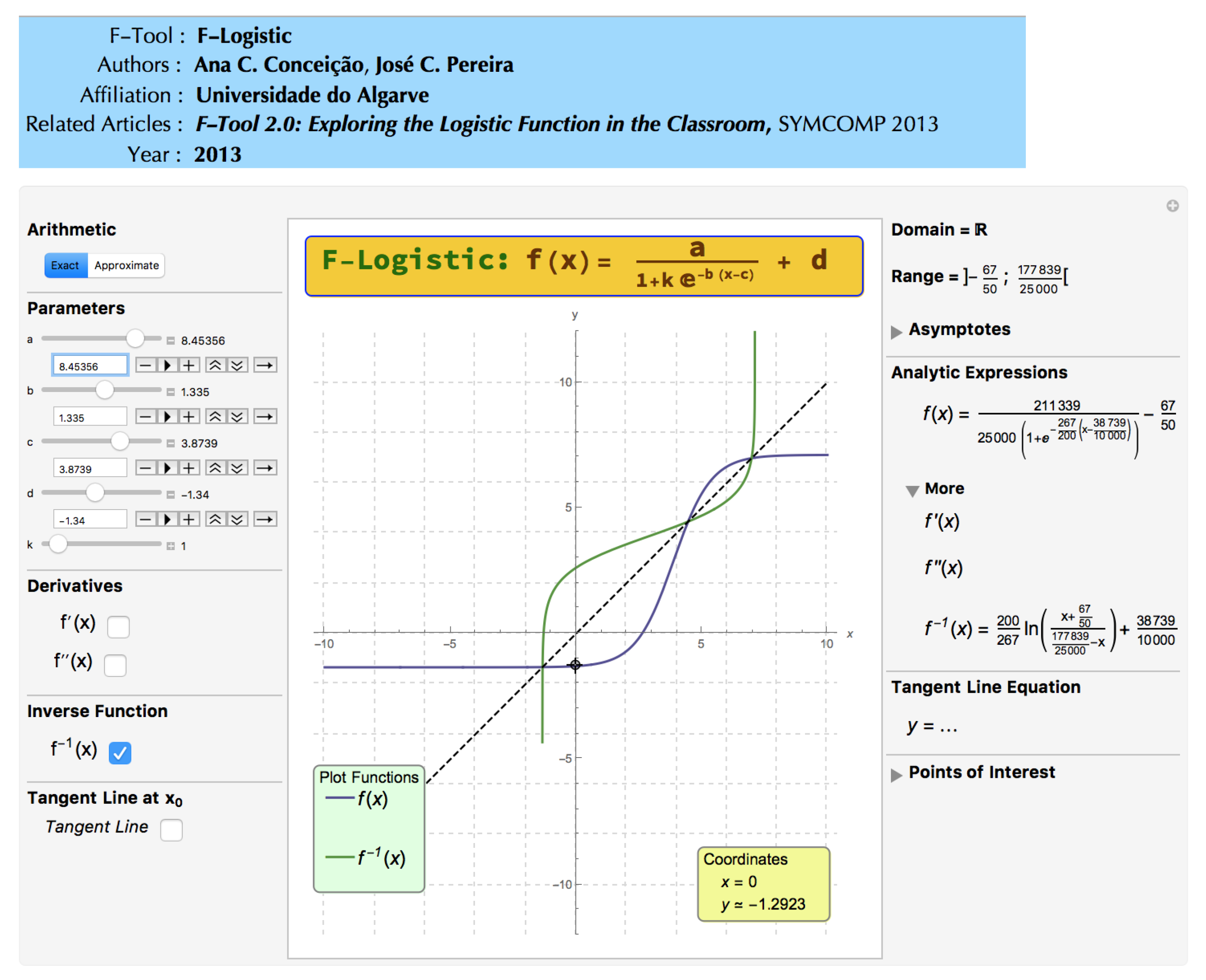
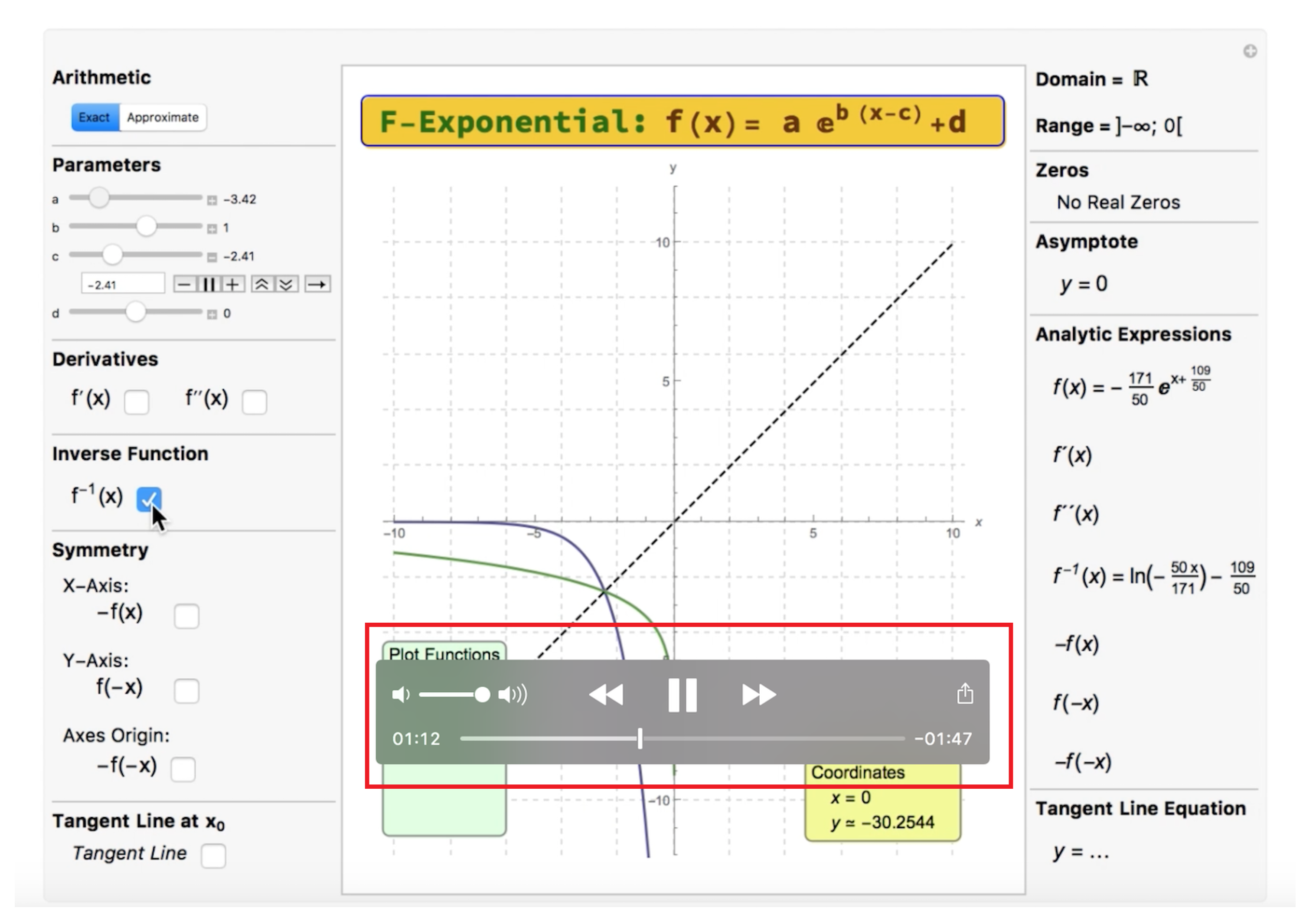
The dynamic and interactive learning tools described in [26,35] can be used to explore in a dynamic, interactive, and visual manner various classes of real functions and features associated with their study. In Figure 4, we can see a usage example of the F-Exponential, one of the already existing F-Tool.

All the F-Tool share a common design and are divided in three main panels:

• Left Panel ↪ In this panel the user can vary the values of one or more parameters, choose which “transformations” of the main function are to be presented, and wether or not to show the tangent line in a chosen tangent point. In addition, the user has the option to see the results in the exact or approximate forms;
• Middle Panel ↪ In this panel all the functions are plotted, according to the options made by the user in the left panel;
• Right Panel ↪ In this panel it is presented all the analytical information concerning the main function and its “transformations”, again in accordance with the options chosen by the user in the left panel.

The available F-Tool can be used in class or in autonomous work, for the creation of short illustrative videos and evaluation exercises (see Section 3.2 and Section 3.3).

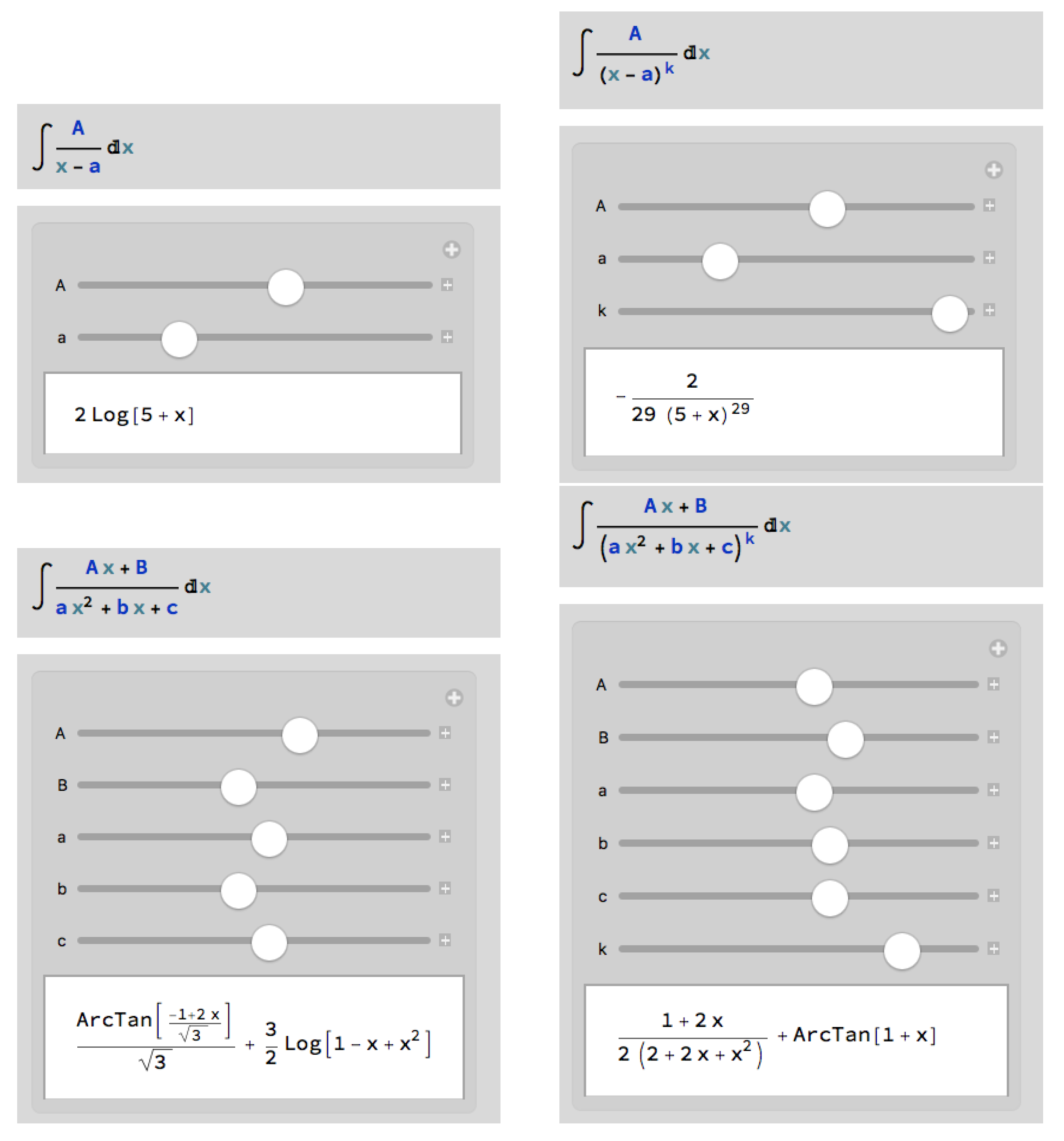
Furthermore, for some particular topics within precalculus, differential calculus, and integral calculus it is possible to design very simple dynamic and interactive tools, with the Manipulate command that can be used as active learning tools, either in a remote or classroom environment (Figure 5 and Figure 6, Figure 9).

One of the advantages of these cdf files is that they can be used without internet access being necessary (useful when the classroom or place of study used by the student has limited internet access). Furthermore, they can be used in an online environment, asking what will happen if a certain parameter is changed. It has been used with great success and active participation by students, through oral contributions or via chat.

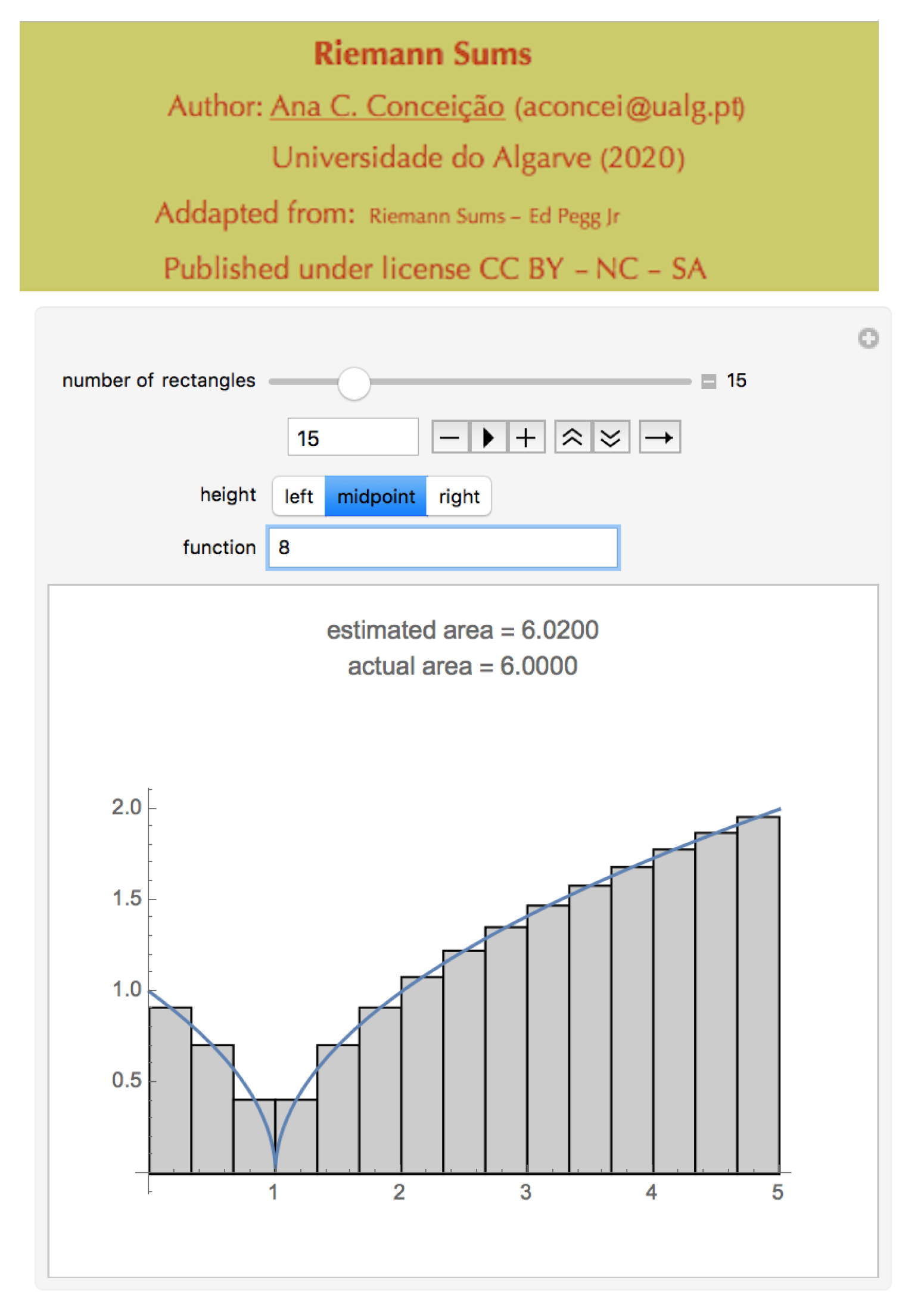
3.1.3. Riemann Sums

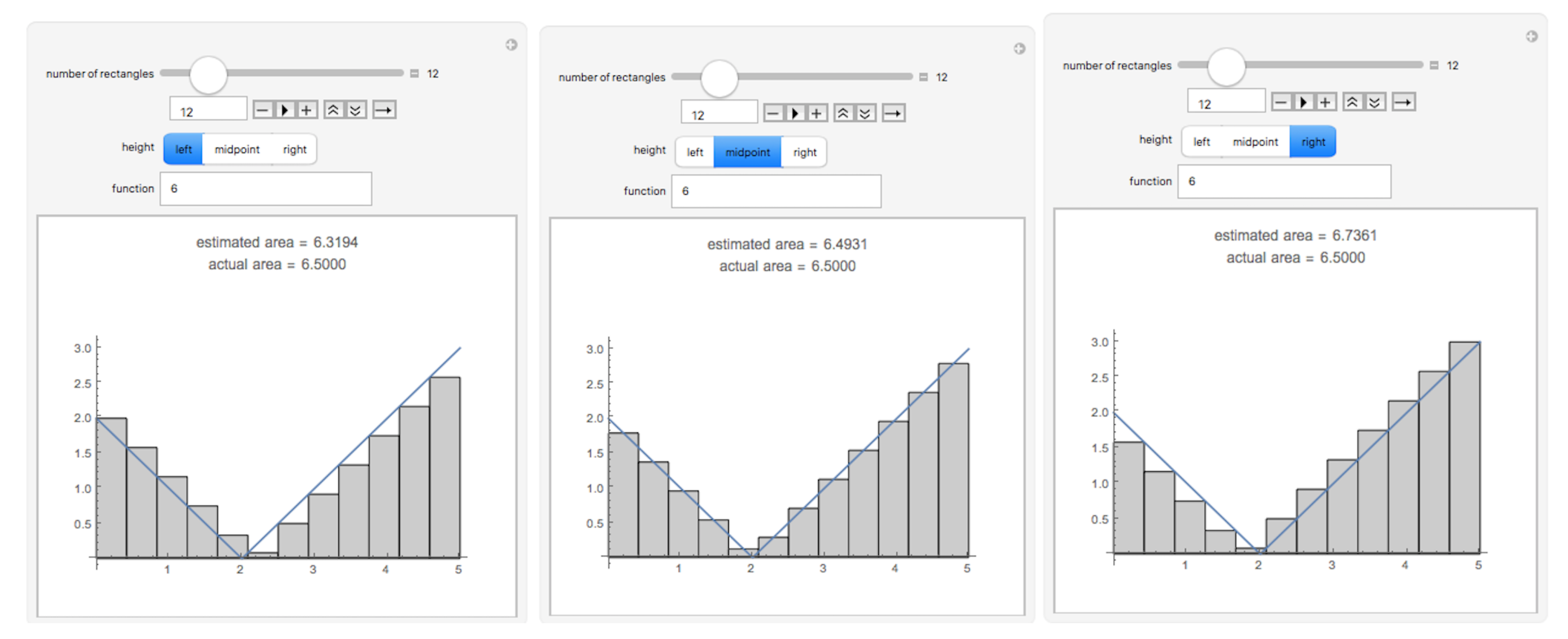
It is not possible to achieve the objectives and skills of a mathematics course concerning the definite integral concept without resorting to graphic concepts since this concept can be more easily apprehended when the students work with a large number and variety of graphics, in an interactive way, with the support of the appropriate technology. Students should be prepared for an intelligent dialogue with the tools they have available. In this sense, it is very useful the creation of a dynamic and interactive tool to explore the Riemann Sum concept.

Through the use of the tool “Riemann Sum” (the “Riemann Sum” tool was created using part of the demonstration code created by Ed Pegg Jr and available at https://demonstrations.wolfram.com/RiemannSums/, accessed on 21 December 2021) (Figure 7), students have available hundreds of different, but similar, exercises. This tool can be used as an active learning tool, either in a remote or classroom environment.

3.1.4. Ordinary Differential Equations

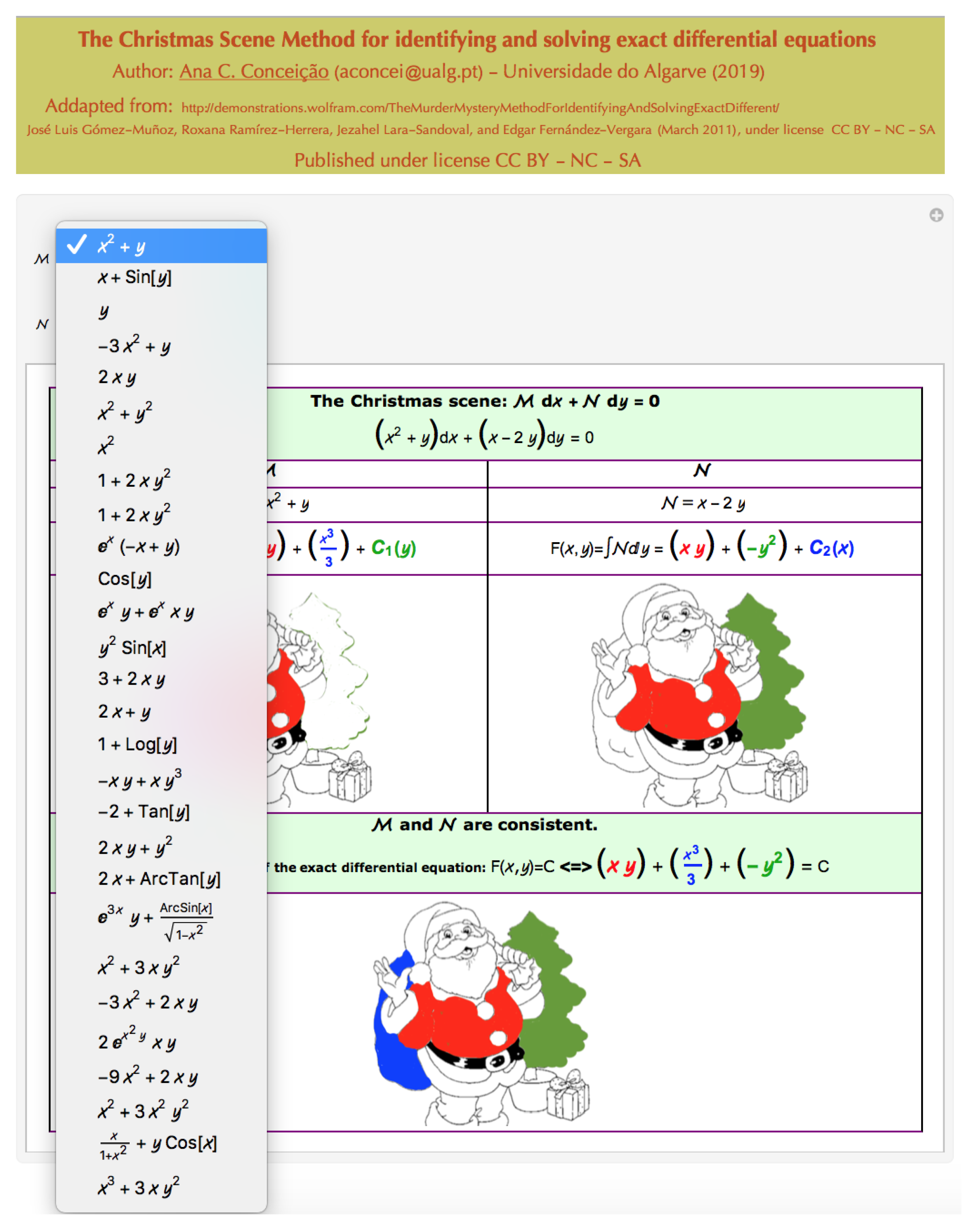
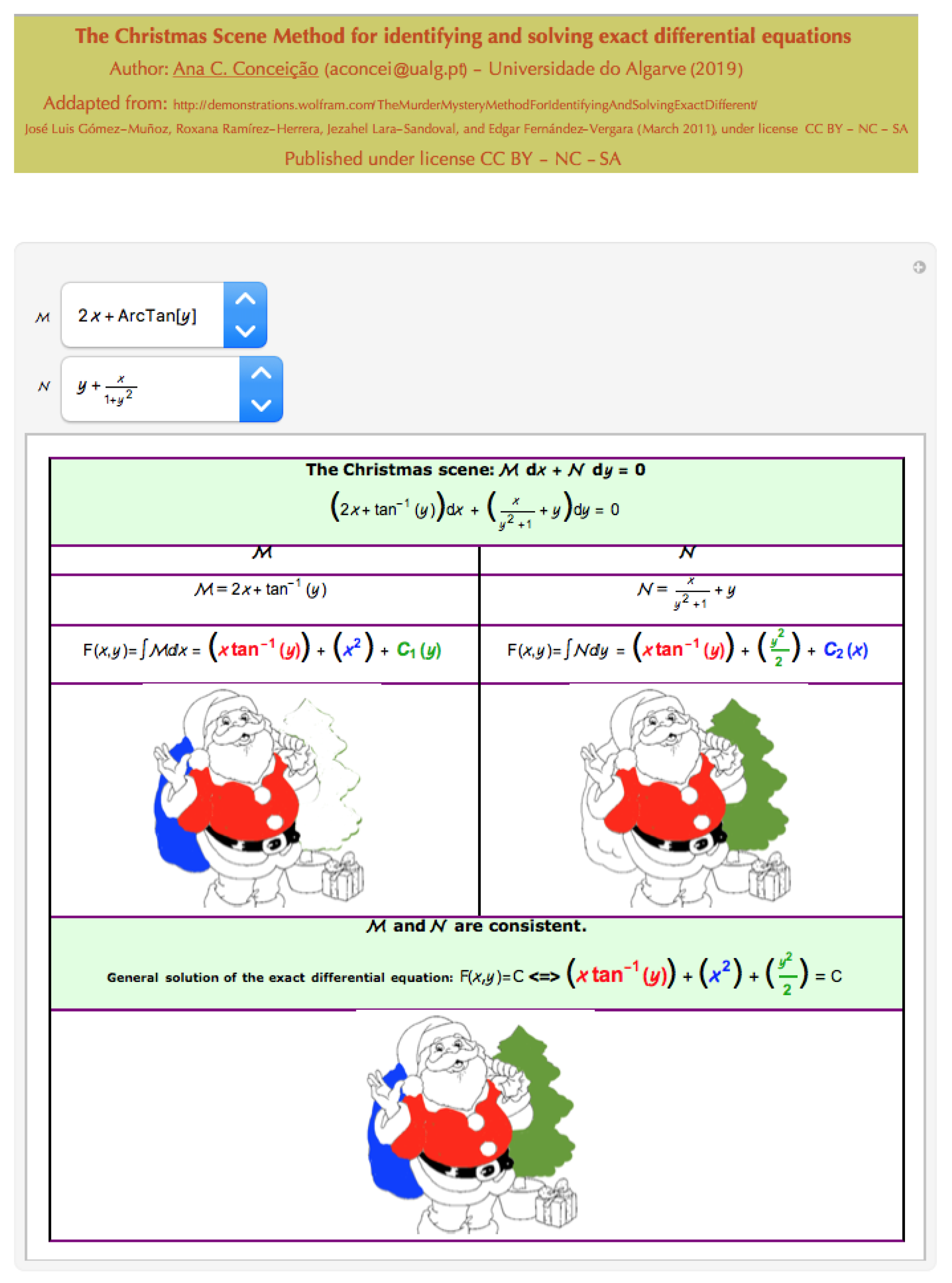
Taking into account the topic of ordinary differential equations that is taught in higher education, the Christmas Scene Method for identifying and solving exact differential equations tool was created in order to be used in autonomous work by students. This tool allows us to identify whether we have an exact ordinary differential equation and, if so, it presents the general solution of the equation. As it was designed to be used in class at Christmas time, in addition to the appropriate adaptations (this dynamic tool for the study of exact ordinary differential equations was adapted on the demonstration available at https://demonstrations.wolfram.com/TheMurderMysteryMethodForIdentifyingAndSolvingExactDifferent/, accessed on 21 December 2021, created by José Luis Gómez-Muñoz, Roxana Ramírez-Herrera, Jezahel Lara-Sandoval, and Edgar Fernández-Vergara) of notations and new lists (Figure 8) of functions, according to the exercises used in the course, it was also considered a Christmas environment.

Through the use of this tool, students have available hundreds of exercises on ordinary differential equations, as well as their solution.

After a brief theoretical justification, students can be suggested to choose, arbitrarily, a function M and a function N, from those available in the tool. If the output is “M and N are not consistent”, then students must justify why it is not an exact ordinary differential equation. If the output is “M and N are consistent”, then students must justify why it is an exact ordinary differential equation and confirm all the computed integrals.

3.2. Dynamic and Interactive Active Learning Tools

Active learning requires students to do meaningful learning activities and think about what they are doing. A student learns better and feels more motivated to achieve their purposes when he/she has a more active role in their learning. It is up to the teacher to create “opportunities for students to practice, create, and reflect on what they have learned” [23].

Faculty members who regularly use strategies to promote active learning typically find several ways to ensure that students learn the assigned content: promoting the dialog and reflection, promoting the acquisition of new knowledge and the transmission of the acquired knowledge and doing short-assessments every week [2,29]. These kind of strategies can be used either in remote or classroom learning environment.

In this subsection we intend to explain how some of the author dynamic and interactive tools can be used in a remote or classroom environment.

3.2.1. Promoting the Dialog and Reflection

Creating a supportive classroom environment involves more than merely having the skills that encourage students to participate and learn in the classroom. More important, instructors must create an intellectual and emotional environment that encourages students to take risks. Demonstrations during a lecture can be used to stimulate the students’ curiosity and to improve their understanding of conceptual material and processes, particularly when the demonstration invites students to participate in the research process through the use of such questions as

“What kind of functions will appear if we …?”.

So, the faculty member can encourage discussion, dialogue and reflection in the classroom, proposing stimulating exercises that lead to a constructive debate in the classroom context (Figure 9).

Another way to promote active participation by students is to use this type of dynamic and interactive tools to encourage students to solve exercises in front of their peers and explain how they solved them. For instance, the exercise illustrated in Figure 10 can be projected using the tool F-Logistic tool [35], and the students asked to solve it in the same classroom/online board (see Figure 11). The student’s name appears on the screen, if the Zoom platform is configured for this purpose.

Then the students can be asked to use the technological tool to confirm the graphical and/or analytical resolution option they had made. In the case of the graphical solution, in particular, the projection made by the educational software would appear to be superimposed on the one represented by the student, if it is correct (Figure 12). These strategies motivate learning in a context of collaborative communication where all entities (teachers and students) are participants [2].

3.2.2. Promoting the Acquisition of New Knowledge and the Transmission of Acquired Knowledge

One of the possibilities to promote the acquisition of new knowledge and the transmission of the acquired knowledge may be done through the production of a short video (Figure 13) on a specific theme and, after its availability and analysis by students, request the resolution of a similar problem that can be projected, in a remote or in a classroom environment, and solved by a student that is invited to explain to their peers the ways used to solve them. Moreover, through the Moodle platform, it is possible to control the visualization of the videos made available by the teacher.

3.2.3. Promoting Self Evaluation through Faculty Evaluation

One way to modify traditional lectures to increase students’ learning is to include a mini test, after a lecture, concerning the subject material recently covered. Some research reveals that the average student immediately recalls 62% of the information presented but this percentage declines to approximately 45% after three or four days and continues to fall down to 24% after eight weeks. If students were asked to take an exam immediately after the lecture, however, they would retain almost twice as much information, both factual and conceptual, after eight weeks [38].

Thus, in an active learning environment it is possible to use the some technological tool, available in the Computable Document Format, to design short quizzes and short-problems related to the concepts acquired/worked during the week. The student must solve the problems individually, being able to consult notes and use available technological tools. In the next class, feedback of the problems resolution should be given to the students and they should be encouraged to analyze all the personalized comments. In this sharing of information between the teacher and the students, the communication and the perception of different forms of resolution and thought are promoted. Figure 14 is an example of a proposed short-problem: “The graphical representation of different types of Riemann sums, given a function and a certain number of intervals.” In this way the teacher can easily create a different version for each student.

3.2.4. Technological Learning Tools and Students’ Autonomous Work

Another faculty members’ strategies to promote active learning can go through the proposal of some challenging problems to be solved autonomously by students. One of the ways to propose those problems is through the use of dynamic and interactive exercises (the challenging problem presented in Figure 15 is part of an educational resource created by the author and nominated for the “Casa das Ciências 2019” award, in Portugal) (Figure 15) using the computable document format [25].

The student must resolve the challenge outside the classroom and send it to the teacher by email or via Moodle. Afterwards, the teacher will be able to give personalized feedback to each student who submits an answer.

This type of dynamic and interactive worksheets can be elaborated with any of the active learning tools created with the computer algebra system Mathematica and transformed into a Computable Document Format.

Another possible strategy is the use of a technological tool such as the Christmas Scene Method for identifying and solving exact differential equations, to encourage the students to solve several exercises on a topic of the course, saying that one of the problem generated by the tool will appear in the next evaluation test (Figure 16 and Figure 17).

3.3. Evaluation Questions

Technological learning tools, correctly used in the classroom, can promote new ways of thinking, teaching and learning.

For example, questions such as the one suggested in Figure 9 have already been used in the classroom (with the exercise projected on the whiteboard) and in online classes (teacher can share the tool and ask oral answers from the students or through the Zoom chat). Taking into account the author’s experience, in an online environment it worked very well because even the most shy students participated as only the names of those who answered correctly were mentioned.

Another advantage of using this type of tool, in terms of short quiz or test/exam question (in person or online), is the ease of creating many different versions with the same degree of difficulty, reducing the possibility of academic fraud (mainly in an online environment). The author has already created thousands of different versions using the tools presented here. 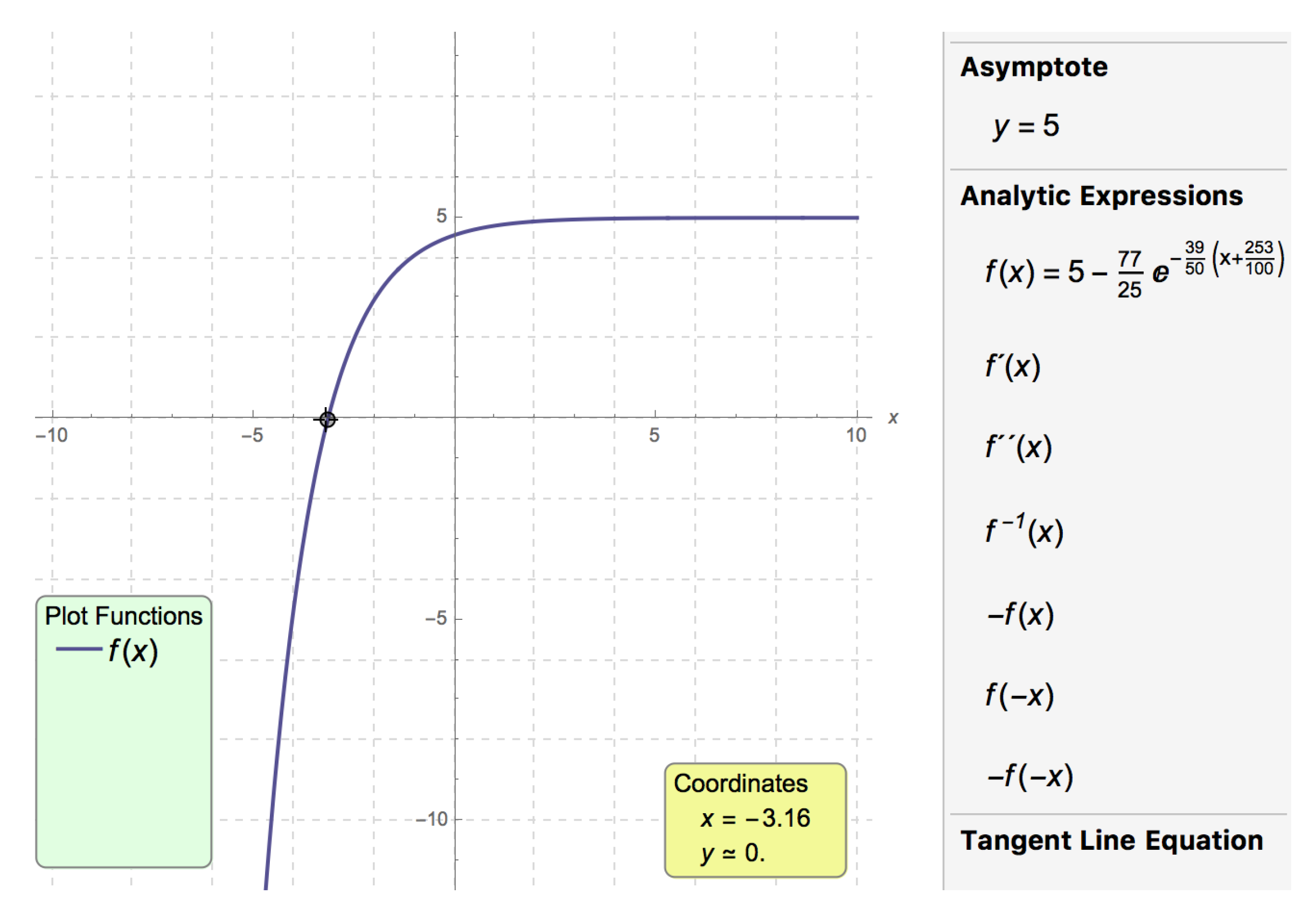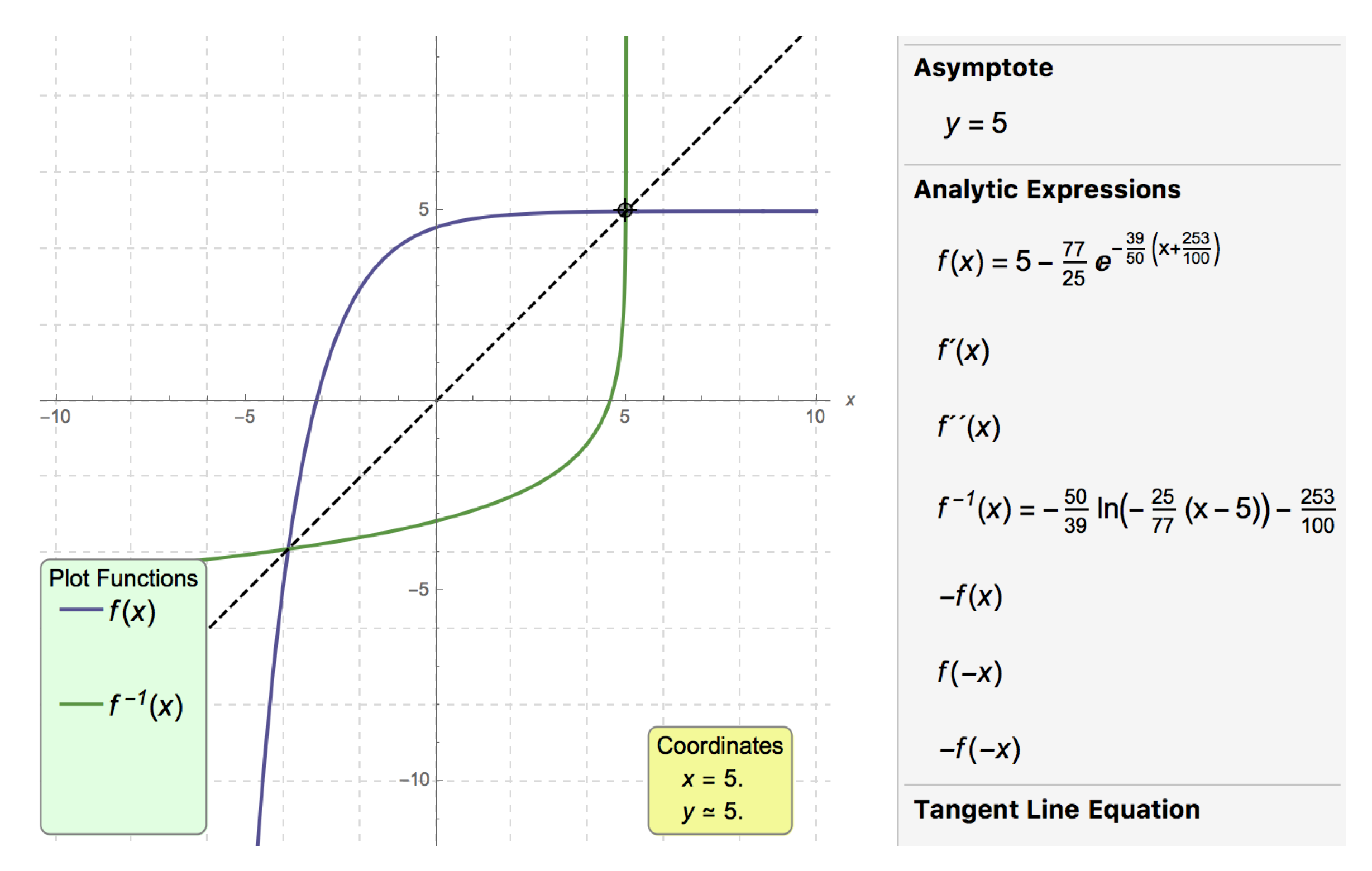For example, using F-Exponential, the teacher can quickly create a similar version of an invertibility question for each student who takes an online assessment (see Figure 18 and Figure 19) and get the solutions immediately (see Figure 20 and Figure 21).

Furthermore, it can also be used to the design of evaluation questions, multiple choice and open response questions, as a part of written tests or exams (to be solved without the use of any technological learning tools).

Another possibility of using this type of dynamic and interactive tools is to create videos (with a short duration) with a theoretical explanation of a topic and place an exercise statement inside, ensuring its visualization by students who want to have some classification for performing an extra task.

Regarding the author’s experience regarding the use of this type of technological learning tools, it is possible to observe, analyzing the before and after the implementation, and the use, of the tool “Christmas Scene Method for identifying and solving exact differential equations”, in the classroom and in self-employed work, that students’ ratings for the concept studied rose by an average of 9.3%. Similar analyzes can be made for other tools used in a remote or classroom learning environment. Obviously, the analysis is done for different groups of students and they may have different preparations in the area of Mathematics. For this reason, the author considers that the most important thing is the increase of motivation on the part of students when, after the presentation of theoretical content on a topic, a dynamic and interactive tool is used to promote the discussion and healthy exchange of ideas. When the tool used makes it possible to carry out numerous exercises on the same topic, it becomes even more efficient.

4. Discussion

Teaching is both an art and a learned skill. The use of dynamic and interactive mathematical tools can provide a context where students and teachers are also invited to contribute, and can also motivate adaptation and innovation in evaluation [2]. In fact, when used appropriately, technological learning tools, can improve a better student activity and engagement in the learning process. Obviously, the use of these kind of tools can be generalized to several curricular units from other scientific areas, creating new teaching methodologies (either in a remote or in a classroom environment).

Although the author has already analyzed some data regarding results obtained by students before and after using various learning tools used in the classroom, a statistically rigorous study to estimate the value of the pedagogical tool could be of great importance. Believing that this study can be an important aid for the future development of this kind of educational tools [29], it is intended to create a working group dedicated to this type of task. Moreover, the author considers that there must be a wide dissemination of tools that promote healthy debate in the classroom. Besides that, the sharing of experiences in scientific and pedagogical meetings is essential for the development of the teaching and learning process.