On the Elicitability and Risk Model Comparison of Emerging Markets Equities
Abstract
:1. Introduction
2. Theoretical Models and Empirical Methodology
2.1. Univariate GAS Model Specification
2.2. The FZL Function
2.3. The MCS Procedure
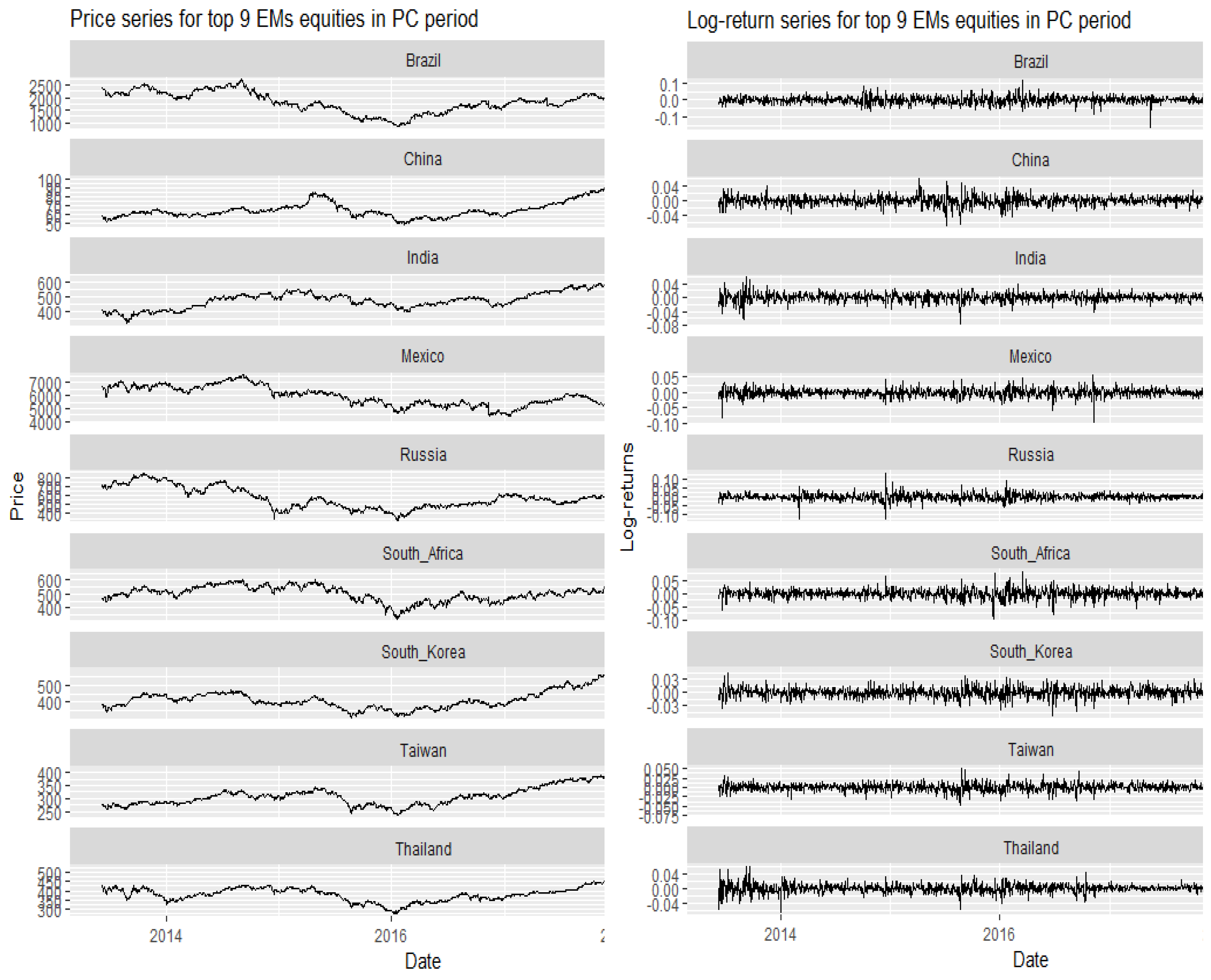
3. Data and Preliminary Analysis
Descriptive Statistics
4. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burzoni, M.; Peri, I.; Ruffo, C.M. On the properties of the Lambda value at risk: Robustness, elicitability and consistency. Quant. Financ. 2017, 17, 1735–1743. [Google Scholar] [CrossRef] [Green Version]
- Cont, R.; Deguest, R.; He, X.D. Loss-based risk measures. Stat. Risk Model. Appl. Financ. Insur. 2013, 30, 133–167. [Google Scholar] [CrossRef] [Green Version]
- Fissler, T.; Ziegel, J.F. Higher order elicitability and Osband’s principle. Ann. Stat. 2016, 44, 1680–1707. [Google Scholar] [CrossRef]
- Fissler, T.; Ziegel, J.F.; Gneiting, T. Expected Shortfall is jointly elicitable with Value at Risk-Implications for backtesting. arXiv 2015, arXiv:1507.00244. [Google Scholar]
- Nolde, N.; Ziegel, J.F. Elicitability and backtesting: Perspectives for banking regulation. Ann. Appl. Stat. 2017, 11, 1833–1874. [Google Scholar] [CrossRef]
- Chang, C.-L.; Jimenez-Martin, J.-A.; Maasoumi, E.; McAleer, M.; Pérez-Amaral, T. Choosing expected shortfall over VaR in Basel III using stochastic dominance. Int. Rev. Econ. Financ. 2019, 60, 95–113. [Google Scholar] [CrossRef] [Green Version]
- Kellner, R.; Rösch, D. Quantifying market risk with Value-at-Risk or Expected Shortfall?—Consequences for capital requirements and model risk. J. Econ. Dyn. Control 2016, 68, 45–63. [Google Scholar] [CrossRef]
- Bernardi, M.; Catania, L. Comparison of Value-at-Risk models using the MCS approach. Comput. Stat. 2016, 31, 579–608. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A.; Nason, J.M. The Model Confidence Set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef] [Green Version]
- Patton, A.J.; Ziegel, J.F.; Chen, R. Dynamic semiparametric models for expected shortfall (and Value-at-Risk). J. Econ. 2019. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Lee, T.-H.; Saltoglu, B. Evaluating predictive performance of value-at-risk models in emerging markets: A reality check. J. Forecast. 2006, 25, 101–128. [Google Scholar] [CrossRef]
- Del Brio, E.B.; Mora-Valencia, A.; Perote, J. VaR performance during the subprime and sovereign debt crises: An application to emerging markets. Emerg. Mark. Rev. 2014, 20, 23–41. [Google Scholar] [CrossRef]
- Hwang, S.; Satchell, S.E. Modelling emerging market risk premia using higher moments. Int. J. Financ. Econ. 1999, 4, 271–296. [Google Scholar] [CrossRef]
- Ji, Q.; Liu, B.-Y.; Zhao, W.-L.; Fan, Y. Modelling dynamic dependence and risk spillover between all oil price shocks and stock market returns in the BRICS. Int. Rev. Financ. Anal. 2020, 68, 101238. [Google Scholar] [CrossRef]
- Miletic, M.; Miletic, S. Performance of Value at Risk models in the midst of the global financial crisis in selected CEE emerging capital markets. Econ. Res.-Ekon. Istraž. 2015, 28, 132–166. [Google Scholar] [CrossRef] [Green Version]
- Kharas, H. The Emerging Middle Class in Developing Countries. Available online: https://www.oecd-ilibrary.org/development/the-emerging-middle-class-in-developing-countries_5kmmp8lncrns-en (accessed on 30 August 2021).
- Aizenman, J.; Binici, M.; Hutchison, M.M. The Transmission of Federal Reserve Tapering News to Emerging Financial Markets (Working Paper No. 19980); National Bureau of Economic Research: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Enginar, O.; Karan, M.B.; Büyükkara, G. Performances of Emerging Stock Exchanges During the Fed’s Tapering Announcements. In Global Approaches in Financial Economics, Banking, and Finance; Dincer, H., Hacioglu, Ü., Yüksel, S., Eds.; Springer: Berlin, Germany, 2018; pp. 415–443. [Google Scholar] [CrossRef]
- Ghosh, S.; Saggar, M. Volatility spillovers to the emerging financial markets during taper talk and actual tapering. Appl. Econ. Lett. 2017, 24, 122–127. [Google Scholar] [CrossRef]
- Mishra, P.; Moriyama, K.; N’Diaye, P.M.P.; Nguyen, L. Impact of Fed Tapering Announcements on Emerging Markets; International Monetary Fund: Washington, DC, USA, 2014. [Google Scholar]
- Blazsek, S.; Hernández, H. Analysis of electricity prices for Central American countries using dynamic conditional score models. Empir. Econ. 2018, 55, 1807–1848. [Google Scholar] [CrossRef]
- Gong, X.-L.; Liu, X.-H.; Xiong, X. Measuring tail risk with GAS time varying copula, fat tailed GARCH model and hedging for crude oil futures. Pac. Basin Financ. J. 2019, 55, 95–109. [Google Scholar] [CrossRef]
- Troster, V.; Tiwari, A.K.; Shahbaz, M.; Macedo, D.N. Bitcoin returns and risk: A general GARCH and GAS analysis. Financ. Res. Lett. 2018, 30, 187–193. [Google Scholar] [CrossRef]
- Owusu Junior, P.; Alagidede, I. Risks in emerging markets equities: Time-varying versus spatial risk analysis. Phys. A Stat. Mech. Appl. 2020, 542, 123474. [Google Scholar] [CrossRef]
- Khalaf, L.; Leccadito, A.; Urga, G. Multilevel and Tail Risk Management. J. Financ. Econom. 2021. [Google Scholar] [CrossRef]
- Kratz, M.; Lok, Y.H.; McNeil, A.J. Multinomial VaR backtests: A simple implicit approach to backtesting expected shortfall. J. Bank. Financ. 2018, 88, 393–407. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, A.K.; Tiwari, A.K. Estimating the market risk of clean energy technologies companies using the expected shortfall approach. Renew. Energy 2021, 177, 95–100. [Google Scholar] [CrossRef]
- Barendse, S. Interquantile Expectation Regression (SSRN Scholarly Paper No. ID 2937665). Available online: https://papers.ssrn.com/abstract=2937665 (accessed on 30 August 2021).
- Dimitriadis, T.; Bayer, S. A Joint Quantile and Expected Shortfall Regression Framework. arXiv 2017, arXiv:1704.02213. [Google Scholar] [CrossRef]
- Couperier, O.; Leymarie, J. Backtesting Expected Shortfall via Multi-Quantile Regression. Available online: https://halshs.archives-ouvertes.fr/halshs-01909375/document (accessed on 30 August 2021).
- Han, A.; Hausman, J.A. Flexible parametric estimation of duration and competing risk models. J. Appl. Econom. 1990, 5, 1–28. [Google Scholar] [CrossRef]
- White, H. A Reality Check for Data Snooping. Econometrica 2000, 68, 1097–1126. [Google Scholar] [CrossRef]
- Romano, J.P.; Wolf, M. Stepwise Multiple Testing as Formalized Data Snooping. Econometrica 2005, 73, 1237–1282. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.R.; Lunde, A. A forecast comparison of volatility models: Does anything beat a GARCH (1, 1)? J. Appl. Econom. 2005, 20, 873–889. [Google Scholar] [CrossRef] [Green Version]
- Giacomini, R.; White, H. Tests of Conditional Predictive Ability. Econometrica 2006, 74, 1545–1578. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.W. Forecasting Value at Risk and Expected Shortfall Using a Semiparametric Approach Based on the Asymmetric Laplace Distribution. J. Bus. Econ. Stat. 2019, 37, 121–133. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar] [CrossRef] [Green Version]
- Dimitrakopoulos, D.N.; Kavussanos, M.G.; Spyrou, S.I. Value at risk models for volatile emerging markets equity portfolios. Q. Rev. Econ. Financ. 2010, 50, 515–526. [Google Scholar] [CrossRef]
- Mollah, S.; Mobarek, A. Global Stock Market Integration: Co-Movement, Crises, and Efficiency in Developed and Emerging Markets; Springer: Berlin, Germany, 2016. [Google Scholar]
- Gneiting, T. Making and Evaluating Point Forecasts. J. Am. Stat. Assoc. 2011, 106, 746–762. [Google Scholar] [CrossRef] [Green Version]
- Weber, S. Distribution-Invariant Risk Measures, Information, and Dynamic Consistency. Math. Financ. 2006, 16, 419–441. [Google Scholar] [CrossRef]
- Creal, D.; Koopman, S.J.; Lucas, A. Generalized autoregressive score models with applications. J. Appl. Econom. 2013, 28, 777–795. [Google Scholar] [CrossRef] [Green Version]
- Harvey, A.C. Dynamic Models for Volatility and Heavy Tails: With Applications to Financial and Economic Time Series (Volume 52); Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ardia, D.; Boudt, K.; Catania, L. Downside Risk Evaluation with the R Package GAS (SSRN Scholarly Paper No. ID 2871444). Available online: https://papers.ssrn.com/abstract=2871444 (accessed on 30 August 2021).
- Mariano, R.S.; Preve, D. Statistical tests for multiple forecast comparison. J. Econom. 2012, 169, 123–130. [Google Scholar] [CrossRef]
- West, K.D. Asymptotic inference about predictive ability. Econom. J. Econom. Soc. 1996, 64, 1067–1084. [Google Scholar] [CrossRef]
- González-Rivera, G.; Lee, T.-H.; Mishra, S. Forecasting volatility: A reality check based on option pricing, utility function, value-at-risk, and predictive likelihood. Int. J. Forecast. 2004, 20, 629–645. [Google Scholar] [CrossRef]
- Bernardi, M.; Catania, L.; Petrella, L. Are news important to predict the Value-at-Risk? Eur. J. Financ. 2017, 23, 535–572. [Google Scholar] [CrossRef]
- Bernardi, M.; Catania, L. The Model Confidence Set Package for R. arXiv 2014, arXiv:1410.8504. [Google Scholar]
- Cajueiro, D.O.; Tabak, B.M. Testing for time-varying long-range dependence in volatility for emerging markets. Phys. A Stat. Mech. Appl. 2005, 346, 577–588. [Google Scholar] [CrossRef]
- McNeil, A.J.; Frey, R. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach. J. Empir. Financ. 2000, 7, 271–300. [Google Scholar] [CrossRef]
- McNeil, A.J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques and Tools—Revised Edition; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Fernández, C.; Steel, M.F.J. On Bayesian Modeling of Fat Tails and Skewness. J. Am. Stat. Assoc. 1998, 93, 359–371. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Galbraith, J.W. A generalized asymmetric Student-t distribution with application to financial econometrics. J. Econom. 2010, 157, 297–305. [Google Scholar] [CrossRef]
- Zhu, D.; Galbraith, J.W. Modeling and forecasting expected shortfall with the generalized asymmetric Student-t and asymmetric exponential power distributions. J. Empir. Financ. 2011, 18, 765–778. [Google Scholar] [CrossRef]
- Kotz, S.; Kozubowski, T.; Podgorski, K. The Laplace Distribution and Generalizations: A Revisit with Applications to Communications, Economics, Engineering, and Finance; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Cheung, Y.-W.; Fatum, R.; Yamamoto, Y. The exchange rate effects of macro news after the global Financial Crisis. J. Int. Money Financ. 2019, 95, 424–443. [Google Scholar] [CrossRef]
- Crotty, J. Structural causes of the global financial crisis: A critical assessment of the ‘new financial architecture’. Camb. J. Econ. 2009, 33, 563–580. [Google Scholar] [CrossRef] [Green Version]
- Martin, R. The local geographies of the financial crisis: From the housing bubble to economic recession and beyond. J. Econ. Geogr. 2011, 11, 587–618. [Google Scholar] [CrossRef] [Green Version]
- Mollah, S.; Quoreshi, A.M.M.S.; Zafirov, G. Equity market contagion during global financial and Eurozone crises: Evidence from a dynamic correlation analysis. J. Int. Financ. Mark. Inst. Money 2016, 41, 151–167. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.H.; Pontell, H.N. Mortgage origination fraud and the global economic crisis. Criminol. Public Policy 2010, 9, 591–612. [Google Scholar] [CrossRef]
- Marcellino, M.; Stock, J.H.; Watson, M.W. A comparison of direct and iterated multistep AR methods for forecasting macroeconomic time series. J. Econom. 2006, 135, 499–526. [Google Scholar] [CrossRef] [Green Version]
- Fundamental Review of the Trading Book. Available online: https://www.bis.org/publ/bcbs265.htm (accessed on 30 August 2021).
- Emerging Markets. Available online: https://www.msci.com/documents/10199/c0db0a48-01f2-4ba9-ad01-226fd5678111 (accessed on 30 August 2021).
- Trucíos, C.; Hotta, L.K.; Ruiz, E. Robust bootstrap forecast densities for GARCH returns and volatilities. J. Stat. Comput. Simul. 2017, 87, 3152–3174. [Google Scholar] [CrossRef]
- Jiménez, I.; Mora-Valencia, A.; Perote, J. Risk quantification and validation for Bitcoin. Oper. Res. Lett. 2020, 48, 534–541. [Google Scholar] [CrossRef]

| China | S. Korea | Taiwan | India | Brazil | S. Africa | Russia | Mexico | Thailand | |
|---|---|---|---|---|---|---|---|---|---|
| EC-GFC periods | |||||||||
| In-sample: 5 January 2007 to 18 April 2011 | |||||||||
| Mean | 0.0003 | 0.0003 | 0.0001 | 0.0003 | 0.0005 | 0.0002 | −0.0002 | 0.0001 | 0.0006 |
| Variance | 0.0005 | 0.0006 | 0.0003 | 0.0005 | 0.0008 | 0.0005 | 0.0009 | 0.0004 | 0.0004 |
| Skewness | 0.03 | −0.13 | –0.20 | 0.19 | −0.34 | −0.26 | −0.40 | 0.02 | −0.59 |
| Excess kurtosis | 5.02 | 17.11 | 2.40 | 6.89 | 7.39 | 4.31 | 13.79 | 6.46 | 6.17 |
| Normtest.W* | 0.94 | 0.86 | 0.96 | 0.94 | 0.90 | 0.95 | 0.85 | 0.91 | 0.94 |
| Observations | 1117 | 1117 | 1117 | 1117 | 1117 | 1117 | 1117 | 1117 | 1117 |
| Out-of-sample: 19 April 2011 to 7 June 2013 | |||||||||
| Mean | −0.0003 | −0.0002 | −0.0001 | −0.0004 | −0.0008 | −0.0003 | −0.0007 | 0.000 | 0.0003 |
| Variance | 0.0002 | 0.0003 | 0.0002 | 0.0002 | 0.0003 | 0.0003 | 0.0003 | 0.0002 | 0.0002 |
| Skewness | −0.077 | −0.248 | −0.167 | 0.030 | −0.401 | −0.082 | −0.477 | −0.533 | 0.034 |
| Excess kurtosis | 2.896 | 2.457 | 1.931 | 1.334 | 2.815 | 1.562 | 2.642 | 3.795 | 2.959 |
| Normtest.W* | 0.959 | 0.965 | 0.970 | 0.985 | 0.971 | 0.982 | 0.963 | 0.961 | 0.967 |
| Observations | 559 | 559 | 559 | 559 | 559 | 559 | 559 | 559 | 559 |
| Post-crises period | |||||||||
| In-sample: 10 June 2013 to 21 July 2017 | |||||||||
| Mean | 0.0002 | 0.0001 | 0.0002 | 0.0002 | −0.0003 | 0.0001 | −0.0002 | −0.0002 | −0.0001 |
| Variance | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0004 | 0.0003 | 0.0004 | 0.0002 | 0.0002 |
| Skewness | −0.17 | −0.16 | −0.15 | −0.51 | 0.18 | −0.25 | −0.03 | −0.60 | −0.07 |
| Excess kurtosis | 3.07 | 1.45 | 2.31 | 4.22 | 1.82 | 2.94 | 7.26 | 4.97 | 3.87 |
| Normtest.W* | 0.96 | 0.98 | 0.97 | 0.95 | 0.98 | 0.97 | 0.93 | 0.96 | 0.95 |
| Observations | 990 | 990 | 990 | 990 | 990 | 990 | 990 | 990 | 990 |
| Out-of-sample: 22 July 2017 to 18 February 2019 | |||||||||
| Mean | 0.0003 | 0.0001 | 0.0001 | 0.0001 | 0.0004 | −0.0002 | 0.0001 | −0.0003 | 0.0004 |
| Variance | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0003 | 0.0003 | 0.0002 | 0.0002 | 0.0001 |
| Skewness | −0.12 | −0.36 | −0.96 | −0.37 | −1.26 | −0.22 | −1.82 | −0.57 | −0.09 |
| Excess kurtosis | 0.57 | 1.71 | 6.98 | 0.87 | 12.68 | 1.21 | 17.03 | 3.08 | 2.23 |
| Normtest.W* | 0.99 | 0.98 | 0.93 | 0.99 | 0.92 | 0.99 | 0.91 | 0.97 | 0.96 |
| Observations | 497 | 497 | 497 | 497 | 497 | 497 | 497 | 497 | 497 |
| Mean | Variance | Skewness | Excess Kurtosis | Normtest.W* | Observations |
|---|---|---|---|---|---|
| EC-GFC periods | |||||
| In-sample: 5 January 2007 to 18 April 2011 | |||||
| 0.0002 | 0.0003 | −0.4159 | 6.3206 | 0.92 | 1117 |
| Out-of-sample: 19 April 2011 to 7 June 2013 | |||||
| −0.0003 | 0.0001 | −0.3898 | 3.4102 | 0.96 | 559 |
| Post-crises period | |||||
| In-sample: 10 June 2013 to 21 July 2017 | |||||
| −0.0001 | 0.0001 | −0.2912 | 1.9301 | 0.98 | 990 |
| Out-of-sample: 22 July 2017 to 18 February 2019 | |||||
| 0.0002 | 0.0001 | −0.5911 | 1.0884 | 0.98 | 497 |
| Model | RankR,M | ti | p-ValueR,M | Loss | Model | RankR,M | ti | p-ValueR,M | Loss |
|---|---|---|---|---|---|---|---|---|---|
| Eurozone and Global Financial Crises (EC-GFC) Periods:19 April 2011 to 7 June 2013 | |||||||||
| Brazil 1% | Brazil 2.5% | ||||||||
| SNORM | 2 | −1.98 | 1.00 | −3.05 | SNORM | 3 | −1.43 | 1.00 | −3.16 |
| STD | 3 | −1.50 | 1.00 | −2.93 | STD | 1 | −2.56 | 1.00 | −3.16 |
| SSTD | 1 | −2.23 | 1.00 | −2.97 | SSTD | 2 | −2.49 | 1.00 | −3.13 |
| AST | 6 | 1.81 | 0.11 | −2.51 | AST | 6 | 1.95 | 0.08 | −2.89 |
| AST1 | 5 | 1.81 | 0.11 | −2.51 | AST1 | 5 | 1.95 | 0.08 | −2.89 |
| ALD | 4 | −1.12 | 1.00 | −2.96 | ALD | 4 | −1.15 | 1.00 | −3.13 |
| p-value | 0.105 | p-value | 0.084 | ||||||
| Mexico 1% | Mexico 2.5% | ||||||||
| SNORM | 2 | −1.32 | 1.00 | −3.17 | SNORM | 4 | −0.77 | 1.00 | −3.32 |
| STD | 4 | 0.13 | 1.00 | −3.05 | STD | 2 | −1.17 | 1.00 | −3.33 |
| SSTD | 1 | −2.96 | 1.00 | −3.13 | SSTD | 1 | −3.47 | 1.00 | −3.32 |
| AST | 6 | 1.43 | 0.29 | −2.93 | AST | 6 | 1.68 | 0.22 | −3.21 |
| AST1 | 5 | 1.43 | 0.29 | −2.93 | AST1 | 5 | 1.68 | 0.22 | −3.21 |
| ALD | 3 | −0.93 | 1.00 | −3.15 | ALD | 3 | −0.87 | 1.00 | −3.32 |
| p-value | 0.292 | p-value | 0.223 | ||||||
| Russia 1% | Russia 2.5% | ||||||||
| SNORM | 2 | −1.11 | 1.00 | −2.69 | SNORM | 2 | −0.21 | 1.00 | −2.88 |
| STD | 3 | 1.08 | 0.44 | −2.60 | STD | 3 | 0.54 | 0.83 | −2.86 |
| SSTD | 4 | 2.06 | 0.06 | −2.54 | SSTD | 4 | 1.89 | 0.10 | −2.82 |
| ALD | 1 | −1.50 | 1.00 | −2.76 | ALD | 1 | −1.78 | 1.00 | −2.93 |
| p-value | 0.059 | p-value | 0.095 | ||||||
| South Africa 1% | South Africa 2.5% | ||||||||
| SNORM | 1 | −0.96 | 1.00 | −2.92 | SNORM | 3 | 1.54 | 0.18 | −3.03 |
| STD | 3 | 0.56 | 0.86 | −2.86 | STD | 2 | −0.16 | 1.00 | −3.07 |
| SSTD | 4 | 1.19 | 0.43 | −2.85 | ALD | 1 | −1.10 | 1.00 | −3.10 |
| ALD | 2 | −0.66 | 1.00 | −2.93 | |||||
| p-value | 0.425 | p-value | 0.180 | ||||||
| China 1% | China 2.5% | ||||||||
| SNORM | 1 | −0.52 | 1.00 | −3.06 | SNORM | 3 | 1.03 | 0.44 | −3.21 |
| STD | 3 | −0.27 | 1.00 | −3.04 | STD | 2 | −0.30 | 1.00 | −3.24 |
| SSTD | 4 | 1.41 | 0.30 | −2.98 | ALD | 1 | −0.57 | 1.00 | −3.25 |
| ALD | 2 | −0.34 | 1.00 | −3.05 | |||||
| p-value | 0.300 | p-value | 0.443 | ||||||
| India 1% | India 2.5% | ||||||||
| SNORM | 4 | 0.23 | 0.97 | −2.90 | SNORM | 4 | 0.86 | 0.62 | −3.08 |
| STD | 1 | −5.01 | 1.00 | −3.17 | STD | 1 | −5.55 | 1.00 | −3.33 |
| SSTD | 2 | −3.92 | 1.00 | −3.08 | SSTD | 2 | −4.11 | 1.00 | −3.22 |
| AST | 6 | 2.17 | 0.06 | −2.66 | AST | 6 | 2.62 | 0.02 | −2.95 |
| AST1 | 5 | 2.17 | 0.06 | −2.66 | AST1 | 5 | 2.62 | 0.02 | −2.95 |
| ALD | 3 | −1.31 | 1.00 | −3.06 | ALD | 3 | −2.66 | 1.00 | −3.28 |
| p-value | 0.061 | p-value | 0.016 | ||||||
| South Korea 1% | South Korea 2.5% | ||||||||
| SNORM | 4 | −0.86 | 1.00 | −2.87 | SNORM | 4 | −0.98 | 1.00 | −3.05 |
| STD | 1 | −2.95 | 1.00 | −2.99 | STD | 1 | −3.53 | 1.00 | −3.14 |
| SSTD | 2 | −1.73 | 1.00 | −2.88 | SSTD | 3 | −1.53 | 1.00 | −3.04 |
| AST | 6 | 1.98 | 0.09 | −2.52 | AST | 6 | 2.43 | 0.03 | −2.81 |
| AST1 | 5 | 1.98 | 0.09 | −2.52 | AST1 | 5 | 2.43 | 0.03 | −2.81 |
| ALD | 3 | −1.26 | 1.00 | −2.95 | ALD | 2 | −1.58 | 1.00 | −3.09 |
| p-value | 0.087 | p-value | 0.031 | ||||||
| Taiwan 1% | Taiwan 2.5% | ||||||||
| SNORM | 3 | −1.36 | 1.00 | −3.12 | SNORM | 3 | −1.26 | 1.00 | −3.28 |
| STD | 1 | −3.52 | 1.00 | −3.08 | STD | 1 | −4.68 | 1.00 | −3.31 |
| SSTD | 4 | −1.31 | 1.00 | −2.89 | SSTD | 4 | −1.21 | 1.00 | −3.16 |
| AST | 6 | 2.03 | 0.06 | −2.25 | AST | 6 | 2.50 | 0.02 | −2.78 |
| AST1 | 5 | 2.03 | 0.06 | −2.25 | AST1 | 5 | 2.50 | 0.02 | −2.78 |
| ALD | 2 | −2.02 | 1.00 | −3.09 | ALD | 2 | −3.08 | 1.00 | −3.32 |
| p-value | 0.064 | p-value | 0.022 | ||||||
| Thailand 1% | Thailand 2.5% | ||||||||
| SNORM | 4 | 0.74 | 0.80 | −2.96 | SNORM | 6 | 1.32 | 0.37 | −3.17 |
| STD | 1 | −4.27 | 1.00 | −3.20 | STD | 1 | −5.55 | 1.00 | −3.41 |
| SSTD | 2 | −2.49 | 1.00 | −3.13 | SSTD | 2 | −2.87 | 1.00 | −3.34 |
| AST | 6 | 1.08 | 0.58 | −2.93 | AST | 5 | 1.02 | 0.55 | −3.20 |
| AST1 | 5 | 1.08 | 0.58 | −2.93 | AST1 | 4 | 1.02 | 0.55 | −3.20 |
| ALD | 3 | −0.36 | 1.00 | −3.07 | ALD | 3 | −0.28 | 1.00 | −3.28 |
| p-value | 0.584 | p-value | 0.367 | ||||||
| Post−crises (PC) period:22 July 2017 to 18 February 2019 | |||||||||
| Brazil 1% | Brazil 2.5% | ||||||||
| SNORM | 2 | −1.62 | 1.00 | −2.59 | SNORM | 4 | −0.85 | 1.00 | −2.95 |
| STD | 4 | −0.91 | 1.00 | −2.57 | STD | 1 | −3.30 | 1.00 | −3.02 |
| SSTD | 1 | −1.81 | 1.00 | −2.60 | SSTD | 3 | −1.09 | 1.00 | −2.96 |
| AST | 6 | 2.17 | 0.06 | −2.32 | AST | 6 | 2.05 | 0.06 | −2.75 |
| AST1 | 5 | 2.17 | 0.06 | −2.32 | AST1 | 5 | 2.05 | 0.06 | −2.75 |
| ALD | 3 | −0.93 | 1.00 | −2.64 | ALD | 2 | −1.14 | 1.00 | −2.98 |
| p-value | 0.058 | p-value | 0.062 | ||||||
| Mexico 1% | Mexico 2.5% | ||||||||
| SNORM | 4 | 0.84 | 0.72 | −2.91 | SNORM | 4 | 0.84 | 0.74 | −3.26 |
| STD | 1 | −3.26 | 1.00 | −3.18 | STD | 1 | −3.74 | 1.00 | −3.41 |
| SSTD | 3 | 0.01 | 1.00 | −3.02 | SSTD | 3 | −0.71 | 1.00 | −3.34 |
| AST | 6 | 1.11 | 0.54 | −2.92 | AST | 6 | 1.45 | 0.35 | −3.23 |
| AST1 | 5 | 1.11 | 0.54 | −2.92 | AST1 | 5 | 1.45 | 0.35 | −3.23 |
| ALD | 2 | −1.09 | 1.00 | −3.17 | ALD | 2 | −1.62 | 1.00 | −3.40 |
| p-value | 0.536 | p-value | 0.349 | ||||||
| Russia 1% | Russia 2.5% | ||||||||
| SNORM | 4 | −0.32 | 1.00 | −2.75 | SNORM | 4 | 0.26 | 0.97 | −3.08 |
| STD | 2 | −2.06 | 1.00 | −2.82 | STD | 1 | −3.94 | 1.00 | −3.22 |
| SSTD | 1 | −2.99 | 1.00 | −2.82 | SSTD | 2 | −3.24 | 1.00 | −3.20 |
| AST | 6 | 1.20 | 0.40 | −2.48 | AST | 6 | 1.03 | 0.54 | −3.01 |
| AST1 | 5 | 1.20 | 0.40 | −2.48 | AST1 | 5 | 1.03 | 0.54 | −3.01 |
| ALD | 3 | −0.56 | 1.00 | −2.79 | ALD | 3 | −0.61 | 1.00 | −3.16 |
| p-value | 0.402 | p-value | 0.536 | ||||||
| South Africa 1% | South Africa 2.5% | ||||||||
| SNORM | 3 | −0.77 | 1.00 | −2.72 | SNORM | 3 | 0.01 | 1.00 | −2.97 |
| STD | 1 | −3.82 | 1.00 | −2.81 | STD | 1 | −3.48 | 1.00 | −3.06 |
| SSTD | 4 | −0.31 | 1.00 | −2.63 | SSTD | 4 | 2.19 | 0.06 | −2.87 |
| AST | 6 | 2.16 | 0.06 | −2.37 | ALD | 2 | −0.46 | 1.00 | −2.99 |
| AST1 | 5 | 2.16 | 0.06 | −2.37 | |||||
| ALD | 2 | −1.49 | 1.00 | −2.78 | |||||
| p-value | 0.063 | p-value | 0.059 | ||||||
| China 1% | China 2.5% | ||||||||
| SNORM | 2 | −0.91 | 1.00 | −3.40 | SNORM | 4 | −1.58 | 1.00 | −3.50 |
| STD | 3 | −0.15 | 1.00 | −3.38 | STD | 1 | −4.80 | 1.00 | −3.55 |
| SSTD | 1 | −1.12 | 1.00 | −3.41 | SSTD | 3 | −1.58 | 1.00 | −3.50 |
| ALD | 4 | 1.38 | 0.26 | −3.31 | AST | 6 | 2.78 | 0.01 | −3.25 |
| AST1 | 5 | 2.78 | 0.01 | −3.25 | |||||
| ALD | 2 | −1.69 | 1.00 | −3.48 | |||||
| p-value | 0.264 | p-value | 0.010 | ||||||
| India 1% | India 2.5% | ||||||||
| SNORM | 2 | −1.24 | 1.00 | −3.53 | SNORM | 4 | −0.72 | 1.00 | −3.67 |
| STD | 1 | −3.21 | 1.00 | −3.59 | STD | 1 | −3.11 | 1.00 | −3.75 |
| SSTD | 3 | −1.21 | 1.00 | −3.52 | SSTD | 3 | −0.80 | 1.00 | −3.67 |
| AST | 5 | 1.92 | 0.09 | −3.18 | AST | 6 | 1.95 | 0.09 | −3.47 |
| AST1 | 6 | 1.92 | 0.09 | −3.18 | AST1 | 5 | 1.95 | 0.09 | −3.47 |
| ALD | 4 | −1.10 | 1.00 | −3.51 | ALD | 2 | −1.95 | 1.00 | −3.71 |
| p-value | 0.08 | p-value | 0.094 | ||||||
| South Korea 1% | South Korea 2.5% | ||||||||
| SNORM | 3 | −0.40 | 1.00 | −3.18 | SNORM | 3 | −0.78 | 1.00 | −3.42 |
| STD | 4 | 1.92 | 0.09 | −3.02 | STD | 4 | 2.08 | 0.06 | −3.30 |
| SSTD | 1 | −1.77 | 1.00 | −3.21 | SSTD | 2 | −1.22 | 1.00 | −3.42 |
| ALD | 2 | −1.18 | 1.00 | −3.26 | ALD | 1 | −1.97 | 1.00 | −3.48 |
| p-value | 0.093 | p-value | 0.063 | ||||||
| Taiwan 1% | Taiwan 2.5% | ||||||||
| SNORM | 4 | −0.94 | 1.00 | −3.04 | SNORM | 4 | −1.42 | 1.00 | −3.44 |
| STD | 1 | −2.10 | 1.00 | −3.13 | STD | 1 | −2.61 | 1.00 | −3.48 |
| SSTD | 3 | −1.21 | 1.00 | −3.06 | SSTD | 3 | −1.49 | 1.00 | −3.45 |
| AST | 5 | 1.73 | 0.14 | −2.56 | AST | 6 | 2.07 | 0.06 | −3.08 |
| AST1 | 6 | 1.73 | 0.14 | −2.56 | AST1 | 5 | 2.07 | 0.06 | −3.08 |
| ALD | 2 | −2.06 | 1.00 | −3.15 | ALD | 2 | −1.97 | 1.00 | −3.48 |
| p-value | 0.140 | p-value | 0.065 | ||||||
| Thailand 1% | Thailand 2.5% | ||||||||
| SNORM | 4 | −0.24 | 1.00 | −3.55 | SNORM | 4 | 1.05 | 0.47 | −3.67 |
| STD | 1 | −4.42 | 1.00 | −3.75 | STD | 1 | −5.34 | 1.00 | −3.95 |
| SSTD | 2 | −2.80 | 1.00 | −3.64 | SSTD | 2 | −2.61 | 1.00 | −3.83 |
| AST | 6 | 1.52 | 0.19 | −3.26 | AST | 6 | 1.44 | 0.24 | −3.63 |
| AST1 | 5 | 1.52 | 0.19 | −3.26 | AST1 | 5 | 1.44 | 0.24 | −3.63 |
| ALD | 3 | −0.86 | 1.00 | −3.60 | ALD | 3 | −1.06 | 1.00 | −3.81 |
| p-value | 0.188 | p-value | 0.245 | ||||||
| Eurozone and Global Financial Crises (EC-GFC) Periods:19 April 2011 to 7 June 2013 | |||||||||
| EM index 1% | EM index 2.5% | ||||||||
| ALD | 1 | −6.03 | 1.00 | −0.02 | ALD | 1 | −5.84 | 1.00 | −0.02 |
| p-value | 0.000 | p-value | 0.000 | ||||||
| Post−crises (PC) period:22 July 2017 to 18 February 2019 | |||||||||
| EM index 1% | EM index 2.5% | ||||||||
| ALD | 1 | −6.00 | 1.00 | −0.024 | ALD | 1 | −5.92 | 1.00 | −0.02 |
| p-value | 0.000 | p-value | 0.000 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owusu Junior, P.; Alagidede, I.P.; Tiwari, A.K. On the Elicitability and Risk Model Comparison of Emerging Markets Equities. Math. Comput. Appl. 2021, 26, 63. https://doi.org/10.3390/mca26030063
Owusu Junior P, Alagidede IP, Tiwari AK. On the Elicitability and Risk Model Comparison of Emerging Markets Equities. Mathematical and Computational Applications. 2021; 26(3):63. https://doi.org/10.3390/mca26030063
Chicago/Turabian StyleOwusu Junior, Peterson, Imhotep Paul Alagidede, and Aviral Kumar Tiwari. 2021. "On the Elicitability and Risk Model Comparison of Emerging Markets Equities" Mathematical and Computational Applications 26, no. 3: 63. https://doi.org/10.3390/mca26030063
APA StyleOwusu Junior, P., Alagidede, I. P., & Tiwari, A. K. (2021). On the Elicitability and Risk Model Comparison of Emerging Markets Equities. Mathematical and Computational Applications, 26(3), 63. https://doi.org/10.3390/mca26030063







