Modeling and Optimizing the Multi-Objective Portfolio Optimization Problem with Trapezoidal Fuzzy Parameters
Abstract
1. Introduction
2. Elements of Fuzzy Theory
2.1. Fuzzy Sets
2.2. Generalized Fuzzy Numbers
- is a continuous function from to the closed interval
- , is strictly increasing on
- , for
- is strictly decreasing on
- , for
2.3. Trapezoidal Addition Operator
2.4. Graded Mean Integration (GMI)
2.5. Order Relation in the Set of the Trapezoidal Fuzzy Numbers
- if only if
- if only if
- if only if
2.6. Pareto Dominance
3. Multi-Objective Portfolio Optimization Problem with Trapezoidal Fuzzy Parameters
3.1. Mathematical Model
3.2. Strategy to Generate the Fuzzy Trapezoidal Instances
- ← Budget as interval
- [ai, a′i] ← Limits of each area I = 1, 2, …, a
- [ri, r′i] ← Limits of each region r = 1, 2, …, r
- [bij, b′ij] ← Benefit from the objective I = 1, 2, ..., m and for each project j = 1, 2, …, p
- {Ci, Ai, Ri} ← Real values of the cost, area and region for each project i = 1, 2, …, p.
| Algorithm 1. o2p25_0I fuzzy interval type instance |
| // Fuzzy interval type value of the total available budget |
| [76800, 83200] |
| // Number of objectives |
| 2 |
| // Number of areas |
| 3 |
| // Fuzzy interval type values of the upper and lower bounds of the available budget // in each area, a row for each area. |
| [13060, 16560] [46245, 49745] |
| [13810, 15810] [47895, 48095] |
| [13210, 16410] [46545, 49445] |
| // Number of regions. |
| 2 |
| // Fuzzy interval type values of the upper and lower bounds of the available budget // in each region, a row for each region. |
| [22775, 24275] [67950, 68050] |
| [23325, 23725] [67900, 68100] |
| // Number of projects |
| 25 |
| // For each project, there is a row that includes the following: fuzzy interval type |
| // value of the project cost, project area, project region, and the fuzzy interval type |
| // value of the benefits obtained with each objective. (only 5 of the 25 projects are |
| // showed) |
| [9308, 10082] [1] [1] [7642, 8278] [231, 249] |
| [8290, 8980] [2] [1] [8506, 9214] [404, 436] |
| [5895, 6385] [3] [1] [3831, 4149] [111, 119] |
| [9053, 9807] [1] [2] [3908, 4232] [399, 431] |
| [6058, 6562] [1] [2] [5760, 6240] [418, 452] |
| Algorithm 2. o2p25_0T fuzzy trapezoidal instance |
| // Fuzzy trapezoidal value of the total available budget |
| [76800, 83200, 0.5, 0.5] |
| // Number of objectives |
| 2 |
| // Number of areas |
| 3 |
| // Fuzzy trapezoidal values of the upper and lower bounds for the available budget // in each area, a row for each area. |
| [13060, 16560, 0.5, 0.5] [46245, 49745, 0.5, 0.5] |
| [13810, 15810, 0.5, 0.5] [47895, 48095, 0.5, 0.5] |
| [13210, 16410, 0.5, 0.5] [46545, 49445, 0.5, 0.5] |
| // Number of regions. |
| 2 |
| // Fuzzy trapezoidal values of the upper and lower bounds for the available budget |
| // in each region, a row for each region. |
| [22775, 24275, 0.5, 0.5] [67950, 68050, 0.5, 0.5] |
| [23325, 23725, 0.5, 0.5] [67900, 68100, 0.5, 0.5] |
| // Number of projects |
| 25 |
| // For each project, there is a row that includes the following: fuzzy trapezoidal value // of the project cost, project area, project region, and the fuzzy trapezoidal values of |
| // the benefits obtained with each objective. (only 5 of the 25 projects are showed) |
| [9308, 10082, 0.5, 0.5] [1] [1] [7642, 8278, 0.5, 0.5] [231, 249, 0.5, 0.5] |
| [8290, 8980, 0.5, 0.5] [2] [1] [8506, 9214, 0.5, 0.5] [404, 436, 0.5, 0.5] |
| [5895, 6385, 0.5, 0.5] [3] [1] [3831, 4149, 0.5, 0.5] [111, 119, 0.5, 0.5] |
| [9053, 9807, 0.5, 0.5] [1] [2] [3908, 4232, 0.5, 0.5] [399, 431, 0.5, 0.5] |
| [6058, 6562, 0.5, 0.5] [1] [2] [5760, 6240, 0.5, 0.5] [418, 452, 0.5, 0.5] |
3.3. Evaluating the Solutions and Verifying the Feasibility
4. Steady-State T-NSGA-II Algorithm
4.1. Representation of the Solutions
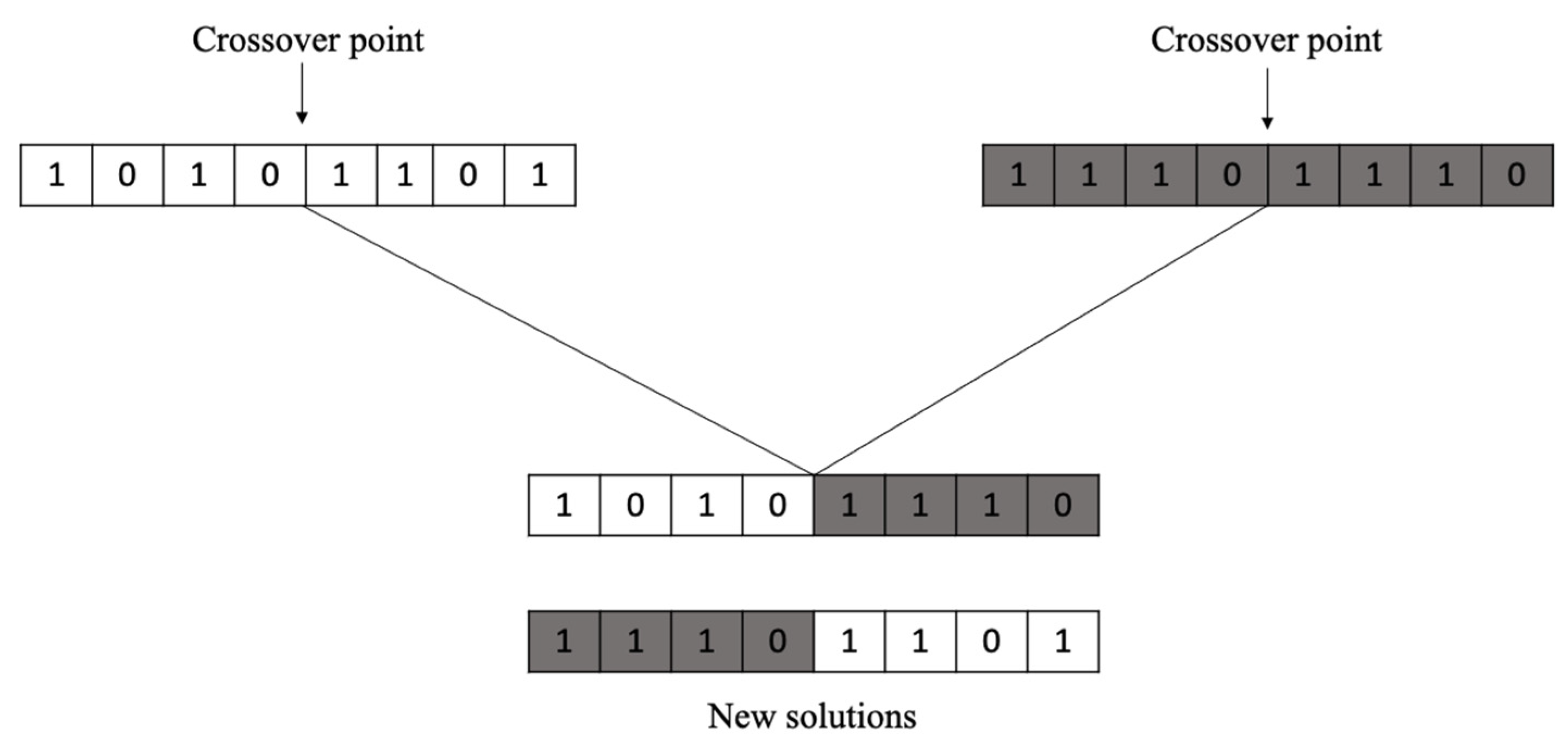
4.2. One-Point Crossover Operator
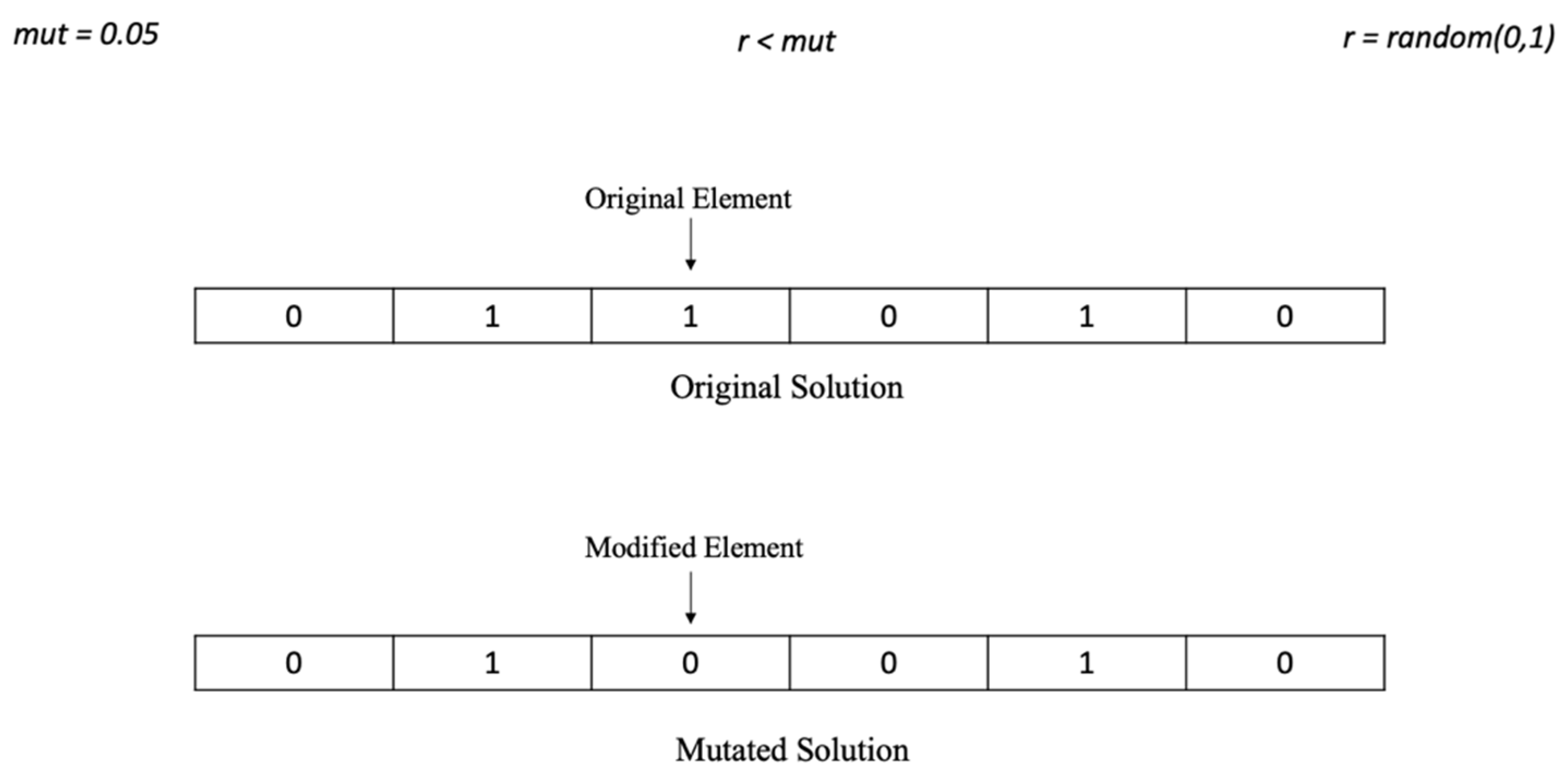
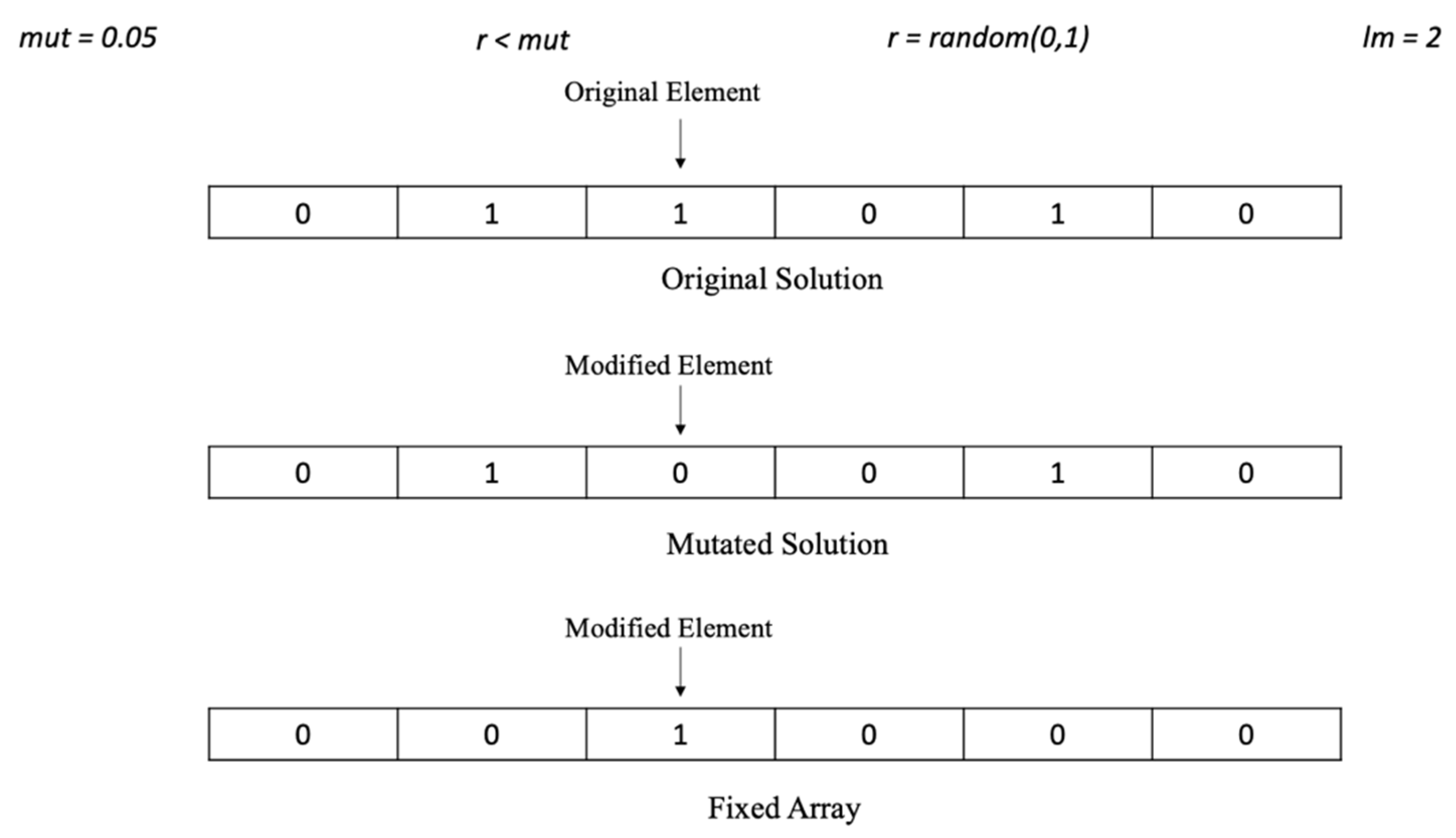
4.3. Uniform Mutation Operator
4.4. Initial Population
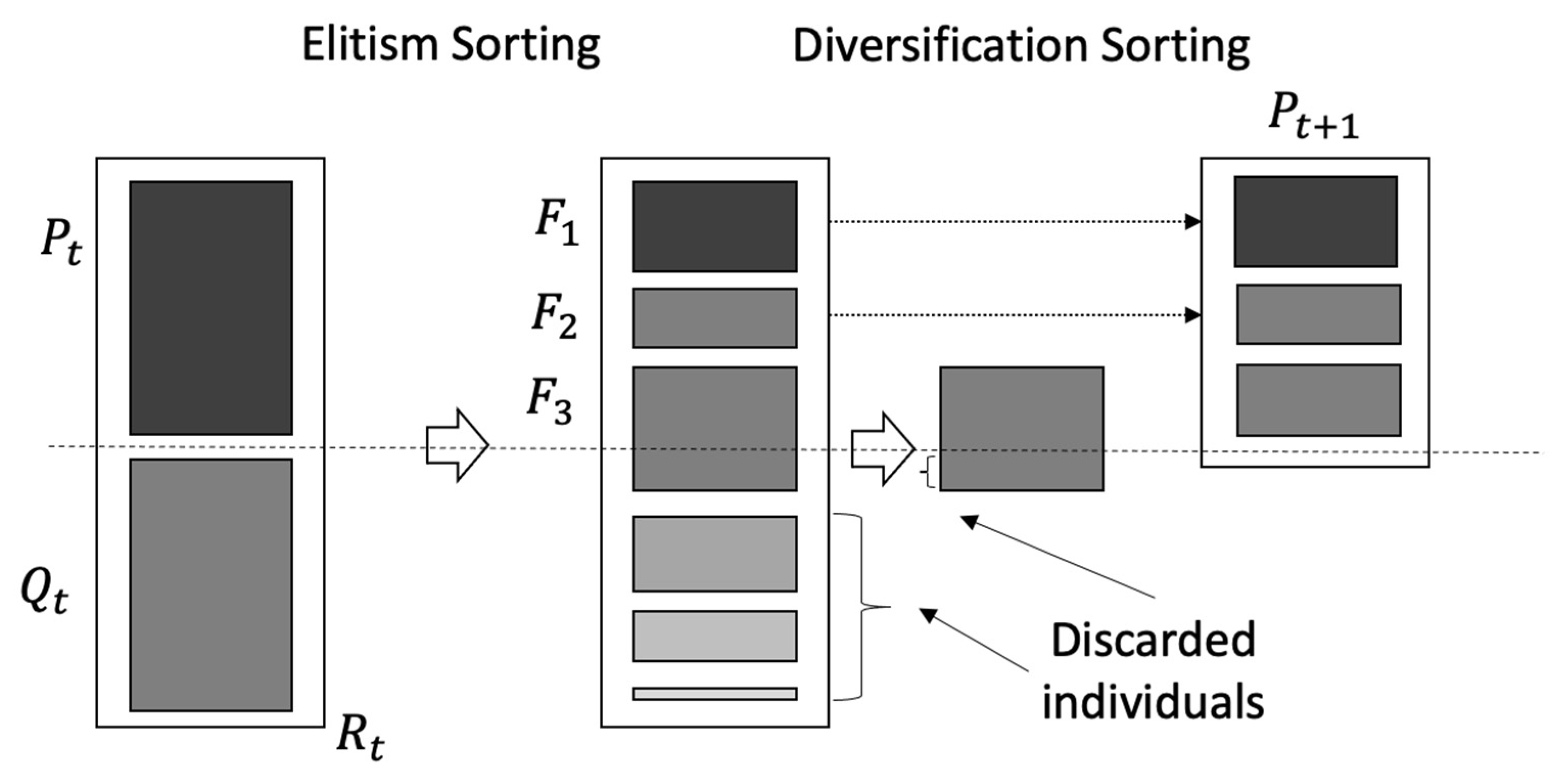
4.5. Population Sorting
4.6. Non-Dominated Sorting
4.7. Calculating the Crowding Distance
4.8. Calculating the Spatial Spread Deviation (SSD)
4.9. Pseudocode of the T-NSGA-II Algorithm
| Algorithm 3. T-NSGA-II pseudocode |
| INPUT: Instance with the trapezoidal parameters of the portfolio problem. OUTPUT: Approximated Pareto Front NOTE: The algorithm is called T-NSGA-II-CD when the Crowding Distance is used, and T-NSGA-II-SSD when is used the Spatial Spread Deviation. *************************************** 1. Create the initial population pop 2. Evaluate all the solutions in pop 3. Order pop using no-dominated Sorting 4. For all solutions in pop calculate Spatial Spread Deviation/Crowding distance |
| 5. pop sorting due to fronts and Spatial Spread Deviation/CD 6. Main loop, until stopping condition is met *** Steady state approach: only one generated individual is considered to include in popc 7. Create popc using crossover operator *********************************************************************** 8. Create popm using mutation operator 9. Join popc and popm to create popj 10. Evaluate solutions in popj and put feasibles in popf 11. Add popf to pop, and calculate objective functions 12. Order pop using no-dominated sorting 13. Calculate Spatial Spread Deviation/Crowding distance 14. pop sorting due to the front ranking and Spatial Spread Deviation/CD 15. Truncate pop to keep a population of original size 16. No-dominated sorting 17. Calculate Spatial Spread Deviation/Crowding distance of the individuals in pop 18. pop sorting due to front ranking and Spatial Spread Deviation/CD 19. End Main loop 20. Return (Front 0). ***Approximated Pareto Front |
5. T-FAME Algorithm
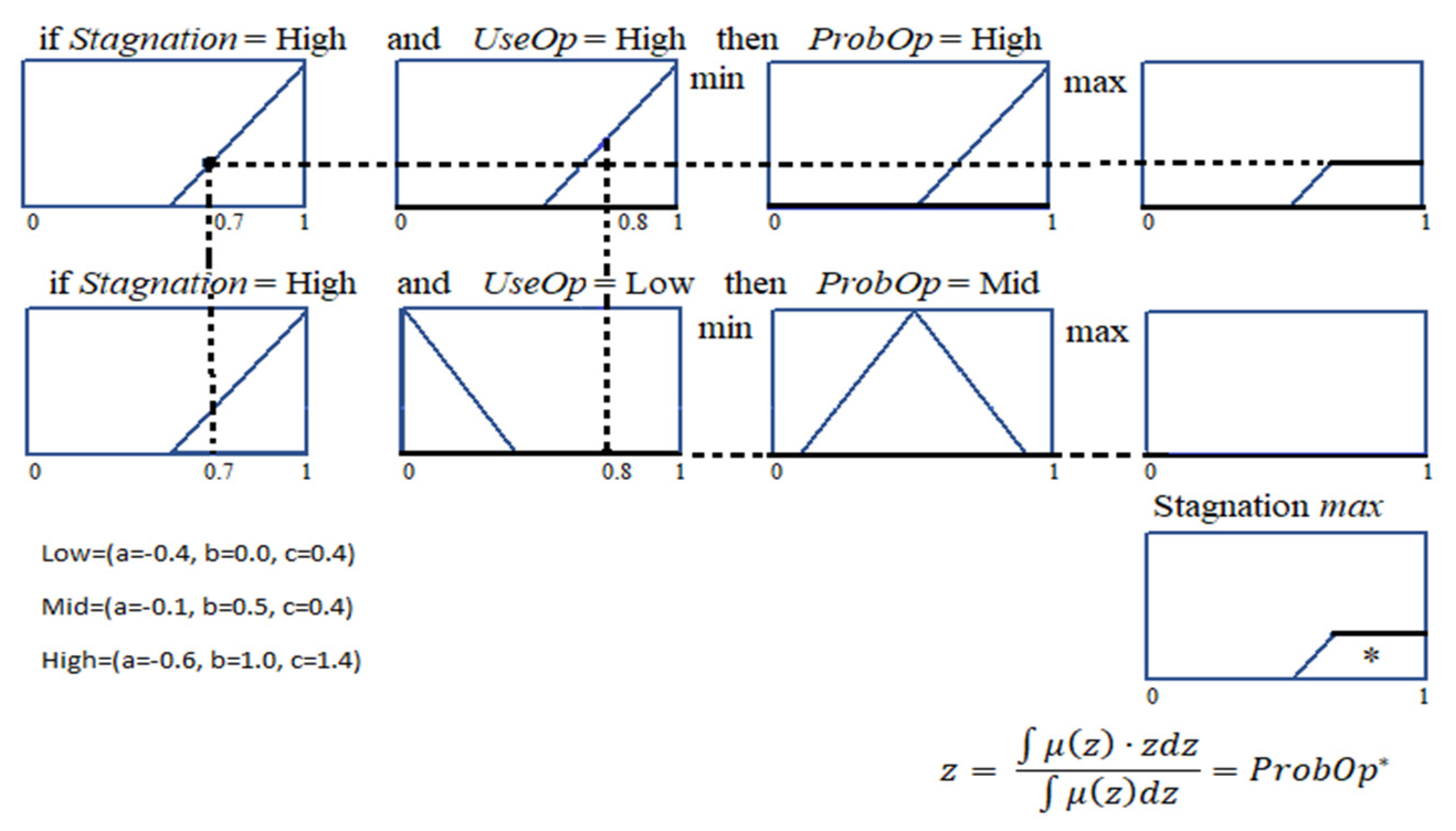
5.1. Fuzzy Controller
| Algorithm 4. Fuzzy controller structure. |
| [System] |
| Name=‘FuzzyController ‘ |
| Type=‘mamdani’ |
| Version=2.0 |
| NumInputs=2 |
| NumOutputs=1 |
| NumRules=9 |
| AndMethod=‘min’ |
| OrMethod=‘max’ |
| ImpMethod=‘min’ |
| AggMethod=‘max’ |
| DefuzzMethod=‘centroid’ |
| [Input1] |
| Name=‘Stagnation’ |
| Range=[0 1] |
| NumMFs=3 |
| MF1=‘Low’:’trimf’,[−0.4 0 0.4] |
| MF2=‘Mid’:’trimf’,[0.1 0.5 0.9] |
| MF3=‘High’:’trimf’,[0.6 1 1.4] |
| [Input2] |
| Name=‘UseOp’ |
| Range=[0 1] |
| NumMFs=3 |
| MF1=‘Low’:’trimf’,[−0.4 0 0.4] |
| MF2=‘Mid’:’trimf’,[0.1 0.5 0.9] |
| MF3=‘High’:’trimf’,[0.6 1 1.4] |
| [Output1] |
| Name=‘ProbOp’ |
| Range=[0 1] |
| NumMFs=3 |
| MF1=‘Low’:’trimf’,[−0.4 0 0.4] |
| MF2=‘Mid’:’trimf’,[0.1 0.5 0.9] |
| MF3=‘High’:’trimf’,[0.6 1 1.4] |
| [Rules] |
| 3 3, 2 (1) : 1 |
| 3 2, 1 (1) : 1 |
| 3 1, 2 (1) : 1 |
| 2 3, 2 (1) : 1 |
| 2 2, 1 (1) : 1 |
| 2 1, 2 (1) : 1 |
| 1 3, 3 (1) : 1 |
| 1 2, 2 (1) : 1 |
| 1 1, 1 (1) : 1 |
5.2. Additional Genetic Operators
5.3. Used Structures to Store the Population and the Approximated Pareto Front
- V(i): vector binary associated to the solution i.
- O1(i) and O2(i): values of the two objectives of the solution i, converted to GMI values.
- r(i): ranking of the solution i is the number of the front in which is located.
- Dominated(i): solutions dominated by the solution i.
- Domines(i): solutions that dominates to solution i.
- CD (i): Crowding Distance value of the solution i.
- SSD(i): Spatial Spread Deviation value of solution i.
- V(i): vector binary associated to the solution i.
- O(i): real vector of the graded mean values of the fuzzy triangular objectives of the solution V(i).
- r(i): ranking of the solution i is the number of the front in which is located.
- Dominated(i): solutions dominated by the solution i.
- Domines(i): solutions that dominates to solution i.
- SSD (i): Spatial Spread Deviation value of the solution i.
5.4. T-FAME Algorithm Pseudocode
| Algorithm 5. T-FAME pseudocode |
| INPUT: Instance with the trapezoidal parameters of the portfolio problem. OUTPUT: Approximated Pareto front Variables pop: Population of solutions (binary vectors) Front: Limited sized set were no-dominated solutions are kept Operator: Vector of size SizeOP that contains the index of the available operators Parents: Vector of size NParents that contains the chosen parents ProbOp(i): Probability that operator i has of being chosen, it has values between 0 and 1 UseOp(i): Normalized Indicator of how much operator i has been used, it has values between 0 and 1 Stagnation: Normalized indicator of the number of generated solutions that couldn’t be inserted into Front, because they were either dominated solutions or there was not space available for them, it can have values between 0 and 1. MAXEVAL: Maximum number of evaluations of the objective function (stopping criterion) Window: Size of the time window. eval: Accumulator of the evaluations of the objective function v: Counter of the time windows that have elapsed Functions |
| CreateaSon(Operator(i), Parents): Generates one solution using the previous chosen operator i with the chosen parents (Steady state) Evaluate(Son): Calculates the objective values of Son and verify feasibility FuzzyController(Stagnation, UseOp(i)): Function that invokes the fuzzy controller with Stagnation and UseOp(i) as input values and returns the probability of selection of all the operators no-dominated_sortingSSD(NewPop): Sorts the fronts of NewPop by dominance and uses as ranking the SSD values of the solutions. EliminateWorstSolutionSSD(NewPop): Eliminates from the last front of NewPop the solution with the worst SSD, and assign NewPop to pop. |
| **************************************************************** 1. Create(pop) **Create random population 2. Front=NoDominated(pop) **Insert in Front the no-dominated solutions of pop 3. 1, UseOp(i)=0 4. v =0; Stagnation = 0; eval=0; 5. while (eval<MAXEVAL) do. **** Stop condition ** Chose |NParents| ** With a probability each parent is taken from Front to intensify) and with 1- from pop to diversify. 6. do 7. if (RandomDouble(0,1) ) then **The parent is chosen from Front 8. Parents[i] ← TournamentSSD(Front) 9. Else **The parent is chosen from pop 10. Parents[i] ← TournamentSSD(pop) *** Roulette to choose an operator with the selection probabilities of the operators 11. sum=0 12. 13. sum=sum+ProbOp(i) 14. while (sum>0) do 15. 16. sum=sum+ProbOp(i) ********** ***** The chosen operator is associated with the last value of i ** ***Steady state approach 17. Son ← CreateaSon(Operator(i), Parents) **** Get the objective vector values corresponding to Son and verify feasibility. 18. Evaluate(Son) 19. eval=eval+1 20. UseOp(Operator(i)) = UseOp(Operator(i))+ 1 . 0/ Window 21. v=v+1 ******************************* 22. If (Son dominates a set S of solutions in Front) 23. then { Front=Front\S; Front=Front Son} 24. else If ( s Front such that s dominates Son) 25. then (Stagnation= Stagnation+1.0/ Window) 26. else if (Sizeof(Front)<100) 27. then (Front=Front Son) 28. else { 29. Front=Front Son ** Front[1 00]=Son 30. Calculate SSD for all the solutions in Front 31. Sort the solutions in Front in ascending order by SSD 32. Eliminate the solution in Front with worst SSD:Front[100] 33. If (Son Front) 34. then Stagnation= Stagnation+1.0/ Window 35. } 36. If (v == Window) then **** The Fuzzy Controller is used to update the selection probability ****of all the operators 37. 38. 39. v =0; Stagnation = 0; 40. End if 41. pop=pop Son 42. NewPop=pop 43. no-dominated_sortingSSD(NewPop) 44. pop ← EliminateWorstSolutionSSD(NewPop) 45. End while 46. Return(Front) *** Approximated Pareto front generated |
6. Experimental Results
6.1. Performance Metrics Used
6.2. Experimental Setup
6.3. Experiment 1. Validating the Implemented Algorithms
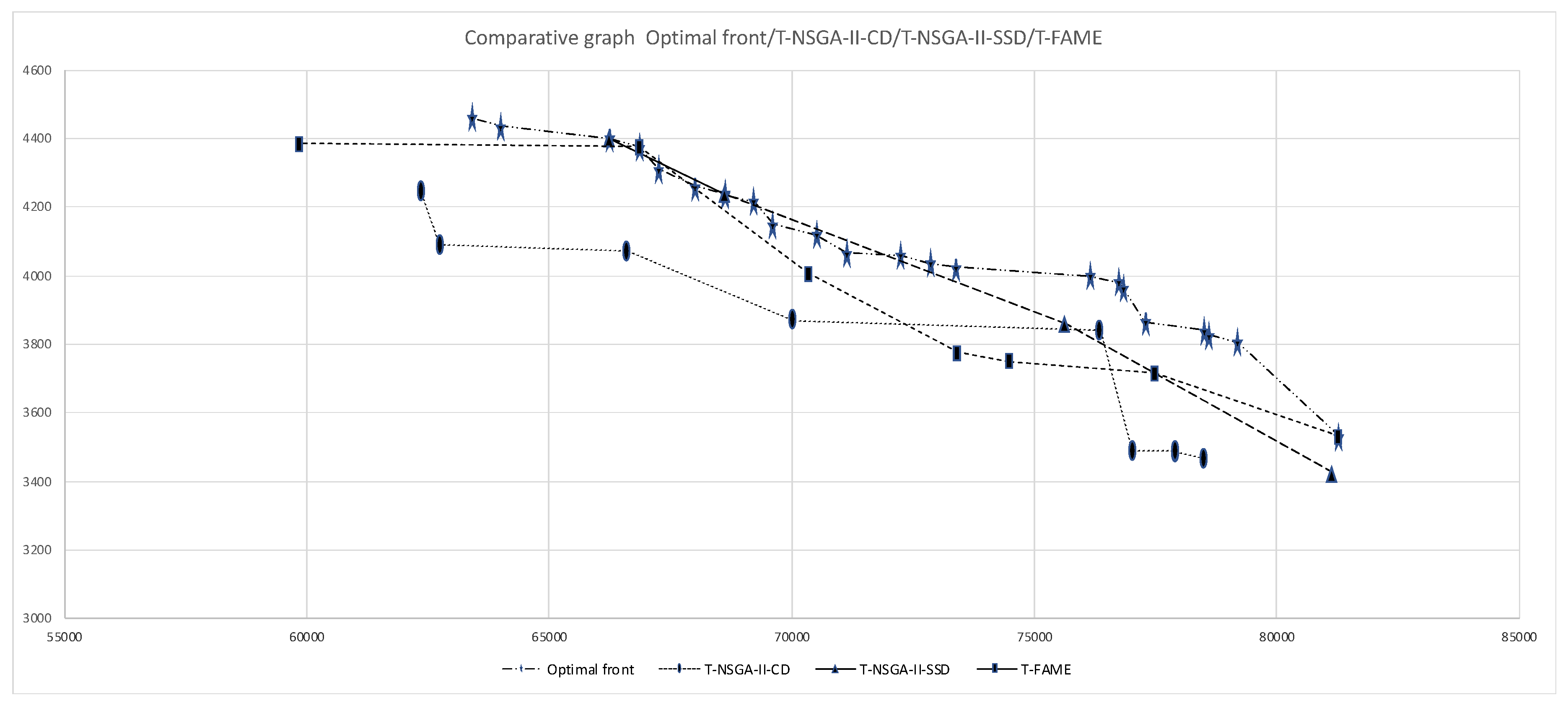
6.4. Experiment 2. Evaluating the Performance of the Algorithms with Instances of 25 Projects
6.5. Experiment 3. Evaluation of the Algorithm’ Perfomances Using Instances with 100 Projects
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Salo, A.; Keisler, J.; Morton, A. Portfolio Decision Analysis: Improved Methods for Resource Allocation; Springer: Berlin/Heidelberg, Germany, 2011; p. 409. [Google Scholar]
- Carlsson, C.; Fuller, R.; Heikkila, M.; Majlender, P. A fuzzy approach to R&D portfolio selection. Int. J. Approx. Reason. 2007, 44, 93–105. [Google Scholar]
- Coffin, M.A.; Taylor, B.W. Multiple criteria R&D project selection and scheduling using fuzzy sets. Comput. Oper. 1996, 23, 207–220. [Google Scholar]
- Klapka, J.; Pinos, P. Decision support system for multicriterial R&D and information systems projects selection. Eur. J. Oper. Res. 2002, 140, 434–446. [Google Scholar]
- Ringuest, J.L.; Graves, S.B.; Case, R.H. Mean–Gini analysis in R&D portfolio selection. Eur. J. Oper. Res. 2004, 154, 157–169. [Google Scholar]
- Stummer, C.; Heidemberger, K. Interactive R&D portfolio analysis with project interdependencies and time profiles of multiple objectives. IEEE Trans. Eng. Manag. 2003, 30, 175–183. [Google Scholar]
- Salo, A.; Keisler, J.; Morton, A. Portfolio Decision Analysis. Improved Methods for Resource Allocation, International Series in Operations Research & Management Science, Chapter An Invitation to Portfolio Decision Analysis; Springer: New York, NY, USA, 2011; pp. 3–27. [Google Scholar]
- Fernandez, E.; Lopez, E.; Lopez, F.; Coello, C. Increasing selective pressure toward the best compromise in Evolutionary Multiobjective Optimization: The extended NOSGA method. Inf. Sci. 2011, 181, 44–56. [Google Scholar] [CrossRef]
- Roy, B. Robustness for Operations Research and Decision Aiding; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Balderas, F.; Fernandez, E.; Gomez, C.; Rangel, N.; Cruz-Reyes, L. An interval-based approach for evolutionary multi-objective optimization of project portfolios. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 1317–1358. [Google Scholar] [CrossRef]
- García, R.R. Hiper-heurístico para Resolver el Problema de Cartera de Proyectos Sociales. Master’s Thesis, Maestro en Ciencias de la Computación, Instituto Tecnológico de Ciudad Madero, Tamps, Mexico, 2010. [Google Scholar]
- Rivera, Z.G. Enfoque Metaheurístico Híbrido para el Manejo de Muchos Objetivos en Optimización de Cartera de Proyectos Interdependientes con Decisiones de Apoyo Parcial. Ph.D. Thesis, Doctorado en Ciencias de la Computación, Instituto Tecnológico de Tijuana, Tamps, Mexico, 2015. [Google Scholar]
- Bastiani, M.S. Solución de Problemas de Cartera de Proyectos Públicos a partir de Información de Ranking de Prioridades. Ph.D. Thesis, Doctorado en Ciencias de la Computación, Instituto Tecnológico de Tijuana, Tamps, Mexico, 2017. [Google Scholar]
- Sánchez, S.P. Incorporación de Preferencias en Metaheurísticas Evolutivas a través de Clasificación Multicriterio. Ph.D. Thesis, Doctorado en Ciencias de la Computación, Instituto Tecnológico de Tijuana, Tamps, Mexico, 2017. [Google Scholar]
- Martínez, V.D. Optimización Multiobjetivo de Cartera de Proyectos con Fenómenos de Dependencias Temporales y Decisiones Dinámicas de Financiamiento. Ph.D. Thesis, Doctorado en Ciencias de la Computación, Instituto Tecnológico de Tijuana, Tamps, Mexico, 2020. [Google Scholar]
- Durillo, J.J.; Nebro, A.J.; Luna, F.; Alba, E. On the Effect of the Steady-State Selection Scheme in Multi-Objective Genetic Algorithms. In Evolutionary Multi-Criterion Optimization. EMO 2009. Lecture Notes in Computer Science; Ehrgott, M., Fonseca, C.M., Gandibleux, X., Hao, J.K., Sevaux, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; p. 5467. [Google Scholar]
- Zadeth, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Vahidi, J.; Rezvani, S. Arithmetic Operations on Trapezoidal Fuzzy Numbers. J. Nonlinear Anal. Appl. 2013, 2013, 1–8. [Google Scholar] [CrossRef][Green Version]
- Kumar, V. Multi-Objective Fuzzy Optimization; Indian Institute of Technology: Kharagpur, India, 2010. [Google Scholar]
- Yao, S.; Jiang, Z.; Li, N.; Zhang, H.; Geng, N. A multi-objective dynamic scheduling approach using multiple attribute decision making in semiconductor manufacturing. Int. J. Prod. Econ. 2011, 130, 125–133. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility Among Combinatorial Problems. Complex. Comput. Comput. 1972, 85–103. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-I. In Proceedings of the Proceedings of the Parallel Problem Solving from Nature VI, Paris, France, 18–20 September 2000; pp. 849–858. [Google Scholar]
- Umbarkar, A.J.; Sheth, P.D. Crossover operators in genetic algorithms: A review. ICTAC J. Soft Comput. 2015, 6, 1083–1092. [Google Scholar]
- Reeves, C.R. Genetic Algorithms. In International Series in Operations Research & Management Science, Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; p. 146. [Google Scholar]
- Santiago, A.; Dorronsoro, B.; Nebro, A.J.; Durillo, J.J.; Castillo, O.; Fraire, H.J. A novel multi-objective evolutionary algorithm with fuzzy logic based adaptive selection of operators: FAME. Inf. Sci. 2019, 471, 233–251. [Google Scholar] [CrossRef]
- Roy, S.; Chakraborty, U. Introduction to Soft Computing: Neurofuzzy and Genetic Algorithms; Dorling-Kindersley: London, UK, 2013. [Google Scholar]
- Rainer, S.; Kenneth, P. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar]
- While, V.; Member, S.; Bradstreet, L.; Barone, V. A Fast Way of Calculating Exact Hypers. IEEE Trans. Evol. Comput. 2012, 16, 86–95. [Google Scholar] [CrossRef]
- Zhou, A.; Jin, Y.; Zhang, Q.; Sendhoff, B.; Tsang, E. Combining Model-based and Genetics-based Offspring Generation for Multi-objective Optimization Using a Convergence Criterion. IEEE Congr. Evol. Comput. 2006, 892–899. [Google Scholar] [CrossRef]


| Work | Algorithm | Instances | Metrics | Preferences | E/D | Parameters | Steady State |
|---|---|---|---|---|---|---|---|
| [11] Social projects | HHGA-SPPv1 HHGA-SPPv2 | (3,4,20) (3,9,100) | No-dominated Solutions | Yes | E | Real | NA |
| [12] Interdependent social projects, several objectives | NO-ACO | (10,4,25) (10,9,100) | No-dominated Solutions, ROI solutions | Yes | E | Real | NA |
| [13] Social projects with priorities and sinergy | ACO-SPRI ACO-SOP ACO-SOP sinergy | (1,ND,25) (1,ND,40) (1,ND,100) | No-dominated Solutions | Yes | E | Real | NA |
| [14] Social projects, several objectives | H-MCSGA I-MCSGA | (3,9,100) (2,9,150) (1,16,500) | No-dominated solutions, higher net flow | Yes | E | Real | No |
| [10] Portfolio selection with interval parameters | I-NSGA-II-CD | (1,2,100) (1,9,100) | Cardinality | Yes | E | Intervals | No |
| [15] Dynamic portfolio selection and several objectives | D-NSGA-II-FF AbYSS-FF D-MOEA\D--FF | (30,2,100) (30,3,100) (30,9,100) | Hypervolume modified, Spread modified, inverted generational distance modified | Yes | D | Real | No |
| This work Portfolio selection with trapezoidal fuzzy numbers | T-NSGA-II-CD T-NSGA-II-SSD T-FAME | (12,2,25) (9,2,100) | Hypervolume, Generalized Spread | No | E | Trapezoidal fuzzy numbers | Yes |
| AND Antecedents | Consequent | |
|---|---|---|
| Stagnation | Utilization | ProbOp |
| High | High | Mid |
| High | Mid | Low |
| High | Low | Mid |
| Mid | High | Mid |
| Mid | Mid | Low |
| Mid | Low | Mid |
| Low | High | High |
| Low | Mid | Mid |
| Low | Low | Low |
| Parameter | Value |
|---|---|
| Evaluation of the objective function | 5000 |
| Population Size | 50 |
| Crossover population % | 70 |
| Mutation population % | 40 |
| Mutation % | 5 |
| Parameter | Value |
|---|---|
| Evaluation of the objective function | 5000 |
| Population Size | 25 |
| Front Size | 100 |
| Tournament Size | 5 |
| Number of parents | 4 |
| Window Size | 13 |
| Differential Evolution Crossover % | 10 |
| Number of mutations in FM | 2 |
| Front choice probability ( | 0.9 |
| Pareto Optimal Front | T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME | |||
|---|---|---|---|---|---|---|
| O2 | O1 | O2 | O1 | O2 | O1 | O2 |
| 3530 | 78,510 | 3465 | 81,155 | 3425 | 81,285 | 3530 |
| 3805 | 62,350 | 4245 | 66,240 | 4400 | 77,480 | 3715 |
| 3825 | 76,360 | 3840 | 75,650 | 3860 | 74,485 | 3750 |
| 3840 | 70,035 | 3870 | 68,610 | 4240 | 73,425 | 3775 |
| 3865 | 77,020 | 3490 | 70,350 | 4005 | ||
| 3965 | 66,605 | 4070 | 66,850 | 4375 | ||
| 3980 | 62,755 | 4090 | 59,865 | 4385 | ||
| 4000 | 77,900 | 3490 | ||||
| 4025 | 77,920 | 3485 | ||||
| 4035 | ||||||
| 4060 | ||||||
| 4065 | ||||||
| 4120 | ||||||
| 4150 | ||||||
| 4215 | ||||||
| 4235 | ||||||
| 4240 | ||||||
| 4260 | ||||||
| 4310 | ||||||
| 4375 | ||||||
| 4400 | ||||||
| 4435 | ||||||
| 4460 | ||||||
| T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Instance | Statistic | p-Value | R | Statistic | p-Value | R | Statistic | p-Value | R | Tests |
| o2p25_0T | 0.9429 | 0.1089 | a | 0.83756 | 0.00034 | r | 0.96919 | 0.51737 | a | t,W |
| o2p25_1T | 0.93655 | 0.07348 | a | 0.92817 | 0.04391 | r | 0.97408 | 0.65561 | a | t,W |
| o2p25_2T | 0.92141 | 0.02918 | r | 0.95491 | 0.22837 | a | 0.96987 | 0.53551 | a | W,t |
| o2p25_3T | 0.94311 | 0.11035 | a | 0.90566 | 0.01159 | r | 0.94528 | 0.12625 | a | t,W |
| o2p25_4T | 0.95413 | 0.21782 | a | 0.93505 | 0.06696 | a | 0.89022 | 0.00488 | r | W,W |
| o2p25_5T | 0.86113 | 0.00107 | r | 0.89584 | 0.00665 | r | 0.94768 | 0.14643 | a | W,W |
| o2p25_6T | 0.9023 | 0.00956 | r | 0.89233 | 0.00548 | r | 0.96519 | 0.41715 | a | W,W |
| o2p25_7T | 0.94961 | 0.16508 | a | 0.86559 | 0.00134 | r | 0.92644 | 0.03953 | r | W,W |
| o2p25_8T | 0.92385 | 0.0338 | r | 0.91474 | 0.01963 | r | 0.85737 | 0.00089 | r | W,W |
| o2p25_9T | 0.94965 | 0.16541 | a | 0.89673 | 0.00699 | r | 0.97209 | 0.59792 | a | t,W |
| o2p25_10T | 0.92989 | 0.04877 | r | 0.78913 | 0.00004 | r | 0.97575 | 0.70469 | a | W,W |
| o2p25_11T | 0.93191 | 0.05518 | a | 0.95357 | 0.21047 | a | 0.96642 | 0.44633 | a | t,t |
| o2p25_12T | 0.94626 | 0.13411 | a | 0.95055 | 0.17491 | a | 0.98323 | 0.9033 | a | t,t |
| o2p100_1T | 0.96346 | 0.37847 | a | 0.96637 | 0.44525 | a | 0.98333 | 0.90552 | a | t,t |
| o2p100_2T | 0.95885 | 0.28944 | a | 0.98951 | 0.98844 | a | 0.9737 | 0.64441 | a | t,t |
| o2p100_3T | 0.93272 | 0.05801 | a | 0.9821 | 0.87827 | a | 0.94779 | 0.14745 | a | t,t |
| o2p100_4T | 0.78768 | 0.00004 | r | 0.78085 | 0.00003 | r | 0.89022 | 0.00488 | r | W,W |
| o2p100_5T | 0.95289 | 0.20189 | a | 0.94588 | 0.13101 | a | 0.93478 | 0.06586 | a | t,t |
| o2p100_6T | 0.94043 | 0.09341 | a | 0.93788 | 0.07976 | a | 0.95224 | 0.194 | a | t,t |
| o2p100_7T | 0.97249 | 0.60937 | a | 0.99025 | 0.99229 | a | 0.94017 | 0.0919 | a | t,t |
| o2p100_8T | 0.96892 | 0.51019 | a | 0.98362 | 0.9115 | a | 0.96805 | 0.48728 | a | t,t |
| o2p100_9T | 0.57553 | 0 | r | 0.52513 | 0 | r | 0.71502 | 0 | r | W,W |
| Instance | Statistic | p-Value | R |
|---|---|---|---|
| o2p25_0T | 8.46563 | 0.00044 | a |
| o2p25_1T | 17.23159 | 0 | a |
| o2p25_2T | 8.53517 | 0.00041 | a |
| o2p25_3T | 11.87763 | 0.00003 | a |
| o2p25_4T | 7.1698 | 0.00131 | a |
| o2p25_5T | 7.60431 | 0.0009 | a |
| o2p25_6T | 7.19194 | 0.00129 | a |
| o2p25_7T | 2.20562 | 0.11631 | a |
| o2p25_8T | 8.18222 | 0.00055 | a |
| o2p25_9T | 4.45024 | 0.01445 | a |
| o2p25_10T | 3.63843 | 0.03037 | a |
| o2p25_11T | 3.98587 | 0.02207 | a |
| o2p25_12T | 9.90574 | 0.00013 | a |
| o2p100_1T | 0.27401 | 0.76098 | a |
| o2p100_2T | 2.14347 | 0.1234 | a |
| o2p100_3T | 0.29369 | 0.74624 | a |
| o2p100_4T | 1.79147 | 0.17281 | a |
| o2p100_5T | 5.98972 | 0.00365 | a |
| o2p100_6T | 1.09354 | 0.33959 | a |
| o2p100_7T | 2.30064 | 0.10626 | a |
| o2p100_8T | 4.20117 | 0.01812 | a |
| o2p100_9T | 1.39539 | 0.25322 | A |
| T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Instance | Statistic | p-Value | R | Statistic | p-Value | R | Statistic | p-Value | R | Tests |
| o2p25_0T | 0.92895 | 0.04606 | r | 0.97607 | 0.71429 | a | 0.9784 | 0.78164 | a | W,t |
| o2p25_1T | 0.98376 | 0.91432 | a | 0.95618 | 0.24658 | a | 0.97193 | 0.59314 | a | t,t |
| o2p25_2T | 0.98074 | 0.84479 | a | 0.97925 | 0.8053 | a | 0.96813 | 0.48946 | a | t,t |
| o2p25_3T | 0.9215 | 0.02934 | r | 0.9225 | 0.03116 | r | 0.96419 | 0.39452 | a | W,W |
| o2p25_4T | 0.95187 | 0.18969 | a | 0.96214 | 0.35091 | a | 0.68255 | 0 | r | W,W |
| o2p25_5T | 0.96913 | 0.51555 | a | 0.95677 | 0.25552 | a | 0.92403 | 0.03416 | r | W,W |
| o2p25_6T | 0.87495 | 0.00216 | r | 0.97296 | 0.62306 | a | 0.958 | 0.27513 | a | W,t |
| o2p25_7T | 0.94053 | 0.094 | a | 0.95631 | 0.24864 | a | 0.94784 | 0.14792 | a | t,t |
| o2p25_8T | 0.9648 | 0.40819 | a | 0.95561 | 0.23827 | a | 0.94282 | 0.10833 | a | t,t |
| o2p25_9T | 0.97001 | 0.53934 | a | 0.97168 | 0.58607 | a | 0.9686 | 0.50171 | a | t,t |
| o2p25_10T | 0.92765 | 0.04254 | r | 0.96999 | 0.53902 | a | 0.97623 | 0.71907 | a | W,t |
| o2p25_11T | 0.91446 | 0.01932 | r | 0.96986 | 0.53537 | a | 0.95816 | 0.27785 | a | W,t |
| o2p25_12T | 0.95492 | 0.22856 | a | 0.98402 | 0.91939 | a | 0.95432 | 0.22029 | a | t,t |
| o2p100_1T | 0.92495 | 0.03611 | r | 0.92054 | 0.02771 | r | 0.94295 | 0.10926 | a | W,W |
| o2p100_2T | 0.9812 | 0.85642 | a | 0.95454 | 0.22326 | a | 0.95353 | 0.21003 | a | t,t |
| o2p100_3T | 0.92278 | 0.03169 | r | 0.86033 | 0.00103 | r | 0.96482 | 0.40857 | a | W,W |
| o2p100_4T | 0.65395 | 0 | r | 0.79925 | 0.00006 | r | 0.68255 | 0 | r | W,W |
| o2p100_5T | 0.91266 | 0.01738 | r | 0.86347 | 0.0012 | r | 0.96541 | 0.4223 | a | W,W |
| o2p100_6T | 0.90797 | 0.01323 | r | 0.91912 | 0.02544 | r | 0.90857 | 0.01369 | r | W,W |
| o2p100_7T | 0.89328 | 0.00578 | r | 0.89889 | 0.00789 | r | 0.96516 | 0.41655 | a | W,W |
| o2p100_8T | 0.94824 | 0.15169 | a | 0.96578 | 0.43096 | a | 0.96071 | 0.32297 | a | t,t |
| o2p100_9T | 0.49141 | 0 | r | 0.68971 | 0 | r | 0.68313 | 0 | r | W,W |
| Instance | Statistic | p-Value | R |
|---|---|---|---|
| o2p25_0T | 0.33509 | 0.71619 | a |
| o2p25_1T | 3.11548 | 0.04934 | a |
| o2p25_2T | 5.44373 | 0.00592 | a |
| o2p25_3T | 7.81001 | 0.00076 | a |
| o2p25_4T | 0.38001 | 0.68498 | a |
| o2p25_5T | 3.01271 | 0.05431 | a |
| o2p25_6T | 1.58378 | 0.21106 | a |
| o2p25_7T | 10.87966 | 0.00006 | a |
| o2p25_8T | 1.51668 | 0.22518 | a |
| o2p25_9T | 19.54345 | 0 | a |
| o2p25_10T | 5.78604 | 0.00437 | a |
| o2p25_11T | 7.0285 | 0.00148 | a |
| o2p25_12T | 15.29209 | 0 | a |
| o2p100_1T | 8.48884 | 0.00043 | a |
| o2p100_2T | 9.53401 | 0.00018 | a |
| o2p100_3T | 3.46674 | 0.0356 | a |
| o2p100_4T | 1.42075 | 0.24708 | a |
| o2p100_5T | 3.96176 | 0.02256 | a |
| o2p100_6T | 4.19408 | 0.01824 | a |
| o2p100_7T | 4.62372 | 0.01235 | a |
| o2p100_8T | 5.30008 | 0.00673 | a |
| o2p100_9T | 0.90643 | 0.40774 | a |
| Hypervolume | |||
|---|---|---|---|
| Instance | T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME |
| o2p25_0T | 0.47470.0858⋁* | 0.31830.3853⋁ | 0.20240.2491 |
| o2p25_1T | 0.38070.0510⋁* | 0.24600.2325⋁ | 0.20030.2876 |
| o2p25_2T | 0.35910.0614⋁ | 0.24670.2042⋁* | 0.16130.1526 |
| o2p25_3T | 0.28320.0549⋁* | 0.27700.2311⋁ | 0.13450.1646 |
| o2p25_4T | 0.35100.0812⋁ | 0.28360.1489⋁ | 0.18750.1673 |
| o2p25_5T | 0.26350.0383⋁ | 0.15290.1495⋁ | 0.10700.1048 |
| o2p25_6T | 0.37970.0609⋁ | 0.24650.1870⋁ | 0.13800.2060 |
| o2p25_7T | 0.23480.2446⋁ | 0.28160.3644⋁ | 0.14270.1694 |
| o2p25_8T | 0.25740.0664⋁ | 0.18380.2259⋁ | 0.16300.1747 |
| o2p25_9T | 0.40260.1184⋁* | 0.24490.2455⋁ | 0.15390.1615 |
| o2p25_10T | 0.25800.0710⋁ | 0.14510.1566⋁ | 0.11260.1070 |
| o2p25_11T | 0.39180.0946⋁* | 0.23270.1687=* | 0.18760.1657 |
| o2p25_12T | 0.29340.0708⋁* | 0.26210.2174=* | 0.23520.1969 |
| Generalized Spread | |||
|---|---|---|---|
| Instance | T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME |
| o2p25_0T | 0.61780.1985⋀ | 0.41900.1534 = * | 0.41540.2064 |
| o2p25_1T | 0.73440.1685⋀* | 0.44770.1289 = * | 0.46610.1128 |
| o2p25_2T | 0.60650.2078⋀* | 0.39290.1025 = * | 0.39830.1047 |
| o2p25_3T | 0.72760.2387⋀ | 0.51810.1370 = | 0.52250.0790 |
| o2p25_4T | 0.64750.3031⋀ | 0.46460.1432⋁ | 0.55110.1078 |
| o2p25_5T | 0.72280.1715⋀ | 0.42040.0925⋀ | 0.41680.1293 |
| o2p25_6T | 0.62580.1539⋀ | 0.40260.0982⋁* | 0.46290.1703 |
| o2p25_7T | 0.83140.5343⋀* | 0.49950.2457⋁* | 0.58330.2388 |
| o2p25_8T | 0.75460.1739⋀* | 0.46930.1447 = * | 0.46460.1059 |
| o2p25_9T | 0.65340.3432⋀* | 0.48250.1435 = * | 0.47260.0690 |
| o2p25_10T | 0.65420.2697⋀ | 0.47930.1031 = * | 0.47790.0891 |
| o2p25_11T | 0.65400.3103⋀ | 0.43690.1073 = * | 0.47840.1629 |
| o2p25_12T | 070790.2465⋀* | 0.46840.0953 = * | 0.46540.0793 |
| Hypervolume (p-Value = 5.68 × 10−6) | Generalized Spread (p-Value = 5.71 × 10−5) | ||
|---|---|---|---|
| Algorithm | Ranking | Algorithm | Ranking |
| T-NSGA-II-CD | 14 | T-NSGA-II-SSD | 19 |
| T-NSGA-II-SSD | 25 | T-FAME | 20 |
| T-FAME | 39 | T-NSGA-II-CD | 39 |
| Hypervolume | |||
|---|---|---|---|
| Instance | T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME |
| o2p100_1T | 0.46810.1948⋀* | 0.50640.1804⋀* | 0.62140.2130 |
| o2p100_2T | 0.40940.1613⋀* | 0.54750.2357=* | 0.51070.2107 |
| o2p100_3T | 0.55240.2781=* | 0.63660.3261=* | 0.59470.2887 |
| o2p100_4T | 0.77380.3543⋀ | 0.92610.5476⋀ | 0.93950.4006 |
| o2p100_5T | 0.28930.1453⋀* | 0.35190.2193⋀* | 0.46110.2668 |
| o2p100_6T | 0.53590.3131=* | 0.54220.4082=* | 0.61630.5234 |
| o2p100_7T | 0.27130.1066⋀* | 0.34770.1816⋀* | 0.48960.2093 |
| o2p100_8T | 0.35500.1282=* | 0.51730.2759⋁* | 0.38940.2611 |
| o2p100_9T | 0.91420.3142⋀ | 10.1428⋁ | 10.0285 |
| Generalized Spread | |||
|---|---|---|---|
| Instance | T-NSGA-II-CD | T-NSGA-II-SSD | T-FAME |
| o2p100_1T | 0.52090.3128⋀ | 0.32100.1922⋀ | 0.30390.1152 |
| o2p100_2T | 0.53600.2984⋀* | 0.31050.1349⋁* | 0.39950.2272 |
| o2p100_3T | 0.48490.1753⋀ | 0.37910.1171⋀ | 0.37770.2171 |
| o2p100_4T | 0.28280.0915⋀ | 0.25550.0661⋁ | 0.26510.0746 |
| o2p100_5T | 0.60080.2320⋀ | 0.37960.2193⋀ | 0.29770.1051 |
| o2p100_6T | 0.37290.2967⋀ | 0.34570.1845⋀ | 0.28760.1838 |
| o2p100_7T | 0.50560.2843⋀ | 0.32210.1803⋀ | 0.31850.1463 |
| o2p100_8T | 0.54240.2142⋀* | 0.31540.1280⋁* | 0.33380.1274 |
| o2p100_9T | 0.40840.0670⋀ | 0.36810.0604= | 0.37180.0489 |
| Hypervolume (p-Value = 0.00104) | Generalized Spread (p-Value = 0.00113) | ||
|---|---|---|---|
| Algorithm | Ranking | Algorithm | Ranking |
| T-FAME | 12.5 | T-FAME | 13 |
| T-NSGA-II-SSD | 14.5 | T-NSGA-II-SSD | 14 |
| T-NSGA-II-CD | 27 | T-NSGA-II-CD | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrada-Padilla, A.; Lopez-Garcia, D.; Gómez-Santillán, C.; Fraire-Huacuja, H.J.; Cruz-Reyes, L.; Rangel-Valdez, N.; Morales-Rodríguez, M.L. Modeling and Optimizing the Multi-Objective Portfolio Optimization Problem with Trapezoidal Fuzzy Parameters. Math. Comput. Appl. 2021, 26, 36. https://doi.org/10.3390/mca26020036
Estrada-Padilla A, Lopez-Garcia D, Gómez-Santillán C, Fraire-Huacuja HJ, Cruz-Reyes L, Rangel-Valdez N, Morales-Rodríguez ML. Modeling and Optimizing the Multi-Objective Portfolio Optimization Problem with Trapezoidal Fuzzy Parameters. Mathematical and Computational Applications. 2021; 26(2):36. https://doi.org/10.3390/mca26020036
Chicago/Turabian StyleEstrada-Padilla, Alejandro, Daniela Lopez-Garcia, Claudia Gómez-Santillán, Héctor Joaquín Fraire-Huacuja, Laura Cruz-Reyes, Nelson Rangel-Valdez, and María Lucila Morales-Rodríguez. 2021. "Modeling and Optimizing the Multi-Objective Portfolio Optimization Problem with Trapezoidal Fuzzy Parameters" Mathematical and Computational Applications 26, no. 2: 36. https://doi.org/10.3390/mca26020036
APA StyleEstrada-Padilla, A., Lopez-Garcia, D., Gómez-Santillán, C., Fraire-Huacuja, H. J., Cruz-Reyes, L., Rangel-Valdez, N., & Morales-Rodríguez, M. L. (2021). Modeling and Optimizing the Multi-Objective Portfolio Optimization Problem with Trapezoidal Fuzzy Parameters. Mathematical and Computational Applications, 26(2), 36. https://doi.org/10.3390/mca26020036








