Derivative-Free Multiobjective Trust Region Descent Method Using Radial Basis Function Surrogate Models
Abstract
1. Introduction
- In [29], a trust region method using Newton steps for functions with positive definite Hessians on an open domain is proposed.
- In [30], quadratic Taylor polynomials are used to compute the steepest descent direction which is used in a backtracking manner to find solutions for unconstrained problems.
- In [33], quadratic Lagrange polynomials are used and the Pascoletti–Serafini scalarization is employed for the descent step calculation.
2. Optimality and Criticality in Multiobjective Optimization
- for all .
- The function is continuous.
- The following statements are equivalent:
- (a)
- The point isnotcritical.
- (b)
- .
- (c)
- .
3. Trust Region Ideas
4. Surrogate Models and the Final Algorithm
4.1. Fully Linear Models
- There are positive constants and such that for any given and for any there is a model function with Lipschitz continuous gradient and corresponding Lipschitz constant bounded by and such that
- the error between the gradient of the model and the gradient of the function satisfies
- the error between the model and the function satisfies
- For this class there exists “model-improvement” algorithm that, in a finite, uniformly bounded (w.r.t. and Δ) number of steps, can:
- either establish that a given model is fully linear on , i.e., it satisfies the error bounds in 1,
- or find a model that is fully linear on .
Algorithm Modifications
- “Relaxing” the (finite) surrogate construction process to try for a possible descent even if the surrogates are not fully linear.
- A criticality test depending on . If this value is very small at the current iterate, then could lie near a Pareto critical point. With the criticality test and Algorithm 1 we ensure that the next model is fully linear and the trust region is not too large. This allows for a more accurate criticality measure and descent step calculation.
- A trust region update that also takes into consideration . The radius should be enlarged if we have a large acceptance ratio and the is small as measured against for a constant .
| Algorithm 1: Criticality Routine. |
 |
- …successful if . The set of successful indices is . The trial point is accepted and the trust region radius can be increased.
- …model-improving if and the models are not fully linear. In these iterations the trial point is rejected and the trust region radius is not changed.
- …acceptable if and the models are fully linear. If , then there are no acceptable indices. The trial point is accepted but the trust region radius is decreased.
- …inacceptable otherwise, i.e., if and are fully linear. The trial point is rejected and the radius decreased.
| Algorithm 2: General Trust Region Method (TRM) for (MOP). |
 |
4.2. Fully Linear Lagrange Polynomials
4.3. Fully Linear Radial Basis Function Models
5. Descent Steps
5.1. Pareto–Cauchy Step
5.2. Modified Pareto–Cauchy Point via Backtracking
- A as in (14) exists.
- There is a constant such that the modified Pareto–Cauchy step satisfies
- 1
- The strict modified Pareto–Cauchy point exists, the backtracking is finite.
- 2
- There is a constant such that
5.3. Sufficient Decrease for the Original Problem
6. Convergence
6.1. Preliminary Assumptions and Definitions
6.2. Convergence Proof
- Because of Assumptions 1 and 6 and Theorem 2 is Cauchy-continuous and with (25) the first term goes to zero.
- Due to Corollary 5 the second term is in and goes to zero.
- Suppose the third term does not go to zero as well, i.e., is bounded below by a positive constant. Due to Assumptions 1 and 7 the iterates are not Pareto critical for (MOPm) and because of and Lemma 10 there would be a successful iteration, a contradiction. Thus the third term must go to zero as well.
7. Numerical Examples
7.1. Implementation Details
- We have an upper bound on the maximum number of iterations and an upper bound on the number of expensive objective evaluations.
- The surrogate criticality naturally allows for a stopping test and due to Lemma 11 the trust region radius can also be used (see also [33] [Sec. 5]). We combine this with a relative tolerance test and stop if
- At a truly critical point the criticality loop Algorithm 1 runs infinitely. We stop after a maximum number of iterations.
- We also employ the common relative stopping criteriato provoke early stopping.
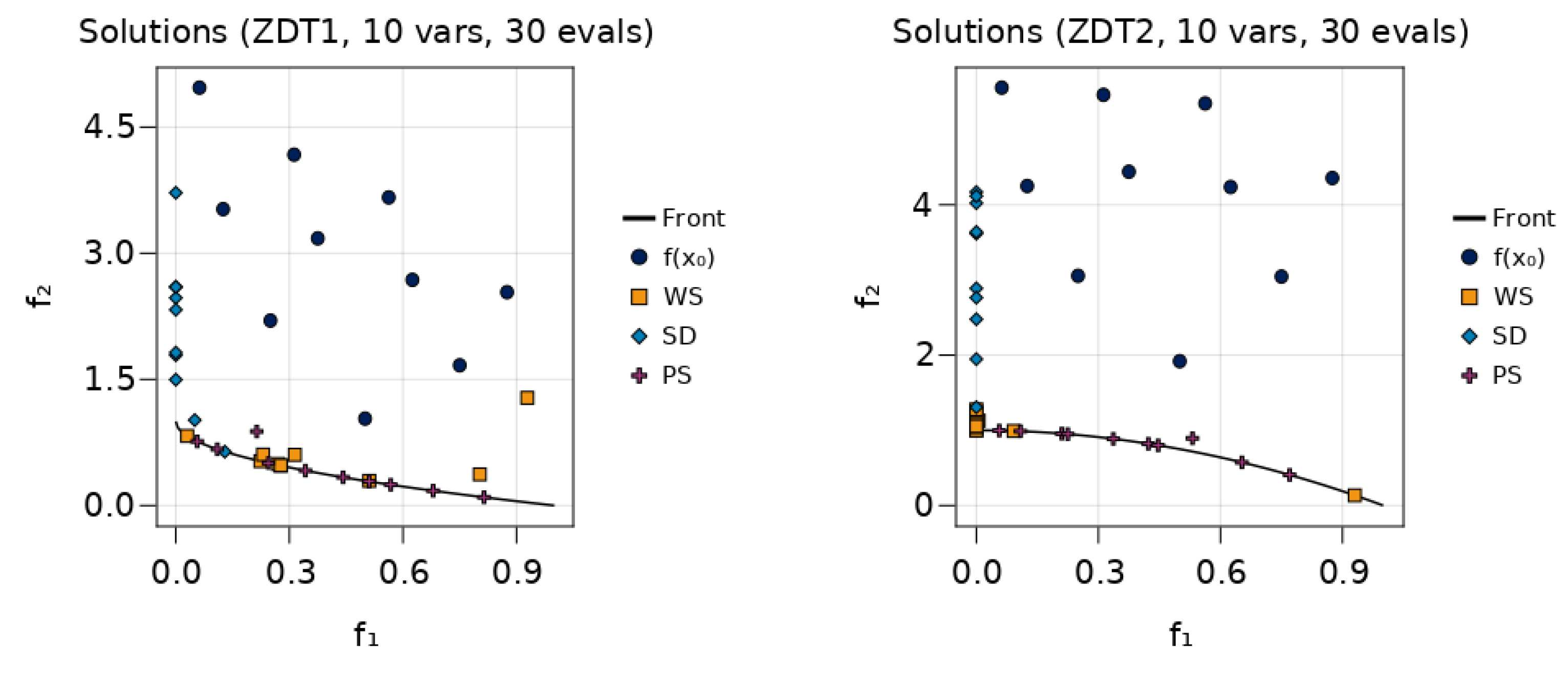
7.2. A First Example
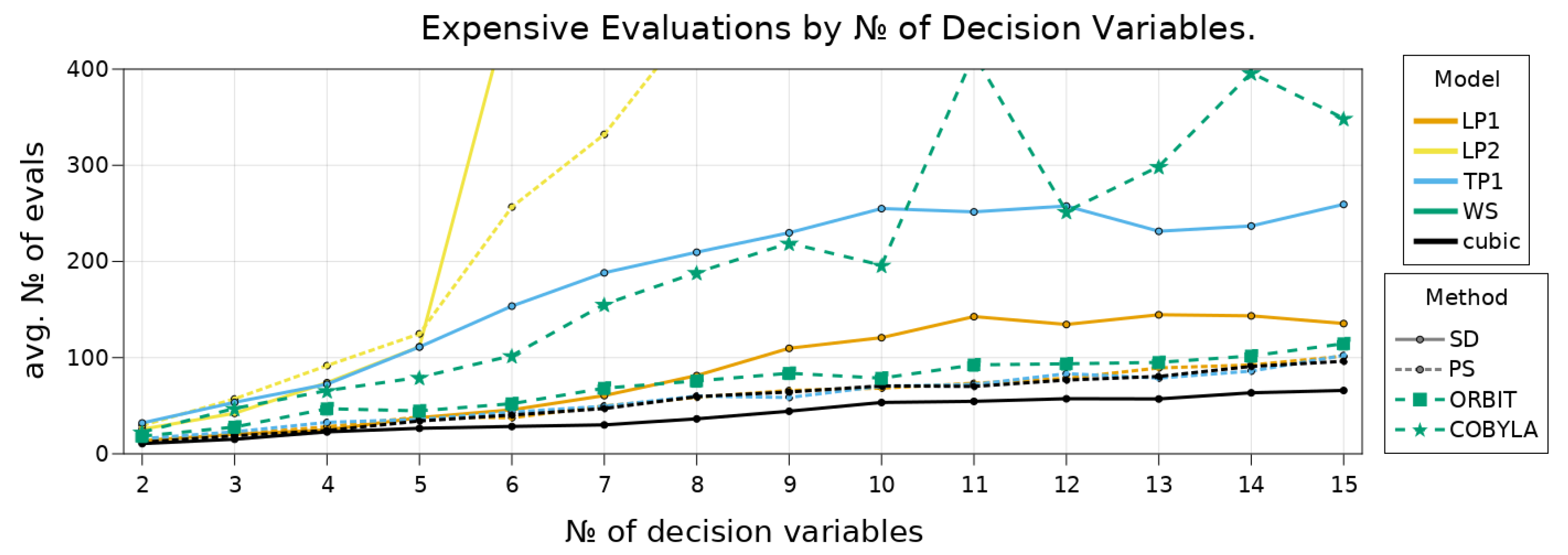
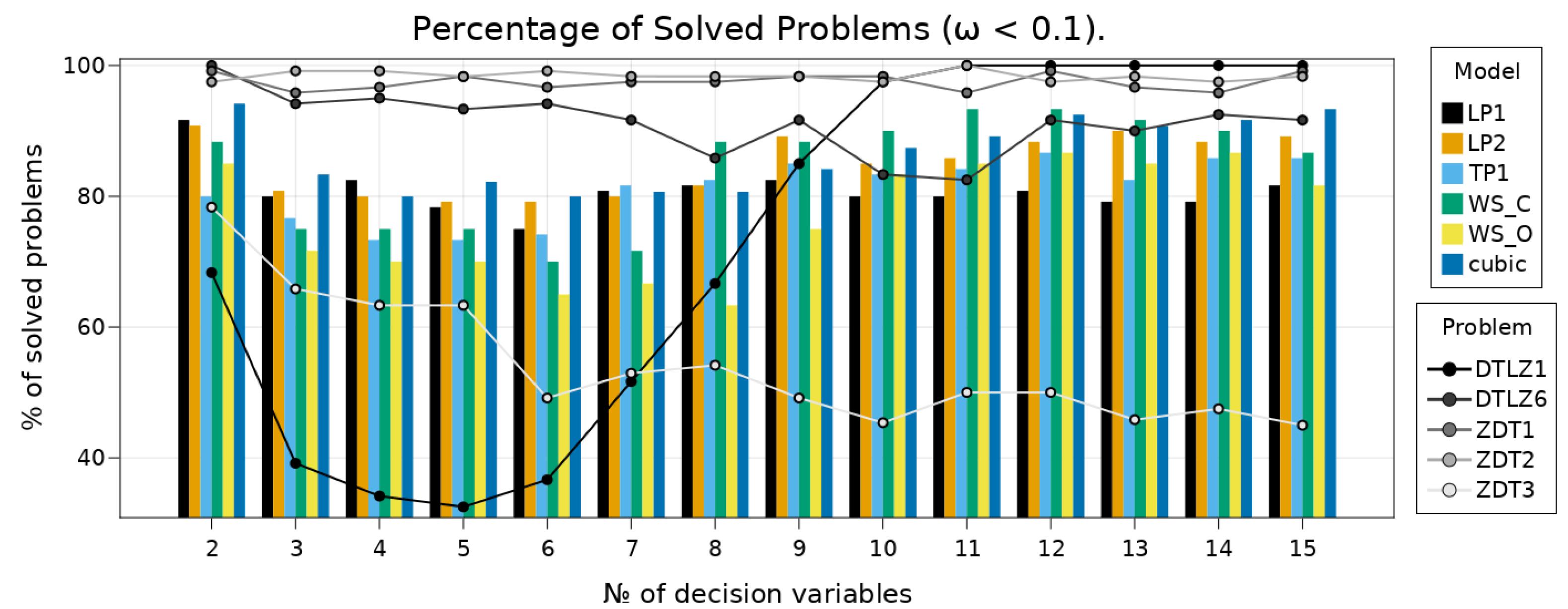
7.3. Benchmarks on Scalable Test-Problems
7.3.1. Solution Quality
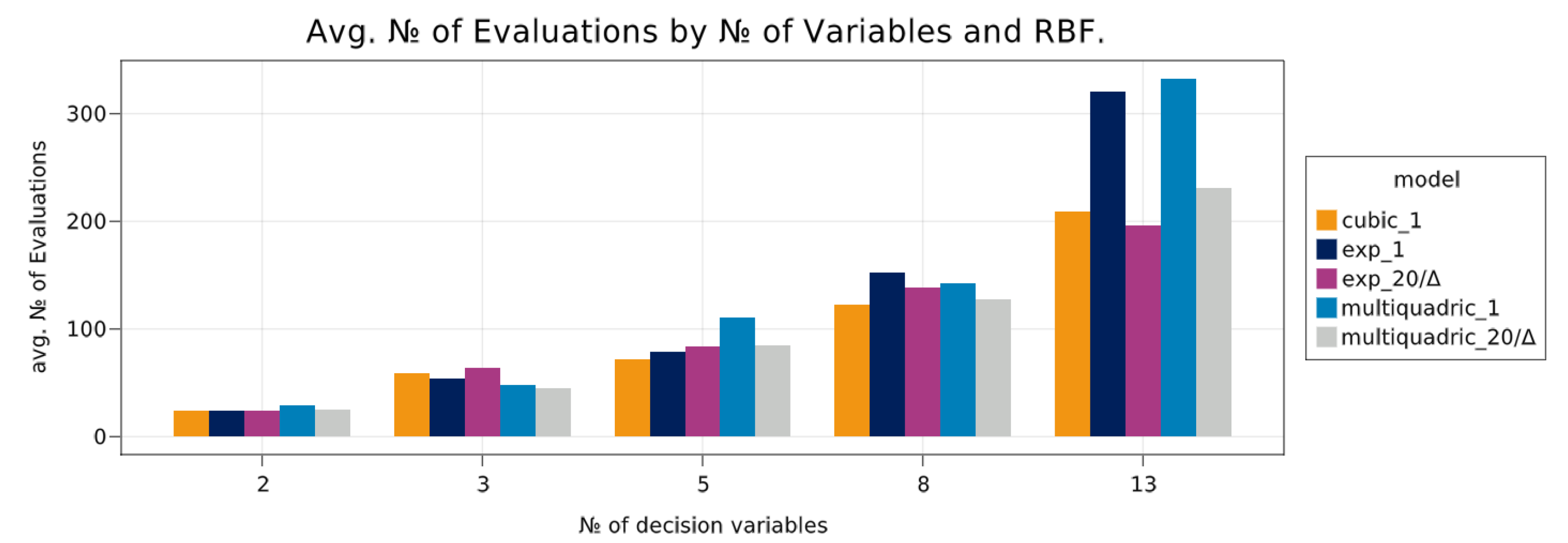
7.3.2. RBF Comparison
8. Conclusions
Supplementary Materials
Author Contributions
Funding

Conflicts of Interest
Appendix A. Miscellaneous Proofs
Appendix A.1. Continuity of the Constrained Optimal Value
- is positively homogenous and hence
- is Lipschitz with constant 1 so thatfor both the maximum and the Euclidean norm.
- because is convex and as well as .
- by the definition of .
- Because of , it follows that .
- Because all objective gradients are continuous, it holds for all that and because is continuous as well, it then follows that
- The last term on the RHS of (A1) vanishes for .
Appendix A.2. Modified Criticality Measures
- If thenNow
- The case can be shown similarly.
- If , then the first inequality follows because of .
- If , then and again the first inequality follows.
Appendix B. Pascoletti–Serafini Step
References
- Ehrgott, M. Multicriteria Optimization, 2nd ed.; Springer: Berlin, Germany, 2005. [Google Scholar]
- Jahn, J. Vector Optimization: Theory, Applications, and Extensions, 2nd ed.; Springer: Berlin, Germany, 2011; OCLC: 725378304. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Berlin, Germany, 2013; OCLC: 1089790877. [Google Scholar]
- Eichfelder, G. Twenty Years of Continuous Multiobjective Optimization. Available online: http://www.optimization-online.org/DB_FILE/2020/12/8161.pdf (accessed on 8 April 2021).
- Eichfelder, G. Adaptive Scalarization Methods in Multiobjective Optimization; Springer: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Fukuda, E.H.; Drummond, L.M.G. A Survay on Multiobjective Descent Methods. Pesqui. Oper. 2014, 34, 585–620. [Google Scholar] [CrossRef]
- Fliege, J.; Svaiter, B.F. Steepest descent methods for multicriteria optimization. Math. Method. Operat. Res. (ZOR) 2000, 51, 479–494. [Google Scholar] [CrossRef]
- Graña Drummond, L.; Svaiter, B. A steepest descent method for vector optimization. J. Comput. Appl. Math. 2005, 175, 395–414. [Google Scholar] [CrossRef]
- Lucambio Pérez, L.R.; Prudente, L.F. Nonlinear Conjugate Gradient Methods for Vector Optimization. SIAM J. Optim. 2018, 28, 2690–2720. [Google Scholar] [CrossRef]
- Lucambio Pérez, L.R.; Prudente, L.F. A Wolfe Line Search Algorithm for Vector Optimization. ACM Transact. Math. Softw. 2019, 45, 1–23. [Google Scholar] [CrossRef]
- Gebken, B.; Peitz, S.; Dellnitz, M. A Descent Method for Equality and Inequality Constrained Multiobjective Optimization Problems. In Numerical and Evolutionary Optimization—NEO 2017; Trujillo, L., Schütze, O., Maldonado, Y., Valle, P., Eds.; Springer: Cham, Switzerland, 2019; pp. 29–61. [Google Scholar]
- Hillermeier, C. Nonlinear Multiobjective Optimization: A Generalized Homotopy Approach; Springer Basel AG: Basel, Switzerland, 2001; OCLC: 828735498. [Google Scholar]
- Gebken, B.; Peitz, S.; Dellnitz, M. On the hierarchical structure of Pareto critical sets. J. Glob. Optim. 2019, 73, 891–913. [Google Scholar] [CrossRef]
- Wilppu, O.; Karmitsa, N.; Mäkelä, M. New Multiple Subgradient Descent Bundle Method for Nonsmooth Multiobjective Optimization; Report no. 1126; Turku Centre for Computer Science: Turku, Sweden, 2014. [Google Scholar]
- Gebken, B.; Peitz, S. An Efficient Descent Method for Locally Lipschitz Multiobjective Optimization Problems. J. Optim. Theor. Appl. 2021. [Google Scholar] [CrossRef]
- Custódio, A.L.; Madeira, J.F.A.; Vaz, A.I.F.; Vicente, L.N. Direct Multisearch for Multiobjective Optimization. SIAM J. Optim. 2011, 21, 1109–1140. [Google Scholar] [CrossRef]
- Audet, C.; Savard, G.; Zghal, W. Multiobjective Optimization Through a Series of Single-Objective Formulations. SIAM J. Optim. 2008, 19, 188–210. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Veldhuizen, D.A.V. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Abraham, A.; Jain, L.C.; Goldberg, R. (Eds.) Evolutionary multiobjective optimization: Theoretical advances and applications. In Advanced Information and Knowledge Processing; Springer: New York, NY, USA, 2005. [Google Scholar]
- Zitzler, E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications. Ph.D. Thesis, ETH, Zurich, Switzerland, 1999. [Google Scholar]
- Peitz, S.; Dellnitz, M. A Survey of Recent Trends in Multiobjective Optimal Control—Surrogate Models, Feedback Control and Objective Reduction. Math. Comput. Appl. 2018, 23, 30. [Google Scholar] [CrossRef]
- Chugh, T.; Sindhya, K.; Hakanen, J.; Miettinen, K. A survey on handling computationally expensive multiobjective optimization problems with evolutionary algorithms. Soft Comput. 2019, 23, 3137–3166. [Google Scholar] [CrossRef]
- Deb, K.; Roy, P.C.; Hussein, R. Surrogate Modeling Approaches for Multiobjective Optimization: Methods, Taxonomy, and Results. Math. Comput. Appl. 2020, 26, 5. [Google Scholar] [CrossRef]
- Roy, P.C.; Hussein, R.; Blank, J.; Deb, K. Trust-Region Based Multi-objective Optimization for Low Budget Scenarios. In Evolutionary Multi-Criterion Optimization; Series Title: Lecture Notes in Computer Science; Deb, K., Goodman, E., Coello Coello, C.A., Klamroth, K., Miettinen, K., Mostaghim, S., Reed, P., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 11411, pp. 373–385. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Introduction to Derivative-Free Optimization; Number 8 in MPS-SIAM Series on Optimization; Society for Industrial and Applied Mathematics/Mathematical Programming Society: Philadelphia, PA, USA, 2009; OCLC: Ocn244660709. [Google Scholar]
- Larson, J.; Menickelly, M.; Wild, S.M. Derivative-free optimization methods. arXiv 2019, arXiv:1904.11585. [Google Scholar] [CrossRef]
- Qu, S.; Goh, M.; Liang, B. Trust region methods for solving multiobjective optimisation. Optim. Method. Softw. 2013, 28, 796–811. [Google Scholar] [CrossRef]
- Villacorta, K.D.V.; Oliveira, P.R.; Soubeyran, A. A Trust-Region Method for Unconstrained Multiobjective Problems with Applications in Satisficing Processes. J. Optim. Theor. Appl. 2014, 160, 865–889. [Google Scholar] [CrossRef]
- Ryu, J.H.; Kim, S. A Derivative-Free Trust-Region Method for Biobjective Optimization. SIAM J. Optim. 2014, 24, 334–362. [Google Scholar] [CrossRef]
- Audet, C.; Savard, G.; Zghal, W. A mesh adaptive direct search algorithm for multiobjective optimization. Eur. J. Oper. Res. 2010, 204, 545–556. [Google Scholar] [CrossRef]
- Thomann, J.; Eichfelder, G. A Trust-Region Algorithm for Heterogeneous Multiobjective Optimization. SIAM J. Optim. 2019, 29, 1017–1047. [Google Scholar] [CrossRef]
- Wild, S.M.; Regis, R.G.; Shoemaker, C.A. ORBIT: Optimization by Radial Basis Function Interpolation in Trust-Regions. SIAM J. Sci. Comput. 2008, 30, 3197–3219. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Global Convergence of General Derivative-Free Trust-Region Algorithms to First- and Second-Order Critical Points. SIAM J. Optim. 2009, 20, 387–415. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. Trust-Region Methods; MPS-SIAM series on optimization; Society for Industrial and Applied Mathematics: Harrisburg, PA, USA, 2000. [Google Scholar]
- Luc, D.T. Theory of Vector Optimization; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Heidelberg, 1989; Volume 319. [Google Scholar] [CrossRef]
- Thomann, J. A Trust Region Approach for Multi-Objective Heterogeneous Optimization. Ph.D. Thesis, TU Ilmenau, Illmenau, Germany, 2018. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research; Springer: Berlin, Germany, 2006; OCLC: Ocm68629100. [Google Scholar]
- Wendland, H. Scattered Data Approximation, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Wild, S.M. Derivative-Free Optimization Algorithms for Computationally Expensive Functions; Cornell University: Ithaca, NY, USA, 2009. [Google Scholar]
- Wild, S.M.; Shoemaker, C. Global Convergence of Radial Basis Function Trust Region Derivative-Free Algorithms. SIAM J. Optim. 2011, 21, 761–781. [Google Scholar] [CrossRef]
- Regis, R.G.; Wild, S.M. CONORBIT: Constrained optimization by radial basis function interpolation in trust regions. Optim. Methods Softw. 2017, 32, 552–580. [Google Scholar] [CrossRef]
- Fleming, W. Functions of Several Variables; Undergraduate Texts in Mathematics; Springer: New York, NY, USA, 1977. [Google Scholar] [CrossRef]
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An operator splitting solver for quadratic programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. Available online: https://nlopt.readthedocs.io/en/latest/ (accessed on 8 April 2021).
- Svanberg, K. A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef]
- Legat, B.; Timme, S.; Weisser, T.; Kapelevich, L.; Rackauckas, C.; TagBot, J. JuliaAlgebra/DynamicPolynomials.jl: V0.3.15. 2020. Available online: https://zenodo.org/record/4153432#.YG5wjj8RVPY (accessed on 8 April 2021).
- Runarsson, T.P.; Yao, X. Search biases in constrained evolutionary optimization. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2005, 35, 233–243. [Google Scholar] [CrossRef]
- Revels, J.; Lubin, M.; Papamarkou, T. Forward-Mode Automatic Differentiation in Julia. arXiv 2016, arXiv:1607.07892. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Test Problems for Evolutionary Multiobjective Optimization. In Evolutionary Multiobjective Optimization; Series Title: Advanced Information and Knowledge Processing; Abraham, A., Jain, L., Goldberg, R., Eds.; Springer: London, UK, 2005; pp. 105–145. [Google Scholar] [CrossRef]
- Powell, M.J. A direct search optimization method that models the objective and constraint functions by linear interpolation. In Advances in Optimization and Numerical Analysis; Gomez, S., Hennart, J.P., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 51–67. [Google Scholar]
- Prinz, S.; Thomann, J.; Eichfelder, G.; Boeck, T.; Schumacher, J. Expensive multi-objective optimization of electromagnetic mixing in a liquid metal. Optim. Eng. 2020. [Google Scholar] [CrossRef]
- Thomann, J.; Eichfelder, G. Representation of the Pareto front for heterogeneous multi-objective optimization. J. Appl. Numer. Optim. 2019, 1, 293–323. [Google Scholar]
- Deshpande, S.; Watson, L.T.; Canfield, R.A. Multiobjective optimization using an adaptive weighting scheme. Optim. Methods Softw. 2016, 31, 110–133. [Google Scholar] [CrossRef]
- Regis, R.G. Multi-objective constrained black-box optimization using radial basis function surrogates. J. Comput. Sci. 2016, 16, 140–155. [Google Scholar] [CrossRef]
- Schütze, O.; Cuate, O.; Martín, A.; Peitz, S.; Dellnitz, M. Pareto Explorer: A global/local exploration tool for many-objective optimization problems. Eng. Optim. 2020, 52, 832–855. [Google Scholar] [CrossRef]
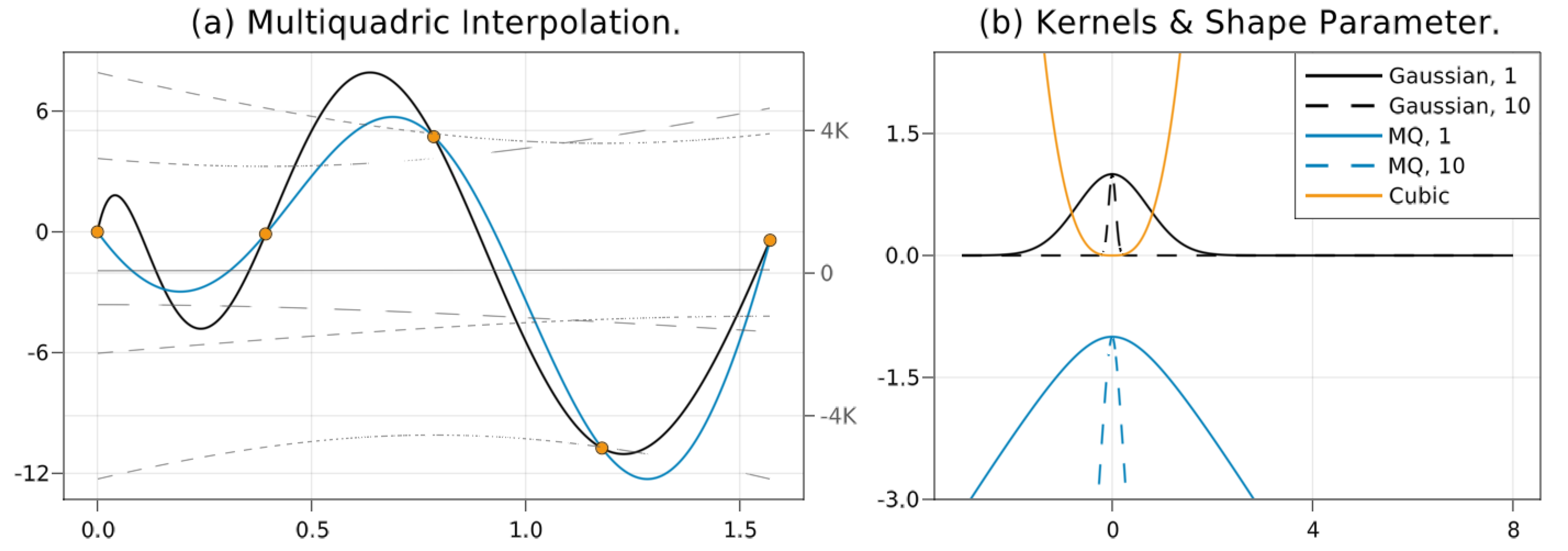


| Name | c.p.d. order D | |
|---|---|---|
| Cubic | 2 | |
| Multiquadric | 1 | |
| Gaussian | 0 |
| Param. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 20 | 2 | 2 |
| Parameter | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 100 | 3 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berkemeier, M.; Peitz, S. Derivative-Free Multiobjective Trust Region Descent Method Using Radial Basis Function Surrogate Models. Math. Comput. Appl. 2021, 26, 31. https://doi.org/10.3390/mca26020031
Berkemeier M, Peitz S. Derivative-Free Multiobjective Trust Region Descent Method Using Radial Basis Function Surrogate Models. Mathematical and Computational Applications. 2021; 26(2):31. https://doi.org/10.3390/mca26020031
Chicago/Turabian StyleBerkemeier, Manuel, and Sebastian Peitz. 2021. "Derivative-Free Multiobjective Trust Region Descent Method Using Radial Basis Function Surrogate Models" Mathematical and Computational Applications 26, no. 2: 31. https://doi.org/10.3390/mca26020031
APA StyleBerkemeier, M., & Peitz, S. (2021). Derivative-Free Multiobjective Trust Region Descent Method Using Radial Basis Function Surrogate Models. Mathematical and Computational Applications, 26(2), 31. https://doi.org/10.3390/mca26020031







