Robust qLPV Tracking Fault-Tolerant Control of a 3 DOF Mechanical Crane
Abstract
1. Introduction
2. Mathematical Modeling
- For the limits are and . The weigthing functions are and . Therefore, can be rewritten as .
- For the limits are and . The weighting functions are and . Therefore, can be rewritten as .
- is bounded as and . The weigthing functions are and , with .
- Finally, is bounded as and . The weighting functions are and , with .
3. Convex Fault-Tolerant Controller
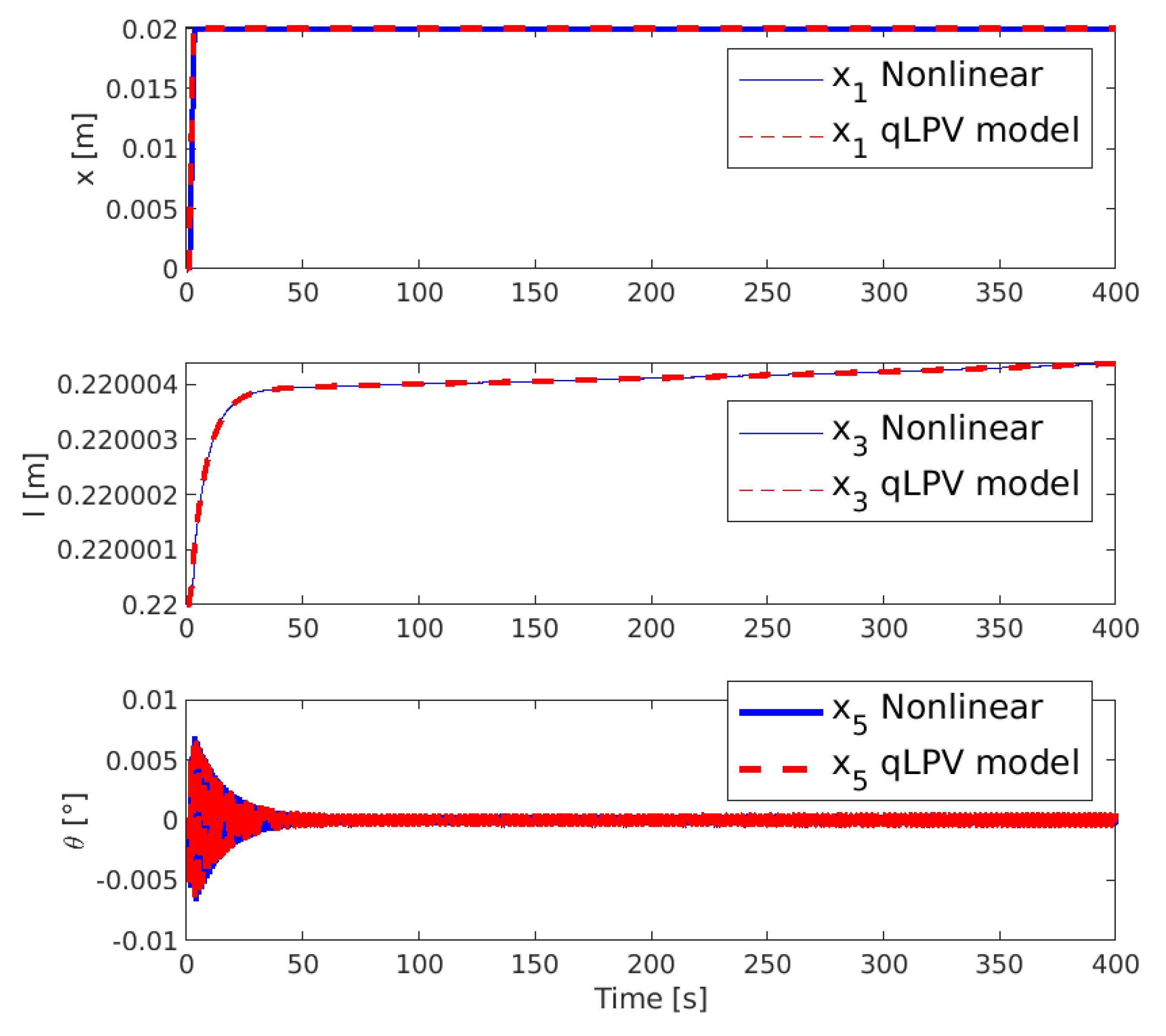
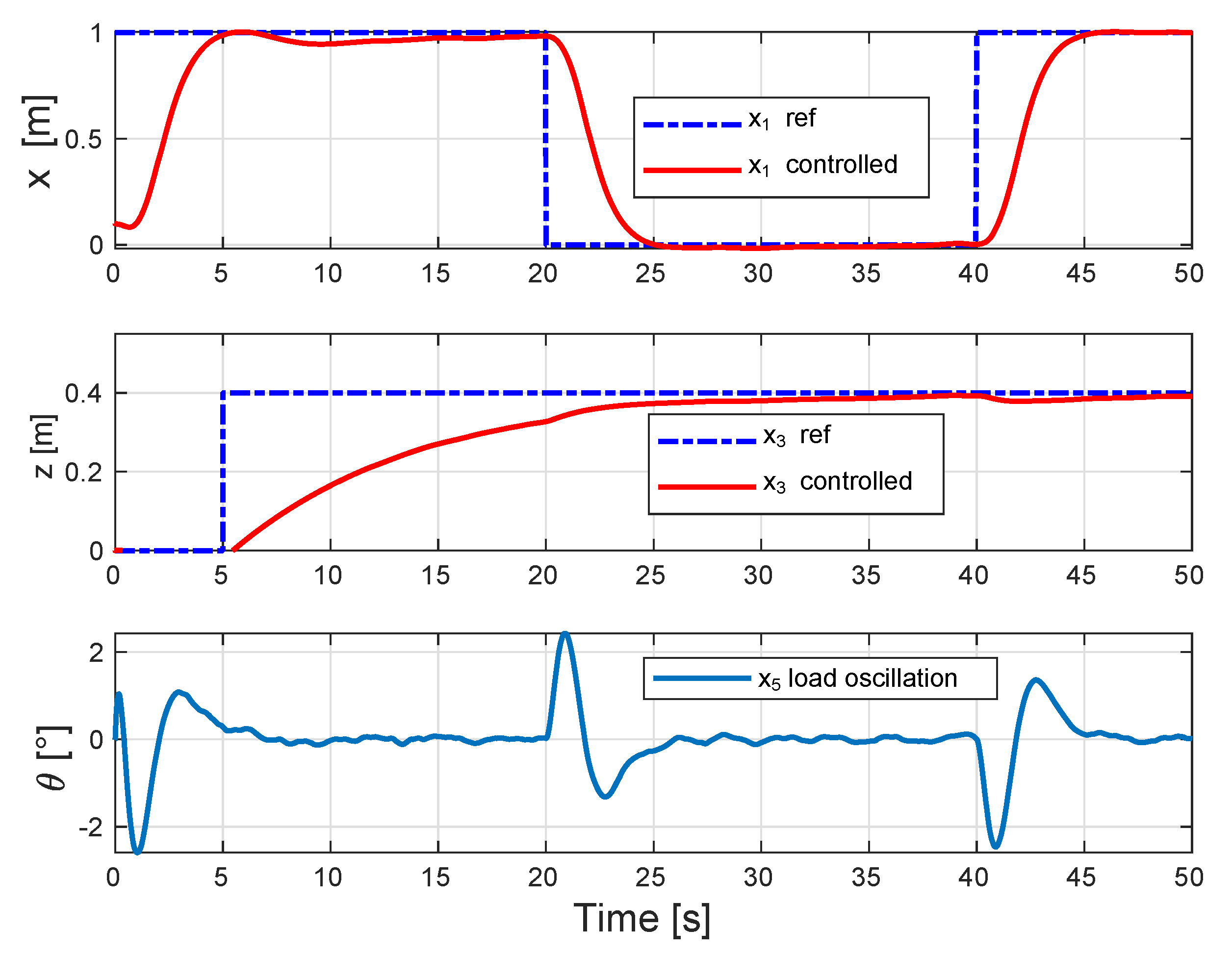
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2006; Volume 691. [Google Scholar]
- Martínez-García, C.; Puig, V.; Astorga-Zaragoza, C.M.; Madrigal-Espinosa, G.; Reyes-Reyes, J. Estimation of Actuator and System Faults Via an Unknown Input Interval Observer for Takagi–Sugeno Systems. Processes 2020, 8, 61. [Google Scholar] [CrossRef]
- Witczak, M. Fault diagnosis and fault-tolerant control strategies for non-linear systems. Lect. Notes Electr. Eng. 2014, 266, 375–392. [Google Scholar]
- García, C.M.; Puig, V.; Astorga-Zaragoza, C.; Osorio-Gordillo, G. Robust fault estimation based on interval takagi–sugeno unknown input observer. IFAC-PapersOnLine 2018, 51, 508–514. [Google Scholar] [CrossRef]
- Nagy-Kiss, A.M.; Ichalal, D.; Schutz, G.; Ragot, J. Fault tolerant control for uncertain descriptor multi-models with application to wastewater treatment plant. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5718–5725. [Google Scholar]
- Wu, Y.; Dong, J. Fault detection for T–S fuzzy systems with partly unmeasurable premise variables. Fuzzy Sets Syst. 2018, 338, 136–156. [Google Scholar] [CrossRef]
- Quintana, D.; Estrada-Manzo, V.; Bernal, M. Real-time parallel distributed compensation of an inverted pendulum via exact Takagi–Sugeno models. In Proceedings of the 2017 14th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 20–22 October 2017; pp. 1–5. [Google Scholar]
- López-Estrada, F.R.; Theilliol, D.; Astorga-Zaragoza, C.M.; Ponsart, J.C.; Valencia-Palomo, G.; Camas-Anzueto, J. Fault diagnosis observer for descriptor Takagi–Sugeno systems. Neurocomputing 2019, 331, 10–17. [Google Scholar] [CrossRef]
- Gómez-Peñate, S.; López-Estrada, F.R.; Valencia-Palomo, G.; Rotondo, D.; Enríquez-Zárate, J. Actuator and sensor fault estimation based on a proportional-integral quasi-LPV observer with inexact scheduling parameters. IFAC-PapersOnLine 2019, 52, 100–105. [Google Scholar] [CrossRef]
- Gómez-Peñate, S.; Valencia-Palomo, G.; López-Estrada, F.R.; Astorga-Zaragoza, C.M.; Osornio-Rios, R.A.; Santos-Ruiz, I. Sensor fault diagnosis based on a sliding mode and unknown input observer for Takagi–Sugeno systems with uncertain premise variables. Asian J. Control 2019, 21, 339–353. [Google Scholar] [CrossRef]
- Chen, L.; Alwi, H.; Edwards, C. On the synthesis of an integrated active LPV FTC scheme using sliding modes. Automatica 2019, 110, 108536. [Google Scholar] [CrossRef]
- Ohtake, H.; Tanaka, K.; Wang, H.O. Fuzzy modeling via sector nonlinearity concept. Integr. Comput. Aided Eng. 2003, 10, 333–341. [Google Scholar] [CrossRef]
- Rotondo, D. Advances in Gain-Scheduling and Fault Tolerant Control Techniques; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- López-Estrada, F.R.; Rotondo, D.; Valencia-Palomo, G. A Review of Convex Approaches for Control, Observation and Safety of Linear Parameter Varying and Takagi–Sugeno Systems. Processes 2019, 7, 814. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Ann. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Y. Design of passive fault-tolerant flight controller against actuator failures. Chin. J. Aeronaut. 2015, 28, 180–190. [Google Scholar] [CrossRef][Green Version]
- Nasiri, A.; Nguang, S.K.; Swain, A.; Almakhles, D. Passive actuator fault tolerant control for a class of MIMO nonlinear systems with uncertainties. Int. J. Control 2019, 92, 693–704. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; He, W. Robust adaptive fault tolerant control for a linear cascaded ODE-beam system. Automatica 2018, 98, 42–50. [Google Scholar] [CrossRef]
- Nemati, F.; Hamami, S.M.S.; Zemouche, A. A nonlinear observer-based approach to fault detection, isolation and estimation for satellite formation flight application. Automatica 2019, 107, 474–482. [Google Scholar] [CrossRef]
- Guzmán-Rabasa, J.A.; López-Estrada, F.R.; González-Contreras, B.M.; Valencia-Palomo, G.; Chadli, M.; Perez-Patricio, M. Actuator fault detection and isolation on a quadrotor unmanned aerial vehicle modeled as a linear parameter-varying system. Meas. Control 2019, 52, 1228–1239. [Google Scholar] [CrossRef]
- Kim, Y.S.; Hong, K.S.; Sul, S.K. Anti-sway control of container cranes: Inclinometer, observer, and state feedback. Int. J. Control Autom. Syst. 2004, 2, 435–449. [Google Scholar]
- Shi, K.; Wang, B.; Yang, L.; Jian, S.; Bi, J. Takagi–Sugeno fuzzy generalized predictive control for a class of nonlinear systems. Nonlinear Dyn. 2017, 89, 169–177. [Google Scholar] [CrossRef]
- Almutairi, N.B.; Zribi, M. Sliding mode control of a three-dimensional overhead crane. J. Vib. Control 2009, 15, 1679–1730. [Google Scholar] [CrossRef]
- Castillo, I.; Vázquez, C.; Fridman, L. Overhead crane control through LQ singular surface design MATLAB Toolbox. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5847–5852. [Google Scholar]
- Maghsoudi, M.J.; Mohamed, Z.; Sudin, S.; Buyamin, S.; Jaafar, H.; Ahmad, S. An improved input shaping design for an efficient sway control of a nonlinear 3D overhead crane with friction. Mech. Syst. Signal Process. 2017, 92, 364–378. [Google Scholar] [CrossRef]
- Vu, N.T.T.; Thanh, P.T.; Duong, P.X.; Phuoc, N.D. Robust Adaptive Control of 3D Overhead Crane System. In Adaptive Robust Control Systems; IntechOpen: London, UK, 2017. [Google Scholar]
- Abdullahi, A.M.; Mohamed, Z.; Selamat, H.; Pota, H.R.; Abidin, M.Z.; Ismail, F.; Haruna, A. Adaptive output-based command shaping for sway control of a 3D overhead crane with payload hoisting and wind disturbance. Mech. Syst. Signal Process. 2018, 98, 157–172. [Google Scholar] [CrossRef]
- Chen, W.; Wu, Q.; Tafazzoli, E.; Saif, M. Actuator fault diagnosis using high-order sliding mode differentiator (HOSMD) and its application to a laboratory 3D crane. IFAC Proc. Vol. 2008, 41, 4809–4814. [Google Scholar] [CrossRef]
- Tan, C.P.; Edwards, C. A robust sensor fault tolerant control scheme implemented on a crane. Asian J. Control 2007, 9, 340–344. [Google Scholar] [CrossRef]
- Chen, W.; Saif, M. Actuator fault diagnosis for a class of nonlinear systems and its application to a laboratory 3D crane. Automatica 2011, 47, 1435–1442. [Google Scholar] [CrossRef]
- Kiriakidis, K. Robust stabilization of the Takagi–Sugeno fuzzy model via bilinear matrix inequalities. IEEE Trans. Fuzzy Syst. 2001, 9, 269–277. [Google Scholar] [CrossRef]
- Adeli, M.; Zarabadipour, H.; Zarabadi, S.H.; Shoorehdeli, M.A. Anti-swing control for a double-pendulum-type overhead crane via parallel distributed fuzzy LQR controller combined with genetic fuzzy rule set selection. In Proceedings of the IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 25–27 November 2011; pp. 306–311. [Google Scholar]
- Hilhorst, G.; Pipeleers, G.; Michiels, W.; Oliveira, R.C.; Peres, P.L.D.; Swevers, J. Reduced-order 2/∞ control of discrete-time LPV systems with experimental validation on an overhead crane test setup. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 125–130. [Google Scholar]
- Zhao, L.; Li, L. Robust stabilization of T–S fuzzy discrete systems with actuator saturation via PDC and non-PDC law. Neurocomputing 2015, 168, 418–426. [Google Scholar] [CrossRef]
- Rabaoui, B.; Rodrigues, M.; Hamdi, H.; BenHadj Braiek, N. A model reference tracking based on an active fault tolerant control for LPV systems. Int. J. Adapt. Control Signal Process. 2018, 32, 839–857. [Google Scholar] [CrossRef]
- Morato, M.M.; Sename, O.; Dugard, L. LPV-MPC Fault Tolerant Control of Automotive Suspension Dampers. IFAC-PapersOnLine 2018, 51, 31–36. [Google Scholar] [CrossRef]
- Petrehuş, P.; Lendek, Z.; Raica, P. Fuzzy modeling and design for a 3D Crane. IFAC Proc. Vol. 2013, 46, 479–484. [Google Scholar] [CrossRef]
- Márquez, R.; Guerra, T.M.; Bernal, M.; Kruszewski, A. Asymptotically necessary and sufficient conditions for Takagi–Sugeno models using generalized non-quadratic parameter-dependent controller design. Fuzzy Sets Syst. 2017, 306, 48–62. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A Toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004. [Google Scholar]
- Sturm, J. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]


| Combination | Combination | ||
|---|---|---|---|
| Parameter | Value | Units |
|---|---|---|
| g | 9.81 | m/s |
| m | 0.50 | kg |
| 1.655 | kg | |
| 0.50 | kg | |
| 100 | Ns/m | |
| 82 | Ns/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Estrada, F.-R.; Santos-Estudillo, O.; Valencia-Palomo, G.; Gómez-Peñate, S.; Hernández-Gutiérrez, C. Robust qLPV Tracking Fault-Tolerant Control of a 3 DOF Mechanical Crane. Math. Comput. Appl. 2020, 25, 48. https://doi.org/10.3390/mca25030048
López-Estrada F-R, Santos-Estudillo O, Valencia-Palomo G, Gómez-Peñate S, Hernández-Gutiérrez C. Robust qLPV Tracking Fault-Tolerant Control of a 3 DOF Mechanical Crane. Mathematical and Computational Applications. 2020; 25(3):48. https://doi.org/10.3390/mca25030048
Chicago/Turabian StyleLópez-Estrada, Francisco-Ronay, Oscar Santos-Estudillo, Guillermo Valencia-Palomo, Samuel Gómez-Peñate, and Carlos Hernández-Gutiérrez. 2020. "Robust qLPV Tracking Fault-Tolerant Control of a 3 DOF Mechanical Crane" Mathematical and Computational Applications 25, no. 3: 48. https://doi.org/10.3390/mca25030048
APA StyleLópez-Estrada, F.-R., Santos-Estudillo, O., Valencia-Palomo, G., Gómez-Peñate, S., & Hernández-Gutiérrez, C. (2020). Robust qLPV Tracking Fault-Tolerant Control of a 3 DOF Mechanical Crane. Mathematical and Computational Applications, 25(3), 48. https://doi.org/10.3390/mca25030048








