A New Approach to Non-Singular Plane Cracks Theory in Gradient Elasticity

Abstract

A non-local solution is obtained here in the theory of cracks, which depends on the scale parameter in the non-local theory of elasticity. The gradient solution is constructed as a regular solution of the inhomogeneous Helmholtz equation, where the function on the right side of the Helmholtz equation is a singular classical solution. An assertion is proved that allows us to propose a new solution for displacements and stresses at the crack tip through the vector harmonic potential, which determines by the Papkovich–Neuber representation. One of the goals of this work is a definition of a new representation of the solution of the plane problem of the theory of elasticity through the complex-valued harmonic potentials included in the Papkovich–Neuber relations represented in a symmetric form, which is convenient for applications. It is shown here that this new representation of the solution for the mechanics of cracks can be written through one harmonic complex-valued potential. The explicit potential value is found by comparing the new solution with the classical representation of the singular solution at the crack tip constructed using the complex potentials of Kolosov–Muskhelishvili. A generalized solution of the singular problem of fracture mechanics is reduced to a non-singular stress concentration problem, which allows one to implement a new concept of non-singular fracture mechanics, where the scale parameter along with ultimate stresses determines the fracture criterion and is determined by experiments.

1. Introduction

The problem of singularities in the theory of elasticity and in fracture mechanics is widely discussed in the related scientific literature [1,2,3]. The singularity of solutions for stresses at the crack tip in the linear theory of elasticity excludes the use of traditional criteria for the strength of bodies with stress concentration. Moreover, the formally obtained singular solutions contradict not only the physical meaning, but also the postulates of the theory of elasticity. Such paradoxes still require an explanation [3]. Gradient elasticity allows one to describe size effects [4], and provides regularization of singular solutions of differential equations of elasticity theory [5,6]. In this regard, it would be quite natural to expect the development of gradient fracture mechanics. Nevertheless, so far only non-singular solutions have been constructed in gradient fracture mechanics for test problems corresponding to cracks of Mode III [7].

For the general theory of gradient deformation, the variational model is described by the density of potential energy:

$$2E=C_{ijkm}{\epsilon }_{ij}{\epsilon }_{km}+C_{ijklnm}{u}_{i,jk}{u}_{l,mn},$$

where $u_i$ is the displacement vector, ε_ij the strain tensor, C_ijkm and $C_{ijklmn}$ are classical and gradient moduli of elasticity respectively, having different dimensions. The force model is determined by the Cauchy stress tensor ${\sigma }_{ij}$ and by the tensor of double stresses of the third rank ${\mu }_{ijk}$. Constitutive equations are obviously given by the following formulas:

$${\sigma }_{ij}=\partial E/\partial {\epsilon }_{ij},{\mu }_{ijk}=\partial E/\partial u_{i,jk},(u_{i,j}=\partial u_i/\partial x_j).$$

In the general case, the physical properties of an isotropic gradient theory are described using seven physical constants, two of which are Lamé constants, and five others determine the tensor of gradient moduli of the sixth rank.

As a rule, one-parameter models are used to solve applied problems. One of the most popular is a model of the continuum in which the tensors of stresses and double stresses are determined by the formulas [8,9]:

$${\sigma }_{ij}=\lambda \vartheta {\delta }_{ij}+2\mu {\epsilon }_{ij},{\mu }_{ijk}=s^2(\lambda {\vartheta }_{,k}{\delta }_{ij}+2\mu {\epsilon }_{ij,k}),$$

and accordingly, the elastic modules have the form:

$$C_{ijkm}=\lambda {\delta }_{ij}{\delta }_{km}+\mu ({\delta }_{ik}{\delta }_{jm}+{\delta }_{im}{\delta }_{jk}),C_{ijklnm}=s^2\lambda {\delta }_{ij}{\delta }_{kn}{\delta }_{lm}+s^2\mu ({\delta }_{il}{\delta }_{jm}{\delta }_{kn}+{\delta }_{im}{\delta }_{jl}{\delta }_{kn}).$$

Here, $\lambda$, $\mu$ are the Lame coefficients, $s$ is the scale parameter, $\vartheta =u_{k,k}$ is the dilation, and ${\delta }_{ij}$ is the Kronecker delta.

The equilibrium equations in such a model are written through the tensor of “total” stresses (see [9]):

$${({\sigma }_{ij}-{\mu }_{ijk,k})}_{,j}=0\mathrm{or}{\tau }_{ij,j}=0,$$

where ${\tau }_{ij}={\sigma }_{ij}-{\mu }_{ijk,k}$. Constitutive equations for such applied gradient models have the following form (see [9]):

$${\tau }_{ij}={\sigma }_{ij}-{\mu }_{ijk,k}={\sigma }_{ij}-s^2{\sigma }_{ij,kk}=(1-s^2\Delta )(\lambda \vartheta \hspace{0.17em}{\delta }_{ij}+2\mu {\epsilon }_{ij}),\vartheta ={\epsilon }_{ij}{\delta }_{ij}$$

(1)

where $\Delta$ is the Laplace operator.

Note that static boundary conditions for the considered gradient model are specified through a linear combination of “classical” stresses ${\tau }_{ij}$ and derivatives of double stresses ${\mu }_{ijk}$. As a result, the boundary conditions cannot be written only through the tensor of stresses ${\tau }_{ij}$, which makes it difficult to obtain solutions. This probably explains why gradient solutions are constructed only for harmonic problems of cracks of Mode III.

Let us note that the problem of the regularization of the classical singular crack fields was still considered in [10,11,12] where the attempts were made to construct non-singular solutions. Furthermore, in [13] these studies were discussed because the obtained solutions did not satisfy the strain compatibility equations. Indeed, in the indicated works, it was possible to construct only approximate non-singular solutions, which is associated with incomplete consideration of the biharmonic components on the right side of the Helmholtz equations. In any case, in the indicated papers there are not the common analytical solutions to problems for cracks of Mode I. In the interesting work [14] the search of solution for the theory of cracks comes down to integral equations.

The complexity of the obtained expressions and the method of constructing approximate solutions using the Chebyshev series did not allow the find of explicit analytical expressions that would show the regularity of the solution. The authors do not provide analytical solutions in an accurate study conducted in [15] using micropolar elasticity, as well as in the fundamental work [16] since, during the construction of an approximate solution, the authors are not able to ensure fully the continuation of the solution directly to the crack tip. In the present work, we are going to construct an exact non-singular solution for Mode I cracks using a new representation of the classical solution for generalized stresses through a complex-valued scalar potential.

The modified variant of the generalized elasticity theory was proposed by the authors of [17,18], where the defining relations are written for the generalized non-local stress tensor and the generalized non-local strain tensor. Note that the idea of the non-local theory of elasticity was proposed in the fundamental works [19,20]. Connection of non-local theory with gradient theories was established in the work [21]. Theoretical aspects of non-local theories and their generalized variants and also their applications in the area of mechanics of nano-structures and nano devices discussed in the interesting works [22,23,24].

We use the applied variant of model when a generalized non-local tensor function is introduced using the averaging operation of a local function on a given finite fragment and then the local function is expanded in a Taylor series on local coordinates on the fragment under consideration with retention of a finite number of terms in the series. As a result, after integrating the resulting finite Taylor series with respect to local coordinates over the considered fragment, the non-local generalized functions are constructed. In the proposed procedure, generalized functions are determined not only through the values of the local function at some point of the fragment, but also in aggregate through its derivatives of the second, fourth, etc. orders, depending on the number of terms held in the Taylor series. Here we can see a difference from the traditional differential calculus where the function or its derivatives are determined by their values at the point. Generalized functions in particular are determined by the corresponding local functions through the Helmholtz operator.

The construction of the solution in the model [17,18] is carried out in two stages. At the first stage, the traditional boundary value problem of the theory of elasticity is considered and non-local stresses and displacements are found. At the second stage, the obtained solutions are substituted on the right-hand side of the Helmholtz equation, which is solved with respect to local functions. Thus, to construct the local solutions it is first proposed to solve the classical elasticity problem for generalized stresses and displacements, and then find local stresses ${\Xi }_{ij}$ and displacements $U_i$, by solving the corresponding Helmholtz equations:

$$U_i-s^2\Delta U_i=u_i,{\Xi }_{ij}-s^2\Delta {\Xi }_{ij}={\sigma }_{ij}$$

(2)

We can see that in using this model for the mechanics of cracks the generalized non-local solutions formally coincide with the classical solution of the static boundary conditions and the local stress field must be found as common solutions of the non-homogeneous Helmholtz equation (2). The solution for local stresses and displacements has the form of a boundary layer.

We note that the procedure for constructing local solutions is similar to the construction of gradient solutions considered in [25]. On the other hand, in the discussed model [18] the constitutive equations are written on non-local generalized stresses and deformations ${\sigma }_{ij}={С}_{ijmn}{\epsilon }_{mn}$, which is quite justified, physically. As is evident, the constitutive equations of the discussed model are different from the constitutive equation (1). For the mechanics of cracks, the generalized non-local solutions formally coincide with the classical solution of the static boundary conditions, and the local stress field must be found as a common solution of the non-homogeneous Helmholtz equations. We assume that the local stresses are important for assessing the strength and that local stresses are involved in the strength criteria. These stresses are found after the definition of generalized stresses (“classical”) ${\sigma }_{ij}$ from the equation ${\sigma }_{ij}=({\Xi }_{ij}-s^2\Delta {\Xi }_{ij})$.

The purpose of this work is to show that, for the model under consideration, the local stress field in the vicinity of the crack tip is regular, i.e., it does not have a singularity. Non-singular solutions could be used as the basis for constructing and testing a new concept of stress concentration in crack mechanics proposed in [26]. We belive that for brittle cracks the non-singular cracks dependences allow us to determine the important role for the scale parameter as a characteristic of fracture for brittle cracks along with tensile strength. In fact, a simular algorithm was implemented in [26] for the case of finite cracks of normal separation in a plane strip. It was shown that the parameter $s$ for a particular brittle material is a constant and can be considered as a critical parameter of fracture, giving with high accuracy a strength forecast for brittle materials.

We propose a new representation of the solution of the plane problem of the theory of elasticity through the complex-valued harmonic potentials included in the Papkovich–Neuber representation in a symmetric form, convenient for applications. A condition is determined under which the solution of plane problems of elasticity can be written through one harmonic potential. This condition is also fulfilled for problems of crack mechanics. As a result, we found the form of solution through one harmonic potential for displacement, and stresses that allow us to construct the non-singular solutions of mechanics of cracks.

2. New Representation of Solution through Harmonic Potential in Mechanics of Cracks

Let us consider the Papkovich–Neuber representation as a convenient analytical tool for describing the stress-strain state of an elastic body [27]. This representation allows us to represent the displacements and the corresponding stresses, through two auxiliary harmonic potentials: $\mathit{f}$ is the vector potential and another $\varphi$ is scalar, ${\nabla }^2\varphi ={\nabla }^2\mathit{f}=0$:

$$\mathit{u}=\frac{\mathit{f}}{\mu }+\frac{\nabla (\varphi -\mathit{r} \mathit{f})}{4\mu (1-\nu )},{\sigma }_{ij}=\frac{\partial f_i}{\partial x_j}+\frac{\partial f_j}{\partial x_i}+\frac{\nu ({\delta }_{ij}\mathrm{div}\mathit{f})}{1-\nu }+\frac{1}{2(1-\nu )}\frac{{\partial }^2(\varphi -\mathit{r}\mathit{f})}{\partial x_i \partial x_j}$$

(3)

here $\mathit{u}=\left\{u_i\right\}$ is the displacement vector, ${\sigma }_{ij}$ is the tensor of stresses, ${\sigma }_{ij}=2\mu \hspace{0.17em}{\epsilon }_{ij}+\lambda {\delta }_{ij}{\epsilon }_{kk}$, where ${\epsilon }_{ij}=(1/2)(u_{i,j}+u_{j,i})$.

We propose a new representation of the solution of the plane problem of the theory of elasticity through the complex-valued harmonic potentials included in the Papkovich–Neuber representation in a symmetric form, convenient for applications. We show that these representations obtained directly from the representation of the general Papkovich–Neuber solution can be reduced to the well-known representations of Kolosov–Muskhelishvili for the plane problem of the theory of elasticity through two complex potentials. However, then we prove that under certain conditions a solution to a plane problem can be represented through one complex-valued harmonic potential. Such a representation is new and is convenient in constructing generalized solutions in crack mechanics.

Lemma 1.

• Papkovich–Neuber’s representation allows us to present a solution to the plane problem of the theory of elasticity through three complex potentials in the following form:

  $$u_x=\mathrm{Re}u,{\sigma }_x=\mathrm{Re}(p+\tau ),u_y=\mathrm{Im}u,{\sigma }_y=\mathrm{Re}(p-\tau ),{\tau }_{xy}=\mathrm{Im}\tau$$

  (4)
• Papkovich–Neuber’s representation leads to the following form of the common solution for complex potentials$u$,$p$,$\tau$of the plane problem of the theory of elasticity through two analytic functions$\Phi (w)$and$F(w)$:

  $$\begin{gathered} u=\frac{F}{\mu }+\frac{1}{4\mu (1-\nu )}\frac{\partial (\overline{\Phi }-\overline{w} F-w \overline{F})}{\partial \overline{w}},p=\frac{1}{2(1-\nu )}\left(\frac{\partial F}{\partial w}+\frac{\partial \overline{F}}{\partial \overline{w}}\right), \\ \tau =\frac{1}{2(1-\nu )}\frac{{\partial }^2(\overline{\Phi }-\overline{w} F-w \overline{F})}{\partial {\overline{w}}^2} \end{gathered}$$

  (5)

  where$w=x+iy$.

Proof. 

We consider the plane problem of the theory of elasticity and write the displacements and stresses in complex form, introducing in (3) complex potentials $u=u_x+i{u}_y$, $f=f_x+i{f}_y$ instead of the corresponding vector expressions $\mathit{u}=\left\{u_x,u_y\right\}$, $\mathit{f}=\left\{f_x,f_y\right\}$ and complex variables $w,$ $\overline{w}$ instead variables $x$, $y$. Also, we use differentiation by complex coordinates $w=x+iy$, $\overline{w}=x-iy$:

$$\frac{\partial }{\partial w}=\frac{1}{2}\left(\frac{\partial }{\partial x}-i\frac{\partial }{\partial y}\right),\frac{\partial }{\partial \overline{w}}=\frac{1}{2}\left(\frac{\partial }{\partial x}+i\frac{\partial }{\partial y}\right).$$

Let us define the first invariant of the stress tensor $p=({\sigma }_x+{\sigma }_y)/2$ and the complex potential $\tau =({\sigma }_x-{\sigma }_y)/2+i{\tau }_{xy}$. Then the components of the displacement vector $u_x$, $u_y$ and the stress tensor ${\sigma }_x={\sigma }_{11}$, ${\sigma }_y={\sigma }_{22}$, ${\tau }_{xy}={\sigma }_{12}$ can be expressed explicitly through the introduced complex potentials in the form of Equation (4). The Equation (3) determines the link between $u$, $p$, $\tau$ and potentials $f=f_x+i f_y$ and $\varphi$. Using representation (3) and taking into account the equalities $\mathit{r}\mathit{f}=x f_x+y f_y=(\overline{w} f+w \overline{f})/2$, $\overline{f}=f_x-i{f}_y$ we can get

$$u=\frac{f}{\mu }+\frac{1}{4\mu (1-\nu )}\frac{\partial (\varphi -\overline{w} f-w \overline{f})}{\partial \overline{w}}$$

(6)

It is easy to establish also the following symmetric expressions for the stresses:

$$\begin{array}{l}{\sigma }_x=2\frac{\partial f_x}{\partial x}+\frac{\nu \mathrm{div}\mathit{f}}{1-\nu }+\frac{1}{4(1-\nu )}\frac{{\partial }^2(\varphi -\overline{w} f-w \overline{f})}{\partial x^2},\hspace{0.17em}\hspace{0.17em}{\sigma }_y=2\frac{\partial f_y}{\partial y}+\frac{\nu \mathrm{div}\mathit{f}}{1-\nu }+\frac{1}{4(1-\nu )}\frac{{\partial }^2(\varphi -\overline{w} f-w \overline{f})}{\partial y^2},\\ {\tau }_{xy}=\frac{\partial f_x}{\partial y}+\frac{\partial f_y}{\partial x}+\frac{1}{4(1-\nu )}\frac{{\partial }^2(\varphi -\overline{w} f-w \overline{f})}{\partial x \partial y},\hspace{1em}\mathrm{div}\mathit{f}=\frac{\partial f_x}{\partial x}+\frac{\partial f_y}{\partial y}=\frac{\partial f}{\partial w}+\frac{\partial \overline{f}}{\partial \overline{w}}\end{array}$$

(7)

We take into account that the potential $f$ is harmonic: $\Delta f=4{\partial }^{2}f/\partial w\partial \overline{w}=0$. Then Equation (7) leads to the following equalities for complex potentials $p$, $\tau$:

$$p=\frac{1}{2(1-\nu )}\left(\frac{\partial f}{\partial w}+\frac{\partial \overline{f}}{\partial \overline{w}}\right),\tau =2\frac{\partial f}{\partial \overline{w}}+\frac{1}{2(1-\nu )}\frac{{\partial }^2(\varphi -\overline{w} f-w \overline{f})}{\partial {\overline{w}}^2}$$

(8)

Furthermore, we take into account that for a plane statement the general complex solution of the Laplace equation $f$ is expressed across two analytical functions $f=F_1(w)+{\overline{F}}_2(w)$. On the other hand, the scalar potential φ in (3) is real and can be written through one analytical function $\phi ={\Phi }_1\left(w\right)+{\overline{\Phi }}_1\left(w\right)$. The following sequence of equalities shows the possibility of writing Equations (6) and (8) through potentials F₁, F₂ and ^Φ₁

$$\begin{array}{l}u=\frac{f}{\mu }+\frac{1}{4\mu (1-\nu )}\frac{\partial (\varphi -\overline{w} f-w \overline{f})}{\partial \overline{w}}=\frac{F_1+{\overline{F}}_2}{\mu }+\frac{\partial }{\partial \overline{w}}\frac{\left({\Phi }_1+{\overline{\Phi }}_1-\overline{w} (F_1+{\overline{F}}_2)-w ({\overline{F}}_1+F_2)\right)}{4\mu (1-\nu )}=\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{F_1}{\mu }+\frac{\partial }{\partial \overline{w}}\frac{\left({\overline{\Phi }}_1+4(1-\nu ){\overline{F}}_2^{(-1)}-\overline{w} {\overline{F}}_2-\overline{w} F_1-w {\overline{F}}_1\right)}{4\mu (1-\nu )}=\frac{F}{\mu }+\frac{\partial }{\partial \overline{w}}\frac{(\overline{\Phi }-\overline{w} F-w \overline{F})}{4\mu (1-\nu )}.\end{array}$$

here $F=F_1(w)$ and $\Phi ={\Phi }_1(w)+4(1-\nu )F_2^{(-1)}(w)-w{F}_2(w)$, and $F_2^{(-1)}$ is the antiderivative function $F_2$. We took into account that the derivative of the analytic function with respect to the conjugate complex variable is equal to zero.

The stresses potentials are converted similarly:

$$\begin{gathered} p=\frac{1}{2(1-\nu )}\left(\frac{\partial f}{\partial w}+\frac{\partial \overline{f}}{\partial \overline{w}}\right)=\frac{1}{2(1-\nu )}\left(\frac{\partial F_1}{\partial w}+\frac{\partial {\overline{F}}_1}{\partial \overline{w}}\right), \\ \tau =2\frac{\partial f}{\partial \overline{w}}+\frac{1}{2(1-\nu )}\frac{{\partial }^2(\varphi -\overline{w} f-w \overline{f})}{\partial {\overline{w}}^2}=\frac{{\partial }^2}{\partial {\overline{w}}^2}\frac{\left({\overline{\Phi }}_1+4(1-\nu ){\overline{F}}_2^{(-1)}-\overline{w} {\overline{F}}_2-\overline{w} F_1-w {\overline{F}}_1\right)}{4\mu (1-\nu )}. \end{gathered}$$

Thus, Equations (6) and (8) are reduced to the form of Equation (5), which are defined with two analytical functions $F(w)$ and $\Phi (w)$. Note that for problems of plane stress state in Equations (3), (5), (6) and (8) the value $\nu$ should be replaced by the value ${\nu }^{*}=\nu /(1+\nu )$. The lemma is proved. □

Theorem 1.

• Equation (5), obtained solely on the basis of the Papkovich–Neuber representation, fully corresponds to the Kolosov–Muskhelishvili representation (see [28]), in which stresses and displacements are expressed through two analytical functions using the formulas:

  $${\sigma }_x+{\sigma }_y=4\mathrm{Re}\left\{{\psi }^{\prime }(w)\right\},{\sigma }_y-{\sigma }_x+2i{\tau }_{xy}=2\left\{\overline{w}\hspace{0.17em}{\psi }^{″}(w)+{\chi }^{″}(w)\right\}$$

  (9)

  $$2\mu (u_x+i{u}_y)=(3-4\nu )\psi (w)-w\overline{{\psi }^{\prime }}(w)-\overline{{\chi }^{\prime }}(w)$$

  (10)

  where$\psi$, χ are Kolosov–Muskhelishvili’s potentials
• There is a relation between the functions$\mathit{f}$and$\varphi$ under which the Papkovich–Neuber relation can be written through one harmonic potential, assuming that $\varphi =0$.
• For problems of crack mechanics, the Pakovich–Neuber representation can always be written through one harmonic vector potential.

Proof. 

• Comparing the right and left parts of Equations (5) and (9) it is easy to see that they are completely consistent with each other, if accept that $\psi =0.5F/(1-\nu )$ , $\chi =-0.5\Phi /(1-\nu )$, or

  $$F=2(1-\nu )\psi ,\Phi =-2(1-\nu )\chi$$

  (11)
  Substitution of the functions $F(w)$ and $\Phi (w)$ from Equation (11) into Equation (5) for complex displacements $u=u_x+i{u}_y$ shows that the resulting equation exactly coincides with the expression for displacements. The first part of the theorem is proved.
• To prove the second part of the theorem, we consider again the representation (3) and show that there is somewhat overdetermined, since between the functions $\mathit{f}$ and $\varphi$ a relationship can be established, which does not change the stress–strain state. Indeed, we can introduce the following harmonic scalar function satisfying the equality:

  $$r\frac{\partial \hspace{0.17em}h}{\partial \hspace{0.17em}r}-4(1-\nu )h=\varphi ,{\nabla }^{2}h=0,\mathit{f}=\nabla h$$

  (12)
  As a result, if Equality (12) holds, then for any harmonic function $\varphi$ it can be resolved with respect to the function $h$ and the Papkovich–Neuber representation (3) can be rewritten by redefining the vector potential $\mathit{f}$ with condition $\varphi =0$.
• Let us briefly consider the cases when relation (12) is not satisfied. We represent the function $\varphi$ in the form $r^{\alpha }\chi (\phi ,\theta )$, where $\phi$ and $\theta$ are the angular coordinates, which are independent from the radial coordinate r. Equality (12) does not satisfied if $\alpha =4(1-\nu )$. For negative values of the exponent, Equation (12) always has a solution, and without loss of generality the relation (3) can be written assuming condition $\varphi =0$. Therefore, for problems of crack mechanics, the Papkovich–Neuber representation can always be written in terms of a single harmonic vector potential. The theorem is proved. □

Thus, the general solution of problems of the plane theory of elasticity can be expressed not only using two analytical functions in the form of Equation (5), but also in equivalent form using one harmonic function $f=F_1(w)+{\overline{F}}_2(w)$ (i.e., through Papkovich–Neuber complex potential):

$$u=\frac{f}{\mu }-\frac{1}{4\mu (1-\nu )}\frac{\partial (\overline{w} f+w \overline{f})}{\partial \overline{w}}$$

(13)

$$p=\frac{1}{2(1-\nu )}\left(\frac{\partial f}{\partial w}+\frac{\partial \overline{f}}{\partial \overline{w}}\right),\tau =2\frac{\partial f}{\partial \overline{w}}-\frac{1}{2(1-\nu )}\frac{{\partial }^2(\overline{w} f+w \overline{f})}{\partial {\overline{w}}^2}$$

(14)

Let us consider the canonical singular problem of the theory of elasticity, which defines the problem of fracture mechanics for the plane problem:

$$y=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\infty <x<0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\sigma }_y={\tau }_{xy}=0,$$

and leads to the determination of the correct solution in stresses, tending to zero when $w\to \infty$ as $O({\left|w\right|}^{1/2})$, $w=x+iy$, $i=\sqrt{-1}$.

It is known that the correct solutions to this problem for a plane problem for normal separation crack and transversal shear, respectively are given through two Kolosov–Muskhelishvili potentials. This solution for a crack open displacement is written as follows (see [1]):

$$u_x=\frac{K_I}{\mu }\sqrt{\frac{r}{2\pi }}\left(1-2\nu +{\sin }^2\frac{\theta }{2}\right)\cos \frac{\theta }{2},u_y=\frac{K_I}{\mu }\sqrt{\frac{r}{2\pi }}\left(2-2\nu -{\cos }^2\frac{\theta }{2}\right)\sin \frac{\theta }{2}$$

(15)

$${\sigma }_x=\frac{K_I}{\sqrt{2\pi r}}\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)\cos \frac{\theta }{2},{\sigma }_y=\frac{K_I}{\sqrt{2\pi r}}\left(1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)\cos \frac{\theta }{2}$$

(16)

$${\tau }_{xy}=\frac{K_I}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\sin \frac{\theta }{2}$$

(17)

Here $u_x$, $u_y$, ${\sigma }_x$, ${\sigma }_y$, ${\tau }_{xy}$ are components of the displacement vector and stress tensor, respectively, $r,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta$ are polar coordinates in the vicinity of the top of the crack $K_I$ is stress intensity factors.

Consider again the Papkovich–Neuber representation (see [27]), which allows us to present a general solution to the problem of the theory of elasticity; that is, both displacement vector $\mathit{u}$ and their corresponding stresses $\mathit{\sigma }(\mathit{u})$ on a surface element with a normal vector $\mathit{n}$, through only one harmonic vector potential $\mathit{f}$ (in accordance with Theorem 1):

$$\mathit{u}=\frac{\mathit{f}}{\mu }-\frac{\nabla (\mathit{r} \mathit{f})}{4\mu (1-\nu )},\mathit{\sigma }(\mathit{u})=\frac{\partial \mathit{f}}{\partial n}+\mathit{n}\nabla \mathit{f}+\frac{\nu (\mathit{n}\mathrm{div}\mathit{f})}{1-\nu }-\frac{1}{2(1-\nu )}\frac{\partial \nabla (\mathit{r}\mathit{f})}{\partial n},\Delta \mathit{f}=0$$

(18)

Here, the differential combination $\mathit{n}\nabla \mathit{f}$ means the expression $\left\{n_j (\partial f_j/\partial x_i)\right\}$, $\mathit{\sigma }(\mathit{u})=\left\{{\sigma }_{ij}{n}_j\right\}$, where ${\sigma }_{ij}$ is the stress tensor. Let us prove that the solution of the classical singular problem (for the example of a crack open displacement (15)–(17)) can be represented also through one harmonic complex-valued potential.

Theorem 2.

An explicit expression exists for the harmonic potential for which the general representation of the solution of the plane Papkovich–Neuber problem (13), (14) is completely equivalent to the classical representation for the singular solution for a crack Mode I given by Equations (15)–(17).

Proof. 

Let us find an explicit expression of the harmonic potential $f$ for a crack Mode I. We first consider the classical solution (13) for the displacement components $u_x$, $u_y$ and transform them, distinguishing the coordinate $y=r\sin \theta =i(w-\overline{w})/2$. We obtain:

$$u_x=\frac{K_I}{\mu }\sqrt{\frac{r}{2\pi }}\left((1-2\nu )\cos \frac{\theta }{2}+\frac{1}{2}\sin \theta \sin \frac{\theta }{2}\right),u_y=\frac{K_I}{\mu }\sqrt{\frac{r}{2\pi }}\left(2(1-\nu )\sin \frac{\theta }{2}-\frac{1}{2}\sin \theta \cos \frac{\theta }{2}\right).$$

Using the written equalities, we can get a complex-valued value of displacements $u=u_x+i{u}_y$:

$$\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}u=u_x+i{u}_y=\frac{K_I}{\sqrt{2\pi }\mu }\left(2(1-\nu )w^{1/2}-i\frac{y}{2}{\overline{w}}^{-1/2}-\mathrm{Re}{w}^{1/2}\right)=\\ =\frac{K_I}{\sqrt{2\pi }\mu }\left(2(1-\nu )w^{1/2}+\frac{\overline{w}-w}{4}{\overline{w}}^{-1/2}-\frac{w^{1/2}+{\overline{w}}^{1/2}}{2}\right)=\frac{K_I}{\sqrt{2\pi }\mu }\left(2(1-\nu )w^{1/2}-\frac{w{\overline{w}}^{-1/2}}{4}-\frac{w^{1/2}}{2}-\frac{{\overline{w}}^{1/2}}{4}\right).\end{array}$$

In the resulting expression, we select the derivative with respect to the coordinate $\overline{w}$:

$$u=K_I\sqrt{\frac{2}{\pi }}(1-\nu )\left(\frac{w^{1/2}}{\mu }-\frac{1}{4\mu (1-\nu )}\frac{\partial }{\partial \overline{w}}\left(w{\overline{w}}^{1/2}+\overline{w}{w}^{1/2}+\frac{{\overline{w}}^{3/2}}{3}\right)\right)$$

(19)

Assuming in (19) that $w^{1/2}=f$, we rewrite the complex value of displacements $u=u_x+i{u}_y$ in the form:

$$u=K_I\sqrt{\frac{2}{\pi }}(1-\nu )\left(\frac{f}{\mu }-\frac{1}{4\mu (1-\nu )}\frac{\partial }{\partial \overline{w}}\left(w\hspace{0.17em}\overline{f}+\overline{w}\hspace{0.17em}f+\frac{{\overline{w}}^{3/2}}{3}\right)\right)$$

(20)

In order to reduce Equation (20) to the form (13) we must show that the last term in Equation (20) can always be compensated by the corresponding choice of the harmonic function. Instead of the harmonic function $f=w^{1/2}$ in Equation (20), we propose to consider another harmonic function $f_I$ obtained as the sum of the function $f=w^{1/2}$ and the harmonic function $A{\overline{w}}^{1/2}$ with some unknown coefficient $A$, so far $f_I=w^{1/2}+A{\overline{w}}^{1/2}$.

It is easy to verify that one can find a constant $A$ such that Expression (20), in which instead of the function $f=w^{1/2}$ stands $f_I$, coincides completely in appearance with Formula (13) for complex displacements, found in accordance with the Papkovich–Neuber representation. Indeed, after some transformations we find $A=-1/(5-8\nu )$. Now the statement of the theorem is verified by direct substitution. Thus, for a crack open displacement in the classical formulation, the field of elastic displacements and stresses in the vicinity of the crack tip is described by the Papkovich–Neuber representation (13) and (14) in complex form with a potential $f_I$ having the following expression through complex variables $w$ and $\overline{w}$:

$$f_I=K_I\sqrt{\frac{2}{\pi }}\left(w^{1/2}-\frac{{\overline{w}}^{1/2}}{5-8\nu }\right)(1-\nu )$$

(21)

We have thus proved that the mathematical description of the crack is based on harmonic functions with a half-integer value of the exponent for the complex variable $w$. The form obtained for representing the solution is based on one complex potential, which represents the solution in a form convenient for construction of the gradient solutions. The theorem is proved. □

The statement proved above is also valid for crack of mode II and crack of mode III. For example, for the classical singular solution mode II:

$$u_x=\frac{K_{II}}{\mu }\sqrt{\frac{r}{2\pi }}\left(2-2\nu +{\cos }^2\frac{\theta }{2}\right)\sin \frac{\theta }{2},u_y=-\frac{K_{II}}{\mu }\sqrt{\frac{r}{2\pi }}\left(1-2\nu -{\sin }^2\frac{\theta }{2}\right)\cos \frac{\theta }{2}$$

(22)

$${\sigma }_x=-\frac{K_{II}}{\sqrt{2\pi r}}\left(2+\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\right)\sin \frac{\theta }{2},{\sigma }_y=\frac{K_{II}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\sin \frac{\theta }{2}$$

(23)

$${\tau }_{xy}=\frac{K_{II}}{\sqrt{2\pi r}}\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)\cos \frac{\theta }{2}$$

(24)

the following harmonic function of complex variables $w, \overline{w}$ can be found:

$$f_{II}=-i\hspace{0.17em}{K}_{II}\sqrt{\frac{2}{\pi }}\left(w^{1/2}-\frac{3{\overline{w}}^{1/2}}{5-8\nu }\right)(1-\nu )$$

(25)

This harmonic function establishes a correspondence of the classical singular solution (22)–(24) with the solution given by the Papkovich–Neuber representation (13) and (14).

Finally, we consider the longitudinal shear crack (Mode III), which in the spatial theory of elasticity is described by the following relations for displacements and stresses:

$$u_z=\frac{K_{III}}{\mu }\sqrt{\frac{2r}{\pi }}\sin \frac{\theta }{2},{\tau }_{xz}=-\frac{K_{III}}{\sqrt{2\pi r}}\sin \frac{\theta }{2},{\tau }_{yz}=\frac{K_{III}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}$$

(26)

It is easy to check that the stress–strain state for this case (26) is also completely described by the spatial version (3) of the Papkovich–Neuber representation with non-zero plane harmonic potential $f_z(x,y)$ and its compensating potential $\varphi =z f_z(x,y)$, where:

$$f_{III}=f_z(x,y)=K_{III}\sqrt{\frac{2}{\pi }}\mathrm{Im}\left(w^{1/2}\right)$$

(27)

Thus, strain–stress state for Mode I, II, and III singular cracks can be described on the basis of the Papkovich–Neuber formulas with the aid of one complex potential with a fractional degree. These forms are convenient for constructing a generalized gradient regular solution.

Remark 1. 

Note that harmonic functions establishing a correspondence between singular classical solutions of crack mechanics and solutions constructed using the Papkovich–Neuber representation are not analytic because, as is easily verifiable, the Cauchy relations are not satisfied for them.

In the future, our goal is to construct the local stresses and displacements associated with classical stresses and displacements through the Helmholtz equation using generalized elasticity. Consequently, the field of local stresses will describe the non-singular crack solutions.

3. Regular Gradient Solutions in Crack Mechanics

Let us construct a regular solution for crack Mode I, using an applied version of the non-local theory of elasticity. Using the algorithm discussed earlier in the Introduction, we can determine the local displacement and stress fields as general solutions of the inhomogeneous Helmholtz Equation (2), on the right-hand sides of which the well-known classical solutions are taken. We rewrite relation (2), introducing on the right-hand sides of the Helmholtz equations the classical solutions written in terms of complex displacements $u(w,\overline{w})$ and complex potentials $p=p(w,\overline{w})$, $\tau =\tau (w,\overline{w})$ (see Equation (4): $p=({\sigma }_x+{\sigma }_y)/2$, $\tau =({\sigma }_x-{\sigma }_y)/2+i{\tau }_{xy}$. The generalized theory of elasticity allows finding the local stresses and displacements associated with classical stresses and displacements through the Helmholtz equation. The fields of local stresses describe the regular crack solutions as:

$$U-s^2 \Delta U=u,\mathrm{P}-s^2 \Delta \mathrm{P}=p,\mathrm{T}-s^2 \Delta \mathrm{T}=\tau$$

(28)

Here $u$, $p$, $\tau$ are the potentials of displacements and stresses expressed through the Papkovich–Neuber potential (21) by the formulas (13) and (14).

The general solution of Equation (28) is constructed as the sum of the general solution of the homogeneous Helmholtz equation and the particular solution of the inhomogeneous Helmholtz equation. It holds the following lemma, indicating the structure of a particular solution of the Helmholtz equation.

Lemma 2. 

Assume that function $\varphi$ is the right-hand side of the Helmholtz equation, written with respect to a function$\Phi$. Assume also that function$\varphi$ is a biharmonic function:

$$\Phi -s^2 \Delta \Phi =\varphi ,$$

(29)

where ${\Delta }^2\varphi =0$. Then, a particular solution of the inhomogeneous Helmholtz equation has the form:

$$\Phi =\varphi +s^2\Delta \varphi .$$

(30)

Proof. 

The lemma is proved by directly substituting Expression (30) into Equation (29). □

The regularity of the generalized solution of Equation (29) is ensured by the structure of a homogeneous solution and the special choice of arbitrary constants in this solution. Since the functions $u$, $p$, $\tau$ in Equation (28) and their particular solutions (see Equation (30)) contain singularities with only a half-integer value of the exponent in the degree of the complex variable $w$, among the solutions of the homogeneous Helmholtz equation we are interested only in singular functions with the same value of the exponent in the degree of the complex variable $w$.

It was shown in [29,30] that a system of such singular solutions can be constructed in an explicit analytical form using radial multipliers satisfying a special recurrence relation:

$${\widehat{\Phi }}_n-s^2\Delta {\widehat{\Phi }}_n=0,{\widehat{\Phi }}_n(w,\overline{w})={\widehat{h}}_n( r)w^{-1/2-n},r={(w\hspace{0.17em}\overline{w})}^{1/2},n\ge 0$$

(31)

$${\widehat{h}}_n(r)=\frac{1}{2}\left(r{\widehat{h^{\prime }}}_{n-1}(r)-(2n-1){\widehat{h}}_{n-1}(r)\right),n\ge 1,{\widehat{h}}_0( r)=e^{- r/s}$$

(32)

Thus, solutions of Equation (28) in the gradient theory of cracks can be constructed by explicitly taking into account Expressions (31) and (32).

A complete representation of the generalized solution (classical solutions) for a crack Mode I for generalized displacements $u_i$ and generalized complex stress potentials $p$, $\tau$ is given by Formulas (13), (14) and (21). As a result, taking into account the statement of Lemma 2 and Relations (31) and (32), we find:

$$U=\frac{f}{\mu }-\frac{1}{4\mu (1-\nu )}\frac{\partial (\overline{w} f+w \overline{f})}{\partial \overline{w}}-\frac{s^2}{\mu (1-\nu )}\frac{{\partial }^2\overline{f}}{\partial {\overline{w}}^2}+{\displaystyle \sum _n{A}_n{\widehat{\Phi }}_n(w,\overline{w})}$$

(33)

$$\mathrm{P}=\frac{1}{2(1-\nu )}\left(\frac{\partial f}{\partial w}+\frac{\partial \overline{f}}{\partial \overline{w}}\right)+{\displaystyle \sum _n{B}_n{\widehat{\Phi }}_n(w,\overline{w})}$$

(34)

$$\mathrm{T}=2\frac{\partial f}{\partial \overline{w}}-\frac{1}{2(1-\nu )}\frac{{\partial }^2(\overline{w} f+w \overline{f})}{\partial {\overline{w}}^2}-\frac{2s^2}{1-\nu }\frac{{\partial }^3\overline{f}}{\partial {\overline{w}}^3}+{\displaystyle \sum _n{C}_n{\widehat{\Phi }}_n(w,\overline{w})}$$

(35)

Here $A_n$, $B_n$, $C_n$ are unknown coefficients that are selected from the compensation condition for singular terms in gradient potentials $U$, ${\rm P}$, ${\rm T}$.

The specific structure of the solutions in the last terms of the above-stated equations, which are general solutions of the homogeneous Helmholtz equations, is found taking into account the order of the singularities in the corresponding particular solutions. So, in Expression (33), the first three terms determine a particular solution of the Helmholtz equation for generalized displacement $U$. They include derivatives with respect to the argument $\overline{w}$ up to the second order, which give rise to singularities of the form $w^{-3/2}$. Therefore, in order to compensate for the singularities in (33), we should use $A_0=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}_1\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}_n=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\ge 2$.

Furthermore, in Equality (34), the first term, which is a particular solution of the Helmholtz equation for the harmonic potential of stresses P, contains only the first derivative with respect to variables $w,\hspace{0.17em}\hspace{0.17em}$$\overline{w}$. Therefore, in the last term we should put ${В}_0\ne 0$, ${В}_n=0$, $n\ge 1$.

Finally, since in Equation (35) a particular solution includes derivatives with respect to the argument $\overline{w}$ up to the third order and contains singularities $w^{-1/2}$, $w\hspace{0.17em}{\overline{w}}^{-3/2}$ and $w^{-5/2}$, then in the term representing the general solution of the homogeneous equation, we should put ${С}_0\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{С}_1=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{С}_2\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{С}_n=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\ge 3$.

The constants $A_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{В}_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{С}_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{С}_2$ in the solution obtained in this way are explicitly found in such a way as to compensate for the singularities in the general solutions (33)–(35). We get:

$$A_1=\frac{K_I\hspace{0.17em}{s}^2}{\sqrt{2\pi }\mu },B_0=-\frac{K_I}{2\sqrt{2\pi }},C_0=\frac{K_I}{4\sqrt{2\pi }},C_2=K_I\sqrt{\frac{2}{\pi }}\hspace{0.17em}{s}^2$$

(36)

Thus, Equalities (33)–(36) allow us to construct regular generalized solutions for complex displacements $U$ and complex stress potentials P and $T$. The components of generalized displacements $U_x$, $U_y$, and generalized stresses ${\Xi }_x$, ${\Xi }_y$, ${\mathrm{T}}_{xy}$ in the gradient theory of elasticity are calculated through the real and imaginary parts of complex potentials (33)–(35) according to the following formulas:

$$U_x=\mathrm{Re}U,U_y=\mathrm{Im}U,{\Xi }_x=\mathrm{Re}(\mathrm{P}+\mathrm{T}),{\Xi }_y=\mathrm{Re}(\mathrm{P}-\mathrm{T}),{\mathrm{T}}_{xy}=\mathrm{Im}\mathrm{T}$$

(37)

As a result, we obtain the following regular generalized solutions describing the non-singular stress–strain state of a normal separation crack in a gradient formulation:

$$U=\frac{K_I}{\sqrt{2\pi }\mu }\left[\left(\frac{3}{2}-2\nu \right)w^{1/2}-\frac{{\overline{w}}^{1/2}}{4}+\frac{s^2}{2}\left(1-\frac{{(r/s)}^2}{2}+2{\widehat{h}}_1(r)\right){\overline{w}}^{-3/2}\right]$$

(38)

$$\mathrm{P}=\frac{K_I}{\sqrt{2\pi }}\frac{1-{\widehat{h}}_0(r)}{2}\left(w^{-1/2}+{\overline{w}}^{-1/2}\right)$$

(39)

$$\mathrm{T}=-\frac{K_I}{4\sqrt{2\pi }}\left[\left(1-{\widehat{h}}_0(r)\right){\overline{w}}^{-1/2}+6s^2\left(1-\frac{{(r/s)}^2}{6}-\frac{4}{3}{\widehat{h}}_2(r) \right){\overline{w}}^{-5/2}\right]$$

(40)

where:

$${\widehat{h}}_0(r)=e^{-r/s},{\widehat{h}}_1(r)=-\frac{r/s+1}{2}{e}^{-r/s},{\widehat{h}}_2(r)=\frac{(r/s{)}^2+3(r/s+1)}{4}{e}^{-r/s}.$$

When deriving (38)–(40), we take into account the relations $w {\overline{w}}^{-1/2}=r^2{\overline{w}}^{-3/2}$, $w {\overline{w}}^{-3/2}=r^2{\overline{w}}^{-5/2}$ in Expressions (39) and (40) written down taking into account (21). We also take into account that functions ${\widehat{h}}_0$, ${\widehat{h}}_1$ and ${\widehat{h}}_2$ are real functions. The coefficients $A_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{В}_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{С}_i$ for the radial multipliers ${\widehat{h}}_0$, ${\widehat{h}}_1$ and ${\widehat{h}}_2$ are chosen so that in the expressions (38)–(40) there are no singular components. We can verify this, if we take into account the specific form of functions ${\widehat{\Phi }}_n(w,\overline{w})$ and the asymptotic behavior of the exponential in functions ${\widehat{h}}_0$, ${\widehat{h}}_1$ and ${\widehat{h}}_2$ in Equations (38)–(40):

$$\left(x+1\right)e^{-x}=1-x^2+O(x^3),(x^2/2+x+1)e^{-x}=1-x^3/6+O(x^4).$$

(41)

Using the polar coordinates $w=r\hspace{0.17em}(\cos \theta +i\sin \theta )$ in Expressions (38)–(40), we obtain an explicit regular everywhere generalized gradient solution for the normal separation crack, written for the components of displacement:

$$U_x=\frac{K_I}{\mu }\sqrt{\frac{r}{2\pi }}\left[\left(1-2\nu +{\sin }^2\frac{\theta }{2}\right)\cos \frac{\theta }{2}+\frac{s^2{r}^{-2}}{2}\left(1-(r/s+1)e^{-r/s}\right)\cos \frac{3\theta }{2}\right]$$

(42)

$$U_y=\frac{K_I}{\mu }\sqrt{\frac{r}{2\pi }}\left[\left(2-2\nu -{\cos }^2\frac{\theta }{2}\right)\sin \frac{\theta }{2}-\frac{s^2{r}^{-2}}{2}\left(1-(r/s+1)e^{-r/s}\right)\sin \frac{3\theta }{2}\right]$$

(43)

and stress components:

$${\Xi }_x=\frac{K_I}{\sqrt{2\pi r}}\left[\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}-\frac{3e^{-r/s}}{4}\right)\cos \frac{\theta }{2}-\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)\cos \frac{5\theta }{2}\right]$$

(44)

$${\Xi }_y=\frac{K_I}{\sqrt{2\pi r}}\left[\left(1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}-\frac{5e^{-r/s}}{4}\right)\cos \frac{\theta }{2}+\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)\cos \frac{5\theta }{2}\right]$$

(45)

$${\mathrm{T}}_{xy}=\frac{K_I}{\sqrt{2\pi r}}\left[\left(\cos \frac{\theta }{2}\cos \frac{3\theta }{2}+\frac{e^{-r/s}}{4}\right)\sin \frac{\theta }{2}-\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)\sin \frac{5\theta }{2}\right]$$

(46)

Note that as the scale parameter tends to zero $s\to 0$, the solutions (42)–(46) go into the classical singular solution.

The asymptotics of Expressions (44)–(46) up to terms of the order of $O(r/s)$ is calculated on the basis of Relation (41), where $x=r/s$. To use (41), we transform the expression in parentheses in (44)–(46) as follows:

$$\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)=\frac{3s^2}{2r^2}\left(1-\left(\frac{r^2}{2s^2}+r/s+1\right)e^{-r/s} \right)+\frac{e^{-r/s}}{4}.$$

As a result, we obtain the asymptotic behavior for stresses, which shows the absence of singularities at the origin:

$$\begin{gathered} {\Xi }_x=\frac{1}{s}{K}_I\sqrt{\frac{r}{2\pi }}\left[\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)\cos \frac{\theta }{2}-\frac{1}{4}\cos \frac{5\theta }{2}\right]+O\left(\frac{r^{3/2}}{s^2}\right), \\ {\Xi }_y=\frac{1}{s}{K}_I\sqrt{\frac{r}{2\pi }}\left[\left(1+\sin \frac{\theta }{2}\cos \frac{3\theta }{2}\right)\cos \frac{\theta }{2}+\frac{1}{4}\cos \frac{5\theta }{2}\right]+O\left(\frac{r^{3/2}}{s^2}\right), \\ {\mathrm{T}}_{xy}=\frac{1}{s}{K}_I\sqrt{\frac{r}{2\pi }}\left[\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}-\frac{1}{4}\sin \frac{5\theta }{2}\right]+O\left(\frac{r^{3/2}}{s^2}\right). \end{gathered}$$

Using the radial multipliers method and the Papkovich–Neuber representations for classical solutions of cracks Mode II and Mode III through the one harmonic potential, the local solutions for displacement and stresses of these modes of cracks were established:

$$U_x=\frac{K_{II}}{\mu }\sqrt{\frac{r}{2\pi }}\left[\left(2-2\nu +{\cos }^2\frac{\theta }{2}\right)\sin \frac{\theta }{2}+\frac{s^2{r}^{-2}}{2}\left(1-(r/s+1)e^{-r/s}\right)\sin \frac{3\theta }{2}\right]$$

(47)

$$U_y=\frac{K_{II}}{\mu }\sqrt{\frac{r}{2\pi }}\left[\left(-1+2\nu +{\sin }^2\frac{\theta }{2}\right)\cos \frac{\theta }{2}+\frac{s^2{r}^{-2}}{2}\left(1-(r/s+1)e^{-r/s}\right)\cos \frac{3\theta }{2}\right]$$

(48)

$${\Xi }_x=-\frac{K_{II}}{\sqrt{2\pi r}}\left[\left(2+\cos \frac{\theta }{2}\cos \frac{3\theta }{2}-\frac{7e^{-r/s}}{4}\right)\sin \frac{\theta }{2}-\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)\sin \frac{5\theta }{2}\right]$$

(49)

$${\Xi }_y=\frac{K_{II}}{\sqrt{2\pi r}}\left[\left(\cos \frac{\theta }{2}\cos \frac{3\theta }{2}+\frac{e^{-r/s}}{4}\right)\sin \frac{\theta }{2}-\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)\sin \frac{5\theta }{2}\right]$$

(50)

$${\mathrm{T}}_{xy}=\frac{K_{II}}{\sqrt{2\pi r}}\left[\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}-\frac{3e^{-r/s}}{4}\right)\cos \frac{\theta }{2}-\frac{s^2}{2r^2}\left(3-\left(\frac{r^2}{s^2}+3(r/s+1)\right)e^{-r/s} \right)\cos \frac{5\theta }{2}\right]$$

(51)

and

$$U_z=\frac{K_{III}}{\mu }\sqrt{\frac{2r}{\pi }}\sin \frac{\theta }{2},T_{xz}=-\frac{K_{III}}{\sqrt{2\pi r}}\left(1-e^{-r/s}\right)\sin \frac{\theta }{2},T_{yz}=\frac{K_{III}}{\sqrt{2\pi r}}\left(1-e^{-r/s}\right)\cos \frac{\theta }{2}$$

(52)

Analytical solutions for displacements and stresses (42)–(46) and (47)–(52) supplement the results presented in the work [29].

Non-singular solutions (44)–(46) are the basis for constructing and testing a new concept of stress concentration in crack mechanics proposed in [26]. Indeed, we can see that for the problem considered above, the normal stresses ${\Xi }_y$ along the crack extension can be represented as ${\Xi }_y=\frac{K_I{с}^{1/2}}{\sqrt{2\pi }}{{\Xi }_y}^0(\overline{r},\lambda )$, $\overline{r}=r/c,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\lambda =c/s$, where $c$ is some parameter of the length. It is easy to verify, that the real value ${{\Xi }_y}^0(\overline{r},\lambda )$ is a function of $\overline{r}$ and is a positive bounded continuous function of the parameter $\overline{r}$ over the entire determination interval $0<\overline{r}<\infty$ that becomes zero when $\overline{r}=0$. The maximum of this function is realized in some neighborhood of the point $\overline{r}=0,\hspace{0.17em}\hspace{0.17em}\overline{r}>0$. 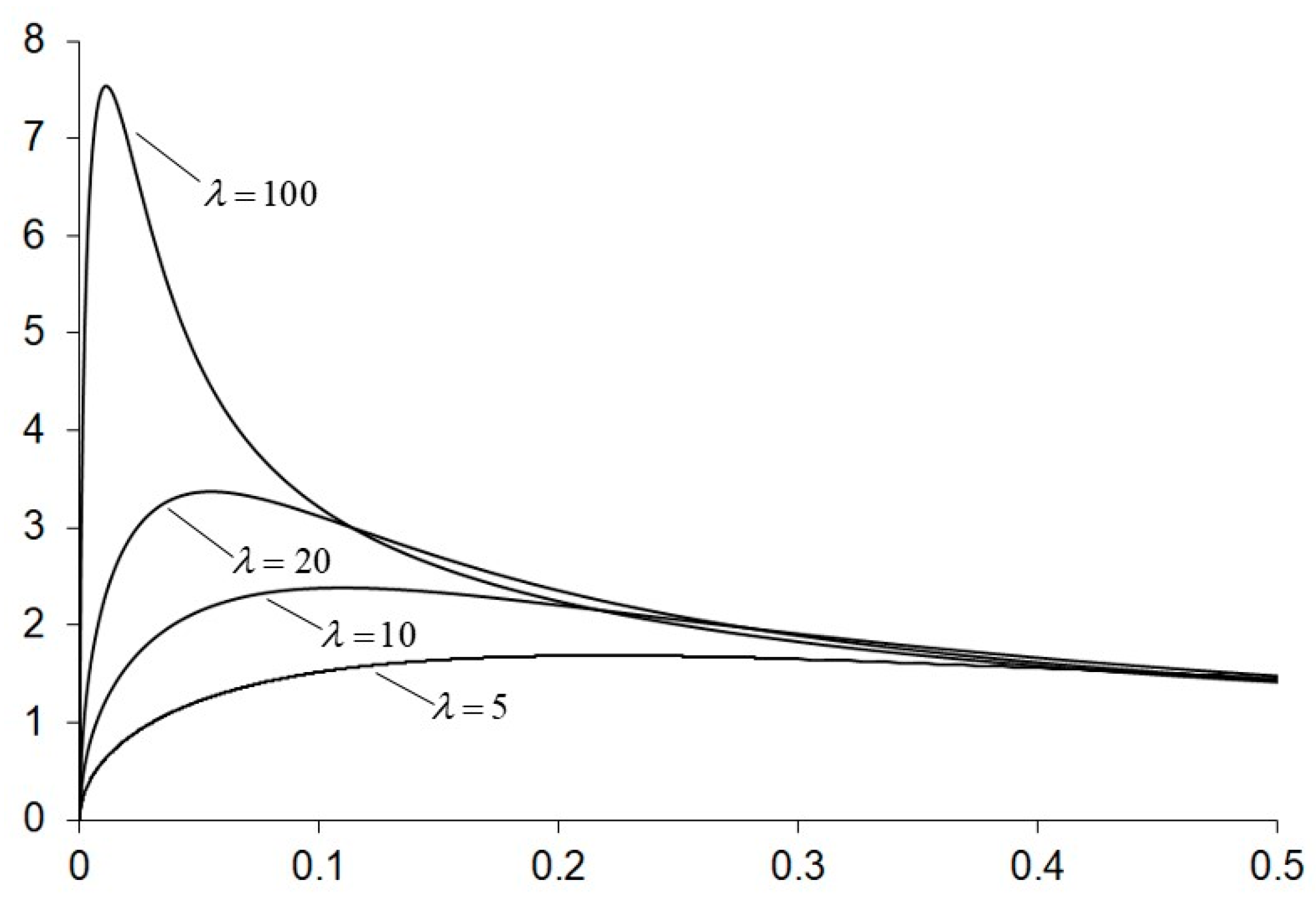Figure 1 shows the distribution of normalized stresses ${{\Xi }_y}^0(\overline{r}\lambda )$ in the vicinity of the crack tip alone the normalized distance from the crack tip ($\theta =0$). Obviously, the distribution of this function over the parameter $\overline{r}$ is a typical picture for stress concentration.

Therefore, to evaluate the strength, it is proposed to use the following procedure. First, the dependence of the maximums of relative stresses ${{\Xi }_y}^0(\overline{r}\lambda )$ on the parameter $\lambda$ is found. Then, using the known explicit Equation (45), the dependence of the maximum points of function ${{\Xi }_y^0}_{\max }(\lambda )$ on the parameter $\lambda$ is constructed. This dependence is essentially a dependence of the stress concentration coefficient on a parameter $\lambda$. In the case when the ultimate stress level characterizing failure is determined by the ultimate stresses ${\sigma }_b$ for brittle cracks, the constructed dependence allows one to determine the relative scale parameter $\lambda =c/s$, which along with tensile strength is characteristic of the fracture for brittle cracks.

4. Conclusions

A new representation is proposed, for the first time, for the classical asymptotic solution for singular cracks through harmonic potentials Equations (21), (25) and (27), which allows explicitly indicating the structure of particular solutions of the equation. On the other hand, the use of the radial factor method made it possible to establish the explicit form of the corresponding general solutions of the homogeneous Helmholtz equation. Together, the representations obtained make it possible to indicate, for the first time, a clear procedure for determining the exact solutions for non-singular local stress fields and the corresponding displacement fields. The complex form of representation of solutions leads not only to compact solutions, but ensures their completeness, eliminating the possibility of losing some components of solutions. We believe that the solutions obtained can be considered as a reference for similar problems in the gradient mechanics of cracks.