Solving Nonholonomic Systems with the Tau Method
Abstract
:1. Introduction
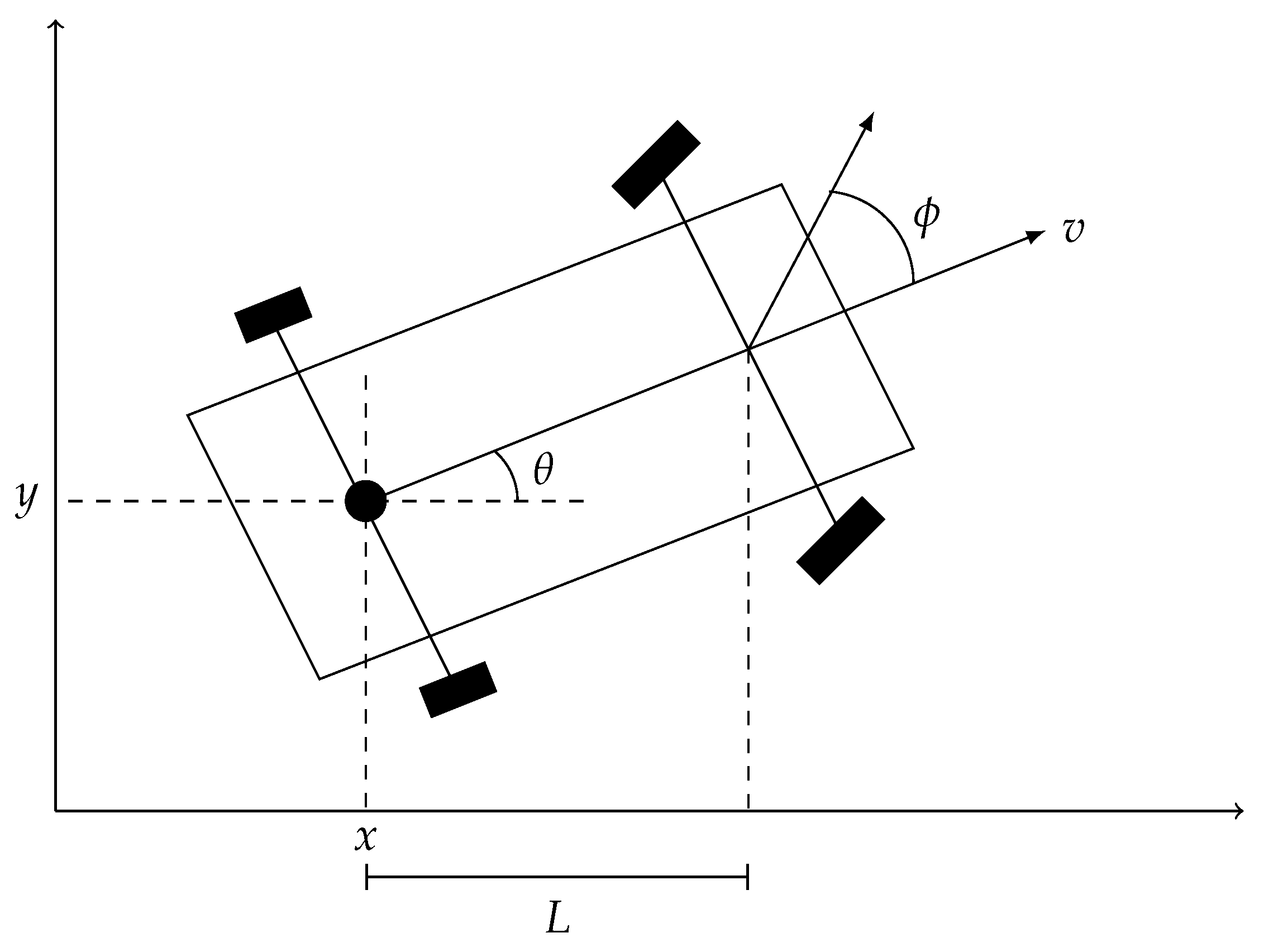
2. Nonholonomic Wheeled Vehicle Model
3. Optimal Control Problems
Pontryagin Maximum Principle
4. Tau Method
4.1. Preliminaries and Notation
4.2. Nonlinear Problems
5. Numerical Experiments
5.1. System Model
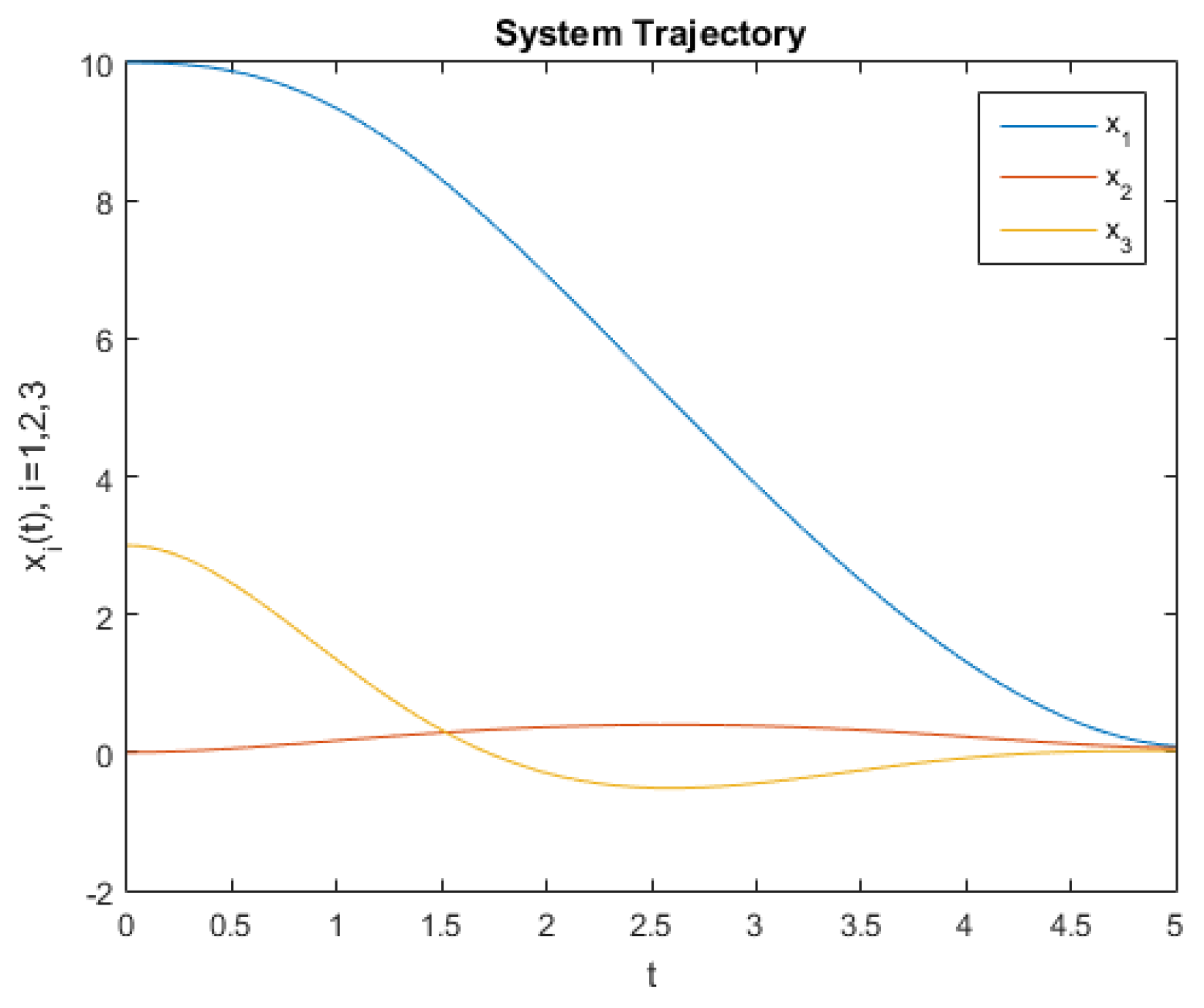
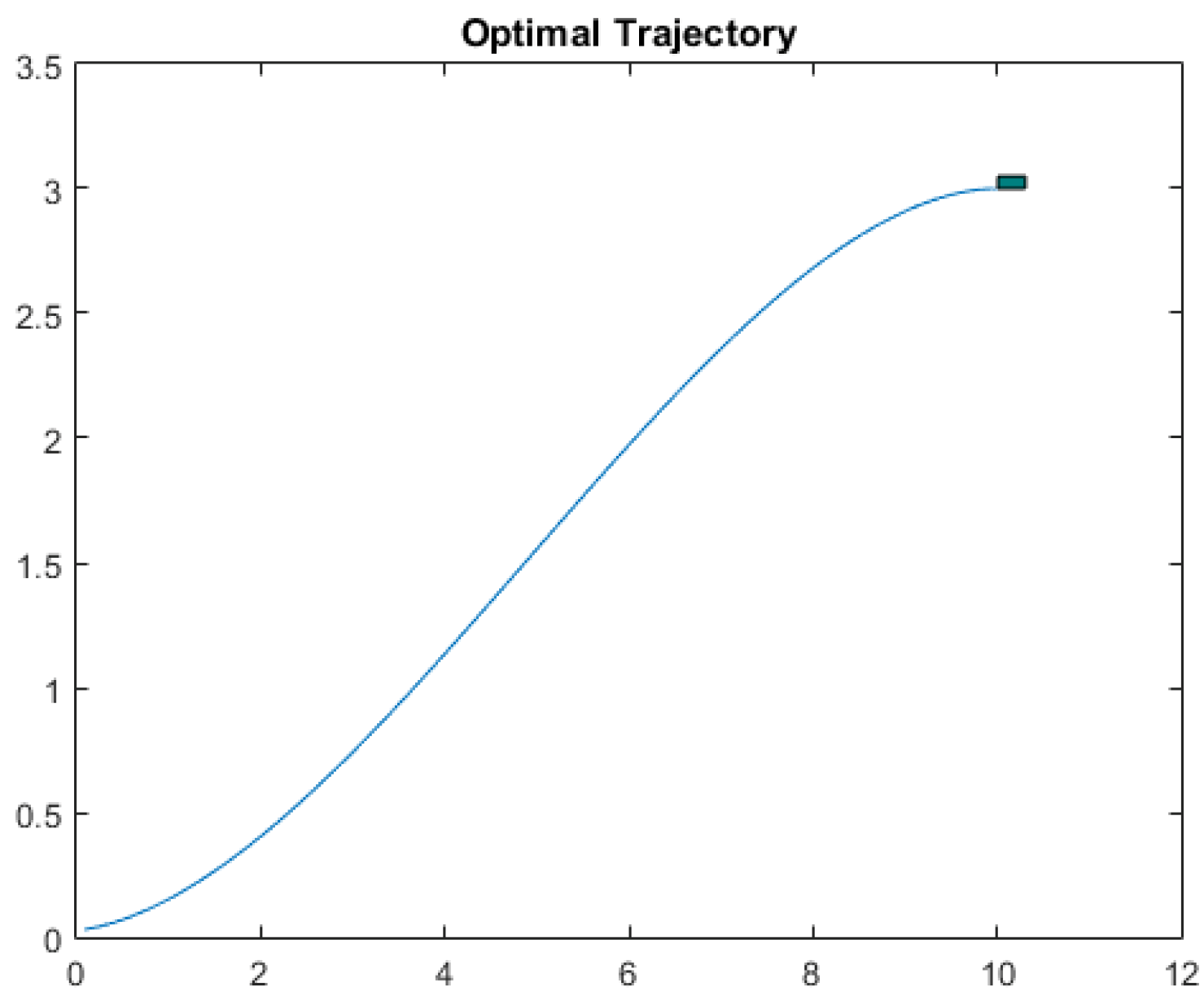
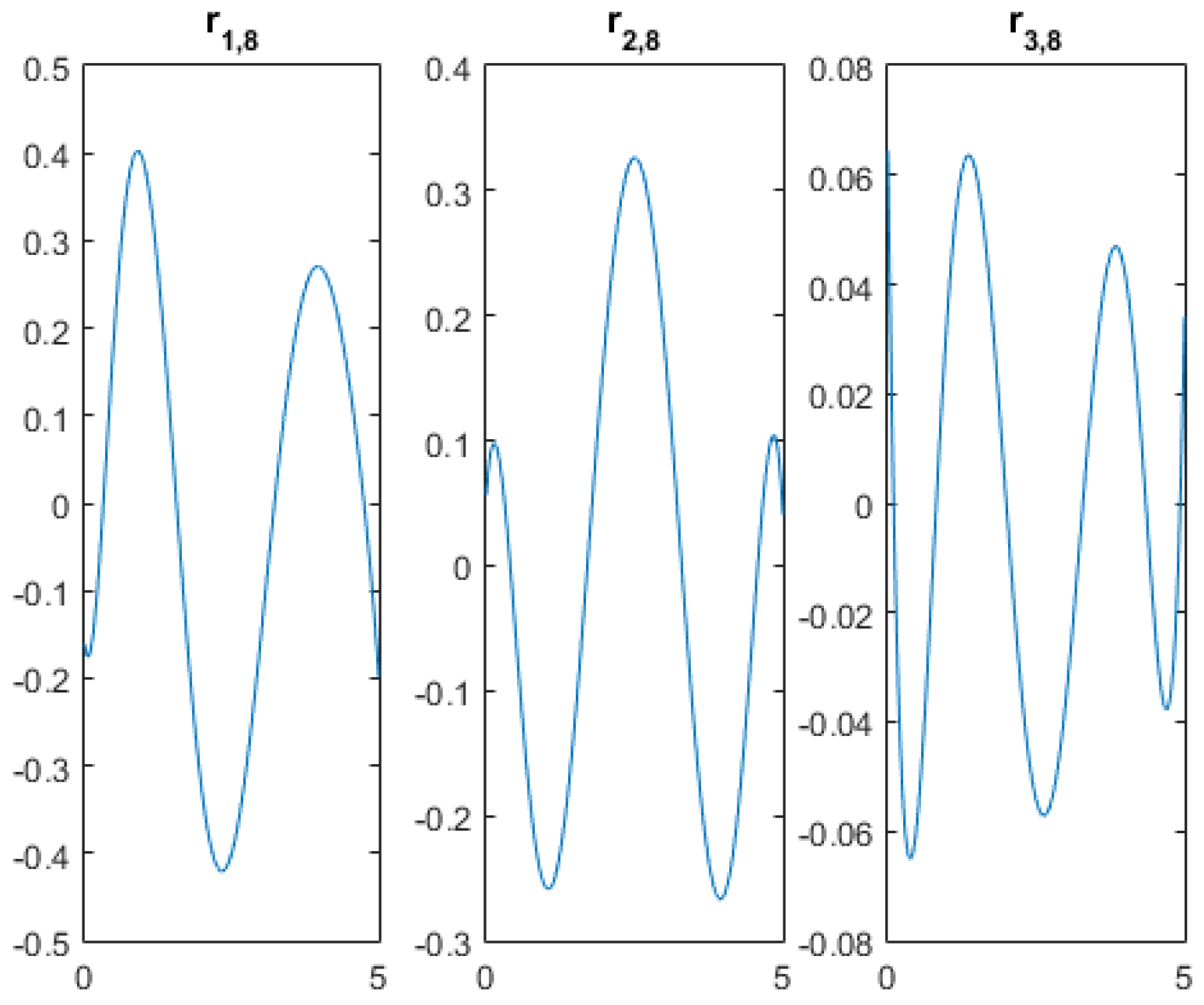
5.2. Numerical Results
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Fontes, F.A.C.C. Discontinuous feedbacks, discontinuous optimal controls, and continuous-time model predictive control. Int. J. Robust Nonlinear Control IFAC Affil. J. 2003, 13, 191–209. [Google Scholar] [CrossRef]
- Kolmanovsky, I.; McClamroch, N.H. Developments in nonholonomic control problems. IEEE Control Syst. Mag. 1995, 15, 20–36. [Google Scholar]
- Athans, M.; Falb, P.L. Optimal Control: An Introduction to the Theory and Its Applications; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Ortiz, E.L.; Samara, H.J. An operational approach to the Tau method for the numerical solution of non-linear differential equations. Computing 1981, 27, 15–25. [Google Scholar] [CrossRef]
- Angeles, J.; Kecskemethy, A. Kinematics and Dynamics of Multi-Body Systems; Springer: Berlin, Germany, 2014. [Google Scholar]
- De Luca, A.; Oriolo, G.; Samson, C. Feedback control of a nonholonomic car-like robot. In Robot Motion Planning and Control; Springer: Berlin, Germany, 1998; pp. 171–253. [Google Scholar]
- Coleman, J. The Lanczos tau-method. IMA J. Appl. Math. 1976, 17, 85–97. [Google Scholar] [CrossRef]
- Lanczos, C. Trigonometric interpolation of empirical and analytical functions. J. Math. Phys. 1938, 17, 123–199. [Google Scholar] [CrossRef]
- Trindade, M.; Matos, J.; Vasconcelos, P.B. Towards a Lanczos’Tau-method toolkit for differential problems. Math. Comput. Sci. 2016, 10, 313–329. [Google Scholar] [CrossRef]
- Vasconcelos, P.; Matos, J.; Trindade, M. Spectral Lanczos’ Tau Method for Systems of Nonlinear Integro-Differential Equations. In Integral Methods in Science and Engineering; Constanda, C., Dalla Riva, M., Lamberti, P., Musolino, P., Eds.; Birkhäuser: Cham, Switzerland, 2017; Volume 1, pp. 305–314. [Google Scholar]
- Gavina, A.; Matos, J.; Vasconcelos, P.B. Improving the Accuracy of Chebyshev Tau Method for Nonlinear Differential Problems. Math. Comput. Sci. 2016, 10, 279–289. [Google Scholar] [CrossRef]
- Yih, C.C.; Ro, P.I. Near-optimal motion planning for nonholonomic systems using multi-point shooting method. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 2943–2948. [Google Scholar]
| Polynomial Degree | Functional Value |
|---|---|
| 5 | 5.0990 |
| 10 | 5.0878 |
| 15 | 5.0880 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavina, A.; Matos, J.M.A.; Vasconcelos, P.B. Solving Nonholonomic Systems with the Tau Method. Math. Comput. Appl. 2019, 24, 91. https://doi.org/10.3390/mca24040091
Gavina A, Matos JMA, Vasconcelos PB. Solving Nonholonomic Systems with the Tau Method. Mathematical and Computational Applications. 2019; 24(4):91. https://doi.org/10.3390/mca24040091
Chicago/Turabian StyleGavina, Alexandra, José M. A. Matos, and Paulo B. Vasconcelos. 2019. "Solving Nonholonomic Systems with the Tau Method" Mathematical and Computational Applications 24, no. 4: 91. https://doi.org/10.3390/mca24040091
APA StyleGavina, A., Matos, J. M. A., & Vasconcelos, P. B. (2019). Solving Nonholonomic Systems with the Tau Method. Mathematical and Computational Applications, 24(4), 91. https://doi.org/10.3390/mca24040091





