Abstract
In the Newtonian approach to mechanics, the concepts of objective tensors of various ranks and types are introduced. The tough classification of objective tensors is given, including tensors of material and spatial types. The diagrams are constructed for non-degenerate (“analogous”) relations between tensors of one and the same (any) rank, and of various types of objectivity. Mappings expressing dependence between objective tensor processes of various ranks and types are considered. The fundamental concept of frame-independence of such mappings is introduced as being inherent to constitutive relations of various physical and mechanical properties in the Newtonian approach. The criteria are established for such frame-independence. The mathematical restrictions imposed on the frame-independent mappings by the objectivity types of connected tensors are simultaneously revealed. The absence of such restrictions is established exclusively for mappings and equations linking tensors of material types. Using this, a generalizing concept of objective differentiation of tensor processes in time, and a new concept of objective integration, are introduced. The axiomatic construction of the generalized theory of stress and strain tensors in continuum mechanics is given, which leads to the emergence of continuum classes and families of new tensor measures. The axioms are proposed and a variant of the general theory of constitutive relations of mechanical properties of continuous media is constructed, generalizing the known approaches by Ilyushin and Noll, taking into account the possible presence of internal kinematic constraints and internal body-forces in the body. The concepts of the process image and the properties of the five-dimensional Ilyushin’s isotropy are generalized on the range of finite strains.
Keywords:
Newtonian mechanics; objective tensors; diagrams; frame-independent mappings; objective derivatives and integrals; generalized theory of stress and strain tensors; axioms of the general theory of constitutive relations; internal kinematic constraints; internal body-forces; Ilyushin’s type process images at finite strains 1. Introduction
The courses in continuum mechanics [1,2,3,4,5,6,7,8,9] are based on the fundamental works of the classics of science [10,11,12,13], which provided the foundations of the modern general theory of the constitutive relations of deformable media and contributed to the solution of the sixth Hilbert problem [14]. With regard to the theoretical description of the mechanical properties of bodies at arbitrary (small and finite) strains and using the numerous results of modern research, the paper offers the results of the author’s research in the following main areas:
- Tensor representation of various characteristics of mechanical processes and states, in the first place, stresses and strains;
- The structure of mappings of these tensors and equations linking them, including differential and integral connections used in constitutive relations of media;
- The basic hypothesis for the construction of constitutive relations of bodies at finite deformations, the general reduced forms of relations, bases of their classification (specialization for classes of bodies and processes), possibilities of their experimental verification and confirmation.
In general, the presented material contributes to the creation and development of new approaches in various fields of Newtonian mechanics, in the branches of classical continuum mechanics. These new approaches are based on fundamental achievements of the science of mechanics [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51] and mathematics [52,53,54,55,56,57,58,59,60,61,62,63,64]. They were carried out by the author [65,66,67,68,69,70,71,72,73] and were realized by his colleagues in different branches: In elasto-plasticity at finite strains [74,75], in constructing models of Cosserat type [75,76,77,78,79], in poromechanics [79,80], in the theory of shape-memory materials [81], in the generalization of the theory of elastic-plastic processes to finite deformations [82], in numerical methods for elastic-plastic problems at finite strains [83], in analytical research in hypo-elasticity [84], and in constructing new models of visco-elasticity at finite strains by using new methods, including the application of different objective derivatives [85,86,87].
2. Newtonian Objectivity
2.1. Objective Tensors and Diagrams
In the framework of Newtonian mechanics, the change of the reference system (change of the frame by the frame ), i.e., the transition from the Eulerian space-time variables to the new variables is expressed by the formulas [3,13]
where the change parameters are the position-valued and time-like a constants, as well as the position-valued and the tensor-valued (orthogonal tensor) functions of time. The transformation (1) expresses a motion of space with a possible reflection. The pair of variables in a new frame means physically the same position and moment of time as the pair in an old frame . The reference systems and are related: They use one and the same decomposition of the world of events in a 3-dimensional affine space of places (positions) and 1-dimensional affine space of time-moments, and the transformation (1) preserves the sense and direction of time, as well as distances between places and durations of time-intervals.
Let us, for a fixed material object (Lagrangian point of a body , particle or body as a whole), consider scalar , vector , and tensor (second rank) , , , mechanical processes to be converted when replacing reference frame (1) by the rules
In the spaces of tensors of arbitrary ranks m, sets of similar tensors can also be distinguished as being transformed by formulas of type (2), namely:
where is a binary multi-index with (), the mapping is composed of the tensors equal to for , and equal to unit tensor for ().
Definition 1.
Using the notation , we shall call objective tensors of type with as materially oriented (or of material type, or simply right), tensors with as spatially oriented (or of spatial type, or left), other objective tensors as of mixed type.
Related mechanical characteristics can be expressed by objective tensors of the same rank and of different types (analogues): vectors , , second rank tensors , , , , which are related pairwise by identities in the form of maps that make up commutative diagrams in the form
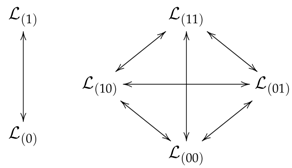 where the arrows indicate the components of the diagram, i.e., the mappings expressed by the formulas
with non-degenerate -objective tensors and , , satisfying the conditions
where the arrows indicate the components of the diagram, i.e., the mappings expressed by the formulas
with non-degenerate -objective tensors and , , satisfying the conditions

We shall call the diagrams (4) simple diagrams, the mappings (5) intertwining (or interweaving) operators, and the tensors (6) transition (or transitional) tensors of these diagrams.
The general form of the intertwining operators for objective tensors of rank m reads as follows:
where the mapping , which transforms an objective tensor of rank m and type into an objective tensor of rank m and type , is composed similarly to interweaving operators (5) by transition tensors () with , .
2.2. Mappings of Objective Tensors
Let and be the sets of mechanical tensor processes and , and let , , and designate their images under the action of the group G of frame-changes (1). Mappings and will be called physically coinciding if
We shall consider the arguments and the images as objective tensors satisfying (3) with certain types and (and ranks m and ), respectively:
Definition 2.
The mapping with and , we call independent of the frame of reference if it is a morphism (concomitant) of the free action of the group G of changes of the frame-reference, that is, the mathematical identity is fulfilled:
This means that the physically coinciding mappings are also mathematically coinciding. The criterion of the frame-independence of mappings is established as the theorem. The theorem, generally speaking, imposes special restrictions on the mathematical type of the mapping depending on the types of objectivity of the tensors and , up to trivial. The corresponding general form of the map is called the general reduced form. Only mappings linking materially oriented tensor processes (tensor processes with and ), named Ilyushin-type maps, do not experience limitations.
The commutativity of simple diagrams provides, accordingly to (7), for each objective tensor process of type and type the uniqueness of its analog of any other type (and of the same rank). This naturally induces (generates) for each specific mapping the single set of maps , binding various analogs of the argument (rank m) and image (rank ) of the original map , and set by the formula
where and are the interweaving operators of type (7) for diagrams of tensor argument and of tensor image respectively.
We shall call the generating mapping inductor, mappings conductors, and their set packet of conductors (or mapping of diagrams). Equalities of type (11) may be called interlacings of conductors.
An inductor determines the properties of all conductors and the package as a whole. Inductors of Ilyushin-type generate packets of conductors possessing the most general species. This is the basis for introducing the new generalizing notion of objective derivatives.
Definition 3.
The objective derivative with respect to time of the type is the mapping from (11) of objective tensor processes of type into objective tensors of type , generated for matching diagrams of arguments and images (, ) by the -inductor owning the form of the total (material) time derivative of the materially oriented tensor —material analog of tensor —at current moment of time t:
For objective scalar, vector, and tensor (of the second rank) processes (2) in accordance with Definition 3 we have:
For the objective derivatives coincide with the usual material derivatives and for they are differential operators of the first order in time, parametrized by the transition tensors of the diagram.
Using the notations
we may derive other (identical) representations of with , which may appear convenient for the Eulerian description method. For (13) they have the form:
The concept of objective derivatives introduced here essentially generalizes and extends the set of known concepts of objective derivatives. Using the notation for the deformation gradient (affinor) with its right polar decomposition ( is the orthogonal tensor of polar rotation, is the right stretch tensor), it can be shown that the corresponding Formulas (13) and (15) represent the derivative of a spatially oriented tensor process as the objective derivative of Oldroyd [36] (for ()); of Cotter–Rivlin [37] (for ()); of Truesdell [38] (, ()); or of Sedov [39,40] (two "skew" derivatives for , and for , ). The corresponding formulas also represent the corotational objective derivatives for which () where is an orthogonal materially oriented tensor, particularly the Zaremba–Jaumann derivative [34,35] (with satisfying the equation ) and the Dienes (“neutral”) derivative (with —unit tensor); as well as the family of corotational derivatives introduced by Finoshkina [74]. The wide class of convective-corotational derivatives of the second rank tensors is studied in [66].
The objective derivative of Hill [42] is nothing more than the derivative of a mixed type objective tensor process with , ().
The introduced notion (12) covers not only objective derivatives of tensors of the second rank and different types, but also the continuum set of time derivatives of objective tensors of various ranks and types.
As inverse operations, the concepts of objective integrals of the type are introduced. The concept of objective integration has not been introduced before.
3. Development of Foundations of Classical Continuum Mechanics
3.1. Generalized Theory of Strain and Stress Tensor Measures
On the base of the theory of objective tensors and their mappings, the new generalized theory of strain and stress tensor measures is constructed. Due to the above-mentioned absence of restrictions on the Ilyushin-type mappings, the basic constructions of new measures are carried out with respect to material-oriented tensor measures. Measures of other types of objectivity can be constructed by use of intertwining operators of respective diagrams.
Axioms are introduced that reflect, in the general sense, the natural properties of stress and strain tensor measures. The most general Lagrangian class of measures is constructed. Using the theorem of energy conjugacy of strains and stresses, the subclass, the complete Lagrangian class, is allocated including the simple Lagrangian class as the subsubclass.
Special attention is put to the family of holonomic tensor measures and the family of corotational measures in the simple Lagrangian class, which have already been applied in constructions of principally new models of deformable media at finite strains, in nonlinear elasticity, hypo-elasticity, viscoelasticity, plasticity and shape-memory theory.
3.2. Constitutive Relations: Foundations of the General Theory
The proposed theory of constitutive relations of mechanical properties of deformable bodies is based on the ideas and approaches of the well known theories by Ilyushin and by Noll. This theory generalizes them with the simultaneous account of kinematic constrictions and internal body-forces in a body.
The new extended definition of dynamic process is introduced.
Definition 4.
For an arbitrary body with a reference configuration , any set (triple) consisting of a motion of that body, a symmetric Cauchy tensor field of the stress process and a vector field of the internal body-forces (mass-densities) , is called a dynamic process:
Any statement (relation) on the dynamic processes, that is valid for a body, we call a physical (mechanical, material) property (or behavior) of this body. The physical property of a given body entailing the fulfillment of all its other physical properties, we call the constitutive physical (mechanical, material) property of this body. The constitutive property of a given body expressed by a mathematical relation (system, set of relations) for dynamic processes, we call the constitutive relation (system, set of constitutive relations) of this body. Any dynamic process that satisfies the constitutive relations of a certain body is called physically (mechanically, materially) acceptable for this body.
The following new triple of axioms (principles) are accepted for constructing the proposed theory of constitutive relations of resistance to deformation: the principle of local separability, the principle of structural-energy determinism, and the principle of material independence of the reference system.
This leads to the general reduced form of the system of constitutive relations
where Equation (17) expresses the internal kinematic constriction of the body ; is the prehistory field of Cauchy measure of deformation ( is the deformation gradient); Equations (18) and (19) determine the physically acceptable tensor field of Cauchy stress and vector field of internal body-forces ; the mapping corresponds to the mechanical properties of the body in the infinitesimal neighborhood of the point , it maps the prehistory fields of symmetric positive definite tensor given in to symmetric tensors; is the mapping of the prehistory fields of symmetric positive definite tensors in the whole body to self-balanced vector fields over ; tensor is the orthogonal polar-rotation tensor; is an arbitrary fixed point of the body ; and t is a moment of time. Field is an arbitrary tensor (symmetric tensor of the second rank) field and is an arbitrary self-balanced vector field both satisfying the conditions
with any physically acceptable fields of velocity and of strain rate .
Other general reduced forms of the system (17)–(19) are also presented in terms of other stress and strain tensors (using intertwining operators of type (5), (7) for tensors and interlacings of conductors of type (11)). In particular, the equivalence of Ilyushin’s and Noll’s relations for simple classic media (simple bodies) is established.
Taking into account the internal body-forces is necessary for the strict derivation of the Cauchy motion equations and for the construction of constitutive relations carried out here. Neglect of internal mass forces is an approximation, which is traditionally used in continuum mechanics.
3.3. Notions of Process Image and Five-Dimensional Isotropy at Finite Strains
Using Ilyushin’s canonical (symmetric orthonormal) tensor basis () permits us to represent the deviators and of any pair of energy conjugate stress and strain measures by the vectors from the five-dimensional Euclidian vector space with the orthonormal basis :
preserving the expression W of the power of the (overcoming of) internal contact forces (stresses):
where and are the values of the spherical parts of the stress and strain tensors.
Then by (21) the general form of the constitutive stress operator can be equivalently represented by the system of relations for vectors , and the spherical parts , of the tensors , :
Then the concept of the process image and the formulation of Ilyushin’s postulate of isotropy (the material property of five-dimensional isotropy in the sense of Ilyushin) are introduced according to the classical definition [2,10,11]. The postulate is expressed by the isotropy properties of the vector and scalar-valued maps and f of (23), namely, by identities for any orthogonal tensor-constant over the space :
The image of a process and the content of the isotropy postulate in the case of finite deformations are entirely determined by the choice of tensor stress and strain measures , . Different variants of the choice of these tensors are studied.
4. Conclusions
The presented theory of objective tensors and their mappings defines their rigid classification and is applicable to all objective tensor processes and their material connections in classical Newtonian mechanics, including the constitutive relations of different mechanical properties of bodies.
The proposed theory of tensor stress and finite strain measures, significantly extends the representations of classical continuum mechanics. The continuum classes and families of introduced measures provide new possibilities to satisfy the experimental data on the mechanical properties of deformable bodies not only due to the mathematical form of the constitutive relations, but also due to the choice of tensor stress and strain measures themselves.
The presented version of the theory of constitutive relations of continuous media is based on the widely used classical statements of the theory by Ilyushin and the theory by Noll, and generalizes them, in a unified form of the system of constitutive relations, taking into account the presence of internal mass forces and the possible presence of internal kinematic constrictions in the body. Further development of the theory provides for the study of specific types of kinematic constrictions and their impact on the form of indeterminate terms of fields of stresses and internal body-forces.
The set of variants of concepts of the process image, and the five-dimensional isotropy opens opportunities for the development of the theory of elastic-plastic processes of Ilyushin on the area of finite deformations.
Acknowledgments
The work was prepared with the financial support of the Russian Foundation for Basic Research (RFBR grant 16-01-00669).
Conflicts of Interest
The author declares no conflict of interest.
References
- Sedov, L.I. Continuum Mechanics; Nauka: Moscow, Russia, 1973. [Google Scholar]
- Ilyushin, A.A. Continuum Mechanics; Moscow University Press: Moscow, Russia, 1990. [Google Scholar]
- Truesdell, C. A First Course in Rational Continuum Mechanics; The Johns Hopkins University: Baltimore, MD, USA, 1972. [Google Scholar]
- Germain, P. Continuum Mechanics; Vysshaya Shkola: Moscow, Russia, 1983. [Google Scholar]
- Jaric, J. Mehanika Kontinuuma; IRO Gradevinska Knjiga: Beograd, Russia, 1988. [Google Scholar]
- Pobedrya, B.E.; Georgievskii, D.V. Foundations of Continuum Mechanics; Fizmatlit: Moscow, Russia, 2006. [Google Scholar]
- Gurtin, M.E.; Fried, E.; Anand, L. The Mechanics and Thermodinamics of Continua; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Eglit, M.E. Lectures on the Basics of Continuum Mechanics; Book House “Librokom”: Moscow, Russia, 2013. [Google Scholar]
- Brovko, G.L. Foundations of Continuum Mechanics; Lomonosov Moscow State University: Moscow, Russia, 2013. [Google Scholar]
- Ilyushin, A.A. On dependence between stresses and small strains in continuum mechanics. Appl. Math. Mech. 1954, 18, 641–666. [Google Scholar]
- Ilyushin, A.A. Plasticity. Foundations of General Mathematical Theory; Academy of Sciences of the USSR: Moscow, Russia, 1963. [Google Scholar]
- Noll, W. A mathematical theory of the mechanical behavior of continuous media. Arch. Ration. Mech. Anal. 1958, 2, 197–226. [Google Scholar] [CrossRef]
- Truesdell, C.A.; Noll, W. The Nonlinear Field Theories of Mechanics; Springer: Berlin, Germany, 1965. [Google Scholar]
- Alexandrov, P.S. Problems of Hilbert. Collection; Nauka: Moscow, Russia, 1969. [Google Scholar]
- Ilyushin, A.A. Works (1946–1966). Plasticity; Fizmatlit: Moscow, Russia, 2004. [Google Scholar]
- Ilyushin, A.A.; Lensky, V.S. Strength of Materials; Fizmatgiz: Moscow, Russia, 1959. [Google Scholar]
- Astarita, G.; Marrucci, G. Principles of Non-Newtonian Fluid Mechanics; McGraw-Hill: London, UK, 1974. [Google Scholar]
- Hill, R. Aspects of invariance in solid mechanics. Adv. Appl. Mech. 1978, 18, 1–75. [Google Scholar]
- Ogden, R.W. On Eulerian and Lagrangean objectivity in continuum mechanics. Arch. Mech. 1984, 36, 207–218. [Google Scholar]
- Tolokonnikov, L.A. Mechanics of Solids; Vysshaya Shkola: Moscow, Russia, 1979. [Google Scholar]
- Lourie, A.I. Nonlinear Theory of Elasticity; Nauka: Mockow, Russia, 1980. [Google Scholar]
- Pozdeyev, A.A.; Trusov, P.V.; Nyashin, Y.I. Large Elastic-Plastic Deformations; Nauka: Moscow, Russia, 1986. [Google Scholar]
- Levitas, V.I. Large Elastic-Plastic Deformations of Materials at High Pressure; Naukova Dumka: Kyiv, Ukraine, 1987. [Google Scholar]
- Kondaurov, V.I.; Nikitin, L.V. Theoretical Foundations of Rheology of Geomaterials; Nauka: Moscow, Russia, 1990. [Google Scholar]
- Chernykh, K.F. Nonlinear Elasticity (Theory and Applications); Solo: St. Petersburg, Russia, 2004. [Google Scholar]
- Zubchaninov, V.G. Mechanics of Processes in Plastic Media; Fizmatlit: Moscow, Russia, 2010. [Google Scholar]
- Markin, A.A.; Sokolova, M.Y. Thermomechanics of Elastic-Plastic Deformations; Fizmatlit: Moscow, Russia, 2013. [Google Scholar]
- Hencky, H. The elastic behavior of vulcanized rubber. J. Appl. Mech. 1933, 1, 45–53. [Google Scholar] [CrossRef]
- Seth, B.R. Generalized strain measures with applications to physical problems. In Second Order Effects in Elasticity, Plasticity and Fluid Dynamics; Reiner, M., Abir, D., Eds.; Pergamon Press: Oxford, UK, 1964; pp. 162–172. [Google Scholar]
- Zhao, Z. Logarithmic strain and plastic constitutive equation at finite strain. In Proceedings of the International Conference on Nonlinear Mechanics, Shanghai, China, 28–31 October 1985; Science Press: Beijing, China, 1985; pp. 651–656. [Google Scholar]
- Novozhilov, V.V.; Chernykh, K.F. On “true” stress and strain measures in nonlinear mechanics of deformable bodies. Proc. Russ. Acad. Sci. Mech. Rigid Solid Bodies 1987, 5, 73–80. [Google Scholar]
- Man, C.S.; Guo, Z.H. A basis-free formula for time rate of Hill’s strain tensors. Int. J. Solids Struct. 1993, 30, 2819–2842. [Google Scholar]
- Xiao, H.; Bruhns, O.T.; Meyers, A. Large strain responses of elastic-perfect plasticity and kinematic hardening plasticity with the logarithmic rate: Swift effect in torsion. Int. J. Plast. 2001, 17, 211–235. [Google Scholar] [CrossRef]
- Zaremba, S. Sur une forme perfectionée de la théorie de la relaxation. Bull. Int. Acad. Sci. Cracovie 1903, 19A, 594–614. [Google Scholar]
- Jaumann, G. Geschlossenes system physikalischer und chemischer differenzialgesetze. Sitzber. Akad. Wiss. Wien 1911, 120, 385–530. [Google Scholar]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. A 1950, 200, 523–541. [Google Scholar]
- Cotter, B.A.; Rivlin, R.S. Tensors assotiated with time-dependent stress. Q. Appl. Math. 1955, 13, 177–188. [Google Scholar] [CrossRef]
- Truesdell, C. Hypo-elasticity. J. Ration. Mech. Anal. 1955, 4, 83–133. [Google Scholar] [CrossRef]
- Sedov, L.I. The concepts of different rates of change of tensors. Appl. Math. Mech. 1960, 24, 393–398. [Google Scholar]
- Sedov, L.I. Introduction to Continuum Mechanics; Fizmatgiz: Moscow, Russia, 1962. [Google Scholar]
- Lehmann, T. Some remarks on a general class of material laws for large elasto-plastic deformations. Eng. Arch. 1972, 41, 279–310. [Google Scholar]
- Kolarov, D.; Baltov, A.; Boncheva, N. Mechanics of Plastic Media; Mir: Moscow, Russia, 1979. [Google Scholar]
- Dienes, J.K. On the analysis of rotation and stress rate in deforming bodies. Acta Mech. 1979, 32, 217–232. [Google Scholar] [CrossRef]
- Nagtegaal, J.C.; de Jong, J.E. Some aspects of nonisotropic work hardening in finite strain plasticity. In Plasticity of Metals at Finite Strain: Theory, Experiment and Computation; Stanford University: Stanford, CA, USA, 1982; pp. 65–102. [Google Scholar]
- Dafalias, Y.F. Corotational rates for kinematic hardening at large plastic deformations. Trans. ASME J. Appl. Mech. 1983, 50, 561–565. [Google Scholar] [CrossRef]
- Atluri, S.N. On constitutive relations at finite strain: Hypo-elasticity and elasto-plasticity with isotropic or kinematic hardening. Comput. Methods Appl. Mech. Eng. 1984, 43, 137–171. [Google Scholar] [CrossRef]
- Markin, A.A.; Tolokonnikov, L.A. Measures and constitutive equations of finite elastoplastic deformation. Appl. Probl. Strength Plast. 1987, 32–37. [Google Scholar]
- Latorre, M.; Montans, F.J. Stress and strain mapping tensors and general work-conjugacy in large strain continuum mechanics. Appl. Math. Model. 2016, 40, 3938–3950. [Google Scholar] [CrossRef]
- Neff, P.; Eidel, B.; Martin, R.J. Geometry of logarithmic strain measures in solid mechanics. Arch. Ration. Mech. Anal. 2016, 222, 507–572. [Google Scholar] [CrossRef]
- Marsden, J.E.; Hughes, T.J.R. Mathematical Foundations of Elasticity; Dover Publications: New York, NY, USA, 1994. [Google Scholar]
- Zhang, M.; Montans, F.J. A simple formulation for large-strain cyclic hyperelasto-plasticity using elastic correctors. Theory and algorithmic implementation. Int. J. Plast. 2019, 113, 185–217. [Google Scholar] [CrossRef]
- Dubrovin, B.A.; Novikov, S.P.; Fomenko, A.T. Contemporary Geometry; Nauka: Moscow, Russia, 1979. [Google Scholar]
- Postnikov, M.M. Lectures on Geometry; Nauka: Moscow, Russia, 1986. [Google Scholar]
- Lang, S. Algebra; Mir: Moscow, Russia, 1968. [Google Scholar]
- Dieudonne, J.; Carrol, J.; Mamford, D. Geometric Theory of Invariants; Mir: Moscow, Russia, 1974. [Google Scholar]
- Vinberg, E.B.; Gorbatsevich, V.V.; Onishchik, A.L. The structure of lie groups and lie algebras. Results Sci. Technol. Mod. Probl. Math. Fundam. Dir. 1989, 41, 5–258. [Google Scholar]
- Skornyakov, L.A. General Algebra; Nauka: Moscow, Russia, 1990. [Google Scholar]
- Kostrikin, A.I. Introduction to Algebra; Fizmatlit: Moscow, Russia, 2004. [Google Scholar]
- Vinberg, E.B. Course of Algebra; Faktorial Press: Moscow, Russia, 2002. [Google Scholar]
- Vinberg, E.B. Representations of classical groups in tensors. In Mathematical Encyclopedia; Sovetskaya Enciklopedia: Moscow, Russia, 1984; pp. 595–598. [Google Scholar]
- Zhelobenko, D.P.; Stern, A.I. Representations of Lie Groups; Nauka: Moscow, Russia, 1983. [Google Scholar]
- Gurevich, G.B. Foundations of the Theory of Algebraic Invariants; OGIZ GITTL: Moscow, Russia, 1948. [Google Scholar]
- Lankaster, P. Theory of Matrices; Nauka: Moscow, Russia, 1982. [Google Scholar]
- Spencer, E. Theory of Invariants; Mir: Moscow, Russia, 1974. [Google Scholar]
- Brovko, G.L. Notions of process image and five-dimensional isotropy of material properties at finite strains. Rep. Acad. Sci. USSR 1989, 308, 565–570. [Google Scholar]
- Brovko, G.L. Properties and integration of some time derivatives of tensor processes in continuum mechanics. Proc. Russ. Acad. Sci. Mech. Rigid Solid Bodies 1990, 1, 54–60. [Google Scholar]
- Brovko, G.L. Material and spatial representations for constitutive relations of deformable media. Appl. Math. Mech. 1990, 54, 814–824. [Google Scholar] [CrossRef]
- Brovko, G.L. On a family of holonomic tensor measures of deformations and stresses. Bull. Mosc. Univ. 1992, 4, 86–91. [Google Scholar]
- Brovko, G.L. Invariance Types of Tensors, Tensor Processes and Their Transforms in Classical Continuum Mechanics. In Proceedings of the Fifth International Seminar on Geometry, Continuum and Microstructures, Sinaia, Romania, 26–28 September 2001; Editura Academiei Romane: Bucuresti, Romania, 2002; pp. 13–24. [Google Scholar]
- Brovko, G.L. On general principles of the theory of constitutive relations in classical continuum mechanics. J. Eng. Math. 2013, 78, 37–53. [Google Scholar] [CrossRef]
- Brovko, G.L. Elements of the Mathematical Apparatus of Continuum Mechanics; Fizmatlit: Moscow, Russia, 2015. [Google Scholar]
- Brovko, G.L. Constitutive Relations of Continuum Mechanics. The Development of Mathematical Apparatus and the Foundations of the General Theory; Nauka: Moscow, Russia, 2017. [Google Scholar]
- Brovko, G.L. General reduced forms of constitutive relations of classical continuum mechanics. Bull. Mosc. Univ. 2018, 2, 67–71. [Google Scholar] [CrossRef]
- Finoshkina, A.S. The use of new objective derivatives in the simplest models of hypoelasticity and plastic flow with kinematic hardening. Bull. Tula State Univ. 2000, 6, 160–166. [Google Scholar]
- Brovko, G.L.; Ivanova, O.A.; Finoshkina, A.S. On geometrical and analytical aspects in formulations of problems of classic and non-classic continuum mechanics. In Operator Theory: Advances and Applications; Birkhäuser Verlag: Basel, Switzerland, 2009; pp. 51–79. [Google Scholar]
- Brovko, G.L.; Ivanova, O.A. Modeling of properties and motions of inhomogeneous one-dimensional continuum with complicated structure of Cosserat type. Proc. Russ. Acad. Sci. Mech. Rigid Solid Bodies 2008, 1, 22–36. [Google Scholar]
- Ivanova, O.A. Model of equipped rod with viscoelastic internal interactions. Mech. Compos. Mater. Struct. 2018, 24, 70–81. [Google Scholar]
- Brovko, G.L.; Kuzichev, S.A. Stability of forced torsional vibrations of an equipped rod. Bull. Mosc. Univ. 2010, 1, 57–62. [Google Scholar] [CrossRef]
- Brovko, G.L.; Grishayev, A.G.; Ivanova, O.A. Continuum models of discrete heterogeneous structures and saturated porous media: Constitutive relations and invariance of internal interactions. J. Phys. Conf. Ser. 2007, 62, 1–22. [Google Scholar] [CrossRef]
- Faskheyev, I.O. Modeling of Mechanical Processes in Saturated Porous Media with Account of Interactive Forces. Ph.D. Thesis, Lomonosov Moscow State University, Moscow, Russia, 2017. [Google Scholar]
- Shutkin, A.S. Approaches to generalization of the constitutive relations of deformable solids to the finite deformation region. Mech. Compos. Mater. Struct. 2010, 16, 166–180. [Google Scholar]
- Muravlev, A.V.; Devyatov, A.S. Development of the theory of elastic-plastic processes of Ilyushin and experimental-theoretical methods of research of viscoplastic properties of materials at finite deformations. Probl. Mech. Eng. Autom. Int. J. 2016, 1, 84–90. [Google Scholar]
- Ovchinnikova, N.V. On tensor measures of stresses and strains used in ANSYS to solve elastic-plastic problems under finite strains. Bull. Mosc. Univ. 2017, 5, 31–36. [Google Scholar]
- Tunguskova, Z.G. Analytical representation of the stress tensor in the problem of the shift of hypoelastic body using corotational derivatives of a certain type. In Elasticity and Anelasticity; Moscow University Press: Moscow, Russia, 2016; pp. 260–262. [Google Scholar]
- Martynova, E.D.; Stetsenko, N.S. The use of one-parameter Gordon–Showalter family of objective derivatives to describe finite deformations of viscoelastic bodies. Bull. Mosc. Univ. 2017, 6, 64–68. [Google Scholar]
- Bykov, D.L.; Martynova, E.D. Identification of characteristics of viscoelastic materials under repeated compression after unloading by numerical-graphical method. Proc. Russ. Acad. Sci. Mech. Rigid Solid Bodies 2018, 2, 3–9. [Google Scholar]
- Martynova, E.D. Processes of torsion of cylindrical specimens made from an incompressible viscoelastic materials of Maxwell type. Appl. Math. Mech. 2019, 83, 95–106. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).