On the Approximation of a Nonlinear Biological Population Model Using Localized Radial Basis Function Method
Abstract
:1. Introduction
2. Description of the Method
2.1. Spatial Approximation
2.2. Temporal Approximation
2.3. Choosing Optimal Shape Parameter
| Algorithm 1: Optimal shape parameter. |
 |
3. Numerical Experiments
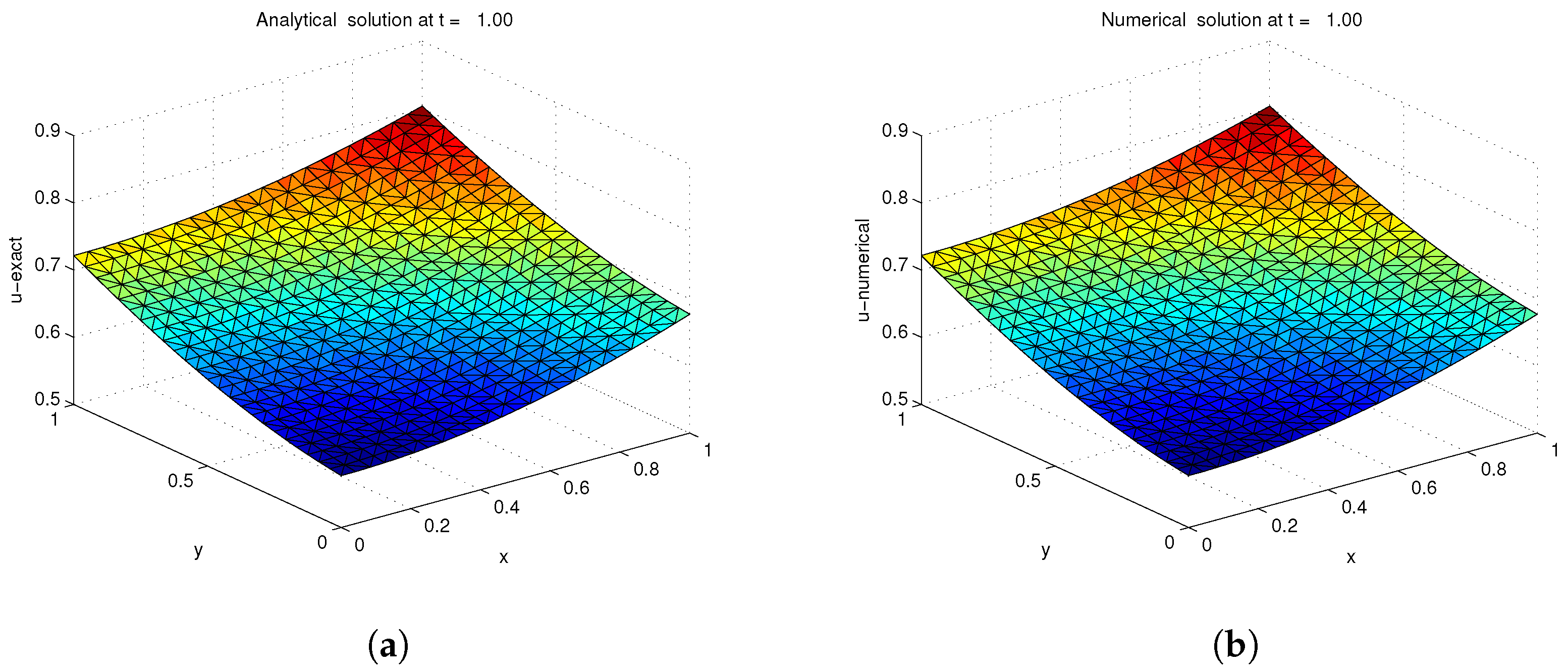
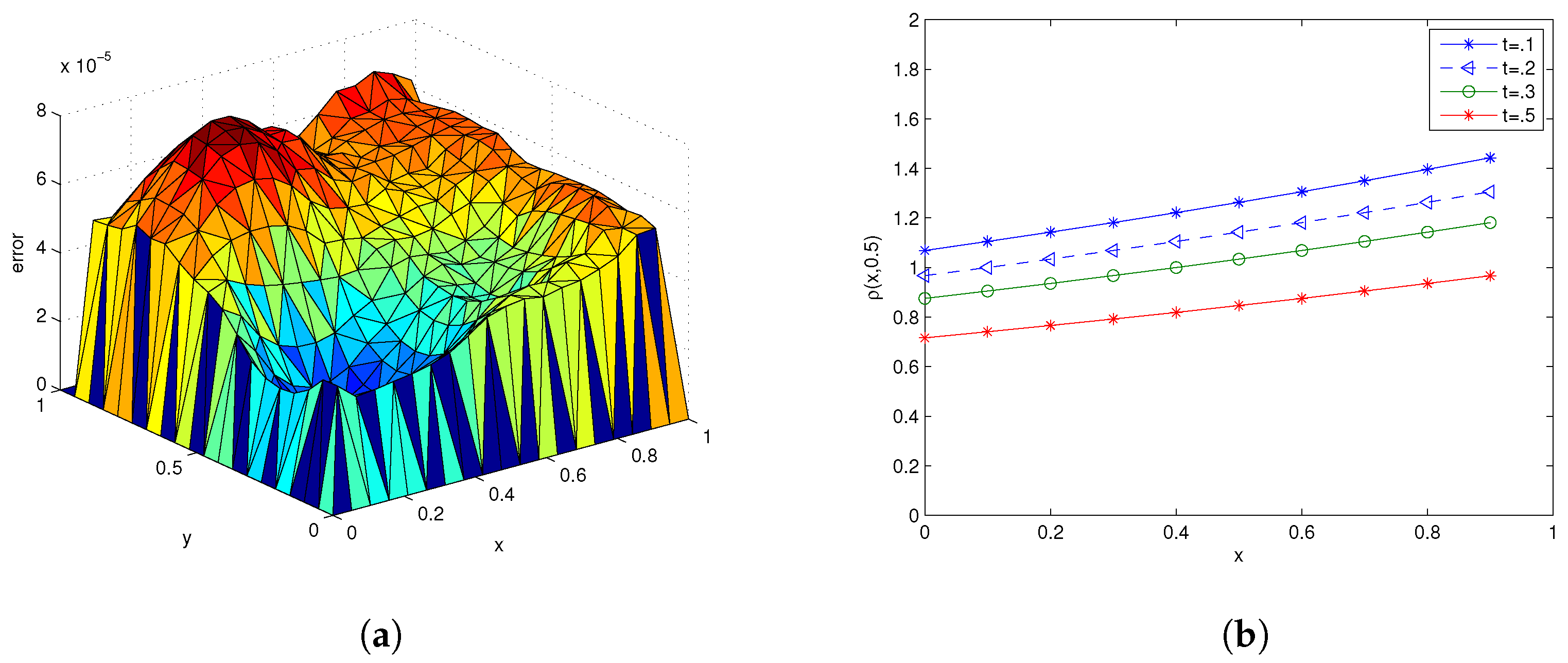
3.1. Example 1
3.2. Example 2
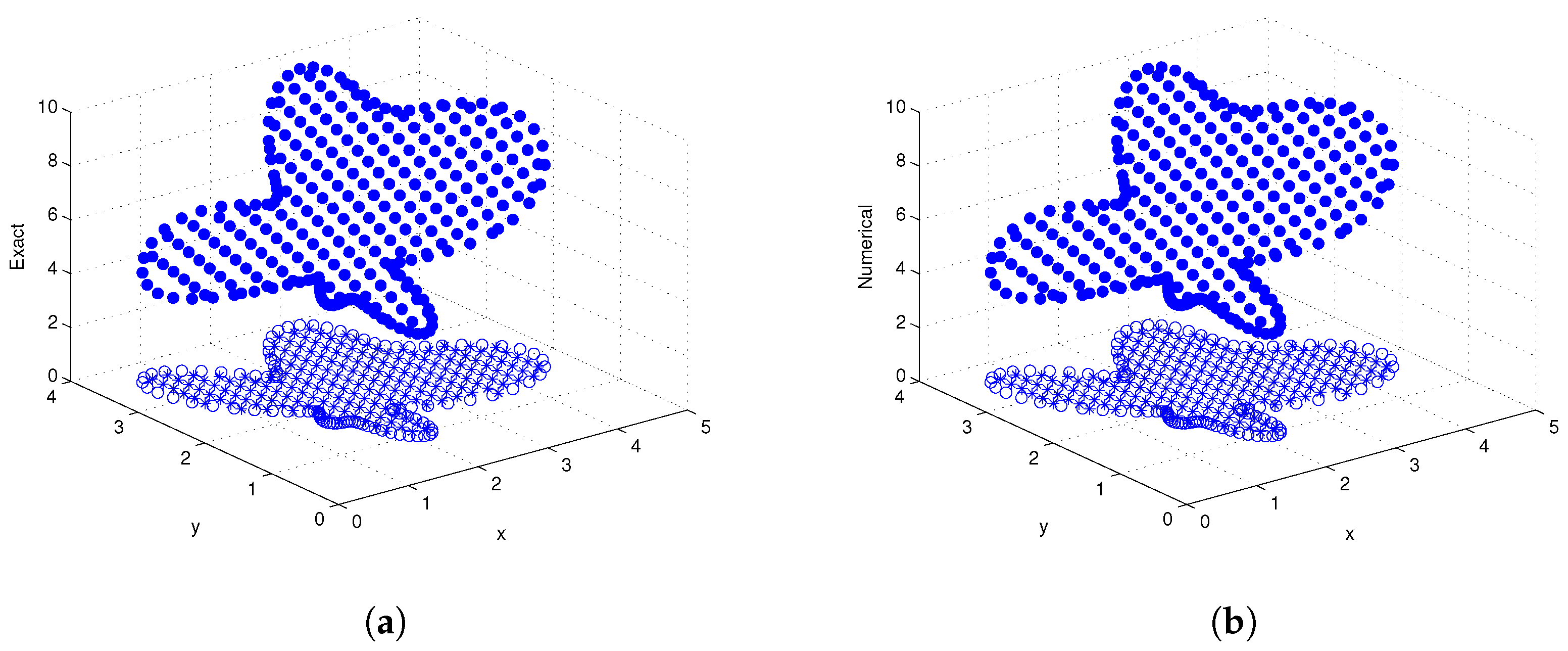
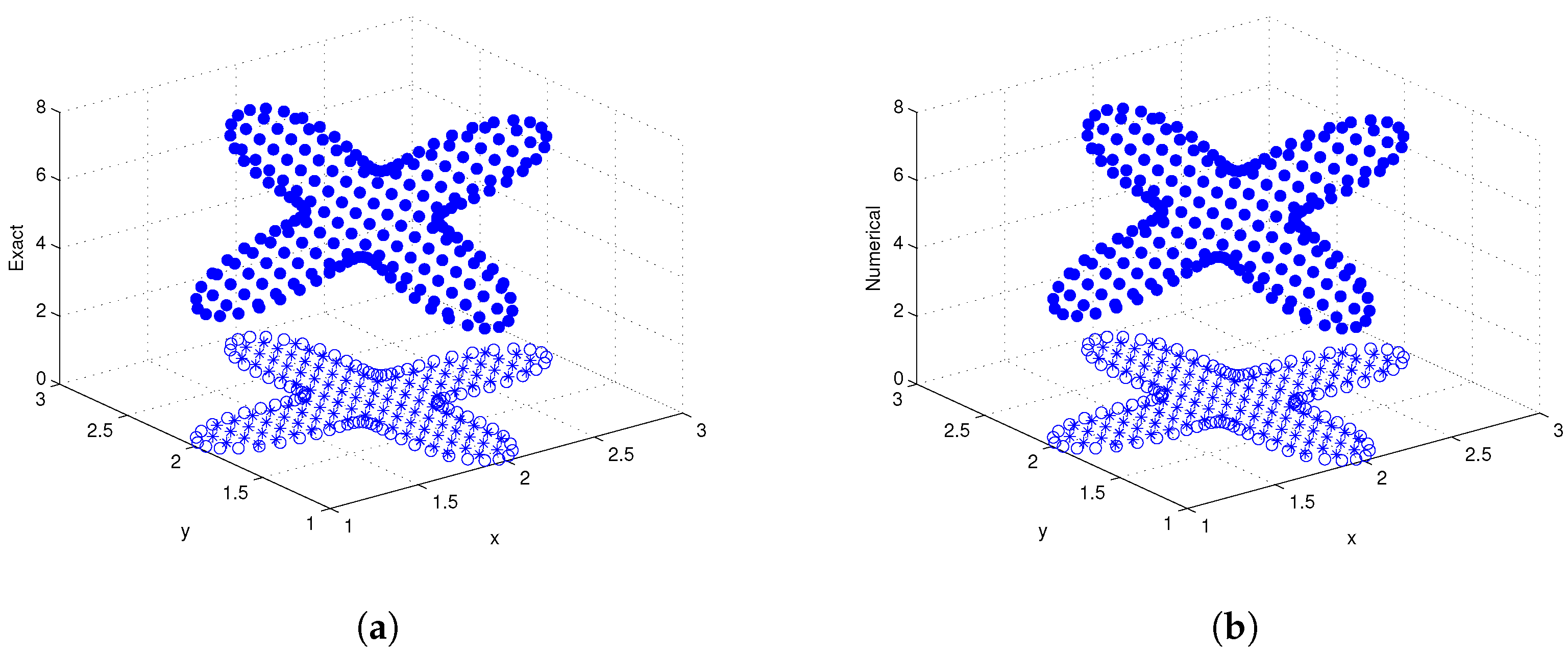
3.3. Example 3
3.4. Example 4
4. Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gurtin, M.E.; MacCamy, R.C. On the diffusion of biological populations. Math. Biosci. 1977, 33, 35–49. [Google Scholar] [CrossRef]
- Gurney, W.; Nisbet, R. The regulation of inhomogeneous populations. J. Theor. Biol. 1975, 52, 441–457. [Google Scholar] [CrossRef]
- Lu, Y.-G. Hölder estimates of solutions of biological population equations. Appl. Math. Lett. 2000, 13, 123–126. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Numerical solution of a biological population model using He’s variational iteration method. Comput. Math. Appl. 2007, 54, 1197–1209. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, Y.; Liew, K. An improved element-free Galerkin method for numerical modeling of the biological population problems. Eng. Anal. Bound. Elem. 2014, 40, 181–188. [Google Scholar] [CrossRef]
- Cheng, R.; Zhang, L.; Liew, K.-M. Modeling of biological population problems using the element-free kp-Ritz method. Appl. Math. Comput. 2014, 227, 274–290. [Google Scholar] [CrossRef]
- Golbabai, A.; Seifollahi, S. Numerical solution of the second kind integral equations using radial basis function networks. Appl. Math. Comput. 2006, 174, 877–883. [Google Scholar] [CrossRef]
- Golbabai, A.; Seifollahi, S. Radial basis function networks in the numerical solution of linear integro-differential equations. Appl. Math. Comput. 2007, 188, 427–432. [Google Scholar] [CrossRef]
- Chen, W. New RBF collocation methods and kernel RBF with applications. In Meshfree Methods for Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003; pp. 75–86. [Google Scholar]
- Monaghan, J.J. An introduction to SPH. Comput. Phys. Commun. 1988, 48, 89–96. [Google Scholar] [CrossRef]
- Gu, L. Moving kriging interpolation and element-free Galerkin method. Int. J. Numer. Methods Eng. 2003, 56, 1–11. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov–Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Duchon, J. Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive Theory of Functions of Several Variables; Springer: Berlin/Heidelberg, Germany, 1977; pp. 85–100. [Google Scholar]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; Volume 12. [Google Scholar]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Solving partial differential equations by collocation with radial basis functions. In Proceedings of Chamonix; Vanderbilt University Press: Nashville, TN, USA, 1996; Volume 1997, pp. 1–8. [Google Scholar]
- Fasshauer, G.E. Solving differential equations with radial basis functions: Multilevel methods and smoothing. Adv. Comput. Math. 1999, 11, 139–159. [Google Scholar] [CrossRef]
- Brown, D.; Ling, L.; Kansa, E.; Levesley, J. On approximate cardinal preconditioning methods for solving PDEs with radial basis functions. Eng. Anal. Bound. Elem. 2005, 29, 343–353. [Google Scholar] [CrossRef]
- Uddin, M.; Minullah, Z.; Ali, A. On the approximation of rapidly oscillatory Hankel transform via radial kernels. Dolomites Res. Notes Approx. 2018, 11, 1. [Google Scholar]
- Uddin, M.; Ali, H.; Ali, A. Kernel-based local meshless method for solving multi-dimensional wave equations in irregular domain. Comput. Model. Eng. Sci. 2015, 107, 463–479. [Google Scholar]
- Uddin, M.; Ali, H. The space–time kernel-based numerical method for Burgers’ equations. Mathematics 2018, 6, 212. [Google Scholar] [CrossRef]
- Bianca, C.; Pappalardo, F.; Pennisi, M.; Ragusa, M. Persistence analysis in a Kolmogorov-type model for cancer-immune system competition. AIP Conf. Proc. 2013, 1558, 1797–1800. [Google Scholar]
- Barbagallo, A.; Ragusa, M.A. On Lagrange duality theory for dynamics vaccination games. Ricerche di Matematica 2018, 67, 969–982. [Google Scholar] [CrossRef]
- Schaback, R.; Wendland, H. Adaptive greedy techniques for approximate solution of large RBF systems. Numer. Algorithms 2000, 24, 239–254. [Google Scholar] [CrossRef]
- Shcherbakov, V.; Larsson, E. Radial basis function partition of unity methods for pricing vanilla basket options. Comput. Math. Appl. 2016, 71, 185–200. [Google Scholar] [CrossRef]
- Hon, Y.; Schaback, R.; Zhou, X. An adaptive greedy algorithm for solving large RBF collocation problems. Numer. Algorithms 2003, 32, 13–25. [Google Scholar] [CrossRef]
- Kosec, G.; Sarler, B. Local RBF collocation method for Darcy flow. Comput. Model. Eng. Sci. 2008, 25, 197. [Google Scholar]
- Shu, C.; Ding, H.; Chen, H.; Wang, T. An upwind local RBF-DQ method for simulation of inviscid compressible flows. Comput. Methods Appl. Mech. Eng. 2005, 194, 2001–2017. [Google Scholar] [CrossRef]
- Fan, C.-M.; Chien, C.-S.; Chan, H.-F.; Chiu, C.-L. The local RBF collocation method for solving the double-diffusive natural convection in fluid-saturated porous media. Int. J. Heat Mass Transf. 2013, 57, 500–503. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge–Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Uddin, M. RBF-PS scheme for solving the equal width equation. Appl. Math. Comput. 2013, 222, 619–631. [Google Scholar] [CrossRef]
- Nie, Q.; Zhang, Y.-T.; Zhao, R. Efficient semi-implicit schemes for stiff systems. J. Comput. Phys. 2006, 214, 521–537. [Google Scholar] [CrossRef]
- Beylkin, G.; Keiser, J.M.; Vozovoi, L. A new class of time discretization schemes for the solution of nonlinear PDEs. J. Comput. Phys. 1998, 147, 362–387. [Google Scholar] [CrossRef]
- Uddin, M. On the selection of a good value of shape parameter in solving time-dependent partial differential equations using RBF approximation method. Appl. Math. Model. 2014, 38, 135–144. [Google Scholar] [CrossRef]
- Schaback, R. Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]

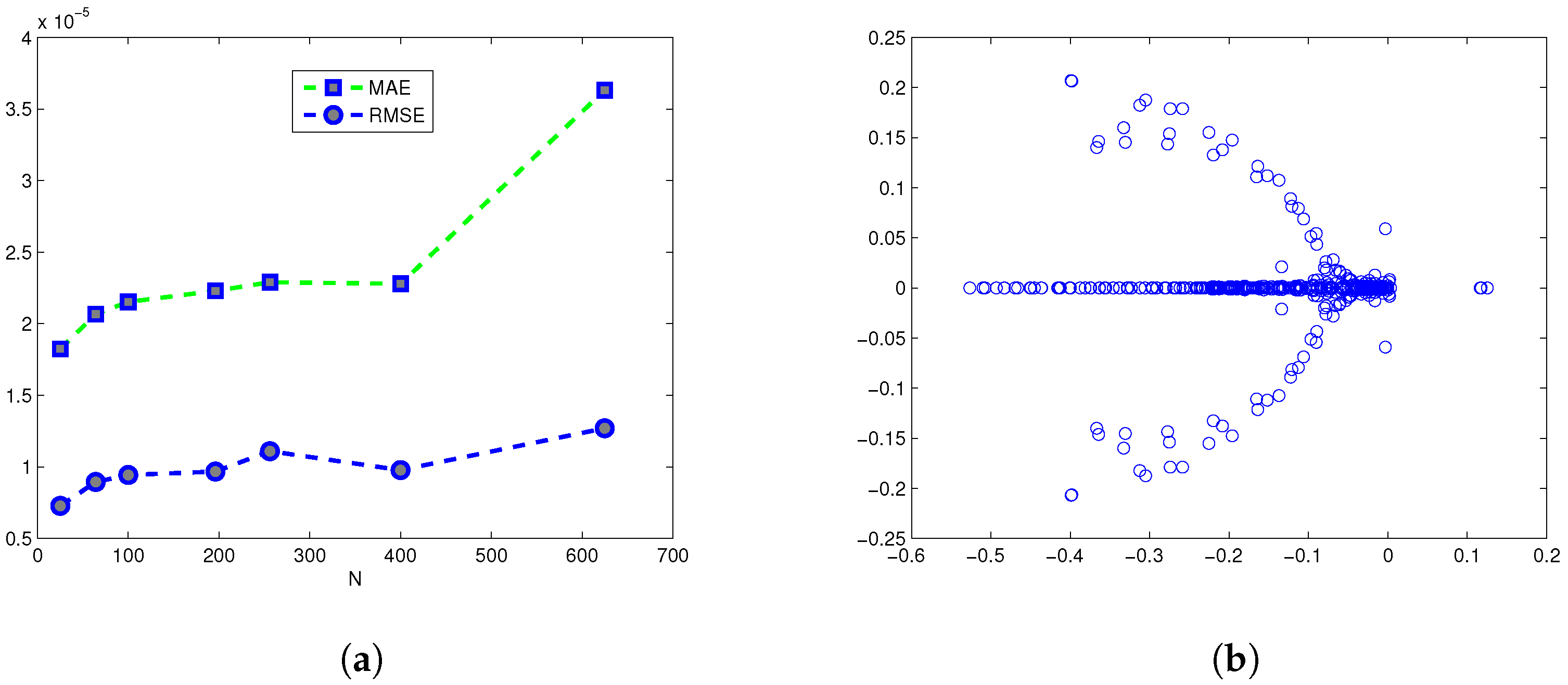
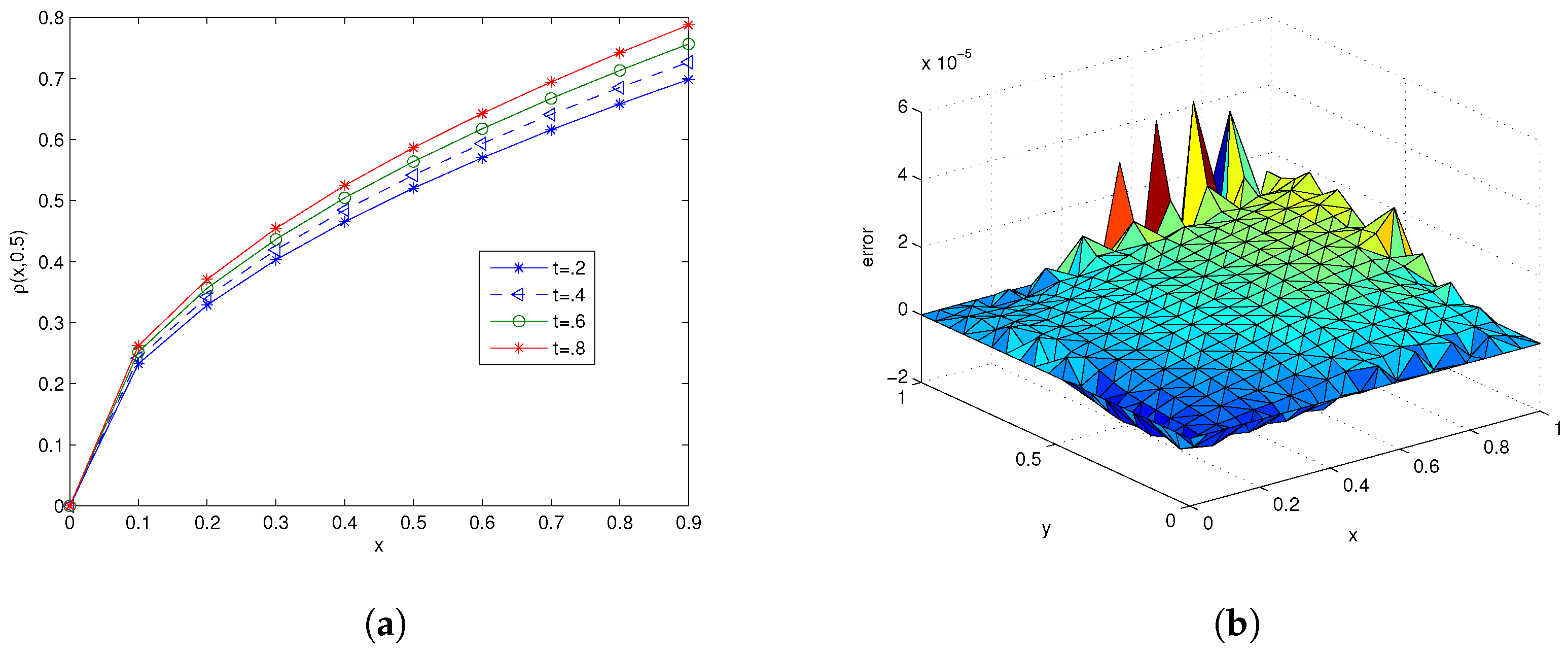
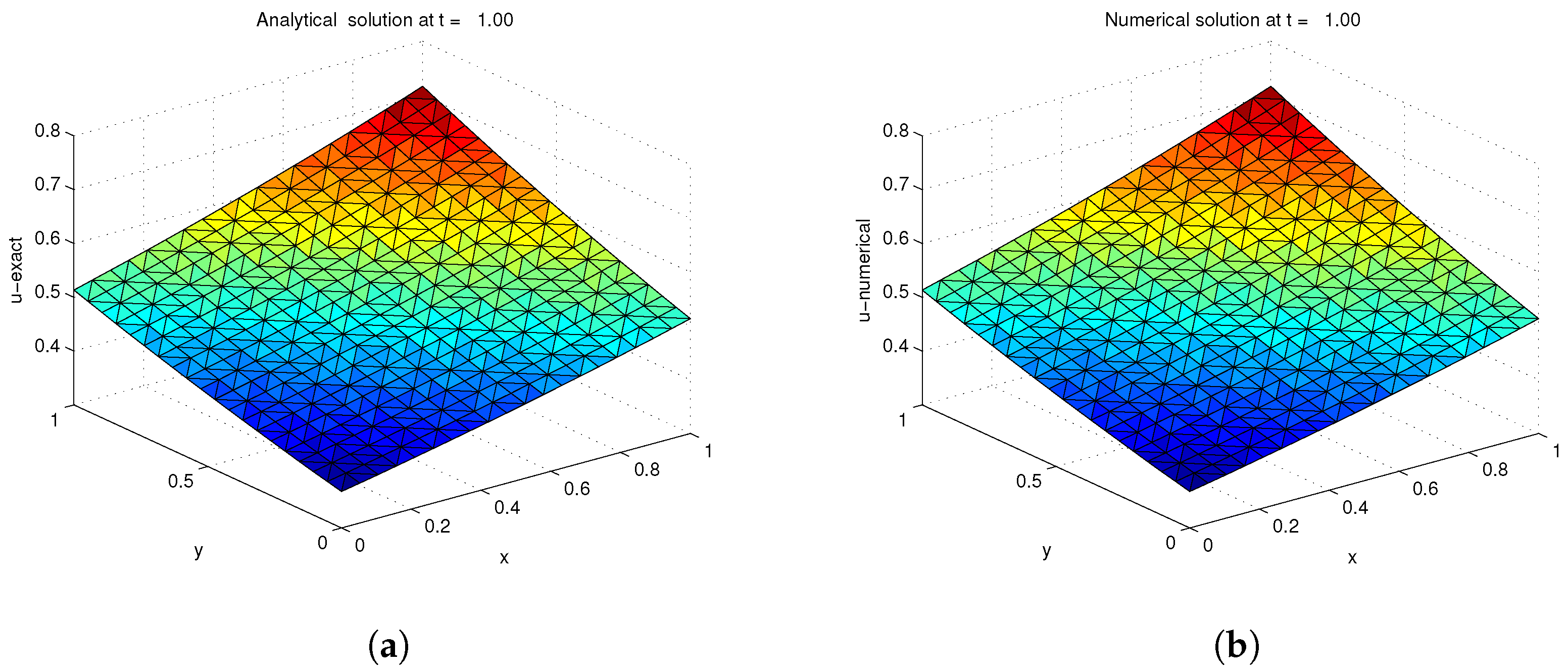
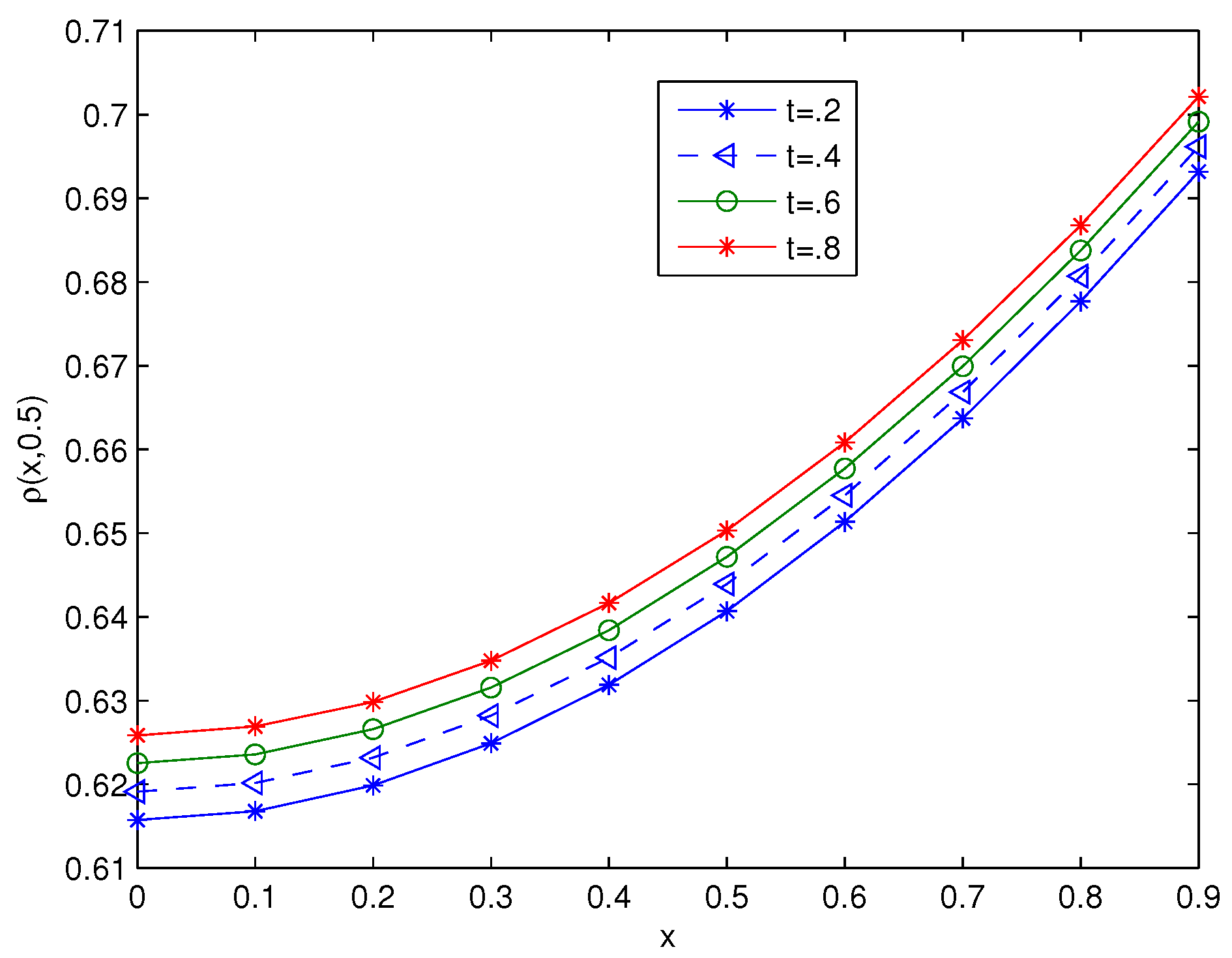

| ns | MCN | MAE | RMSE | C-Time | Shape (c) | |
|---|---|---|---|---|---|---|
| RK4 (MQ RBF) | 5 | 3.099 | 1.931 | 8.336 | 0.950 | 0.010 |
| 11 | 1.241 | 1.915 | 7.935 | 0.858 | 0.520 | |
| 21 | 7.732 | 1.215 | 7.643 | 2.319 | 1.160 | |
| 49 | 2.929 | 4.109 | 1.269 | 1.869 | 1.990 | |
| 60 | 2.941 | 2.725 | 1.121 | 2.504 | 2.150 | |
| 80 | 5.096 | 2.961 | 1.287 | 4.199 | 2.320 |
| Number of Nodes = 13 × 13 | |||||
|---|---|---|---|---|---|
| Present Solution | 1.2628 | 1.1426 | 1.0339 | 0.9355 | 0.8465 |
| Zhang et al. Solution [5] | 1.2574 | 1.1382 | 1.0302 | 0.9325 | 0.844 |
| Exact Solution | 1.2628 | 1.1426 | 1.0339 | 0.9355 | 0.8465 |
| ns | MCN | MAE | RMSE | C-Time | Shape (c) | |
|---|---|---|---|---|---|---|
| RK4 (MQ RBF) | 5 | 3.099 | 1.35 | 8.85 | 0.14538 | 0.01 |
| 10 | 5.136 | 6.93 | 4.70 | 0.76946 | 0.43 | |
| 15 | 4.549 | 6.90 | 4.75 | 0.77773 | 0.85 | |
| 25 | 1.367 | 7.50 | 5.47 | 0.88658 | 1.41 | |
| 50 | 3.225 | 7.34 | 4.67 | 1.26577 | 1.99 | |
| 70 | 3.558 | 6.92 | 4.72 | 1.57271 | 2.26 | |
| 80 | 5.096 | 7.53 | 4.53 | 1.74231 | 2.32 |
| Number of Nodes = 13 × 13 | |||||
|---|---|---|---|---|---|
| Present Solution | 1.2628 | 1.1426 | 1.0339 | 0.9355 | 0.8465 |
| Zhang et al. Solution [5] | 1.2574 | 1.1382 | 1.0302 | 0.9325 | 0.844 |
| Exact Solution | 1.2628 | 1.1426 | 1.0339 | 0.9355 | 0.8465 |
| Ameoba | Cassini | |||
|---|---|---|---|---|
| ns | MAE | RMSE | MAE | RMSE |
| 5 | 9.40 | 3.52 | 1.63 | 1.02 |
| 15 | 2.40 | 2.21 | 7.33 | 4.32 |
| 30 | 3.20 | 9.12 | 6.36 | 3.82 |
| 45 | 1.78 | 1.51 | 2.51 | 1.56 |
| 60 | 1.20 | 2.12 | 4.45 | 2.22 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uddin, M.; Ali, H.; Taufiq, M. On the Approximation of a Nonlinear Biological Population Model Using Localized Radial Basis Function Method. Math. Comput. Appl. 2019, 24, 54. https://doi.org/10.3390/mca24020054
Uddin M, Ali H, Taufiq M. On the Approximation of a Nonlinear Biological Population Model Using Localized Radial Basis Function Method. Mathematical and Computational Applications. 2019; 24(2):54. https://doi.org/10.3390/mca24020054
Chicago/Turabian StyleUddin, Marjan, Hazrat Ali, and Muhammad Taufiq. 2019. "On the Approximation of a Nonlinear Biological Population Model Using Localized Radial Basis Function Method" Mathematical and Computational Applications 24, no. 2: 54. https://doi.org/10.3390/mca24020054
APA StyleUddin, M., Ali, H., & Taufiq, M. (2019). On the Approximation of a Nonlinear Biological Population Model Using Localized Radial Basis Function Method. Mathematical and Computational Applications, 24(2), 54. https://doi.org/10.3390/mca24020054





