Seeking a Chaotic Order in the Cryptocurrency Market

Abstract

In this study, we investigate the existence of chaos in the global cryptocurrency market. Specifically, we analyze parameters of chaotic order, nonlinearity, sensitivity to the initial conditions, monofractality, and multifractality. For this purpose, we conduct a comprehensive series of tests, including Brock–Dechert–Scheinkman (BDS) test, largest Lyapunov exponent, box-counting, and monogram analysis for fractal dimension, and multiple tests for long-range dependence (Aggregated Variances, Peng, Higuchi, R/S Analysis, and Multifractal Detrended Fluctuation Analysis (MFDFA)). All tests are performed over a variety of major cryptocurrencies: Bitcoin, Litecoin, Ethereum, and Ripple. The empirical results support the existence of chaos in the cryptocurrency market. Accordingly, cryptocurrency returns are not random and follow a chaotic order. Therefore, long term predictions are not possible, contrary to most of the discussions ongoing in the media and the public.

1. Introduction

Chaos theory is the science of surprises. Informally, it teaches us to expect the unexpected and can be highly effective in modeling the behavior of virtually unpredictable complex nonlinear systems. Chaos theory, having numerous introductive resources, such as Alligood et al. [1] and Strogatz [2], has found applications in physics, biology, chemistry, and engineering. Among the practically infinite and ever-increasing examples, some are weather patterns [3], biological systems [4], food chains [5], crude oil markets [6], and brain states [7]. In terms of the variety of fields of study, the cases where chaos is present are extensive, and this renders chaos applicable to broad and interdisciplinary areas of study. Chaos theory may help us understand how our ecosystems, social systems, and economic systems work, and as such, it naturally paves its way to applications in economics and finance. A fundamental question for a particular system is whether chaos theory applies or not; if yes, to what extent does it apply? In this study, we attempt to examine the chaotic behavior of a relatively new financial product: cryptocurrencies. The main motivation of the study is to seek whether chaotic features are present in the cryptocurrency market in the context of predictability. As this market has had considerable investor attention in recent years, there is an intense discussion regarding its future. However, rather than telling the cryptocurrency market’s fortune, scientific evidence is required to determine if there is a foreseeable path in this market. We believe that statistical evidence can pave the way for a better investor mindset in these instruments and predictions in market trends.

Since the inception of cryptocurrencies, their main criticism has been the absence of an underlying theoretical background and their wild volatility. As of 2017, the spike in the cryptocurrency market raised the attention of the media and the public. However, putting the marketing of the issuers and possibly optimistic investors aside, there is no evidence in the literature to justify this soaring. The common sense is ‘this market is very risky’, ‘the mechanism is way too complicated’, and the lack of theoretical clarification has escalated the perspectives of everyday citizens. Bitcoin and cryptocurrencies, in general, seem to be uncorrelated with global stock market trends, monetary policy decisions, such as Federal Reserve policies, and the major events in the world, and the average individual keeps their distance due to common sentiment that “bitcoin is baseless” or that “it does not rely on anything”. Even amongst investors, the psychology is two-sided and ranges between the two extremes of “bitcoin is going to take over the world tomorrow” and “it is worth nothing”. Cheah and Fry [8] put forward the psychological, bubble-oriented behavior in bitcoin markets via a critical approach. As observed by Glaser et al. [9], for the current state of the market, it can be argued that users are primarily interested in investment and the holding value of bitcoin, rather than using it as an alternative monetary transaction system. On the other hand, a report of multinational investment company Morgan–Stanley [10] stated that Bitcoin and altcoins constitute a new institutional investment class, and have already attracted some retail venture. Even under the assumption of an innovative asset price behavior, the idiosyncratic nature of bitcoin involves many uncertainties and legislative question marks as it typically resides in a legal grey zone in most countries.

Apart from the above, statistically speaking, there may be some order in the behavior of this market. According to chaos theory, apparently random processes might have a hidden order, as chaotic dynamics are generated from nonlinear deterministic systems. Therefore, the process in which the price formation is determined might have chaotic characteristics, provided that certain features of chaos theory are held. As stated by Kortian [11], along with the supply and demand, many other parameters, such as self-fulfilling expectations, mass psychology, herd behavior, and manipulations, take a role in the determination of asset prices. The combination of these factors creates a market equilibrium price for any asset. However, the price formed does not guarantee fairness of value unless the market is fully efficient. In a market which is inefficient, the formed price might create opportunities due to undervaluing or overvaluing of the asset. The efficient market hypothesis assumes that the price innovations are fully random and unpredictable. This randomness requires the rejection of the existence of chaos in the market, and any departures from randomness can be considered/evaluated as a sign of chaos. From this point of view, this study attempts to seek chaotic price evidence in the cryptocurrency market, being tempted by the idea of investors that this market has opaque complexity. Although a few studies have examined the presence of chaos in the cryptocurrency market, to the best of our knowledge, these studies are often quite limited in their methodologies for investigating the characteristics of chaos. While chaotic dynamics require testing of multiple aspects of asset prices, from the self-similarity to sensitivity to the initial conditions, existing studies usually employ single-sided methodologies representing one aspect only.

2. Literature Review

Having been proposed under a pseudonymous name [12], and being the first of its kind, bitcoin has led the way for a variety of cryptocurrencies, which are considered as a nontraditional asset class. Due to its notorious price increase since its inception, bitcoin has arguably been the most successful currency in terms of demand so far, and without doubt, a highly controversial one. In parallel to the public interest in media and social media platforms and enthusiasm among investors, studies related to different divisions of cryptocurrencies are growing exponentially. There is a wide range of studies regarding anonymity, protocol proposals, security, transaction costs, scalability, energy consumption, and legislation related to cryptocurrencies, whereas our focus is on the financial and statistical aspects. Unlike centralized banking networks, the transaction capabilities of blockchain-based networks are highly related to the underlying technology, the limitations of which are yet to appear as it is still under development. Various aspects, such as governance, are covered in [13]. A heavily debated topic is transaction costs, which have risen over time as indicated in a relatively early work [14]. However, the technology is still evolving. Although a highly decentralized structure such as the core bitcoin network, per se, is not scalable, promising technologies such as the so-called “lightning network” emerge to overcome these problems, as described in [15], and have already been deployed and in practical use as of 2018. This solution, allowing transactions to not rely on miners, also has the potential to decrease the highly criticized redundant energy consumption of bitcoin miners at the cost of centralization of transaction entities. Nevertheless, the native scalability shortcoming of bitcoin is also one of the reasons that has led academics to develop alternative protocol proposals, such as in [16]. Another aspect is anonymity, which has been studied extensively by Reid and Harrigan [17]. Another is security; a recent study involved devising an algorithm that can track tokens that are stolen from exchanges [18]. We will briefly discuss the blockchain mechanism and the academic interest on it, as without some basic understanding, from a purely financial perspective, one cannot really comprehend cryptocurrencies. Indeed, the underlying blockchain technology of bitcoin, although having been most notably utilized for tokenizing digital assets, has the capability of acting as a trusted third party, enabling a large number of applications other than cryptocurrencies, as discussed in Underwood [19]. Among the numerous fields that employ blockchain, one can discuss its usage for digital identity management and protecting personal data with the additional benefit of auditability, as studied by Zyskind and Nathan [20] and how it may be used to construct e-voting mechanisms as in [21]. Reyna et al. [22], in particular, discuss how blockchain can be integrated into the internet of things. Furthermore, blockchain, along with RFID technologies, are frequently discussed to restructure supply chain traceability systems, as argued by Tian [23]. In addition, a major discussion is that blockchain may have significant applications in banking and have potential financial implications as discussed in [24,25]. Studies investigating the relationship of cryptocurrencies and other economic or financial variables are also extensive in the literature. Gandal et al. [26] studied bitcoin price manipulation. Viglione [27] argues that relative bitcoin price within a country is inversely correlated with the economic freedom therein. The speculative aspect of bitcoin is studied by Bouoiyour and Selmi [28] and in [29], along with the relationship between the supply–demand fundamentals and its price. Dyhrberg [30] classifies bitcoin as somewhere in between gold and the US dollar, while identifying its attributes as a medium of exchange versus a store of value. A related work by Katsiampa [31] estimates the volatility of bitcoin via a comparison of GARCH models. Brauneis and Mestel [32] argue that cryptocurrencies become less predictable/inefficient as liquidity increases.

The current literature on the cryptocurrency market is quite limited in the context of nonlinear behaviors of these instruments. The recent studies which discuss the chaotic dynamics of cryptocurrencies can be summarized as follows: Takaishi [33] and Lahmiri and Bekiros [34] independently studied the multifractality properties of bitcoin. Urquhart [35] studied the market inefficiency of bitcoin via random walks, whereas Bariviera [36] revisited the same topic by using Hurst exponent. Bariviera et al. [37] further studied long-range dependence of bitcoin again by Hurst exponents. In a recent related study, Garnier et al. [38] observed orderly correlation in the bitcoin market. There are alternate views on Bitcoin regarding its chaoticity and its complexity. Santos [39] claims that bitcoin can neither be regarded as a complex system nor exhibits chaotic features. Pilkington [40] also studied bitcoin through the perspective of complexity theory. Al-Yahyae et al. [41] compared the multifractality properties of bitcoin compared to gold, stock, and global currency markets and their findings show that the bitcoin market is the most inefficient compared to others. In a similar study, Bouri et al. [42] also tested for nonlinear short-term and long-term relationships between bitcoin, aggregate commodity, and gold prices. Khuntia and Pattanayak [43] considered the adaptive market hypothesis and evolving return predictability in the bitcoin market. Khuntia and Pattanayak [44] also evaluated the adaptive pattern of long memory in the volatility of day-trading bitcoin returns while testing the impact of the trading volume on time-varying long memory. Jiang et al. [45] also studied time-varying long-term memory in the bitcoin market by considering Hurst exponents and found inefficiency. Jang and Lee [46] used a different and interesting approach in the prediction of bitcoin prices via Bayesian neural networks. Apart from the cryptocurrency-related studies in the literature, chaos and its features have already been examined with a great deal of interest. Following the seminal paper of Lorenz [47], many researchers have attempted to examine chaos in different fields. Chaos was mathematically defined by Li and Yorke [48] by three properties: the dependence on the initial value of the system, boundedness, and nonperiodicity. Some relatively early work was performed by Brock [49], providing a rigorous mathematical introduction to the tests that help distinguish between random and deterministic systems. Related results are given in [50].

In practice, the determination of chaos is conducted through different types of tests (Hurst exponent for self-similarity analysis, Lyapunov exponent, BDS tests, fractal dimension, etc.), such that each test measures the examined feature of chaos. For example, Grassberger and Procaccia [51] studied a variety of algorithms for describing attractors of a dynamic chaotic system. An attractor is said to be strange if it has a fractal structure. In this case, the system exhibits dependence on initial conditions. The study of Takens [52] is recognized as a reliable mathematical foundation for detecting attractors. Adeli et al. [53] use EEGs (electroencephalograms) and certain sub-bands through a wavelet-chaos methodology to detect seizure and epilepsy. Becks et al. [54] empirically demonstrated the existence of chaos in a biological predator–prey setting in bacterial species. Lee et al. [55], a study in aeronautical engineering, analyzed nonlinear aeroelastic analysis of airfoils. Gunay [56] examined chaos in the stock markets of BRIC countries and Turkey through various methods and stated that the evidence is too weak to accept the presence of chaos. Barkoulas et al. [57] searched for the existence of chaos in the Athens Stock Exchange, whereas Serletis et al. [58] claimed that there is no evidence of chaos, due to some dependence on the US stock market. Among other theoretical chaos work, Eissa et al. [59] studied a specific comparison within the boundaries of vibrations and dynamic chaos and Cai et al. [60] studied secure communication between two different chaotic systems. Needless to say, the use of Lyapunov exponents in the context of chaos has been studied in various other markets, such as in future markets, as in [61]. The BDS test, a powerful tool for detecting serial dependence in time series, was first devised by Brock [62]. The test was later modified by Brock et al. [62]. Brock [63] provided a recent related survey on analyzing causality, chaos, and prediction in economics and finance. While there are alternative methods for revealing nonlinearities in financial time series, the BDS test has gained widespread acceptance. McKenzie [64] applied the BDS test in the context of chaotic behavior in the national stock market indices. However, not being indicative of chaos, a large number of studies employ the test in a complementary fashion. Among them, Opong et al. [65] studied the behavior of certain UK equity markets employing Hurst exponents as well as the BDS test. Serletis and Gogas [66] studied chaos in East European black market exchange rates using the Lyapunov exponent estimator alongside the BDS test. The previously mentioned work of Barkoulas et al. [57] also employed the BDS test and a number of others. On the other hand, the fractal dimension, also utilized in the examination of chaotic features, was first studied by Mandelbrot [67] and algorithmic implementations were studied in [68]. Many resources, such as [69], were presented for financial chaos theory applications and fractal market analysis. Diego and Giampiero [70] applied fractal dimensions to earth sciences and specifically analyzed geochemically linked groups to reveal magmatic interaction. Tsonis and Elsner [71] applied the box-counting method as a measurement of fractal dimension to identify chaotic behavior in weather patterns. Among the financial studies, while Vassilicos et al. [72] provided yet another study in which no evidence of chaos was observed in the foreign exchange and the stock markets but the presence of multifractals was noticed. Lindsay and Campbell [73] applied the box-counting method to predict bankruptcies within a chaos theory approach. On the other hand, Sun et al. [74] studied the predictability of the Hang Seng stock index in Hong Kong via multifractal analysis and the box counting method. The study of Hurst exponents, also used in the determination of chaotic signals in asset prices, depends on the seminal study of Hurst [75] that was conducted to detect long memory in hydrologic time series. The method was made popular by Mandelbrot and Wallis [76], where rescaled range (R/S) analysis was studied. Mandelbrot [77] later interpreted this statistic for financial time series. A historically significant relevant study was due to [78]. For a survey displaying variations on Hurst exponent, see [79] and for theory and various applications of long-range dependence, see [80]. Even though predicting stock markets and futures markets is a challenging task, some studies have attempted to describe their behavior via chaos theory. Serletis and Rosenberg [81] and He and Chen [82] studied the Hurst exponent in energy futures prices and agricultural futures markets, respectively. Qian and Rasheed [83] employed the Hurst exponent to show that not all periods of the stock markets were equally random. Another work applying the Hurst exponent was by Zunino et al. [84], who studied stock markets’ inefficiency.

3. Methodology

3.1. BDS Test

The BDS test was originally designed by Brock et al. [49,62] in order to detect serial dependence in price data. The BDS test is essentially a statistic based on the correlation dimension of the residuals that result from the fitted linear autoregressive model. In other words, the inquiry is whether there is a simple linear dependence or certain daily seasonality in the data. Such dependence is meant to be filtered out before testing for nonlinearity. The BDS test indeed has strength against linear and nonlinear alternative tests that can be employed for the same purpose [85]. Given a time series, we first compute the “m-histories” of the series; that is, we embed the series into a set of m-dimensional vectors as follows: $\left\{x_t^m\right\}$ = $\left(x_t,x_{t+\tau },\dots ,x_{t+\tau \left(m-1\right)}\right)$, where $t=1,\dots ,T-m$ is the time, $m$ is the embedding dimension, and $\tau$ is the delay. We then compute the correlation integral as follows

$$C_m\left(\epsilon \right)=\frac{1}{\left(T-m+1\left(T-m\right)\right)}{\displaystyle \sum }_{\forall t,s}{I}_{\epsilon }\left(x_t^m,x_s^m\right)$$

where, $I_{\epsilon }\left(x_t^m,x_s^m\right)$ is the indicator function, that is $I_{\epsilon }=1$ if $\Vert x_t^m-x_s^m\Vert \le \epsilon$ (points are close enough) and is 0 otherwise. The BDS test is now stated as:

$$C_{m,T}\left(\epsilon \right)=\frac{\sqrt{T}\left[(C_T(\epsilon )-C_1{\left(\epsilon \right)}^m\right]}{{\sigma }_{m,\tau }(\epsilon )}$$

where ${\sigma }_{m,\tau }\left(\epsilon \right)=4\left[K^m+2\left({{\displaystyle \sum }}_{j=1}^{m-1}{K}^{m-j}C{\left(\epsilon \right)}^{2j}\right)+{\left(m-1\right)}^{2}C{\left(\epsilon \right)}^{2m}-m^{2}KC{\left(\epsilon \right)}^{2m-2}\right]$ and $K\left(\epsilon \right)$ is computed by $K\left(\epsilon \right)=\frac{6{{\displaystyle \sum }}_{t,s,r}{h}_{\epsilon }\left(x_t^m,x_s^m,x_r^m\right)}{\left[Tm\left(Tm-1\right)\left(Tm-2\right)\right]}$ and $h_{\epsilon }\left(x_t^m,x_s^m,x_r^m\right)=\frac{1}{3} \left[I_{\epsilon }\left(i,j\right)I_{\epsilon }\left(j,k\right)+I_{\epsilon }\left(i,k\right)I_{\epsilon }\left(k,j\right)+I_{\epsilon }\left(j,i\right)I_{\epsilon }\left(i,k\right)\right]$.

3.2. Largest Lyapunov Exponent

Sensitivity to the initial conditions can be measured by the largest Lyapunov exponent and positive values of this test statistic for time series produced by dynamical systems is postulated as a sign of chaos. Calculating the largest Lyapunov exponent from a given time series as in [86] is accurate, and robust to changes in quantities such as the embedding dimension, the size of data set, the noise level, and the reconstruction delay. One may use the method to calculate the correlation dimension. Hence, one sequence of computations helps simultaneous estimation of both the level of chaos and the system’s complexity. As we construct rows by $\left\{X_i\right\}=\left(x_i,x_{i+J},\dots ,x_{i+J\left(m-1\right)}\right)$, $J$ being the delay and $m$ being the embedding dimension, each row being a vector, we obtain the $M\times m$ trajectory matrix $X$ such that $\left\{X\right\}={\left[X_1,X_2,\dots ,X_M\right]}^T$. Letting ${\lambda }_1$ be the largest of the Lyapunov exponents ${\lambda }_i,1\le i\le n$, and $d\left(t\right)=C{e}^{{\lambda }_{1}t}$ be the average divergence at time $t$ where $C$ is a constant that normalizes the initial separation, we assume that the $j^{th}$ pair of nearest neighbors diverge at the rate of the largest Lyapunov exponent, that is, $d_j\left(i\right)\approx C_j{e}^{{\lambda }_1\left(i.\Delta t\right)}$ or $\ln d_j\left(i\right)\approx \ln C_j+{\lambda }_1\left(i.\Delta t\right)$. The largest Lyapunov exponent is obtained by using a least-squares fit to the “average” of these lines defined as $y\left(i\right)=\frac{1}{\Delta t}<\ln d_j\left(i\right)>$ where $<\cdots >$ is the average over all values of $j$.

3.3. Fractal Dimension: Box-Counting Method

By following the definition of Gneiting et al. [87], let $N\left(ϵ\right)$ be the number of boxes required at scale $ϵ$ and let $u$ be the range of the data so that $u={\max }_{0\le j\le n} X_{j/n}-{\min }_{0\le j\le n} X_{j/n}$. We assume a scale ${ϵ}_k=2^{k-K}$ where $k=0,1,\dots ,K$. At the largest scale ${ϵ}_k=1$, the graph can be covered by a box whose width is 1 and height is $u$, which is called the bounding box. It is observed that the bounding box can be tiled by $4^{K-k}$ boxes each with the height $u{2}^{k-K}$ and the width $2^{k-K}$. Among these, let $N\left({ϵ}_k\right)$ denote the number of such boxes which intersects with the linearly interpolated data graph. Then, the box estimator is

$${\widehat{D}}_{BC}=-\left\{{\displaystyle {\displaystyle \sum }_{k=0}^K}\left(s_k-\overline{s}\right)\log N\left({ϵ}_k\right)\right\}{\left\{{\displaystyle {\displaystyle \sum }_{k=0}^K}{\left(s_k-\overline{s}\right)}^2\right\}}^{-1}$$

where $s_k=\log {ϵ}_k$ and $\overline{s}$ is the mean of $s_0,s_1,\dots ,s_K$. We also employ generalized variation estimators again as in [87],

$${\widehat{D}}_{V;p}=1-\frac{1}{p}\frac{\log {\widehat{V}}_p\left(\frac{2}{n}\right)-\log {\widehat{V}}_p\left(\frac{1}{n}\right)}{\log 2},$$

such that

$${\widehat{V}}_p\left(l/n\right)=-\frac{1}{2\left(n-l\right)}{\displaystyle {\displaystyle \sum }_{k=0}^K}{\left|X_{i/n}-X_{\left(i-l\right)/n}\right|}^p,$$

where $X$ is the point set, $n$ is the sample size, ${ϵ}_l=l/n$ is the scales used. When $p=1$, we obtain a madogram.

3.4. Long-Memory (Long Range Dependence)

3.4.1. Rescaled Range

The original statistical approach of long memory, called rescaled range analysis (R/S range), was presented in [75] and is a simple and useful tool for analyzing the time series. We adopt the formulation as in [88], which can be described as the rescaled range statistic $\frac{R_t}{s_t}$ as follows:

$$R_t=\underset{0\le j\le T}{\max } \left\{{\displaystyle {\displaystyle \sum }_{j=1}^r}\left(y_j-j\overline{y}\right)\right\}-\underset{0\le j\le T}{\min }\left\{{\displaystyle {\displaystyle \sum }_{j=1}^r}\left(y_j-j\overline{y}\right)\right\}.$$

Here $R$ is the range,$\overline{y}$ is the sample mean and $s_T$ is the standard deviation where $s_T={\left\{\frac{1}{T}{{\displaystyle \sum }}_{j=1}^r{\left(y_t-\overline{y}\right)}^2\right\}}^{\frac{1}{2}}$.

3.4.2. Modified DFA

The Detrended Fluctuation Analysis (DFA) was originally due to [89]. We adopt the formulation as in [90]. Let us first describe DFA (without modification) as below. Given $\left(i\right), i=1,2,\dots ,N$, we aim to find the correlation between $x_i$ and $x_{i+s}$. Let $\overline{x_i}=x_i-<x>$ where $<x>=\frac{1}{N}$ ${{\displaystyle \sum }}_{i=1}^n{x}_i$ is the mean. Now the quantitative correlation between $x_i$ and $x_{i-s}$ is

$$C\left(s\right)=<{\overline{x}}_i,{\overline{x}}_{i+s}>=\frac{1}{N-s}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\overline{x}}_i.{\overline{x}}_{i+s}.$$

Note that $C\left(s\right)$ declines as a power-law for long-range correlations, that is, $C\left(s\right)\propto s^{-\gamma }$, $0<\gamma <1$.

$$Y\left(i\right)={\displaystyle {\displaystyle \sum }_{k=1}^i}{x}_k-<x>$$

is computed for the record $\left(x_i\right)$ of length $N$. Afterwards, we cut the profile $Y\left(i\right)$ into $N_s\equiv \left[N/s\right]$ non-overlapping segments each with length s. Now we calculate the local trend for each segment. For that, we apply a least-square fit of the data. Then let $Y_s\left(i\right)=Y\left(i\right)-p_v\left(i\right)$, which is the difference between the time series and the fits. For each of the $2N_s$ segments, we calculate the variance $F_s^2\left(v\right)=<Y_s^2\left(i\right)>=\frac{1}{s}{{\displaystyle \sum }}_{i=1}^s{Y}_s^2\left[\left(v-1\right)s+i\right]$. Finally, by averaging over all segments, the DFA fluctuation function is $F\left(s\right)={\left[\frac{1}{2N_s}{{\displaystyle \sum }}_{v=1}^{2N_s}{F}_s^2\left(v\right)\right]}^{1/2}$. In the case of the modified DFA, the distinction is that we simply divide the DFA fluctuation functions $F\left(s\right)$ above by the corresponding correction function $K_{\alpha }^{\left(n\right)}\left(s\right)=\frac{<{\left[F^{\left(n\right)}\left(s\right)\right]}^2{>}^{1/2} s^{\prime \alpha }}{<{\left[F^{\left(n\right)}\left(s^{\prime }\right)\right]}^2{>}^{1/2} s^{\alpha }}$ for $s^{\prime }\gg 1$. In particular, we divide $F^{\left(n\right)}\left(s\right)$ by $K_{1/2}^{\left(n\right)}\left(s\right)$.

3.4.3. Higuchi’s Method

This method was originally presented [91] for calculating the length of a curve and obtaining the fractal dimension of large-scale fluctuations of the interplanetary magnetic field. Higuchi [92] modified the method, in particular, the way the curve length is defined, turning it into a generic one and popularizing it. This method is widely referred to as Higuchi’s method, which we adopt, and can be stated as follows. Given $X_i,\dots ,X_N$, a time series of length $N$, and assuming a block size $m$, we first calculate $Y\left(n\right)={{\displaystyle \sum }}_{i=1}^n{X}_i$ where $n$ is picked as an arbitrarily large number such as $n>1000$. Here, the purpose is to produce fractional Brownian motion from fractional Gaussian noise. Then, we find the normalized length of the curve via the formula

$$L\left(M\right)=\frac{N-1}{m^3}{\displaystyle {\displaystyle \sum }_{i=1}^m}{\left[\frac{N-i}{m}\right]}^{-1}{\displaystyle {\displaystyle \sum }_{k=1}^{\left[\left(N-i\right)/m\right)]}}\left|Y\left(i+km\right)-Y\left(i+\left(k-1\right)m\right)\right|,$$

where $[ ]$ denotes the greatest integer function. We have $EL\left(m\right)~C_H{m}^{-D}$, where $D=2-H$. Drawing $L\left(m\right)$ versus m logarithmically will produce a straight line with a slope $D=2-H$.

3.4.4. Aggregated Variance Method

The Aggregated Variance Method [93] is described below. Divide the time series $\left\{X_i, i\ge 1\right\}$ into blocks of size $m$ and define

$$X^{\left(m\right)}=\frac{1}{m} {\displaystyle {\displaystyle \sum }_{i=\left(k-1\right)m+1}^{km}}X\left(i\right) k=1,2,\dots$$

for all values of $m$, where blocks are labeled by the index $k$. Now compute the sample variance of $X^{\left(m\right)}\left(k\right), k=1,2,\dots$ for each block, which is an estimator of $Var{X}^{\left(m\right)}$. With partitioning the data $X_i,\dots ,X_n$ into $N/m$ blocks each of size $m$, we calculate $\widehat{Var} X^{\left(m\right)}$ using $X^{\left(m\right)}\left(k\right)$ for $k=1,2,\dots ,N/m$, for different values of $m$, where

$$\widehat{Var} X^{\left(m\right)}=\frac{1}{N/m}{\displaystyle {\displaystyle \sum }_{i=1}^{N/m}}{(X^{\left(m\right)}\left(k\right))}^2-{\left(\frac{1}{N/m}{\displaystyle {\displaystyle \sum }_{i=1}^{N/m}}{X}^{\left(m\right)}\left(k\right)\right)}^2,$$

Here, note that $\widehat{Var} X^{\left(m\right)}$ is an estimate for $Var{X}^{\left(m\right)}$. Finally, we plot the logarithm of the sample variance $\widehat{Var} X^{\left(m\right)}$ versus log m.

4. Empirical Analysis

We investigate the presence of chaos in the cryptocurrency market for four main assets: Bitcoin, Litecoin, Ripple, and Ethereum, which are recognized as the major cryptocurrencies with a mature price history. Selection of cryptocurrencies is based on the market capitalizations as of January 13, 2018. As discussed by Higgins [94] and Rickles et al. [95], the leading properties of chaotic systems are nonlinearity, nonrandom deterministic behavior, sensitivity to initial conditions, and fractality (self-similarity and fractal dimensions). Statistically proven existence of these features leads us to conclude that the respective time series display chaotic features. In other words, the presence of these elements helps distinguish chaos from randomness. To that end, in our study, we run three main tests: the estimation of the Hurst Exponent through monofractal and multifractal analysis, fractal dimension analysis (fractality), the BDS test (nonlinearity), and the Lyapunov Exponent (sensitivity to the initial conditions). By considering the preassumptions of the BDS test, we also conduct an autoregressive fractionally integrated moving average (ARFIMA) and a fractionally integrated generalized autoregressive conditionally heteroskedastic (FIGARCH) model estimations for the corresponding times series. The data used in the study is obtained from the widely recognized price aggregator www.coinmarketcap.com with a daily frequency and covers the period 28 April 2013 to 13 January 2018.

Fractality Test: Hurst Exponent and Fractal Dimension

As discussed by Williams [96], fractals deal with quantitative ways of characterizing geometric patterns. Chaos, on the other hand, is a certain evolution in time, and its underlying characteristics distinguish itself. Fractals and chaos often occur together. Most chaotic attractors have a fractal striped texture. Chaotic attractors of invertible maps are typically fractals. Because of such close relationships, we say that fractals help detect chaos. The fractality feature of chaotic time series can be observed through long memory (long-range dependence) or self-similarity analysis in which we compute the Hurst exponent (H). There are plenty of methods to compute the Hurst exponent. Nonetheless, regardless of the method employed, the Hurst exponent varies between 0 and 1, and interpretation of the coefficient is as follows: For $0.5<H<1$, the process has stationary long memory; For $H=0.5$, the time series obeys random walk; In the case where $0<H<0.5$, the series is said to be antipersistent.

Before the interpretation of the coefficient, determination of the most robust method would increase the accuracy of the study. In

Table 1. Hurst exponent estimations.

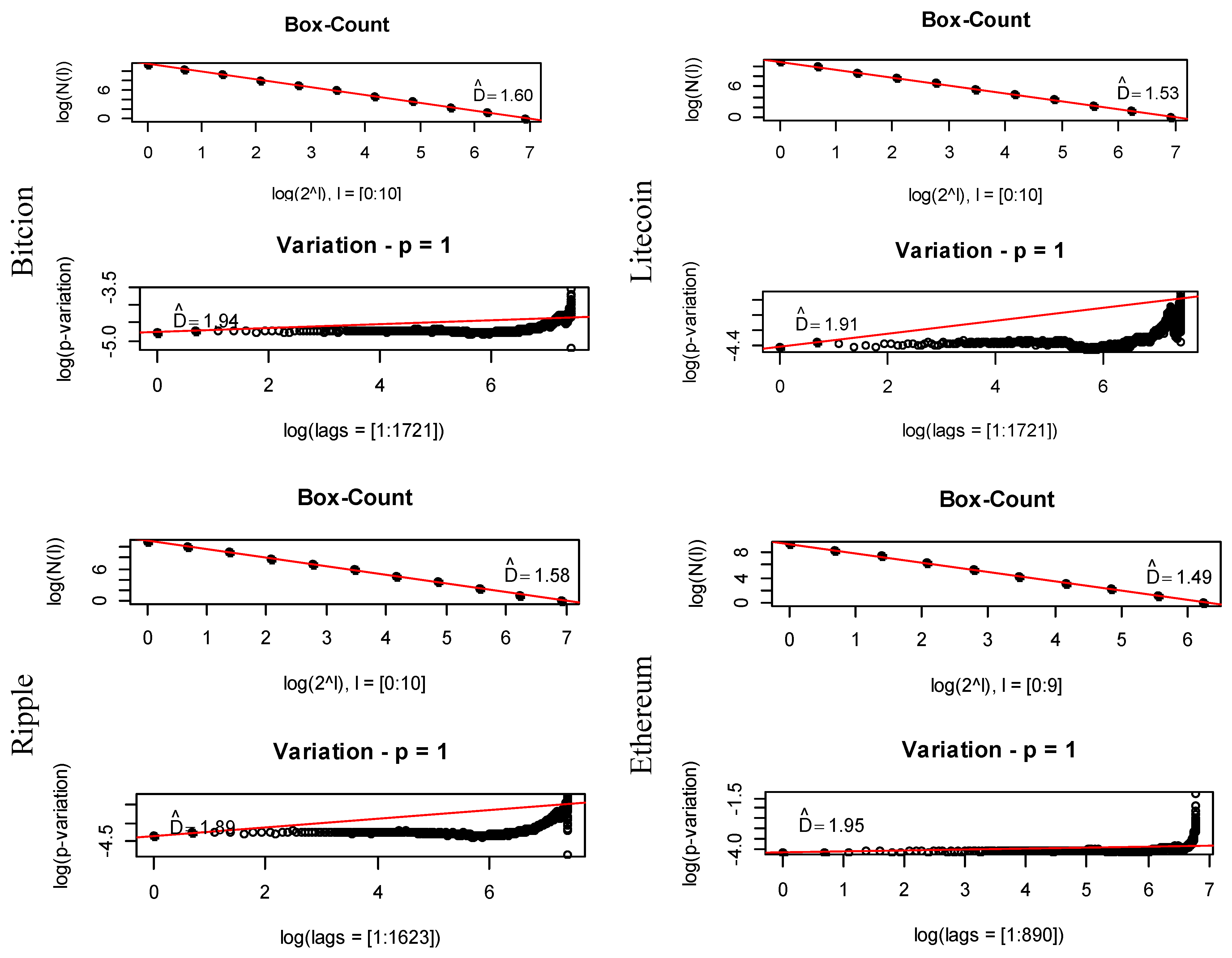
	Bitcoin	Litecoin	Ripple	Ethereum
Aggregated Variances	0.5696 ***	0.5530 ***	0.5041 ***	0.5754 ***
	−0.8609	−0.8940	−0.9918	−0.8492
	0.0184	0.0223	0.0585	0.0265
Peng Method	0.5391 ***	0.5321 ***	0.5618 ***	0.5629 ***
	1.0782	1.0643	1.1236	1.1258
	0.0138	0.0150	0.0145	0.0132
Higuchi Method	0.5983 ***	0.6194 ***	0.5743 ***	0.6661 ***
	−1.4017	−1.3806	−1.4257	−1.3339
	0.0336	0.0470	0.0496	0.0422
R/S Method	0.5908 ***	0.5523 ***	0.6197 ***	0.5713 ***
	0.5908	0.5523	0.6197	0.5713
	0.0264	0.0292	0.0151	0.0176

*** denotes significance at 99% confidence level. Source: Estimated by the authors through the R implementation of [98].

, we present various methods for the estimation of the Hurst exponent and each method has its own pros and cons. As stated by Gunay [97], while Aggregated Variances and the Peng Method are quite robust, the Higuchi Method and R/S Analysis have a strong bias. Considering those findings, we focus on the first two out of the four tests. According to the results of the Aggregated Variances and Peng Method, we can argue for a significant presence of long memory for all times series. As the larger Hurst exponent presents a greater intensity of long-range dependence, we can say that Ethereum returns display a higher order of dependence or persistence.

The Hurst exponent can also be interpreted as self-similarity indicator. As discussed by Rickles et al. [95], a chaotic system’s time series depicts fractality features such as self-similarity. Self-similarity can be defined as a property of an object which yields the same appearance under different scales. For example, a time series might appear to exhibit the same behavior under annual, monthly, and daily frequencies. For a time series, self-similarity can be observed in a distributional sense. In this case, for different scales, time series would depict the same correlation structure. Therefore, for a self-similar time series, we might witness long memory feature [99]. From this point of view, the results in Table 1 also indicate that the corresponding time series shows self-similarity, and therefore chaotic features. However, this is a preliminary analysis and we need to support this finding through further research by running corresponding tests. In order to raise the robustness of the paper, we have also calculated the multifractal Hurst exponent. Unlike the monofractal theory, the multifractal approach states that some asset returns might display multiple scaling exponents rather than single ones. In modeling the scaling behavior of different subsets of data, Kantelhardt et al. [100] introduced multifractal detrended fluctuation analysis (MFDFA). Results of the MFDFA are presented in

Table 2. Multifractality analysis.

	$\mathbf{H}\left(\mathbf{q}=-5\right)$	$\mathbf{H}\left(\mathbf{q}=0\right)$	$\mathbf{H}\left(\mathbf{q}=5\right)$
Bitcoin	0.8396	0.6567	0.5376
Litecoin	0.9164	0.6984	0.4093
Ripple	0.9129	0.6768	0.3992
Ethereum	0.8773	0.6957	0.5219

Source: Authors’ estimation through the Matlab implementation of Ihlen [101].

.

Large variation in H(q) is an indicator of a multifractal time series. According to the findings, the MFDFA yields different H values (different scaling behaviors) for each utilized q-orders (−5, 0, and 5). The indication of multifractality also supports the existence of chaos that was asserted in monofractal analysis. As pointed by Rickles et al. [95], fractals are a spatial type of chaos and another way to extract the fractality feature from a time series is examining its fractal dimension.

As stated by Peters [102], the fractal dimension defines the roughness or smoothness of a time series. While in Euclidean geometry dimensions are integers and can take a value such as 1 (line), 2 (planes), or 3 (solids), in fractal geometry, dimensions might have noninteger values. The fractal dimension of a time series is related to scaling in time. For a time series, the fractal dimension will have values between 1 and 2. Considering the relationship $D=H+2$, a random walk processes $D=1.5$. Hence, for a given time series, with any $D$ value different than 1.5, one can infer the absence of randomness as a signal of chaos. Results exhibited in

Table 3. Fractal dimension statistics.

	Madogram	Box-Count
Bitcoin	1.94	1.60
Litecoin	1.91	1.53
Ripple	1.89	1.58
Ethereum	1.95	1.49

Source: Estimated by the authors through the R implementation of [103].

indicate that all D values are different, and there is random walk behavior. In Figure 1, for each cryptocurrency, we provide two graphs, where the one depicts the results of the box-count and the graph below is the madogram output. Recalling that the box-count estimator is the slope in an ordinary least squares regression fit of $\log N\left(l\right)$ on $\log \left(l\right)$, where $N\left(l\right)$ is the number of boxes required at scale $l$, for the box count outputs in charts in Figure 1, $\log \left(2^l\right)$ and $\log N\left(l\right)$ are represented over x and y axes, respectively. Note that ϵ in the methodology description of the box-counting method is replaced by l for the sake of feasibility in representation in computer software. For the madogram outputs, the x-axis represents lags $l/n$ where $l=1$, and the corresponding p-variation is on the y-axis. Again, a log–log regression fit over our data for the variation estimator is presented for order $p=1$ madogram. However, test results aside, inferring chaos requires more evidence that satisfies other features of chaos. Therefore, in the following section, we fulfill the tests regarding nonlinearity and sensitivity to the initial conditions.

As we discussed before, the investigation of chaos also requires the test of nonlinear behavior in data. In this section of the paper, we execute the BDS test. As discussed by Brock et al. [62], this test is implemented to detect if the time series is related to a process that generates chaotic data. Implementation of the BDS test has a prerequisite. The test is implemented to forecast errors of the fitted model, such as ARMA, ARIMA, or ARFIMA. The null hypothesis of the model tests whether the time series is independently and identically distributed. As our earlier analysis revealed the existence of long memory in series, here, for BDS test, we execute the ARFIMA model which considers long-range dependence.

An ARFIMA ($p,d,q$) process is the combination of the AR and MA models along with a fractionally (noninteger) differencing parameter. As the results in Table 3 indicate, we have utilized different orders $p$ and $q$ to determine the best fitting model for the data. For the appropriate order selection, we employed Akaike Information Criteria (AIC). The models attained with the minimum AIC values are presented in

Table 4. ARFIMA model estimation.

	Bitcoin ARFIMA (4.d.2)	Litecoin ARFIMA (2.d.3)	Ripple ARFIMA (1.d.1)	Ethereum ARFIMA (1.d.1)
AR-1	0.6023 *** (0.0538)	−1.2109 *** (0.0438)	0.3917 ** (0.1749)	1.7037 *** (0.1096)
AR-2	−0.9488 *** (0.0349)	−0.8625 *** (0.0579)		−0.7732 *** (0.1021)
AR-3	−0.0728 ** (0.0357)
AR-4	−0.0661 ** (0.0332)
d	0.1098 *** (0.0354)	0.0700 ** (0.0355)	0.1409 ** (0.0636)	0.2284 *** (0.0873)
MA-1	−0.7121 (0.0282)	1.1789 *** (0.0695)	−0.4843 ** (0.1943)	−1.8493 *** (0.0527)
MA-2	0.9385 *** (0.0205)	0.7666 *** (0.1008)		0.8909 *** (0.0550)
MA-3		−0.0928 * (0.0491)
Constant	0.0012 *** (0.0008)	0.0010 (0.0011)	0.0017 (0.0020)	0.0027 (0.0034)
Log-likelihood	4369	3594	3147	1675
AIC	−5.0640	−4.1649	−3.8688	−3.7451

*, ** and *** denotes significance at 90%, 95% and 99% confidence levels, respectively. Source: Authors’ estimation.

. Results show that Bitcoin and Litecoin have higher lags in the AR and MA processes than Ripple and Ethereum. Besides this, for all variables, the fractional differencing parameter $d$ is statistically significant, indicating that returns of all variables have long memory (long-range dependence). This also means that return in the cryptocurrency market does not obey the weak form of market efficiency and does not follow random walk. Deviation from randomness can also be interpreted as a sign of chaotic behavior.

As discussed before, the benefit of incorporating an ARFIMA $\left(p,d,q\right)$ model is filtering the linear structure of time series. The residuals of the ARFIMA models will be used in the BDS test to see whether the return series emerge from an IDD process. As discussed by Brooks [104], beside a linear model, the BDS test can also be implemented to the residuals of GARCH type models. However, as in this case, the critical values of the BDS test will be different from the standard normal distribution. We need to utilize the values provided by Hsieh [105]. By following this recommendation in our analysis, we run the FIGARCH model as well to see if further determinism, already filtered in the ARFIMA and FIGARCH models, is still present in the series.

According to the reference, ranges for fractionally differencing parameter $d$ given by Baillie [88], volatility of the variables also has long memory. As discussed by the author, for $0<d<0.5$, the time series has long memory and its autocorrelation function decays hyperbolically. In the case where $-0.5<d<0$, the process has short memory. Accordingly, in

Table 5. FIGARCH model estimation.

	Bitcoin FIGARCH (1.d.1)	Litecoin FIGARCH (1.d.1)	Ripple FIGARCH (1.d.1)	Ethereum FIGARCH (1.d.1)
cm	0.0008 ** (0.0003)	−0.0005 (0.0005)	−0.0017 *** (0.0006)	0.0010 (0.0010)
c v	0.0965 (0.0638)	0.2157 *** (0.0776)	1.8985 *** (0.7269)	0.5213 ** (0.2466)
d	0.5486 *** (0.1486)	0.9707 *** (0.1312)	0.6493 *** (0.1092)	0.8071 *** (0.1740)
a	0.2819 ** (0.1157)	0.1575 (0.1501)	−0.3680 *** (0.1236)	0.1933 (0.1488)
b	0.6223 *** (0.1446)	0.8868 *** (0.0166)	−0.2310 * (0.1193)	0.5979 *** (0.1645)
Log-likelihood	4691	3940	3702	1831
AIC	−5.4422	−4.5706	−4.5532	−4.0976

*, ** and *** denote significance at 90%, 95% and 99% confidence levels, respectively. Source: Authors’ estimation.

, we can state that the volatility of the process for all variables displays a hyperbolic decay for the influence of lagged squared innovations. Following the estimation of ARFIMA and FIGARCH models, we extract the residuals of these estimations. Employed BDS test results for these residuals are presented in

Table 6. BDS test results.

	e	ARFIMA par	FIGARCH par		Residuals of ARFIMA			Residuals of FIGARCH
					m = 3	m = 5	m = 7	m = 3	m = 5	m = 7
Bitcoin	0.5	0.2086	0.4139	w	19.28	33.29	59.11	21.06	36.56	64.77
				c	0.05	0.02	0.01	0.06	0.02	0.01
	1	0.4873	0.6622	w	16.03	20.86	26.92	16.44	21.39	27.60
				c	0.26	0.17	0.11	0.27	0.17	0.12
	1.5	0.6798	0.8015	w	13.06	14.94	17.04	13.42	15.30	17.56
				c	0.47	0.36	0.29	0.48	0.37	0.30
	2	0.8009	0.8796	w	11.65	12.69	13.72	12.10	13.16	14.32
				c	0.65	0.55	0.48	0.65	0.56	0.49
Litecoin	0.5	0.2086	0.4943	w	25.54	39.41	65.37	22.53	34.15	54.61
				c	0.11	0.06	0.03	0.12	0.06	0.03
	1	0.4873	0.7241	w	18.50	21.90	26.52	17.79	21.10	25.18
				c	0.37	0.26	0.20	0.38	0.27	0.21
	1.5	0.6798	0.8380	w	14.13	15.19	16.39	14.07	15.10	16.34
				c	0.56	0.46	0.38	0.57	0.47	0.39
	2	0.8009	0.8994	w	12.11	12.26	12.49	12.12	12.12	12.43
				c	0.71	0.62	0.55	0.71	0.62	0.55
Ripple	0.5	0.2086	0.4938	w	23.77	33.18	52.17	23.91	33.64	52.88
				c	0.12	0.06	0.03	0.12	0.06	0.03
	1	0.4873	0.7291	w	20.23	22.83	25.94	20.37	22.96	26.02
				c	0.40	0.29	0.22	0.41	0.30	0.23
	1.5	0.6798	0.8425	w	17.52	18.58	19.84	18.02	18.90	20.00
				c	0.61	0.51	0.44	0.61	0.52	0.45
	2	0.8009	0.8996	w	14.50	15.00	15.62	15.21	15.49	15.93
				c	0.73	0.65	0.59	0.73	0.65	0.59
Ethereum	0.5	0.2086	0.4297	w	16.99	27.97	55.46	13.74	20.32	36.82
				c	0.06	0.02	0.01	0.06	0.02	0.01
	1	0.4873	0.6841	w	12.87	15.79	19.96	12.59	14.98	18.81
				c	0.29	0.19	0.13	0.30	0.19	0.13
	1.5	0.6798	0.8253	w	10.34	11.39	11.98	10.40	11.07	11.65
				c	0.52	0.41	0.33	0.53	0.42	0.34
	2	0.8009	0.9054	w	9.46	9.72	9.50	8.50	8.63	8.48
				c	0.70	0.61	0.54	0.70	0.62	0.55

Source: Authors’ estimation through the Matlab implementation of [109].

.

The test statistic of BDS analysis makes use of the correlation function, the asymptotic distribution of which is known under the assumption of the null hypothesis. Therefore, the BDS test can be employed to produce a formal statistical test against arbitrary dependence [106]. The BDS test is two-sided and the greater test statistic than the critical value requires the rejection of the null hypothesis. For both residuals of the ARFIMA and FIGARCH models, we employed four epsilon values (0.5, 1, 1.5, 2) following the recommendation of Hsieh and LeBaron [107], and three embedding dimensions (3, 5, 7). The critical values for the BDS tests provided by Brock et al. [62] are as follows: 1.960 and 2.575 at 95% and 99% confidence levels, respectively, for a linear filtration model. For GARCH type filtrations, critical values provided by Hsieh [105] range from 1.85 to 2.90 for epsilon from 0.5 to 2 and dimension from 2 to 5 at 97.5% confidence level. For these reference values, as can be seen in Table 6, the null hypothesis of the BDS test is rejected for all epsilon values and dimensions. As discussed by Hsieh [105], this proves that the cryptocurrency market is governed by low complexity chaotic dynamics. Therefore, fluctuation in returns and volatilities of cryptocurrencies is not random.

As discussed by Peters [102], one of the most important features of chaotic dynamics is its sensitivity to initial conditions. This property expresses the difficulty of specifying the problem. The further we travel in time, the less accurate our forecasts will be. Another aspect is that randomness is created by the system itself through a mixing process. Hence, when the system reaches a certain point, information about early stages is lost. Here, we utilize the Largest Lyapunov exponent to examine its sensitivity to initial conditions in the cryptocurrency market, which is proven to be a highly useful diagnostic for chaotic systems. Largest Lyapunov exponent (or in general Lyapunov exponents in the spectrum) is described by the average exponential rates of divergence of nearby orbits in the phase space. Here, nearby orbits refer to nearly identical states, and exponential divergence of orbits corresponds to systems whose initial differences are negligible and will soon behave quite differently. In this case, predictive ability is rapidly lost. A system containing a positive largest Lyapunov Exponent is defined to be chaotic in the magnitude of the exponent, which reflects the time scale on which the system’s dynamics become unpredictable [108]. In this study, estimation of the largest Lyapunov exponent is conducted through the Rosenstein algorithm [86]. Since, by using the flexibility provided in the code, we do not have a priori knowledge concerning the embedding lag (tau) of the system, we left the selection of optimum tau value to the software to be picked as default. As for the embedding dimension, we use the three-dimension level (m): 3, 5, 7. According to the results in

Table 7. Largest Lyapunov exponent results (tau = 1).

	m = 3	m = 5	m = 7
Bitcoin	0.2522	0.1513	0.0875
Litecoin	0.1799	0.1473	0.2070
Ripple	0.1853	0.1773	0.1992
Ethereum	0.2482	0.1767	0.0772

Source: Authors’ estimation through the Matlab implementation of [110].

, all the largest Lyapunov exponents are positive and this points the existence of chaotic behaviors in the cryptocurrency market for the samples of Bitcoin, Litecoin, Ripple, and Ethereum. However, it should be kept in mind that the conclusion resulting from the Lyapunov exponent should be interpreted along with our previous findings. Chaos theory requires the differentiation of randomness from chaos itself. The evidence in our study indicates that the cryptocurrency market display a different path from the random walk. This conclusion supports the proposition of long memory theory. Accordingly, it is stated that a time series exhibits long memory in returns (or in volatilities), unlike the random walk theory, where predictions might be possible for the future behavior of this series. Beside long memory, since in our study chaotic features were observed, we indeed assert that the predictability cannot be long-term. This is due to the fact that sensitivity to initial conditions would not allow for long-term predictions. Hence, we conclude that predictability has a constraint in terms of time scale rather than full predictability (such as linear time series) or no predictability (such as complete randomness).

5. Conclusions

Cryptocurrency market has considerably raised investor attention in recent years, and the ongoing discussions in the media and in the public are largely focused on the markets’ trend and the sustainability of the cryptocurrency market. Unfortunately, a large amount of ongoing debate on these markets is not distinguishable from rumors and fortune-telling, and barely has any evidence to support their arguments. Absence of scientific evidence does not add value to investors’ strategies. To that end, in this paper, we attempt to examine statistics referring to the most essential features of the cryptocurrency market through the perspective of chaos. One of the criticisms for cryptocurrencies is the lack of existence of an underlying fundamental theory, and another is the independence of the cryptocurrency market from global financial indicators. This self-ordained behavior raises concerns and makes investors vulnerable to wild volatilities despite the inception of derivative markets for the cryptocurrency instruments. These concerns raise the question of whether these instruments act through a hidden order in their behaviors and paths they follow, or they are totally unpredictable. The main motivation of this study is to confirm whether or not the cryptocurrency market follows any hidden pattern, in the context of chaos theory. Considering the characteristics of chaotic time series, for each feature we have utilized the corresponding test: monofractality and multifractality (Hurst exponent and fractal dimension analysis), nonlinearity (BDS test), and sensitivity to initial conditions (largest Lyapunov exponent). Hurst exponent test results were performed through the most robust methods (Aggregated Variances and Peng Method). Results indicate the existence of long-range dependence in time series. Similar results are also observed through fractal dimension analysis. Although the Box-Count method yields values close to 1.5, for the madogram, we obtained numbers significantly greater than 1.5, meaning that the characteristics of the data are different from randomness. As for the BDS test employed to determine the residuals of the ARFIMA and FIGARCH models, it is indicated that all variables exhibit nonlinear features as the test statistic is greater than the corresponding critical values, meaning that the returns and volatilities are not random, although they may appear so. Final evidence is provided by means of largest Lyapunov exponent. According to the Rosenstein algorithm, all test statistics that are greater than zero imply further evidence for the existence of chaos. Overall results indicate that the statistical behavior of cryptocurrencies is not random and displays chaotic dynamics. In practice, this means that short term forecasts might be achievable in the cryptocurrency market and investors might profit with an appropriate strategy, while the long-term behavior of these time series are not predictable at all. The wild volatility of the market, immature market background, and weak and insufficient regulations suggest that the cryptocurrency market is too risky for naive investors and riskier than the image illustrated in media, portals, and other corresponding platforms.