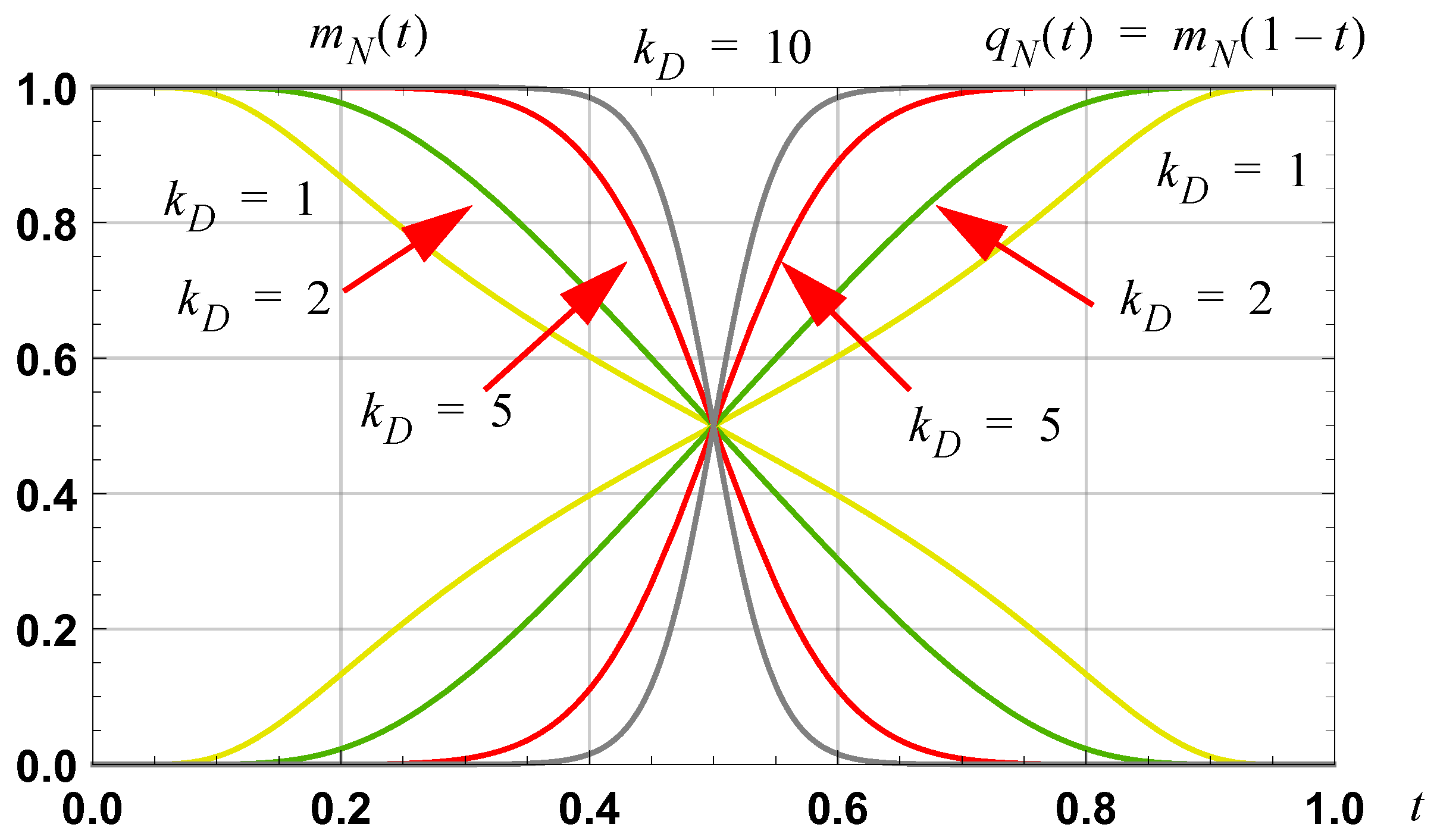
Figure 1.
Illustration of the normalized demarcation functions and .
Figure 1.
Illustration of the normalized demarcation functions and .
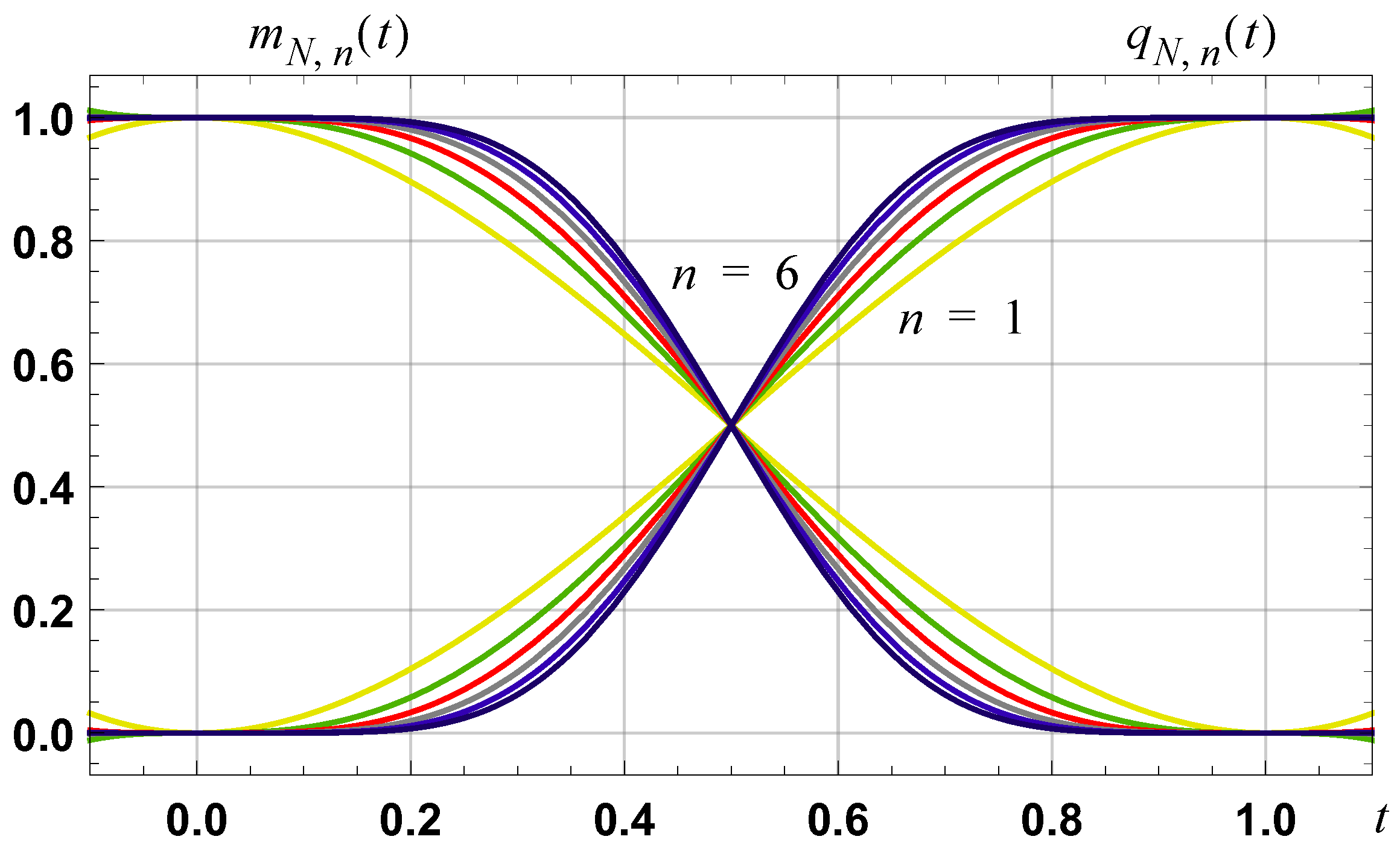
Figure 2.
Graph of the normalized demarcation functions and as defined by (16). Such functions are infinitely differentiable on (0, 1), and have right and left hand derivatives, of all orders, that are zero, respectively, at the points of zero and one.
Figure 2.
Graph of the normalized demarcation functions and as defined by (16). Such functions are infinitely differentiable on (0, 1), and have right and left hand derivatives, of all orders, that are zero, respectively, at the points of zero and one.
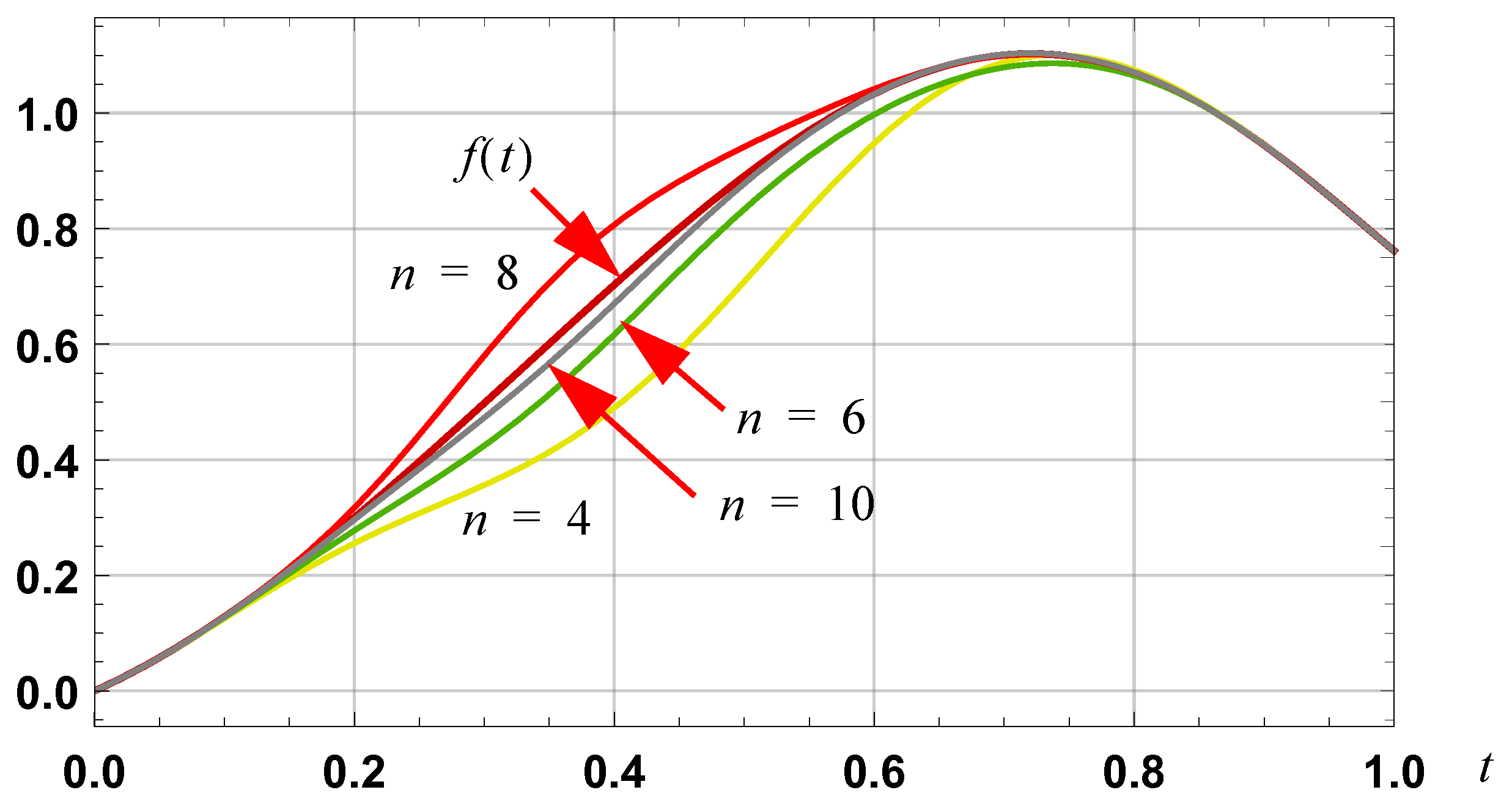
Figure 3.
Graph of the normalized polynomial demarcation functions, of orders one to six, for the interval [0, 1].
Figure 3.
Graph of the normalized polynomial demarcation functions, of orders one to six, for the interval [0, 1].
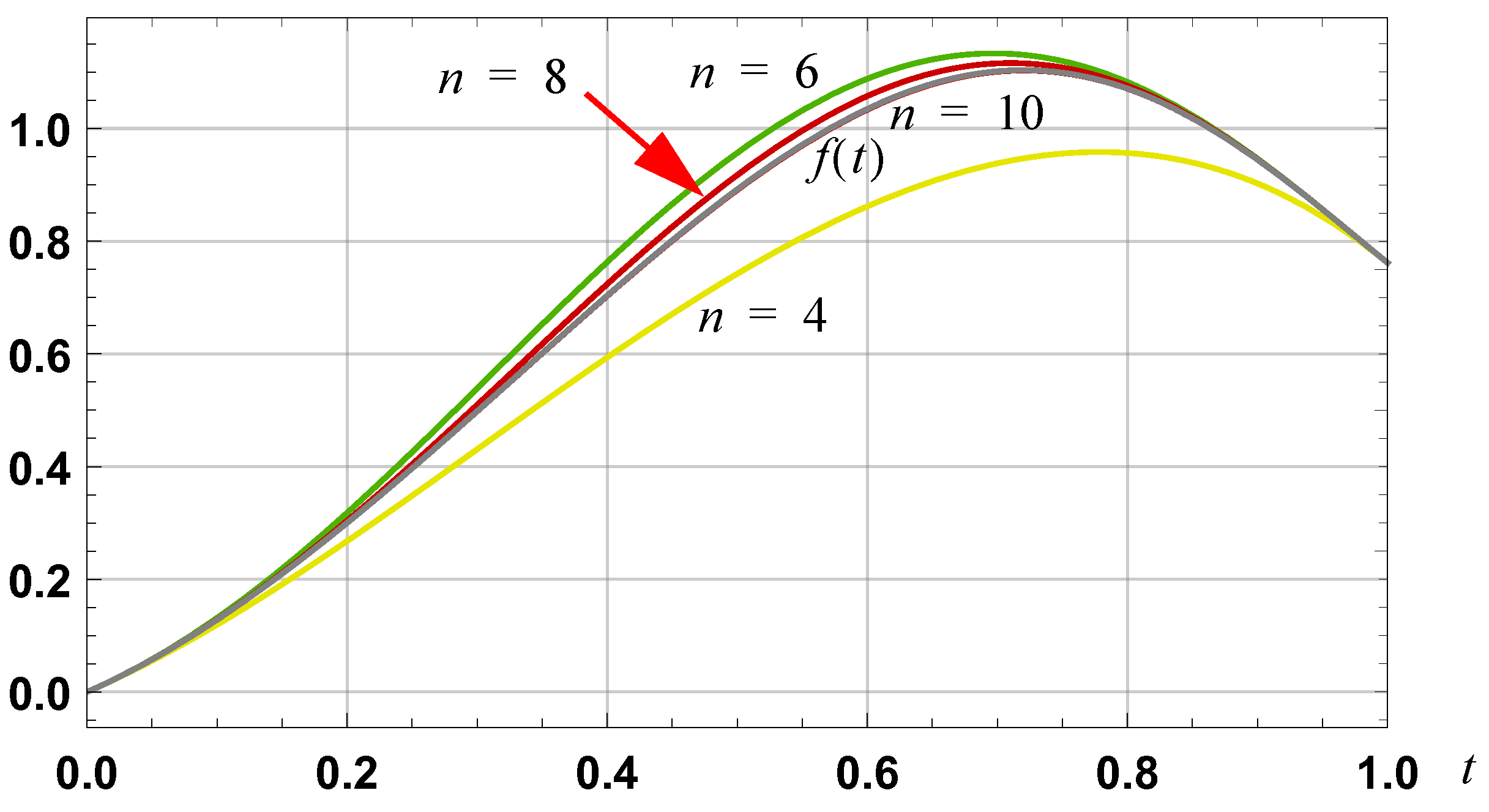
Figure 4.
Graph of the 4th, 6th, 8th and 10th order dual Taylor series approximations, based on the interval [0, 1], for the function defined by (33).
Figure 4.
Graph of the 4th, 6th, 8th and 10th order dual Taylor series approximations, based on the interval [0, 1], for the function defined by (33).
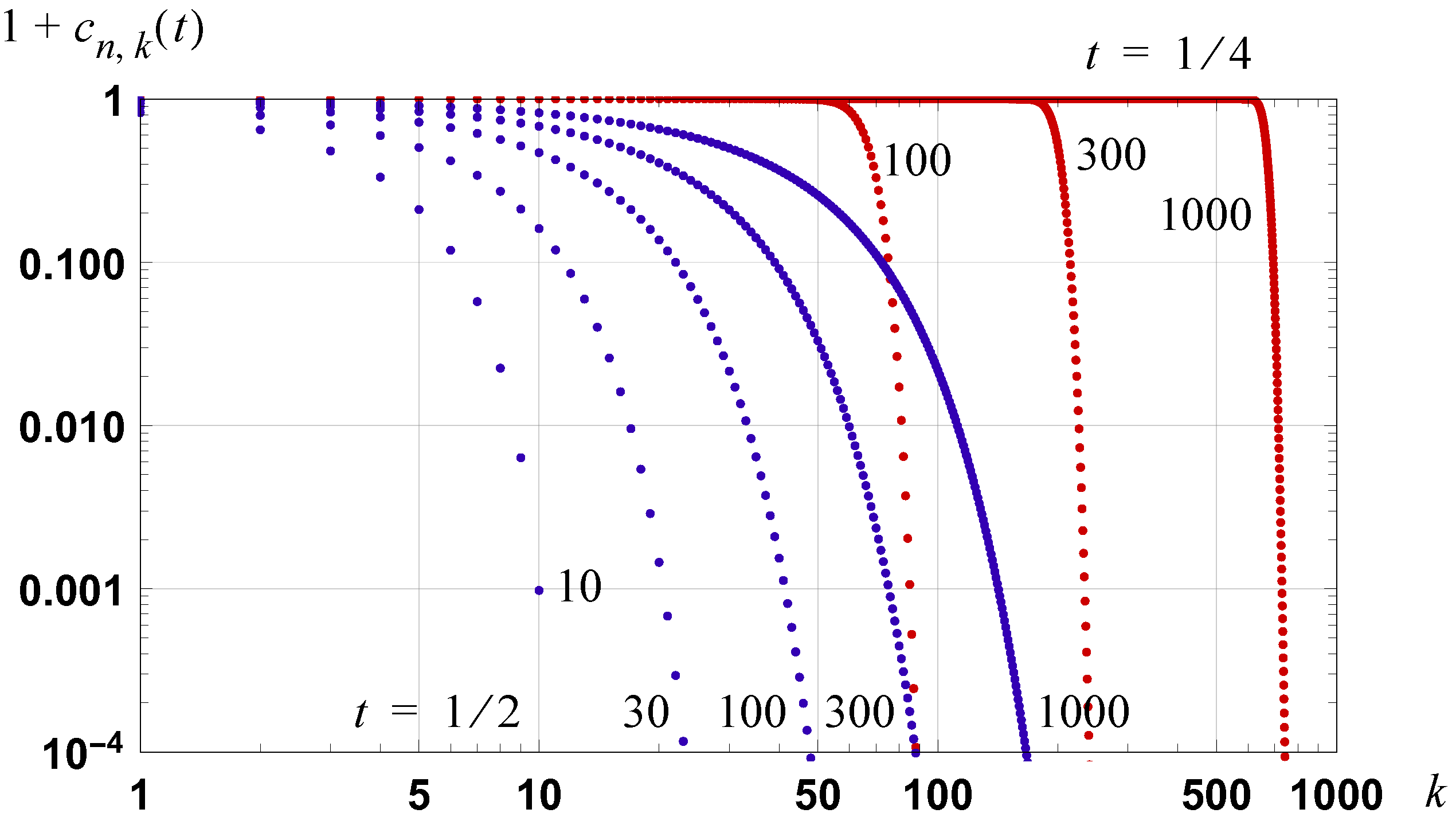
Figure 5.
Graph of , for the case of and and for and . Results are shown for when and when .
Figure 5.
Graph of , for the case of and and for and . Results are shown for when and when .
Figure 6.
Graph of 4th, 6th, 8th and 10th order spline approximations, based on the interval [0, 1], for the function defined by (33).
Figure 6.
Graph of 4th, 6th, 8th and 10th order spline approximations, based on the interval [0, 1], for the function defined by (33).
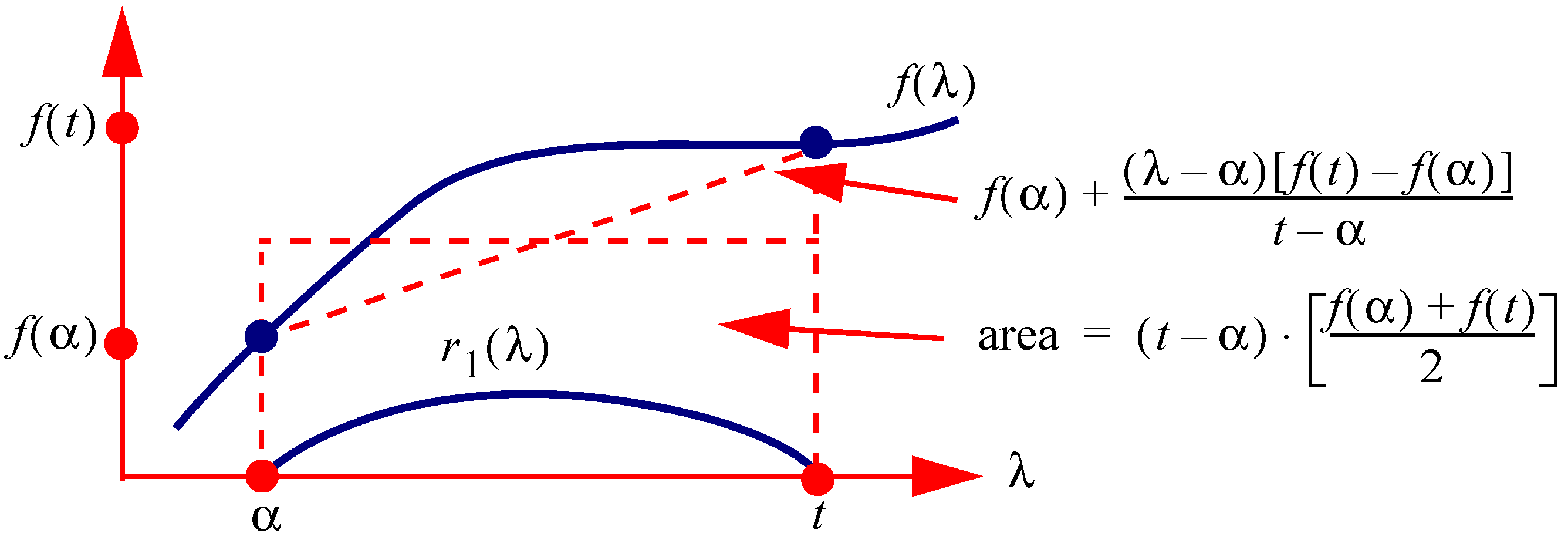
Figure 7.
Illustration of the area defined by a zeroth order approximation to an integral and the residual function .
Figure 7.
Illustration of the area defined by a zeroth order approximation to an integral and the residual function .
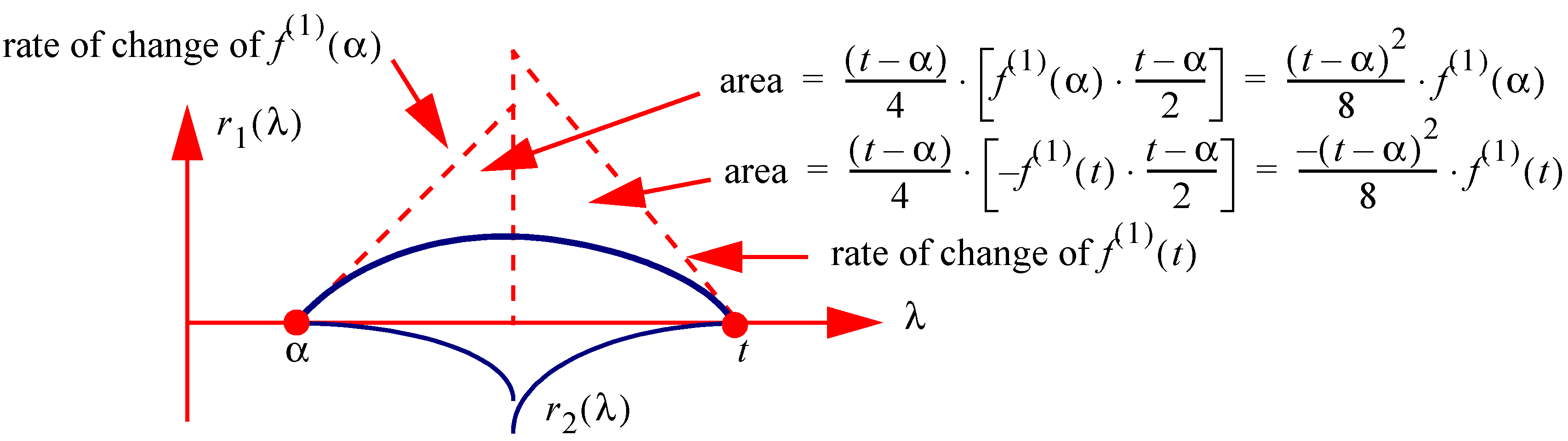
Figure 8.
Illustration of the residual function , the areas as defined by linear change at the points and t and the second residual function .
Figure 8.
Illustration of the residual function , the areas as defined by linear change at the points and t and the second residual function .
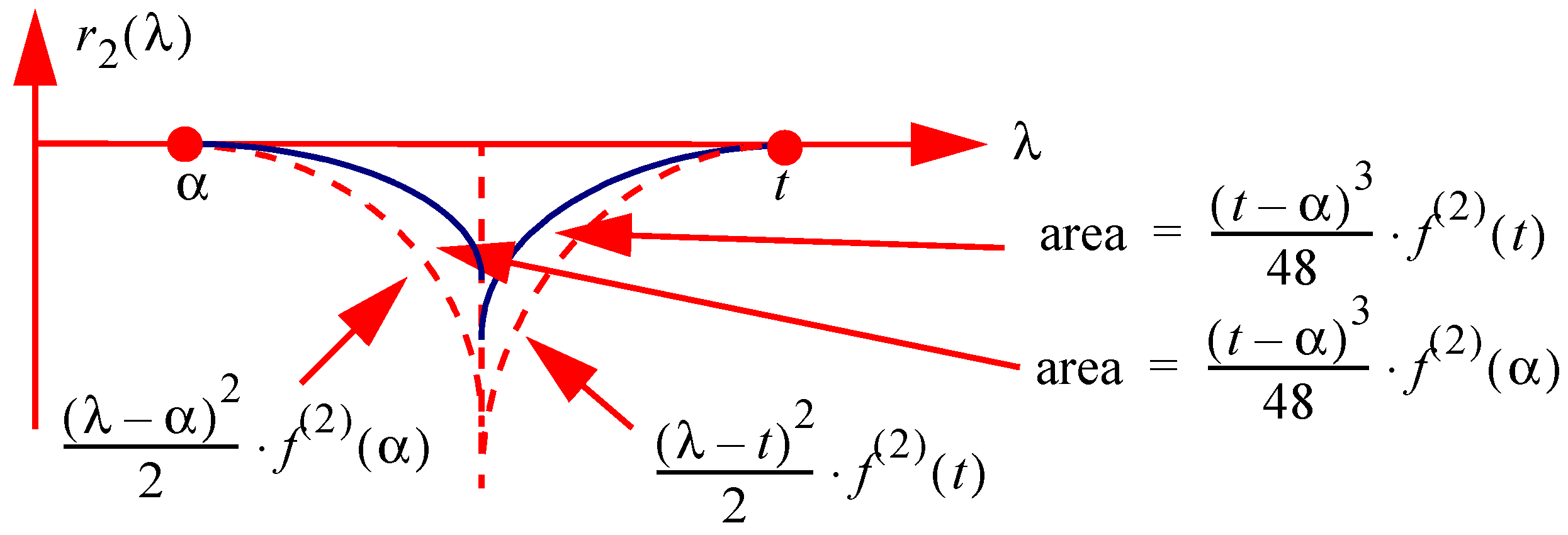
Figure 9.
Illustration of the areas defined by a quadratic approximation to the residual function and based on and .
Figure 9.
Illustration of the areas defined by a quadratic approximation to the residual function and based on and .
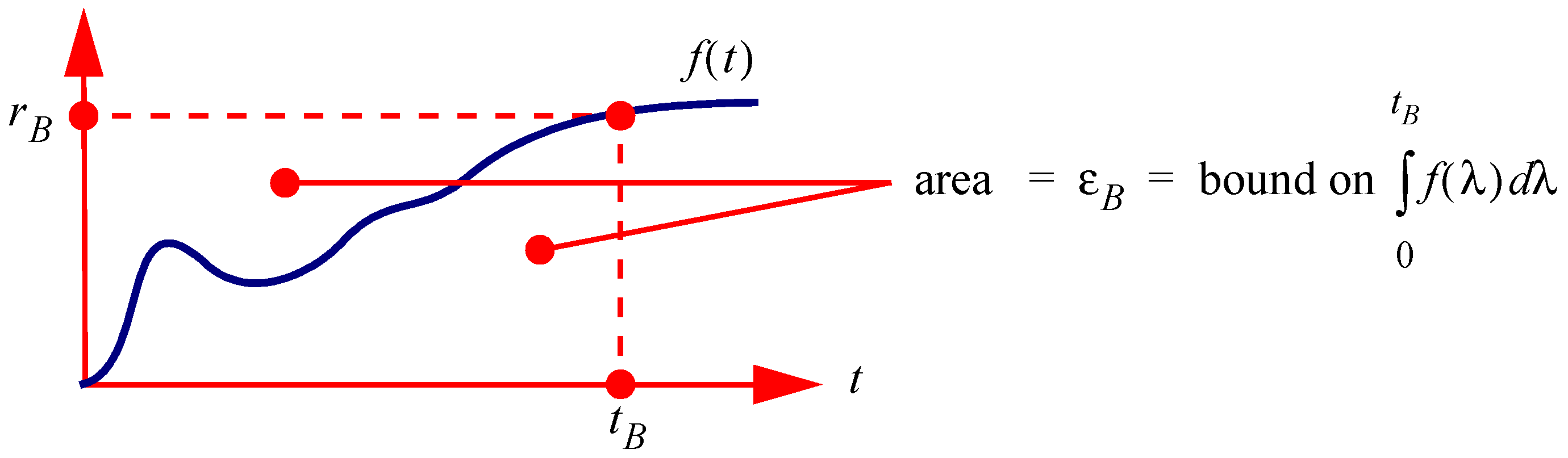
Figure 10.
The area bound defined by the first passage time of a positive function to a set level.
Figure 10.
The area bound defined by the first passage time of a positive function to a set level.
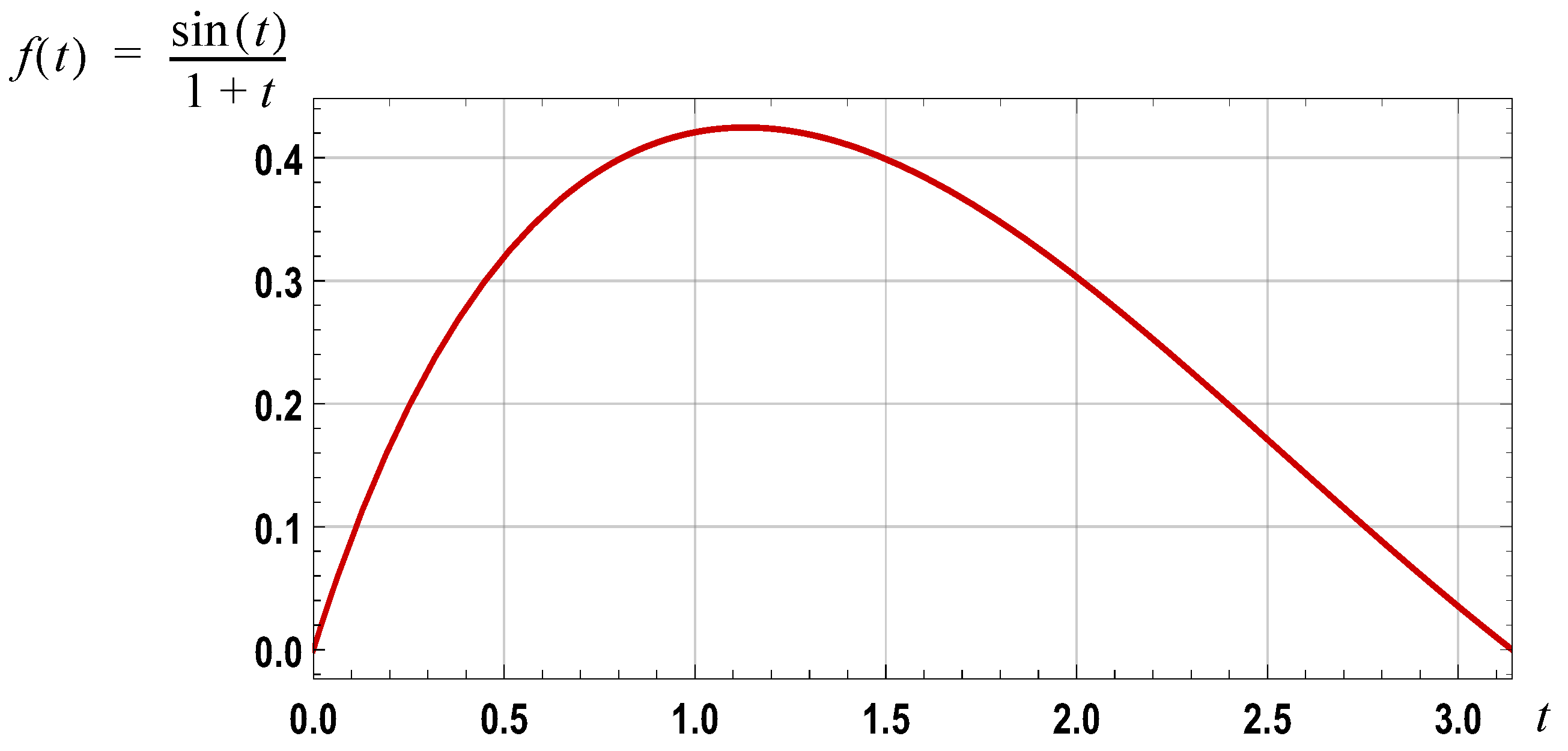
Figure 11.
Graph of over the interval [0, ].
Figure 11.
Graph of over the interval [0, ].
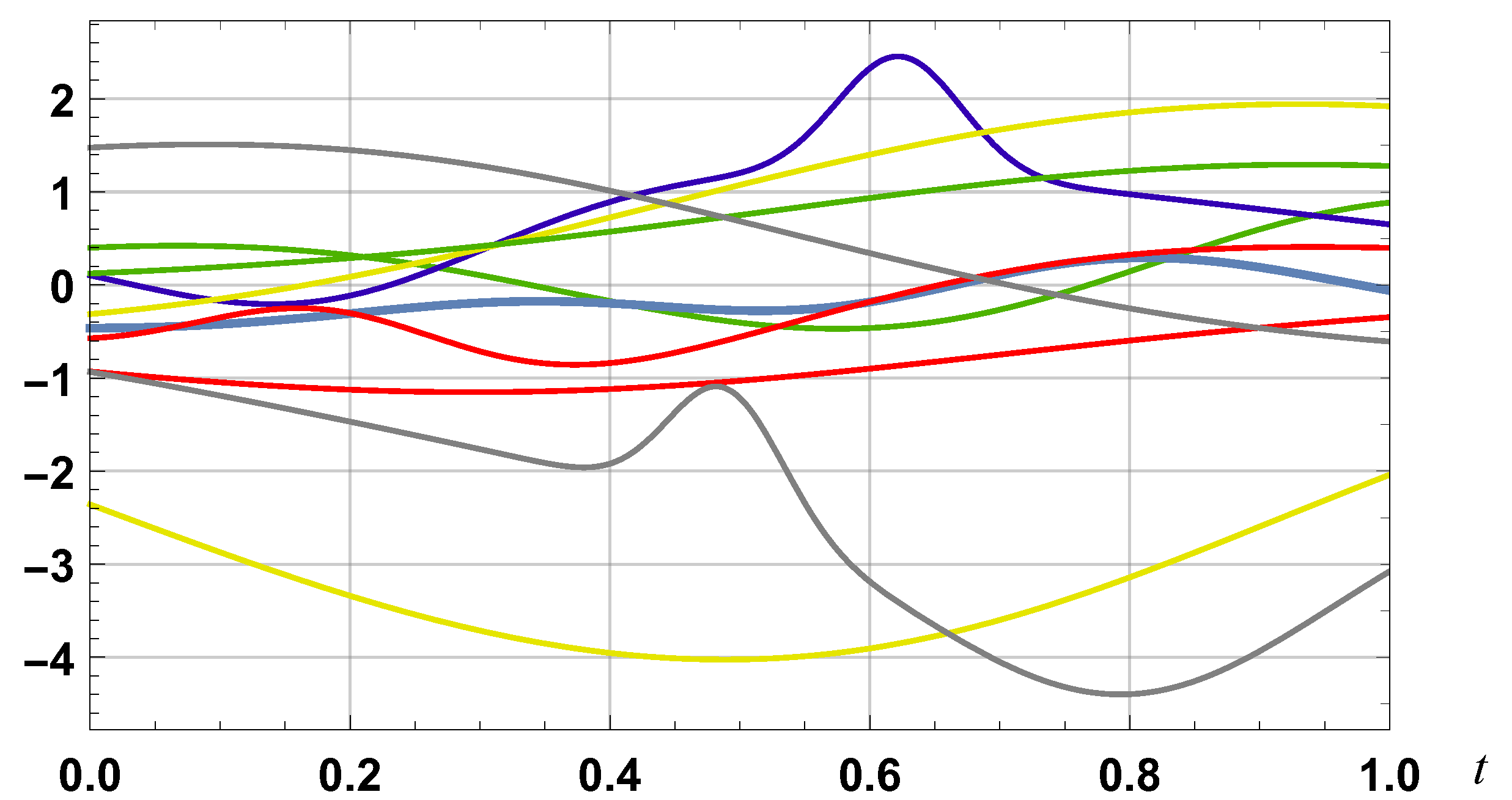
Figure 12.
Examples of test functions as defined by (73).
Figure 12.
Examples of test functions as defined by (73).
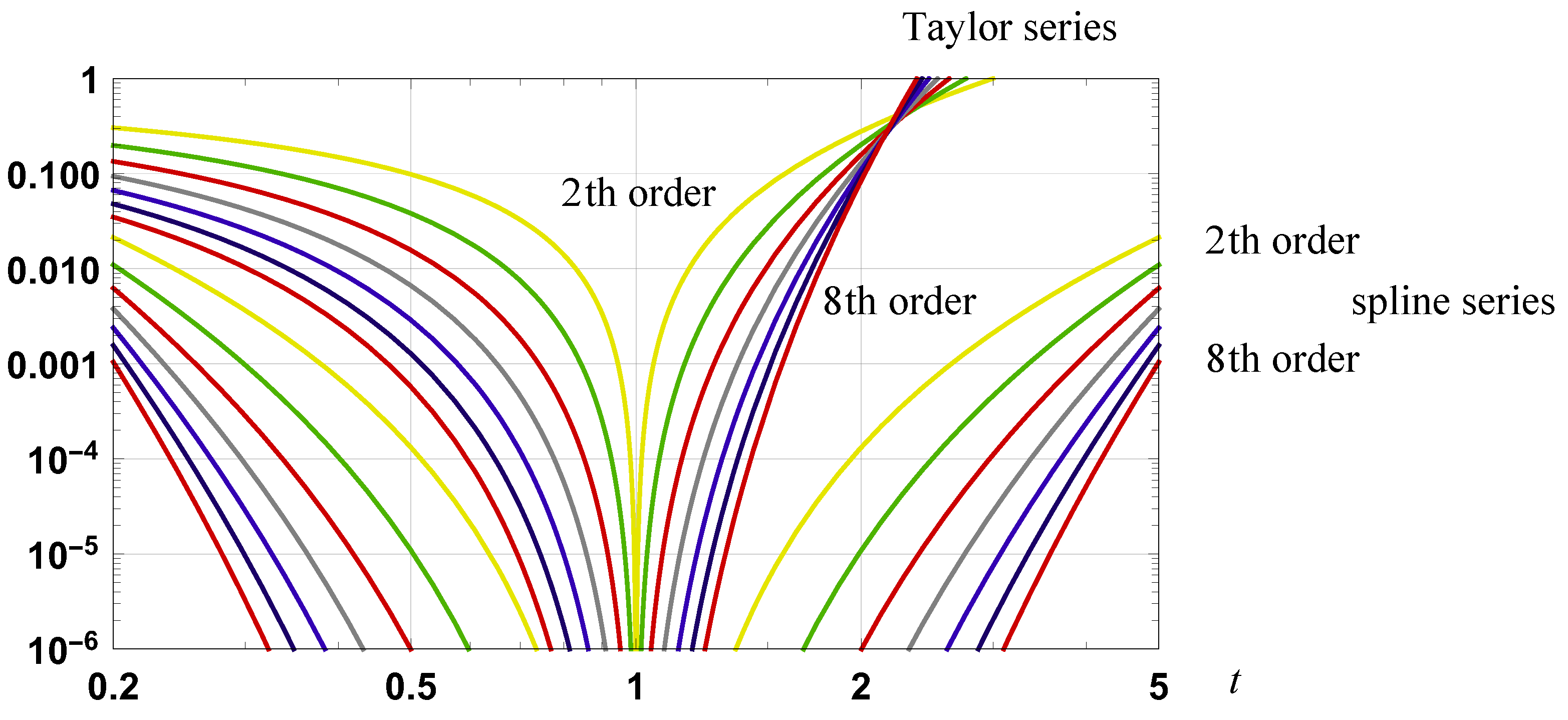
Figure 13.
Graph of the relative error in approximations to exp(−t): fourth to eighth order spline based approximations along with eighth to sixteen order Taylor series approximations.
Figure 13.
Graph of the relative error in approximations to exp(−t): fourth to eighth order spline based approximations along with eighth to sixteen order Taylor series approximations.
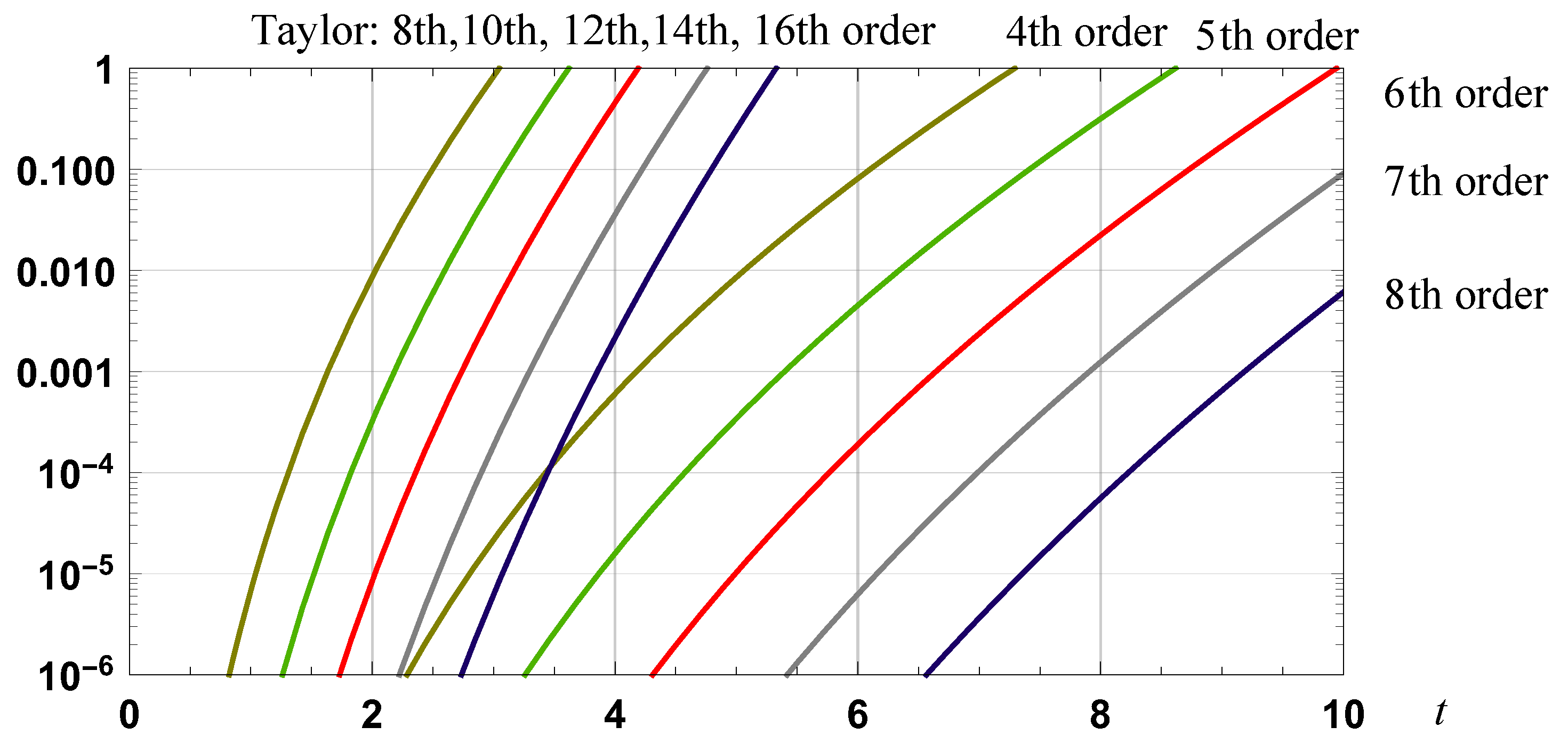
Figure 14.
Graph of the relative error in approximations to ln(t): second to eighth order Taylor series and spline based series approximation.
Figure 14.
Graph of the relative error in approximations to ln(t): second to eighth order Taylor series and spline based series approximation.
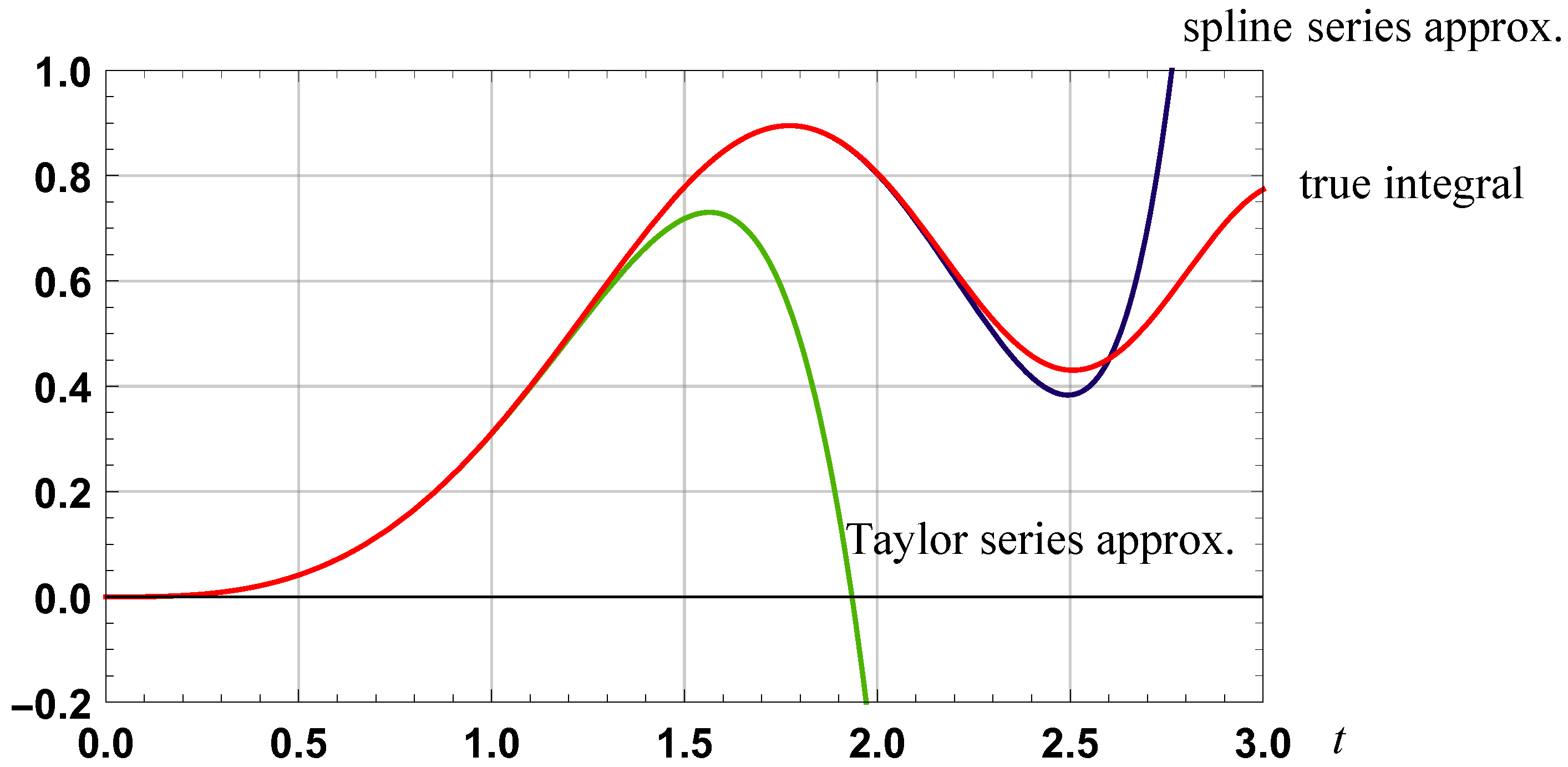
Figure 15.
Graph of approximations (order 6) to the integral of sin(t2).
Figure 15.
Graph of approximations (order 6) to the integral of sin(t2).
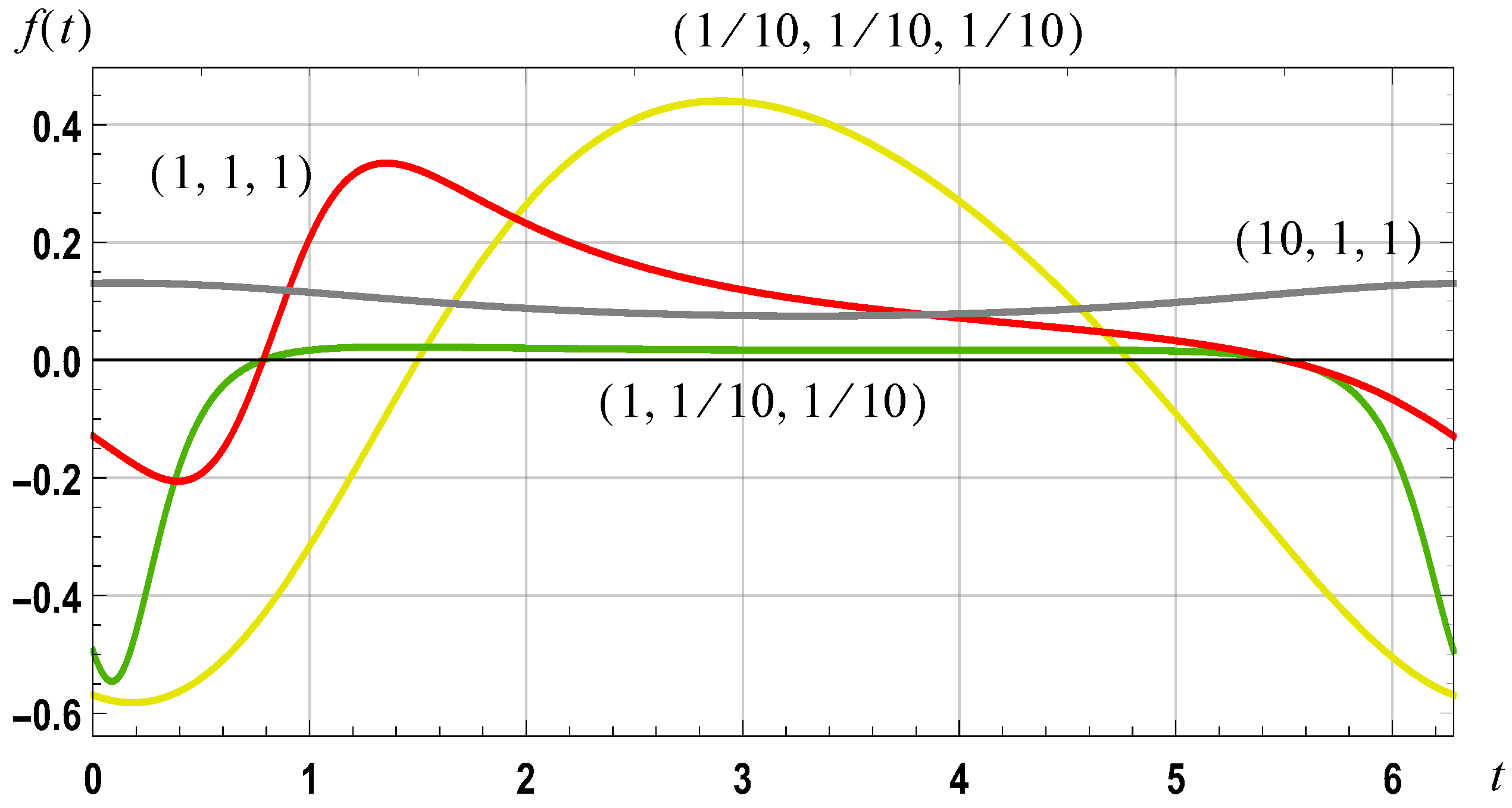
Figure 16.
Graph of f(t) for the case of a = 1, b = 0. For the case of (10, 1, 1) a scaling factor of 10 has been used; for the case of (1, 1/10, 1/10) a scaling factor of 0.1 has been used.
Figure 16.
Graph of f(t) for the case of a = 1, b = 0. For the case of (10, 1, 1) a scaling factor of 10 has been used; for the case of (1, 1/10, 1/10) a scaling factor of 0.1 has been used.
Figure 17.
Graph of g(t). For the case of (10, 1, 1) a scaling factor of 10 has been used; for the case of (1, 1/10, 1/10) a scaling factor of 0.1 has been used.
Figure 17.
Graph of g(t). For the case of (10, 1, 1) a scaling factor of 10 has been used; for the case of (1, 1/10, 1/10) a scaling factor of 0.1 has been used.
Table 1.
Interval of integration for a spline based approximation and for a specified error bound of .
Table 1.
Interval of integration for a spline based approximation and for a specified error bound of .
| Order of Integral Approx. n | | Magnitude of Error in Integral Approx. over |
|---|
| 1 | 0.47 | 2.4 × 10−4 |
| 2 | 0.83 | 1.9 × 10−4 |
| 3 | 1.17 | 1.5 × 10−4 |
| 4 | 1.47 | 1.3 × 10−4 |
| 6 | 1.96 | 1.0 × 10−4 |
| 8 | 2.33 | 8.2 × 10−5 |
| 10 | 2.62 | 6.9 × 10−5 |
| 12 | 2.85 | 6.0 × 10−5 |
Table 2.
Summary of function and integral approximations.
Table 2.
Summary of function and integral approximations.
| | Function Approximation for | Integral Approximation: |
|---|
| Antiderivative Series | | |
| Taylor Series | | |
| Dual Taylor Series | | |
| Spline Series | | |
Table 3.
Summary of remainder terms.
Table 3.
Summary of remainder terms.
| | Remainder in Integral Approximation: |
|---|
| Antiderivative Series | |
| Taylor Series | |
| Dual Taylor Series | |
| Spline Series | |
Table 4.
Proportion of integral approximations, based on a set of 1000 test functions, with a relative error less than 0.01.
Table 4.
Proportion of integral approximations, based on a set of 1000 test functions, with a relative error less than 0.01.
| Integral Approximation | 4th Order Approx. | 6th Order Approx. | 8th Order Approx. | 10th Order Approx. |
|---|
| Antiderivative Series | < 0.01 | 0.01 | 0.03 | 0.09 |
| Taylor Series | < 0.01 | 0.01 | 0.02 | 0.08 |
| Dual Taylor Series | 0.13 | 0.34 | 0.40 | 0.48 |
| Spline Series | 0.56 | 0.71 | 0.78 | 0.84 |
Table 5.
Relative error in evaluation of e.
Table 5.
Relative error in evaluation of e.
| Order of Approx. n | Fractional Power m | Magnitude of Relative Error |
|---|
| 2 | 1 | 1.0 × 10−5 |
| | 10 | 9.9 × 10−12 |
| | 100 | 9.9 × 10−18 |
| | 1000 | 9.9 × 10−24 |
| 4 | 1 | 1.0 × 10−10 |
| | 10 | 9.9 × 10−21 |
| | 100 | 9.9 × 10−31 |
| | 1000 | 9.9 × 10−41 |
| 8 | 1 | 1.7 × 10−22 |
| | 10 | 1.7 × 10−40 |
| | 100 | 1.7 × 10−58 |
| | 1000 | 1.7 × 10−76 |
| 16 | 1 | 4.2 × 10−50 |
| | 10 | 4.1 × 10−84 |
| | 100 | 4.1 × 10−118 |
| | 1000 | 4.1 × 10−152 |
Table 6.
Relative error in evaluation of ln(t) for the case of t = 100. For the case of m = 1 the relative error is high for all orders of approximation.
Table 6.
Relative error in evaluation of ln(t) for the case of t = 100. For the case of m = 1 the relative error is high for all orders of approximation.
| Order of Approx. n | Fractional Power m | Magnitude of Relative Error |
|---|
| 2 | 10 | 1.1 × 10−5 |
| | 100 | 1.1 × 10−11 |
| | 1000 | 1.1 × 10−17 |
| 4 | 10 | 1.6 × 10−8 |
| | 100 | 1.5 × 10−18 |
| | 1000 | 1.5 × 10−28 |
| 8 | 10 | 5.7 × 10−14 |
| | 100 | 5.2 × 10−32 |
| | 1000 | 5.2 × 10−50 |
| 16 | 10 | 1.6 × 10−24 |
| | 100 | 1.3 × 10−58 |
| | 1000 | 1.3 × 10−92 |
Table 7.
Relative error in evaluation of for the case of , h = 6 and an initial estimate for of 9/5. .
Table 7.
Relative error in evaluation of for the case of , h = 6 and an initial estimate for of 9/5. .
| Spline Approximation Order: n | Iteration order | Magnitude of Relative Error |
|---|
| 3 | 1 | 5.1 × 10−3 |
| | 2 | 4.2 × 10−18 |
| | 3 | 7.2 × 10−154 |
| 6 | 1 | 6.7 × 10−4 |
| | 2 | 2.0 × 10−42 |
| | 3 | 3.2 × 10−620 |
Table 8.
Relative error in approximation of based on an approximation to atan(1).
Table 8.
Relative error in approximation of based on an approximation to atan(1).
| Order of Spline Approx. n | Order of Angle Sub-division i | Magnitude of Relative Error |
|---|
| 1 | 1 | 4.4 × 10−3 |
| | 2 | 2.1 × 10−5 |
| | 4 | 7.3 × 10−8 |
| | 10 | 4.3 × 10−15 |
| | 100 | 1.8 × 10−123 |
| 2 | 1 | 1.7 × 10−5 |
| | 2 | 1.6 × 10−7 |
| | 4 | 3.2 × 10−11 |
| | 10 | 4.5 × 10−22 |
| | 100 | 1.3 × 10−184 |
| 4 | 1 | 3.6 × 10−8 |
| | 2 | 1.2 × 10−11 |
| | 4 | 7.5 × 10−18 |
| | 10 | 6.3 × 10−36 |
| | 100 | 7.4 × 10−307 |
| 8 | 1 | 2.5 × 10−13 |
| | 2 | 1.3 × 10−19 |
| | 4 | 6.1 × 10−31 |
| | 10 | 1.7 × 10−63 |
| | 100 | 3.6 × 10−551 |
Table 9.
Magnitude of relative error in evaluation of using four sub-intervals and eight sub-intervals for the point (1, 0.1, 0.1).
Table 9.
Magnitude of relative error in evaluation of using four sub-intervals and eight sub-intervals for the point (1, 0.1, 0.1).
| Order of Approx. n | Point: (0.1, 0.1, 0.1) | Point: (1, 0.1, 0.1) (8 Intervals) | Point: 90 (1, 1, 1) | Point: (10, 1, 1) |
|---|
| 2 | 0.015 | 0.15 | 0.067 | 3.1 × 10−4 |
| 4 | 2.9 × 10−4 | 4.6 × 10−3 | 2.4 × 10−2 | 5.3 × 10−6 |
| 8 | 2.6 × 10−8 | 2.3 × 10−3 | 2.6 × 10−3 | 1.1 × 10−9 |
| 16 | 3.6 × 10−16 | 2.9 × 10−5 | 2.7 × 10−5 | 2.1 × 10−17 |