Construction of Regular Developable Bézier Patches
Abstract
:1. Introduction
2. Mathematical Formulations of the Regular Developable Bézier Patches
3. Construction of the Regular Developable Bézier Patches
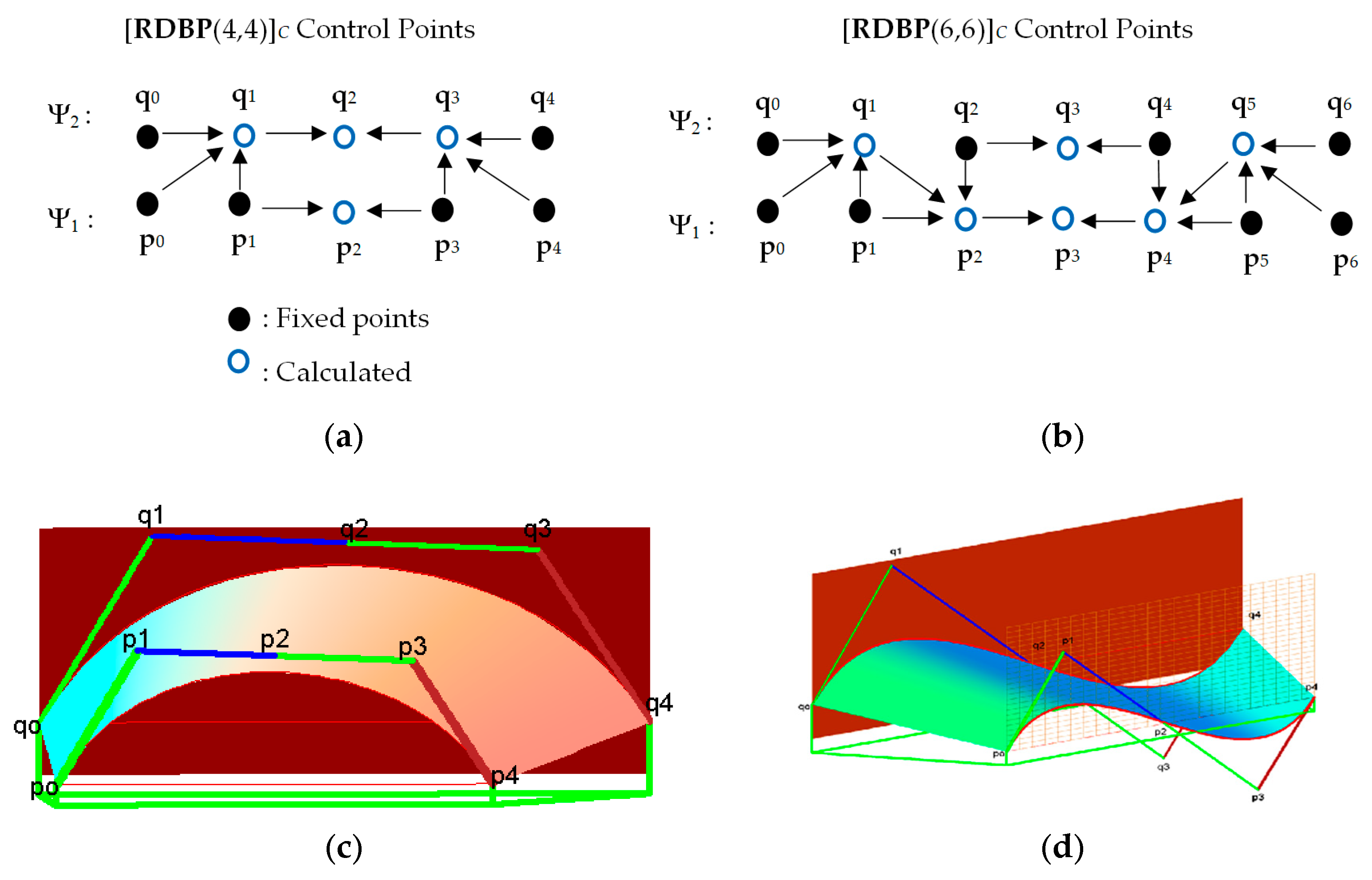
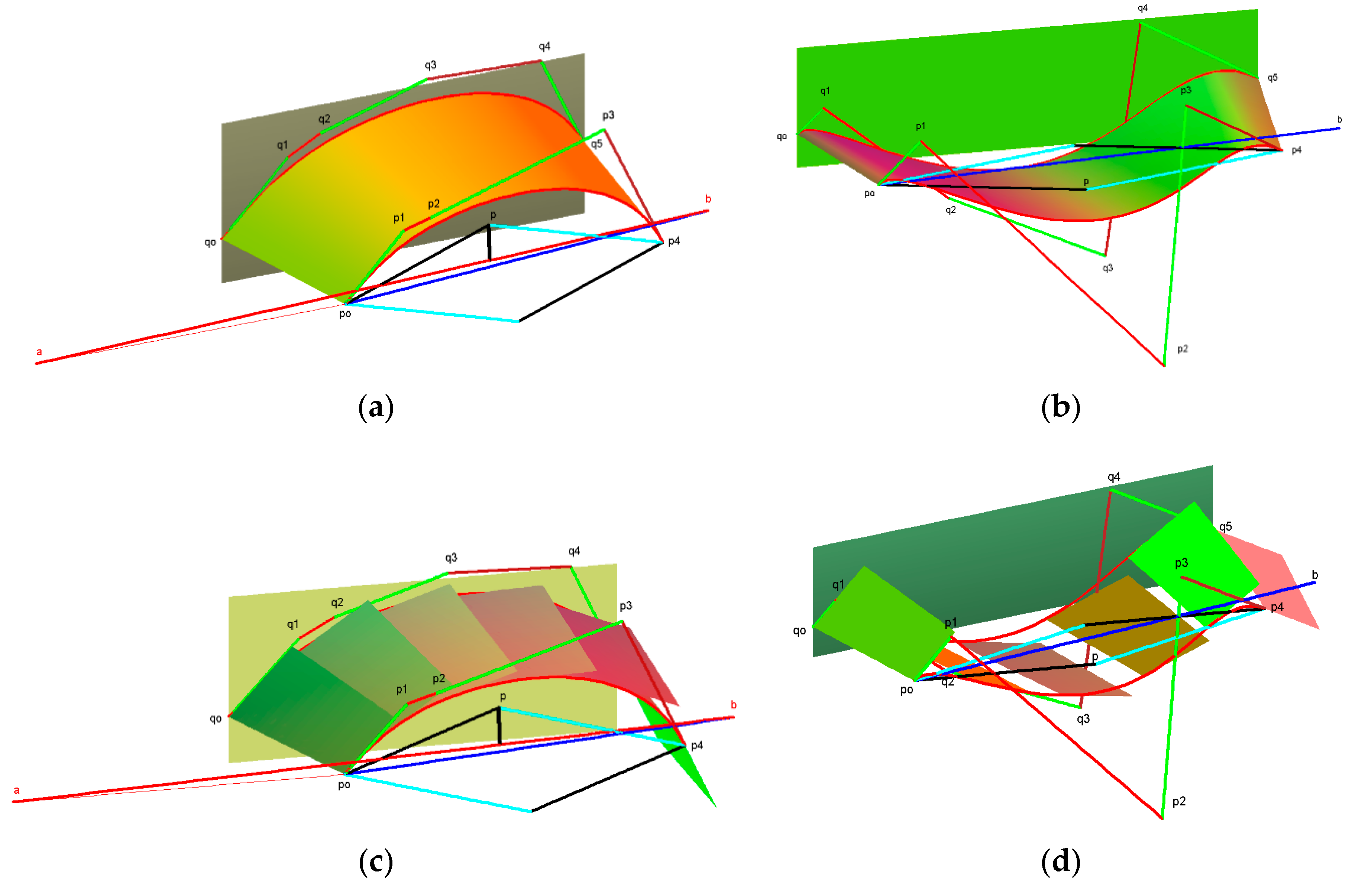
3.1. Case: ρ(u) Constant
- The two vectors parallel (qn − q0) and (pn − p0) must be in the same direction to determine α value;
- Every i = 0, …, n − 1) the vector (qi+1 − qi) and (pi+1 − pi) must be parallel and proportional to α.
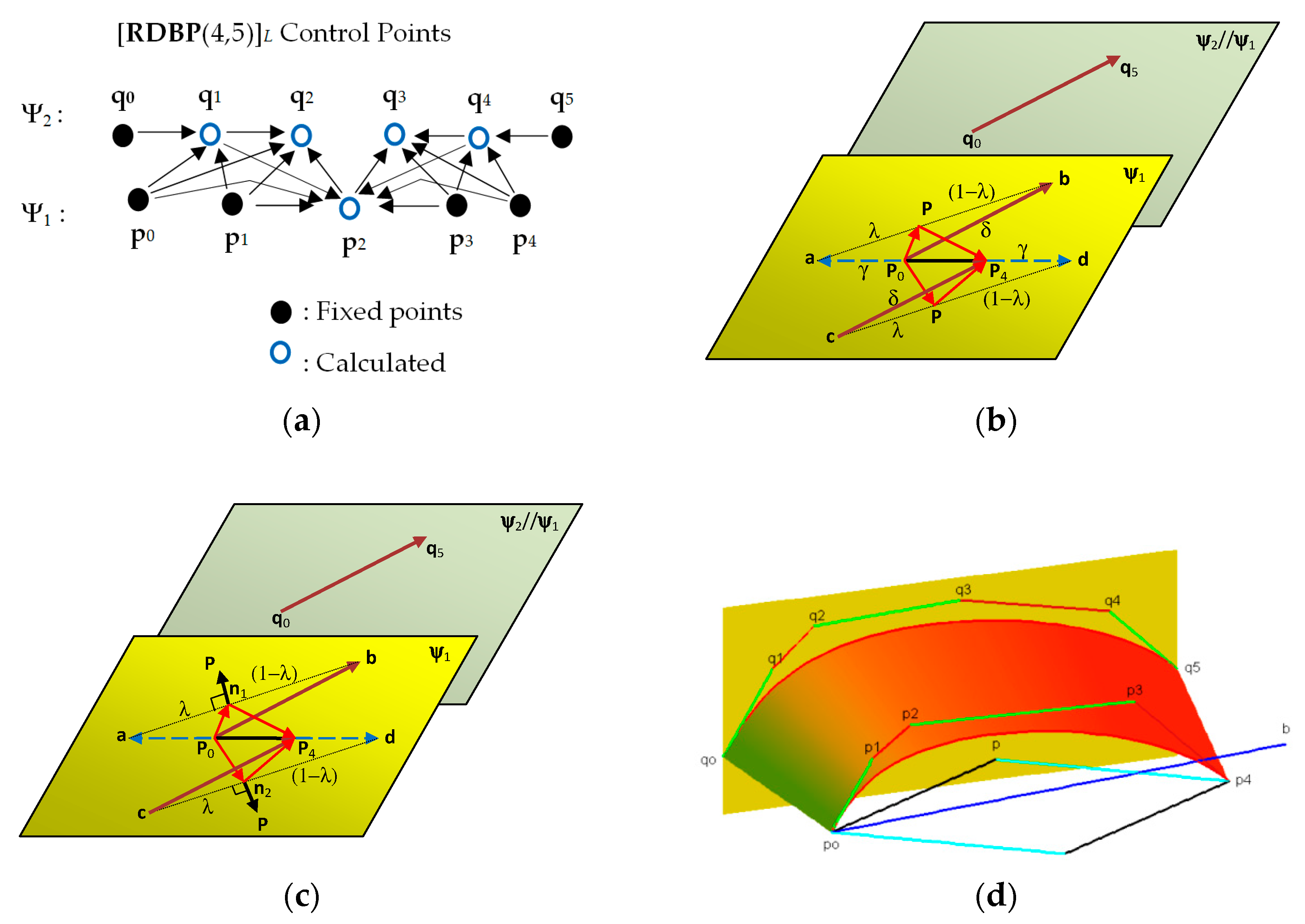
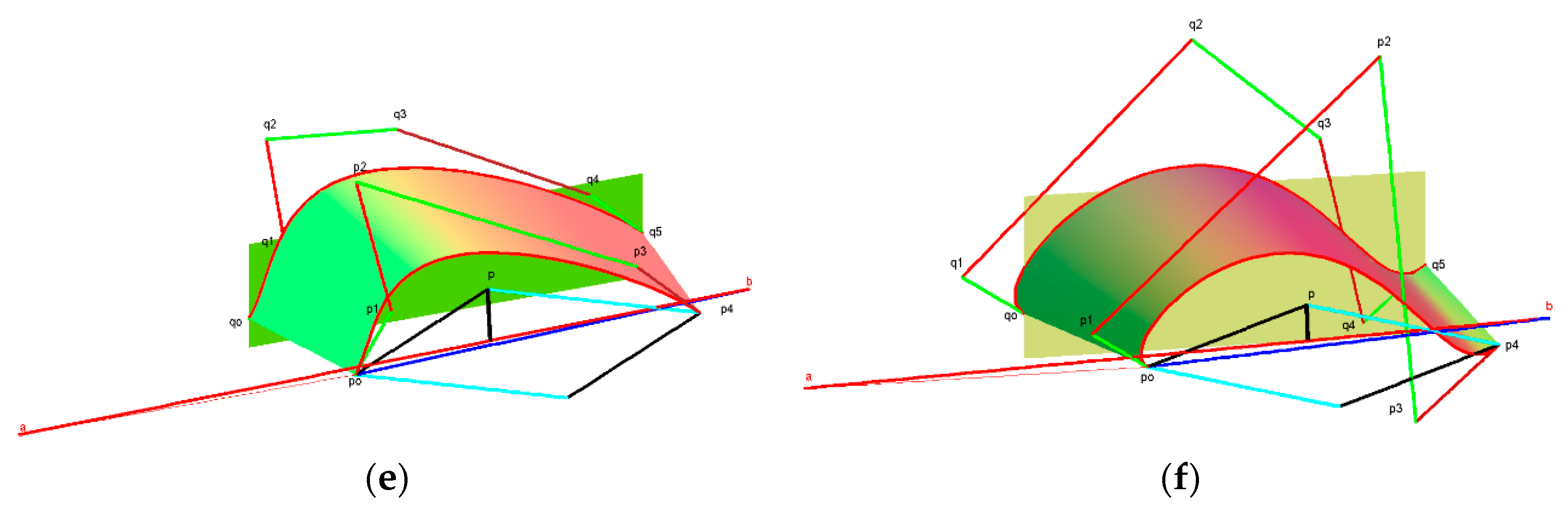
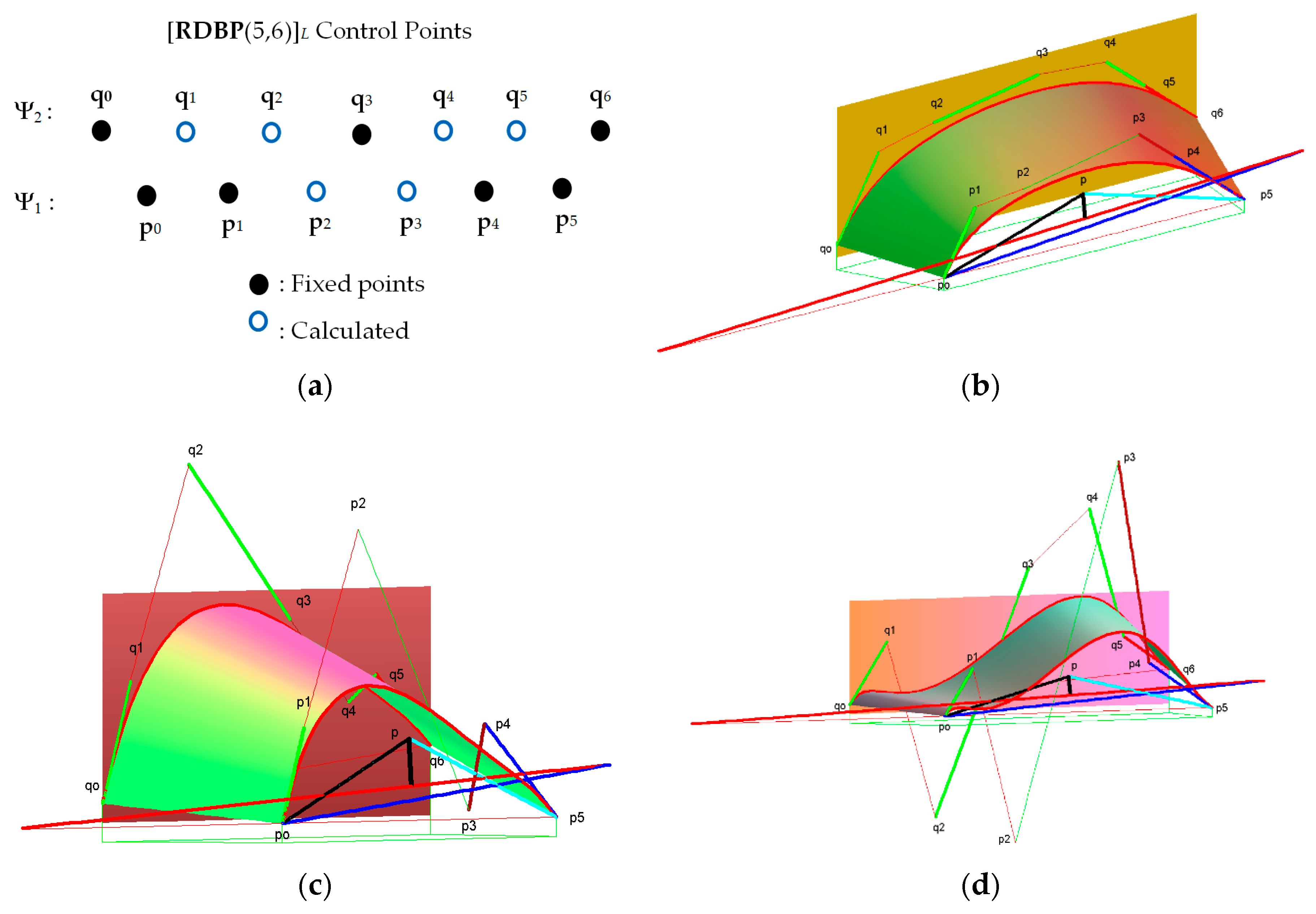
3.2. Case: ρ(u) Linear
- N1 = (n + k2 + 1 − i)(n + k2 + 2 − i)…(n + k2 + k1 − i) if k1 ≥ 1, if not 1;
- N2 = (i − k2 + 1)(i − k2 + 2)…(i), if k2 ≥ 1, if not 1;
- D = (n + 1)(n + 2)…(n + k1 + k2), if (k1 + k2) ≥ 1, if not 1.
- Because α0 and α1 must be positive, the position of the vector (qn − q0) in Equation (10) must lie on the interior of the angle between two vectors (p − p0) and (pn − p). If the control points [p0,pn,q0,qn+1] are fixed, then the selection of the centroid point p must satisfy the conditions that the direction of the vector (p − p0) and (pn − p) are in the different sides to the vector (qn − q0).
- The value of α0 and α1 in Equation (10) can be calculated by
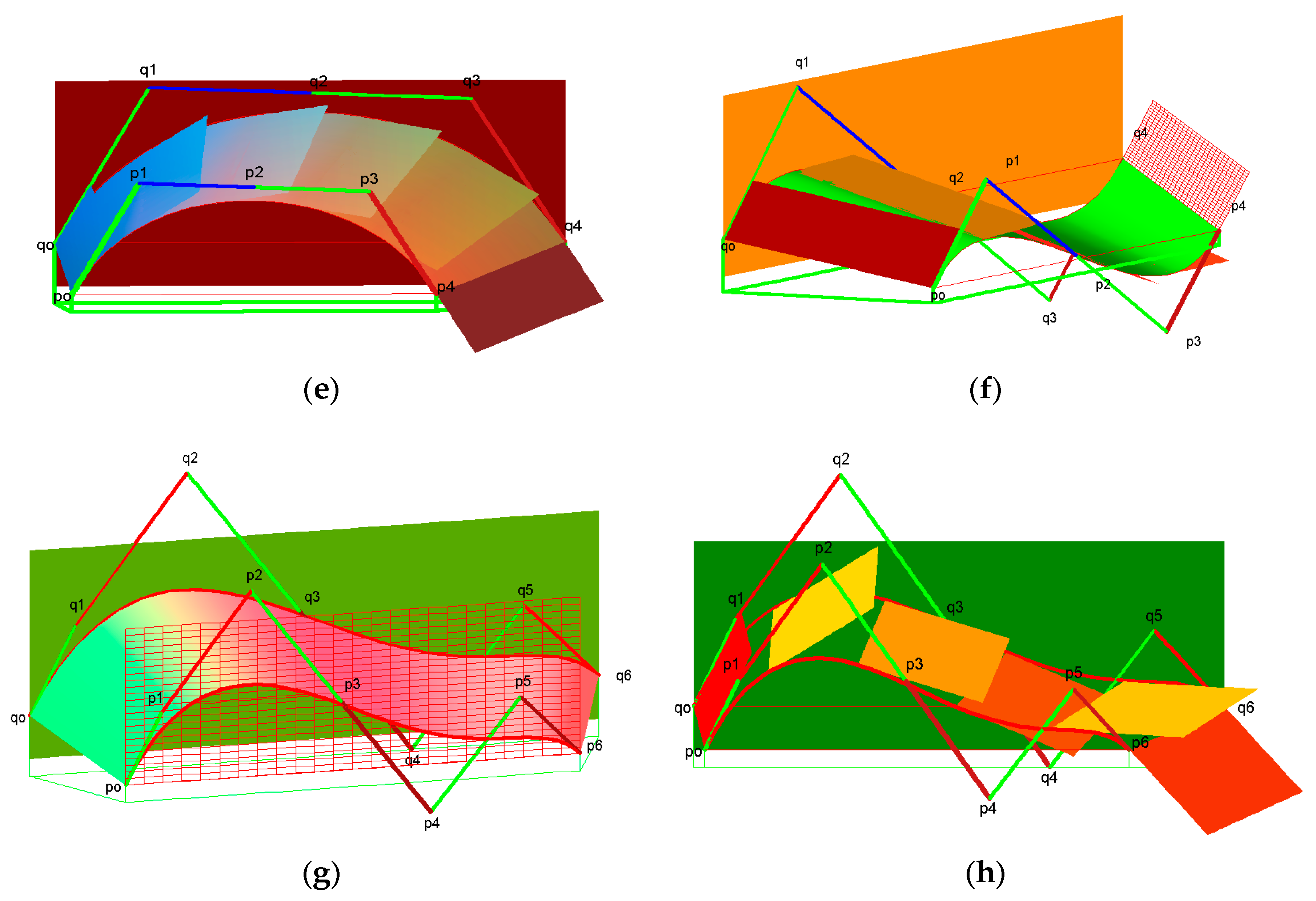
- To find the unique solution of the system (9), we use the strategy as follows. It has to determine (n + 2) control points of (2n + 3) control points in the system, such that the number (n + 1) calculated control points are the same as the number of these equations, i.e., (n + 1) equations. Also, the determinant of its coefficients matrix of the system must be different from zero. In relation to treating the geometric continuity order 1 between two adjacent joined patches, it is necessary that the points [p0,p1,pn−1,pn,q0,qn+1] are included in the list of the (n + 2) fixed points.
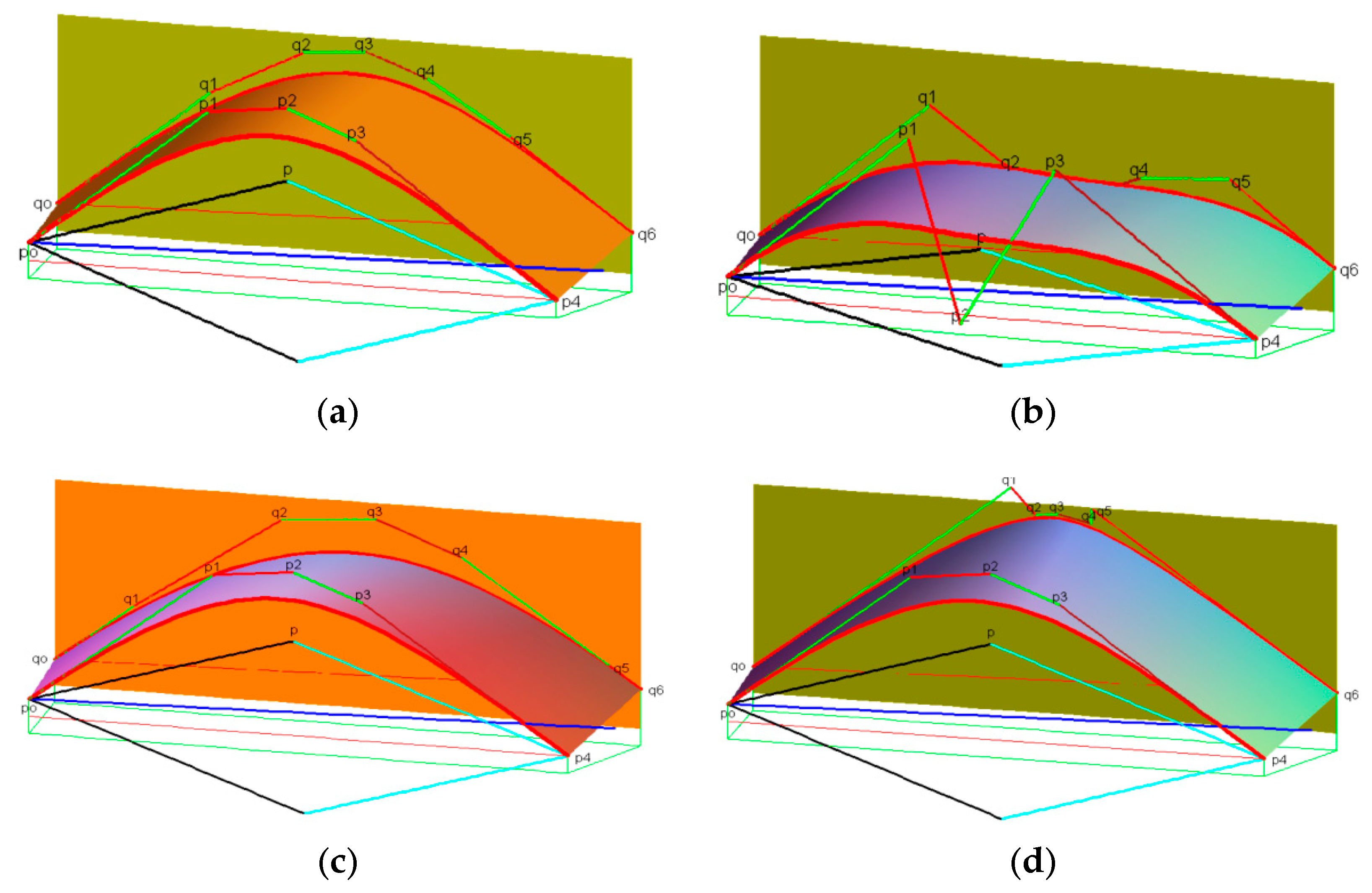
3.3. Case: ρ(u) Quadratic
- Because α0 and α1 must be positive, the election α1 in Equation (19) must verify the expression (20) or the vector [(qn+2 − q0) − α1 v] in Equation (19) must lie on the interior of the angle between two vectors (p − p0) and (pn − p).
- Calculation of the value α0 and α1 in Equation (19) is like the formula (11).
- To find the exact solution of the system (18), we have to determine (n + 2) control points of (2n + 4) control points in the system, such that the number (n + 2) calculated control points are the same as the number of these Equation (18). The determinant of its coefficients matrix is different from zero and the control points [p0,p1,pn,pn−1,q0,qn+2] must be included in the list of the (n + 2) fixed control points.
- w1 = [30q1 − 12 α0 p2 + 4 (α0 + 2α1 + α2) (p1 − p0)];
- w2 = [6 α0 p3 − 6(α0 + 2 α1 + α2) p1 + 2 α2 (p1 − p0)];
- w3 = [2 α0 (p4−p3) + 6(α0 + 2α1 +α2) p3 − 6 α2 p1];
- w4 = [−30 q5 + 4(α0 + 2α1 +α2) (p4−p3) + 2 α2 p3].
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Aumann, G. Interpolation with developable Bézier patches. CAGD 1991, 23, 409–420. [Google Scholar] [CrossRef]
- Frey, W.H.; Bindschadler, D. Computer-Aided Design of a Class of Developable Bézier Surfaces; General Motors R&D Publication: Detroit, MI, USA, 1993. [Google Scholar]
- Chu, C.H.; Séquin, C.H. Developable Bézier patches: Properties and design. CAGD 2002, 34, 511–527. [Google Scholar] [CrossRef]
- Aumann, G. A simple algorithm for designing developable Bézier surfaces. CAGD 2002, 20, 601–616. [Google Scholar] [CrossRef]
- Chalfant, J.S. Analysis and Design of Developable Surfaces for Shipbuilding. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Zhao, H.; Wang, G. A new method for designing a developable surface utilizing the surface pencil through a given curve. Prog. Nat. Sci. 2008, 18, 105–110. [Google Scholar] [CrossRef]
- Al-Ghefari, R.A.; Abdel-Baky, R.A. An approach for designing developable surface with a common geodesic curve. Int. J. Contemp. Math. Sci. 2013, 8, 875–891. [Google Scholar] [CrossRef]
- Park, F.C.; Yu, Y.; Chun, C.; Ravani, B. Design of developable surfaces using optimal control. Trans. ASME 2002, 124, 602–608. [Google Scholar] [CrossRef]
- Elber, G. Approximation algorithm for developable surfaces. CAGD 1995, 16, 539–556. [Google Scholar]
- Sun, M.; Fiume, E. A Technique for Constructing Developable Surfaces; University of Toronto: Toronto, ON, Canada, 1996; pp. 176–185. [Google Scholar]
- Xu, G.; Rabczuk, T.; Güler, E.; Wu, Q.; Hui, K.; Wang, K. Quasi-harmonic Bézier approximation of minimal surfaces for finding forms of structural membranes. Comput. Struct. 2015, 161, 55–63. [Google Scholar] [CrossRef]
- Xu, G.; Li, M.; Mourrain, B.; Rabczuk, T.; Xu, J.; Bordas, S.P.A. Constructing IGA-suitable planar parameterization from complex CAD boundary by domain partition and global/local optimization. Comput. Methods Appl. Mech. Eng. 2017, 328, 175–200. [Google Scholar] [CrossRef]
- Bodduluri, R.M.C.; Ravani, B. Design of developable surfaces using duality between plane and point geometries. CAGD 1993, 25, 621–632. [Google Scholar] [CrossRef]
- Pottmann, H.; Farin, G. Developable rational Bézier and B-spline surfaces. CAGD 1995, 12, 513–531. [Google Scholar] [CrossRef]
- Pottmann, H.; Wallner, J. Model fabrication using surface layout projection. CAD 1999, 27, 283–291. [Google Scholar]
- Hu, G.; Wu, J.L.; Qin, X.Q. A new approach in designing of local controlled developable H-Bézier surfaces. Adv. Eng. Softw. 2018, 121, 26–38. [Google Scholar] [CrossRef]
- Hu, G.; Cao, H.X.; Zhang, S.X.; Guo, W. Developable Bézier-like surfaces with multiple shape parameters and its continuity conditions. Appl. Math. Model. 2017, 45, 728–747. [Google Scholar] [CrossRef]
- Kusno. Contribution à la Solution du Problème de Construction et de Raccordement Géometrique de Surfaces Développable Régulièrs à L’aide des Carreaux de Bézier. Ph.D. Thesis, Université de Metz, Metz, France, 1998. (In French). [Google Scholar]
- Hui, D.W. Etude sur la Représentation des Surfaces Complexes: Application à la Reconstruction de Surfaces Echantillonées. Ph.D. Thesis, Télécom ParisTech (ENST), Paris, France, 1988. (In French). [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusno. Construction of Regular Developable Bézier Patches. Math. Comput. Appl. 2019, 24, 4. https://doi.org/10.3390/mca24010004
Kusno. Construction of Regular Developable Bézier Patches. Mathematical and Computational Applications. 2019; 24(1):4. https://doi.org/10.3390/mca24010004
Chicago/Turabian StyleKusno. 2019. "Construction of Regular Developable Bézier Patches" Mathematical and Computational Applications 24, no. 1: 4. https://doi.org/10.3390/mca24010004
APA StyleKusno. (2019). Construction of Regular Developable Bézier Patches. Mathematical and Computational Applications, 24(1), 4. https://doi.org/10.3390/mca24010004



