Global Sensitivity Analysis to Study the Impacts of Bed-Nets, Drug Treatment, and Their Efficacies on a Two-Strain Malaria Model
Abstract
:1. Introduction
- Proposing a simple model of the mosquito biting rate as a non-linear function of ITN usage and including a parameter in the function that represents ITN efficacy. This will form the basis for studying ITN usage and its efficacy.
- Investigating a wide range of intervention strategies through global sensitivity analysis to determine the impacts of drug treatment and its efficacy and ITN usage and its efficacy in controlling malaria.
- Conducting a global sensitivity analysis to determine the influence of ITN usage, drug treatment, and their efficacies and other model parameters on the dynamics of malaria transmission. This could help in devising optimal intervention strategies that will offer more realistic predictions towards controlling malaria’s spread.
2. Model Formulation
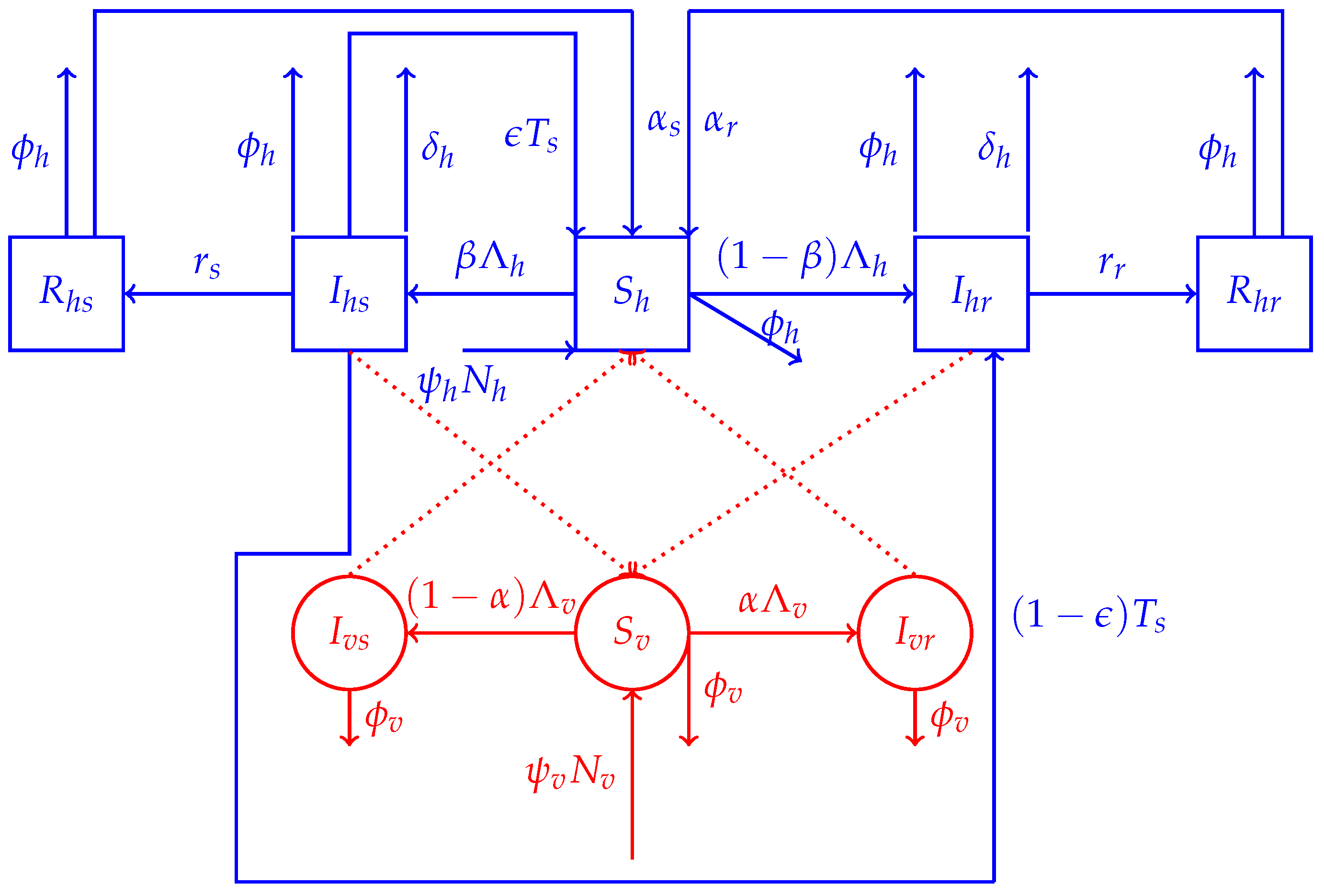
2.1. Model Structure
2.1.1. Human Dynamics
2.1.2. Mosquitoes’ Dynamics
2.2. The Model
3. Basic Properties of the Model
3.1. Basic Properties of the Model
3.2. Possibility of Backward Bifurcation
3.3. Scaling and Non-Existence of Backward Bifurcation
3.4. Stability of the Disease-Free Equilibrium Point
3.5. Global Stability of the DFE
3.6. Boundary Equilibria
3.6.1. Boundary Equilibria for the Drug-Sensitive Strain Only
3.6.2. Local Stability of
3.6.3. Boundary Equilibria for the Drug-Resistant Strain Only
3.6.4. Local Stability of
3.7. Coexistence Equilibrium Point
3.8. Global Stability of the Coexistence Equilibrium Point
4. Numerical Simulations of the Model
4.1. Baseline Parameter Values
5. Intervention Strategies and Global Sensitivity Analysis
5.1. Analytic Intervention Strategies
5.2. Numerical Intervention Strategies and Global Sensitivity Analysis
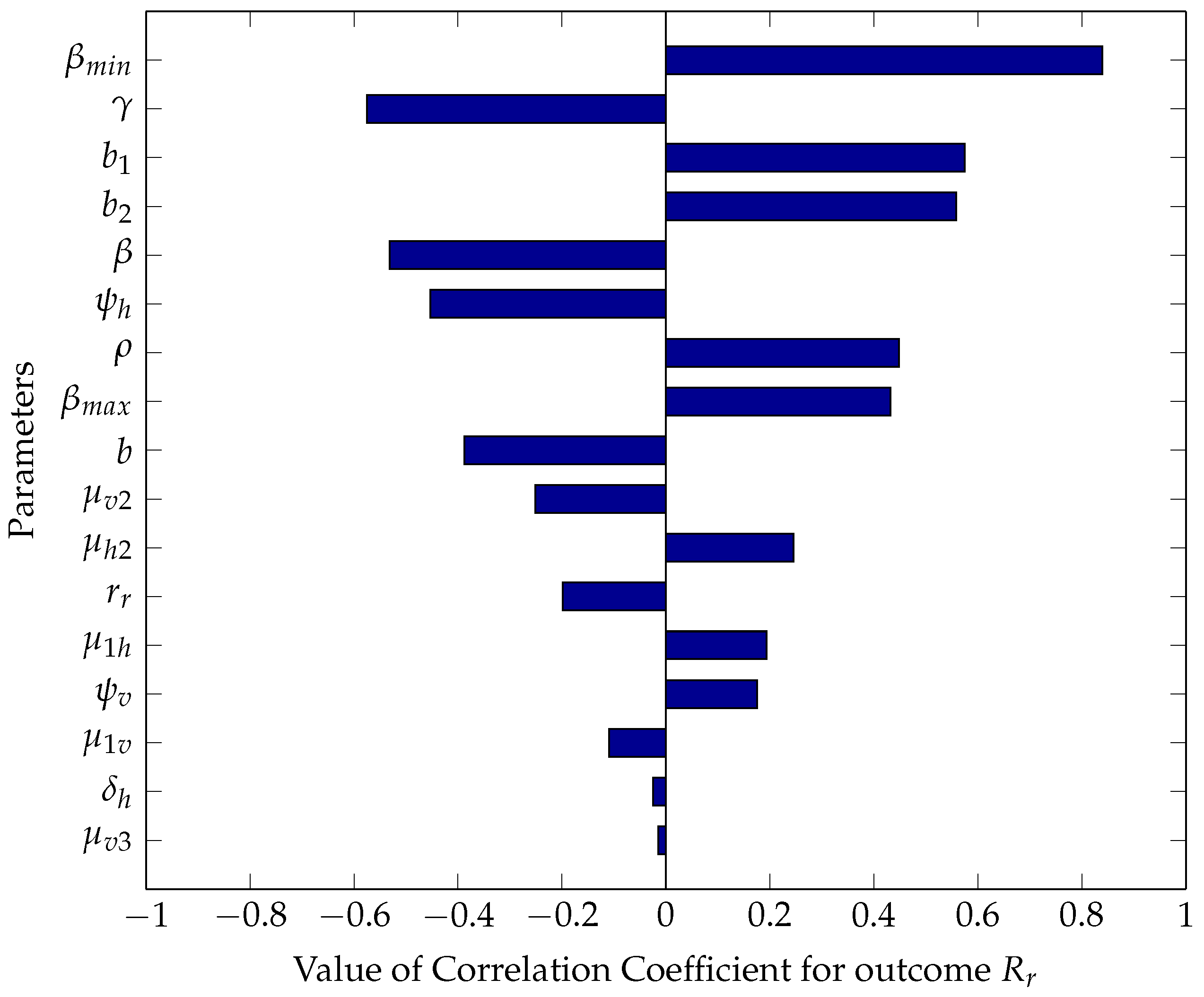
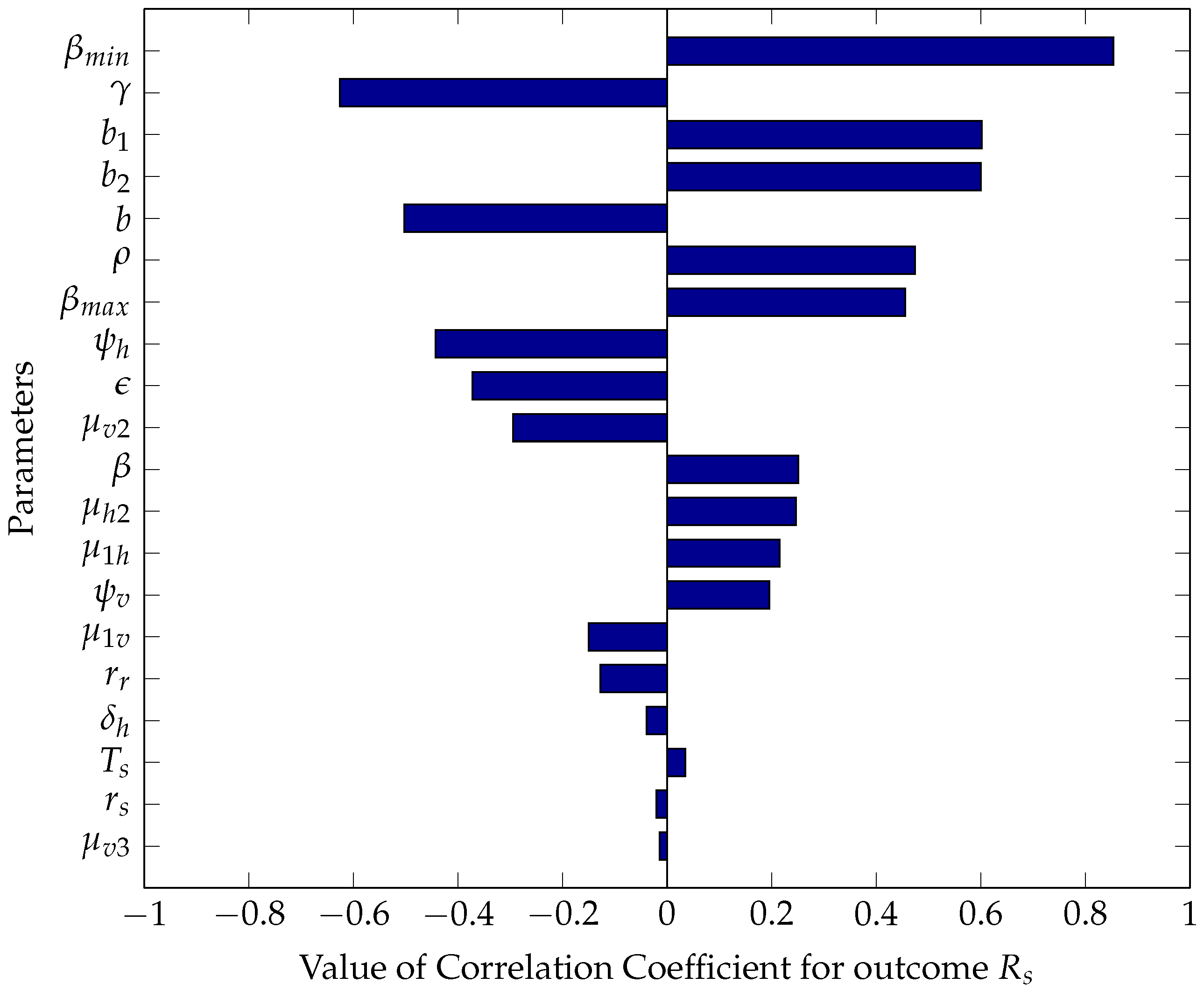
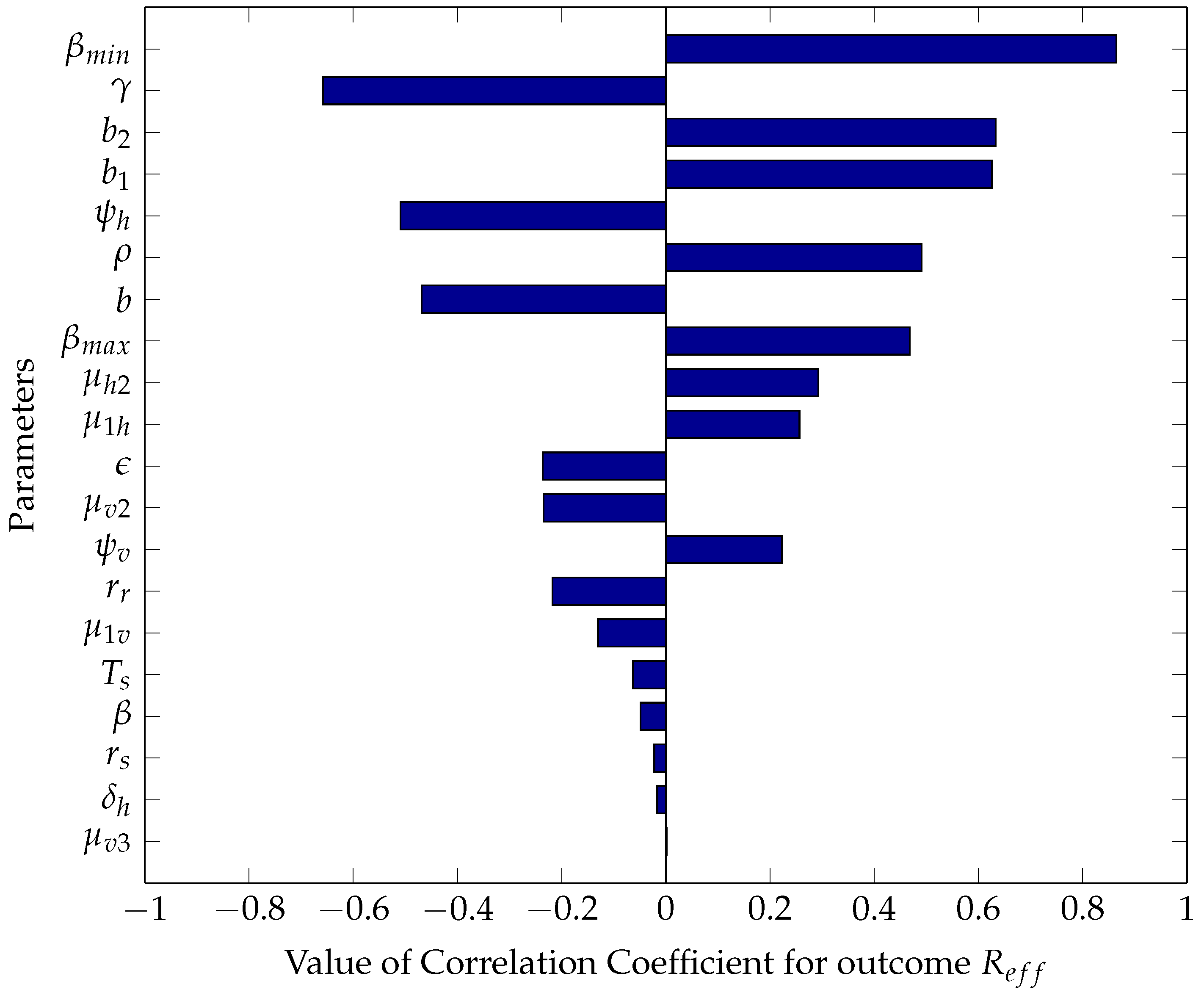
5.2.1. Sensitivity Analysis Using Partial Rank Correlation Coefficients
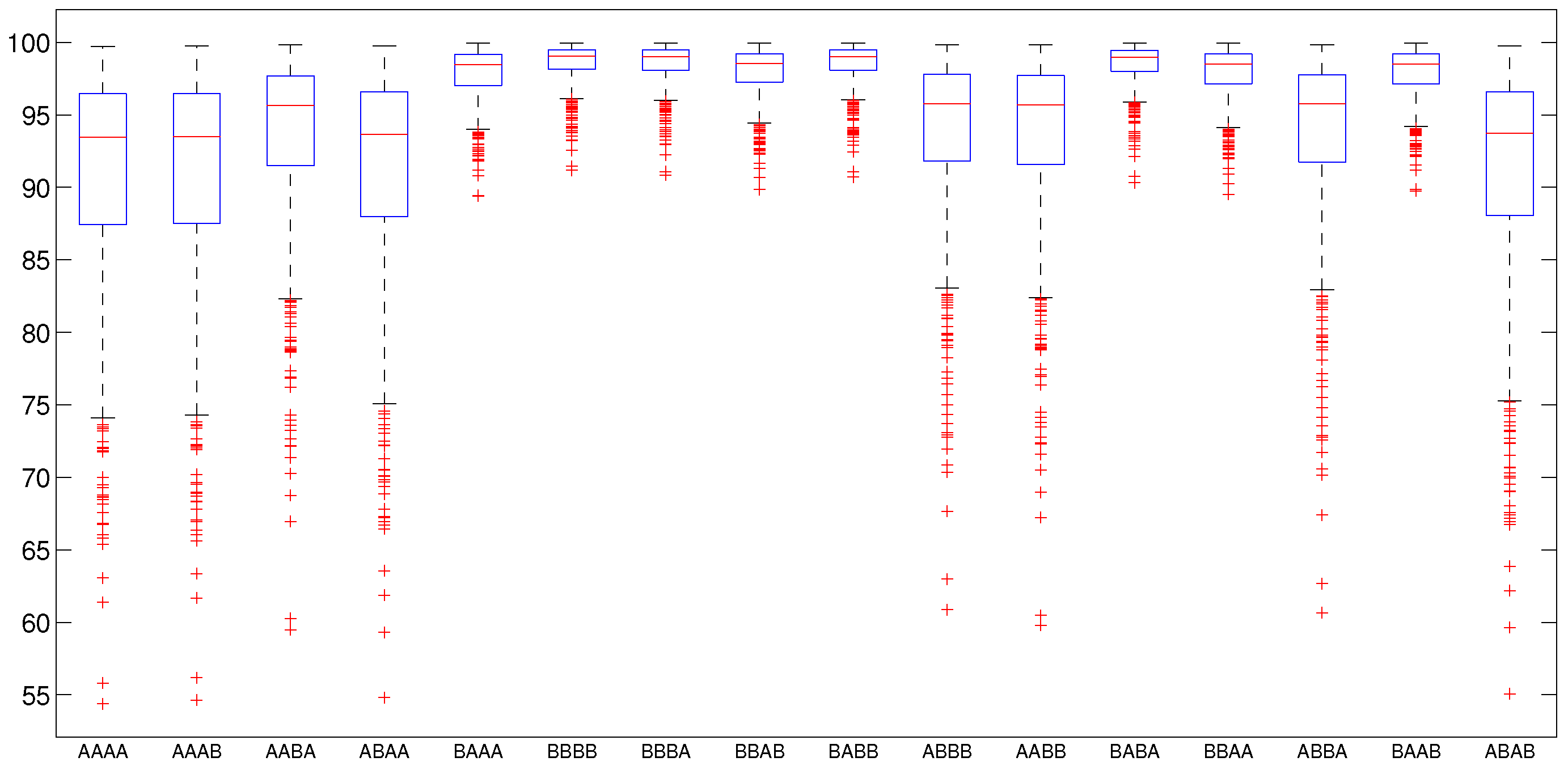
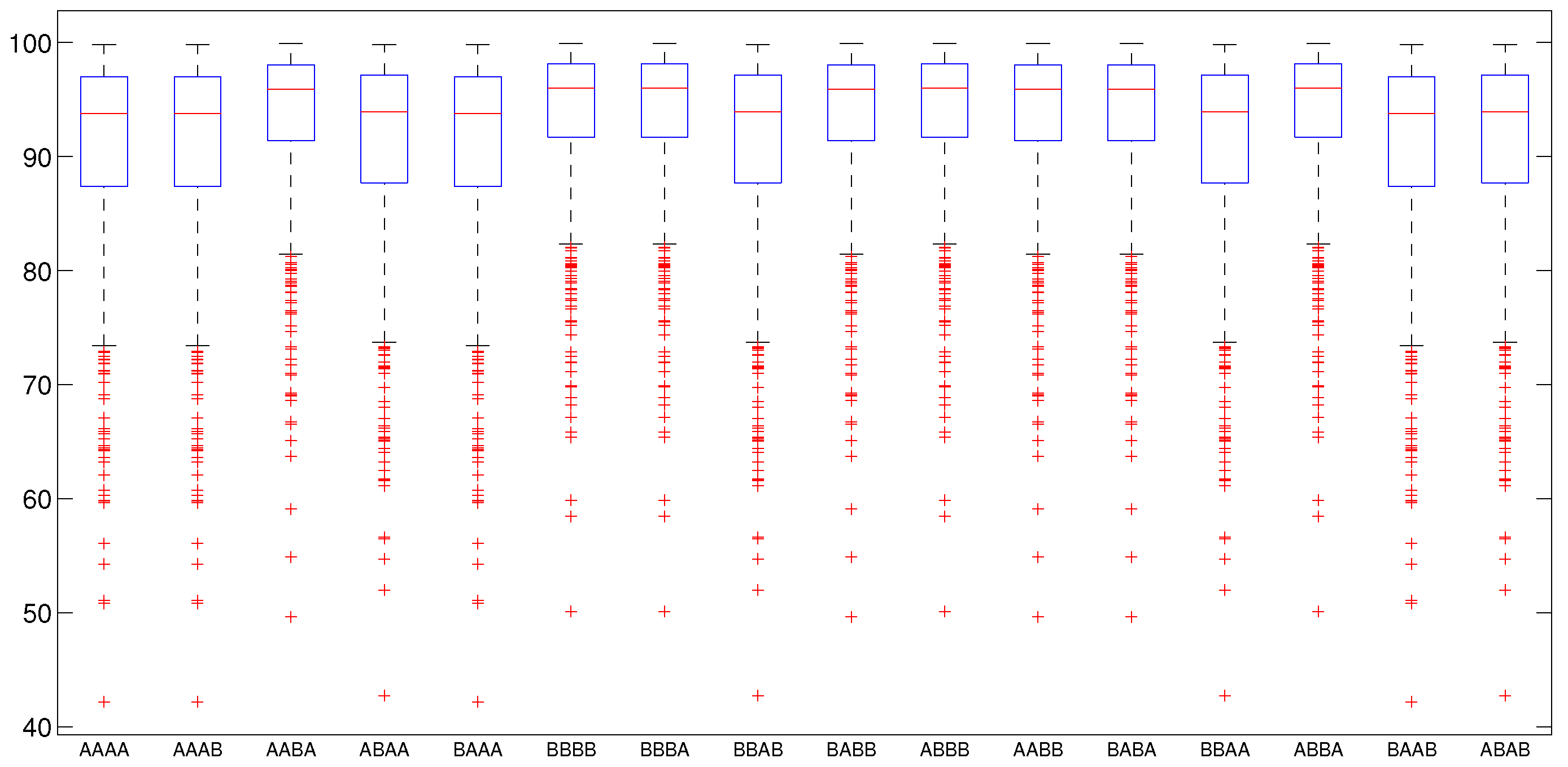
5.2.2. Numerical Intervention Strategies
6. Discussion
7. Conclusions
Author Contributions
Conflicts of Interest
References
- WHO. Global Technical Strategy for Malaria 2016–2030. Available online: https://www.who.int/malaria/publications/atoz/9789241564991/en/ (accessed on 7 March 2019).
- Hove-Musekwa, S.D. Determining effective spraying periods to control malaria via indoor residual spraying in sub-saharan Africa. Adv. Decis. Sci. 2008, 2008, 745463. [Google Scholar]
- Dawaki, S.; Al-Mekhlafi, H.M.; Ithoi, I.; Ibrahim, J.; Atroosh, W.M.; Abdulsalam, A.M.; Sady, H.; Elyana, F.N.; Adamu, A.U.; Yelwa, S.I.; et al. Is Nigeria winning the battle against malaria? Prevalence, risk factors and KAP assessment among Hausa communities in Kano State. Malar. J. 2016, 15, 351. [Google Scholar] [CrossRef]
- Kamgang, J.C.; Kamla, V.C.; Tchoumi, S.Y. Modeling the dynamics of malaria transmission with bed net protection perspective. Appl. Math. 2014, 5, 3156. [Google Scholar] [CrossRef]
- Yang, G.G.; Kim, D.; Pham, A.; Paul, C.J. A Meta-Regression Analysis of the Effectiveness of Mosquito Nets for Malaria Control: The Value of Long-Lasting Insecticide Nets. Int. J. Environ. Res. Public Health 2018, 15, 546. [Google Scholar] [CrossRef]
- Brock, A.; Gibbs, C.; Ross, J.; Esterman, A. The Impact of Antimalarial Use on the Emergence and Transmission of Plasmodium falciparum Resistance: A Scoping Review of Mathematical Models. Trop. Med. Infect. Dis. 2017, 2, 54. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Novak, R.J. Predicting the impact of insecticide-treated bed nets on malaria transmission: The devil is in the detail. Malar. J. 2009, 8, 256. [Google Scholar] [CrossRef]
- Phuc, H.K.; Andreasen, M.H.; Burton, R.S.; Vass, C.; Epton, M.J.; Pape, G.; Fu, G.; Condon, K.C.; Scaife, S.; Donnelly, C.A.; et al. Late-acting dominant lethal genetic systems and mosquito control. BMC Biol. 2007, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Forouzannia, F.; Gumel, A. Dynamics of an age-structured two-strain model for malaria transmission. Appl. Math. Comput. 2015, 250, 860–886. [Google Scholar] [CrossRef]
- Atkinson, M.P.; Su, Z.; Alphey, N.; Alphey, L.S.; Coleman, P.G.; Wein, L.M. Analyzing the control of mosquito-borne diseases by a dominant lethal genetic system. PNAS 2007, 104, 9540–9545. [Google Scholar] [CrossRef]
- Youdom, S.W.; Tahar, R.; Basco, L.K. Comparison of anti-malarial drug efficacy in the treatment of uncomplicated malaria in African children and adults using network meta-analysis. Malar. J. 2017, 16, 311. [Google Scholar] [CrossRef]
- Wurtz, N.; Pascual, A.; Marin-Jauffre, A.; Bouchiba, H.; Benoit, N.; Desbordes, M.; Martelloni, M.; de Santi, V.P.; Richa, G.; Taudon, N.; et al. Early treatment failure during treatment of Plasmodium falciparum malaria with atovaquone-proguanil in the Republic of Ivory Coast. Malar. J. 2012, 11, 146. [Google Scholar] [CrossRef]
- Olagunju, A.; Adeagbo, B.; Bolaji, O.; Izevbekhai, O. Quality of artemisinin-based antimalarial drugs marketed in Nigeria. Trans. R. Soc. Trop. Med. Hyg. 2017, 111, 90–96. [Google Scholar]
- Tivura, M.; Asante, I.; van Wyk, A.; Gyaase, S.; Malik, N.; Mahama, E.; Hostetler, D.M.; Fernandez, F.M.; Asante, K.P.; Kaur, H.; et al. Quality of artemisinin-based combination therapy for malaria found in Ghanaian markets and public health implications of their use. BMC Pharmacol. Toxicol. 2016, 17, 48. [Google Scholar] [CrossRef]
- Bassat, Q.; Tanner, M.; Guerin, P.J.; Stricker, K.; Hamed, K. Combating poor-quality anti-malarial medicines: A call to action. Malar. J. 2016, 15, 302. [Google Scholar] [CrossRef]
- Kaur, H.; Allan, E.L.; Mamadu, I.; Hall, Z.; Green, M.D.; Swamidos, I.; Dwivedi, P.; Culzoni, M.J.; Fernandez, F.M.; Garcia, G.; et al. Prevalence of substandard and falsified artemisinin-based combination antimalarial medicines on Bioko Island, Equatorial Guinea. BMJ Glob. Health 2017, 2, e000409. [Google Scholar] [CrossRef]
- WHO. Malaria. Available online: https://www.who.int/malaria/en/ (accessed on 7 March 2019).
- Esteva, L.; Gumel, A.B.; de LeóN, C.V. Qualitative study of transmission dynamics of drug-resistant malaria. Math. Comput. Model. 2009, 50, 611–630. [Google Scholar] [CrossRef]
- Tumwiine, J.; Hove-Musekwa, S.D.; Nyabadza, F. A Mathematical Model for the Transmission and Spread of Drug Sensitive and Resistant Malaria Strains within a Human Population. ISRN Biomath. 2014, 2014, 636973. [Google Scholar] [CrossRef]
- Pongtavornpinyo, W.; Yeung, S.; Hastings, I.M.; Dondorp, A.M.; Day, N.P.; White, N.J. Spread of anti-malarial drug resistance: Mathematical model with implications for ACT drug policies. Malar. J. 2008, 7, 229. [Google Scholar] [CrossRef]
- Klein, E.Y.; Smith, D.L.; Laxminarayan, R.; Levin, S. Superinfection and the evolution of resistance to antimalarial drugs. Proc. R. Soc. Lond. B Biol. Sci. 2012, 279, 3834–3842. [Google Scholar] [CrossRef]
- Klein, E.Y.; Smith, D.L.; Boni, M.F.; Laxminarayan, R. Clinically immune hosts as a refuge for drug-sensitive malaria parasites. Malar. J. 2008, 7, 67. [Google Scholar] [CrossRef]
- Newton, P.N.; Caillet, C.; Guerin, P.J. A link between poor quality antimalarials and malaria drug resistance? Expert Rev. Anti-Infect. Ther. 2016, 14, 531–533. [Google Scholar] [CrossRef]
- Chitnis, N.; Cushing, J.M.; Hyman, J. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J. Appl. Math. 2006, 67, 24–45. [Google Scholar] [CrossRef]
- Chiyaka, C.; Garira, W.; Dube, S. Transmission model of endemic human malaria in a partially immune population. Math. Comput. Model. 2007, 46, 806–822. [Google Scholar] [CrossRef]
- Huo, H.F.; Qiu, G.M. Stability of a mathematical model of malaria transmission with relapse. Abstr. Appl. Anal. 2014, 2014, 289349. [Google Scholar] [CrossRef]
- Ngwa, G.A.; Shu, W.S. A mathematical model for endemic malaria with variable human and mosquito populations. Math. Comput. Model. 2000, 32, 747–763. [Google Scholar] [CrossRef]
- Wyse, A.P.P.; Bevilacqua, L.; Rafikov, M. Simulating malaria model for different treatment intensities in a variable environment. Ecol. Model. 2007, 206, 322–330. [Google Scholar] [CrossRef]
- Jäger, W. A quantitative model of population dynamics in malaria with drug treatment. J. Math. Biol. 2014, 69, 659–685. [Google Scholar]
- White, M.T.; Griffin, J.T.; Churcher, T.S.; Ferguson, N.M.; Basáñez, M.G.; Ghani, A.C. Modelling the impact of vector control interventions on Anopheles gambiae population dynamics. Parasites Vectors 2011, 4, 1. [Google Scholar] [CrossRef]
- McKenzie, F.E.; Smith, D.L.; O’Meara, W.P.; Riley, E.M. Strain theory of malaria: the first 50 years. Adv. Parasitol. 2008, 66, 1–46. [Google Scholar]
- Agyingi, E.; Ngwa, M.; Wiandt, T. The dynamics of multiple species and strains of malaria. Lett. Biomath. 2016, 3, 29–40. [Google Scholar] [CrossRef]
- Koella, J.; Antia, R. Epidemiological models for the spread of anti-malarial resistance. Malar. J. 2003, 2, 3. [Google Scholar] [CrossRef]
- Bacaër, N.; Sokhna, C. A reaction-diffusion system modeling the spread of resistance to an antimalarial drug. Math. Biosci. Eng. 2005, 2, 227–238. [Google Scholar]
- Garba, S.M.; Gumel, A.B.; Bakar, M.A. Backward bifurcations in dengue transmission dynamics. Math. Biosci. 2008, 215, 11–25. [Google Scholar] [CrossRef]
- Brauer, F. Backward bifurcations in simple vaccination models. J. Math. Anal. Appl. 2004, 298, 418–431. [Google Scholar] [CrossRef]
- Keegan, L.T.; Dushoff, J. Population-level effects of clinical immunity to malaria. BMC Infect. Dis. 2013, 13, 428. [Google Scholar] [CrossRef]
- Gimba, B.; Bala, S.I. Modeling the impact of bed-net use and treatment on malaria transmission dynamics. Int. Sch. Res. Not. 2017, 2017, 6182492. [Google Scholar] [CrossRef]
- Ngonghala, C.N.; Mohammed-Awel, J.; Zhao, R.; Prosper, O. Interplay between insecticide-treated bed-nets and mosquito demography: implications for malaria control. J. Theor. Biol. 2016, 397, 179–192. [Google Scholar] [CrossRef]
- Hadeler, K.P.; van den Driessche, P. Backward bifurcation in epidemic control. Math. Biosci. 1997, 146, 15–35. [Google Scholar] [CrossRef]
- Feng, X.; Ruan, S.; Teng, Z.; Wang, K. Stability and backward bifurcation in a malaria transmission model with applications to the control of malaria in China. Math. Biosci. 2015, 266, 52–64. [Google Scholar] [CrossRef]
- Baba, I.A.; Kaymakamzade, B.; Hincal, E. Two-strain epidemic model with two vaccinations. Chaos Solitons Fractals 2018, 106, 342–348. [Google Scholar] [CrossRef]
- Baba, I.A.; Hincal, E. Global stability analysis of two-strain epidemic model with bilinear and non-monotone incidence rates. Eur. Phys. J. Plus 2017, 132, 208. [Google Scholar] [CrossRef]
- Filipe, J.A.; Riley, E.M.; Drakeley, C.J.; Sutherland, C.J.; Ghani, A.C. Determination of the processes driving the acquisition of immunity to malaria using a mathematical transmission model. PLoS Comput. Biol. 2007, 3, e255. [Google Scholar] [CrossRef]
- Pinkevych, M.; Petravic, J.; Chelimo, K.; Kazura, J.W.; Moormann, A.M.; Davenport, M.P. The Dynamics of Naturally Acquired Immunity to Plasmodium falciparum Infection. PLoS Comput. Biol. 2012, 8. [Google Scholar] [CrossRef] [PubMed]
- Altizer, S.; Dobson, A.; Hosseini, P.; Hudson, P.; Pascual, M.; Rohani, P. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 2006, 9, 467–484. [Google Scholar] [CrossRef]
- Beck-Johnson, L.M.; Nelson, W.A.; Paaijmans, K.P.; Read, A.F.; Thomas, M.B.; Bjørnstad, O.N. The effect of temperature on Anopheles mosquito population dynamics and the potential for malaria transmission. PLoS ONE 2013, 8, e79276. [Google Scholar] [CrossRef]
- Lunde, T.M.; Bayoh, M.N.; Lindtjørn, B. How malaria models relate temperature to malaria transmission. Parasites Vectors 2013, 6, 1. [Google Scholar] [CrossRef]
- Ermert, V.; Fink, A.H.; Morse, A.P.; Jones, A.E.; Paeth, H.; di Giuseppe, F.; Tompkins, A.M. Development of dynamical weather-disease models to project and forecast malaria in Africa. Malar. J 2012, 11. [Google Scholar] [CrossRef]
- Agusto, F.B.; del Valle, S.Y.; Blayneh, K.W.; Ngonghala, C.N.; Goncalves, M.J.; Li, N.; Zhao, R.; Gong, H. The impact of bed-net use on malaria prevalence. J. Theor. Biol. 2013, 320, 58–65. [Google Scholar] [CrossRef]
- Childs, D.Z.; Boots, M. The interaction of seasonal forcing and immunity and the resonance dynamics of malaria. J. R. Soc. Interface 2010, 7, 309–319. [Google Scholar] [CrossRef]
- Caminade, C.; Kovats, S.; Rocklov, J.; Tompkins, A.M.; Morse, A.P.; Colón-González, F.J.; Stenlund, H.; Martens, P.; Lloyd, S.J. Impact of climate change on global malaria distribution. PNAS 2014, 111, 3286–3291. [Google Scholar] [CrossRef]
- Hoshen, M.B.; Morse, A.P. A weather-driven model of malaria transmission. Malar. J. 2004, 3, 1. [Google Scholar] [CrossRef]
- Stuckey, E.M.; Smith, T.; Chitnis, N. Seasonally dependent relationships between indicators of malaria transmission and disease provided by mathematical model simulations. PLoS Comput. Biol. 2014, 10, e1003812. [Google Scholar] [CrossRef]
- Chitnis, N.; Hardy, D.; Smith, T. A periodically-forced mathematical model for the seasonal dynamics of malaria in mosquitoes. Bull. Math. Biol. 2012, 74, 1098–1124. [Google Scholar] [CrossRef]
- Ngonghala, C.N.; del Valle, S.Y.; Zhao, R.; Mohammed-Awel, J. Quantifying the impact of decay in bed-net efficacy on malaria transmission. J. Theor. Biol. 2014, 363, 247–261. [Google Scholar] [CrossRef]
- Silva, C.J.; Torres, D.F. An optimal control approach to malaria prevention via insecticide-treated nets. Conf. Pap. Math. 2013, 2013, 658468. [Google Scholar] [CrossRef]
- Chiyaka, C.; Tchuenche, J.M.; Garira, W.; Dube, S. A mathematical analysis of the effects of control strategies on the transmission dynamics of malaria. Appl. Math. Comput. 2008, 195, 641–662. [Google Scholar] [CrossRef]
- Pinto, C.M.; Machado, J.T. Fractional model for malaria transmission under control strategies. Comput. Math. Appl. 2013, 66, 908–916. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Hoare, A.; Regan, D.G.; Wilson, D.P. Sampling and sensitivity analyses tools (SaSAT) for computational modelling. Theor. Biol. Med. Model. 2008, 5, 1. [Google Scholar] [CrossRef]
- WHO. Vector Control Technical Expert Group Report to MPAC September 2013. Available online: https://www.who.int/malaria/mpac/mpac_sep13_vcteg_llin_survival_report.pdf?ua=1 (accessed on 7 March 2019).
- Smith, N.R.; Trauer, J.M.; Gambhir, M.; Richards, J.S.; Maude, R.J.; Keith, J.M.; Flegg, J.A. Agent-based models of malaria transmission: A systematic review. Malar. J. 2018, 17, 299. [Google Scholar] [CrossRef] [PubMed]
- Steinhardt, L.C.; St Jean, Y.; Impoinvil, D.; Mace, K.E.; Wiegand, R.; Huber, C.S.; Alexandre, J.S.F.; Frederick, J.; Nkurunziza, E.; Jean, S.; et al. Effectiveness of insecticide-treated bednets in malaria prevention in Haiti: A case-control study. Lancet Glob. Health 2017, 5, e96–e103. [Google Scholar] [CrossRef]
- Mukhtar, A.Y.; Munyakazi, J.B.; Ouifki, R.; Clark, A.E. Modelling the effect of bednet coverage on malaria transmission in South Sudan. PLoS ONE 2018, 13, e0198280. [Google Scholar] [CrossRef] [PubMed]
- Okuneye, K.; Gumel, A.B. Analysis of a temperature-and rainfall-dependent model for malaria transmission dynamics. Math. Biosci. 2017, 287, 72–92. [Google Scholar] [CrossRef]
- Larson, P.S.; Minakawa, N.; Dida, G.O.; Njenga, S.M.; Ionides, E.L.; Wilson, M.L. Insecticide-treated net use before and after mass distribution in a fishing community along Lake Victoria, Kenya: Successes and unavoidable pitfalls. Malar. J. 2014, 13, 466. [Google Scholar] [CrossRef]
- Pulkki-Brännström, A.M.; Wolff, C.; Brännström, N.; Skordis-Worrall, J. Cost and cost effectiveness of long-lasting insecticide-treated bed nets—A model-based analysis. Cost Eff. Resour. Alloc. 2012, 10, 5. [Google Scholar] [CrossRef]
| Variable | Description |
|---|---|
| Population of susceptible humans | |
| Population of infected humans with the sensitive strain | |
| Population of infected humans with the resistant strain | |
| Population of recovered humans with the sensitive strain | |
| Population of recovered humans with the resistant strain | |
| Total human population | |
| Population of susceptible mosquitoes | |
| Population of infected mosquitoes with the sensitive strain | |
| Population of infected mosquitoes with the resistant strain | |
| Total population of mosquitoes |
| Parameters | Description and Dimension |
|---|---|
| Recruitment rate into human population (humans ) | |
| Recruitment rate into the mosquitoes’ population (mosquitoes ) | |
| Treatment rate of infected humans with the sensitive strain () | |
| a | Average daily biting rate by a single mosquito of humans () |
| Probability of transmission of infection from infected humans to susceptible mosquitoes | |
| Probability of transmission of infection from infected mosquitoes to susceptible humans | |
| Number of mosquitoes per human host | |
| b | Proportion of ITN usage |
| Maximum biting rate per mosquito () | |
| Minimum biting rate per mosquito () | |
| Treatment efficacy () | |
| ITN efficacy () | |
| Rate at which humans with sensitive strains lose immunity () | |
| Rate at which humans with resistant strains lose immunity () | |
| Proportion of infected vectors that developed resistance | |
| Rate at which humans with resistant strains acquire immunity () | |
| Rate at which humans with sensitive strains acquire immunity () | |
| Proportion of susceptible humans who become infected with the sensitive strain | |
| Disease-induced death rate for infected humans () | |
| Density-dependent part of the death and emigration rate for humans (human ) | |
| Density-independent part of the death rate for humans (human ) | |
| Density-independent part of the death rate for mosquitoes (mosquitoes ) | |
| Density-dependent part of the death rate for mosquitoes () | |
| ITN-induced death rate for mosquitoes () |
| Parameter | Baseline Value/Source | Range/Source | Distribution for Sensitivity Analysis |
|---|---|---|---|
| 9.3614 [38] | [6.0849, 12.17] estimated | Uniform | |
| 0.4478, [38] | [0.2911, 0.7], estimated, [19] | Uniform | |
| 0.35, [19] | [0.2275, 0.455], estimated | Uniform | |
| 0.75, [19] | [0.1, 0.8], assumed | Uniform | |
| 0.5342, [38] | [0.072, 0.64], [56] | Uniform | |
| 7, assumed | [2, 8], [38] | Uniform | |
| b | 0.53, [56] | [0.1325, 0.6625], estimated | Triangular, peak 0.5 |
| 0.6334, [38] | [0.1, 1], [56] | Uniform | |
| 0.0696, [38] | [0, 0.1], [56] | Uniform | |
| 0.4, assumed | [0.01, 0.61], [19] | Uniform | |
| 0.5, assumed | [0.2, 1], [58] | Uniform | |
| 0.0017, [19] | [0.001105, 0.00221], estimated | Uniform | |
| 0.0017, [19] | [0.001105, 0.00221], estimated | Triangular, peak 0.0017 | |
| 0.3, assumed | [0.195, 0.39], estimated | Uniform | |
| 0.0078, [18] | [0.00507, 0.01014], estimated | Triangular, peak 0.0078 | |
| 0.0078, [18] | [0.00507, 0.01014], estimated | Uniform | |
| 0.7, [19] | [0.455, 0.91], estimated | Uniform | |
| [58] | [0.00065, 0.0013], estimated | Uniform | |
| 1 [24] | [6.5, 13] , estimated | Uniform | |
| 4.212 [24] | [2.74, 5.48] , estimated | Uniform | |
| 0.1429, [24] | [0.092885, 0.18577], estimated | Uniform | |
| 2.28 [24] | [1.48, 2.96] , estimated | Uniform | |
| 0.0995, [38] | [0.064675, 0.12935], estimated | Uniform |
| Parameter | b | |||
|---|---|---|---|---|
| A | 0.75 | 0.75 | 0.75 | 0.75 |
| B | 0.95 | 0.95 | 0.95 | 0.95 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bala, S.; Gimba, B. Global Sensitivity Analysis to Study the Impacts of Bed-Nets, Drug Treatment, and Their Efficacies on a Two-Strain Malaria Model. Math. Comput. Appl. 2019, 24, 32. https://doi.org/10.3390/mca24010032
Bala S, Gimba B. Global Sensitivity Analysis to Study the Impacts of Bed-Nets, Drug Treatment, and Their Efficacies on a Two-Strain Malaria Model. Mathematical and Computational Applications. 2019; 24(1):32. https://doi.org/10.3390/mca24010032
Chicago/Turabian StyleBala, Saminu, and Bello Gimba. 2019. "Global Sensitivity Analysis to Study the Impacts of Bed-Nets, Drug Treatment, and Their Efficacies on a Two-Strain Malaria Model" Mathematical and Computational Applications 24, no. 1: 32. https://doi.org/10.3390/mca24010032
APA StyleBala, S., & Gimba, B. (2019). Global Sensitivity Analysis to Study the Impacts of Bed-Nets, Drug Treatment, and Their Efficacies on a Two-Strain Malaria Model. Mathematical and Computational Applications, 24(1), 32. https://doi.org/10.3390/mca24010032





