An Elastodiffusive Orthotropic Euler–Bernoulli Beam Considering Diffusion Flux Relaxation
Abstract
:1. Introduction
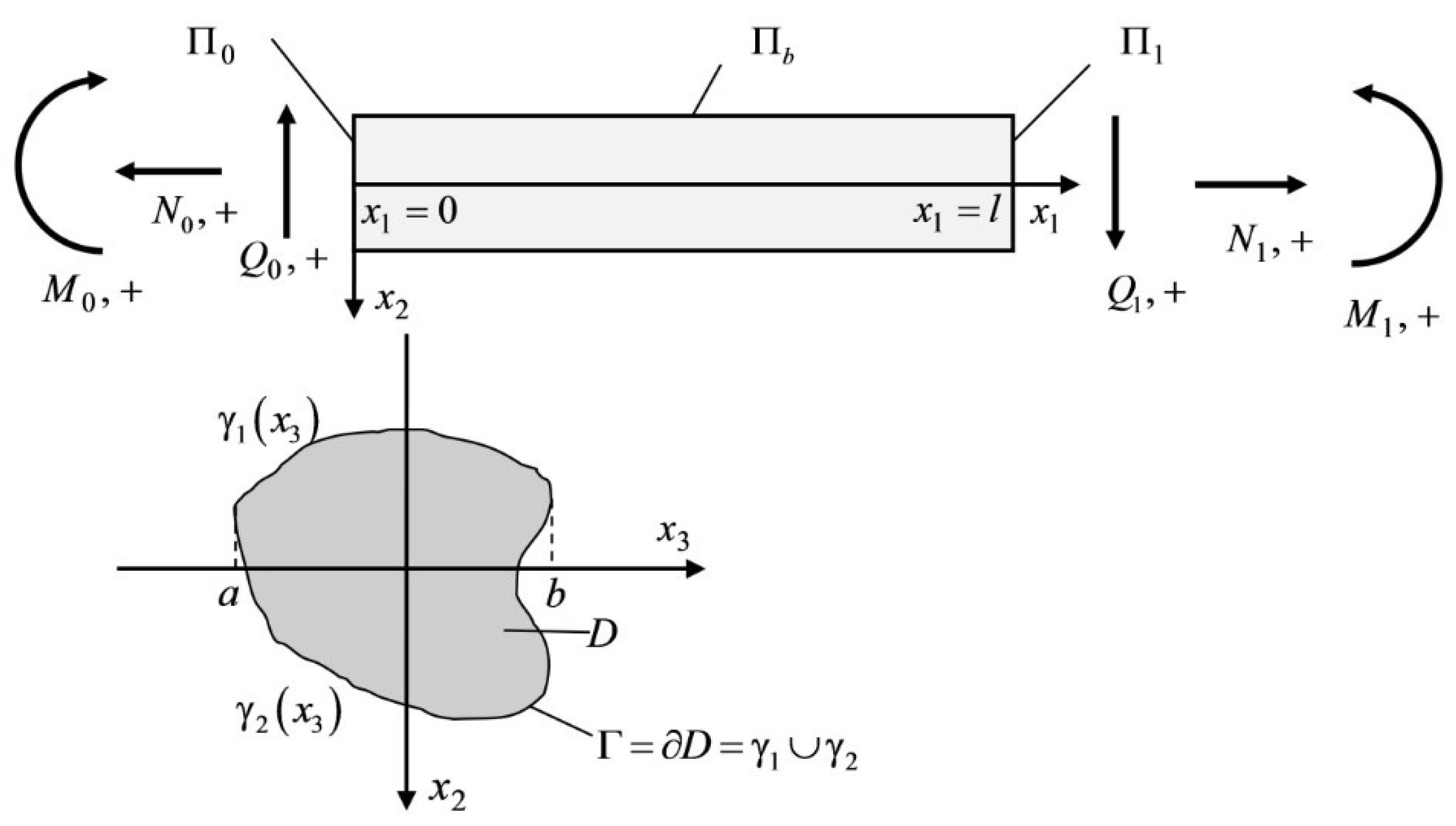
2. Problem Formulation
- The axis is the central axis of the cross section. In this case,
- The side surface is free from mechanical loads, i.e.,
- We also assume that there is no mass transfer through the side surface,
- The beam material is a homogeneous ortotropic continuum.The bending of beam is considered in plane . Then ; ; . Mass transfer occurs also in the plane , i.e., η(q) = η(q)(x1,x2,τ).
- Transverse deflections are considered small. Then, the linearization of the unknown quantities with respect to the variable will have the following form:
- is the cross-sectional area,
- is moment of inertia of the beam section relative to the axis ,
- is the linearly distributed axial load,
- is the linearly distributed moment,
- is the linearly distributed transverse load,
- is the linear density of bulk mass transfer sources,
3. Method of Solution
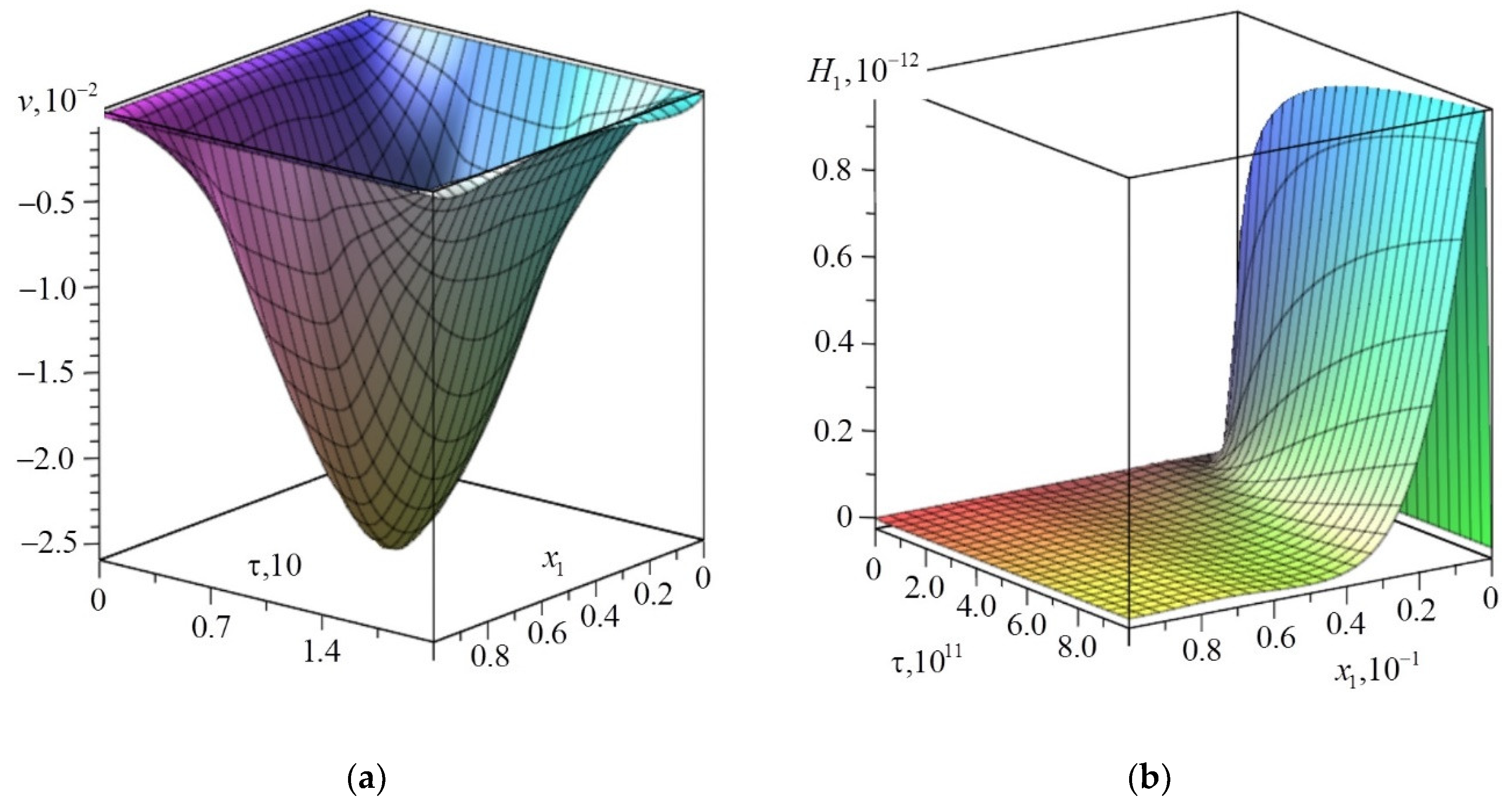
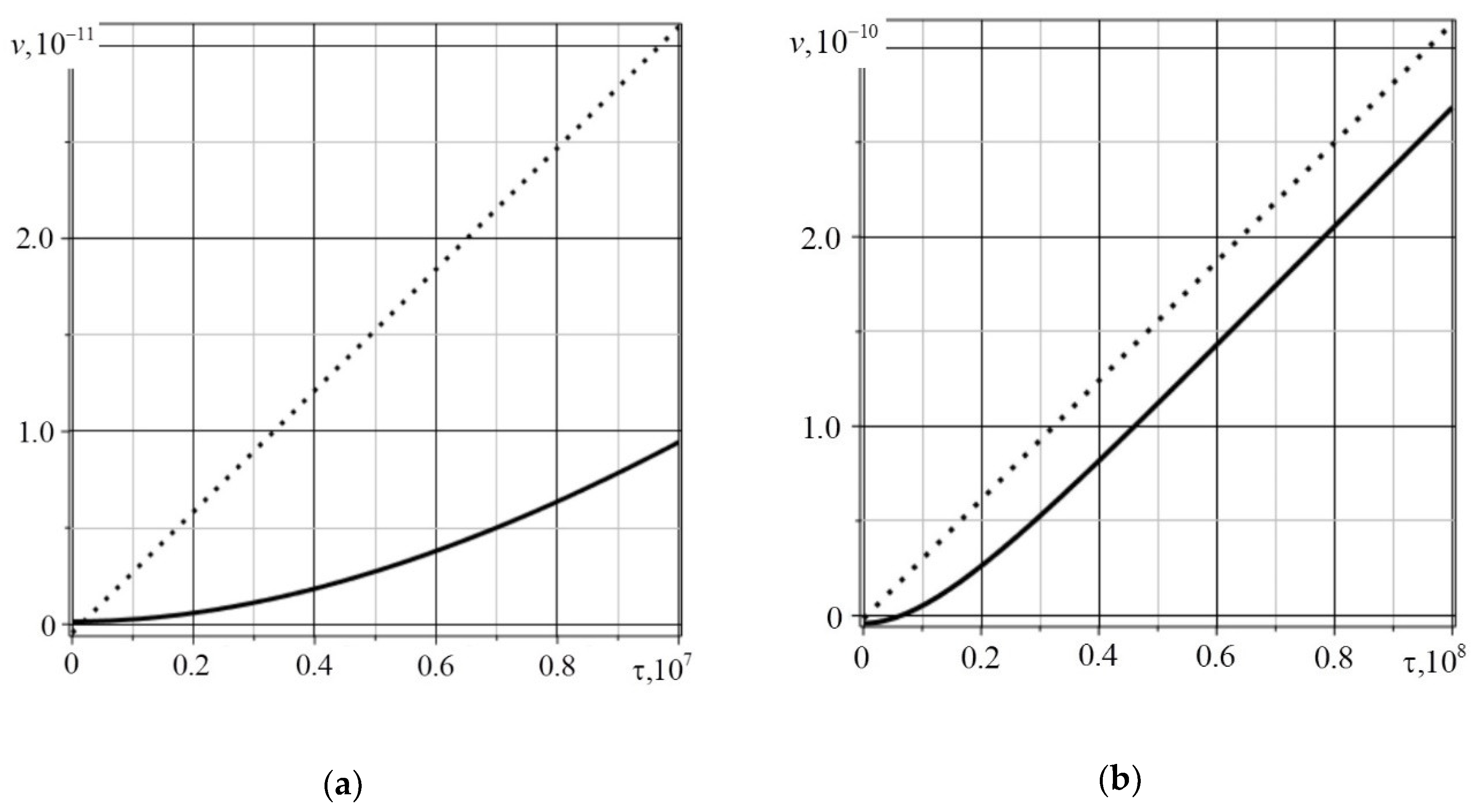
4. Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Afram, A.Y.; Khader, S.E. 2D Problem for a Half-Space under the Theory of Fractional Thermoelastic Diffusion. Am. J. Sci. Ind. Res. 2014, 6, 47–57. [Google Scholar]
- Atwa, S.Y.; Egypt, Z. Generalized Thermoelastic Diffusion with Effect of Fractional Parameter on Plane Waves Temperature-Dependent Elastic Medium. J. Mater. Chem. Eng. 2013, 1, 55–74. [Google Scholar]
- Belova, I.V.; Murch, G.E. Thermal and diffusion-induced stresses in crystalline solids. J. Appl. Phys. 1995, 77, 127–134. [Google Scholar] [CrossRef]
- Choudhary, S.; Deswal, S. Mechanical Loads on a Generalized Thermoelastic Medium with Diffusion. Meccanica 2010, 45, 401–413. [Google Scholar] [CrossRef]
- Elhagary, M.A. Generalized thermoelastic diffusion problem for an infinitely long hollow cylinder for short times. Acta Mech. 2011, 218, 205–215. [Google Scholar] [CrossRef]
- El-Sayed, A.M. A two-dimensional generalized thermoelastic diffusion problem for a half-space. Math. Mech. Solids 2016, 21, 1045–1060. [Google Scholar] [CrossRef]
- Knyazeva, A.G. Model of medium with diffusion and internal surfaces and some applied problems. Mater. Phys. Mech. 2004, 7, 29–36. [Google Scholar]
- Kumar, R.; Chawla, V. Green’s Functions in Orthotropic Thermoelastic Diffusion Media. Eng. Anal. Bound. Elem. 2012, 36, 1272–1277. [Google Scholar] [CrossRef]
- Olesiak, Z.S.; Pyryev, Yu.A. A coupled quasi-stationary problem of thermodiffusion for an elastic cylinder. Int. J. Eng. Sci. 1995, 33, 773–780. [Google Scholar] [CrossRef]
- Pidstryhach, Y.S. Differential equations of the problem of thermodiffusion in a solid deformable isotropic body. Dop. Akad. Nauk USSR 1961, 2, 169–172. [Google Scholar]
- Sherief, H.H.; El-Maghraby, N.M. A Thick Plate Problem in the Theory of Generalized Thermoelastic Diffusion. Int. J. Thermophys. 2009, 30, 2044–2057. [Google Scholar] [CrossRef]
- Aouadi, M. Variable electrical and thermal conductivity in the theory of generalized thermoelastic diffusion. Z. Angew. Math. Phys. 2005, 57, 350–366. [Google Scholar] [CrossRef]
- Deswal, S.; Kalkal, K. A two-dimensional generalized electro-magneto-thermoviscoelastic problem for a half-space with diffusion. Int. J. Therm. Sci. 2011, 50, 749–759. [Google Scholar] [CrossRef]
- Tarlakovskii, D.V.; Vestyak, V.A.; Zemskov, A.V. Dynamic Processes in Thermoelectromagnetoelastic and Thermoelastodiffusive Media. In Encyclopedia of Thermal Stress; Springer: London, UK, 2014; Volume 2, pp. 1064–1071. [Google Scholar]
- Zhang, J.; Li, Y. A Two-Dimensional Generalized Electromagnetothermoelastic Diffusion Problem for a Rotating Half-Space. Hindawi Publ. Corp. Math. Probl. Eng. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Chu, J.L.; Lee, S. Diffusion-induced stresses in a long bar of square cross section. J. Appl. Phys. 1993, 73, 3211–3219. [Google Scholar] [CrossRef]
- Freidin, A.B.; Korolev, I.K.; Aleshchenko, S.P.; Vilchevskaya, E.N. Chemical affinity tensor and chemical reaction front propagation: Theory and FE-simulations. J. Fract. 2016, 202, 245–259. [Google Scholar] [CrossRef]
- Hwang, C.C.; Chen, K.M.; Hsieh, J.Y. Diffusion-induced stresses in a long bar under an electric field. J. Phys. D Appl. Phys. 1994, 27, 2155–2162. [Google Scholar] [CrossRef]
- Indeitsev, D.A.; Semenov, B.N.; Sterlin, M.D. The Phenomenon of Localization of Diffusion Process in a Dynamically Deformed Solid. Dokl. Phys. 2012, 57, 171–173. [Google Scholar] [CrossRef]
- Crump, K. Numerical Inversion of Laplace Transforms Using a Fourier Series Approximation. J. Assoc. Comput. Mach. 1976, 23, 89–96. [Google Scholar] [CrossRef]
- Durbin, F. Numerical inversion of Laplace transforms: An efficient improvement to Dubner and Abate’s method. Comput. J. 1974, 17, 371–376. [Google Scholar] [CrossRef]
- Honig, G.; Hirdes, U. A method for the numerical inversion of Laplace transforms. J. Comput. Appl. Math. 1984, 10, 113–132. [Google Scholar] [CrossRef]
- Poroshina, N.I.; Ryabov, V.M. Methods for Laplace Transform Inversion; Vestnik of the St. Petersburg 239 University: Cambridge, UK, 2011; Volume 44, pp. 214–222. [Google Scholar]
- Mikhailova, E.Yu.; Tarlakovskii, D.V.; Fedotenkov, G.V. Obshchaya Teoriya Uprugikh Obolochek; MAI: Moscow, Russia, 2018. [Google Scholar]
- Gorshkov, A.G.; Medvedsky, A.L.; Rabinsky, L.N.; Tarlakovsky, D.V. Volny v Sploshnykh Sredakh; Fizmatlit: Moscow, Russia, 2004. [Google Scholar]
- Davydov, S.A.; Zemskov, A.V.; Tarlakovskii, D.V. An Elastic Half-Space under the Action of One-Dimensional Time-Dependent Diffusion Perturbations. Lobachevskii J. Math. 2015, 36, 503–509. [Google Scholar] [CrossRef]
- Davydov, S.A.; Vestyak, A.V.; Zemskov, A.V.; Tarlakovskii, D.V. Unsteady one-dimensional problem of thermoelastic diffusion for homogeneous multicomponent continuum with a plane boundaries. Uchenye Zapiski Kazanskogo Univ. Ser. Fiziko-Matematicheskie Nauki 2018, 160, 183–196. [Google Scholar]
- Davydov, S.A.; Zemskov, A.V. Unsteady One-dimensional Perturbations in Multicomponent Thermoelastic Layer with Cross-diffusion Effect. J. Phys. Conf. Ser. 2018, 1129, 012009. [Google Scholar] [CrossRef]
- Zemskov, A.V.; Tarlakovskiy, D.V. Method of the equivalent boundary conditions in the unsteady problem for elastic diffusion layer. Mater. Phys. Mech. 2015, 23, 36–41. [Google Scholar]
- Davydov, S.A.; Zemskov, A.V.; Igumnov, L.A.; Tarlakovskiy, D.V. Non-stationary model of mechanical diffusion for half-space with arbitrary boundary conditions. Mater. Phys. Mech. 2016, 28, 72–76. [Google Scholar]
- Grigoriev, I.S.; Meylikhov, I.Z. Fizicheskiye Velichiny: Sprovochnik; Energoatomizdat: Moscow, Russia, 1991. [Google Scholar]
- Polyanin, A.D.; Vyazmin, A.V. differential-difference heat-conduction and diffusion models and equations with a finite relaxation time. Theor. Found. Chem. Eng. 2013, 47, 217–224. [Google Scholar] [CrossRef]
- Szekeres, A.; Fekete, B. Continuummechanics—Heat Conduction—Cognition. Period. Polytech. Mech. Eng. 2015, 59, 8–15. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarlakovskii, D.; Zemskov, A. An Elastodiffusive Orthotropic Euler–Bernoulli Beam Considering Diffusion Flux Relaxation. Math. Comput. Appl. 2019, 24, 23. https://doi.org/10.3390/mca24010023
Tarlakovskii D, Zemskov A. An Elastodiffusive Orthotropic Euler–Bernoulli Beam Considering Diffusion Flux Relaxation. Mathematical and Computational Applications. 2019; 24(1):23. https://doi.org/10.3390/mca24010023
Chicago/Turabian StyleTarlakovskii, Dmitry, and Andrei Zemskov. 2019. "An Elastodiffusive Orthotropic Euler–Bernoulli Beam Considering Diffusion Flux Relaxation" Mathematical and Computational Applications 24, no. 1: 23. https://doi.org/10.3390/mca24010023
APA StyleTarlakovskii, D., & Zemskov, A. (2019). An Elastodiffusive Orthotropic Euler–Bernoulli Beam Considering Diffusion Flux Relaxation. Mathematical and Computational Applications, 24(1), 23. https://doi.org/10.3390/mca24010023




