1. Introduction
Theoretical research and field observations have established the prevalence of various infectious diseases amongst the majority of the ecosystem population. In the ecological system, the impact of such infectious diseases is an important area of research for ecologists and mathematicians. The processes of merging ecology and epidemiology in the past few decades have been challenging and interesting. By nature, species are always dependent on other species for its food and living space. It is responsible for spreading infectious diseases and also competes against and is predated by other species. The dynamical behavior of such systems is analyzed using mathematical models that are described by differential equations. Mathematical epidemic models have gained much attention from researchers after the pioneering work of Kermack and McKendrick [
1] on the SIRS (Susceptible-Infective-Removal-Susceptible) system, in which the evolution of a disease which gets transmitted upon contact is described. The influence of epidemics on predation was first studied by Anderson and May [
2,
3]. Hadler and Freedman [
4] considered the prey–predator model in which predation is more likely on infected prey. In their model, they considered that predators only became infected from infected prey by predation. Haque and Venturino [
5,
6] discussed the models of diseases spreading in symbolic communities. Mukhopadhyay [
7] studied the role of harvesting and switching on the dynamics of disease propagation and/or eradication. The role of prey infection on the stability aspects of a prey–predator models with different functional responses was studied by Bairagi et al. [
8]. Han et al. [
9] analyzed four epidemiological models for SIS (Susceptible-Infectious-Susceptible) and SIR (Susceptible-Infectious-Recovered) diseases with standard and mass action incidents. Das [
10] showed that parasite infection in predator populations stabilized prey–predator oscillations. Pal and Samanta [
11] studied the dynamical behavior of a ratio-dependent prey–predator system with infection in the prey population. They proved that prey refuge had a stabilizing effect on the prey–predator interaction. Numerous examples of the prey–predator relationship with infection in the prey population have been found in various studies [
12,
13,
14,
15,
16,
17].
Adaptation is a fundamental characteristic of living organisms, such as in the prey–predator system and other ecological models, since they attempt to maintain physiological equilibrium in the midst of changing environmental conditions. Adaptive control is an active field in the design of control systems that helps deal with uncertainties. Back-stepping is a technique for designing stability controls for a nonlinear dynamical system, and this approach is a recursive method for stabilizing the origin of the system. The control process terminates when the final external control reaches. El-Gohary and Al-Ruzaiza [
18,
19] discussed the chaos and adaptive control of a three-species, continuous-time prey–predator model. Recently, Madhusudanan et al. [
20] studied back-stepping control in a diseased prey–predator system. They proved that the system was globally asymptotically stable at the origin with the help of nonlinear feedback control. Numerous examples of control techniques in the prey–predator system have been found in various studies [
21,
22].
The rest of the paper is structured as follows. In
Section 2, we formulate a mathematical model with an assumption, and the positivity and boundedness of the deterministic model is also discussed.
Section 3 deals with the existence of equilibrium points with a feasible condition. In
Section 4, local stability analysis of equilibrium points is discussed.
Section 5 deals with global stability analysis of the interior equilibrium point
. We discuss the condition for permanence of the system in
Section 6. In
Section 7, we introduce adaptive back-stepping control in the prey–predator system. In
Section 8, we compute the population intensity of fluctuation due to the incorporation of noise, which leads to chaos in reality. In
Section 9, we propose and analyze a delayed prey–predator system. Numerical simulation of the proposed model is presented in
Section 10. Finally, the discussion is presented in
Section 11 and conclusions are presented in the final section.
2. Mathematical Model
In this section, a continuous-time prey–predator system with susceptible, infected prey and a predator is considered. It is assumed that the susceptible prey population was developed on the basis of logistic law, and that only infected prey are predated. The disease is inherited only from the prey population, and they remain infected and do not recover.
Here, the parameters
,
, and
denote the susceptible prey, infected prey, and predator populations, respectively. The parameters
a,
d,
b,
f,
, and
denote the rate of transmission from the susceptible to infected prey population, death rate of predators, searching efficiency of the predator, conversion-efficiency rate of the predator, and constant harvesting rate of susceptible prey and infected prey, respectively. Now, we will analyze system (
1) with the following initial conditions:
Positiveness and Boundedness of the System
In theoretical eco-epidemiology, boundedness of the system implies that the system is biologically well-behaved. The following theorems ensure the positivity and boundedness of the system (
1):
Theorem 1. All solutions of of system (1) with the initial condition (2) are positive for all Proof. From (
1), it is observed that
where
.
Integrating in the region
, we get
for all
t. From (
1), it is observed that
where
Integrating in region
we get
for all
t. From (
1), it is observed that
where
.
Integrating in the region , we get for all t. Hence, all solutions starting from interior of the first octant remain positive for the future. □
Theorem 2. All the non-negative solutions of the model system (1) that initiate in are uniformly bounded. Proof. Let
be any solution of system (
1). Since from (1)
we have
Let
therefore,
Substituting Equation (
1) in Equation (
3), we get
where
m and
are positive constants. Applying Lemma on differential inequalities [
23], we obtain
and, for
, we have
Thus, all solutions of system (
1) enter into the region
This completes the proof. □
6. Permanence of the System
In this section, our main intuition is that the long time survival of species in an ecological system. Many notions and terms are identified in the literature to discuss and analyze the long-term survival of populations. Out of such, permanence and persistence are the ones to better analyze the system. From an ecological point of view, permanence of a system means that the long-term survival of all populations of the system.
Definition 1. The system (1) is said to be permanent if ∃
, such that for any solution of of system (1), , Now, we show that system (
1) is uniformly persistent. The survival of all populations of the system in the future time is nothing but persistence in the view of ecology.
In the mathematical point of view, persistence of a system means that a strictly positive solution does not have omega limit points on the boundary of the non-negative cone.
Definition 2. A population is said to be uniformly persistent if there exists , independent of where , such that Theorem 5. The system (1) is uniformly persistent if Proof. We will prove this theorem by the method of Lyapunov average function.
Let the average Lyapunov function for the system (
1) be
, where
p,
q,
r are positive constants. Clearly,
is non-negative function defined in
D of
, where
Then, we have
Furthermore, there are no periodic orbits in the interior of positive quadrant of
x–
y plane. Thus, to prove the uniform persistence of the system, it is enough to show that
in
for a suitable choice of
We noticed that, by increasing the value of
p, while
,
,
can be made positive. Thus, the inequality (
9) holds. If
, then
is positive. Thus, the inequality (
10) holds. If the inequality in Equation (
7) holds, then (
11) is satisfied. □
8. Stochastic Analysis
All usual occurrences explicitly in the ecosystem are continuously under random fluctuations of the environment. The stochastic examination of any ecosystem gives an enhanced vision on the dynamic forces of the populace by means of population variances. In a stochastic model, the model parameters oscillate about their average values [
24,
25,
26,
27]. Therefore, the steady state which we anticipated as permanent will now oscillate around the mean state. The method to measure the mean-square fluctuations of population is proposed by [
24] and it was applied by [
28] nicely. Furthermore, many researchers like Samanta [
29], Maiti, Jana and Samanta [
30] have investigated critically the stochastic analysis to interpret local as well as global stability using mean-square fluctuations on population variances.
Now, this segment is meant for the extension of the deterministic model (
1), which is formed by adding a noisy term. There are several ways in which environmental noise may be incorporated in the model system (
1). External noise may arise from random fluctuations of a finite number of parameters around some known mean values of the population densities around some fixed values. Since the aquatic ecosystem always has unsystematic fluctuations of the environment, it is difficult to define the usual phenomenon as a deterministic ideal. The stochastic investigation enables us to get extra intuition about the continuous changing aspects of any ecological unit. The deterministic model (
1) with the effect of random noise of the environment results in a stochastic system (
41)–(
43) given in the following discussion:
where
are the real constants and
is a three-dimensional Gaussian white noise process.
where
;
where
;
is the Kronecker delta function;
is the Dirac delta function.
The linear parts of (
41), (
42) and (
43) are (using (
44) and (
45))
Taking the Fourier transform on both sides of (
46), (
47) and (
48), we get
The matrix form of (
49)–(
51) is
where
Equation (
52) can also be written into
where
and
Here,
where
, where
and
If the function
has a zero mean value, then the fluctuation intensity (variance) of its components in the frequency interval
is
is the spectral density of
Y and is defined as
If
Y has a zero mean value, the inverse transform of
is the auto covariance function
The corresponding variance of fluctuations in
is given by
and the auto-correlation function is the normalized auto-covariance
For a Gaussian white noise process, it is
Hence, by (
61) and (
62), the intensities of fluctuations in the variable
are given by
and by (
54), we obtain
If we are interested in the dynamics of stochastic process (
41)–(
69) with either
or
or
the population variances are
if then
If then
If then
Equations (
67)–(
69) give three variations of the inhabitants. The integrations over the real line can be estimated, which gives the variations of the inhabitants.
9. Mathematical Model with Delay
In this section, we establish some conditions for oscillations of all positive solutions of the delay system
Here, the parameter is the delay. This proposed system is concerned not only with the present number of predator and prey but also with the number of predator and prey in the past. If t is the present time, then (t-) is the past.
According to Krisztin [
31], a solution of (
70)–(
72),
is called
oscillatory if every component has arbitrary large zeros; otherwise,
is said to be a
non-oscillatory solution. Whenever all solutions of (
70)–(
72) are oscillatory, we will say that (
70)–(
72) is an
oscillatory system.
In [
32], Kubiaczyk and Saker studied the oscillatory behavior of the delay differential equation
where
Using similar methods to liberalize each equation of the delay system, we will establish conditions for oscillations of all positive solutions of the system.
Now, we will analyze the system of (
70)–(
72) with the following initial conditions:
Using the same arguments that we got in Theorem 1, we can establish the following theorem:
Theorem 7. All solutions of of systems (70)–(72) with the initial condition (73) are positive for all Easily, we can see that the equilibrium point remains the same when we have the delay system. However, it is important to know the oscillatory behavior of the solutions around the equilibrium points.
Theorem 8. If there exist a such thatwhere , and ; then, all solutions of the system (70)–(72) oscillate around . Proof. Let us consider the system (
70)–(
72). Let
Then,
oscillate around
if
oscillate around
From (
70)–(
72) and (
75)–(
77), we have
Moreover, since
is the equilibrium point
, we have
Thus, the linearized system associated with the system (
75)–(
77) is given by
and every solution of (
79)–(
81) oscillates if and only if the characteristic equation has no real roots (see Theorem 5.1.1 in [
21]), i.e.,
for all
Equation (
82) is equivalent to the equation
where
,
and
In fact,
and
Then, by (
74) and (
78), systems (
79)–(
81) will start oscillating and then all the solutions of systems (
75)–(
77) will also oscillate. □
Example 1. Let the parameters of systems (70)–(72) be and In this case, condition (74) becomesand consequently all solutions of the system oscillate around the equilibrium point 10. Numerical Simulations
Analytical studies can never complete without numerical verification of the results. Moreover, it may be noted that, as the parameters of the model are not based on the real world observation, the main features described by the simulations presented in this section should be considered from a qualitative rather than a quantitative point of view. We choose the parameters of system (
1) as
with the initial densities
and observe the dynamical behaviour of system (
1).
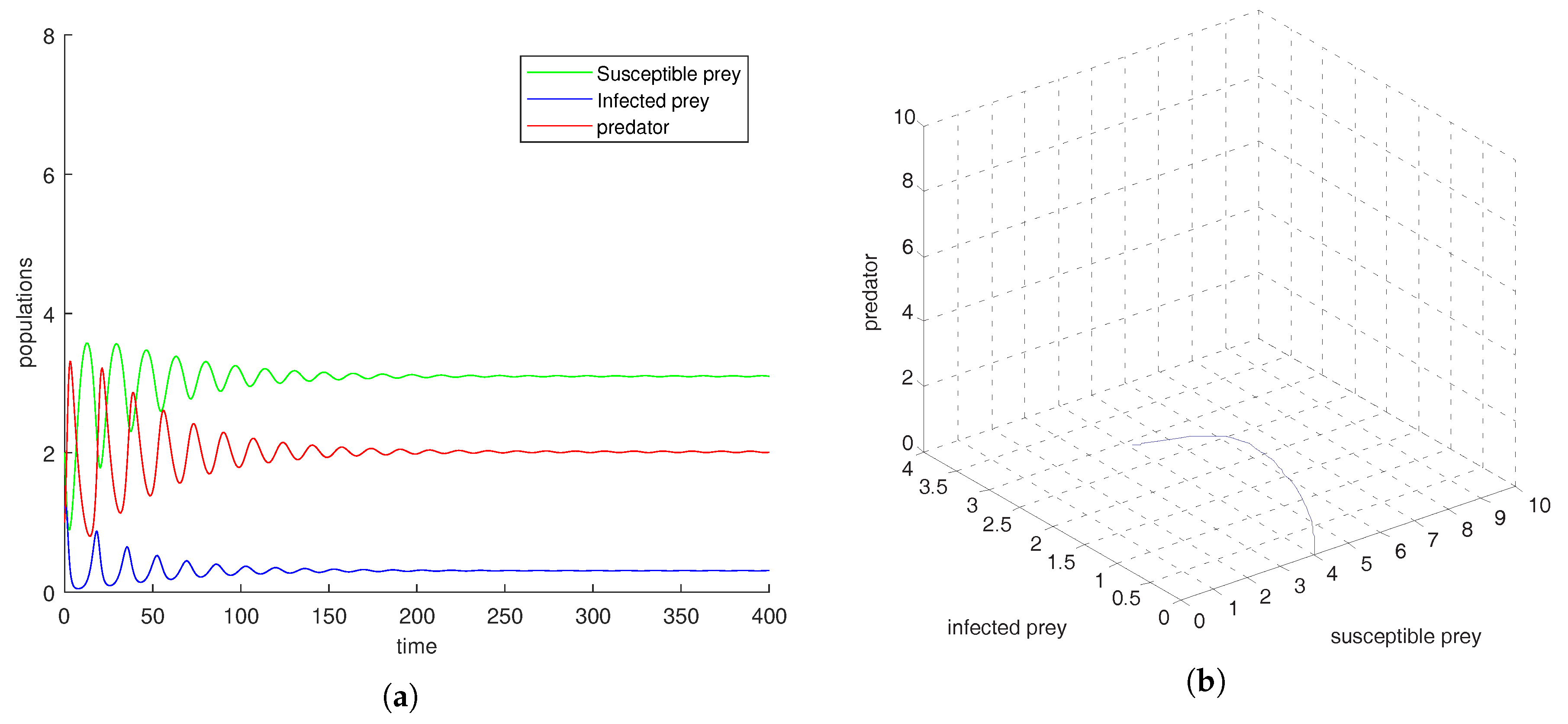
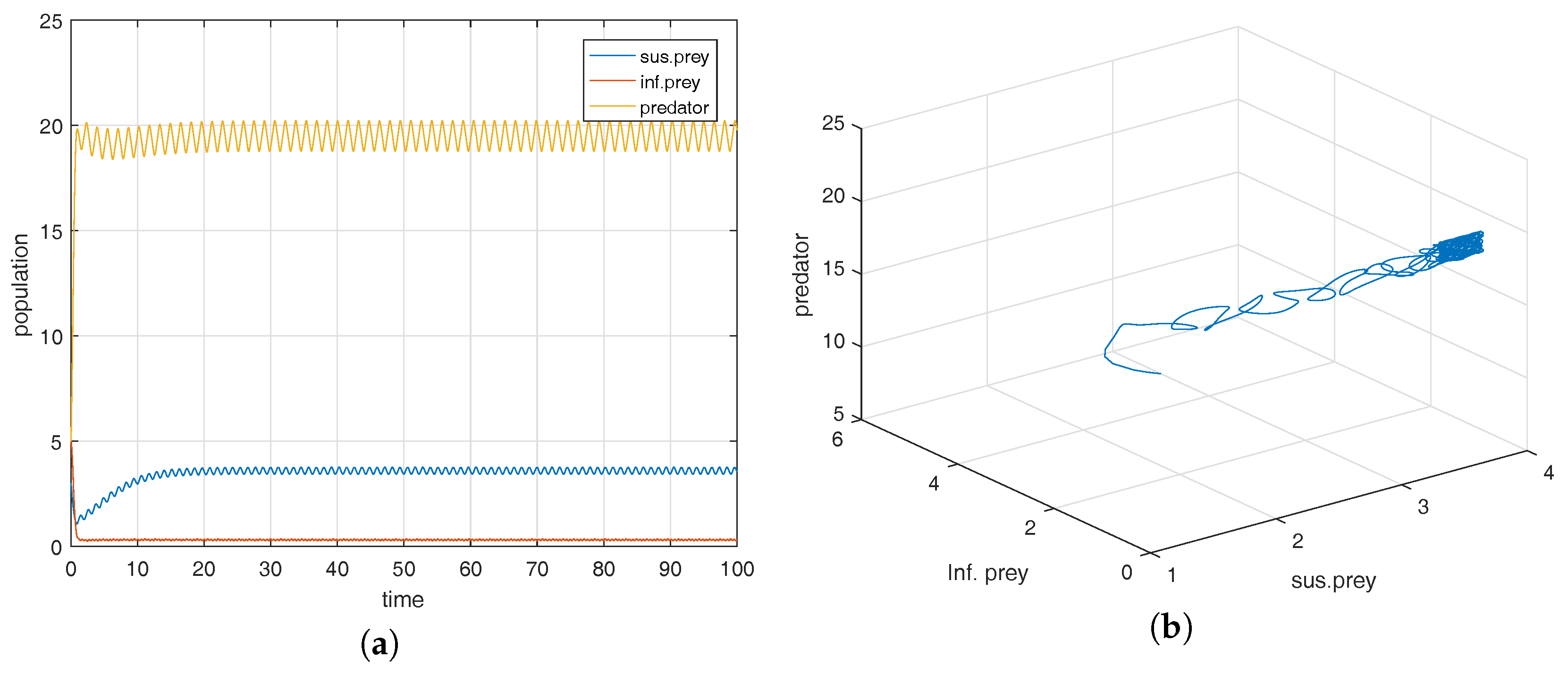
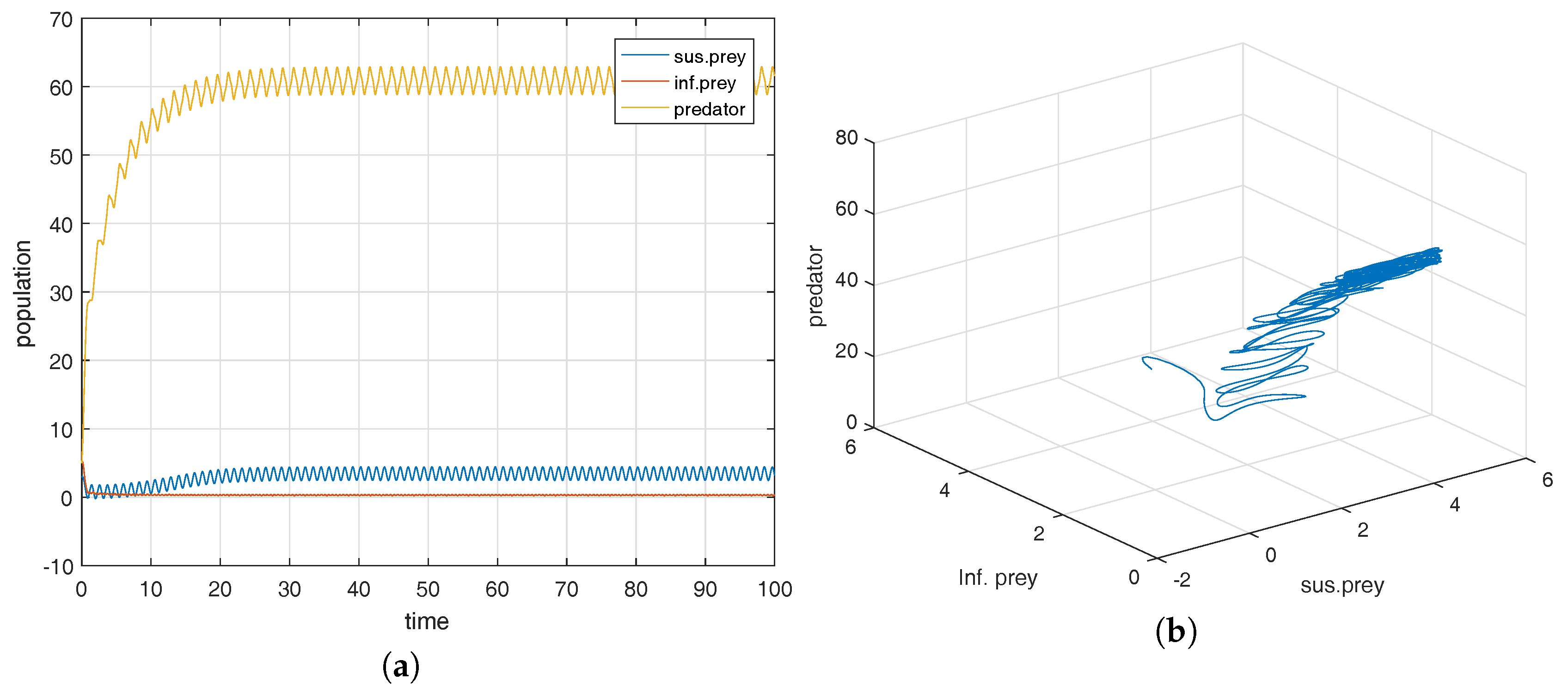
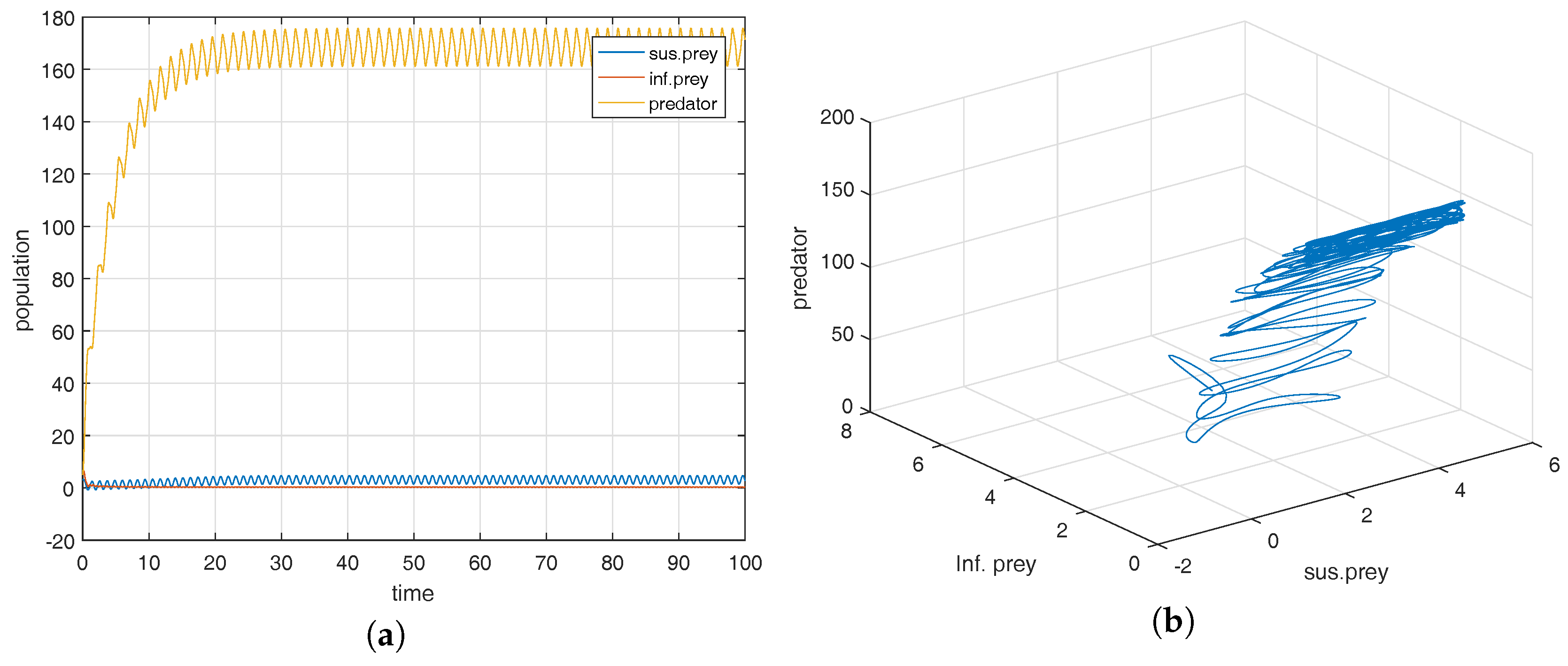
Figure 1a shows that the equilibrium point
is locally asymptotically stable and the corresponding phase-portrait is shown in
Figure 1b.
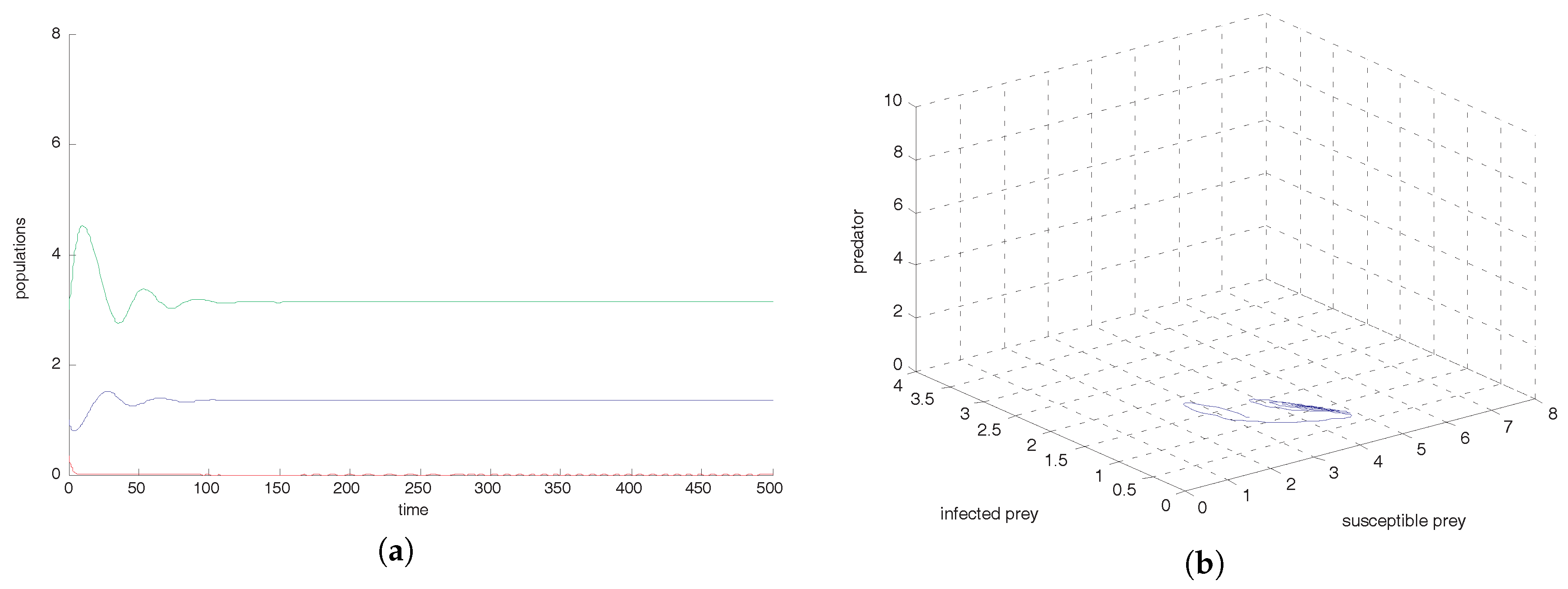
Figure 2a shows that the equilibrium point
is locally asymptotically stable and the corresponding phase-portrait is shown in
Figure 2b.
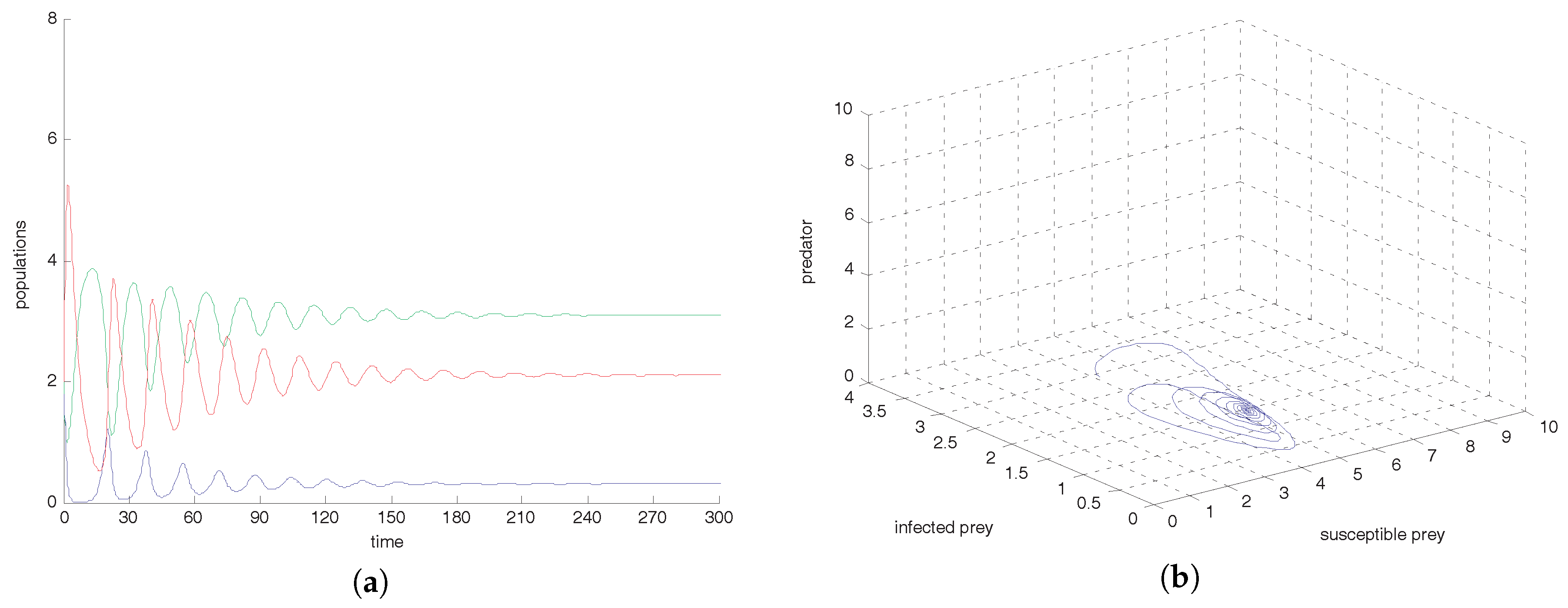
Figure 3a shows that the co-existence equilibrium point
is locally asymptotically stable and the corresponding phase portrait is shown in
Figure 3b. From
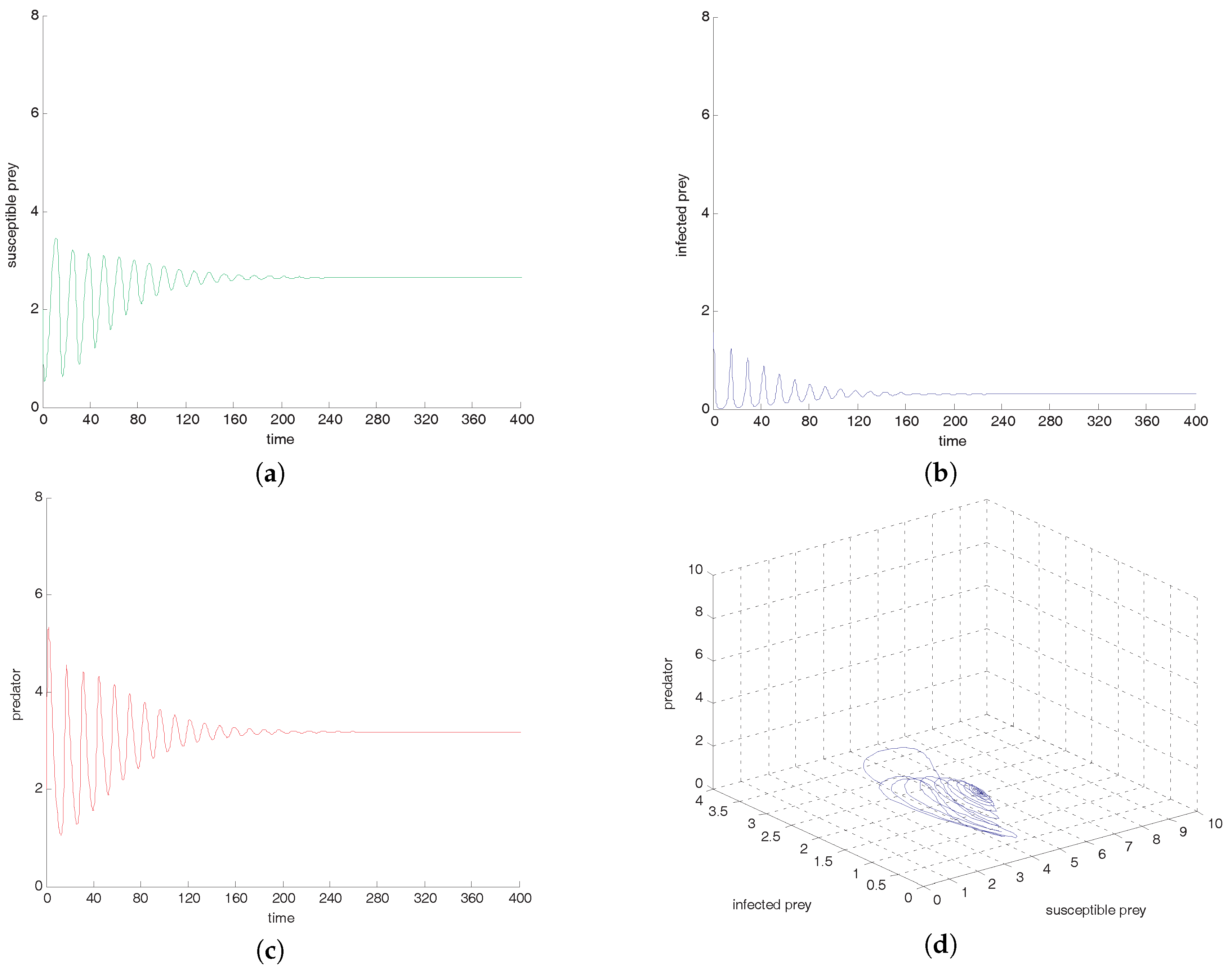
Figure 4a–d, if all other parameters are fixed and varying transmission rate
to
, we observe that oscillation settles down into a stable situation for all three of the species. Stability around this state implies extinction of the infected prey. This study interestingly suggests that the harvesting of both prey prevent limit cycle oscillations and the combined effect of both harvests also prevent disease propagation in the system. We also conclude that the inclusion of stochastic perturbation creates a significant change in the intensity of populations because change of responsive noise parameters causes chaotic dynamics with low, medium and high variances of oscillations (see
Figure 5,
Figure 6 and
Figure 7).